Mapping Solar–Wind Complementarity with BARRA
Abstract
1. Introduction
2. Materials and Methods
2.1. Reanalysis Data
2.1.1. Solar Resource
2.1.2. Wind Resource
2.2. Analysis Approach
2.2.1. Central Tendency Measures
2.2.2. Variability
2.2.3. Reliability
2.2.4. Intermittency
2.2.5. Synergy Metrics
3. Results
3.1. Central Tendency Measures
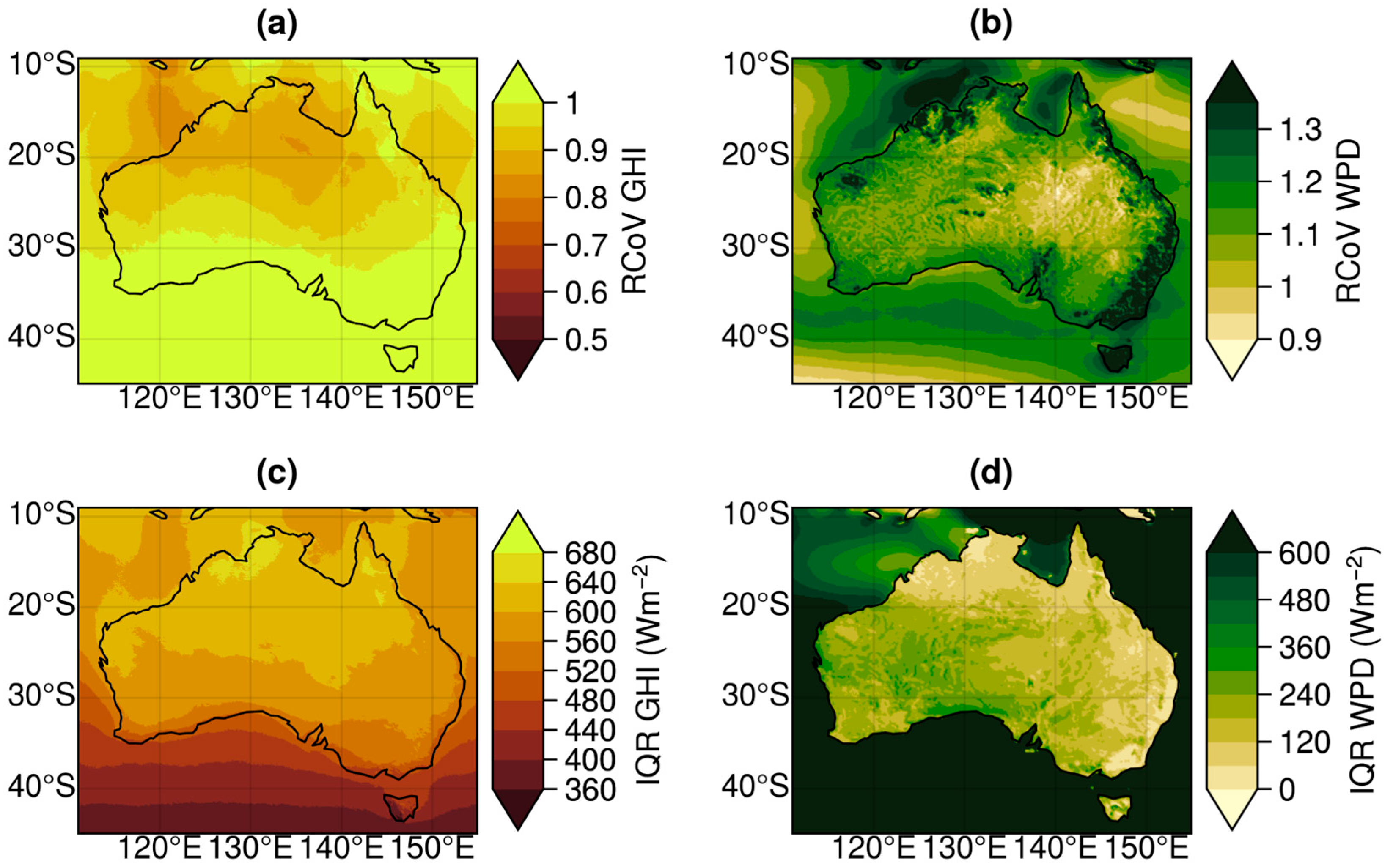
3.2. Variability
3.3. Reliability
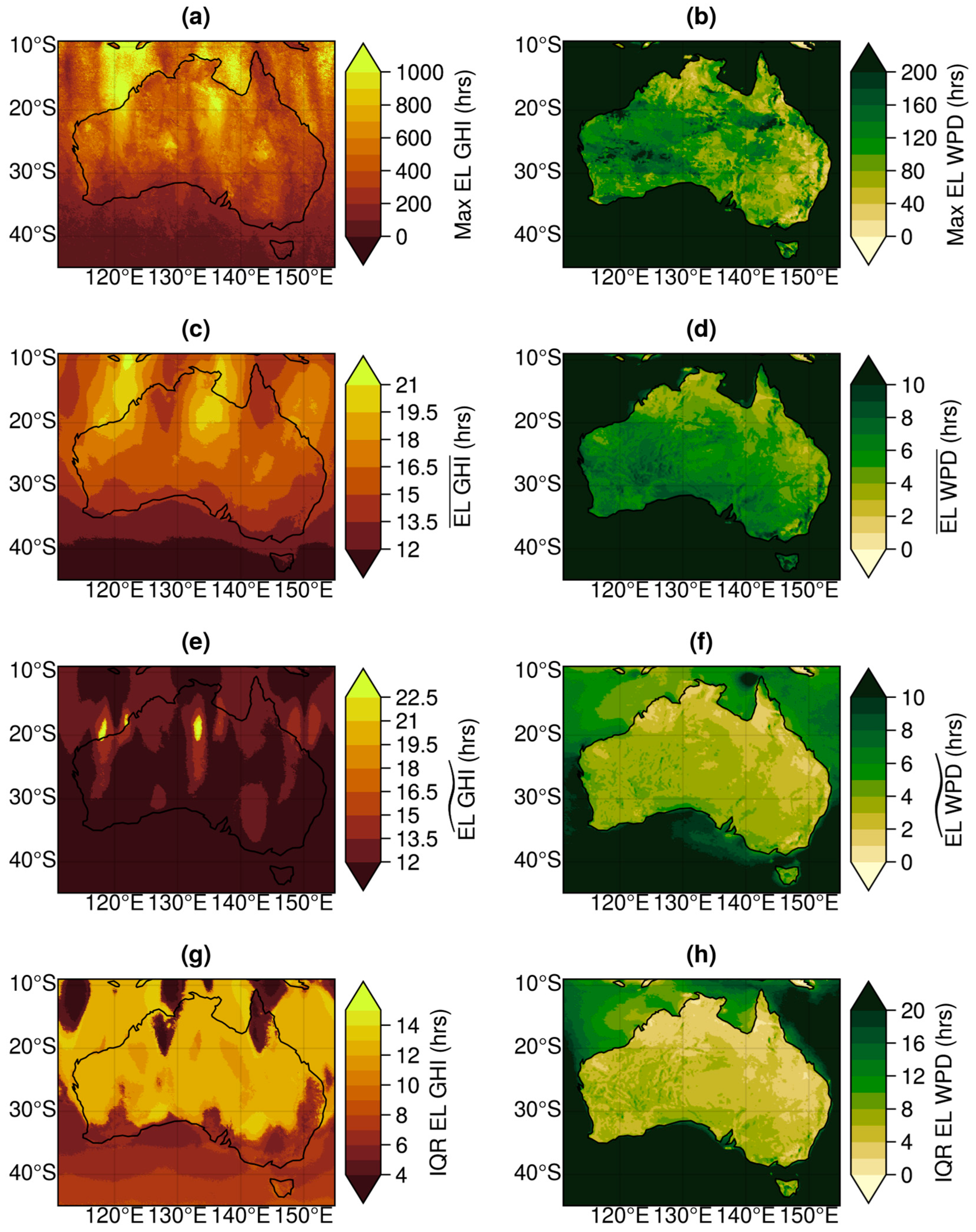
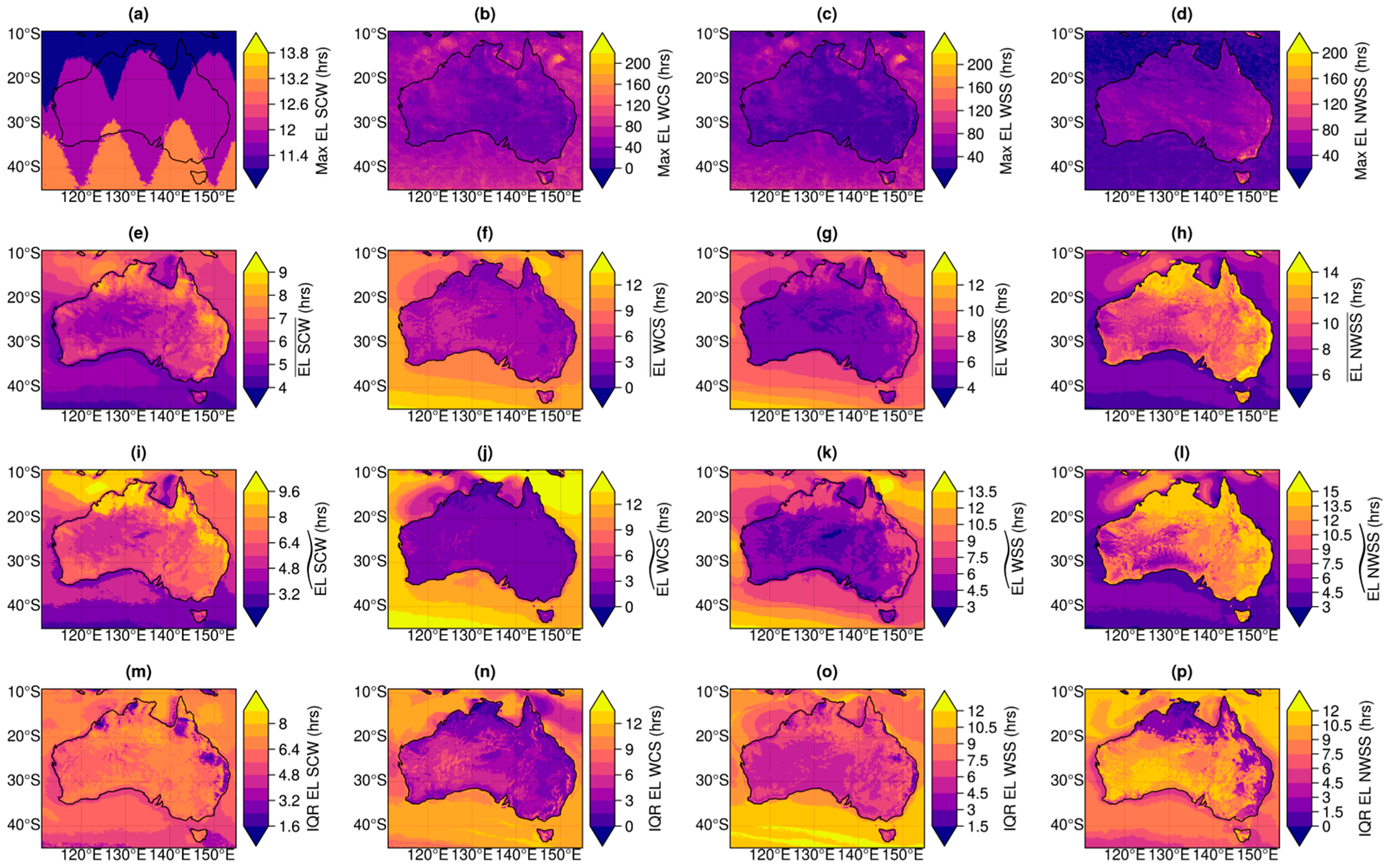
3.4. Intermittency
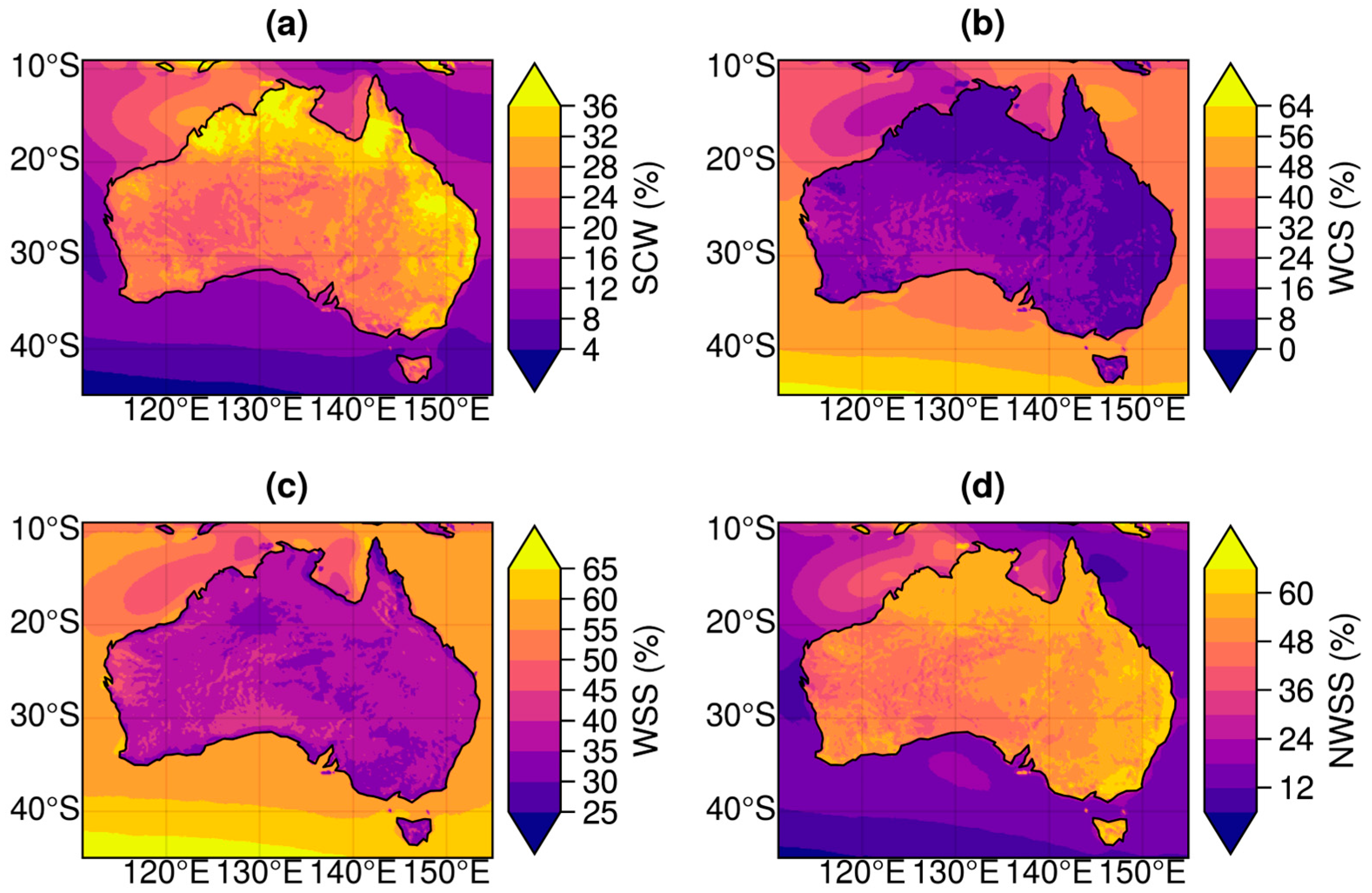
3.5. Synergy
3.6. Case Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, H.; West, S.R. Co-optimisation of wind and solar energy and intermittency for renewable generator site selection. Heliyon 2024, 10, 5. [Google Scholar] [CrossRef]
- Henao, F.; Viteri, J.P.; Rodríguez, Y.; Gómez, J.; Dyner, I. Annual and interannual complementarities of renewable energy sources in Colombia. Renew. Sustain. Energy Rev. 2020, 134, 110318. [Google Scholar] [CrossRef]
- Jurasz, J.; Canales, F.A.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- de Andrade Melo, G.; Cyrino Oliveira, F.L.; Maçaira, P.M.; Meira, E. Exploring complementary effects of solar and wind power generation. Renew. Sustain. Energy Rev. 2025, 209, 115139. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of solar and wind resource synergy in Australia. Appl. Energy 2017, 190, 354–367. [Google Scholar] [CrossRef]
- Weschenfelder, F.; de Novaes Pires Leite, G.; Araújo da Costa, A.C.; de Castro Vilela, O.; Ribeiro, C.M.; Villa Ochoa, A.A.; Araújo, A.M. A review on the complementarity between grid-connected solar and wind power systems. J. Clean. Prod. 2020, 257, 120617. [Google Scholar] [CrossRef]
- IRENA. Renewable Capacity Statistics 2025; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2025. [Google Scholar]
- Busby, J.; Baker, K.; Bazilian, M.; Gilbert, A.; Grubert, E.; Rai, V.; Rhodes, J.; Shidore, S.; Smith, C.; Webber, M. Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 2021, 77, 102106. [Google Scholar] [CrossRef]
- Prasad, A.A.; Yang, Y.; Kay, M.; Menictas, C.; Bremner, S. Synergy of solar photovoltaics-wind-battery systems in Australia. Renew. Sustain. Energy Rev. 2021, 152, 111693. [Google Scholar] [CrossRef]
- Pedruzzi, R.; Silva, A.R.; Soares dos Santos, T.; Araujo, A.C.; Cotta Weyll, A.L.; Lago Kitagawa, Y.K.; Nunes da Silva Ramos, D.; Milani de Souza, F.; Almeida Narciso, M.V.; Saraiva Araujo, M.L.; et al. Review of mapping analysis and complementarity between solar and wind energy sources. Energy 2023, 283, 129045. [Google Scholar] [CrossRef]
- Chen, W.-B. Assessing global land-based solar–wind complementarity using high-resolution climate reanalysis for hybrid renewable energy design. Energy Convers. Manag. 2025, 343, 120267. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The climatological relationships between wind and solar energy supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef]
- Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Huld, T.; Monforti-Ferrario, F. Local Complementarity of Wind and Solar Energy Resources over Europe: An Assessment Study from a Meteorological Perspective. J. Appl. Meteorol. Climatol. 2017, 56, 217–234. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’Isidoro, M.; Lacal-Arántegui, R. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Z.; Liu, Y. The spatial and temporal variation features of wind-sun complementarity in China. Energy Convers. Manag. 2017, 154, 138–148. [Google Scholar] [CrossRef]
- Jurasz, J.; Beluco, A.; Canales, F.A. The impact of complementarity on power supply reliability of small scale hybrid energy systems. Energy 2018, 161, 737–743. [Google Scholar] [CrossRef]
- Widen, J. Correlations Between Large-Scale Solar and Wind Power in a Future Scenario for Sweden. IEEE Trans. Sustain. Energy 2011, 2, 177–184. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Lara-Fanego, V.; Tovar-Pescador, J. Analysis of spatiotemporal balancing between wind and solar energy resources in the southern Iberian Peninsula. J. Appl. Meteorol. Climatol. 2012, 51, 2005–2024. [Google Scholar] [CrossRef]
- López Prol, J.; de Llano Paz, F.; Calvo-Silvosa, A.; Pfenninger, S.; Staffell, I. Wind-solar technological, spatial and temporal complementarities in Europe: A portfolio approach. Energy 2024, 292, 130348. [Google Scholar] [CrossRef]
- Kapica, J.; Canales, F.A.; Jurasz, J. Global atlas of solar and wind resources temporal complementarity. Energy Convers. Manag. 2021, 246, 114692. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Gallardo, R.P. Chapter 12—A comparative study of correlation coefficients used to assess the solar and wind complementarity in Mexico. In Complementarity of Variable Renewable Energy Sources; Jurasz, J., Beluco, A., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 269–290. [Google Scholar]
- Yan, J.; Qu, T.; Han, S.; Liu, Y.; Lei, X.; Wang, H. Reviews on characteristic of renewables: Evaluating the variability and complementarity. Int. Trans. Electr. Energy Syst. 2020, 30, e12281. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, N.; Jiang, H.; Yao, L. Evaluation of Reanalysis Surface Incident Solar Radiation Data in China. Sci. Rep. 2020, 10, 3494. [Google Scholar] [CrossRef]
- Samal, R.K. Assessment of wind energy potential using reanalysis data: A comparison with mast measurements. J. Clean. Prod. 2021, 313, 127933. [Google Scholar] [CrossRef]
- Yang, D.; Wang, W.; Xia, X. A Concise Overview on Solar Resource Assessment and Forecasting. Adv. Atmos. Sci. 2022, 39, 1239–1251. [Google Scholar] [CrossRef]
- Quansah, A.D.; Dogbey, F.; Asilevi, P.J.; Boakye, P.; Darkwah, L.; Oduro-Kwarteng, S.; Sokama-Neuyam, Y.A.; Mensah, P. Assessment of solar radiation resource from the NASA-POWER reanalysis products for tropical climates in Ghana towards clean energy application. Sci. Rep. 2022, 12, 10684. [Google Scholar] [CrossRef]
- Du, Y.; Shi, H.; Zhang, J.; Xia, X.; Yao, Z.; Fu, D.; Hu, B.; Huang, C. Evaluation of MERRA-2 hourly surface solar radiation across China. Sol. Energy 2022, 234, 103–110. [Google Scholar] [CrossRef]
- Rabbani, R.; Zeeshan, M. Exploring the suitability of MERRA-2 reanalysis data for wind energy estimation, analysis of wind characteristics and energy potential assessment for selected sites in Pakistan. Renew. Energy 2020, 154, 1240–1251. [Google Scholar] [CrossRef]
- Berger, M.; Radu, D.; Fonteneau, R.; Henry, R.; Glavic, M.; Fettweis, X.; Le Du, M.; Panciatici, P.; Balea, L.; Ernst, D. Critical time windows for renewable resource complementarity assessment. Energy 2020, 198, 117308. [Google Scholar] [CrossRef]
- Nyenah, E.; Sterl, S.; Thiery, W. Pieces of a puzzle: Solar-wind power synergies on seasonal and diurnal timescales tend to be excellent worldwide. Environ. Res. Commun. 2022, 4, 055011. [Google Scholar] [CrossRef]
- Sterl, S.; Liersch, S.; Koch, H.; van Lipzig, N.P.M.; Thiery, W. A new approach for assessing synergies of solar and wind power: Implications for West Africa. Environ. Res. Lett. 2018, 13, 094009. [Google Scholar] [CrossRef]
- Doddy Clarke, E.; Griffin, S.; McDermott, F.; Monteiro Correia, J.; Sweeney, C. Which Reanalysis Dataset Should We Use for Renewable Energy Analysis in Ireland? Atmosphere 2021, 12, 624. [Google Scholar] [CrossRef]
- Gualtieri, G. Analysing the uncertainties of reanalysis data used for wind resource assessment: A critical review. Renew. Sustain. Energy Rev. 2022, 167, 112741. [Google Scholar] [CrossRef]
- Kaiser-Weiss, A.K.; Borsche, M.; Niermann, D.; Kaspar, F.; Lussana, C.; Isotta, F.A.; van den Besselaar, E.; van der Schrier, G.; Undén, P. Added value of regional reanalyses for climatological applications. Environ. Res. Commun. 2019, 1, 071004. [Google Scholar] [CrossRef]
- Ridal, M.; Bazile, E.; Le Moigne, P.; Randriamampianina, R.; Schimanke, S.; Andrae, U.; Berggren, L.; Brousseau, P.; Dahlgren, P.; Edvinsson, L.; et al. CERRA, the Copernicus European Regional Reanalysis system. Q. J. R. Meteorol. Soc. 2024, 150, 3385–3411. [Google Scholar] [CrossRef]
- Su, C.-H.; Eizenberg, N.; Steinle, P.; Jakob, D.; Fox-Hughes, P.; White, C.J.; Rennie, S.; Franklin, C.; Dharssi, I.; Zhu, H. BARRA v1.0: The Bureau of Meteorology Atmospheric high-resolution Regional Reanalysis for Australia. Geosci. Model Dev. 2019, 12, 2049–2068. [Google Scholar] [CrossRef]
- Gleeson, E.; Whelan, E.; Hanley, J. Met Éireann high resolution reanalysis for Ireland. Adv. Sci. Res. 2017, 14, 49–61. [Google Scholar] [CrossRef]
- Rasmussen, R.M.; Chen, F.; Liu, C.H.; Ikeda, K.; Prein, A.; Kim, J.; Schneider, T.; Dai, A.; Gochis, D.; Dugger, A.; et al. CONUS404: The NCAR–USGS 4-km Long-Term Regional Hydroclimate Reanalysis over the CONUS. Bull. Am. Meteorol. Soc. 2023, 104, E1382–E1408. [Google Scholar] [CrossRef]
- Acharya, S.C.; Nathan, R.; Wang, Q.J.; Su, C.H.; Eizenberg, N. An evaluation of daily precipitation from a regional atmospheric reanalysis over Australia. Hydrol. Earth Syst. Sci. 2019, 23, 3387–3403. [Google Scholar] [CrossRef]
- Chandra Acharya, S.; Nathan, R.; Wang, Q.J.; Su, C.H.; Eizenberg, N. Ability of an Australian reanalysis dataset to characterise sub-daily precipitation. Hydrol. Earth Syst. Sci. 2020, 24, 2951–2962. [Google Scholar] [CrossRef]
- May, P.T.; Trewin, B.; Su, C.H.; Ostendorf, B. Verification of moist surface variables over northern Australia in a high-resolution reanalysis (BARRA). J. South. Hemisph. Earth Syst. Sci. 2021, 71, 194–202. [Google Scholar] [CrossRef]
- Cowin, E.; Wang, C.; Walsh, S.D.C. Assessing Predictions of Australian Offshore Wind Energy Resources from Reanalysis Datasets. Energies 2023, 16, 3404. [Google Scholar] [CrossRef]
- Palmer, G.; Dargaville, R.; Su, C.H.; Wang, C.; Hoadley, A.; Honnery, D. Validation of BARRA2 and comparison with MERRA-2 and ERA5 using historical wind power generation. J. South. Hemisph. Earth Syst. Sci. 2025, 75, ES24028. [Google Scholar] [CrossRef]
- Fox-Hughes, P.; Su, C.H.; Eizenberg, N.; White, C.; Steinle, P.; Jakob, D.; Black, M.; Dowdy, A.; Brown, A.; Nathan, R.; et al. A review of early severe weather applications of high-resolution regional reanalysis in Australia. Meteorol. Appl. 2022, 29, e2087. [Google Scholar] [CrossRef]
- Gualtieri, G.; Secci, S. Methods to extrapolate wind resource to the turbine hub height based on power law: A 1-h wind speed vs. Weibull distribution extrapolation comparison. Renew. Energy 2012, 43, 183–200. [Google Scholar] [CrossRef]
- Lopez-Villalobos, C.A.; Martínez-Alvarado, O.; Rodriguez-Hernandez, O.; Romero-Centeno, R. Analysis of the influence of the wind speed profile on wind power production. Energy Rep. 2022, 8, 8079–8092. [Google Scholar] [CrossRef]
- Sherman, P.; Song, S.; Chen, X.; McElroy, M. Projected changes in wind power potential over China and India in high resolution climate models. Environ. Res. Lett. 2021, 16, 034057. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, Y.; Xue, X.; Li, Y.; Zhang, M.; Li, Y.; Ji, X. China’s future wind energy considering air density during climate change. Renew. Sustain. Energy Rev. 2024, 199, 114452. [Google Scholar] [CrossRef]
- Dehghani, F.; Shafiyi, M.A. Integration of hybrid renewable energy sources with the power system considering their economic complementarity. IET Renew. Power Gener. 2023, 17, 3638–3650. [Google Scholar] [CrossRef]
- Richardson, D.; Pitman, A.J.; Ridder, N.N. Climate influence on compound solar and wind droughts in Australia. Npj Clim. Atmos. Sci. 2023, 6, 184. [Google Scholar] [CrossRef]
- Gunn, A.; Dargaville, R.; Jakob, C.; McGregor, S. Spatial optimality and temporal variability in Australia’s wind resource. Environ. Res. Lett. 2023, 18, 114048. [Google Scholar] [CrossRef]
- Sun, Z.; Li, J.; He, Y.; Li, J.; Liu, A.; Zhang, F. Determination of direct normal irradiance including circumsolar radiation in climate/NWP models. Q. J. R. Meteorol. Soc. 2016, 142, 2591–2598. [Google Scholar] [CrossRef]




| Metrics | GHI | WPD | SCW | WCS | WSS | NWSS | |
|---|---|---|---|---|---|---|---|
| Key Statistics | 431 | 146 | - | - | - | - | |
| 392 | 53 | - | - | - | - | ||
| Variability | 105 | 142 | - | - | - | - | |
| 560 | 177 | - | - | - | - | ||
| Reliability | 38 | 20 | - | - | - | - | |
| 71 | 34 | - | - | - | - | ||
| Synergy | - | - | 23 | 9 | 32 | 53 | |
| Intermittency | 442 | 70 | 12 | 36 | 36 | 46 | |
| 15 | 6 | 5 | 3 | 5 | 11 | ||
| 12 | 4 | 5 | 2 | 4 | 12 | ||
| 8 | 7 | 6 | 4 | 5 | 8 | ||
| 91 | 537 | 144 | 623 | 47 | 90 | ||
| 14 | 26 | 18 | 34 | 10 | 10 | ||
| 14 | 15 | 16 | 19 | 10 | 10 | ||
| 3 | 20 | 6 | 35 | 11 | 5 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prasad, A.; Kay, M. Mapping Solar–Wind Complementarity with BARRA. Energies 2025, 18, 5452. https://doi.org/10.3390/en18205452
Prasad A, Kay M. Mapping Solar–Wind Complementarity with BARRA. Energies. 2025; 18(20):5452. https://doi.org/10.3390/en18205452
Chicago/Turabian StylePrasad, Abhnil, and Merlinde Kay. 2025. "Mapping Solar–Wind Complementarity with BARRA" Energies 18, no. 20: 5452. https://doi.org/10.3390/en18205452
APA StylePrasad, A., & Kay, M. (2025). Mapping Solar–Wind Complementarity with BARRA. Energies, 18(20), 5452. https://doi.org/10.3390/en18205452







