Thermodynamic Analysis of Pumped Thermal Energy Storage System Combined Cold, Heat, and Power Generation
Abstract
:1. Introduction
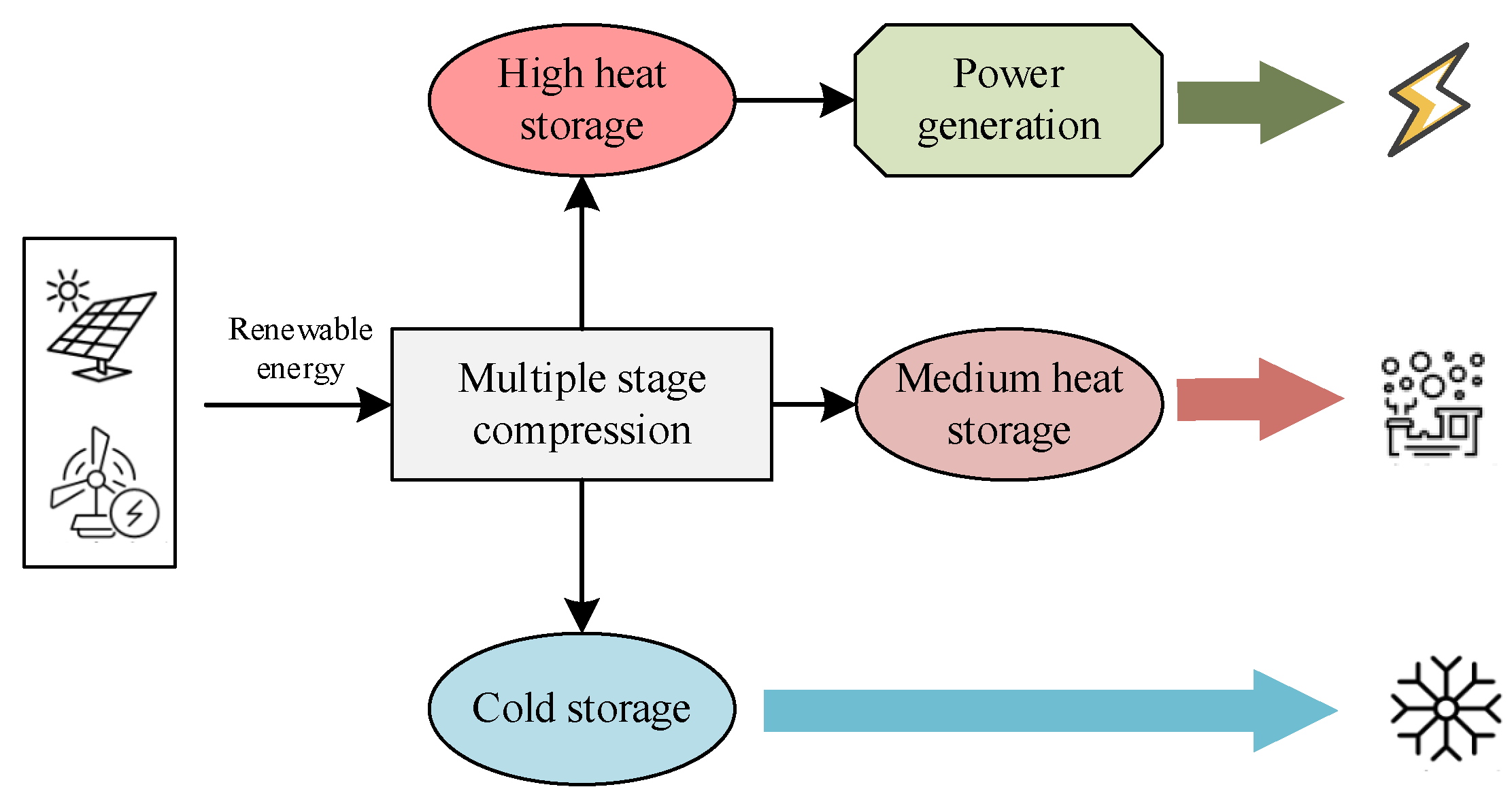
2. System Description
2.1. System Principle
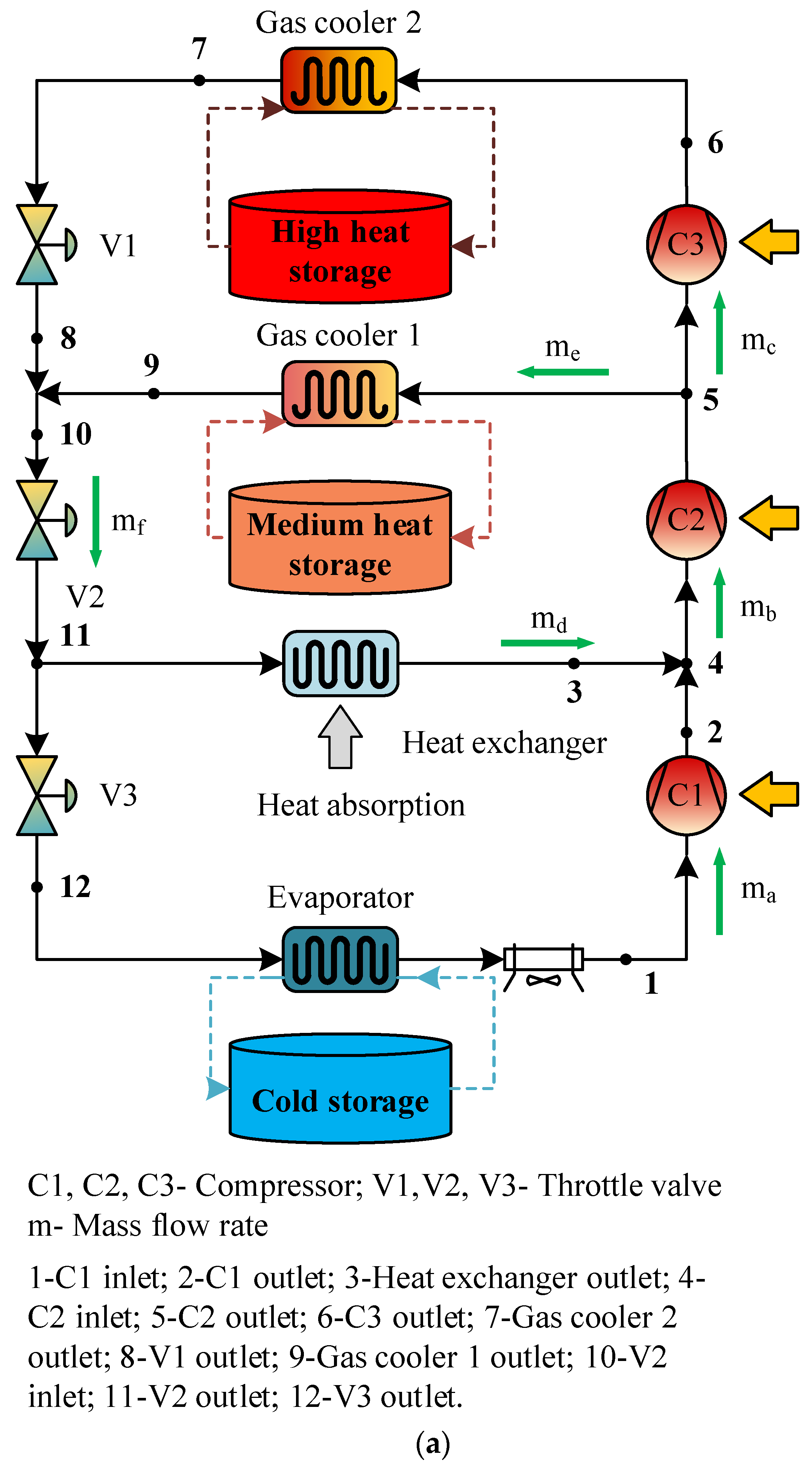
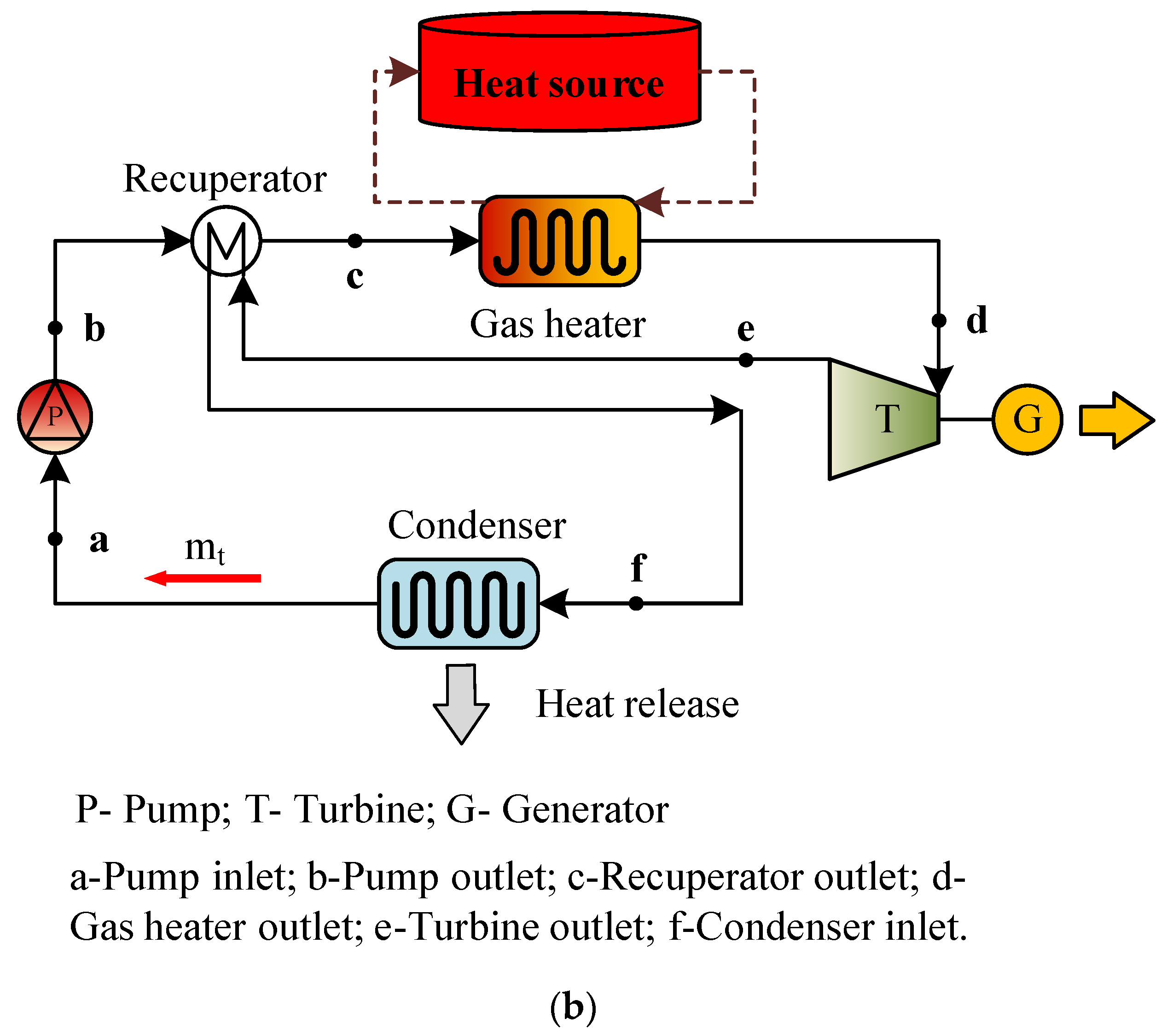
2.2. System Process
- (1)
- As shown in Figure 2a, when the system performs the energy storage process, the cycle operation mode is similar to that of a multistage compression heat pump. The initial state of the working fluid of the cycle is 1. From state 1 to 2 is the first stage of compression. The low-temperature and low-pressure CO2 (ma) is mixed with the working fluid (md) after the first stage of compression (C1), becoming stage 4. From state 4 to 5 is the second stage of compression; the mixed working fluid (mb) enters the second stage compressor (C2) to become the medium-temperature and -pressure working fluid. From state 11 to 3 is the heat equilibrium process. The heat exchanger on the md branch is designed to balance the heat of the system by absorbing heat from the air to achieve the thermal balance of the first stage compression circuit. From state 5 to 6 is the third stage of compression. From state 5 to 9 is the process of medium-temperature heat storage in gas cooler 1. After diverting the working fluid after the second-stage compressor, some working fluid (me) is heat exchanged with water in gas cooler 1 for medium-temperature heat storage (50 °C), and the other (mc) enters the third-stage compressor. From state 6 to 7 is the process of high-temperature heat storage in gas cooler 2. After three stages of compression, the working fluid reaches a high-temperature and high-pressure state, and this part of the high-temperature heat is stored in water through the gas cooler 2 for high-temperature heat storage (120 °C). From state 7 to 8 is the process of throttling in throttle valve 1. From state 10 to 11 is the process of throttling in throttle valve 2. The working fluid of the outflow gas cooler is medium-temperature and high-pressure supercritical CO2, which enters the first-stage throttle to become the medium-temperature and medium-pressure working fluid, and then, enters the second-stage throttle after mixing (mf) with the medium-temperature heat transfer working fluid (me). From state 11 to 12 is the process of throttling in throttle valve 3. From state 12 to 1 is the cooling process in the evaporator. After two throttling processes, the working fluid is divided into two ways: one way (md) absorbs environmental heat for heat balance, and the other way (ma) carries out the third-stage throttling to become low-temperature and low-pressure working fluid, absorbs the heat of the coolant in the evaporator, and restores the initial state of the working fluid.
- (2)
- As shown in Figure 2b, the energy release process is the heat engine cycle. From state a to b is the pressurization process in the pump. The low-temperature, low-pressure working fluid (mt) is pressurized by the pump to become the low-temperature, high-pressure working fluid. From state b to c is the heating process in the recuperator. The low-temperature working fluid at state b of the recuperator is exchanged with the waste heat at the turbine outlet. From state c to d is the heating process in the gas heater. From state d to e is the expansion process of the turbine. The working fluid flows into the gas heater and uses the high-temperature heat stored in the energy storage cycle to heat the working fluid, thus becoming the high-temperature, high-pressure supercritical CO2 in the turbine expansion power generation. From state f to a is the cooling process in the condenser. The medium-temperature fluid at the turbine outlet can preheat the working fluid at the outlet of the pump, and the CO2 after heat exchange can further release excess heat to the environment and return to the initial state.
3. Materials and Methods
3.1. Mathematical Models
- (1)
- The system is in a stable operation state and does not consider the specific heat transfer process;
- (2)
- The heat transfer loss between the internal and external pipes and compressors and the external environment is ignored;
- (3)
- The pressure drop of CO2 and energy storage medium in the flow process is ignored, and the flow rate and temperature are evenly distributed;
- (4)
- Mass conservation is satisfied at each part of the system; that is, the outlet flow of the connected component is equal to the inlet mass of the next component.
3.1.1. Heat Pump Modeling
3.1.2. Heat Engine Modeling
3.1.3. Energy Balance Equations and Other Correlations
3.2. Thermodynamic Performance Evaluation Indexes
3.2.1. Energy Efficiency
3.2.2. Total UA Value
3.3. Model Validation
4. Results and Discussion
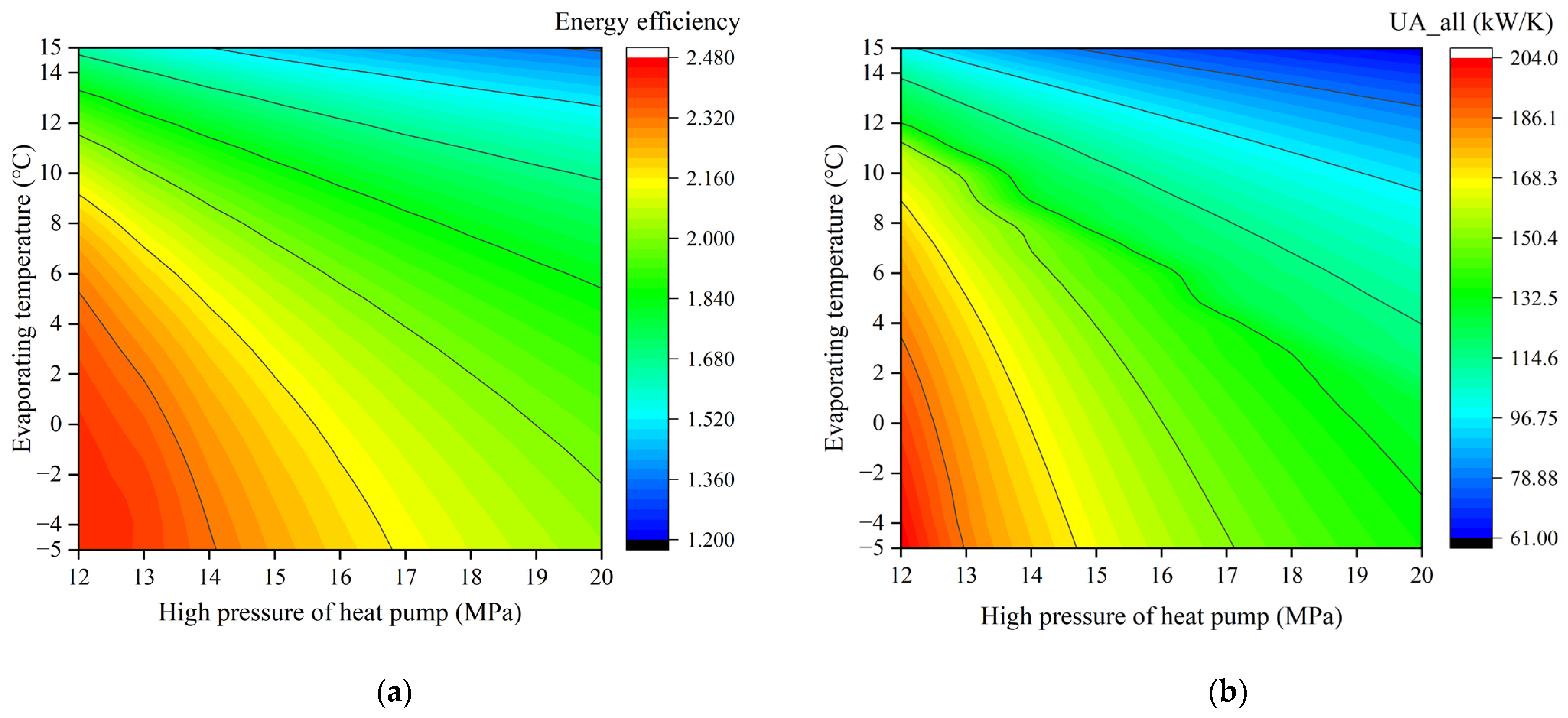
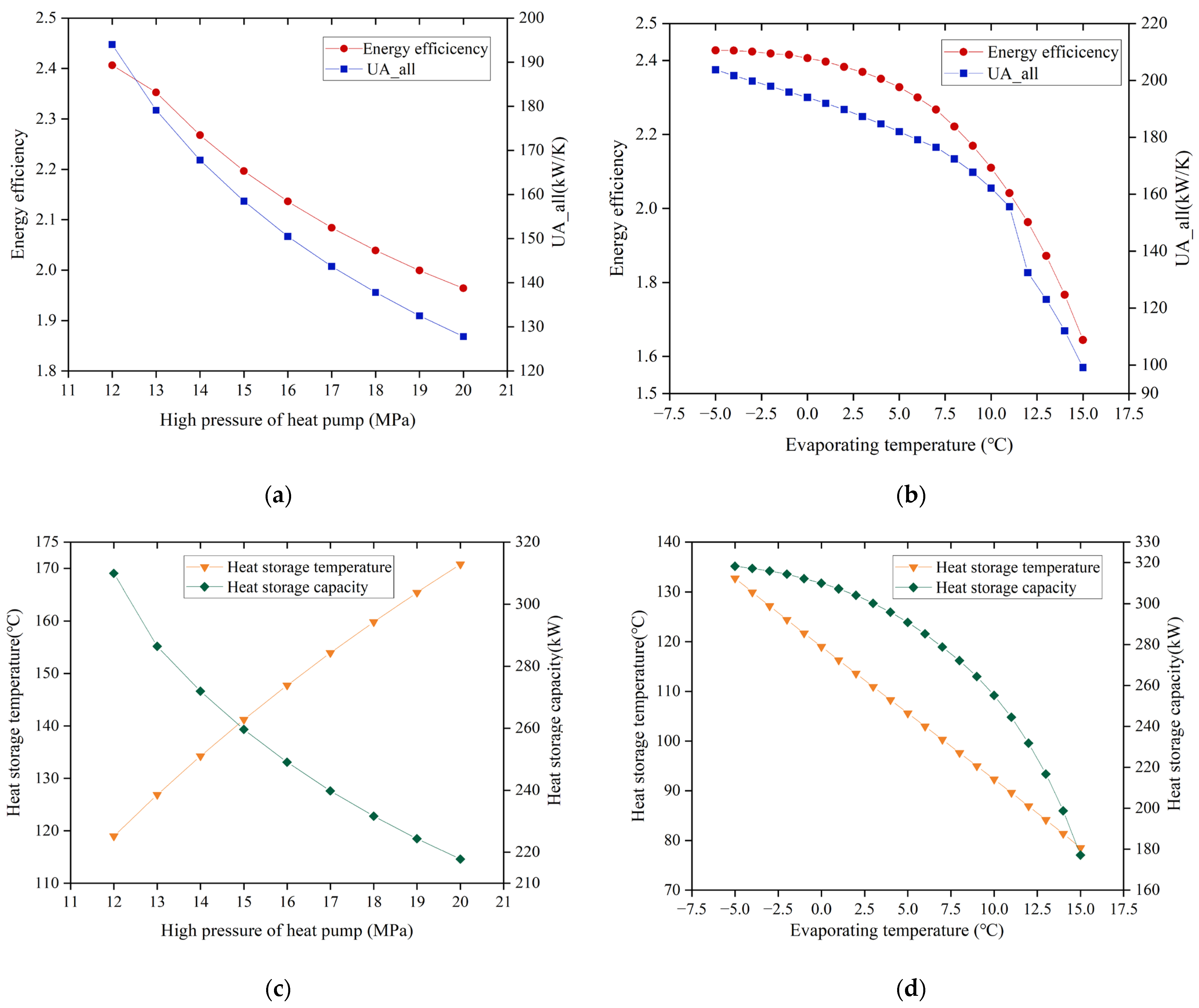
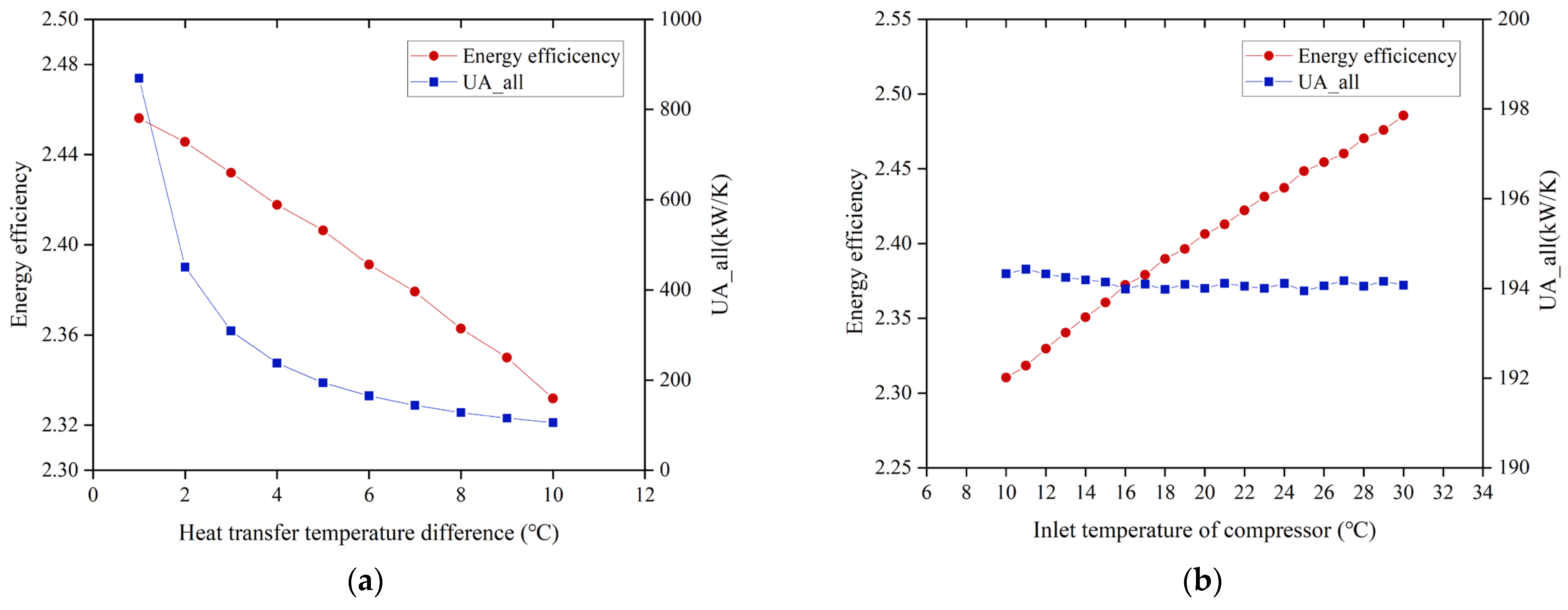
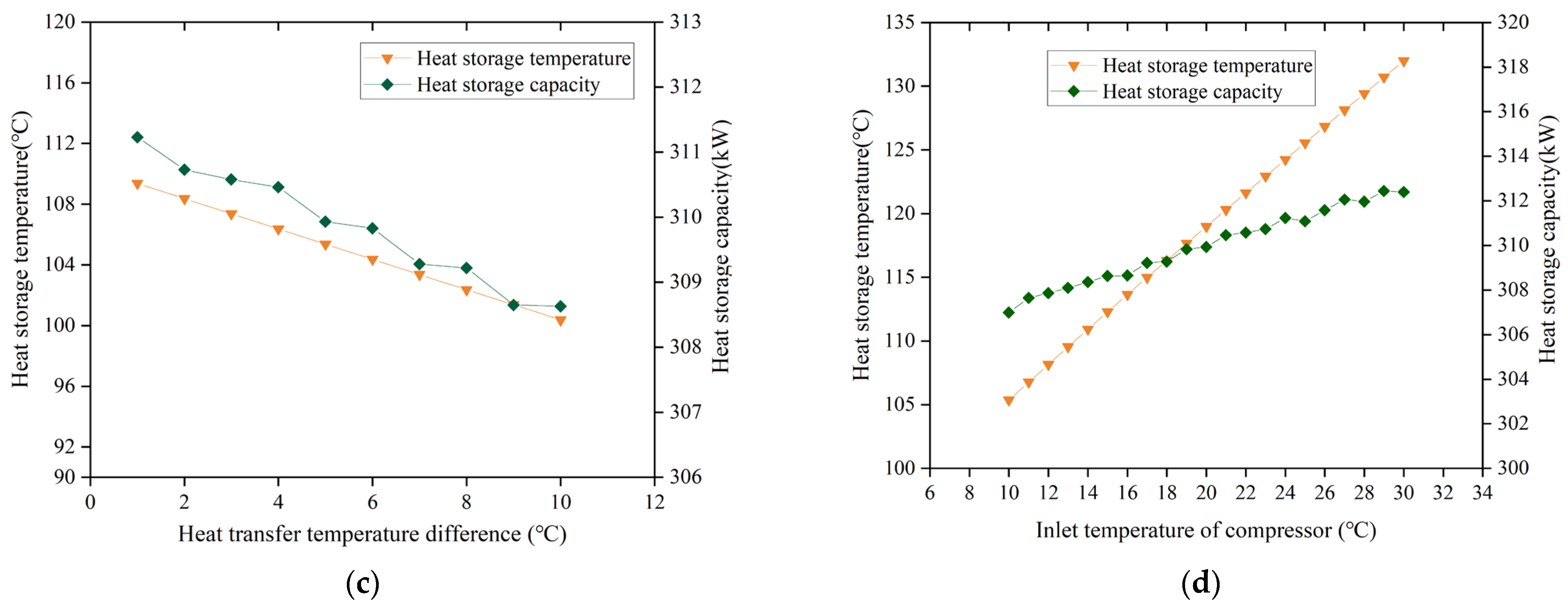
4.1. Critical Parameters of Heat Pump
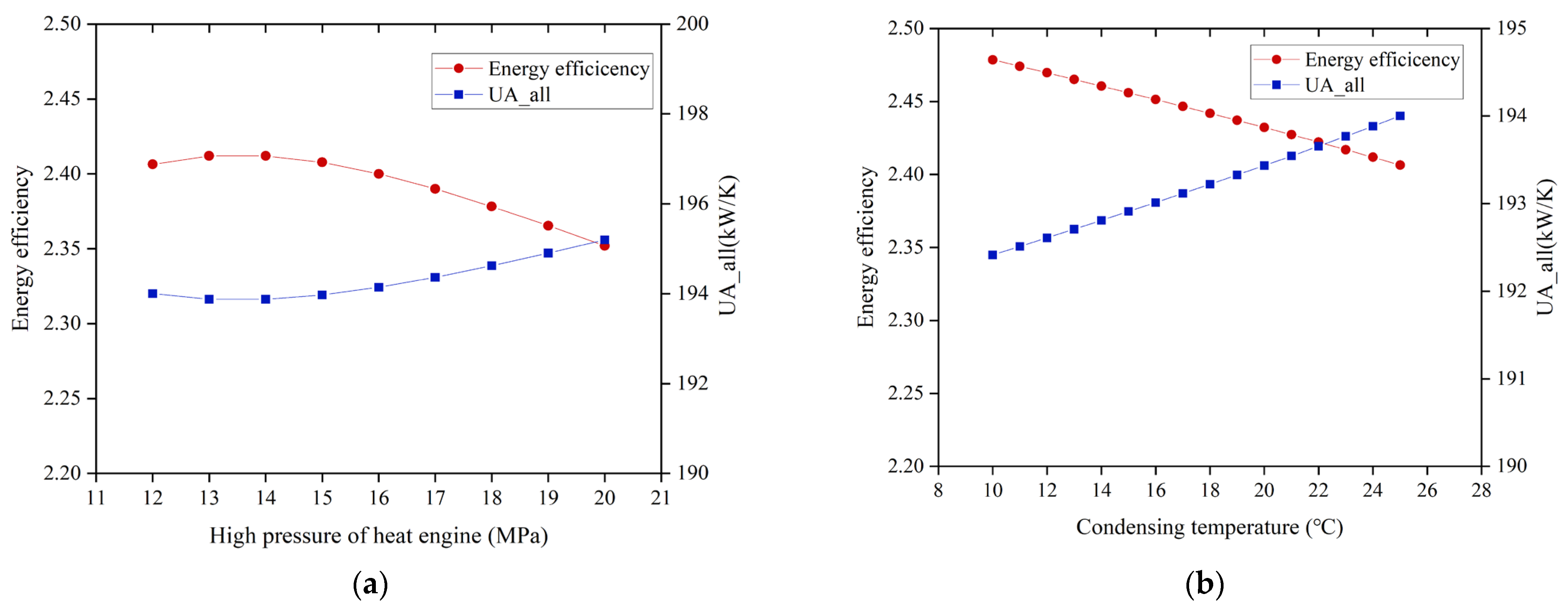
4.2. Critical Parameters of Heat Engine
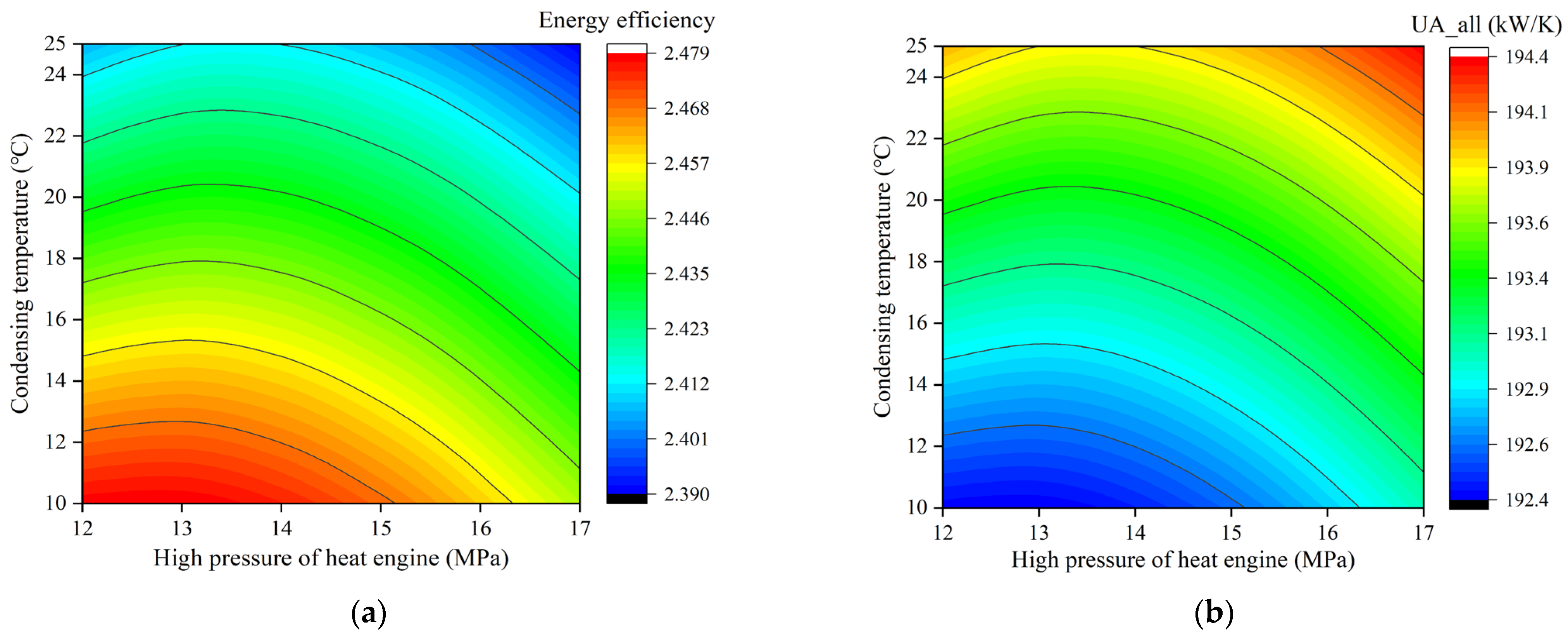
4.3. Coupling Parameters of Charge/Discharge System
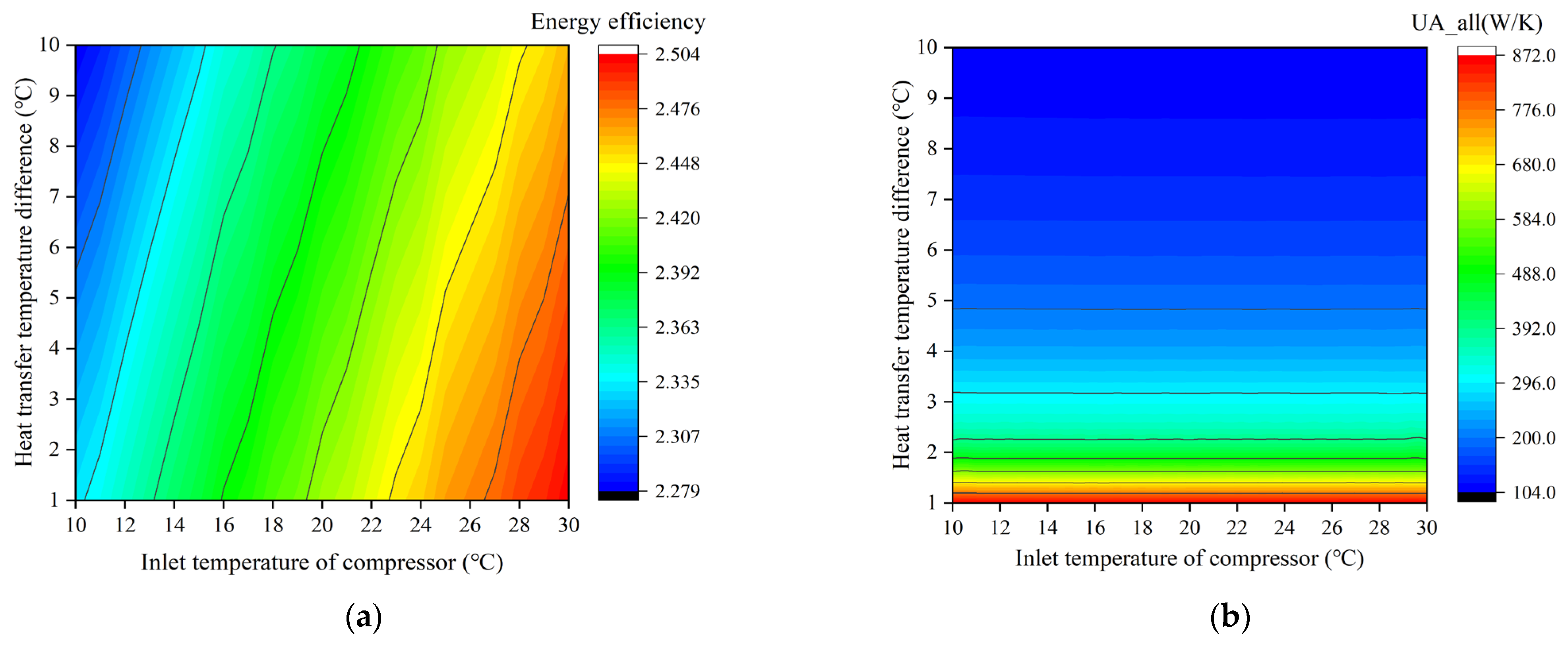
4.4. Mechanical Component Efficiency of System
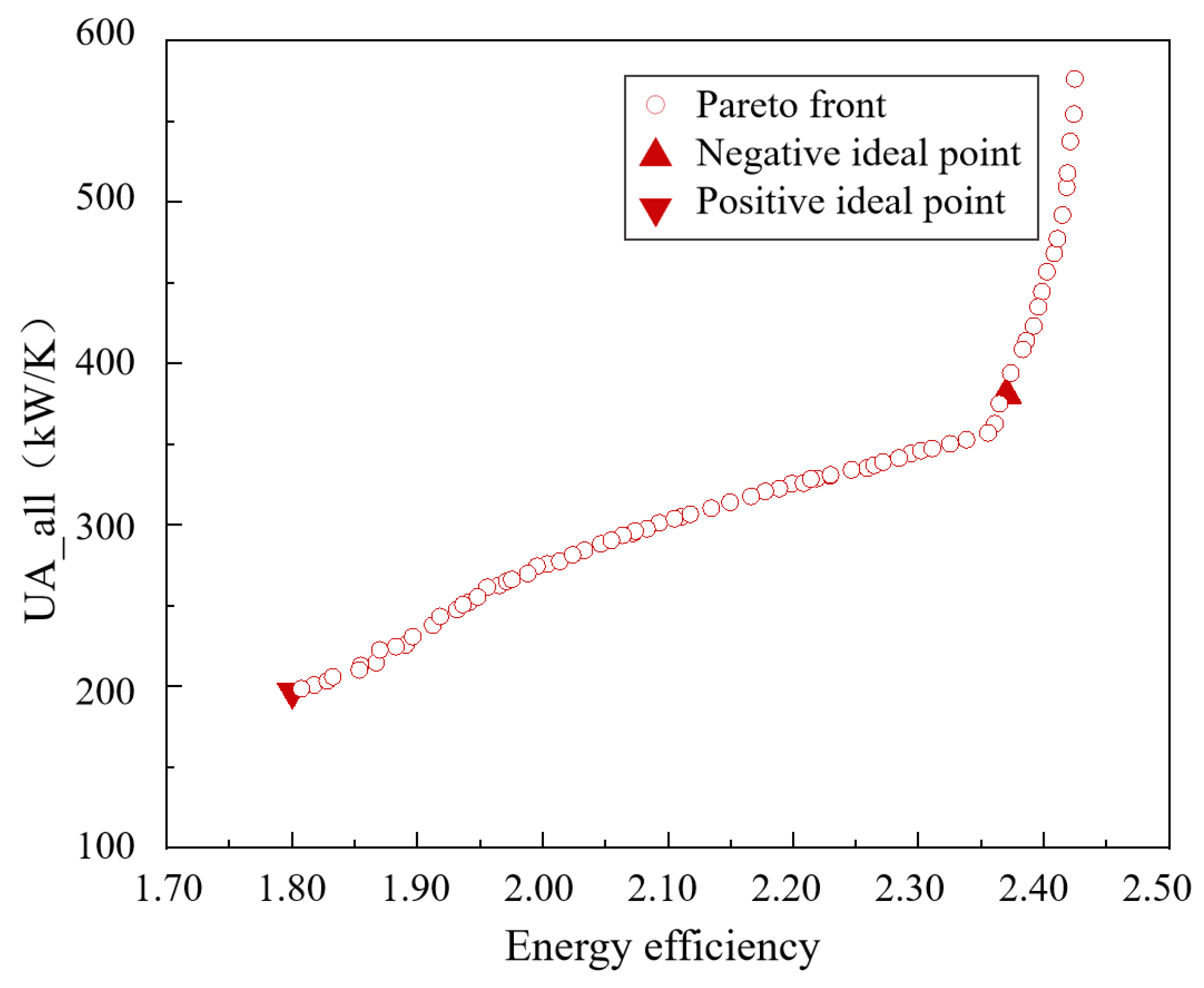
4.5. Multi-Objective Optimization and Decision Making
5. Conclusions
- (1)
- Through the form of the multistage compression heat pump cycle, the PTES system achieved a cascade heat storage pattern. The system can store about 0 °C of cold capacity, used to meet the needs of the cooling load. At the same time, it can store approximately 50 °C medium-temperature hot water, used to provide domestic hot water for the user side, and store the high-temperature heat above 115 °C for driving the turbine to generate electricity. The system not only can store renewable power, but also realize the flexible regulation of storage/release of power and meet the demand of multiple loads of heating and cooling in different periods.
- (2)
- Through the comprehensive analysis of the key parameters of the system, it is found that the effect of the heat pump parameters on the system performance is greater than that of the heat engine parameters. When and , the of the system reaches the highest value of 2.43. The change trend of is the same as that of , and the minimum value of is 61.32 kW/K when and are used. However, and do not show a simple linear relationship with the change in heat engine parameters.
- (3)
- The genetic algorithm is used to realize the comprehensive optimization of the PTES system. In addition, the optimal solution of the Pareto front solution set is obtained by the TOPSIS decision-making method. The optimal energy efficiency of the system is 2.39, and the total UA value is 357.4 kW/K.
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Specific enthalpy, kJ/kg | |
| Mass flow rate, kg/s | |
| Input electric power, kW | |
| Output electric power, kW | |
| Heat rate, kW | |
| Temperature, °C | |
| Greek Symbols | |
| Temperature difference, K | |
| Isentropic efficiency of mechanical components | |
| Energy efficiency of the system | |
| Thermodynamic efficiency of the heat engine | |
| Subscripts | |
| Heat pump | |
| Heat engine | |
| Compressor | |
| Cooling capacity | |
| Medium-temperature water | |
| High-temperature water | |
| Evaporator | |
| Condenser | |
| Abbreviations | |
| Pumped thermal energy storage | |
| Heat exchanger performance |
References
- Bp. Energy Outlook. Available online: https://www.bp.com/en/global/corporate/energy-economics/energy-outlook.html (accessed on 1 October 2024).
- Rostirolla, G. A Survey of Challenges and Solutions for the Integration of Renewable Energy in Datacenters. Renew. Sustain. Energy Rev. 2022, 155, 111787. [Google Scholar] [CrossRef]
- Wang, S. Economic Study on the Application of Energy Storage in Regional Electricity Market System. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Erixno, O.; Rahim, N.A.; Ramadhani, F.; Adzman, N.N. Energy Management of Renewable Energy-Based Combined Heat and Power Systems: A Review. Sustain. Energy Technol. Assess. 2022, 51, 101944. [Google Scholar] [CrossRef]
- He, Z.; Qi, W.; Song, J.; Cui, S.; Li, H. The thermodynamic analysis of a liquefied air energy storage system coupled with liquefied natural gas. Energy Storage Sci. Technol. 2020, 10, 1589–1596. [Google Scholar]
- Liang, T.; Vecchi, A.; Knobloch, K.; Sciacovelli, A.; Engelbrecht, K.; Li, Y.; Ding, Y. Key Components for Carnot Battery: Technology Review, Technical Barriers and Selection Criteria. Renew. Sustain. Energy Rev. 2022, 163, 112478. [Google Scholar] [CrossRef]
- Novotny, V.; Basta, V.; Smola, P.; Spale, J. Review of Carnot Battery Technology Commercial Development. Energies 2022, 15, 647. [Google Scholar] [CrossRef]
- Saher, S.; Johnston, S.; Esther-Kelvin, R.; Pringle, J.M.; MacFarlane, D.R.; Matuszek, K. Trimodal Thermal Energy Storage Material for Renewable Energy Applications. Nature 2024, 636, 622–626. [Google Scholar] [CrossRef]
- Dumont, O. Carnot Battery Technology: A State-of-the-Art Review. J. Energy Storage 2020, 32, 101756. [Google Scholar] [CrossRef]
- Strasser, M.N. A Cost and Performance Comparison of Packed Bed and Structured Thermocline Thermal Energy Storage Systems. Sol. Energy 2014, 108, 390–402. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Xu, Y.; Chen, H. Research progress in pumped heat electricity storage system: A review. Proc. CSEE 2018, 38, 178–185. [Google Scholar]
- Wang, L. Unbalanced Mass Flow Rate of Packed Bed Thermal Energy Storage and Its Influence on the Joule-Brayton Based Pumped Thermal Electricity Storage. Energy Convers. Manag. 2019, 185, 593–602. [Google Scholar] [CrossRef]
- Mercangöz, M. Electrothermal Energy Storage with Transcritical CO2 Cycles. Energy 2012, 45, 407–415. [Google Scholar] [CrossRef]
- Morandin, M. Conceptual Design of a Thermo-Electrical Energy Storage System Based on Heat Integration of Thermodynamic Cycles—Part A: Methodology and Base Case. Energy 2012, 45, 375–385. [Google Scholar] [CrossRef]
- Morandin, M. Conceptual Design of a Thermo-Electrical Energy Storage System Based on Heat Integration of Thermodynamic Cycles—Part B: Alternative System Configurations. Energy 2012, 45, 386–396. [Google Scholar] [CrossRef]
- Morandin, M. Thermoeconomic Design Optimization of a Thermo-Electric Energy Storage System Based on Transcritical CO2 Cycles. Energy 2013, 58, 571–587. [Google Scholar] [CrossRef]
- Carro, A.; Chacartegui, R.; Ortiz, C.; Carneiro, J.; Becerra, J.A. Energy Storage System Based on Transcritical CO2 Cycles and Geological Storage. Appl. Therm. Eng. 2021, 193, 116813. [Google Scholar] [CrossRef]
- Benato, A. Heat Transfer Fluid and Material Selection for an Innovative Pumped Thermal Electricity Storage System. Energy 2018, 147, 155–168. [Google Scholar] [CrossRef]
- Sun, P. Design and Application of Pumped Thermal Energy Storage System Based on High and Low Temperature Energy Storage. Master’s Thesis, Zhejiang University, Hangzhou, China, 2023. [Google Scholar]
- Laterre, A.; Dumont, O.; Lemort, V.; Contino, F. Is Waste Heat Recovery a Promising Avenue for the Carnot Battery? Techno-Economic Optimisation of an Electric Booster-Assisted Carnot Battery Integrated into Different Data Centres. Energy Convers. Manag. 2024, 301, 118030. [Google Scholar] [CrossRef]
- Kasaeian, A. Solar-Driven Polygeneration Systems: Recent Progress and Outlook. Appl. Energy 2020, 264, 114764. [Google Scholar] [CrossRef]
- Yu, L.; Zhu, Y.; Wu, Y. Medium and Low Temperature Waste Heat Power Generation Technology, 1st ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2015; pp. 123–125. [Google Scholar]
- Kim, Y.-M.; Shin, D.-G.; Lee, S.-Y.; Favrat, D. Isothermal Transcritical CO2 Cycles with TES (Thermal Energy Storage) for Electricity Storage. Energy 2013, 49, 484–501. [Google Scholar] [CrossRef]
- Hu, S.; Yang, Z.; Li, J.; Duan, Y. Thermo-Economic Analysis of the Pumped Thermal Energy Storage with Thermal Integration in Different Application Scenarios. Energy Convers. Manag. 2021, 236, 114072. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Nondy, J. Exergoeconomic Investigation and Multi-Objective Optimization of Different ORC Configurations for Waste Heat Recovery: A Comparative Study. Energy Convers. Manag. 2021, 245, 114593. [Google Scholar] [CrossRef]
- Yu, X. Sensitivity Analysis of Thermophysical Properties on PCM Selection under Steady and Fluctuating Heat Sources: A Comparative Study. Appl. Therm. Eng. 2021, 186, 116527. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Li, H. Multi-Objective Optimization and off-Design Evaluation of Organic Rankine Cycle (ORC) for Low-Grade Waste Heat Recovery. Energy 2020, 203, 117809. [Google Scholar] [CrossRef]
- Hwang, C.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]

| Parameter | Physical Meaning | Value |
|---|---|---|
| Low pressure of heat pump | 1.8 MPa | |
| High pressure of heat pump | 12.2 MPa | |
| Inlet temperature of compressor | 9.7 °C | |
| Outlet temperature of gas cooler | 5.6 °C | |
| Low pressure of heat engine | 2.1 MPa | |
| High pressure of heat engine | 14.4 MPa | |
| Inlet temperature of turbine | 175.8 °C |
| Parameter | Calculated Value | Reference Value | Relative Error |
|---|---|---|---|
| Power consumption of compressor | 132.12 kW | 130.6 kW | 1.2% |
| Output work of turbine | 95.24 kW | 99.4 kW | −4.2% |
| Power consumption of pump | 17.36 kW | 16.8 kW | 3.3% |
| Heat storage by heat pump | 358.8 kW | 352 kW | 1.9% |
| Heat consumption of heat engine | 337.36 kW | 336.4 kW | 0.3% |
| Parameter | Physical Meaning | Value |
|---|---|---|
| Total input power | 100 kW | |
| Isentropic efficiency of compressor | 86% | |
| Isentropic efficiency of pump | 85% | |
| Isentropic efficiency of turbine | 88% | |
| Ambient temperature | 25 °C | |
| High pressure of heat pump | 12 MPa | |
| Evaporating temperature of heat pump | 0 °C | |
| Medium heat storage temperature | 55 °C | |
| High heat storage temperature | 115 °C | |
| Inlet temperature of compressor | 20 °C | |
| High pressure of heat engine | 12 MPa | |
| Condensing temperature of heat pump | 25 °C | |
| Water pressure | 0.5 MPa | |
| Heat transfer temperature difference of evaporator | 5 °C | |
| Pinch point temperature difference | 1 °C |
| Parameter | Physical Meaning | Value Range |
|---|---|---|
| High pressure of heat pump | 12~20 MPa | |
| Evaporating temperature of heat pump | −5~15 °C | |
| High pressure of heat engine | 12~20 MPa | |
| Condensing temperature of heat pump | 10~30 °C | |
| Inlet temperature of compressor | 10~30 °C | |
| Heat transfer temperature difference | 1~10 °C |
| Parameter | Physical Meaning | Optimal Value |
|---|---|---|
| High pressure of heat pump | 16.1 MPa | |
| Evaporating temperature of heat pump | −0.12 °C | |
| High pressure of heat engine | 12.2 MPa | |
| Condensing temperature of heat pump | 10.7 °C | |
| Inlet temperature of compressor | 15.08 °C | |
| Heat transfer temperature difference | 3.1 °C |
| Energy Efficiency | Total UA Value | Thermal Storage Capacity | Cold Storage Capacity | Thermal Storage Temperature | Cold Storage Temperature | Output Electricity |
|---|---|---|---|---|---|---|
| 2.39 | 357.4 W/K | 38.2 kW | 195.8 kW | 136.9 °C | 2.2 °C | 37.7 kW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yin, Y.; Kang, Z.; Fan, J. Thermodynamic Analysis of Pumped Thermal Energy Storage System Combined Cold, Heat, and Power Generation. Energies 2025, 18, 525. https://doi.org/10.3390/en18030525
Wang Y, Yin Y, Kang Z, Fan J. Thermodynamic Analysis of Pumped Thermal Energy Storage System Combined Cold, Heat, and Power Generation. Energies. 2025; 18(3):525. https://doi.org/10.3390/en18030525
Chicago/Turabian StyleWang, Yijing, Yonggao Yin, Zhanxiao Kang, and Jintu Fan. 2025. "Thermodynamic Analysis of Pumped Thermal Energy Storage System Combined Cold, Heat, and Power Generation" Energies 18, no. 3: 525. https://doi.org/10.3390/en18030525
APA StyleWang, Y., Yin, Y., Kang, Z., & Fan, J. (2025). Thermodynamic Analysis of Pumped Thermal Energy Storage System Combined Cold, Heat, and Power Generation. Energies, 18(3), 525. https://doi.org/10.3390/en18030525








