A Review of Ignition Characteristics and Prediction Model of Combustor Under High-Altitude Conditions

Abstract

High-altitude relight is a critical challenge for aero-engines, directly impacting the safety and emergency response capabilities of aircraft. This paper systematically reviews the physical mechanisms, key factors, and relevant prediction models of high-altitude relight, highlighting the detrimental effects of extreme conditions such as low pressure and temperature on fuel evaporation rates, flame propagation speeds, and turbulent combustion processes. A comprehensive overview of the current state of high-altitude relight research is presented, alongside recommendations for enhancing the ignition performance of aero-engines under extreme conditions. This paper focuses on the development of ignition prediction models, including early empirical and semi-empirical models, as well as physics-based models for turbulent flame propagation and flame kernel tracking, assessing their applicability in high-altitude relight scenarios. Although flame kernel tracking has shown satisfactory performance in predicting ignition probability, it still overly relies on manually set parameters and lacks precise descriptions of the physical processes of flame kernel generation. Future studies on some topics, including refining flame kernel modeling, strengthening the integration of experimental data and numerical simulations, and exploring the incorporation of new ignition technologies, are needed, to further improve model reliability and predictive capability.

1. Introduction

Gas turbine engines play a critical role in modern aviation, as their operational stability directly determines flight missions. These engines rely on efficient fuel-air combustion to generate thrust, making ignition a vital process. Failure in ignition can result in engine startup failure or sudden shutdown, posing significant risks to flight safety [1].

During normal operation, ignition occurs either during engine startup on the ground or after a flameout at high altitude. Ignition is typically achieved by depositing a significant amount of energy locally to initiate a flame kernel and lead to full combustion [2]. Lefebvre [3], Mastorakos [4,5], and Yang [6] state that the ignition transient involves three phases: kernel generation, flame growth, and burner-scale flame establishment (including flame stabilization over a single burner and burner-to-burner propagation, known as “light-round”). In the first stage, the flame kernel develops into a flame, requiring sufficient energy to initiate droplet evaporation, sustain fuel pyrolysis, and ensure rapid oxidation of pyrolysis products. In the second stage, the flame generates enough heat within the initial ignition region to propagate to the central recirculation zone (CRZ) without extinguishing. This process is strongly influenced by fuel-air ratios (FAR) and the efficient evaporation of small droplets. Finally, in the third stage, the heat release rate continues to increase until the flame spreads to a stable position. If the flame can reach this stage, the ignition process is likely to succeed [5,7].

For the ignition process of gas turbines under ground-level conditions, extensive experimental and simulation studies have already been conducted by previous researchers [5], revealing that it is influenced by various factors, primarily including airflow speed [8,9], combustion chamber pressure drop, nozzle pressure drop, droplet size [10], inlet air temperature [11], geometric dimensions of the combustion chamber [12,13], the aerodynamic characteristics of the combustion chamber (such as cooling air near the igniter) and the energy output and frequency of the igniter [3].

In contrast, ignition at high altitudes introduces significant challenges due to reduced ambient pressure, temperature, and air density. These conditions disrupt the flow field within the combustion chamber and hinder critical processes such as atomization, evaporation, and flame propagation. The low-pressure environment slows the growth and propagation of the flame kernel, as the rarefied air decreases flame propagation speed. Additionally, the low-temperature conditions reduce the evaporation rate of liquid fuel, delaying its conversion into combustible gas. High-speed airflow further complicates the process by destabilizing the flame kernel, increasing the risk of ignition failure [3]. Addressing these challenges requires a deeper understanding of flame kernel generation and flame stability mechanisms under high-altitude conditions.

In recent years, high-altitude relight research has advanced significantly, evolving from theoretical foundations and experimental optimizations to the application of advanced technologies and prediction model development. Lefebvre [14] established a theoretical framework for Minimum Ignition Energy (MIE) under high-altitude conditions. Building on this, Chen [15] explored oxygen enrichment as a strategy to enhance ignition performance in low-oxygen environments. Structural optimizations have also been studied, with Read [16] and Linassier [17] investigating ignition performance in lean direct injection (LDI) and multi-sector combustors, respectively, revealing the influence of design configurations on ignition efficiency. Advanced diagnostic and ignition technologies have been employed by Mosbach [18] and Mehdi [19], who used laser diagnostics and plasma-assisted methods to analyze the dynamic effects of fuel injection and plasma excitation. Rosa [20] and Giusti [21] additionally combined numerical simulations and experiments to study two-phase flow ignition in liquid fuels, while Cambridge University researchers [22,23] developed and validated a low-order ignition model using Rolls-Royce data, advancing high-altitude relight prediction models. These studies, through the integration of theoretical, experimental, and technological approaches, have provided systematic support for high-altitude relight research.

High-altitude relight is critical for aviation safety, directly affecting aircraft performance and emergency response capabilities. Understanding flame propagation and ignition mechanisms under high-altitude conditions is essential not only for improving current aero-engine performance but also for guiding the development of future low-emission engines. However, the lack of comprehensive analysis of flame propagation characteristics and predictive methods for combustors under extreme conditions has become a limiting factor for flight safety after flame blowoff in combustors. This paper aims to address these gaps by providing a detailed review of the physical mechanisms and key factors influencing high-altitude relight. It will analyze airflow dynamics, fuel atomization, and evaporation processes, as well as flame propagation and stability theories. The advantages and limitations of current ignition prediction models will also be evaluated, with a focus on their applicability and accuracy for high-altitude conditions. Finally, the paper will identify current research gaps and propose directions for future work in high-altitude relight.

2. Ignition and Flame Establishment Mechanisms

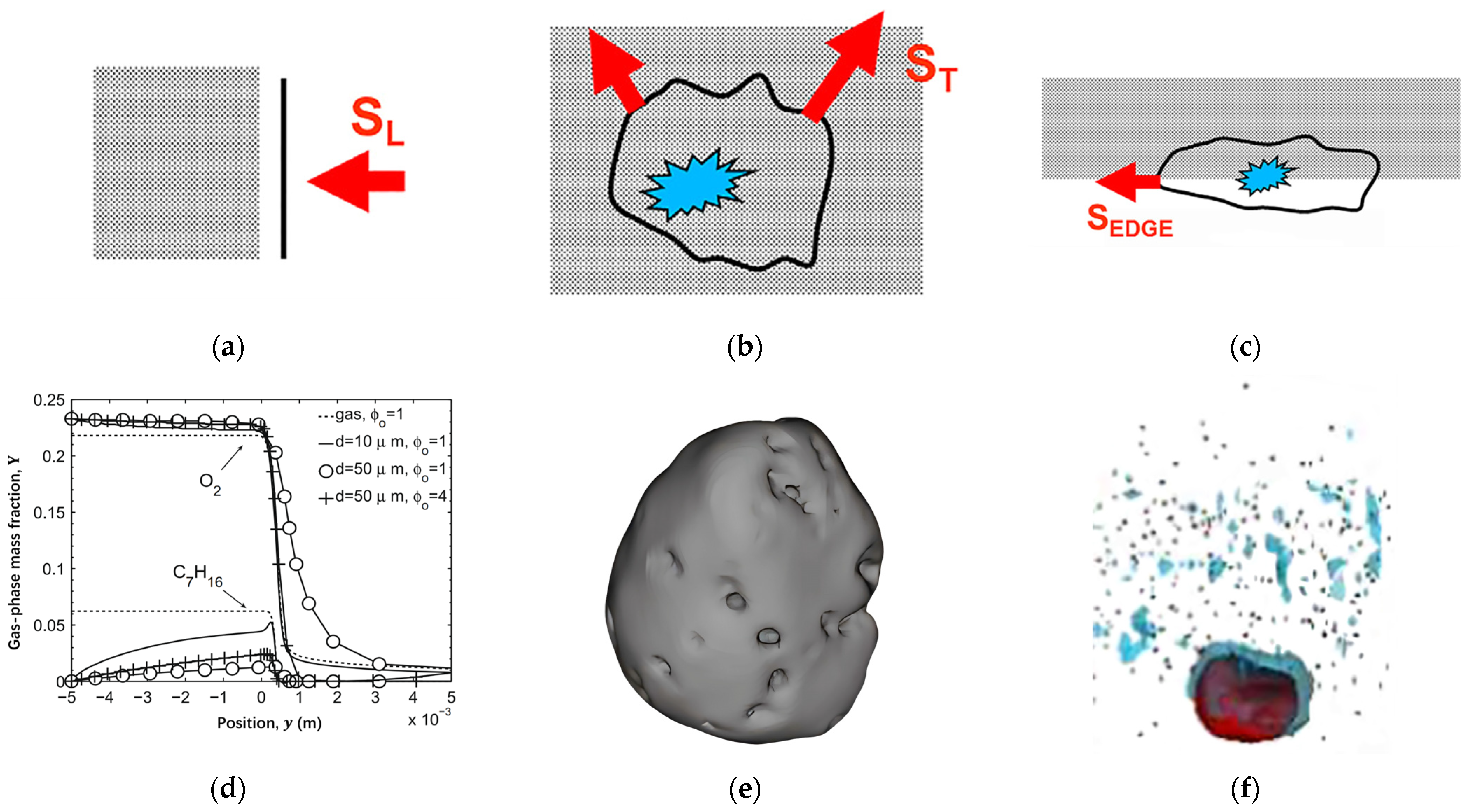
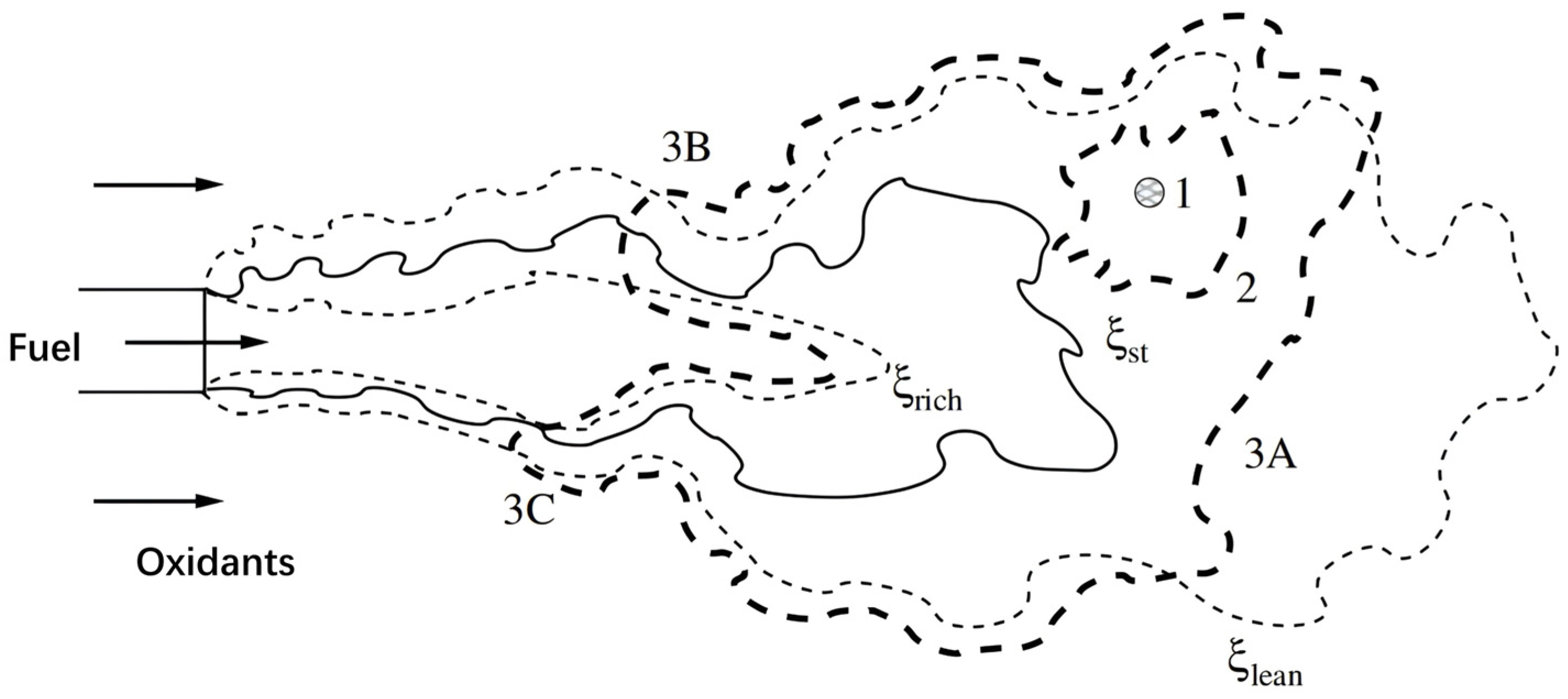
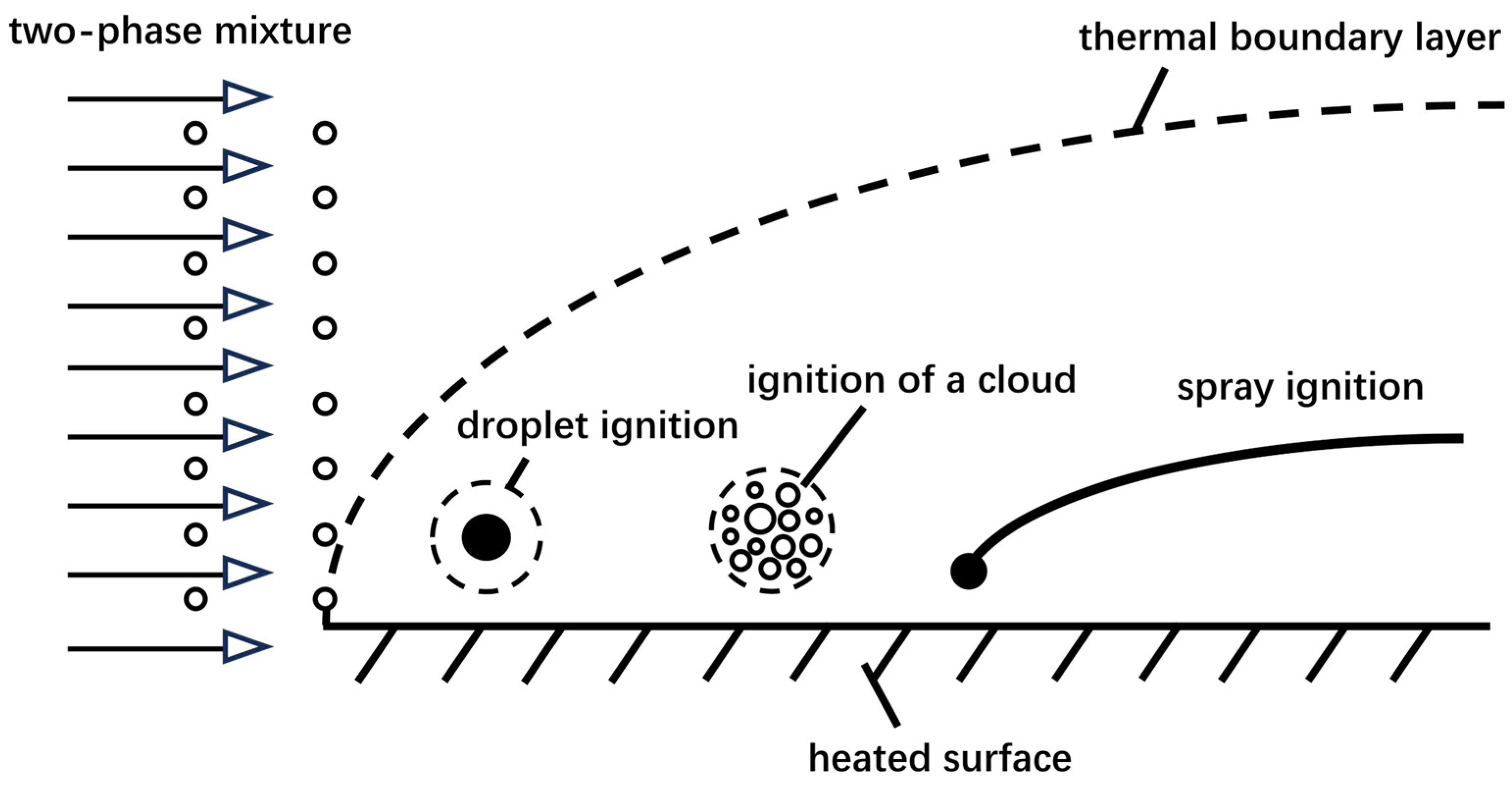
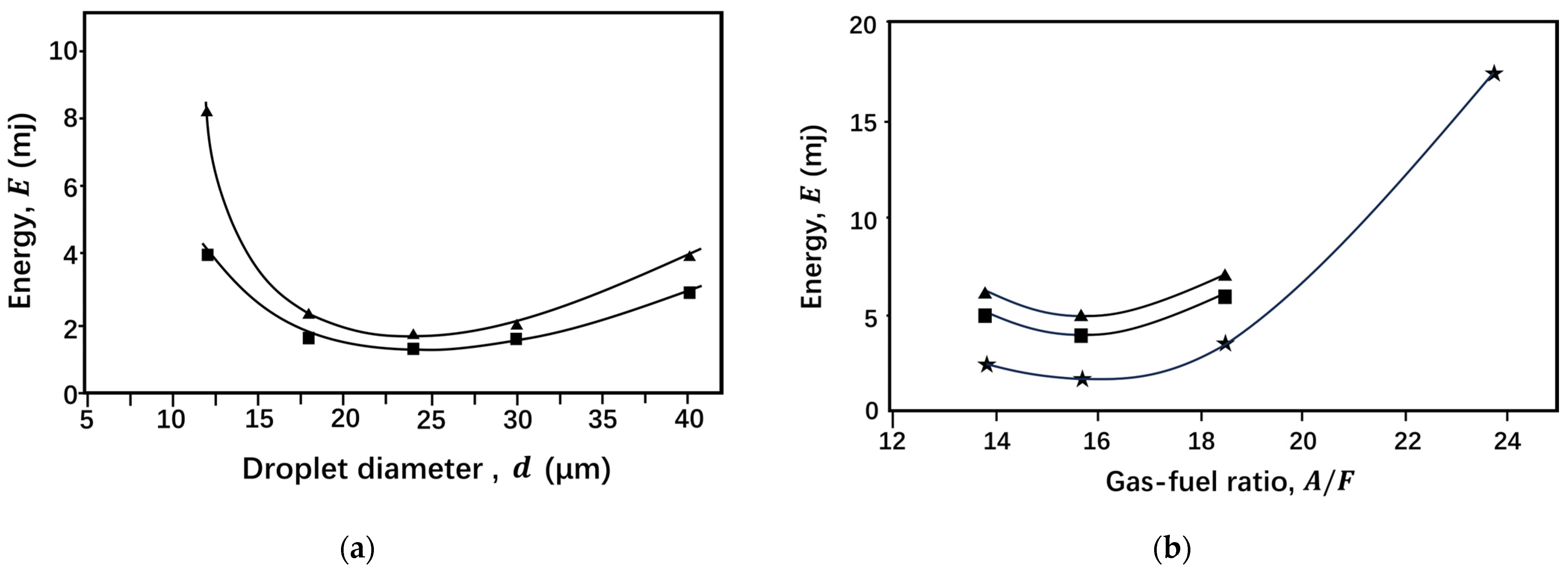
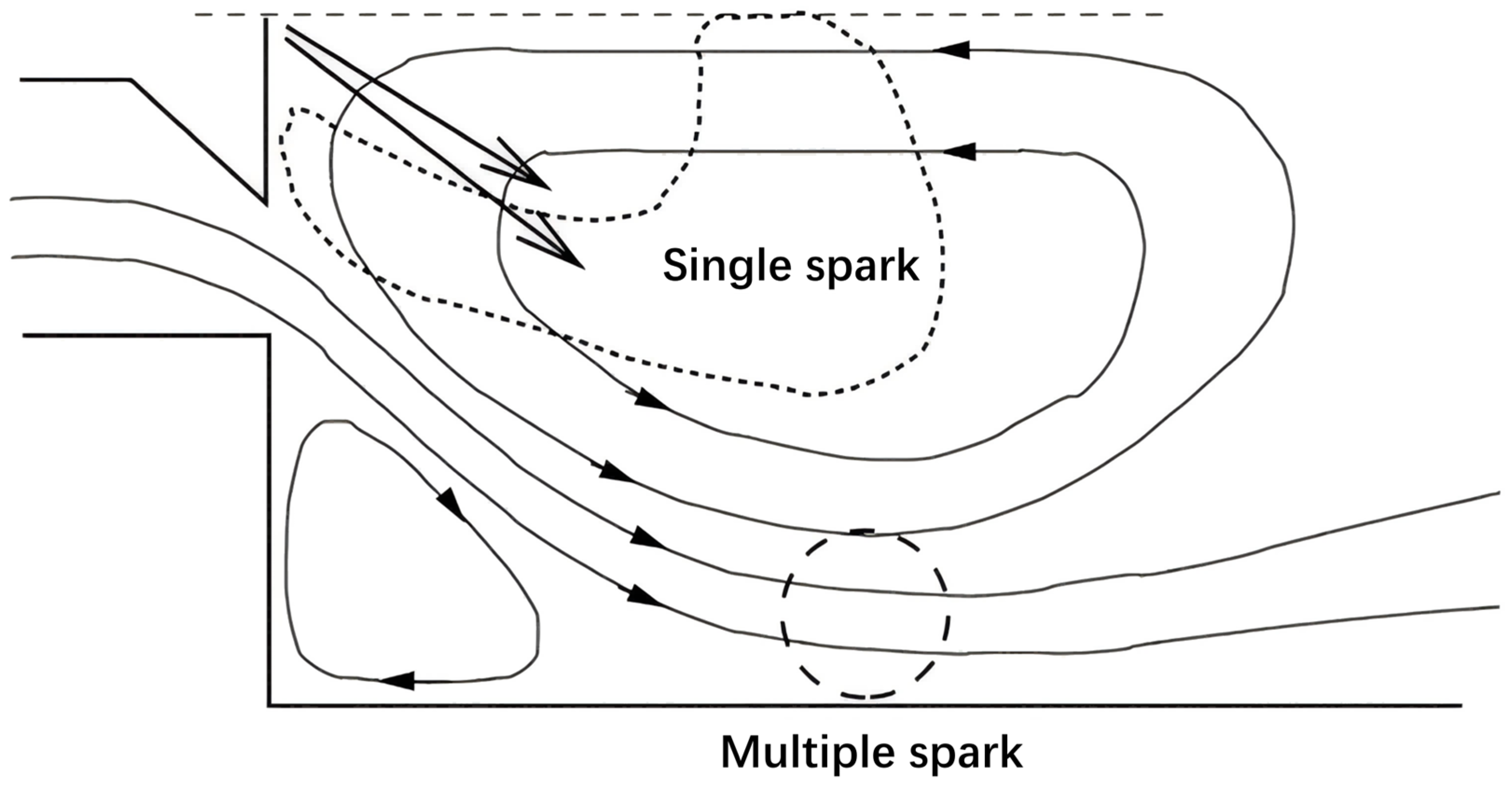
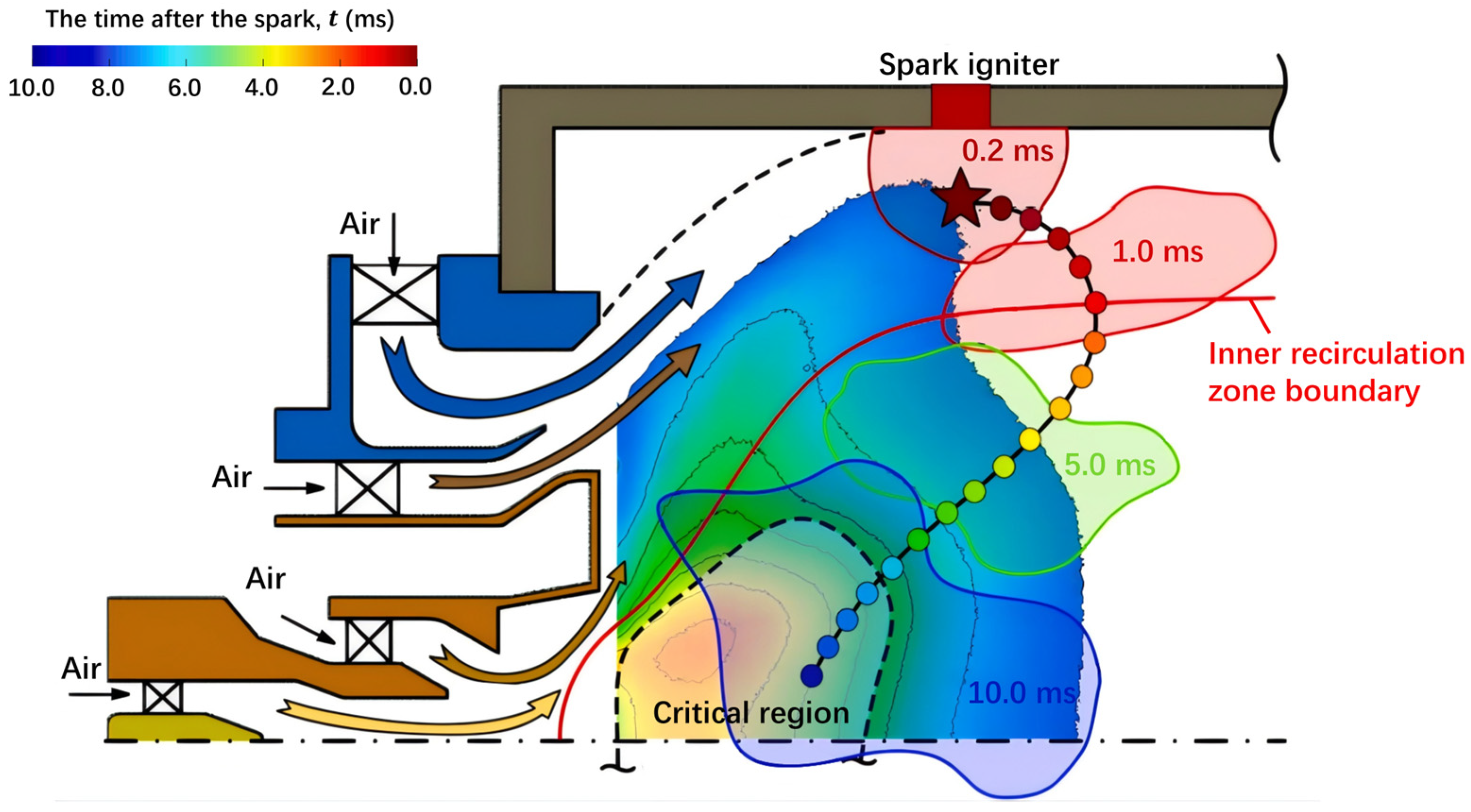
2.1. Current Research Status on Ignition Characteristics

Ignition is a highly intricate and multifaceted area of combustion research. Its performance plays a pivotal role in determining the operating envelope of an aircraft and the combustor volume, which in turn influences engine weight, energy losses, and emissions. Forced ignition refers to the initiation of combustion in a mixture through externally imposed energy sources such as electrical or laser-induced sparks [24,25,26,27], plasma jets [28,29], or heated surfaces [5]. In turbulent combustion, flames are broadly classified into premixed flames [8,30,31] and non-premixed flames [4,32], the latter can be further categorized into stratified flames [33] and spray flames [5,34,35,36], with spray flames being the most prevalent type in aero-engine applications. Figure 1 depicts canonical flame propagation, illustrating laminar flame propagation in a uniform liquid spray field, spark ignition in a uniform liquid spray, and flame propagation in a non-uniform liquid spray.

Researchers globally have conducted extensive studies on ignition stages and flame propagation characteristics. For the kernel generation stage, Mastorakos [5] summarized three probabilistic factors to describe the stochastic nature of ignition. The likelihood of finding a combustible mixture in the spark region is defined as the flammability factor, expressed as:

$$F={\int }_{{\xi }_{lean}}^{{\xi }_{rich}}P(\eta )d(\eta )$$

(1)

Here, $P\left(\eta \right)$ denotes the probability density function of the local equivalence ratio $\eta$, while ${\xi }_{rich}$ and ${\xi }_{lean}$ collectively define the flammable range. Variations in the ionization path between electrodes, local droplet distribution, and turbulence strain rate influence the kernel establishment probability $P_{ker}$, which in turn impacts the overall ignition probability $P_{ign}$. Successful ignition requires the spark to release sufficient energy for the kernel diameter to exceed the quenching diameter [40]. Typically, the ignition energy that can form a flame in 50% of ignition events is referred to as the Minimum Ignition Energy (MIE) [5]. Shy described two statistical methods for determining the MIE at 50% ignitability [8]: the midpoint approximation method and the logistic regression method. The midpoint method estimates ignition probabilities at different energy levels through interpolation and progressively approaches 50% ignition probability to determine MIE. Its advantage lies in its intuitive process and clear experimental results, but it requires numerous test points, making it labor-intensive. The logistic regression method, on the other hand, relies on the cumulative distribution of ignition probabilities and uses statistical modeling to calculate MIE, including confidence intervals. This method is more robust and requires fewer experiments but demands advanced data processing and statistical modeling capabilities.

Neophytou [41] proposed that the success of ignition depends on the number of droplets surrounding the ignition kernel. In the initial ignition phase, a highly wrinkled flame surface forms around the droplets, with high reaction rates near them and low reaction rates in the gaps. Heat diffusion in the reaction zone triggers the ignition of nearby cold droplets, further sustaining the combustion process. The timescale of droplet evaporation interacts with chemical and diffusion timescales, determining the overall ignition process. If the droplet evaporation rate is too slow, this interaction may compete with chemical reactions, potentially leading to flame extinction. Figure 2 schematically illustrates features of forced ignition in turbulent non-premixed flames, focusing on flame propagation in turbulent fuel jets through cold air after successful ignition.

Aggarwal [10] proposed that ignition in two-phase mixtures occurs in three different modes (see Figure 3): droplet ignition, droplet cluster ignition, and spray ignition. An optimal droplet size and equivalence ratio for ignition in liquid fuel sprays correspond to the minimum ignition delay time (or ignition energy). Figure 4 illustrates the variation of MIE with droplet size and air-fuel ratio.

In the context of premixed flame ignition, Shy [8] investigated the phenomenon of spark ignition transition in premixed turbulent combustion. The study explored how factors such as spark gap, Lewis number, and turbulence velocity influence the MIE, with a particular focus on two distinct ignition phenomena: monotonic MIE transition and non-monotonic MIE transition. Yu [42] further advanced the theoretical understanding of premixed flame ignition, particularly the generation and expansion of flame kernels during forced ignition. Key ignition parameters, such as critical flame radius, MIE, and minimum ignition power, were analyzed, along with prediction models under various theoretical frameworks, including homogeneous explosion theory, hot spot ignition theory, flame ball theory, and transient ignition theory. These studies highlighted advancements in theoretical models for predicting critical ignition conditions, especially when considering the complex interactions between chemical kinetics and fluid dynamics.

During the flame growth phase, once a kernel is generated and a sufficiently large flame forms around the stoichiometric mixture fraction isosurface, the flame can propagate along it as a non-premixed edge flame [4]. Rosa [20] demonstrated experimentally that the successful propagation of the flame kernel depends on its movement within the fuel spray region. The axial spark position significantly impacts ignition performance and the flame propagation process. The propagation trajectory of the flame kernel is related to the ignition location and is primarily influenced by the non-reactive flow field and fuel concentration, warranting further investigation [43]. Marchione [12] summarized the optimal ignition locations for bluff-body flames under single-spark and multiple-spark conditions through multiple experiments, as shown in Figure 5. It was observed that, under high-frequency ignition conditions, the optimal position of the igniter is at the axial location corresponding to the widest radial extent of the recirculation zone.

During the flame propagation phase, the process is complex and variable, influenced significantly by boundary conditions and operating parameters [44]. The flame propagation mode is determined by the flow conditions, injection patterns, and flame shape. Flow structure and injection patterns establish potential flammable pathways for flame propagation, while flame morphology dictates the motion path of the flame front during ignition. Gao [45] proposed three mechanisms for injector-to-injector flame propagation patterns in annular combustors based on flame front behavior: spanwise upstream pattern, archlike-entrainment pattern, and spanwise-entrainment pattern (see Figure 6). The solid green lines show flame paths, and the black dashed lines outline recirculation zones. The spanwise-upstream pattern demonstrates the flame’s azimuthal and upstream movement, igniting downstream droplets before stabilizing in the unignited injector’s recirculation zone, which occurs under low velocity and high equivalence ratio conditions. The archlike-entrainment pattern shows the flame forming an arch shape as it moves across the merging jets, becoming entrained in the adjacent injector’s recirculation zone, and stabilizing as a kernel, typically under lean conditions. The spanwise-entrainment pattern describes a flame pathway characterized by radial movement and recirculation zone entrainment, prevalent under high-velocity conditions where the flame is short and wide. Similarly, Wang [46], from the perspective of local interactions in the flow field and combustion process, summarized the flame propagation modes in annular combustors with centrally staged swirl burners as the kindled-swirling pattern, entrained-swirling pattern, and sweeping pattern.

Topperwien [44] discovered that the volumetric expansion of combustion gases induces azimuthal flow acceleration, which serves as the primary driving mechanism for flame propagation. In the wake of rotating jets, droplets accumulate ahead of the propagating flame front, forming a characteristic sawtooth pattern in the trajectory of the leading points. Compared to non-staged combustors, staged combustors exhibit a more intricate “sawtooth” pattern during the light-round process. During this process, flame-leading points follow a zigzag motion, with counterclockwise trajectories closer to the inner wall and clockwise trajectories closer to the outer wall [47].

Microwave plasma extends combustion limits and shortens ignition delay, offering greater flexibility and stability compared to traditional spark ignition, particularly under lean burn and high-altitude conditions.

For advanced ignition technologies, plasma-assisted ignition, using low-temperature non-equilibrium plasma, has been demonstrated to effectively improve ignition and combustion performance under low pressure and temperature conditions. Mehdi et al. [19] investigates plasma-assisted ignition for re-igniting aeroengines under high-altitude, low-pressure conditions. The results show that plasma significantly reduces ignition delay times, with a reduction from 1.1 × 10⁻³ s to 3.5 × 10⁻⁵ s at 1 bar. At lower pressures (0.6 bar and 0.4 bar), the effect is less pronounced but still beneficial. Plasma improves fuel/air mixture mixing and enhances active radicals (H, O, OH, CH et al.), accelerating ignition. Lin et al. [29] used multi-channel nanosecond discharge plasma to achieve successful ignition of premixed fuels at low pressures, showcasing the effectiveness of microwave plasma ignition in comparison to other ignition methods. He et al. [48] provided a review of microwave plasma ignition, highlighting its potential in modern combustion technology to widen the ignition range, improve combustion efficiency, and reduce emissions.

Laser ignition technology has also been rapidly advancing. O’Briant et al. [49] reviewed the application of laser ignition in aerospace propulsion systems, noting that laser ignition provides precise timing for ignition, improves ignition efficiency, and extends the operational limits of aero-engines, especially under high-pressure and hypersonic flight conditions. Mulla et al. [26] studies the development of flame kernels in laser-induced spark ignition mixtures, focusing on their growth over time in different fuel mixtures. Using OH-PLIF imaging, the study tracks the flame kernel’s formation from 3 µs to 1000 µs. It finds that factors like fuel composition, equivalence ratio, and laser energy significantly affect kernel growth. Hydrogen mixtures show a larger flame kernel spread and higher laser energy leads to greater flame kernel expansion. The study conducted by de Oliveira et al. [50] investigates the ignition of droplet-laden turbulent flows using laser sparks, examining the effects of laser energy, equivalence ratio, and fuel pre-vaporization on flame kernel formation. It finds that small droplets enhance ignition by reducing the MIE and improving flame propagation, whereas larger droplets may hinder ignition. A critical kernel size of 1 mm is identified for successful ignition. The ignition probability is significantly increased by higher laser energies (80 mJ) and partial fuel pre-vaporization. Moreover, a positive correlation is observed between kernel size and absorbed energy. Yi et al. [51] studied the laser ignition characteristics of aviation kerosene droplets under different pressures and initial diameters and developed a droplet ignition model to calculate the MIE of RP-3 droplets at specific diameters and pressures. These studies highlight the potential of laser ignition technology in high-pressure, low-temperature, and lean fuel conditions, providing crucial theoretical support for the development of ignition techniques in aerospace propulsion systems.

This section reviews key advancements in ignition and flame propagation research, revealing the complex mechanisms from flame kernel generation to flame propagation. It also explores the impact of combustor design, fuel characteristics, environmental conditions, and advanced ignition technologies on ignition performance. Under high-altitude, low-temperature, and complex operating conditions, novel technologies such as microwave plasma and laser ignition have significant potential to extend combustion limits, accelerate flame propagation, and improve ignition probability. Optimizing ignition performance relies not only on improvements to individual factors but also on achieving higher integration through the synergistic interaction of combustor design, fuel compatibility, and ignition technologies.

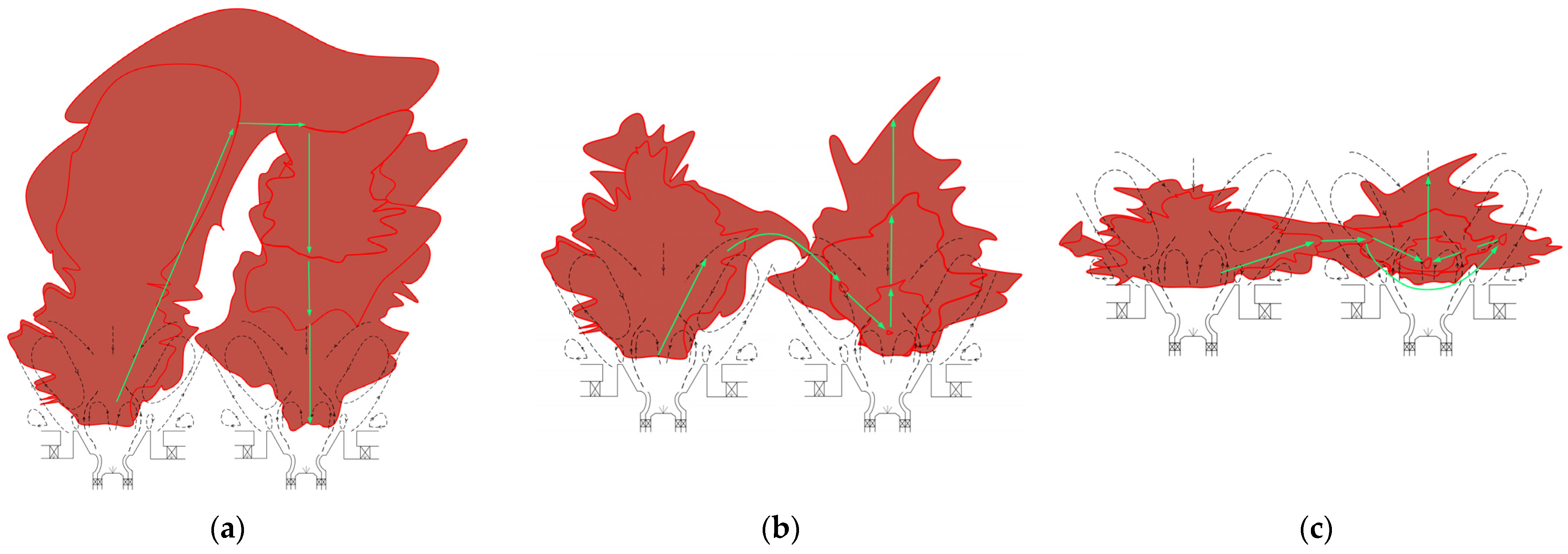
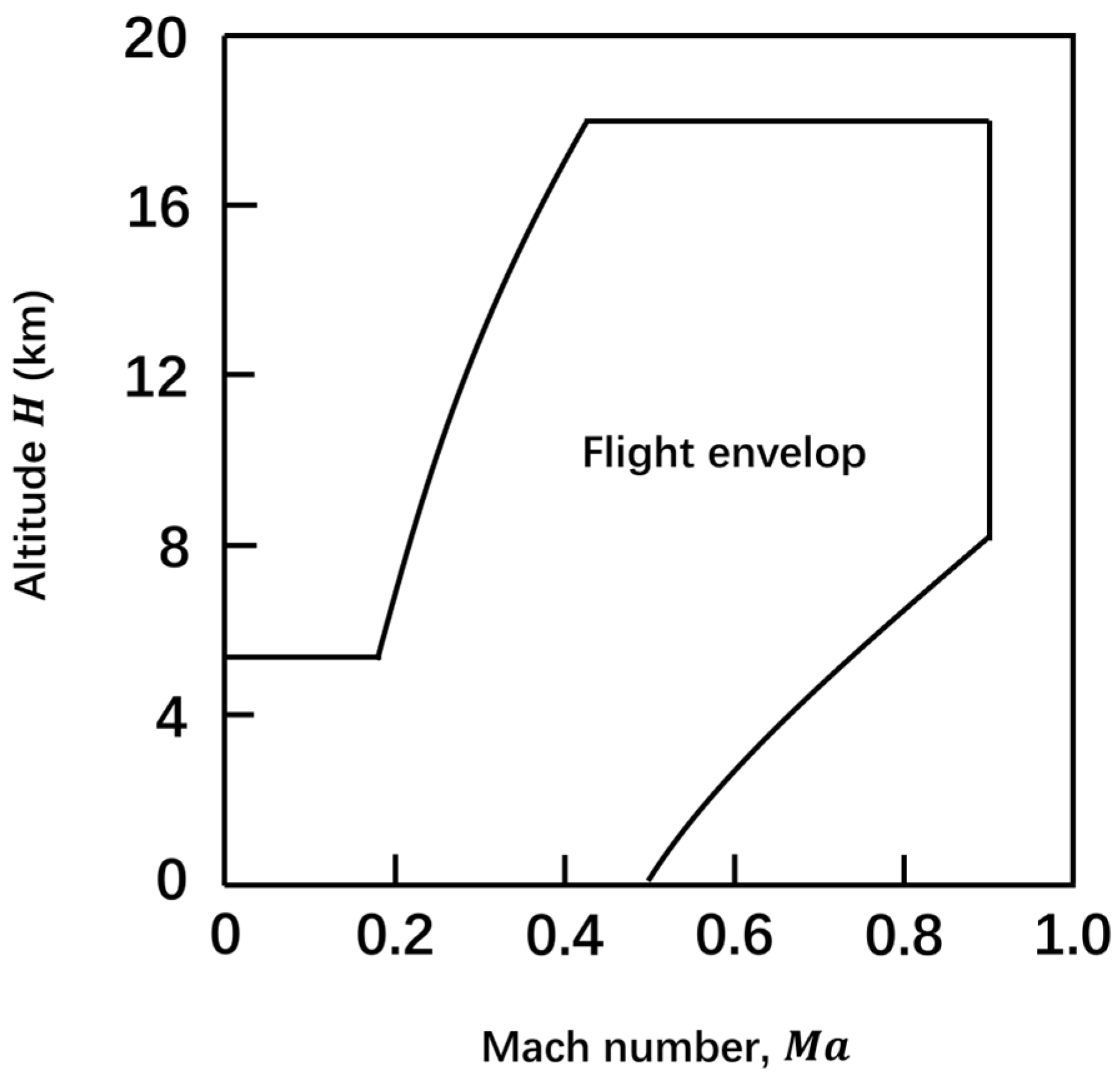
2.2. Ignition Under High-Altitude Conditions

When an aero-engine experiences a flameout due to specific incidents, the loss of energy causes the turbine to cease generating power, leaving the engine in a windmill state, where the fan and compressor are passively rotated by external airflow without active ignition. Reigniting the combustor in this state is referred to as high-altitude relight [52]. High-altitude relight characteristics are typically described by relating relight altitude to aircraft flight speed. These characteristics define the relight flight envelope of an aircraft under different flight speeds. Currently, the international standard for high-altitude relight reaches altitudes of 8–12 km. Figure 7 illustrates the typical aero-engine flight envelope.

Under high-altitude conditions, significant reductions in air pressure, temperature, and density deteriorate flow and spray conditions, making ignition in the combustor more challenging. As air density and pressure decrease, turbulence intensity weakens, reducing the shear effect on fuel [53], increasing droplet size, and slowing evaporation rates. These factors degrade fuel atomization, leading to locally low FAR, which in turn reduces the efficiency of fuel-air mixing, increases ignition difficulty, and negatively impacts flame propagation speed and stability during the ignition process. Figure 8 illustrates the trend of minimum ignition FAR as the altitude increases. As shown by the red line in the figure, the minimum ignition FAR increases as temperature and pressure conditions deteriorate. Low temperatures at high altitudes slow fuel evaporation, preventing the formation of a sufficient concentration of combustible mixtures and causing longer ignition delays or even ignition failure [15].

In numerical simulations, reduced fuel temperature under high-altitude conditions significantly decreases fuel-air mixing uniformity. This uneven distribution of fuel in the combustion zone, with locally over-rich or lean areas, further increases the likelihood of ignition failure [17]. Zhao [55] found in the study of a multi-swirl staged combustor equipped with a pre-filming airblast atomizer that low-temperature and low-pressure conditions can significantly weaken the turbulent kinetic energy and tangential shear force of the swirling air, leading to larger atomized droplets, deeper penetration of droplet groups, and further deterioration of fuel distribution quality. In a study of high-altitude ignition processes in aero-engines with and without effusion cooling, Martinos [54] concluded that increasing FAR can compensate for the negative effects of low pressure and temperature on combustion reactions.

The generation and propagation of the flame kernel, and the alignment of fuel with the spark plug, are key challenges in high-altitude ignition. MIE is a critical parameter for understanding ignition processes, particularly under high-altitude conditions. Studies by Ballal and Lefebvre [56] have demonstrated that the MIE increases significantly as air pressure and temperature decrease. Their experimental measurements under sub-atmospheric pressures showed that MIE for liquid sprays is highly sensitive to spray SMD, airflow velocity, and equivalence ratio. They found that reduced air pressure and temperature not only lead to a significant increase in MIE but also necessitate higher spark energy and longer ignition duration. This indicates that atomization quality and fuel spray properties play a crucial role in achieving reliable ignition under such extreme conditions. Future research could focus on refining these relationships and expanding experimental studies to quantify MIE under high-altitude environments, where low turbulence intensity and suppressed flame kernel growth further complicate ignition.

Under high-altitude conditions, turbulent flame propagation modes directly influence the formation and expansion of flame kernel [18]. Read et al. [16] conducted high-speed imaging of the ignition process at Rolls-Royce’s high-altitude relight test rig in Derby, UK. They found that the success of ignition strongly depends on the overall FAR of the combustor and, to a great extent, on the trajectory of the flame kernel. Flame kernels that enter the CRZ of the combustor typically lead to flame stabilization, while those flowing toward the combustor exit tend to extinguish. Mosbach [18] further revealed that the success of ignition depends on the flame kernel’s ability to move upstream from the igniter to the fuel atomization region. Flame kernels that successfully develop into sustained ignition typically exhibit pronounced upstream movement, while those that fail to ignite remain localized downstream and eventually extinguish, primarily due to adverse turbulence effects or insufficient energy. Zhao [57] summarized a high-probability flame propagation pattern (dipper-type propagation, see Figure 9), which supports this conclusion.

Linassier [17] found that the flame kernel is typically generated in fuel-rich regions within the combustor, and its propagation path is significantly influenced by airflow and fuel distribution. The study showed that a successful ignition process relies on the flame kernel quickly propagating from the spark plug to the fuel atomization region. If the flame kernel cannot move upstream and reach the fuel injection region within a short period, ignition is highly likely to fail [16]. Figure 10 illustrates four trajectories of the flame centroid, corresponding to flame kernel failure following high-altitude relight attempts. The spark plug position and discharge energy intensity significantly impact flame kernel formation and propagation path [58]. Adjusting the axial position of the igniter or increasing its discharge energy can substantially improve the probability of high-altitude ignition [18]. Vincenti [58] demonstrated that flame kernel generation and propagation depend on fuel atomization quality and igniter position. In regions with uneven fuel distribution, ignition probability significantly drops. Adjusting the igniter’s position increases the probability from 50% to over 80%. Doubling the igniter’s discharge energy compared to standard systems improves the probability by 20%.

The geometry of the combustor has a significant impact on high-altitude ignition performance, and the optimization of different components within the combustor plays a crucial role in improving ignition reliability under adverse conditions.

For the combustor dome, Wang et al. [59] demonstrated the critical influence of two-stage axial swirlers on ignition characteristics. By reducing the outer swirl number, the shear strength between inner and outer swirling airflows was enhanced, improving fuel atomization and ignition stability. Furthermore, adjusting the effective area ratio between the swirlers and modifying the Venturi throat radius optimized ignition performance under low-pressure and high-altitude conditions. Fu et al. [60] investigated the effect of step heights at the dome outlet in centrally staged combustors. They found that increasing step height significantly improved lean ignition performance under high-altitude conditions, particularly due to enhanced fuel atomization. This impact was more pronounced under low-pressure conditions, emphasizing the importance of step height in stabilizing ignition.

For the combustor liner, Li et al. [61] systematically studied the effects of sleeve length and large cooling holes (LCHs) on ignition processes in reverse-flow combustors. Their research showed that plugging LCHs and shortening the sleeve length enhanced the recirculation zone and facilitated better energy and radical transfer, resulting in improved ignition performance even at altitudes of 8.5 km. Yang et al. [62] explored the axial positioning of primary holes along the combustor liner. Their study revealed that aligned primary holes expanded the recirculation zone and reduced the reference velocity, creating a more stable flame and minimizing the quenching probability of the flame kernel. This configuration supports flame propagation and ensures ignition reliability under low-temperature and low-pressure conditions.

By integrating these findings, it becomes evident that a synergistic approach to combustor design, encompassing swirler configuration, dome outlet step height, cooling hole management, sleeve length, and primary hole positioning, enhances ignition reliability and advances the development of high-efficiency combustors for aviation applications.

One of the challenges in high-altitude relight testing is that ground-based test equipment must accurately simulate real high-altitude conditions, which imposes high demands on the complexity and cost of the experimental setup. The high-altitude environment features extremely low pressure and temperature, requiring the test equipment to create a similar vacuum environment and maintain a high-precision temperature control system to ensure that the engine can relight under realistic conditions.

There are several renowned ignition testing platforms worldwide. The Rolls-Royce Strategic Research Centre (SRC) altitude-relight test rig in Derby, UK, has been used to test the high-altitude relight performance of a lean fuel injector and combustor. This test rig can operate a sector combustor with an inlet pressure as low as 0.2 bar (20 kPa), an inlet temperature of 243 K, and an airflow of up to 1.77 lb/s (800 g/s). Flame behavior can be observed through quartz windows in the sidewall of the combustion chamber and pressure vessel [18]. Researchers, including Read [16] from the University of Cambridge and Mosbach [18] from the German Aerospace Center (DLR), studied the high-altitude relight performance of lean fuel at operating pressures of 50 kPa and 41.7 kPa, respectively, based on this testing platform. Nicolás [20] from Toulouse University and Linassier [17] from France conducted high-altitude studies on single-head and multi-sector combustor models using the MERCATO (Moyen Expérimental de Recherche en Combustion Aérobie par Techniques Optiques) test rig at ONERA Fauga-Mauzac. This facility analyzes two-phase flow injection systems and reproduces high-altitude combustor conditions, with pressures as low as 0.4 bar and air-fuel temperatures down to 233 K. For more information, refer to refs. [63,64].

The Combustion and Fire Research Laboratory (CFRL) at the University of Cincinnati designed and constructed the High Altitude Relight Test Facility (HARTF) [65,66]. HARTF successfully simulates the atmospheric environment in the combustor region from sea level to altitudes above 10,700 m. Diagnostic methods compatible with this facility include high-speed flame imaging, combustion emission analysis, laser sheet spray visualization, phase Doppler particle analysis (PDPA), and high-speed particle image velocimetry (HSPIV). The ISCAR (“Ignition under Sub-atmospheric Conditions Altitude Relight”) rig was designed and manufactured at the Engler-Bunte Institute of Karlsruhe Institute of Technology (KIT), where Majcherczyk et al. studied the impact of turbulence on spark ignition [67], and Martinos investigated ignition processes in aero-engine combustors under high-altitude conditions with and without effusion cooling [54]. Zhao’s [34,68] ignition experiments are conducted in the gas turbine model combustor facility at the Institute of Engineering Thermophysics (IET), Chinese Academy of Sciences (CAS) to investigate the influence of sub-atmospheric pressure under high-altitude conditions on relight performance, flame propagation modes, and the lean blowout dynamics of spray flames. The test rig can achieve conditions as low as 0.1 bar in pressure and 213 K in temperature.

The operating conditions of the test rigs summarized from the above literature are shown in

Table 1. The rough range of operating conditions of some test rigs.

Test Rig	Pressure Range	Temperature Range
SCR	Down to 0.2 bar [18]	243 K or less [18]
MERCATO	0.5 to 1 bar [66]	233 K to 473 K [66]
HARTF	Down to 0.276 bar [65]	Down to 227 K [65]
ISCAR	Down to 0.4 bar [54]	Down to 253 K [54]
IET	Down to 0.1 bar	Down to 213 K

. Rigs like Rolls-Royce’s SRC rig and ONERA’s MERCATO excel in optical diagnostics, providing high-resolution visualization of flame propagation, spray breakup, and two-phase flow interactions under simulated high-altitude conditions. These capabilities are essential for studying flame stability and ignition boundary dynamics in lean combustor designs. Facilities such as HARTF and ISCAR place greater emphasis on turbulence effects and particle-level interactions, utilizing advanced diagnostic techniques like PDPA and HSPIV to analyze ignition turbulence and flame kernel dynamics. The SRC rig operates at pressures as low as 0.2 bar and temperatures below 243 K, while the MERCATO rig covers a wider range with pressures from 0.5 to 1 bar and temperatures as low as 233 K. HARTF achieves pressures down to 0.276 bar and temperatures down to 227 K, whereas ISCAR operates at pressures of 0.4 bar and temperatures of 253 K. The IET rig from CAS enables relatively more extreme conditions, achieving pressures as low as 0.1 bar and temperatures down to 213 K. These high-altitude relight testing rigs not only provide valuable data for the design and optimization of aero-engines but also establish a foundation for addressing the challenges of more efficient and environmentally friendly combustion systems in future aviation technologies.

It is worth noting that under high-altitude conditions, the reduced air density and pressure are often accompanied by microgravity-like effects, which significantly affect flame propagation dynamics. Research has shown that in the absence of gravity, the lack of buoyancy leads to different flame behaviors. In microgravity, flames tend to become more spherical, and the transport of heat and mass relies solely on diffusion, affecting flame propagation dynamics [69]. Studies indicate that buoyancy effects in normal gravity can stabilize flames by producing vorticity that opposes flame wrinkling. In microgravity, the removal of this stabilizing mechanism results in increased flame wrinkling amplitude and flame speed [70]. These findings are highly relevant to high-altitude ignition scenarios, where similar low-gravity effects may influence ignition probabilities and flame stabilization mechanisms.

High-altitude ignition processes are fundamentally constrained by low pressure, temperature, and density, which influence fuel atomization, evaporation, and mixing with air, thereby influencing flame kernel generation and propagation. A critical aspect is the matching between the spatial distribution of fuel and the concentration field required for effective flame propagation, which significantly affects ignition performance and the trajectory of the flame kernel. The generation and propagation of flame kernels toward the CRZ are critical for ignition success, with key influencing factors including droplet size, turbulence intensity, and local equivalence ratio. The findings emphasize that optimizing combustor geometry, such as swirler configurations and igniter positioning, can improve fuel-air mixing and stabilize the flame. Increasing the overall FAR can partially mitigate the negative effects of low-temperature and low-pressure environments on ignition.

To expand the high-altitude ignition boundary, future research should prioritize improving fuel atomization through advanced atomizers or modified swirler designs to enhance droplet breakup and mixing efficiency. In addition, advanced ignition technologies, such as plasma-assisted or laser ignition, hold promise for reducing MIE requirements and increasing flame stability under extreme conditions, thereby further extending the ignition boundary.

3. Prediction Models of High-Altitude Relight

High-altitude relight prediction models are crucial for studying ignition probability and flame propagation in aero-engines under conditions of rarefied air, low pressure, and low temperatures. These models combine numerical simulations with experimental data to predict engine ignition performance under extreme conditions and provide theoretical support for optimizing ignition systems. With the continuous advancement of computational fluid dynamics (CFD) and turbulence combustion models, significant progress has been made in high-altitude relight prediction models in recent years.

3.1. Empirical Models

Initial high-altitude relight prediction primarily relied on empirical models, which used extensive experimental data, simplified assumptions, and empirical formulas to estimate the influence of key parameters on ignition boundaries. Ballal and Lefebvre’s classic ignition model simplified the fuel-air mixture and turbulence characteristics in the combustion chamber to estimate the MIE in relation to pressure, turbulence intensity, and fuel injection speed [71,72]. These empirical models were practical in the early design stages, particularly for preliminary assessments. However, they heavily relied on experimental data, limiting their applicability under extreme conditions, where they struggled to capture complex turbulence-combustion coupling phenomena.

To more accurately simulate the physical phenomena during ignition, researchers gradually transitioned to models based on physical and chemical mechanisms, which better explain flame propagation and ignition processes under different conditions. The characteristic time model proposed by Peters and Mellor [73,74] further optimized the description of ignition and flame propagation by introducing key combustion and fluid dynamics parameters. This model effectively considered the relationship between the characteristic time of flame propagation and the reaction time of the fuel-air mixture, laying the foundation for more complex turbulent combustion models.

3.2. Turbulent Flame Propagation Model and Numerical Computation

As the understanding of turbulent combustion processes advanced, researchers introduced turbulent flame propagation models to capture the complex turbulence effects during the generation, growth, and propagation of the flame kernel. Mastorakos [39] proposed a turbulence-based flame propagation model that analyzed turbulence effects on ignition processes, leading to more accurate predictions of ignition probability under high-altitude conditions. Direct Numerical Simulation (DNS) was used to simulate turbulent droplet-laden mixing layers with hydrocarbon fuels, incorporating detailed chemical reaction mechanisms to capture edge flame dynamics and spark-turbulence interactions. In this model, flame kernel generation is crucial for ignition. Turbulence enhances flame propagation but also increases the risk of flame kernel extinction. Ahmed and Mastorakos [75] conducted experimental and numerical studies on non-premixed bluff-body flames, exploring flame stabilization mechanisms and employing detailed combustion chemistry to model turbulent ignition processes. They found that the ignition probability of turbulent non-premixed bluff-body flames is significantly influenced by factors such as fuel and air velocities, mixing distribution, and turbulence intensity. The ignition location plays a critical role in determining the flame propagation direction. Swirl improves mixing but may lead to overly lean or rich mixtures in the CRZ, reducing ignition probability in this region.

With the advancement of computational capabilities, Large Eddy Simulation (LES) and DNS have emerged as the predominant methodologies for investigating high-altitude relight phenomena. LES is effective in capturing large-scale turbulence structures and providing detailed insights into flame propagation and the interactions between turbulence and combustion, while DNS solves the Navier-Stokes equations with high fidelity, simulating all turbulence scales throughout the flame propagation process, making it suited for studies involving small-scale geometries or simple configurations.

Barré et al. [76] investigated the influence of head spacing on flame propagation using LES, demonstrating good agreement between numerical and experimental results. Similarly, Boileau et al. [77] applied LES to simulate ignition processes in annular combustors, revealing that flame propagation speeds are significantly influenced by thermal expansion and head interactions, exceeding theoretical turbulent flame speeds. These studies underscore the capability of LES to capture complex flow and ignition phenomena, particularly in annular combustors with intricate flow structures. Eyssartier et al. [78] used LES to simulate ignition in a two-phase flow combustor, incorporating detailed two-phase interaction models with simplified chemistry for computational efficiency and proposed local ignition success criteria based on fuel droplet size, turbulence intensity, and spark energy to predict flame propagation and ignition reliability. Mesquita and Mastorakos [79] employed DNS to conduct a comprehensive analysis of the high-altitude relight process, demonstrating the profound impact of turbulence on flame kernel generation and expansion, particularly in complex low-pressure environments. Tang [80] developed a numerical model that integrates LES with a hybrid chemical reaction tabulation method to predict the probability of forced ignition in high-altitude turbulent non-premixed combustion (see Figure 11). The main innovation of Tang’s model lies in the introduction of a novel tabulation approach, which combines the flamelet-progress variable (FPVA) model with a homogeneous reaction model, allowing for a more precise representation of the transition from homogeneous reaction to diffusion-controlled flame behavior within the ignition kernel. In addition, the model incorporates the stochastic nature of turbulence and spark discharge, using multiple simulations to statistically estimate ignition probability, providing an efficient and reliable framework for the numerical prediction of high-altitude relight.

Although LES and DNS provide highly accurate results, their high computational cost limits their widespread application in engineering. To address this, researchers have developed RANS-LES hybrid models, which combine LES for simulating large-scale turbulence structures and RANS for modeling small-scale turbulence, significantly reducing computational costs while maintaining accuracy. The RANS-LES hybrid model strikes an effective balance between simulation accuracy and computational efficiency, making it a promising direction for future high-altitude relight prediction models. Among hybrid methods, Detached Eddy Simulation (DES) blends RANS and LES capabilities, effectively modeling near-wall flows with RANS and transitioning to LES for separated or large-scale turbulent regions. DES has been widely applied in numerous studies. However, its application to high-altitude ignition remains limited due to several factors. DES relies heavily on fine grid resolution for smooth RANS-LES transitions, which is challenging in complex ignition flows. In addition, its integration with detailed combustion models, including flame propagation and ignition dynamics, is underexplored, and its computational cost, while lower than LES, remains higher than traditional RANS-LES models. Despite these challenges, DES complements existing RANS-LES approaches by resolving large-scale turbulence with greater detail, offering opportunities for improving ignition modeling under extreme conditions. Continued development of DES and hybrid CFD methods holds potential for optimizing combustor performance in high-altitude relight scenarios.

The French research team developed the MIST (Model for Ignition STatistics), a statistical model designed to predict ignition probability in gas turbine combustors [81,82,83]. This model uses non-reactive flow field statistics to generate ignition probability maps, eliminating the need for extensive reactive flow simulations. It processes instantaneous non-reactive flow data to construct potential flame kernel trajectories, combining local turbulence intensity, flammability, and flow direction to predict ignition probability at various locations. Since the MIST only requires a single non-reactive flow simulation to produce a global ignition probability distribution, it significantly reduces computation time and cost, making it particularly well-suited for complex combustor geometries. In addition, this model has been validated across multiple combustion modes (such as premixed, non-premixed, and two-phase flows), providing an accurate and cost-effective prediction tool for ignition system design and optimization—an essential asset for ensuring reliable ignition in combustor design.

3.3. Flame Kernel Tracking and Improved Models

In high-altitude relight prediction models, flame kernel tracking has emerged as a widely adopted method due to its ability to evaluate ignition probability under cold flow field conditions. This approach monitors the generation and expansion of flame kernels, utilizing the Karlovitz number as a critical metric to assess whether a flame kernel will extinguish due to turbulence-induced stretching or successfully ignite the surrounding combustible mixture [4,78]. The Karlovitz number quantitatively describes the impact of turbulence on flame stability, with its calculation depending on local flow characteristics and mixture properties. By tracking the evolution of the flame kernel, researchers can predict whether it will propagate to regions of higher FAR and ultimately form a stable flame. This methodology has been validated in a range of canonical cases, such as bluff-body flames, counterflow turbulent flames, and spray flames, under controlled conditions.

One notable application of this method is the SPINTHIR code, developed by the University of Cambridge. This code has been employed by Rolls-Royce for predicting high-altitude ignition probabilities in low-emission aero-engines, demonstrating its practical relevance in engineering contexts [22]. The SPINTHIR model, as one of the pioneering frameworks in ignition prediction, simulates the trajectories of individual flame elements originating from a spark within generic flow fields containing droplets. Figure 12a illustrates the initial steps of this model as described in [23], where this process is repeated for different spark locations and spark shapes. The resulting statistics of ${\pi }_{ign}$ are then compared to assess the relative performance of the sparks and their placement. Here, ${\pi }_{ign}$ is the ignition progress factor, which is defined as the ratio of the number of cells in a burnt state to the total number of cells. The detailed steps of the model are as follows:

• The fluid domain is divided into a regular grid of cells, with each cell can have two states: cold (unburnt) or burnt. All cells start in the cold state.
• The simulation begins by defining a spark volume representing the ignition source, which is based on experimental observations. All grid cells overlapping the spark volume are switched to the burnt state, releasing a “flame particle” at their center. The size and shape of the spark volume are key parameters of the ignition system.
• The particle position in direction $i$ evolves according to the stochastic differential equation:

  $$d{X}_{p,i}=U_{p,i}dt$$

  (2)

  where $U_{p,i}$ is the particle velocity in direction $i.$ A flame particle is tracked using a Langevin model within the cold CFD field. Each particle is assigned a velocity and mixture fraction that consists of both mean and random components derived from the CFD solution. The $U_{p,i}$ consists of a linear drift towards the local Favre averaged velocity of the flow and an added isotropic diffusion term:

  $$d{U}_{p,i}=-\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{4}}{C}_0\right){\omega }_p\left(U_{p,i}-{\tilde{U}}_i\right)dt+{\left(C_0{ϵ}_{p}dt\right)}^{1/2}{N}_{p,i}$$

  (3)

  where $C_0$ is a constant with a value of 2.0 [84], ${\omega }_p$ is the inverse turbulent timescale at the particle location, ${\tilde{U}}_i$ is the local Favre averaged velocity in direction $i$, ${ϵ}_p$ is the turbulent dissipation rate at the particle location, and $N_{p,i}$ is a random number following a standard normal distribution (mean of 0, variance of 1), assumed to be independent for each particle. The detailed calculation formulas for these parameters are provided in Appendix A. The particle mixture fraction ${\xi }_p$ is defined as:

  $$d{\xi }_p=-{\displaystyle \frac{1}{2}}{C}_{\xi }\omega \left({\xi }_p-\stackrel{\mathrm{~}}{\xi }\right)dt+(1-{\xi }_p){\displaystyle \frac{{\overline{\Gamma }}_m}{\overline{\rho }}}dt$$

  (4)

  where $C_{\xi }$ is a constant with a value of 2.0 [84], ${\xi }_p$ is the particle mixture fraction, $\stackrel{\mathrm{~}}{\xi }$ is the local Favre averaged mixture fraction, $\rho$ is the local flow density, and ${\Gamma }_m$ is the mass source term due to evaporation. As the particle moves along its trajectory, it may extinguish based on a criterion determined by the Karlovitz number, which depends on the turbulence properties and equivalence ratio, as described below.

  $${Ka}_p=0.157(\nu {\displaystyle \frac{(u_p^{\prime }{)}^3}{L_{turb,p}}}{)}^{1/2}{\displaystyle \frac{1}{S_{L,p}^2}}$$

  (5)

  where $\nu$ is the mixture kinematic viscosity, $u_p^{\prime }$ is the standard deviation of $u_p$, $L_{turb,p}$ is the integral scale of turbulent length, and $S_{L,p}$ is the laminar flame speed. Once extinguished, the particle is removed from further computation.
• When a particle visits a grid cell in the cold state, that cell is switched to the burnt state, releasing a new flame particle at its center with its own velocity and mixture fraction, governed by the same stochastic equations.
• During the simulation, the proportion of cells in the burnt state relative to the total number of cells, referred to as the ignited volume fraction, is calculated over time. This proportion, denoted by the symbol ${\pi }_{ign}$, is called the “ignition progress factor” and serves as the primary raw output of the model.
• At the end of each simulation, ${\pi }_{ign}$ is compared to a critical threshold ${\pi }_{crit}$. If ${\pi }_{ign}$ > ${\pi }_{crit}$, the ignition event is deemed successful; otherwise, it is considered a failure. The process is repeated for various spark locations to generate a spatial map of ignition probability, which can be compared with experimental data for validation.

The nomenclature table provides the definitions of key symbols.

Building on the SPINTHIR model, subsequent researchers have gradually introduced various extensions and improvements to meet the growing demands of practical applications and more complex combustion environments. The original SPINTHIR model assumed that as soon as a burning particle enters an incombustible cell, it extinguishes. This is equivalent to infinitely fast heat losses, resulting in limited flame particle propagation and prematurely terminating the ignition simulation. However, hot gas can also lead to ignition even when no burning flame is present. Soworka [85] introduced the concept of the “hot gas state” into the model (see Figure 12b): after encountering an incombustible cell, the particle first switches to the hot gas state and continues its movement and ignition capability for a certain period, referred to as the extinction time $t_{ext}$. After $t_{ext}$, the particle transitions to the extinguished state and is excluded from further computations. This adjustment mitigates the overly strict distinction between incombustible and combustible cells, providing a more realistic representation of flame propagation in complex environments.

In recent years, researchers have further developed the SPINTHIR model to predict flame stabilization in annular combustors. De Oliveira et al. [1], investigated the effect of spray’s poly-disperse characteristics, considering fuel fluctuations in the context of the low-order ignition model SPINTHIR. Their study focused on a Rolls-Royce developmental RQL gas turbine combustor under relight conditions, which better captures uncertainties in flame propagation while enhancing computational efficiency.

Mesquita [86] introduced Flame Generated Turbulent Intensity (FGTI) and imposed turbulent flame speed on flame particles to improve the numerical prediction of the flame light-round process in premixed annular combustors. In the simulation of the light-round transient, Ciardiello [87] further refined the light-round transient simulation by incorporating the effects of dilatation and a stochastic component in the quenching criterion, which captured the bending behavior of turbulent flame speed with turbulent intensity more accurately. Tao et al. [88], based on the SPINTHIR model, incorporated a kd-tree algorithm into the stochastic particle tracking ignition model (SIMSPaT) to improve the simulation of flame kernel propagation within complex annular combustor geometries. By directly associating flame particles with the cold flow field, their approach eliminates interpolation errors, thereby significantly enhancing the accuracy of ignition predictions. The model simulation results of the light-round process and the comparison of the tests are shown in Figure 13. These innovations significantly enhance the applicability of the SPINTHIR model in simulating complex multi-chamber flame stabilization processes, providing new tools for analyzing and optimizing annular combustor performance.

In summary, the SPINTHIR model has laid a significant theoretical foundation for combustion and ignition prediction, particularly in providing a framework for low-order modeling of complex flame propagation processes. Subsequent technical extensions and validations based on this model have enhanced its ability to address multifaceted challenges, such as fuel variability and turbulent flame dynamics, driving the field toward more comprehensive and accurate predictions. Future research is likely to focus on developing more precise prediction models within the SPINTHIR framework, potentially integrating advanced techniques such as machine learning or high-fidelity simulations. These advancements will further refine the model’s capability to simulate complex combustion phenomena and expand its application in modern combustion systems.

4. Conclusions and Future Research

4.1. Conclusions

This review summarizes the high-altitude relight characteristics of aero-engines and the advancements in related prediction models. The main conclusions are as follows:

• Under high-altitude conditions, reduced air pressure, temperature, and density significantly increase ignition difficulty, affecting fuel evaporation, flame propagation, and combustion stability. Addressing these challenges requires a deep understanding of the underlying physical processes and the development of accurate prediction models. High-altitude relight test rigs play a vital role in simulating real high-altitude conditions, providing critical experimental data for model validation and technological advancements. Numerical methods, including LES and DNS, offer detailed insights into turbulent structures and flame kernel behavior but are computationally expensive. Hybrid RANS-LES models, including DES, which balance accuracy and efficiency, represent a promising direction for future prediction models.
• Existing models have evolved from empirical and semi-empirical models to advanced physics-based and numerical methods. Empirical models, while effective during initial design stages, struggle to capture the complex ignition dynamics of high-altitude conditions. Advanced models, such as SPINTHIR and flame kernel tracking, have made significant progress in predicting ignition by better describing flame kernel formation, turbulent flame propagation, and the role of turbulent mixing. However, these models still rely on manually set parameters and exhibit limitations in modeling flame kernel generation under complex flow conditions.

4.2. Future Research

To further advance high-altitude relight research, future work could prioritize two critical areas: the development of advanced numerical simulation methods and the exploration of emerging ignition technologies.

• The dynamic interaction between flame kernel generation, propagation, and turbulence remains a significant challenge in current high-altitude ignition prediction models. Current research primarily focuses on the variation of ignition performance with increasing altitude, the mechanisms and pathways of flame propagation, and trajectory tracking algorithms. Existing studies often rely on a combination of low-cost numerical simulations and theoretical modeling to estimate ignition probabilities in combustors. However, the inherent complexity of turbulent flame ignition significantly limits the accuracy and refinement of these models. Multi-scale modeling approaches, which integrate LES with fine-scale turbulence modeling, can offer a comprehensive understanding of flame kernel behavior, spanning from its microscopic initiation to macroscopic propagation. In addition, exploring transient turbulence modeling can further uncover the impact of unsteady turbulence on flame kernel lifespan and propagation pathways, enabling the optimization of turbulent flame propagation models. Such advancements are expected to improve the predictive accuracy of ignition probability models and provide more reliable solutions for high-altitude ignition challenges. Future research should aim to develop more precise semi-empirical predictive models by incorporating dynamic parameters, such as turbulence scale variations and local equivalence ratio non-uniformity, to better capture the processes of flame kernel formation and propagation.
• Emerging ignition technologies, such as plasma-assisted and laser ignition, have shown potential to extend ignition limits and improve efficiency under extreme high-altitude conditions. Future research could explore combining these technologies with traditional spark ignition systems to achieve synergistic effects. For example, plasma-assisted ignition could complement conventional methods by enhancing kernel stability and reducing ignition energy requirements. Novel approaches, such as microwave-assisted ignition, could provide additional advantages in challenging environments by enabling non-intrusive energy deposition and improving ignition reliability.

In conclusion, while significant progress has been made in understanding and modeling high-altitude relight, continued efforts are needed to optimize physical models, strengthen experimental-numerical synergies, and incorporate new ignition technologies. These advancements are expected to enhance combustor design, improve fuel injection systems, and ultimately boost the ignition performance and operational efficiency of aero-engines under high-altitude conditions, providing vital technical support for the safety and reliability of future aviation.