Power Coefficient for Large Wind Turbines Considering Wind Gradient Along Height
Abstract
1. Introduction
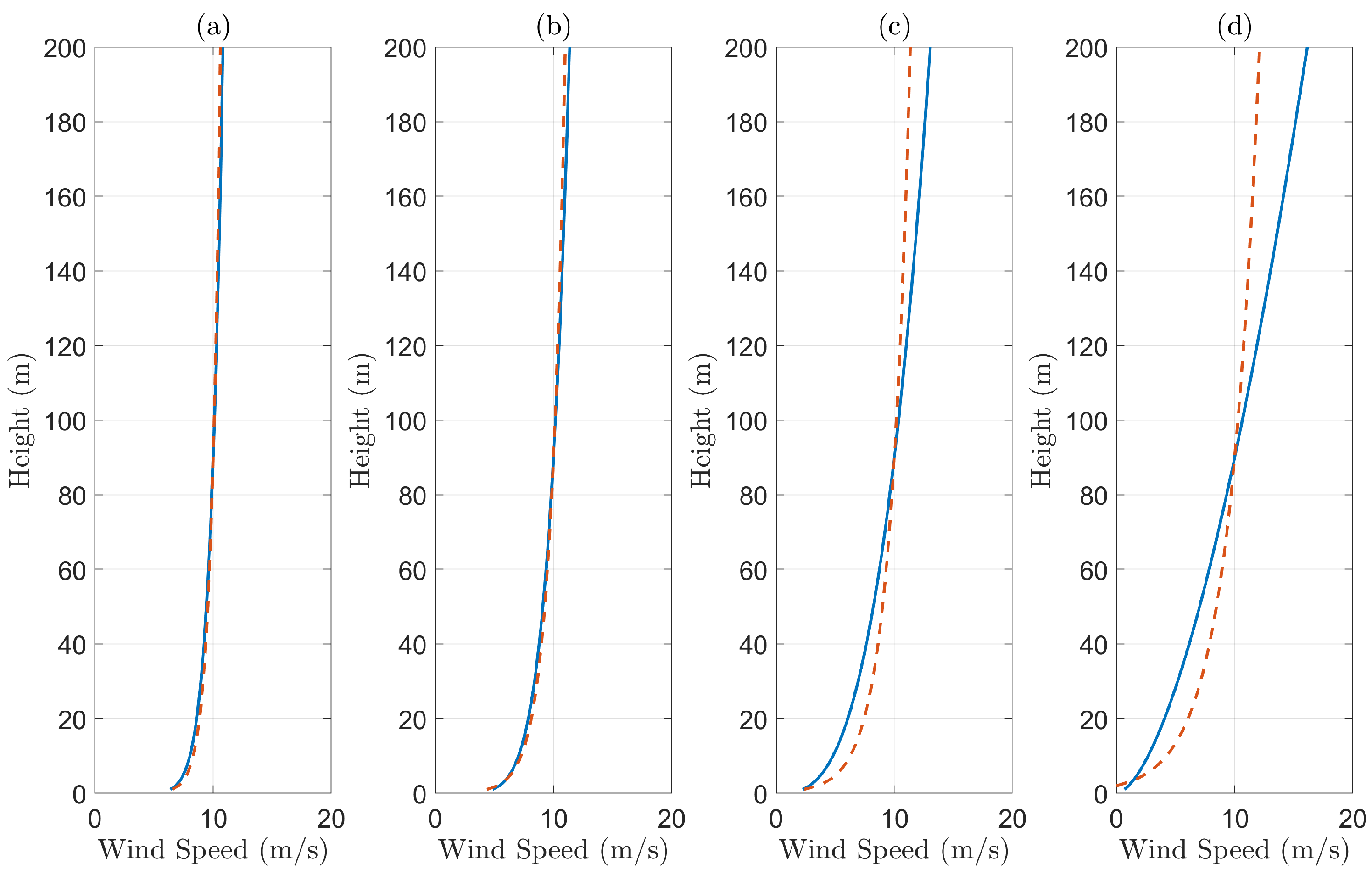
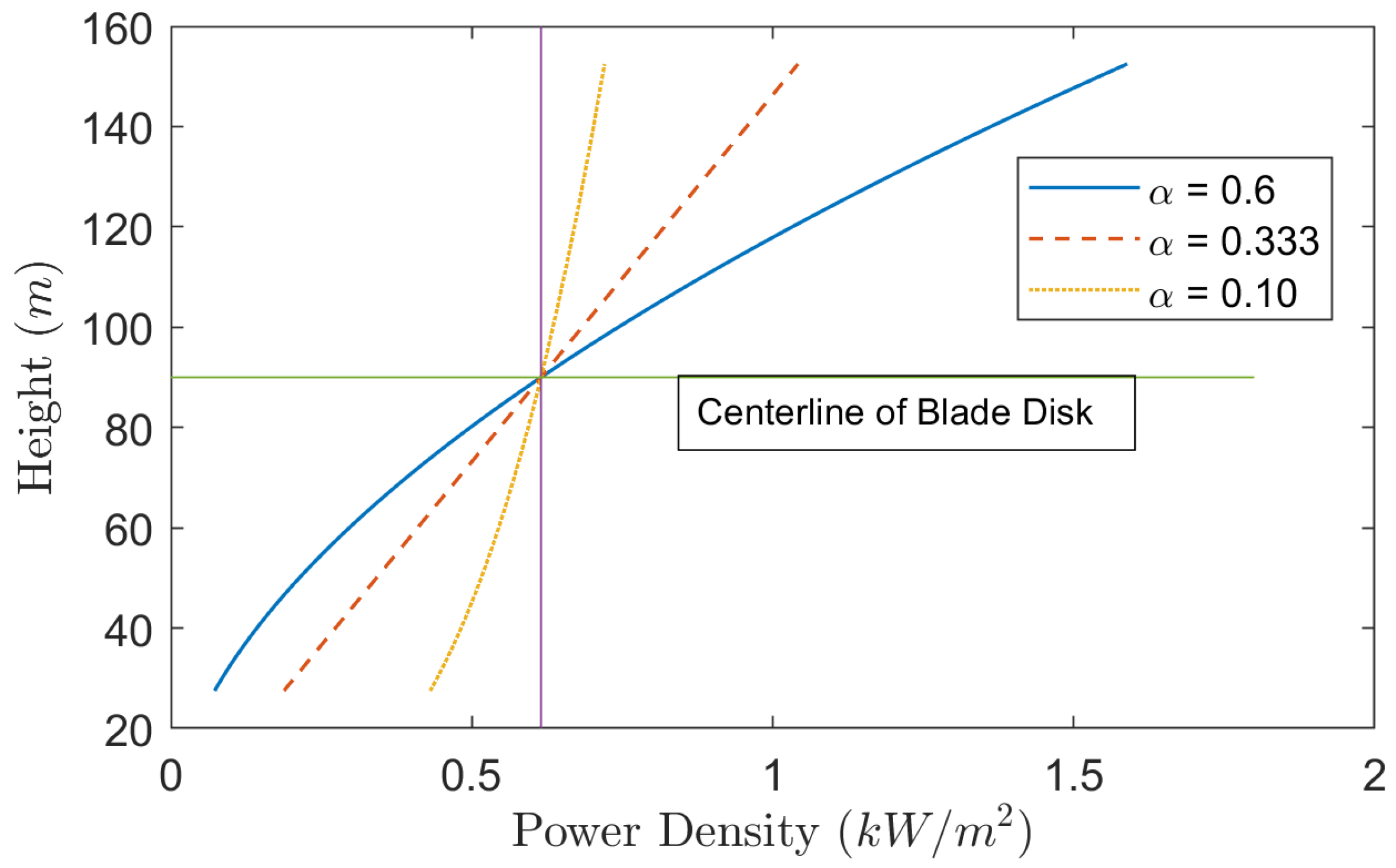
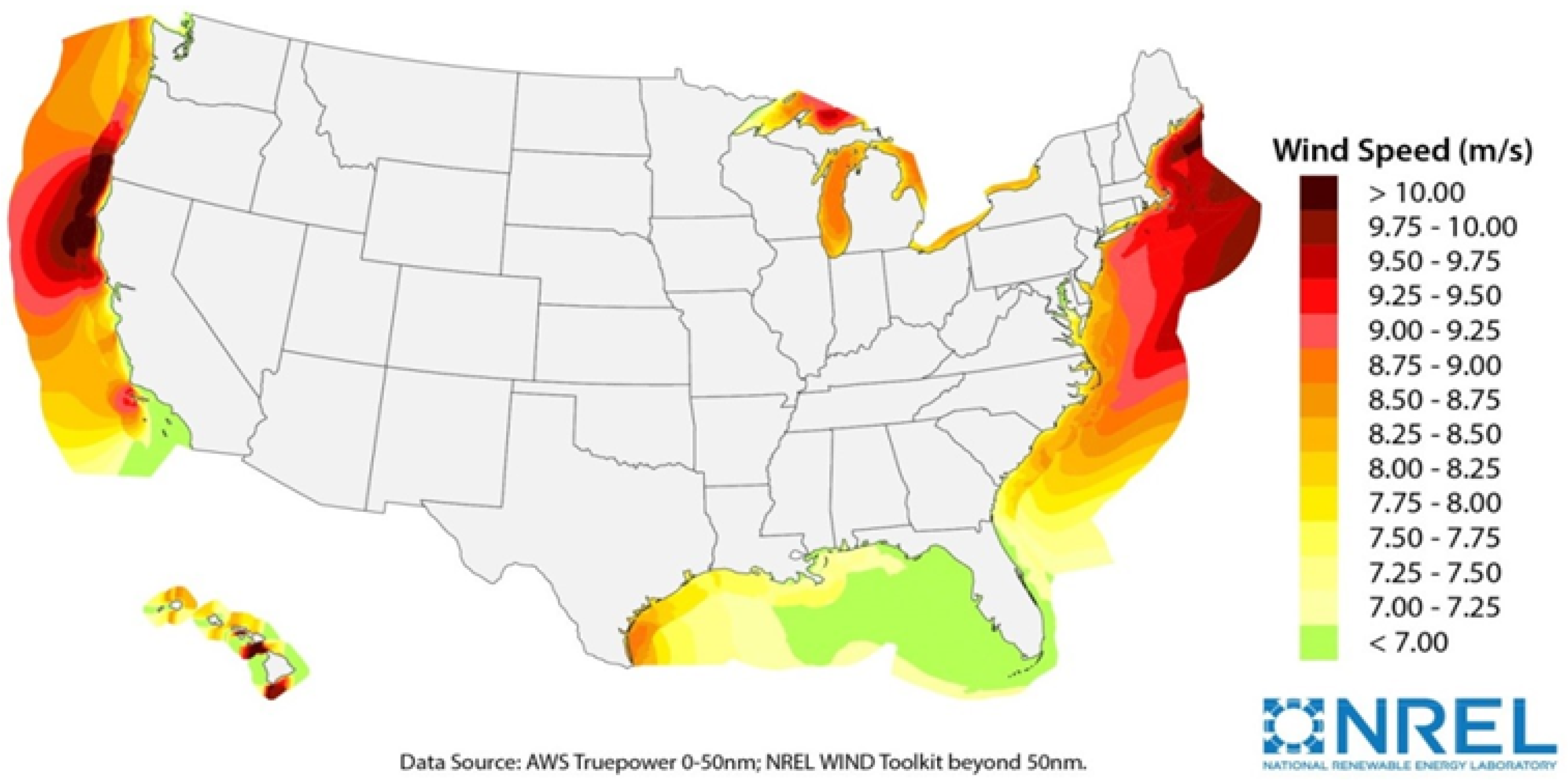
2. Wind Gradient
- Power Law Exponent Model: The power law exponent model [3,4,14] is an empirical equation which describes the wind speed in relation to a reference speed at a known altitude:where is the wind speed at a reference height , which is usually taken to be 10 m, and is the Hellmann exponent. The Hellmann exponent depends on the location, topology of the terrain, and atmospheric stability, referenced as turbulent air or neutral air. Table 1 [4,15] shows some examples of the Hellmann exponent.Table 1. Hellmann exponent examples.
Location Unstable air above open water 0.06 Neutral air above open water 0.10 Unstable air above flat, open coast 0.11 Neutral air above flat, open coast 0.16 Stable air above open water 0.27 Unstable air above human-inhibited areas 0.27 Neutral air above human-inhibited area 0.34 Stable air above flat, open coast 0.40 Stable air above human-inhibited areas 0.60 - Logarithmic Model: A physical model of wind gradients is given by the logarithmic model [16,17,18]:where is the wind speed at the reference altitude , is the roughness length or roughness height, is the Karman constant, and is the friction velocity. Atmospheric stability is included in this model using the function . In a neutral atmosphere, the above equation simplifies toTypical values of have been estimated from experimental observations [5] to be in the range of 0.0001–2 m and above, where a higher value of indicates more obstructions to wind flow from, for example, trees and buildings. As in the case of the power law exponent model, the reference height is usually taken to be 10 m. Table 2 [19] shows some typical values of the roughness length .
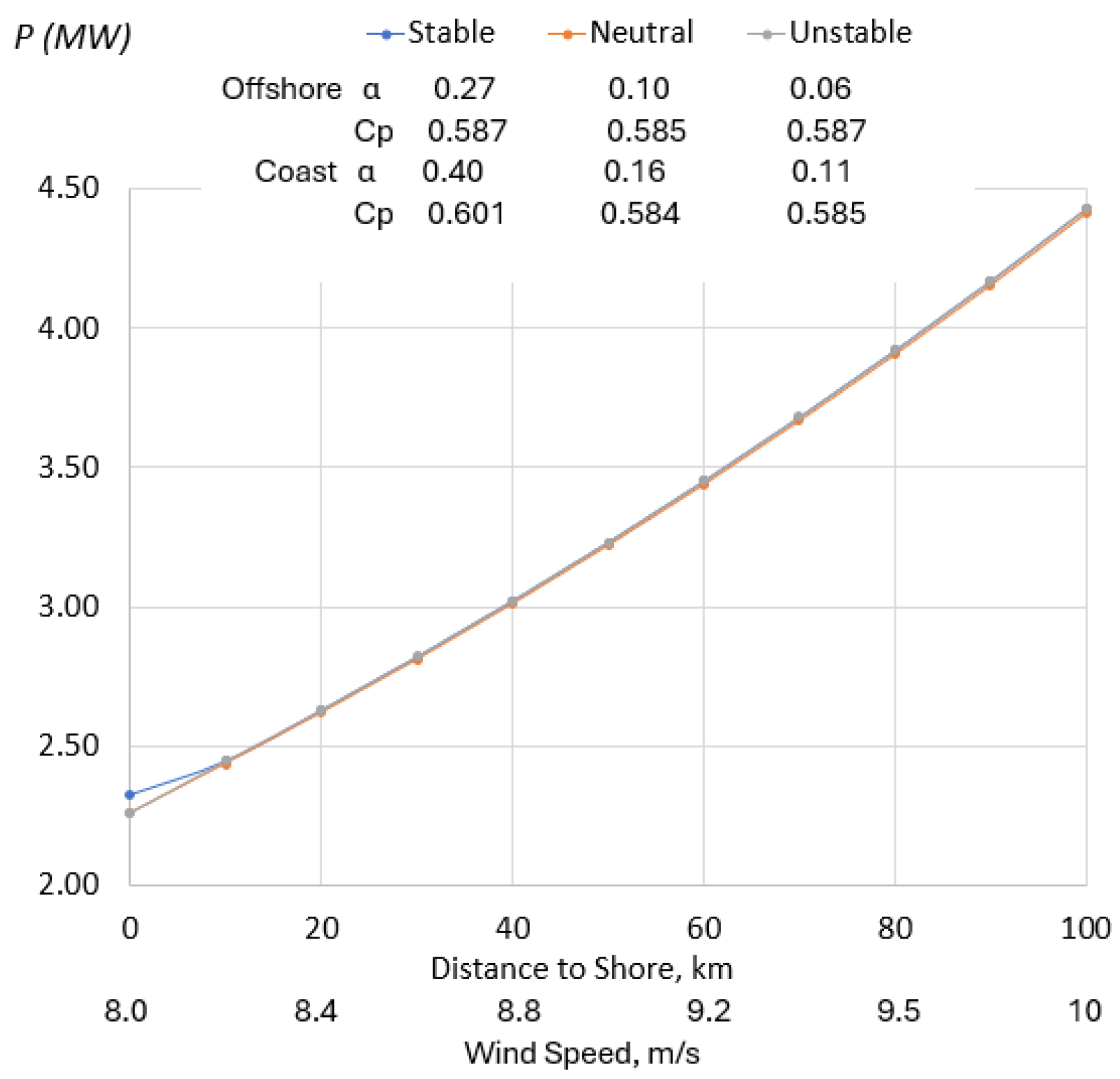
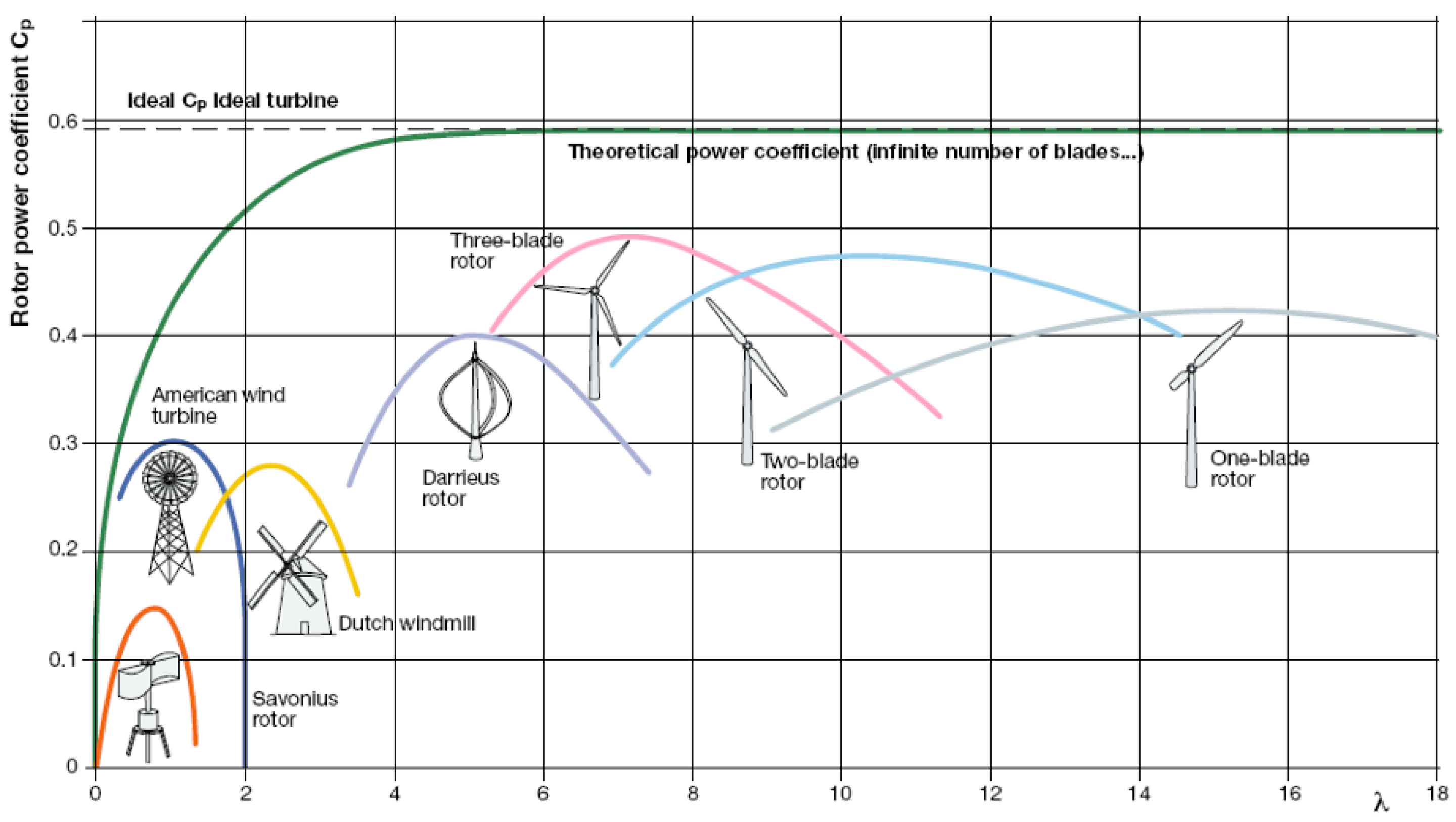
3. Power Coefficient for Large Wind Turbines
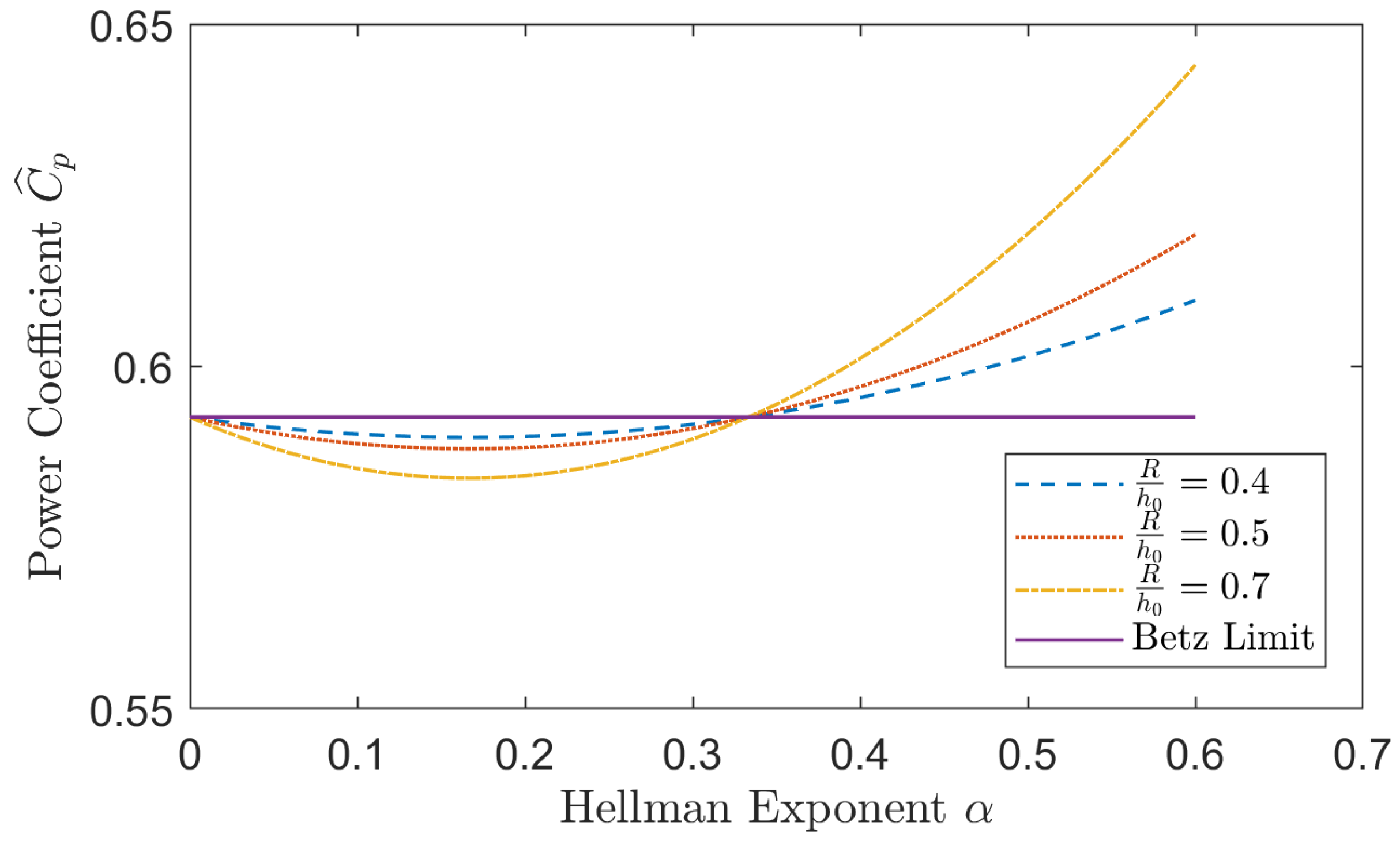
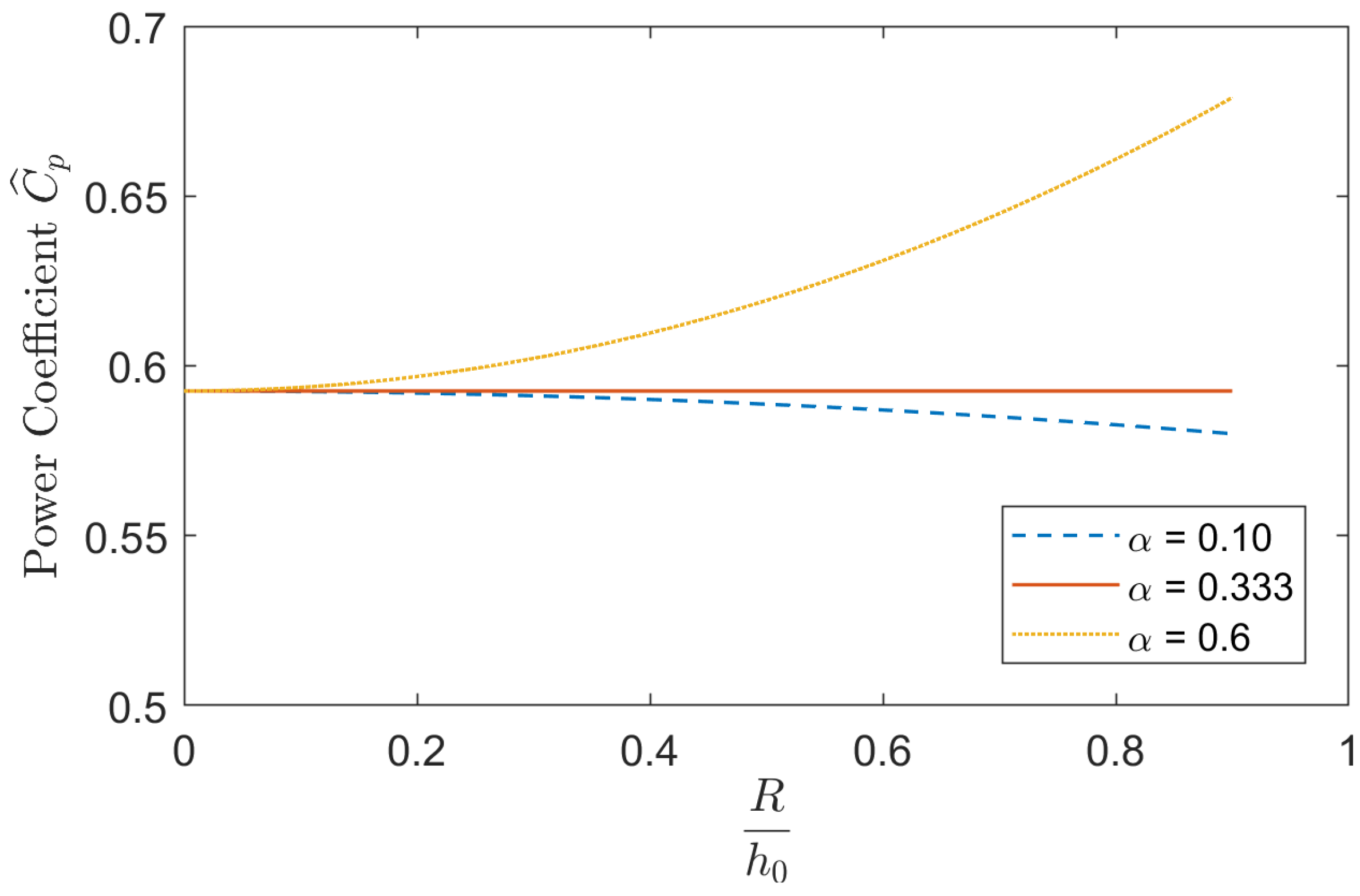
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Renewable Energy Agency. Available online: https://www.irena.org/Energy-Transition/Technology/Wind-energy (accessed on 6 July 2024).
- US Department of Energy. Available online: https://www.energy.gov/eere/articles/wind-turbines-bigger-better (accessed on 17 June 2024).
- Harrison, R.; Hau, E.; Snel, H. Large Wind Turbines: Design and Economics; John Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kaltschmitt, M.; Streicher, W.; Wiese, A. Renewable Energy Technology, Economics and Environment; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: London, UK, 1997. [Google Scholar]
- Li, Q.; Zhi, L.; Hu, F. Boundary Layer Wind Structure from Observations on a 325m Tower. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 818–832. [Google Scholar] [CrossRef]
- Betz, A. Das Maximum der theoretischen Ausnutzung des Windes durch Windmotoren. Z. Für Das Gesamte Turbinenwesen 1920, 26, 307–309. [Google Scholar]
- Manwell, J.F.; Branlard, E.; McGowan, J.G.; Ram, B. Wind Energy Explained: On Land and Offshore, 3rd ed.; Wiley: Hoboken, NJ, USA, 2024. [Google Scholar]
- Vennel, R. Exceeding the Betz limit with tidal turbines. Renew. Energy 2013, 55, 277–285. [Google Scholar] [CrossRef]
- Liew, J.; Heck, K.S.; Howland, M.F. Unified momentum model for rotor aerodynamics across operating regimes. Nat. Commun. 2024, 15, 6658. [Google Scholar] [CrossRef] [PubMed]
- Madsen, H.A.; Larsen, T.J.; Pirrung, G.R.; Li, A.; Zahle, F. Implementation of the blade element momentum model on a polar grid and its aeroelastic load impact. Wind Energ. Sci. 2020, 5, 1–27. [Google Scholar] [CrossRef]
- Moriarty, P.J.; Hansen, A.C. Aerodyn Theory Manual. 2005. Available online: https://www.nrel.gov/docs/fy05osti/36881.pdf (accessed on 8 December 2024).
- Chen, J.S.; Chen, Z.; Biswas, S.; Miau, J.; Hsieh, C. Torque and Power Coefficients of a Vertical Axis Wind Turbine With Optimal Pitch Control. In Proceedings of the ASME 2010 Power Conference, Chicago, IL, USA, 13–15 July 2010; pp. 655–662. [Google Scholar] [CrossRef]
- Heier, S. Grid Integration of Wind Energy Conversion Systems; Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-470-86899-7. [Google Scholar]
- Hsu, S.A. Coastal Meteorology; Academic Press: London, UK, 1988. [Google Scholar]
- Sukumar, P.; Selig, M.S. Dynamic Soaring of Sailplanes over Open Fields. J. Aircr. 2013, 50, 1420–1430. [Google Scholar] [CrossRef]
- van den Berg, G.P. Wind gradient statistics up to 200 m altitude over flat ground. In Proceedings of the First International Meeting on Wind Turbine Noise: Perspectives for Control, Berlin, Germany, 17–18 October 2005. [Google Scholar]
- Houshuo, J.H.; James, B.; Edson, J.B. Characterizing marine atmospheric boundary layer to support offshore wind energy research. J. Physics Conf. Ser. 2020, 1452, 012027. [Google Scholar]
- Wieringa, J. Updating the Davenport Roughness Classification. J. Wind. Eng. Ind. Aerodyn. 1992, 41, 357–368. [Google Scholar] [CrossRef]
- Li, C.; Liu, L.; Lu, X.; Stevens, R.J.A.M. Analytical model of fully developed wind farms in conventionally neutral atmospheric boundary layers. J. Fluid Mech. 2022, 948, A43. [Google Scholar] [CrossRef]
- Wen-Ring, H.; Hong-Biao, Z.; Zu-Rong, D. Computational Study of the Aerodynamics of Sails in a Twisted Wind. J. Shanhgai Jiaotong Univ. 2008, 42, 1900–1903. [Google Scholar]
- Mortimer, I.A. A Comparison of Downwind Sail Coefficients from Tests in Diffeent Wind Tunnels. Ocean. Eng. 2014, 90, 62–71. [Google Scholar] [CrossRef]
- Bower, G.C. Boundary Layer Dynamic Soaring for Autonomous Aircraft Design and Validation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2011. [Google Scholar]
- Deittert, M.; Richards, A.; Toomer, C.A.; Pipe, A. Engineless Unmanned Aerial Vehicle Propulsion dy Dynamic Soaring. J. Guid. Control. Dyn. 2009, 32, 1446–1457. [Google Scholar] [CrossRef]
- Sachs, G.; Bussotti, P. Application of Optimal Control Theory to Dynamic Soaring of Seabirds. In Variational Analysis and Applications; Giannessi, F., Maugeri, A., Eds.; Springer: New York, NY, USA, 2005; Volume 79, pp. 975–994. [Google Scholar]
- Holmes, D. Wind Loading of Structures; Spon Press: New York, NY, USA, 2001. [Google Scholar]
- Li, C.; Wang, H.; Sun, P. Study on the Influence of Gradient Wind on the Aerodynamic Characteristics of a Two-Element Wingsail for Ship-Assisted Propulsion. J. Mar. Sci. Eng. 2023, 11, 134. [Google Scholar] [CrossRef]
- Suemoto, H.; Hara, N.; Nihei, Y.; Konishi, K. Experimental Testing on Blade Load Mitigation of wind Turbines with Individual Blade Pitch Control under Wind Shear. In Proceedings of the IEEE 4th International Conference on Advanced Robotics and Mechatronics, Toyonaka, Japan, 3–5 July 2019. [Google Scholar] [CrossRef]
- Kotur, D.; Durišić, Z. Individual Pitch Control for Wind Turbine Load Reduction Recognizing Atmospheric Stability. In Proceedings of the Wind Europe Summit 2016, Hamburg, Germany, 27–30 September 2016. [Google Scholar]
- Offshore Wind. Available online: https://atb-archive.nrel.gov/electricity/2019/index.html?t=ow&s=ov (accessed on 14 January 2025).
- Jung, C.; Schindler, D. The Properties of the Global Wind Turbine Fleet. Renew. Sustain. Energy Rev. 2023, 186, 113667. [Google Scholar] [CrossRef]
- Ebrahimpour, M.; Shafaghat, R.; Alamian, R.; Safdari, M.S. Numerical Investigation of the Savonius Vertical Axis Wind Turbine and Evaluation of the Effect of the Overlap Parameter in Both Horizontal and Vertical Directions on Its Performance. Symmetry 2019, 11, 821. [Google Scholar] [CrossRef]
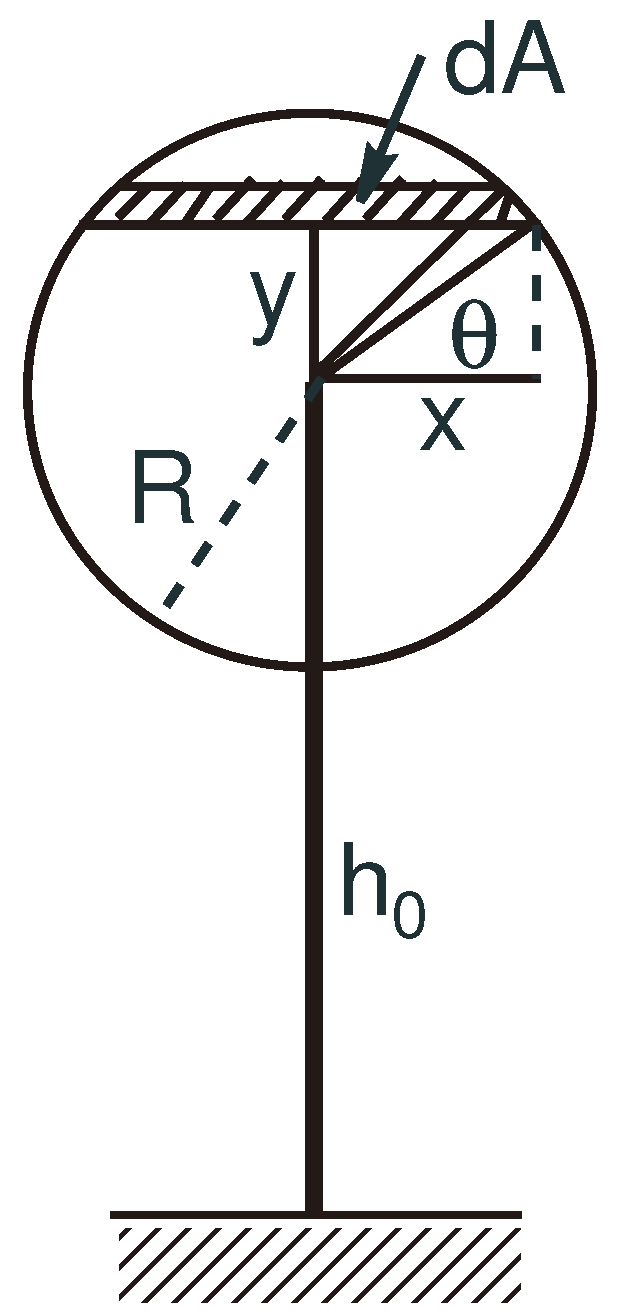
| Terrain | |
|---|---|
| Open sea | 0.0002 |
| Open mud flat, snow, no vegetation, no obstacles | 0.005 |
| Open flat terrain, grass, few obstacles | 0.03 |
| Low crop, some large obstacles | 0.10 |
| High crop, scattered obstacles | 0.25 |
| Parkland, bushes, many obstacles | 0.5 |
| Large obstacles, forests | 1.0 |
| City with high-rise buildings | >2.0 |
| Terms in the Infinite Series (Equation (15)) | Power Coefficient | |
|---|---|---|
| Up to second-degree terms | 0.64403 | |
| Up to fourth-degree terms | 0.64428 | |
| Up to sixth-degree terms | 0.64429 | |
| Power coefficient based on Equation (10) | 0.64430 | |
| Betz limit | 0.59259 | |
| Up to second-degree terms | 0.58509 | |
| Up to fourth-degree terms | 0.58440 | |
| Up to sixth-degree terms | 0.58434 | |
| Power coefficient based on Equation (10) | 0.58424 | |
| Betz limit | 0.59259 |
| Average Power Density (kW/m2) | Total Power (MW) | |||||
|---|---|---|---|---|---|---|
| Hellmann Exponent | Upper Half of Rotor Disk | Lower Half of Rotor Disk | Hub | Total Power Available in Rotor Disk | Maximum Extractible (This Paper) | Maximum Extractible (Betz Limit) |
| 0.6 | 0.993 | 0.344 | 0.615 | 8.2057 | 5.2845 | 4.4679 |
| 0.796 | 0.433 | 0.615 | 7.5472 | 4.4679 | 4.4679 | |
| 0.663 | 0.549 | 0.615 | 7.4408 | 4.3536 | 4.4679 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, S.; Chen, J.S.-J. Power Coefficient for Large Wind Turbines Considering Wind Gradient Along Height. Energies 2025, 18, 740. https://doi.org/10.3390/en18030740
Biswas S, Chen JS-J. Power Coefficient for Large Wind Turbines Considering Wind Gradient Along Height. Energies. 2025; 18(3):740. https://doi.org/10.3390/en18030740
Chicago/Turabian StyleBiswas, Saroj, and Jim Shih-Jiun Chen. 2025. "Power Coefficient for Large Wind Turbines Considering Wind Gradient Along Height" Energies 18, no. 3: 740. https://doi.org/10.3390/en18030740
APA StyleBiswas, S., & Chen, J. S.-J. (2025). Power Coefficient for Large Wind Turbines Considering Wind Gradient Along Height. Energies, 18(3), 740. https://doi.org/10.3390/en18030740








