Investigations on the Aerodynamic Interactions Between Turbine and Diffuser System by Employing the Kriging Method
Abstract
1. Introduction
2. Simulation and Test
2.1. Geometric Models and Numerical Simulation Methods
2.2. Test Method
3. The Flow Field in Diffuser Changes with the Operational Conditions
3.1. Flow Field in the Last-Stage Turbine
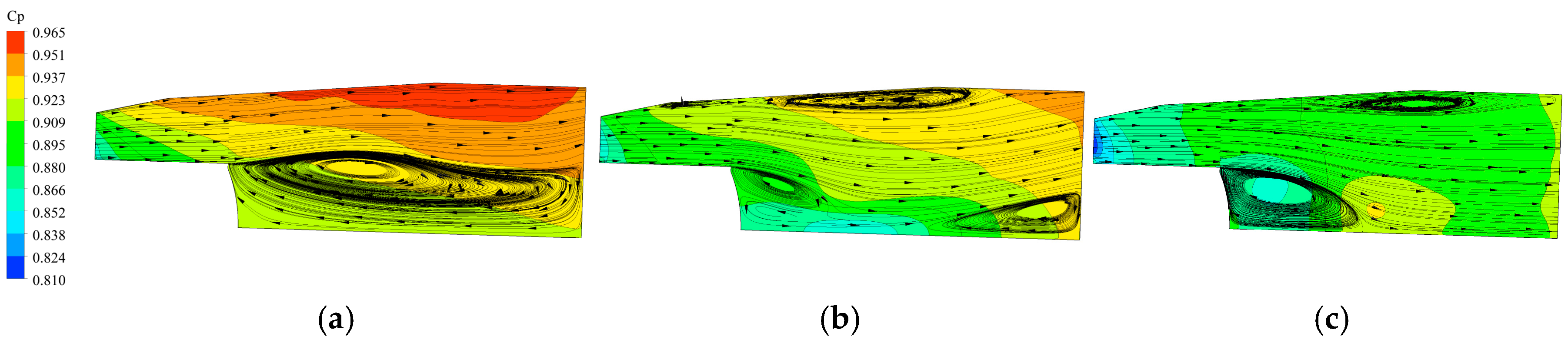
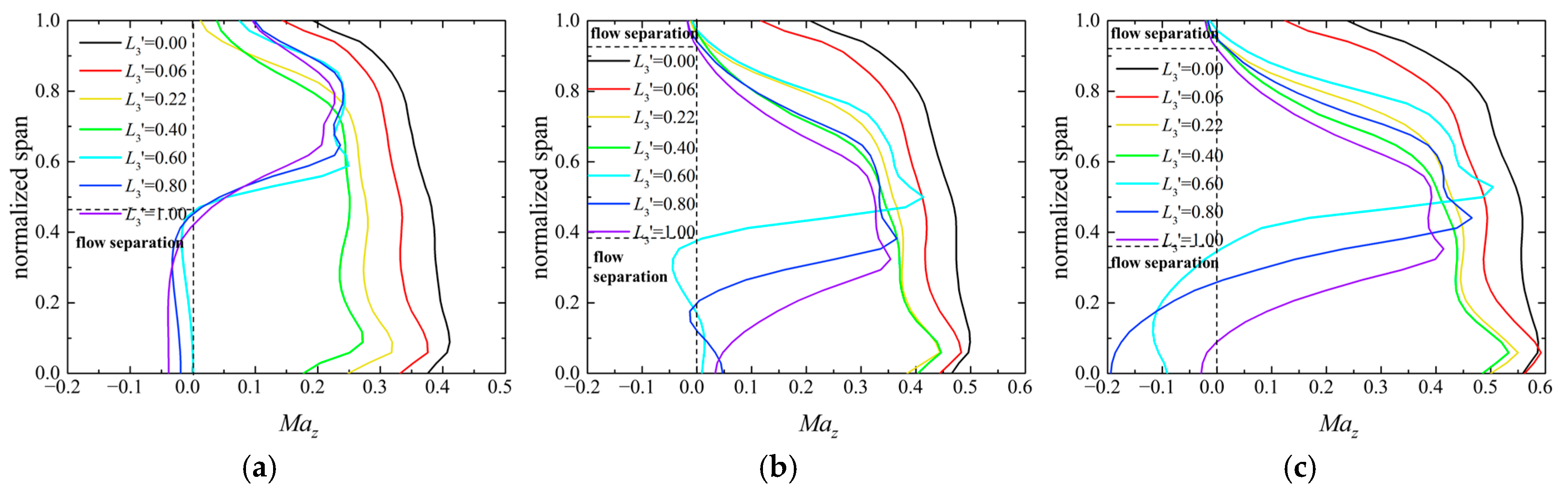
3.2. Flow Field in the Exhaust Diffuser
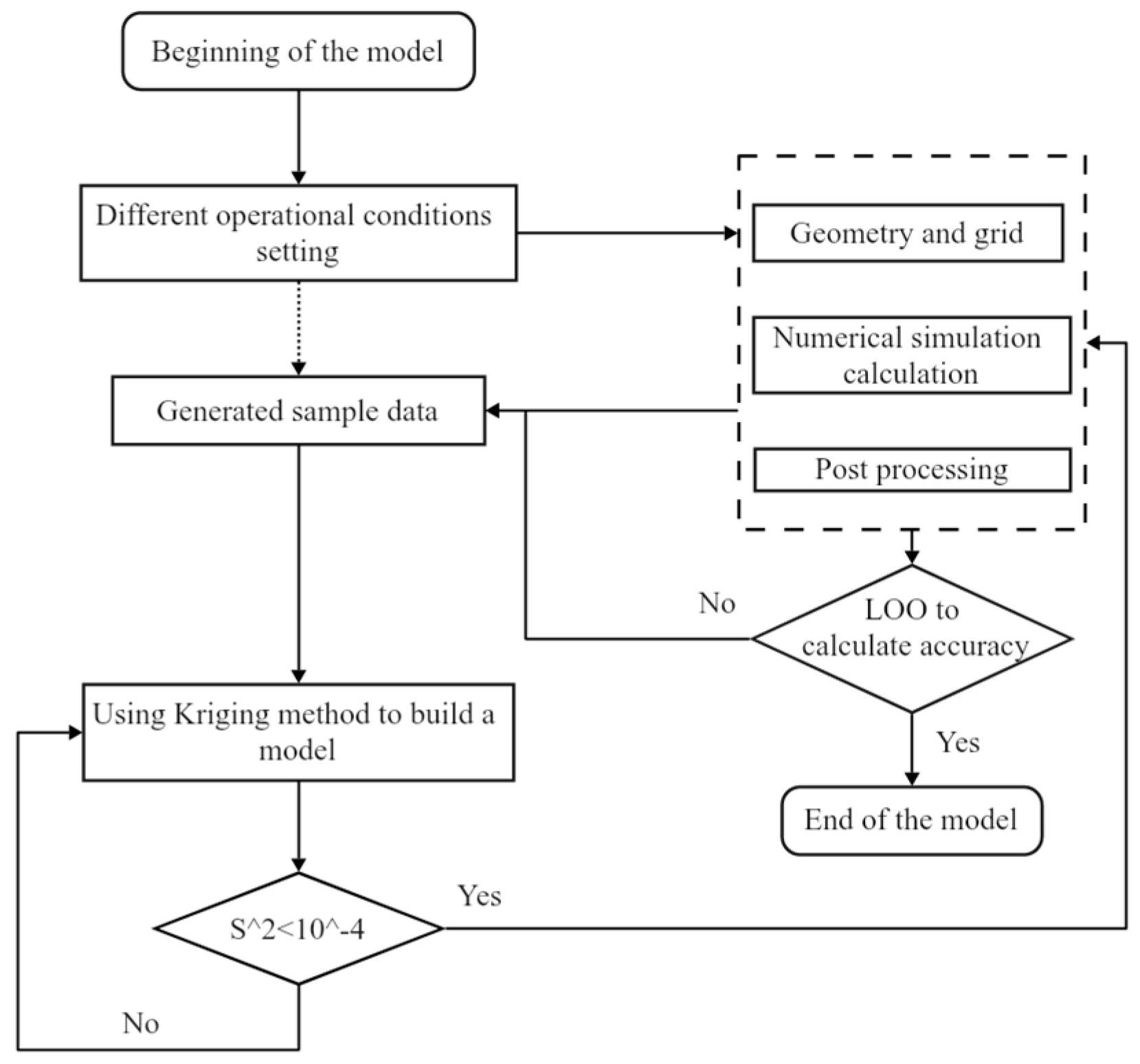
4. The Process of the Kriging Surrogate Model
5. The Reliability and Applications of the Model
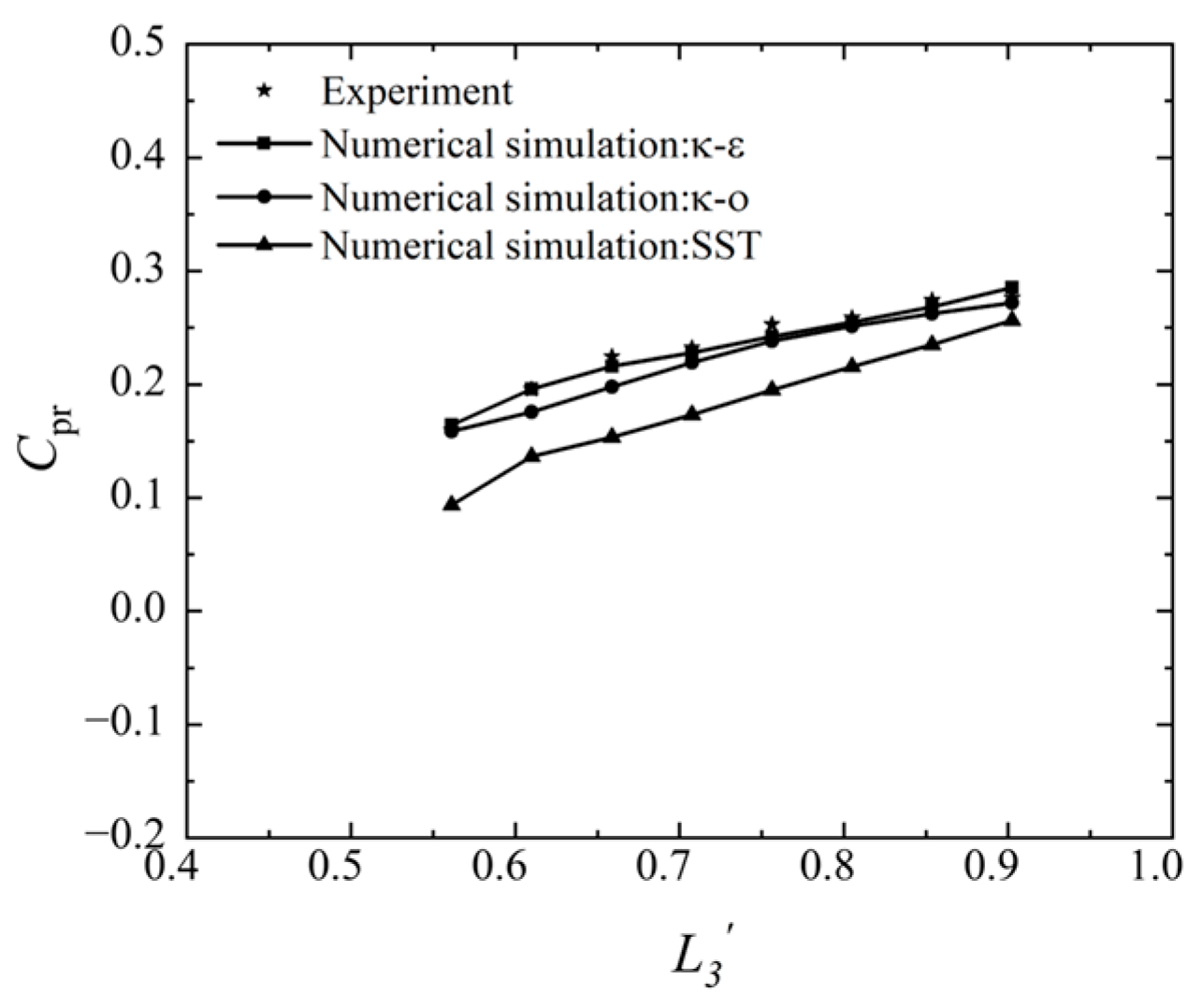
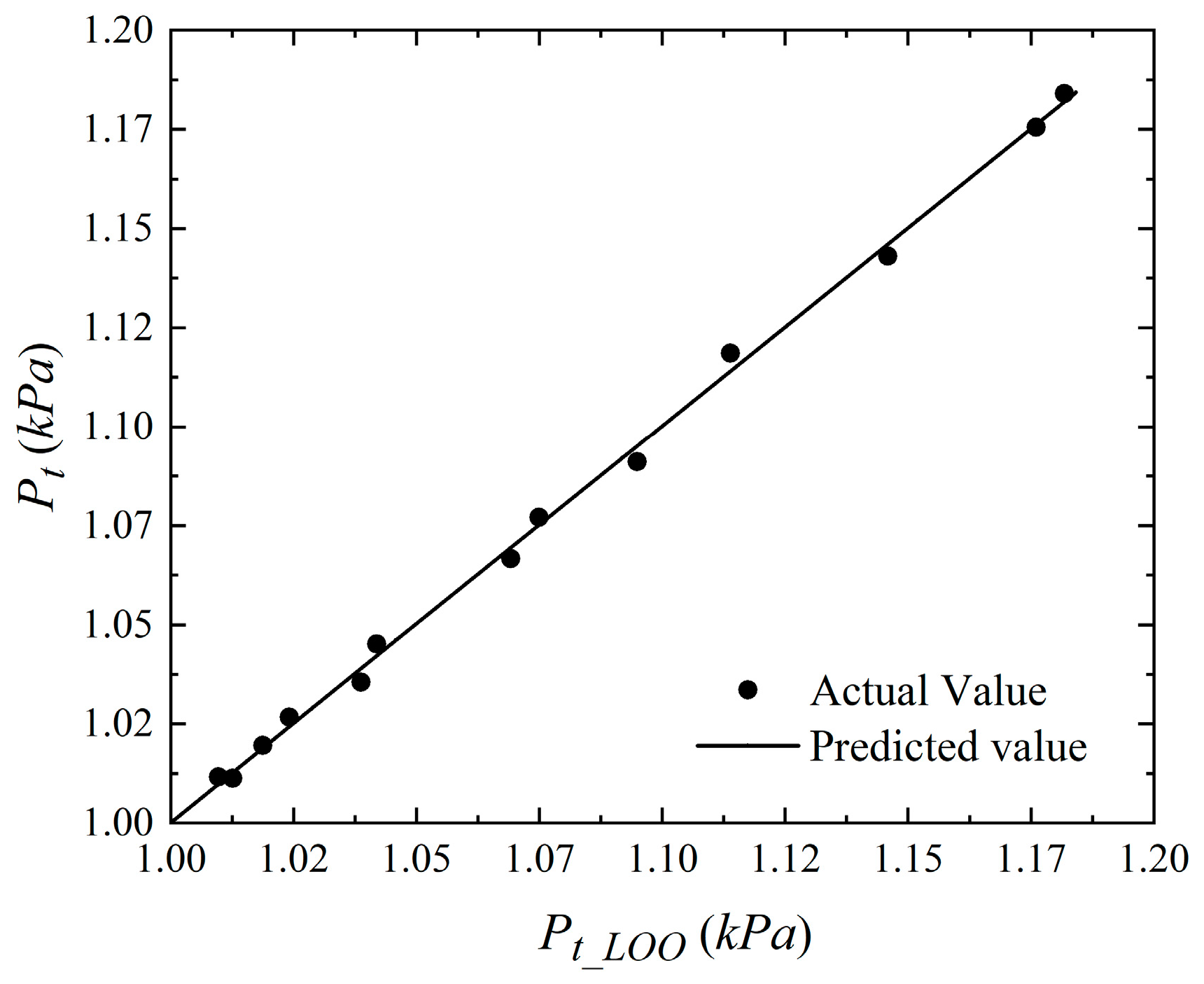
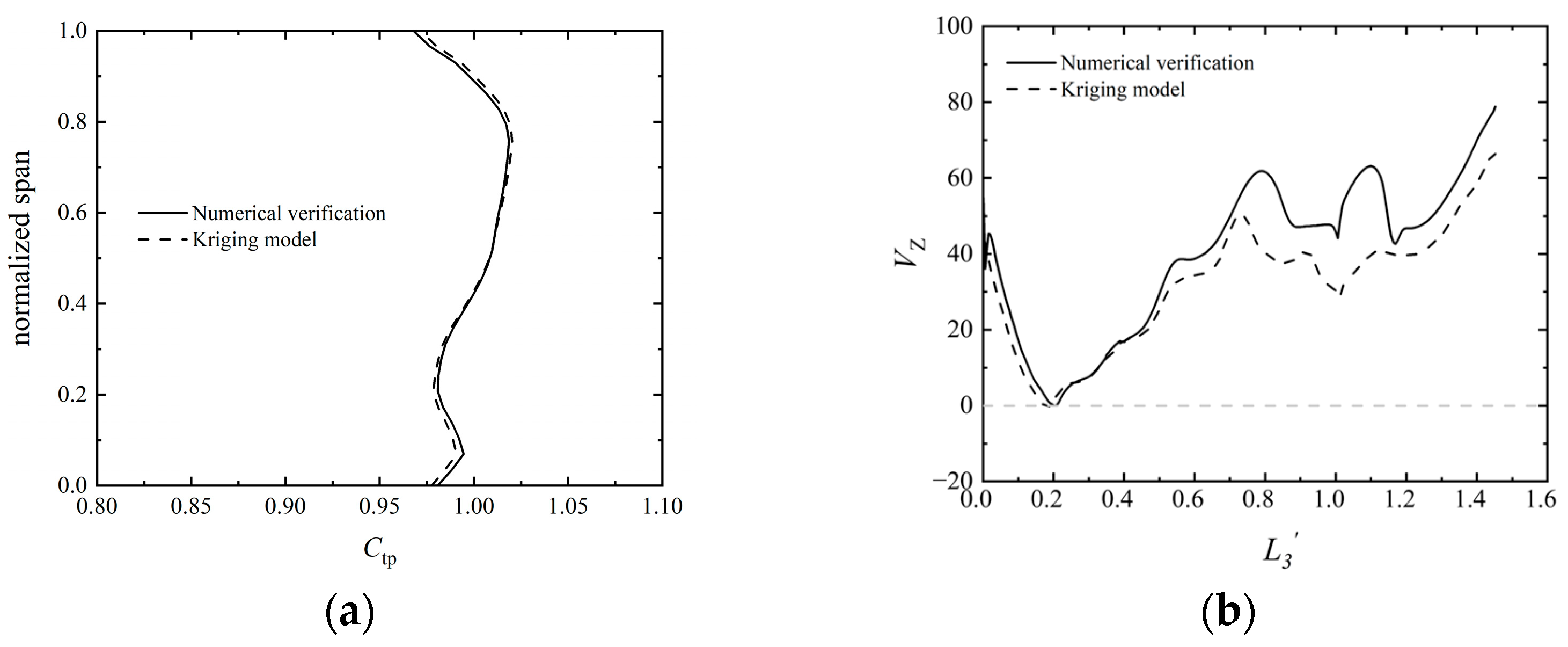
5.1. Accuracy Analysis
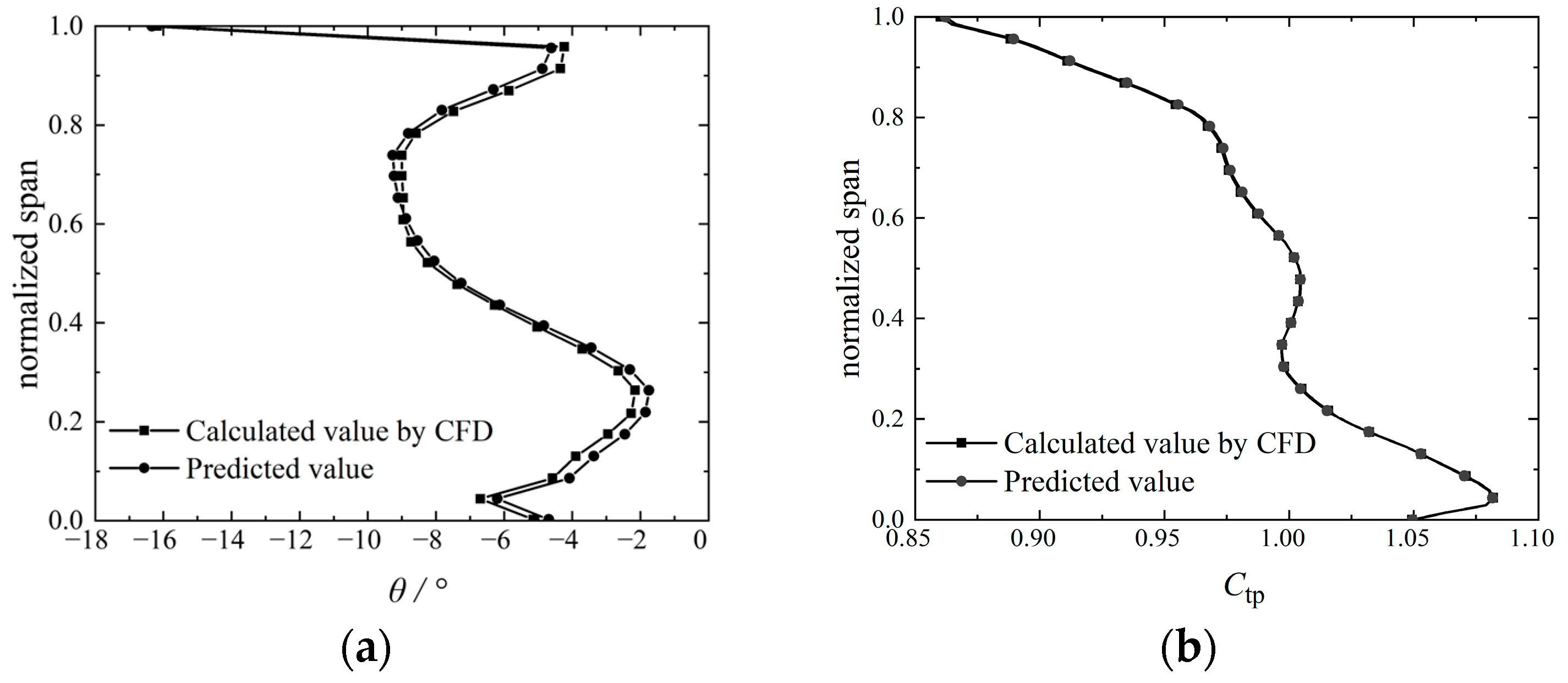
5.2. Comparison of Predicted Results
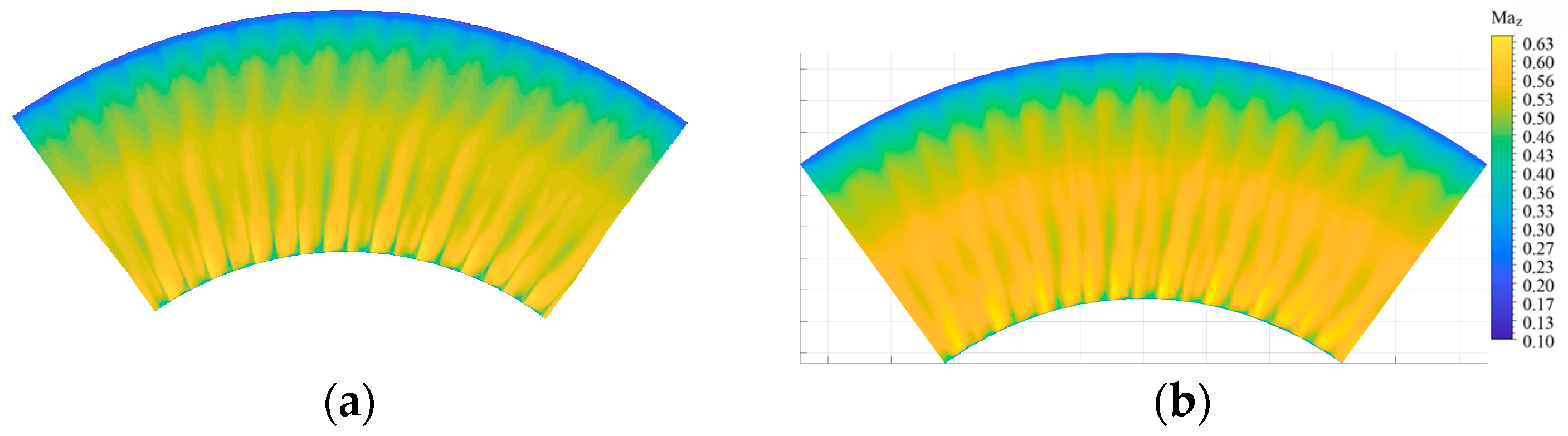
5.3. Application of the Kriging Surrogate Model to Describe the Flow Interaction Between Turbine and Exhaust Diffuser
6. Conclusions
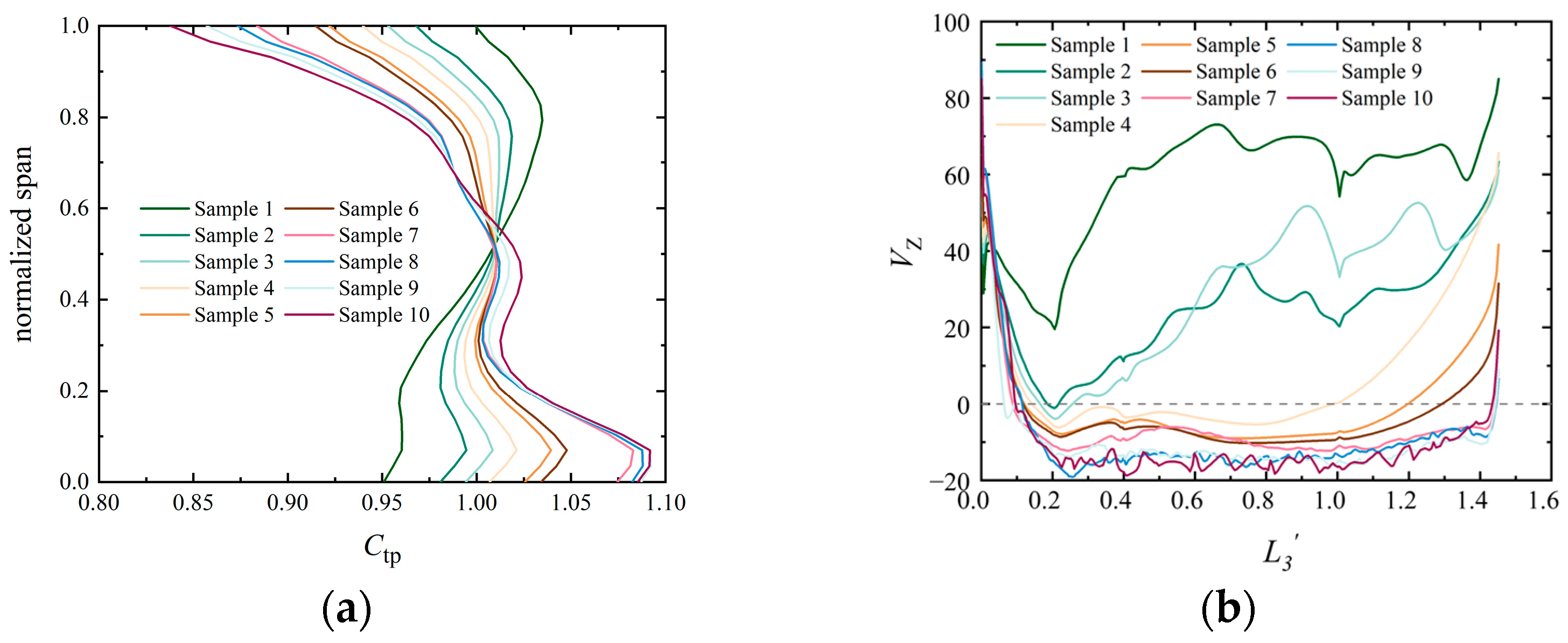
- The differences in the aerodynamic performance of the coupled turbine–diffuser system under various operational conditions are primarily attributed to the flow structure in the annular diffuser and the conical diffuser. The radial distribution profiles of total pressure and the axial velocity values are identified as the two key factors influencing the flow field evolution with changing operational conditions.
- A radial negative gradient in the total pressure at the turbine outlet tends to induce flow separation near the outer end-wall of the diffuser, thereby reducing the pressure recovery capacity. The axial velocity at the turbine outlet hub directly influences the strength of the backflow vortex in the conical diffuser, which in turn affects the total pressure loss. Quantitatively, the slope of the total pressure change along the blade height near the casing is k = −4.37, indicating a significant pressure drop that correlates with flow separation and vortex formation.
- A surrogate model was developed using a database generated by running a CFD solver and employing the Kriging interpolation method. This model provides a quantitative description of the relationships between operational conditions and key flow field characteristics in the coupled system. For the prediction of radial two-dimensional parameters, the maximum error of the axial Mach number (Maz) prediction is 18.81%, the minimum error is 0.84%, and the average error is 7.23%. The normalized total pressure prediction is more accurate, with an error of less than 0.5%. Additionally, the maximum error in the axial Mach number prediction is 15.3%, the minimum error is 0.18%, and the average error is 7.45%. The total pressure prediction error ranges from 0.78% to 3.8%, with an average error of 1.98%. The time consumed by the proposed surrogate model is much shorter than that of the CFD solver.
- The Kriging surrogate model presented in this paper uses Matérn functions to describe data with varying smoothness within a single model, which can better capture complex spatial correlation structures. The remaining method can reoptimize the hyperparameters and further improve the accuracy of the model. In the future, neural networks with more powerful nonlinear modeling capabilities will be added to further improve and deepen this area of research, and the methodology will be extended to other turbomachinery applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, D.S.; Kumar, K.L. Effect of swirl on pressure recovery in annular diffusers. J. Mech. Eng. Sci. 1980, 22, 305–313. [Google Scholar] [CrossRef]
- Babu, M.; Bhatia, D.; Shukla, R.K.; Pradeep, A.M.; Roy, B. Effect of turbine tip leakage flows on exhaust diffuser performance. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Babu, M.; Shukla, R.K.; Maru, A.; Pradeep, A.M.; Roy, B. Boundary layer control in turbine exhaust diffusers using casing injection and design modifications. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Zimmermann, C.; Stetter, H. Experimental determination of the flow field in the tip region of a LP steam turbine. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993. [Google Scholar]
- Vassiliev, V.; Irmisch, S.; Abdel-Wahab, S.; Granovskiy, A. Impact of the inflow conditions on the heavy-duty gas turbine exhaust diffuser performance. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Kluß, D.; Wiedermann, A.; Volgmann, W. Impact of gas turbine outflow on diffuser performance—A numerical study. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Kuschel, M.; Drechsel, B.; Kluß, D.; Seume, J.R. Influence of turbulent flow characteristics and coherent vortices on the pressure recovery of annular diffusers: Part A—Experimental results. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Drechsel, B.; Müller, C.; Herbst, F.; Seume, J.R. Influence of turbulent flow characteristics and coherent vortices on the pressure recovery of annular diffusers: Part B—Scale-resolving simulations. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Steven, S.J.; Williams, Q.J. The influence of inlet conditions on the performance of annular diffusers. J. Fluids Eng. 1980, 102, 357–363. [Google Scholar] [CrossRef]
- Vassiliev, V.; Irmisch, S.; Florjancic, S. CFD analysis of industrial gas turbine exhaust diffusers. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002. [Google Scholar]
- Vassiliev, V.; Irmisch, S.; Claridge, M.; Richardson, D.P. Experimental and numerical investigation of the impact of swirl on the performance of industrial gas turbines exhaust diffusers. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003. [Google Scholar]
- Tsoutsanis, E.; Meskin, N. Derivative-driven window-based regression method for gas turbine performance prognostics. Energy 2017, 128, 302–311. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C.; Chen, J.; Tian, H. Optimal design of aeroengine turbine disc based on kriging surrogate models. Comput. Struct. 2011, 89, 27–37. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, X.; Du, Z. Aerodynamic optimization for low pressure turbine exhaust hood using kriging surrogate model. Int. Commun. Heat Mass Transf. 2010, 37, 998–1003. [Google Scholar] [CrossRef]
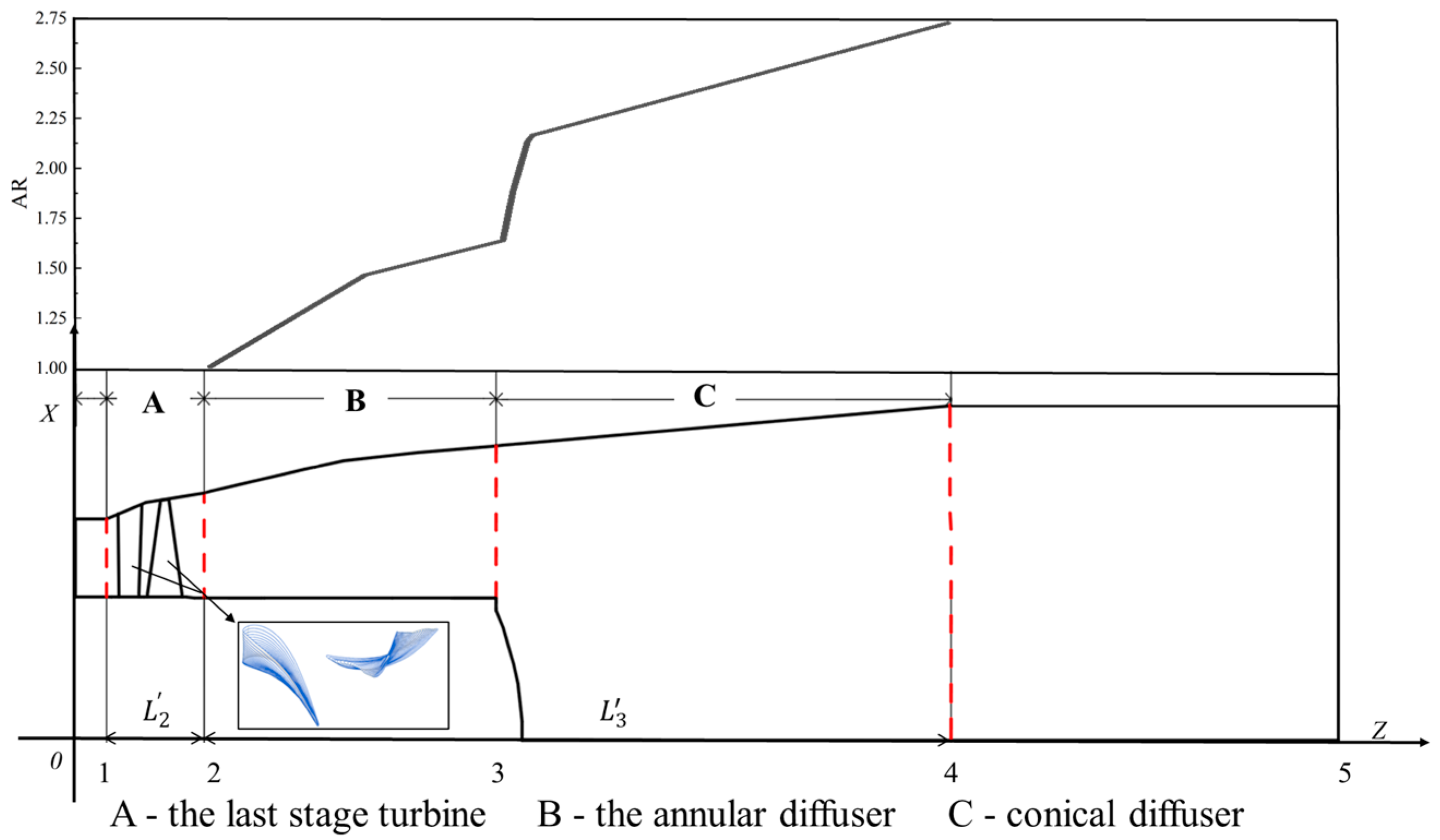








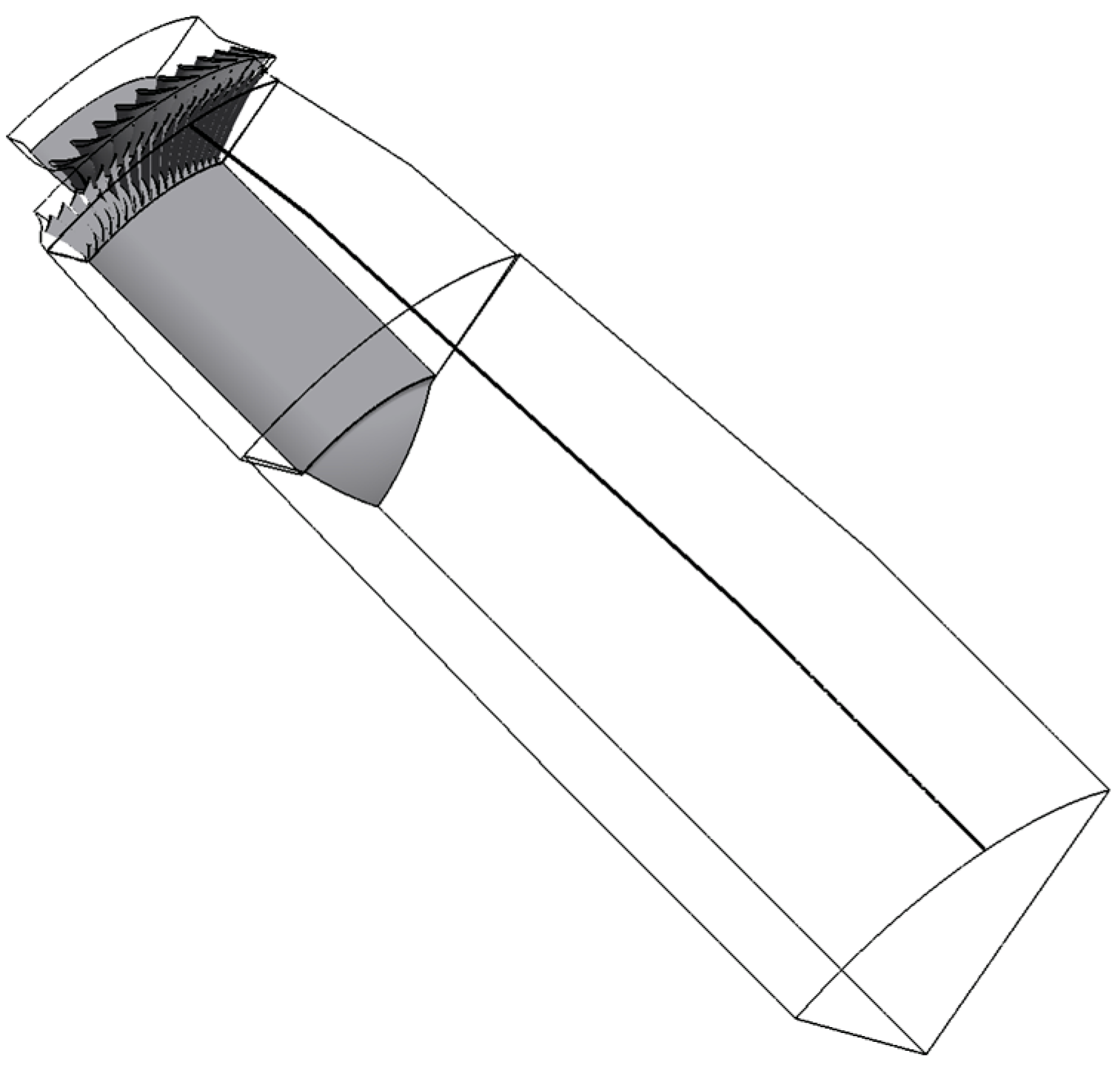
| Case | Case | Case | |||
|---|---|---|---|---|---|
| 1 | 1.579 | 2 | 1.974 | 3 | 2.270 |
| Stator | Rotor | Diffuser | |
|---|---|---|---|
| Number of passages | 10 | 18 | 1 |
| The circumferential angle of the domain | 72° | 72° | 72° |
| Stator | Rotor | Diffuser | |
|---|---|---|---|
| Number of nodes | 2.62 million | 8.15 million | 3.63 million |
| The Circumference Is Uniform | The Circumference Is Not Uniform | |||
|---|---|---|---|---|
| Swirl Angle | Ctp | Ma | Ctp | |
| Error | max/min/ave (%) | max/min/ave (%) | max/min/ave (%) | max/min/ave (%) |
| 18.81/0.84/7.23 | 0.23/0.01/0.06 | 15.3/0.18/7.45 | 3.8/0.78/1.98 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, B.; Fu, J.; Kong, X.; Zhang, H.; Yu, Q. Investigations on the Aerodynamic Interactions Between Turbine and Diffuser System by Employing the Kriging Method. Energies 2025, 18, 921. https://doi.org/10.3390/en18040921
Qiu B, Fu J, Kong X, Zhang H, Yu Q. Investigations on the Aerodynamic Interactions Between Turbine and Diffuser System by Employing the Kriging Method. Energies. 2025; 18(4):921. https://doi.org/10.3390/en18040921
Chicago/Turabian StyleQiu, Bin, Jinglun Fu, Xiangling Kong, Hongwu Zhang, and Qiang Yu. 2025. "Investigations on the Aerodynamic Interactions Between Turbine and Diffuser System by Employing the Kriging Method" Energies 18, no. 4: 921. https://doi.org/10.3390/en18040921
APA StyleQiu, B., Fu, J., Kong, X., Zhang, H., & Yu, Q. (2025). Investigations on the Aerodynamic Interactions Between Turbine and Diffuser System by Employing the Kriging Method. Energies, 18(4), 921. https://doi.org/10.3390/en18040921






