Research on Export Oil and Gas Concentration Prediction Based on Machine Learning Methods
Abstract
:1. Introduction
2. Model Basis
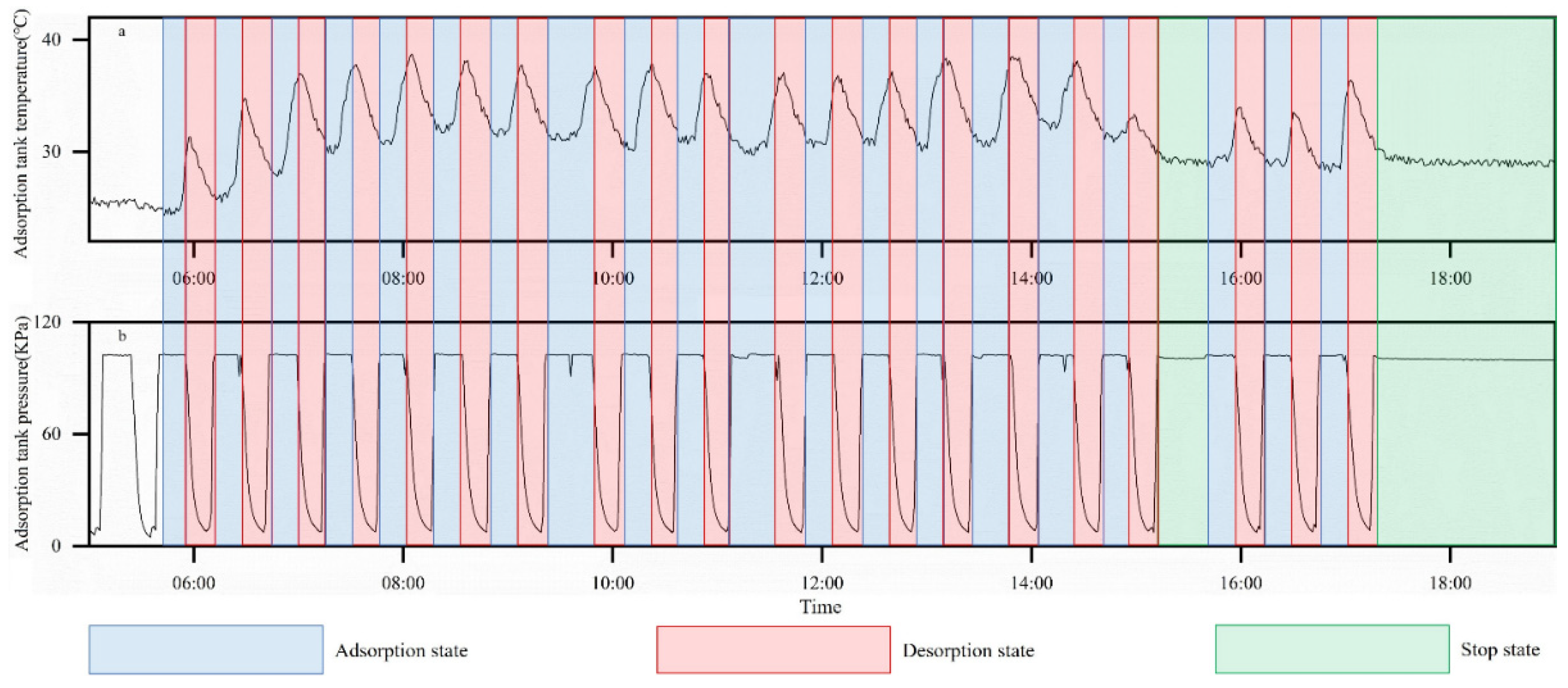
2.1. Process Flow Analysis
2.2. Data Processing
3. Methodology
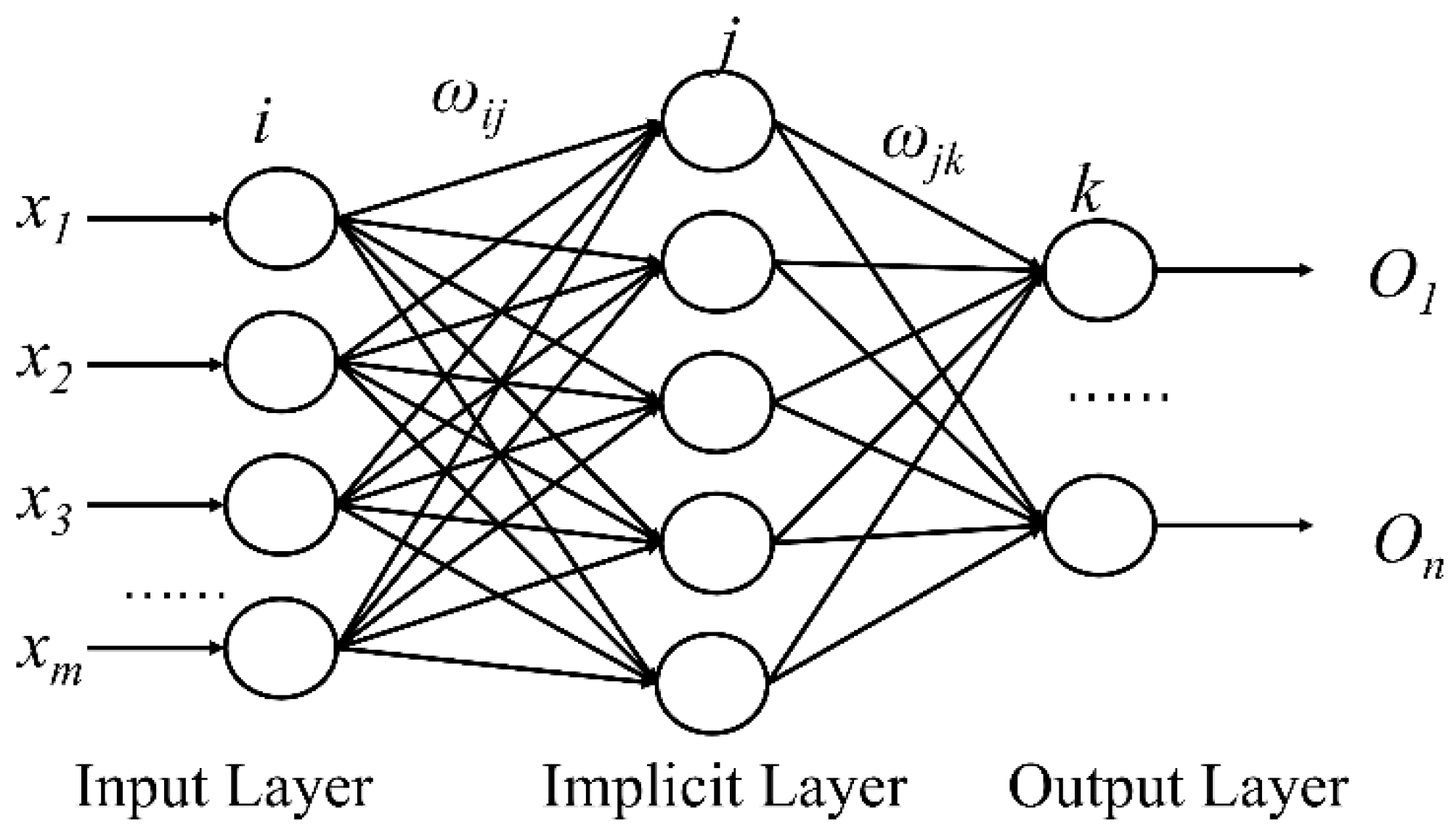
3.1. BP Neural Network
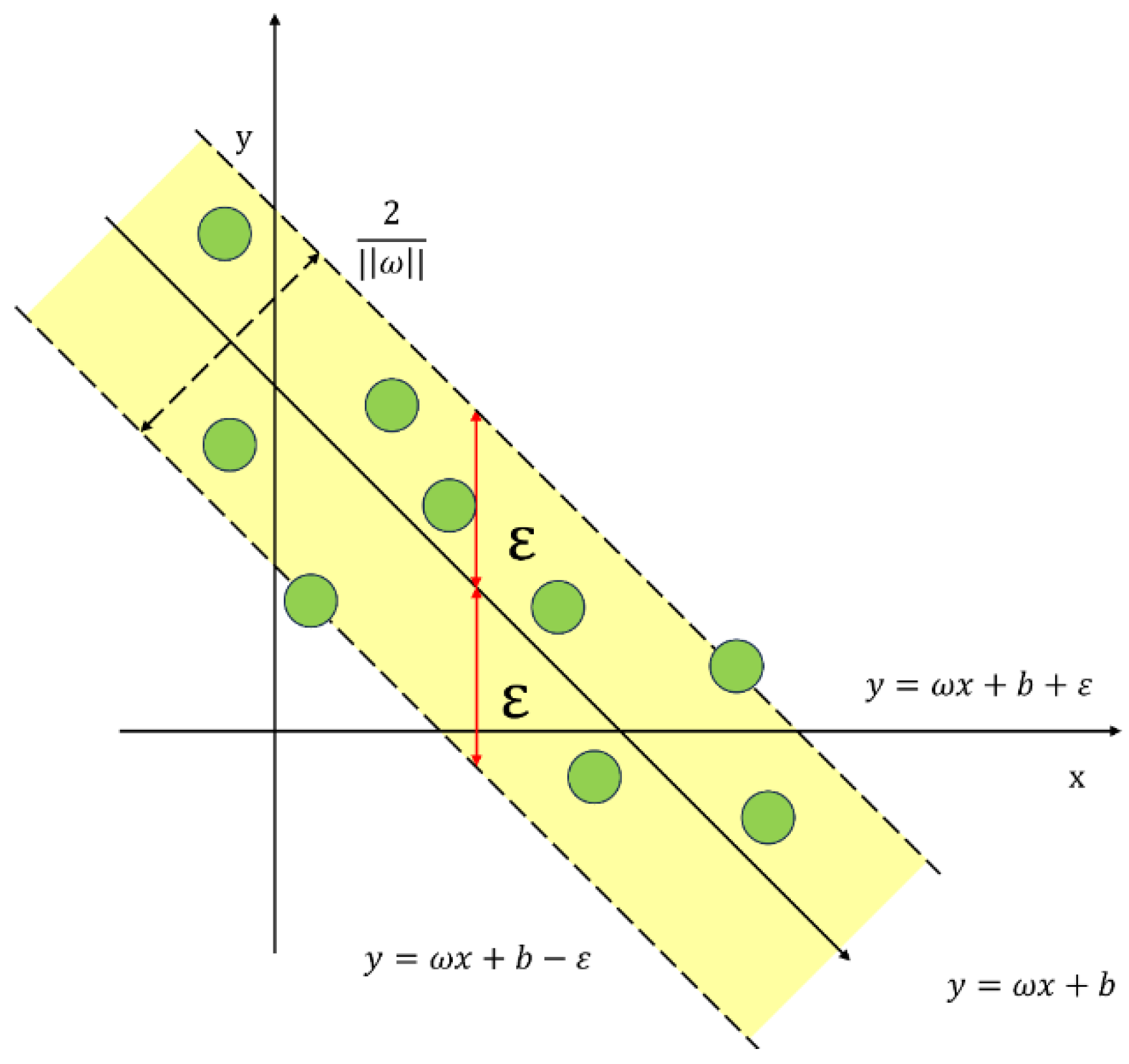
3.2. Support Vector Machines
3.3. Random Forests
3.4. BP Neural Network Algorithm Based on Particle Swarm Optimization
3.5. Support Vector Machine Algorithm Based on Particle Swarm Optimization
- Initialize the position and velocity of the particle swarm.
- One SVM model is trained for each particle, and performance metrics are calculated.
- Update the velocity and position of the particles to determine the optimal hyperparameter combination.
- After meeting the iteration condition, the final training is conducted using the optimal parameters.
3.6. Genetic-Algorithm-Based BP Neural Network
4. Results and Discussion
4.1. Data Correlation Analysis
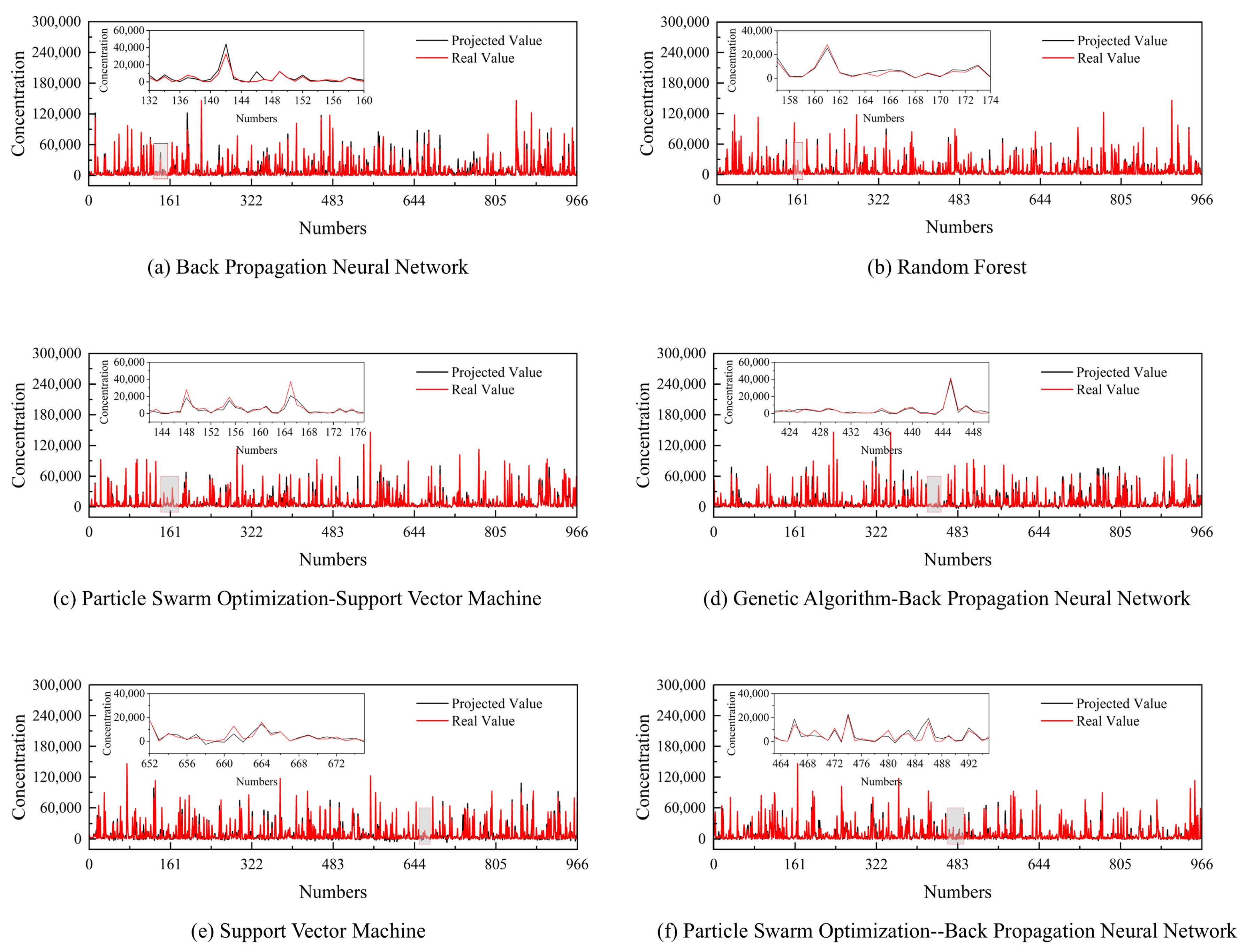
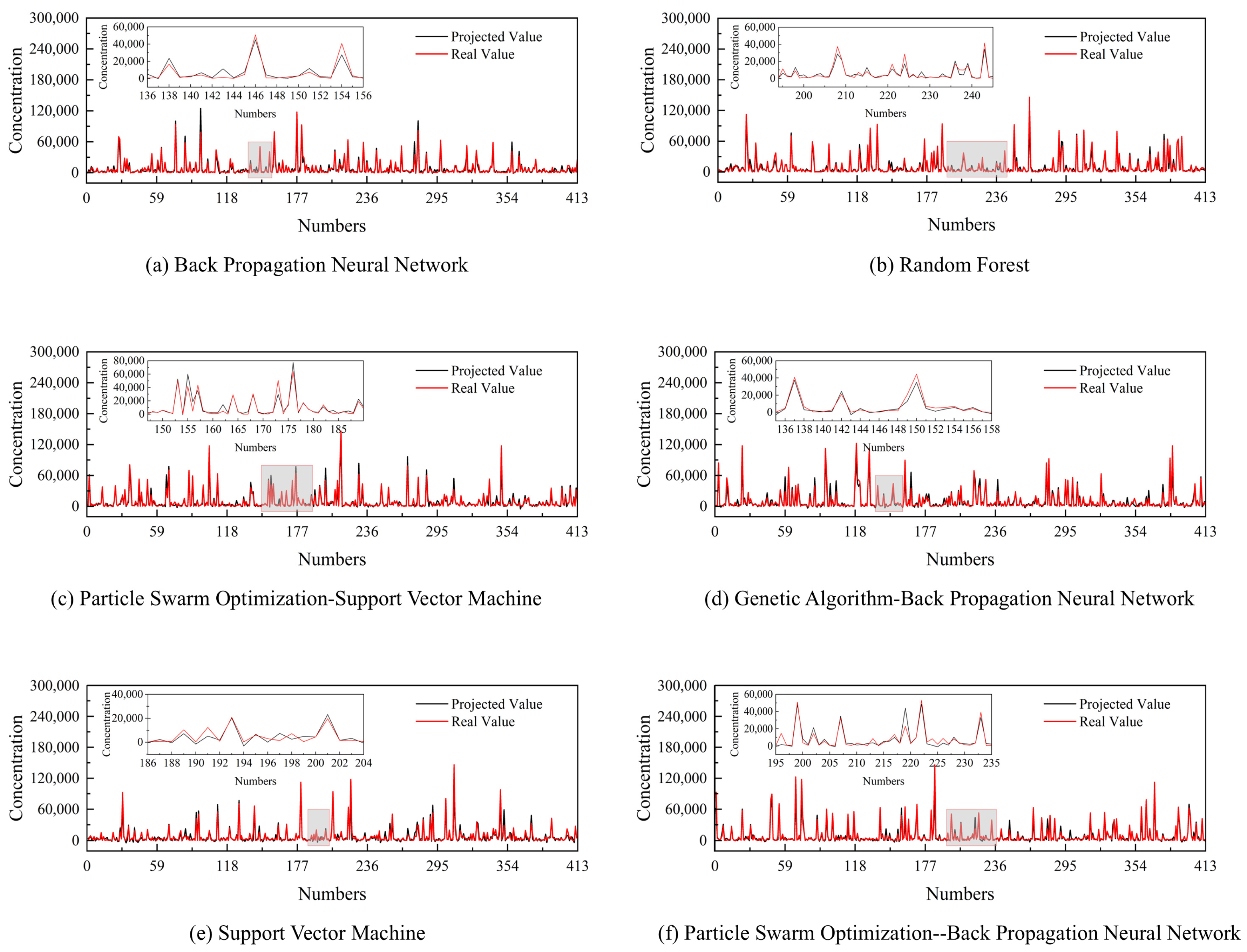
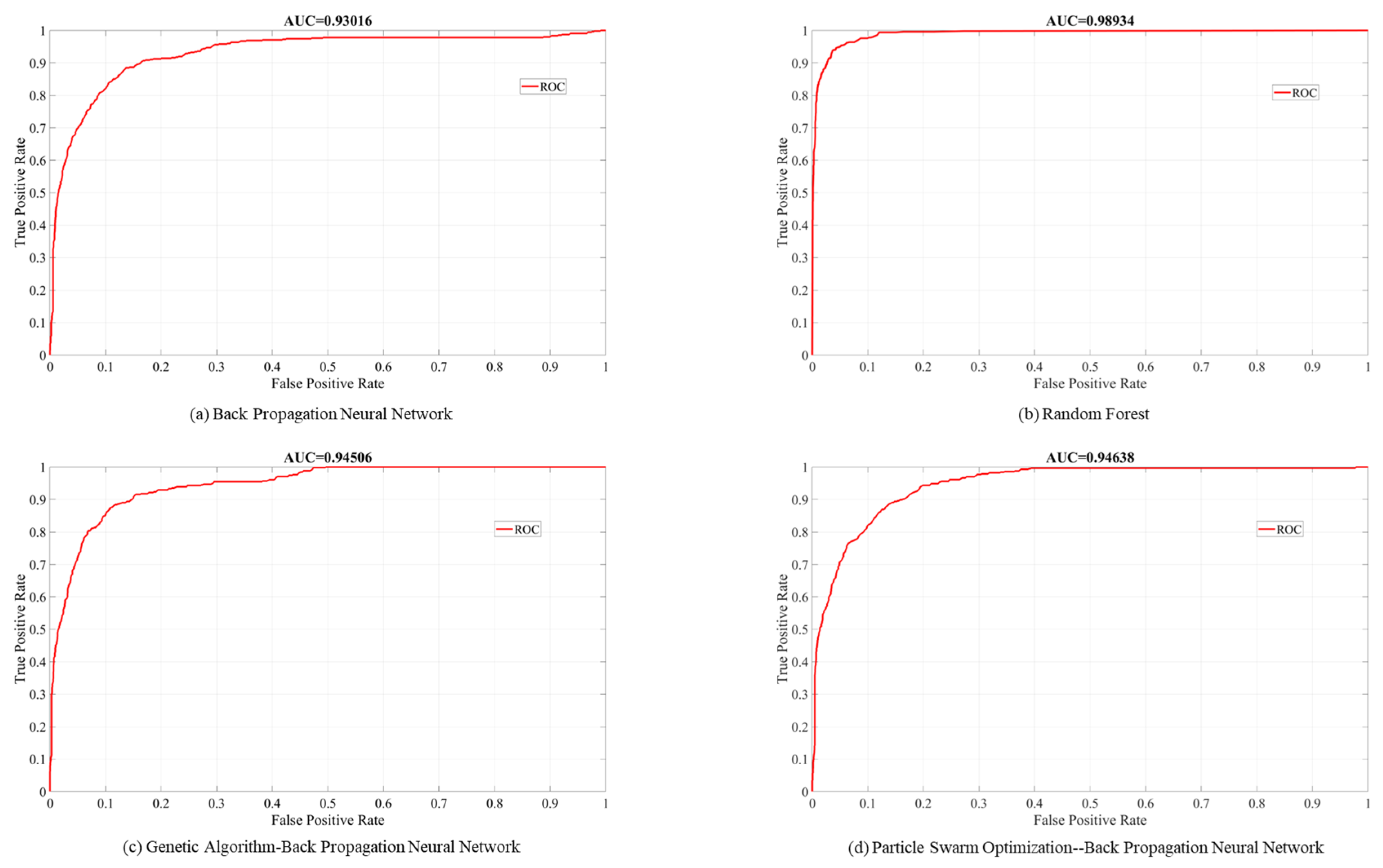
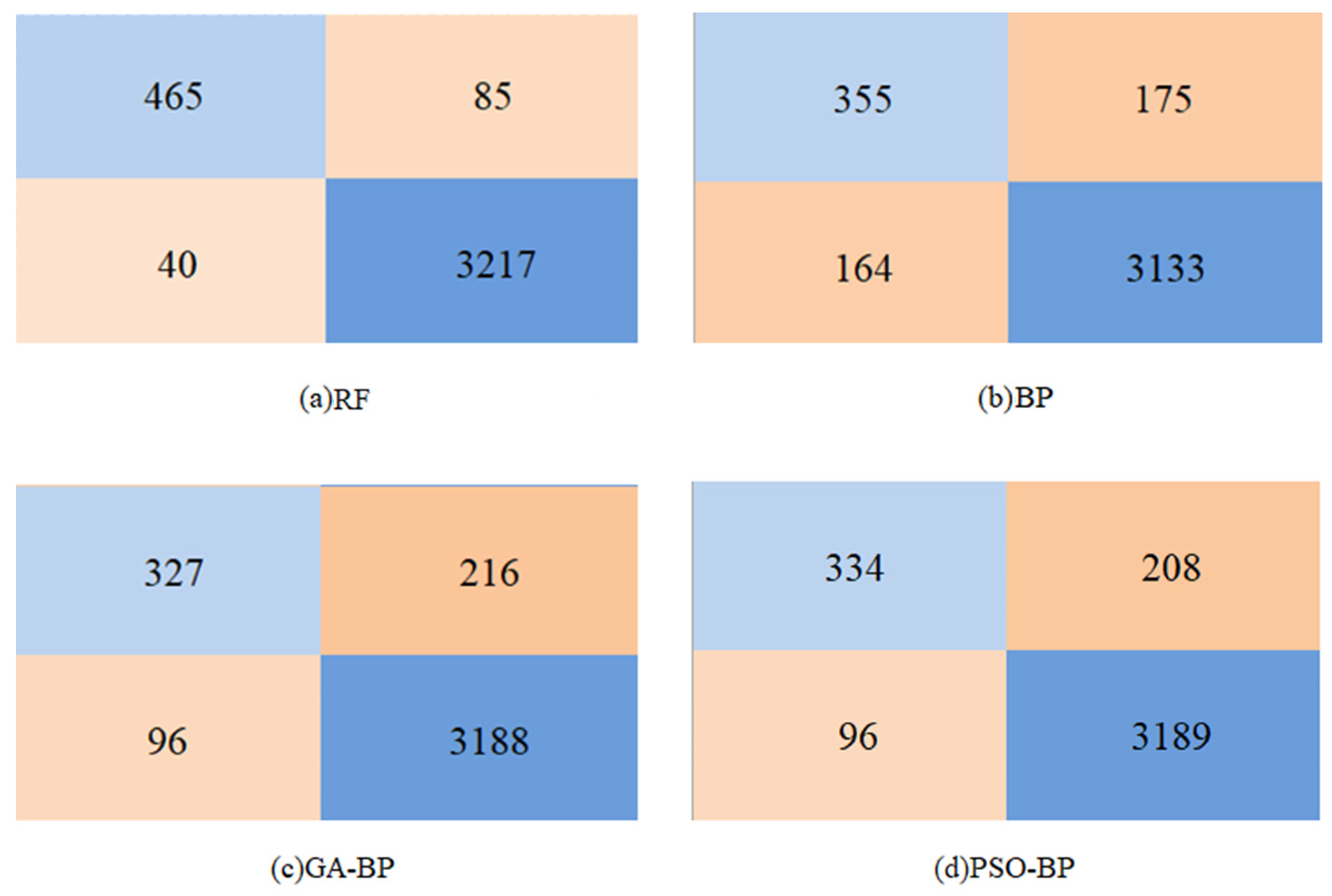
4.2. Comparison of Machine Learning Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahsan, M.; Tian, L.; Du, R.; Alhussan, A.A.; El-Kenawy, E.-S.M. Optimizing Environmental Impact: MCDM-Based Approaches for Petrochemical Industry Emission Cuts. IEEE Access 2024, 12, 35309–35324. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Q.; Yuan, Y.; Tang, X.; Zhao, S.; Yi, H. Adsorption Behavior of Mo-MEL Zeolites for Reducing VOCs from Cooking Oil Fumes. Sep. Purif. Technol. 2023, 322, 124059. [Google Scholar] [CrossRef]
- Al-Muhtaseb, S.A. Effects of Adsorbent Characteristics on Adiabatic Vacuum Swing Adsorption Processes for Solvent Vapor Recovery. Chem. Eng. Technol. 2006, 29, 1323–1332. [Google Scholar] [CrossRef]
- Shie, J.-L.; Lu, C.-Y.; Chang, C.-Y.; Chiu, C.-Y.; Lee, D.-J.; Liu, S.-P.; Chang, C.-T. Recovery of Gasoline Vapor by a Combined Process of Two-Stage Dehumidification and Condensation. J. Chin. Inst. Chem. Eng. 2003, 34, 605–616. [Google Scholar] [CrossRef]
- Shi, L.; Huang, W. Sensitivity Analysis and Optimization for Gasoline Vapor Condensation Recovery. Process Saf. Environ. Protect. 2014, 92, 807–814. [Google Scholar] [CrossRef]
- Nitsche, V.; Ohlrogge, K.; Stürken, K. Separation of Organic Vapors by Means of Membranes. Chem. Eng. Technol. 1998, 21, 925–935. [Google Scholar] [CrossRef]
- Roizard, D.; Lapicque, F.; Favre, E.; Roizard, C. Potentials of Pervaporation to Assist VOCs’ Recovery by Liquid Absorption. Chem. Eng. Sci. 2009, 64, 1927–1935. [Google Scholar] [CrossRef]
- Chiang, C.-Y.; Liu, Y.-Y.; Chen, Y.-S.; Liu, H.-S. Absorption of Hydrophobic Volatile Organic Compounds by a Rotating Packed Bed. Ind. Eng. Chem. Res. 2012, 51, 9441–9445. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, Y.; Huang, J. Hyper-Cross-Linked Phenolic Hydroxyl Polymers with Hierarchical Porosity and Their Efficient Adsorption Performance. Ind. Eng. Chem. Res. 2020, 59, 11275–11283. [Google Scholar] [CrossRef]
- Fu, L.; Zuo, J.; Liao, K.; Shao, M.; Si, W.; Zhang, H.; Gu, F.; Huang, W.; Li, B.; Shao, Y. Preparation of Adsorption Resin and Itas Application in VOCs Adsorption. J. Polym. Res. 2023, 30, 167. [Google Scholar] [CrossRef]
- Feng, X.; Sourirajan, S.; Tezel, F.H.; Matsuura, T.; Farnand, B.A. Separation of Volatile Organic Compound/Nitrogen Mixtures by Polymeric Membranes. Ind. Eng. Chem. Res. 1993, 32, 533–539. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Q.; Zhang, Z.; Lin, J.; Wu, Q. Study on Separation of CO2 Condensation from Natural Gas Based on Cellular Automaton Method. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 3663–3683. [Google Scholar] [CrossRef]
- Sikiru, S.; Soleimani, H.; Shafie, A.; Olayemi, R.I.; Hassan, Y.M. Prediction of Electromagnetic Properties Using Artificial Neural Networks for Oil Recovery Factors. Colloid J. 2023, 85, 151–165. [Google Scholar] [CrossRef]
- Ghanem, A.; Gouda, M.F.; Alharthy, R.D.; Desouky, S.M. Predicting the Compressibility Factor of Natural Gas by Using Statistical Modeling and Neural Network. Energies 2022, 15, 1807. [Google Scholar] [CrossRef]
- Wang, F.; Tang, X.; Deng, C.; Li, J. Application of BP Neural Network to Prediction of Recovery Effect of Air-Foam Flooding in Heavy Oil. Pet. Sci. Technol. 2022, 40, 1914–1924. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.; Wen, Y.; Li, L.; Zhang, X.; Wang, Y. Comparison of Ethane Recovery Processes for Lean Gas Based on a Coupled Model. J. Clean. Prod. 2024, 434, 139726. [Google Scholar] [CrossRef]
- Orru, P.F.; Zoccheddu, A.; Sassu, L.; Mattia, C.; Cozza, R.; Arena, S. Machine Learning Approach Using MLP and SVM Algorithms for the Fault Prediction of a Centrifugal Pump in the Oil and Gas Industry. Sustainability 2020, 12, 4776. [Google Scholar] [CrossRef]
- Yue, M.; Dai, Q.; Liao, H.; Liu, Y.; Fan, L.; Song, T. Prediction of ORF for Optimized CO2 Flooding in Fractured Tight Oil Reservoirs via Machine Learning. Energies 2024, 17, 1303. [Google Scholar] [CrossRef]
- Hong, B.-Y.; Liu, S.-N.; Li, X.-P.; Fan, D.; Ji, S.-P.; Chen, S.-H.; Li, C.-C.; Gong, J. A Liquid Loading Prediction Method of Gas Pipeline Based on Machine Learning. Pet. Sci. 2022, 19, 3004–3015. [Google Scholar] [CrossRef]
- Cen, X.; Chen, Z.; Chen, H.; Ding, C.; Ding, B.; Li, F.; Lou, F.; Zhu, Z.; Zhang, H.; Hong, B. User Repurchase Behavior Prediction for Integrated Energy Supply Stations Based on the User Profiling Method. Energy 2024, 286, 129625. [Google Scholar] [CrossRef]
- R Azmi, P.A.; Yusoff, M.; Mohd Sallehud-din, M.T. A Review of Predictive Analytics Models in the Oil and Gas Industries. Sensors 2024, 24, 4013. [Google Scholar] [CrossRef] [PubMed]
- Zhai, S.; Geng, S.; Li, C.; Gong, Y.; Jing, M.; Li, Y. Prediction of Gas Production Potential Based on Machine Learning in Shale Gas Field: A Case Study. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 6581–6601. [Google Scholar] [CrossRef]
- GB 20950-2007; Emission Standard of Air Pollutant for Bulk Gasoline Terminals. National Standards of People’s Republic of China: Beijing, China, 2007.
- Cui, K.; Jing, X. Research on Prediction Model of Geotechnical Parameters Based on BP Neural Network. Neural Comput. Appl. 2019, 31, 8205–8215. [Google Scholar] [CrossRef]
- Wang, C.-D.; Xi, W.-D.; Huang, L.; Zheng, Y.-Y.; Hu, Z.-Y.; Lai, J.-H. A BP Neural Network Based Recommender Framework With Attention Mechanism. IEEE Trans. Knowl. Data Eng. 2022, 34, 3029–3043. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.; Sun, T.; Xu, B. A Constrained Optimization Method Based on BP Neural Network. Neural Comput. Appl. 2018, 29, 413–421. [Google Scholar] [CrossRef]
- Wang, L.-L.; Ngan, H.Y.T.; Yung, N.H.C. Automatic Incident Classification for Large-Scale Traffic Data by Adaptive Boosting SVM. Inf. Sci. 2018, 467, 59–73. [Google Scholar] [CrossRef]
- Aisyah, S.; Simaremare, A.A.; Adytia, D.; Aditya, I.A.; Alamsyah, A. Exploratory Weather Data Analysis for Electricity Load Forecasting Using SVM and GRNN, Case Study in Bali, Indonesia. Energies 2022, 15, 3566. [Google Scholar] [CrossRef]
- Jakkula, V. Tutorial on Support Vector Machine (Svm); School of EECS, Washington State University: Pullman, WA, USA, 2006; Volume 37, p. 3. [Google Scholar]
- Khan, A.U.; Salman, S.; Muhammad, K.; Habib, M. Modelling Coal Dust Explosibility of Khyber Pakhtunkhwa Coal Using Random Forest Algorithm. Energies 2022, 15, 3169. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, H.; Huang, T.; Wu, Y.; Guo, B.; Liu, Z.; Luo, H.; Tang, J.; Zhou, H.; Wang, L.; et al. Improved Random Forest Algorithms for Increasing the Accuracy of Forest Aboveground Biomass Estimation Using Sentinel-2 Imagery. Ecol. Indic. 2024, 159, 111752. [Google Scholar] [CrossRef]
- Tian, K.; Kang, Z.; Kang, Z. A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network. Energies 2024, 17, 3482. [Google Scholar] [CrossRef]
- Xu, C.; Li, L.; Li, J.; Wen, C. Surface Defects Detection and Identification of Lithium Battery Pole Piece Based on Multi-Feature Fusion and PSO-SVM. IEEE Access 2021, 9, 85232–85239. [Google Scholar] [CrossRef]
- Dong, Q.; Fu, X. Prediction of Thermal Conductivity of Litz Winding by Least Square Method and GA-BP Neural Network Based on Numerical Simulations. Energies 2023, 16, 7295. [Google Scholar] [CrossRef]
- Wang, M.; Xiong, C.; Shang, Z. Predictive Evaluation of Dynamic Responses and Frequencies of Bridge Using Optimized VMD and Genetic Algorithm-Back Propagation Approach. J. Civil. Struct. Health Monit. 2024, 15, 173–190. [Google Scholar] [CrossRef]


| Data 1 | Data 2 | Data 3 | Data 4 | Data 5 | Data XXX | |
|---|---|---|---|---|---|---|
| TI121 (°C) | 31.95 | 36.21 | 35.32 | 35.47 | 33.91 | 34.49 |
| PI101 (KPa) | −0.39 | −0.75 | −0.96 | −0.39 | −0.16 | −0.36 |
| AT101 (mg m−3) | 150,651.00 | 150,712.00 | 150,638.00 | 150,675.00 | 150,602.00 | 150,663.00 |
| TI101 (°C) | 24.33 | 27.30 | 29.36 | 29.41 | 23.87 | 26.53 |
| TI301 (°C) | 23.85 | 23.59 | 23.86 | 23.64 | 24.07 | 23.69 |
| TI201A (°C) | 75.72 | 72.28 | 73.82 | 76.54 | 73.86 | 75.76 |
| TI201B (°C) | 71.84 | 67.02 | 69.2 | 72.98 | 66.22 | 70.28 |
| FI101 (m3 h−1) | 945.6 | 929.69 | 929.69 | 929.69 | 929.69 | 929.69 |
| NMHC (mg m−3) | 21,352.99 | 122,504.00 | 113,168.40 | 90,060.49 | 66,273.78 | 64,245.71 |
| Maximum Values | Minimum Value | Average Value | (Statistics) Standard Deviation | |
|---|---|---|---|---|
| TI121(°C) | 39.84 | 22.85 | 30.99 | 3.06 |
| PI101 (KPa) | 1.44 | −1.11 | 0.17 | 0.43 |
| AT101 (mg m−3) | 151,312.00 | 75,913.00 | 113,011.10 | 23,648.61 |
| TI101 (°C) | 36.52 | 19.52 | 25.23 | 3.49 |
| TI301 (°C) | 26.13 | 6.17 | 16.59 | 6.06 |
| TI201A (°C) | 80.16 | 31.00 | 66.63 | 9.72 |
| TI201B (°C) | 79.22 | 28.44 | 62.64 | 8.67 |
| FI101 (m3 h−1) | 1063.80 | 0.00 | 390.68 | 282.4685 |
| NMHC (mg m−3) | 146,168.10 | 201.09 | 9752.58 | 18,219.62 |
| Correlation with Non-Methane Hydrocarbon (NMHC) | TI121 | PI101 | FI101 | AT101 | TT101 | TI301 | TI201A | TI201B |
|---|---|---|---|---|---|---|---|---|
| Spearman’s coefficient | 0.512 | −0.432 | −0.046 | 0.432 | 0.126 | 0.586 | 0.382 | 0.414 |
| Coefficient of two-sided significance test | 0.000 | 0.000 | 0.087 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Training Set R2 | Test Set R2 | The Average R2 After Cross-Validation | Training Set MAE | Test Set MAE | The Average MAE After Cross-Validation | |
|---|---|---|---|---|---|---|
| BP | 0.8897 | 0.8422 | 0.8758 | 3677.3227 | 3935.7610 | 3421.2937 |
| SVM | 0.8906 | 0.8724 | 0.8621 | 2999.3626 | 3079.9374 | 3381.9632 |
| RF | 0.9438 | 0.9314 | 0.9081 | 1814.3089 | 2533.9995 | 2602.8601 |
| PSO-BP | 0.9010 | 0.8964 | 0.8880 | 3430.7646 | 3627.3885 | 3252.7312 |
| PSO-SVM | 0.9165 | 0.9011 | 0.8816 | 2498.2642 | 2969.0997 | 3232.0596 |
| GA-BP | 0.9101 | 0.9036 | 0.8894 | 3074.3935 | 3075.3705 | 3314.7126 |
| Training Set NMAE | Test Set NMAE | |
|---|---|---|
| BP | 0.29296 | 0.32769 |
| SVM | 0.29113 | 0.3414 |
| RF | 0.17776 | 0.26125 |
| PSO-BP | 0.31286 | 0.32712 |
| PSO-SVM | 0.28781 | 0.34514 |
| GA-BP | 0.30623 | 0.3394 |
| Arithmetic | Accuracy | Precision | Recall | FPR |
|---|---|---|---|---|
| BP | 91.6% | 68.4% | 67.0% | 5.0% |
| RF | 97.2% | 92.1% | 84.5% | 1.2% |
| GA-BP | 91.8% | 77.3% | 60.2% | 3.0% |
| PSO-BP | 92.1% | 77.7% | 61.6% | 2.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhu, B.; Zheng, H.; Wang, J.; Chen, Z.; Hong, B. Research on Export Oil and Gas Concentration Prediction Based on Machine Learning Methods. Energies 2025, 18, 1078. https://doi.org/10.3390/en18051078
Wang X, Zhu B, Zheng H, Wang J, Chen Z, Hong B. Research on Export Oil and Gas Concentration Prediction Based on Machine Learning Methods. Energies. 2025; 18(5):1078. https://doi.org/10.3390/en18051078
Chicago/Turabian StyleWang, Xiaochuan, Baikang Zhu, Huajun Zheng, Jiaqi Wang, Zhiwei Chen, and Bingyuan Hong. 2025. "Research on Export Oil and Gas Concentration Prediction Based on Machine Learning Methods" Energies 18, no. 5: 1078. https://doi.org/10.3390/en18051078
APA StyleWang, X., Zhu, B., Zheng, H., Wang, J., Chen, Z., & Hong, B. (2025). Research on Export Oil and Gas Concentration Prediction Based on Machine Learning Methods. Energies, 18(5), 1078. https://doi.org/10.3390/en18051078





