A Data Reconciliation-Based Method for Performance Estimation of Entrained-Flow Pulverized Coal Gasification
Abstract
:1. Introduction
2. Materials and Methods
2.1. Coal Gasification Unit and the Operational Data
2.2. Data Reconciliation-Based Method for Performance Estimation
2.3. Data Reconciliation
2.4. ANN Model
3. Results and Discussion
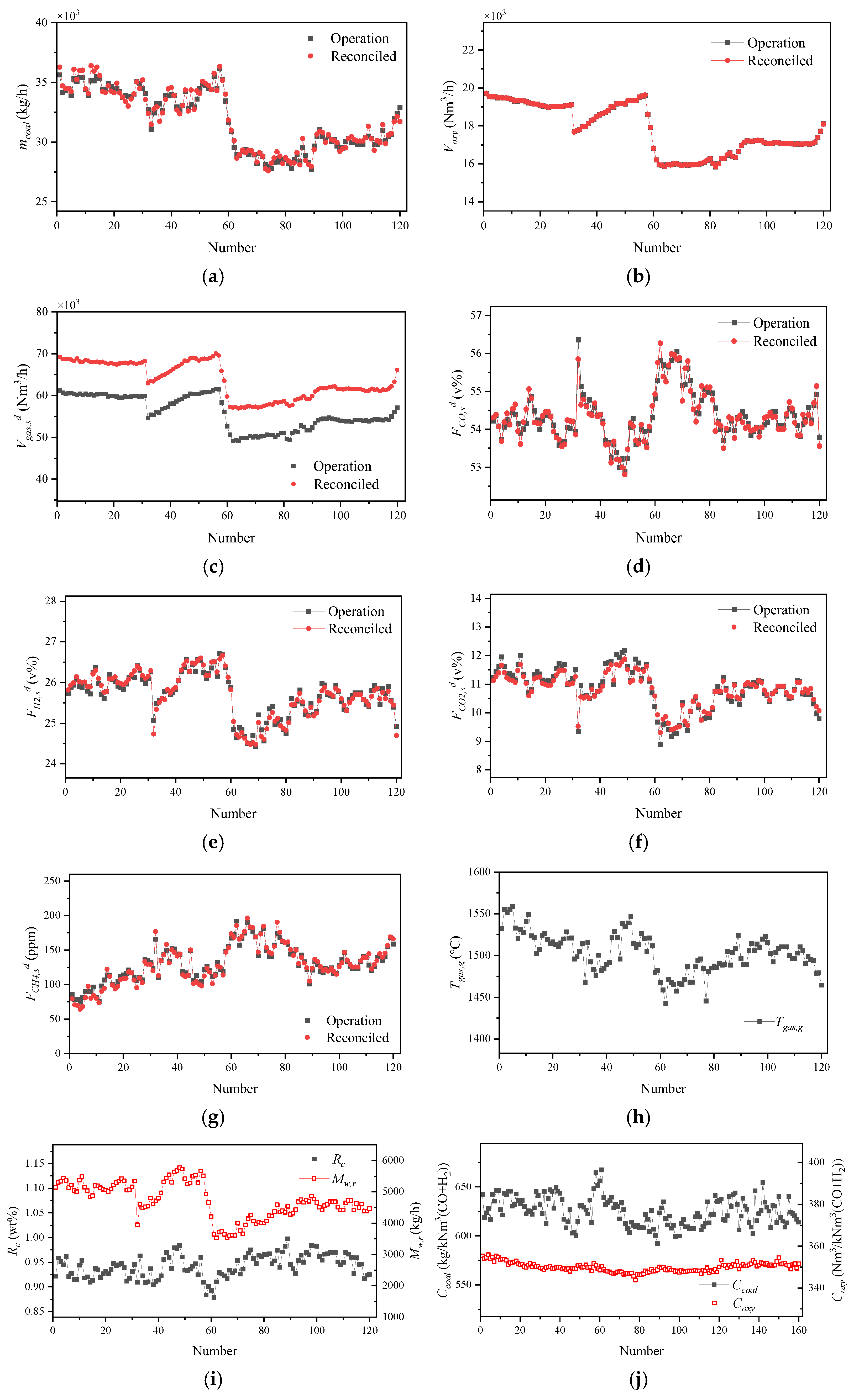
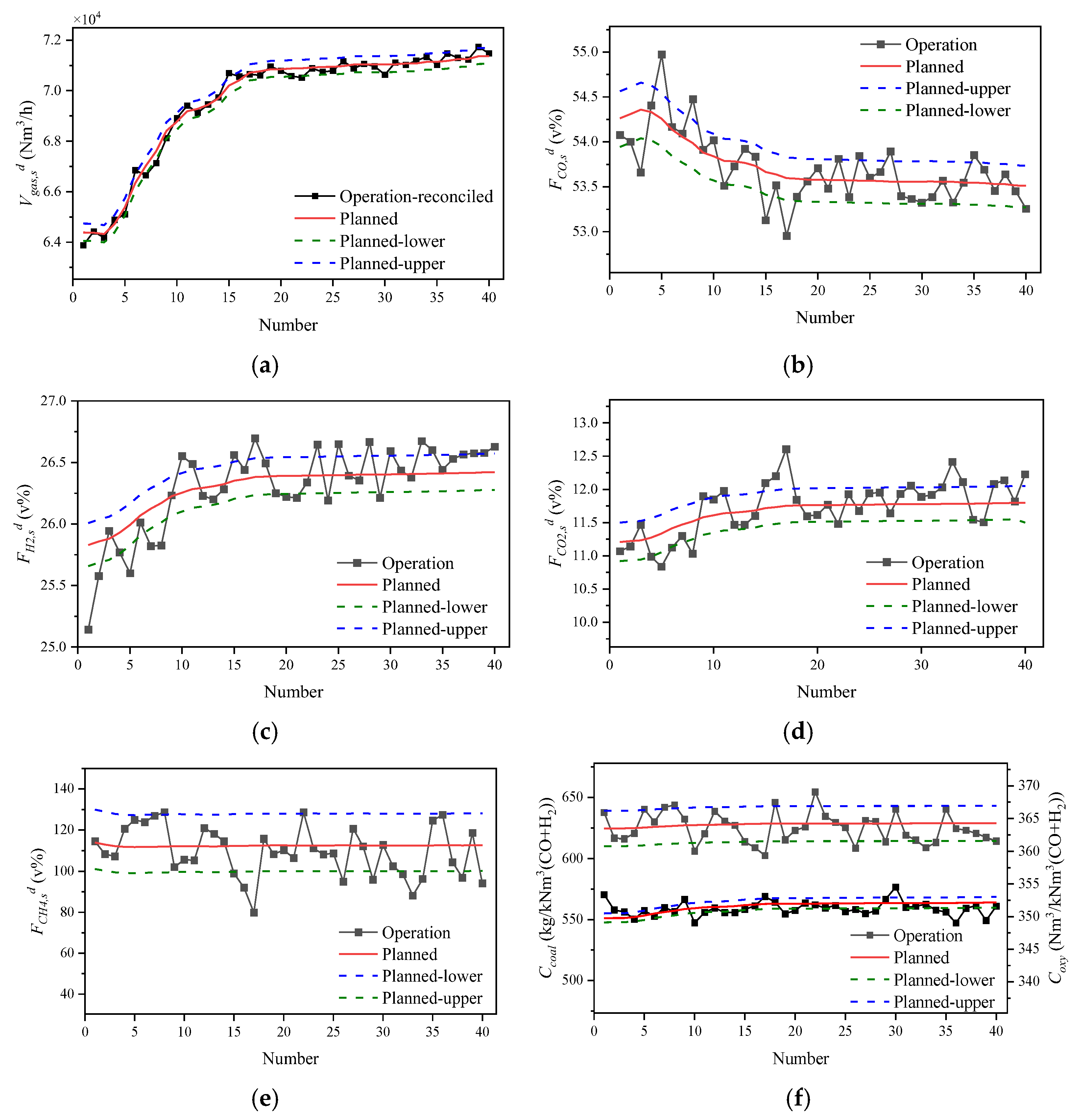
3.1. Results of Data Reconciliation
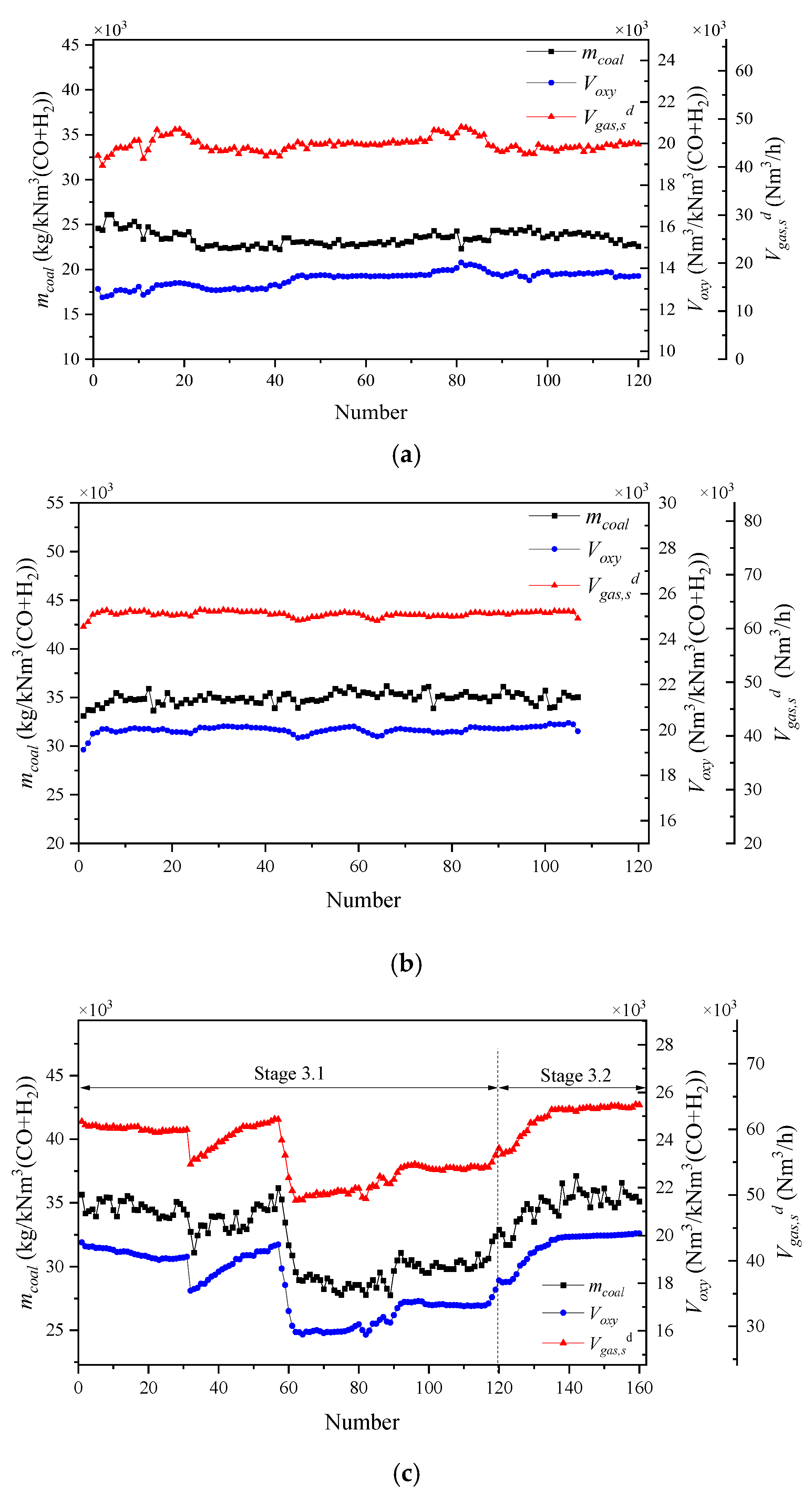
3.1.1. Operational Data in Three Operating Stages
3.1.2. Data Reconciliation Results of Stable Operating Conditions
3.1.3. Data Reconciliation Results of Variable Operating Conditions
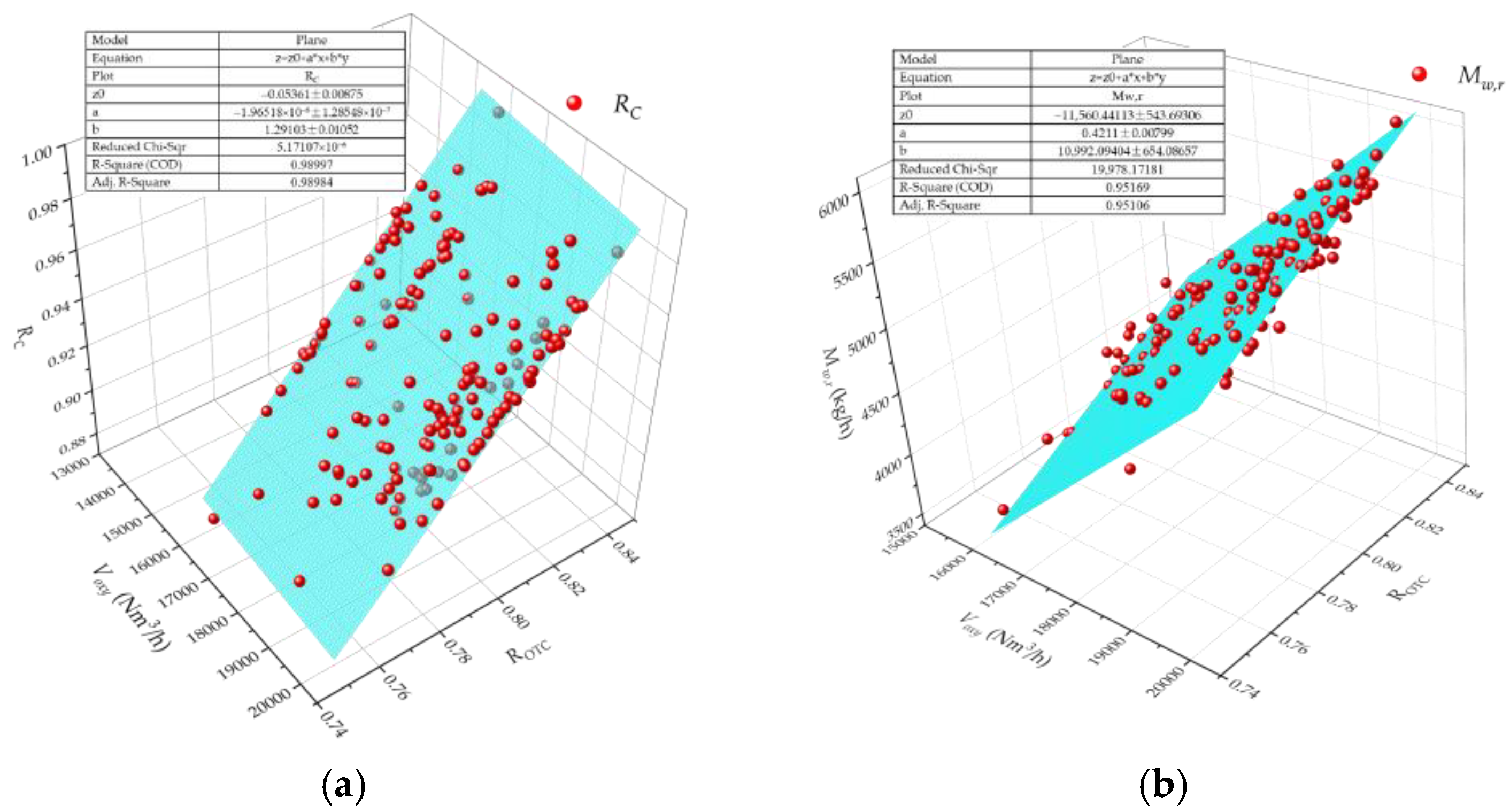
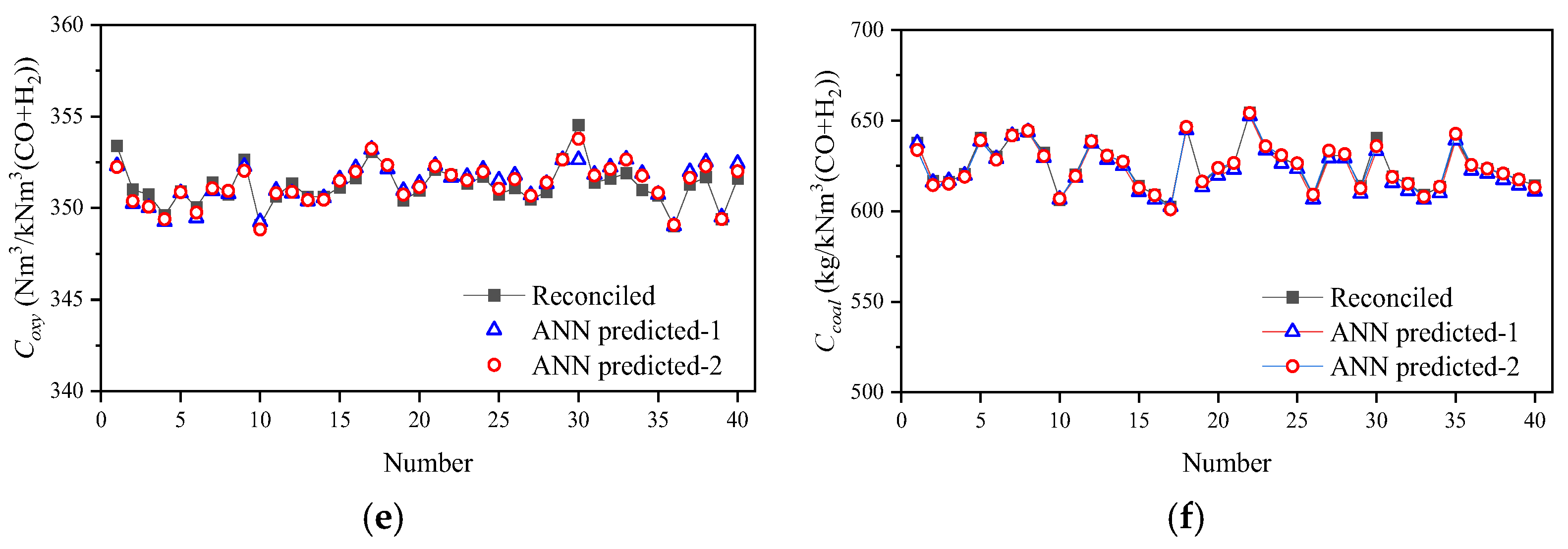
3.2. Results of the Offline Prediction Module
3.3. Results of the Online Estimation Module
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Janajreh, I.; Adeyemi, I.; Raza, S.S.; Ghenai, C. A review of recent developments and future prospects in gasification systems and their modeling. Renew. Sustain. Energy Rev. 2021, 138, 110505. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Shang, C.; Huang, D. Operation optimization of Shell coal gasification process based on convolutional neural network models. Appl. Energy 2021, 292, 116847. [Google Scholar] [CrossRef]
- Chen, C.-J.; Hung, C.-I.; Chen, W.-H. Numerical investigation on performance of coal gasification under various injection patterns in an entrained flow gasifier. Appl. Energy 2012, 100, 218–228. [Google Scholar] [CrossRef]
- Watanabe, H.; Kurose, R. Modeling and simulation of coal gasification on an entrained flow coal gasifier. Adv. Powder Technol. 2020, 31, 2733–2741. [Google Scholar] [CrossRef]
- Mularski, J.; Pawlak-Kruczek, H.; Modlinski, N. A review of recent studies of the CFD modelling of coal gasification in entrained flow gasifiers, covering devolatilization, gas-phase reactions, surface reactions, models and kinetics. Fuel 2020, 271, 117620. [Google Scholar] [CrossRef]
- Kim, M.; Ye, I.; Jo, H.; Ryu, C.; Kim, B.; Lee, J. New reduced-order model optimized for online dynamic simulation of a Shell coal gasifier. Appl. Energy 2020, 263, 114634. [Google Scholar] [CrossRef]
- Kim, H.J.; Li, R.; Yang, Z.; Duan, Y. Modeling, prediction and multi-objective optimization of the coal gasification system. In Proceedings of the E3S Web of Conferences, the 7th International Conference on Renewable Energy Technologies (ICRET 2021), Lumpur, Malaysia, 8–10 January 2021; Volume 242. [Google Scholar]
- Feng, L.; Zhang, G.; Zhai, R. Study on gasification reaction and energy conversion characteristics of the entrained flow coal gasification based on chemical kinetics simulation. Heliyon 2024, 10, e30997. [Google Scholar] [CrossRef] [PubMed]
- Dang, Q.; Zhang, X.; Zhou, Y.; Jia, X. Prediction and optimization of syngas production from a kinetic-based biomass gasification process model. Fuel Process. Technol. 2021, 212, 106604. [Google Scholar] [CrossRef]
- Prabhakar, A.; Kumar Gupta, A.; Kumar Sadhukhan, A.; Gupta, P. Estimation of gasification kinetics of coal char fines in steam ambience. Mater. Today Proc. 2022, 68, 905–909. [Google Scholar] [CrossRef]
- Netter, T.; Fendt, S.; Spliethoff, H. A collection of model parameters describing the gasification behavior of different fuels under entrained flow conditions. Fuel 2021, 296, 120536. [Google Scholar] [CrossRef]
- Shabbar, S.; Janajreh, I. Thermodynamic equilibrium analysis of coal gasification using Gibbs energy minimization method. Energy Convers. Manag. 2013, 65, 755–763. [Google Scholar] [CrossRef]
- Zhou, B.; Chang, J.; Li, J.; Hong, J.; Wang, T.; Zhu, Z.; Zhang, L.; Ma, C. Two-stage gasification process simulation and optimization of pulverized coal for hydrogen-rich production using Aspen plus. Int. J. Hydrog. Energy 2024, 49, 849–860. [Google Scholar] [CrossRef]
- Li, J.; Xu, K.; Yao, X.; Chen, S. Prediction and optimization of syngas production from steam gasification: Numerical study of operating conditions and biomass composition. Energy Convers. Manag. 2021, 236, 114077. [Google Scholar] [CrossRef]
- Gazzani, M.; Manzolini, G.; Macchi, E.; Ghoniem, A.F. Reduced order modeling of the Shell–Prenflo entrained flow gasifier. Fuel 2013, 104, 822–837. [Google Scholar] [CrossRef]
- Safarian, S.; Ebrahimi Saryazdi, S.M.; Unnthorsson, R.; Richter, C. Artificial neural network integrated with thermodynamic equilibrium modeling of downdraft biomass gasification-power production plant. Energy 2020, 213, 118800. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Xu, K. A comprehensive model integrating BP neural network and RSM for the prediction and optimization of syngas quality. Biomass Bioenergy 2021, 155, 106278. [Google Scholar] [CrossRef]
- Wang, H.; Chaffart, D.; Ricardez-Sandoval, L.A. Modelling and optimization of a pilot-scale entrained-flow gasifier using artificial neural networks. Energy 2019, 188, 116076. [Google Scholar] [CrossRef]
- Wang, H.; Ricardez-Sandoval, L.A. Dynamic optimization of a pilot-scale entrained-flow gasifier using artificial recurrent neural networks. Fuel 2020, 272, 117731. [Google Scholar] [CrossRef]
- Ayub, Y.; Hu, Y.; Ren, J. Estimation of syngas yield in hydrothermal gasification process by application of artificial intelligence models. Renew. Energy 2023, 215, 118953. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, D.; Li, Z.J.; Dariva, C.; Cao, Y.; Ellis, N. Predicting and optimizing syngas production from fluidized bed biomass gasifiers: A machine learning approach. Energy 2023, 263, 125900. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.C.; Hazarika, M.K. Artificial neural network based modeling of biomass gasification in fixed bed downdraft gasifiers. Biomass Bioenergy 2017, 98, 264–271. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, L.; Miao, H.; Shang, Y.; Yin, H.; Dong, M. An innovative application of machine learning in prediction of the syngas properties of biomass chemical looping gasification based on extra trees regression algorithm. Energy 2023, 275, 127438. [Google Scholar] [CrossRef]
- Ascher, S.; Sloan, W.; Watson, I.; You, S. A comprehensive artificial neural network model for gasification process prediction. Appl. Energy 2022, 320, 119289. [Google Scholar] [CrossRef]
- Ren, S.; Wu, S.; Weng, Q. Physics-informed machine learning methods for biomass gasification modeling by considering monotonic relationships. Bioresour Technol 2023, 369, 128472. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, J.; Zhou, J.; Zhao, L.; Zhang, D. A hybrid data-driven machine learning framework for predicting the performance of coal and biomass gasification processes. Fuel 2023, 346, 128338. [Google Scholar] [CrossRef]
- Antonio Vélez Godiño, J.; José Jiménez-Espadafor Aguilar, F. Joint data reconciliation and artificial neural network based modelling: Application to a cogeneration power plant. Appl. Therm. Eng. 2024, 236, 121720. [Google Scholar] [CrossRef]
- Narasimhan, S.; Jordache, C. Data Reconciliation and Gross Error Detection: An Intelligent Use of Process Data, 2nd ed.; Gulf Publishing Company: Houston, TX, USA, 2000. [Google Scholar]
- Zhang, Z.; Chuang, Y.-Y.; Chen, J. Methodology of data reconciliation and parameter estimation for process systems with multi-operating conditions. Chemom. Intell. Lab. Syst. 2014, 137, 110–119. [Google Scholar] [CrossRef]
- Loyola-Fuentes, J.; Smith, R. Data reconciliation and gross error detection in crude oil pre-heat trains undergoing shell-side and tube-side fouling deposition. Energy 2019, 183, 368–384. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, P.; Li, Z. Data reconciliation and gross error detection for operational data in power plants. Energy 2014, 75, 14–23. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, P.; Li, Z. data reconciliation for sensor fault monitoring. J. Tsinghua Univ. (Sci. Technol.) 2014, 54, 6. [Google Scholar]
- Zhang, T.; Gräbner, M.; Xu, S. Data reconciliation of an industrial coal gasification plant. Comput. Chem. Eng. 2021, 155, 107503. [Google Scholar] [CrossRef]
- Yu, J.; Han, W.; Chen, K.; Liu, P.; Li, Z. Gross error detection in steam turbine measurements based on data reconciliation of inequality constraints. Energy 2022, 253, 124009. [Google Scholar] [CrossRef]
- Yu, J.; Petersen, N.; Liu, P.; Li, Z.; Wirsum, M. Hybrid modelling and simulation of thermal systems of in-service power plants for digital twin development. Energy 2022, 260, 125088. [Google Scholar] [CrossRef]
- Yu, J.; Liu, P.; Li, Z. Data reconciliation-based simulation of thermal power plants for performance estimation and digital twin development. Comput. Chem. Eng. 2022, 168, 108063. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Z.; Huang, B.; Wang, Y.; Liu, H.; Gong, X. Influence of Water Quench on Syngas Composition of Entrained Flow Pulverized Coal Gasification Process. J. East China Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 44, 6. [Google Scholar]
- Wiinikka, H.; Carlsson, P.; Marklund, M.; Grönberg, C.; Pettersson, E.; Lidman, M.; Gebart, R. Experimental investigation of an industrial scale black liquor gasifier. Part 2: Influence of quench operation on product gas composition. Fuel 2012, 93, 117–129. [Google Scholar] [CrossRef]
- Wiinikka, H.; Carlsson, P.; Granberg, F.; Löfström, J.; Marklund, M.; Tegman, R.; Lindblom, M.; Gebart, R. Design and methodology of a high temperature gas sampling system for pressurized black liquor gasification. Fuel 2010, 89, 2583–2591. [Google Scholar] [CrossRef]
- Higman, C.; van der Burgt, M. Gasification, 2nd ed.; Gulf Professional Publishing: Houston, TX, USA, 2003; ISBN 0-7506-7707-4. [Google Scholar]
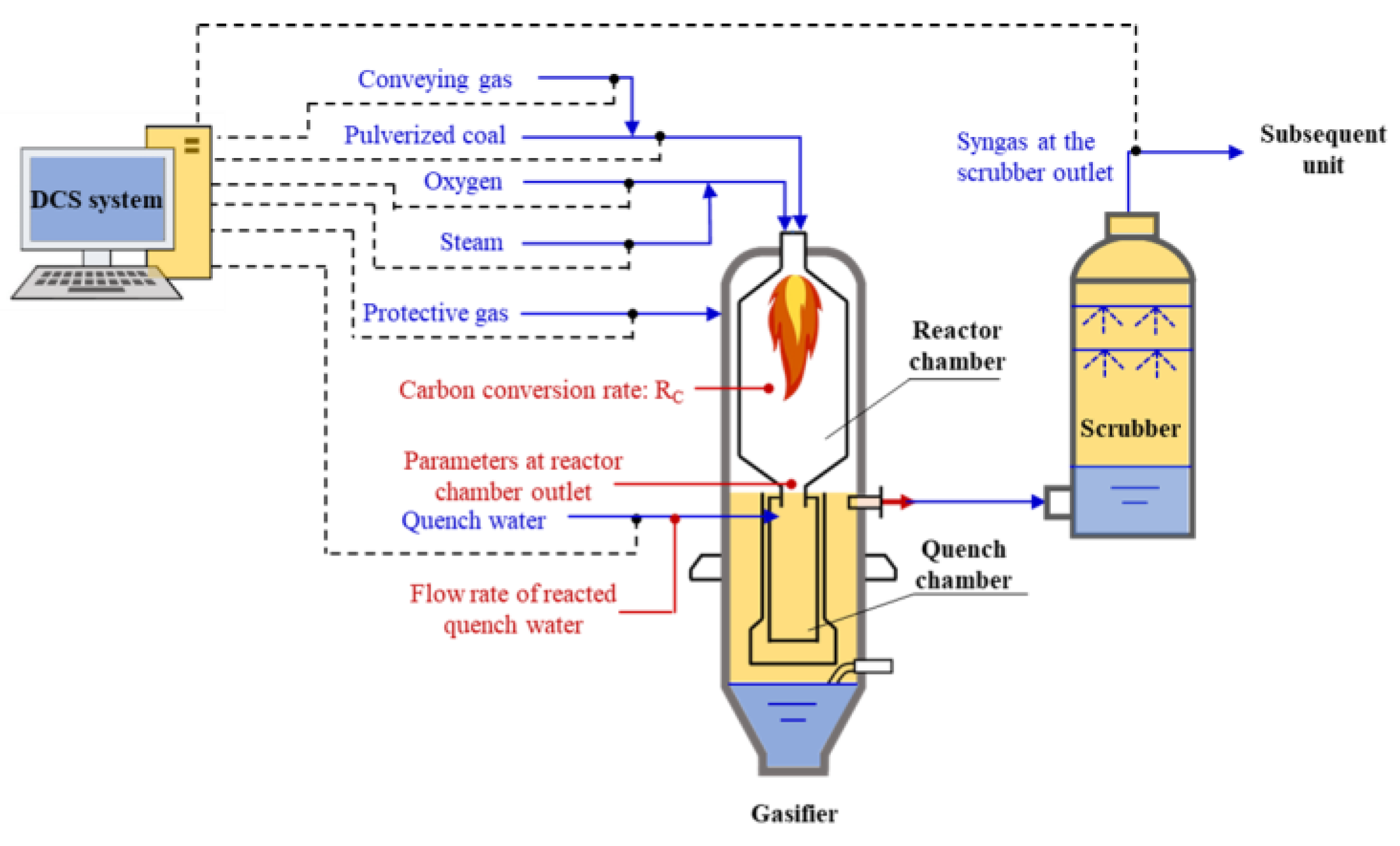



| Proximate Analysis (wt%) | Ultimate Analysis (wt%) | Heat Value (MJ/kg) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mad | Vdaf | Aad | Cad | Had | Oad | Nad | Sad | Qgr,ad |
| 2.3 | 8.90 | 19.2 | 71.9 | 2.0 | 2.6 | 0.5 | 1.5 | 26.3 |
| Parameter Name | Symbol | Unit | Accuracy |
|---|---|---|---|
| Measured parameters: | |||
| Flow rate of coal | mcoal | kg/h | 3% |
| Flow rate of oxygen | Voxy | Nm3/h | 1% |
| Flow rate of steam entering the gasifier | mst | kg/h | 1% |
| Flow rate of coal conveying gas | Vcon | Nm3/h | 2% |
| Flow rate of protective gas | Vpro | Nm3/h | 1% |
| Pressure of the gasifier | Pgas,s | MPaG | 1% |
| Flow rate of wet syngas at the scrubber outlet | Vgas,s | Nm3/h | 2% |
| Temperature of wet syngas at the scrubber outlet | Tgas,s | °C | 1% |
| Pressure of wet syngas at the scrubber outlet | Pgas,s | MPaG | 1% |
| Compositions of syngas at the scrubber outlet: CO | FCO,sd | v% | 2% |
| Flow rate of protective gas | Vpro | Nm3/h | 1% |
| H2 | FH2,sd | v% | 2% |
| CO2 | FCO2,sd | v% | 2% |
| CH4 | FCH4,sd | ppm | 2% |
| N2 | FN2,sd | v% | 2% |
| Unmeasured parameters: | |||
| Carbon conversion rate | Rc | wt% | - |
| Flow rate of reacted quench water | mw,r | kg/h | - |
| Temperature of syngas at the reactor chamber outlet | Tgas,g | °C | - |
| Flow rate of wet syngas at the reactor chamber outlet | Vgas,g | Nm3/h | |
| Compositions of wet syngas at the reactor chamber outlet: CO | FCO,g | v% | - |
| H2 | FH2,g | v% | - |
| CO2 | FCO2,g | v% | - |
| CH4 | FCH4,g | ppm | - |
| N2 | FCO,g | V% | - |
| Performance metrics: | |||
| Coal consumption | Ccoal | kg/kNm3(CO+H2) | - |
| Oxygen consumption | Coxy | Nm3/kNm3(CO+H2) | - |
| Parameter | Stag 1 | Stage 2 | ||||
|---|---|---|---|---|---|---|
| Measured | Reconciled | Adjusted Percentage | Measured | Reconciled | Adjusted Percentage | |
| mcoal | 23,462.0 | 23,979.5 | 2.21% | 34,945.6 | 34,552.4 | −1.1% |
| Voxy | 13,472.9 | 13,466.2 | −0.05% | 19,999.6 | 19,989.6 | 0.0% |
| mst | 1769.7 | 1776.3 | 0.37% | 2857.1 | 2876.2 | 0.7% |
| Vcon | 2331.1 | 2385.0 | 2.31% | 3609.2 | 3552.4 | −1.6% |
| Vpro | 1733.2 | 1729.5 | −0.21% | 1935.1 | 1924.8 | −0.5% |
| Vgas,sd | 44,609.7 | 49,641.4 | 11.28% | 62,678.0 | 70,527.5 | 12.5% |
| Vgas,sd-2 (1) | 50,200.0 | - | - | 71,068.0 | - | - |
| FCO,sd | 56.19 | 56.23 | 0.07% | 54.29 | 54.27 | 0.0% |
| FH2,sd | 22.89 | 22.84 | −0.23% | 26.23 | 26.26 | 0.1% |
| FCO2,sd | 8.18 | 8.19 | 0.13% | 11.44 | 11.43 | −0.1% |
| FCH4,sd | 183.48 | 187.46 | 2.17% | 111.82 | 108.83 | −2.7% |
| FN2,sd | 12.72 | 12.72 | −0.01% | 8.03 | 8.03 | 0.0% |
| Rc | 95.0 (2) | 95.81 | 0.86% | 96.0 (2) | 97.35 | 1.4% |
| mw,r | - | 2941.65 | - | - | 5877.92 | - |
| Tgas | - | 1440 | - | - | 1573 | - |
| Vgas,g | - | 46,339.7 | - | - | 64,013.2 | - |
| FCO,g | - | 67.82 | - | - | 70.91 | - |
| FH2,g | - | 16.44 | - | - | 17.37 | - |
| FCO2,g | - | 0.83 | - | - | 1.11 | - |
| FH2O,g | - | 0.77 | - | - | 1.24 | - |
| FCH4,g | - | 199.76 | - | - | 119.30 | - |
| FN2,g | - | 13.62 | - | - | 8.84 | - |
| Ccoal | 680 | 611 | −10.13% | 685 | 608 | −11.15% |
| Coxy | 382 | 343 | −10.17% | 396 | 352 | −11.19% |
| Roff2 | RMSE | RRMSE | Roff2 | RMSE | RRMSE | ||
|---|---|---|---|---|---|---|---|
| Vgas,sd | 0.9212 | 240.33 | 0.35% | FCH4,sd | 0.8134 | 12.410 | 11.03% |
| FCO,sd | 0.8548 | 0.2739 | 0.51% | Ccoal | 0.8240 | 12.777 | 2.04% |
| FH2,sd | 0.7819 | 0.2174 | 0.83% | Coxy | 0.6763 | 1.2961 | 0.37% |
| FCO2,sd | 0.7247 | 0.3033 | 2.60% |
| Parameter | ANN Predicted-1 | ANN Predicted-2 | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | RRMSE | R2 | RMSE | RRMSE | |
| RC | 0.9689 | 0.0034 | 0.36% | 0.9945 | 0.0014 | 0.15% |
| Mw,r | 0.9083 | 114.63 | 2.07% | 0.9898 | 38.303 | 0.69% |
| Tgas,g | 0.8792 | 5.7766 | 0.38% | 0.9597 | 3.3371 | 0.22% |
| Vgas,sd | 0.8423 | 907.10 | 1.30% | 0.9560 | 479.16 | 0.69% |
| Ccoal | 0.9583 | 2.4903 | 0.40% | 0.9859 | 1.4461 | 0.23% |
| Coxy | 0.7345 | 0.6325 | 0.18% | 0.8573 | 0.6780 | 0.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yue, K.; Yuan, C.; Xiang, J. A Data Reconciliation-Based Method for Performance Estimation of Entrained-Flow Pulverized Coal Gasification. Energies 2025, 18, 1079. https://doi.org/10.3390/en18051079
Zhang Y, Yue K, Yuan C, Xiang J. A Data Reconciliation-Based Method for Performance Estimation of Entrained-Flow Pulverized Coal Gasification. Energies. 2025; 18(5):1079. https://doi.org/10.3390/en18051079
Chicago/Turabian StyleZhang, Yan, Kai Yue, Chang Yuan, and Jiahao Xiang. 2025. "A Data Reconciliation-Based Method for Performance Estimation of Entrained-Flow Pulverized Coal Gasification" Energies 18, no. 5: 1079. https://doi.org/10.3390/en18051079
APA StyleZhang, Y., Yue, K., Yuan, C., & Xiang, J. (2025). A Data Reconciliation-Based Method for Performance Estimation of Entrained-Flow Pulverized Coal Gasification. Energies, 18(5), 1079. https://doi.org/10.3390/en18051079







