Combined State-of-Charge Estimation Method for Lithium-Ion Batteries Using Long Short-Term Memory Network and Unscented Kalman Filter

Abstract

The state of charge (SOC) of lithium-ion batteries (LIBs) is a pivotal metric within the battery management system (BMS) of electric vehicles (EVs). An accurate SOC is crucial to ensuring both the safety and the operational efficiency of a battery. The unscented Kalman filter (UKF) is a classic and commonly used method among the various SOC estimation algorithms. However, an unscented transform (UT) utilized in the algorithm struggles to completely simulate the probability density function of actual data. Additionally, inaccuracies in the identification of battery model parameters can lead to performance degradation or even the divergence of the algorithm in SOC estimation. To address these challenges, this study introduces a combined UKF-LSTM algorithm that integrates a long short-term memory (LSTM) network with the UKF for the precise SOC estimation of LIBs. Firstly, the particle swarm optimization (PSO) algorithm was utilized to accurately identify the parameters of the battery model. Secondly, feature parameters that exhibited a high correlation with the estimation error of the UKF were selected to train an LSTM network, which was then combined with the UKF to establish the joint algorithm. Lastly, the effectiveness of the UKF-LSTM was confirmed under various conditions. The outcomes demonstrate that the average absolute error (MAE) and the root mean square error (RMSE) for the SOC estimation by the algorithm were less than 0.7%, indicating remarkable estimation accuracy and robustness.

1. Introduction

Amid escalating environmental degradation and dwindling oil reserves, electric vehicles (EVs) have gained widespread adoption, owing to their high efficiency, environmental friendliness, and energy-conservation benefits [1]. Meanwhile, the popularity of EVs has also driven a boom in research on energy storage devices. Lithium-ion batteries (LIBs), as one of the power source types in EVs, have gradually become the focus of research due to their high energy density, long cycle life, and minimal self-discharge rate [2,3,4,5]. The state of charge (SOC) plays an important role in the battery management system (BMS), essential for ensuring that a battery operates safely and stably. However, this parameter cannot be measured directly by sensors. Therefore, an accurate SOC estimation method is key in battery research [6].

An accurate SOC value is crucial for ensuring the stable operation of the BMS. Accordingly, to enhance the precision and robustness of SOC estimation, researchers have proposed various methods. Currently, the primary SOC estimation methods are categorized into the following three types.

Experiment-based methods are utilized to establish the mapping relationship between experimental test parameters and the SOC, which includes the open-circuit voltage method and the Coulomb counting method. The open-circuit voltage (OCV) method utilizes the nonlinear relationship between the OCV and the SOC to determine the SOC value. Nevertheless, during the measurement of the OCV, the battery must be allowed a prolonged resting period. Therefore, the method is unsuitable for use in online SOC estimation [7]. The Coulomb counting method uses current-to-time integration to achieve SOC estimation, but it has cumulative errors over time [8]. Although experiment-based methods are reliable, their applications are limited, making them difficult to be widely used [9]. Therefore, the methods are primarily employed to acquire benchmark data for comparative analysis with alternative methods or for utilization during laboratory calibration sessions.

Model-based methods primarily utilize Kalman filter (KF) algorithms combined with battery models to obtain the SOC. The main KF includes the extended Kalman filter (EKF) and the unscented Kalman filter (UKF) [10,11]. In contrast to the EKF, the UKF is widely used because it can avoid linearization errors and provide an accurate value of battery SOC estimation with relatively low computational cost [12]. For example, Sangeetha et al. [13] employed the Thevenin model in conjunction with the EKF to obtain a battery SOC. Results indicated that this approach could effectively estimate the battery SOC. However, the EKF relies on Taylor series expansion to linearize the nonlinear system, inevitably introducing linear errors in the process. To address the issue, Vedhanayaki et al. [14] proposed the UKF combined with the Coulomb counting method. Unlike the EKF, the UKF applies the unscented transform (UT) to simulate a linear system, enhancing the precision of the estimation results. Additionally, the method utilizes Coulomb counting to circumvent the issue of capacity degradation due to battery usage, maintaining the error of the SOC estimation within 1%. Wang et al. [15] introduced an online algorithm for SOC estimation utilizing a modified square root-untraced Kalman filter (SR-UKF). Accurate SOC estimates are obtained by avoiding the negative definite of the state matrix during the state update process and by considering the impact of the temperature on battery capacity changes. However, although the UKF demonstrates superior performance in SOC estimation, it requires higher model accuracy and is more sensitive to system noise. Consequently, these constraints hinder the effectiveness of the UKF in estimating battery SOCs. To overcome this issue, the UKF is frequently integrated with alternative techniques to improve the precision of SOC estimation.

Data-driven methods use machine learning and deep learning techniques to construct a correlation between the SOC and battery characteristic parameters [16,17,18]. Meanwhile, the methods can obtain more accurate estimation results and demonstrate strong nonlinear processing capabilities. For instance, Mao et al. [19] utilized a particle swarm optimization algorithm optimized by Levy’s flight strategy (LPSO) to determine the weights and thresholds within the backpropagation (BP) neural network for estimating the LIB SOC. The results indicate that the BP network, refined with the LPSO, achieves some improvements in SOC prediction accuracy. However, this method still has the potential to further improve due to the simplistic structure of the BP network and the absence of consideration for temporal variations in the information transfer process. To avoid this issue, Almaita et al. [20] used a long short-term memory (LSTM) neural network to estimate the SOC in a high-capacity LIB storage system. The LSTM network was trained and validated using actual data from the Al-Manara photovoltaic power plant. The results indicated that the mean squared error (MSE) for the feedforward neural network ranged from 5.37% to 9.22%, while for the deep feedforward neural network, it ranged from 4.03% to 7.37%. In contrast, the MSE of the LSTM network was less than 0.62%. This significant reduction was attributed to the memory cell and forget gate of the LSTM network, which enhanced prediction performance for time-varying battery data. In addition, Chai et al. [21] enhanced the LSTM network by employing a random search algorithm to select optimal network parameters, thereby improving the SOC estimation precision of the LSTM network. However, data-driven methods lack clear explicit physical interpretation and comprehensibility, and their efficacy is profoundly affected by the quality of the data [22]. Therefore, the methods exhibit a strong dependence on training sets and lack reliability.

The analysis above indicates that although various SOC estimation methods rely on their respective characteristics to estimate battery SOCs, achieving accurate SOC estimation through a singular method continues to be challenging. Consequently, with ongoing innovations in research methods, certain combined estimation methods have gained significant attention from researchers. For instance, Zhao et al. [23] integrated the EKF with the Coulomb counting method to develop an SOC estimation method that identifies errors and formulated error equations under various error sources. Based on this, the method is proposed for sensor fault identification correction and model parameter error estimation. However, the study overlooks the issue of linear errors introduced by the EKF when approximating the linearization of the model in the Taylor expansion. Additionally, Zeng et al. [24] introduced an integrated SOC estimation method that combines modeling and dual data driving. The approach simultaneously inputs SOC estimates from both the UKF and the LSTM network into another LSTM network to achieve optimal SOC estimation. However, the method overlooks the problem of error accumulation over time, and its practical value still needs further verification. Meanwhile, Pei et al. [25] utilized a BP network optimized through the tuna swarm optimization (TSO) algorithm to perform online error compensation in the EKF. The validation indicated that the TSO-BP can effectively reduce the estimation error of the EKF and enhance SOC estimation accuracy due to the error correction principle. However, the BP network in the method does not take into account the influence of time on the data model and fails to capture the time-varying information during the battery charge and discharge process. Consequently, the SOC estimation accuracy of the method will gradually decrease over time.

In studies of joint-method SOC estimation, certain joint methods have enhanced SOC estimation accuracy compared to traditional algorithms. However, common joint estimation methods of model-based methods combined with data-driven methods mostly fail to take into account the impact of the differences in the KF algorithms themselves on the performance of the algorithms, as well as the strong time-varying nonlinear nature of the battery system. The joint SOC estimation method of using LSTM to optimize the UKF (UKF-LSTM) is proposed in this study to address these issues.

The main contributions of this study are as follows:

(1)

A Thevenin model was established. Then, the particle swarm optimization (PSO) algorithm was utilized to determine the unknown parameters of the battery model. The model accuracy was verified under specified working conditions.

(2)

To obtain key parameters involved in the UKF estimation errors, combined with identified battery model parameters, the UKF was utilized to preliminarily calculate the battery SOC under the training condition. These key characteristic parameters were subsequently used to train the LSTM network. The trained LSTM network was employed to mitigate the UKF estimation errors, thereby enhancing the estimation performance of the UKF.

(3)

The UKF-LSTM was evaluated under different working conditions. The verified results demonstrate that the joint estimation approach proposed in this research yields precise SOC estimation, surpassing the accuracy of the EKF and UKF.

2. Experiment of Battery

The experimental platform for the LIB was established, as shown in Figure 1. It included the ARBIN BT-5HC-5V-100A battery test instrument produced by Arbin Instruments in College Station, TX, USA, the RGD-500 temperature and humidity chamber produced by Lab Companion in Dongguan, China, and the host computer. During the experiment, the battery was placed in the temperature chamber to ensure a constant temperature. The ARBIN test instrument was used to load the test program, monitor the current, voltage, capacity, and other parameters of the battery in the experiment in real time, and transmit them to the host computer. The parameters of the selected NMC LIB are shown in

Table 1. Parameters of the battery.

Normal Capacity	Normal Voltage	Voltage Range	Temperature Range
2 Ah	3.6 V	[3.0, 4.1] V	[−10, 45] °C

.

To obtain the dynamic characteristics of the battery under various excitations, three experiments were designed: the hybrid pulse power characterization (HPPC) test, the dynamic stress test (DST), and the urban dynamometer driving schedule (UDDS) test. These tests were performed at 25 °C. Charging and discharging currents were defined as positive values and negative values, respectively. The experimentally collected current and voltage versus time curves are shown in Figure 2.

3. Battery Model and Parameter Identification

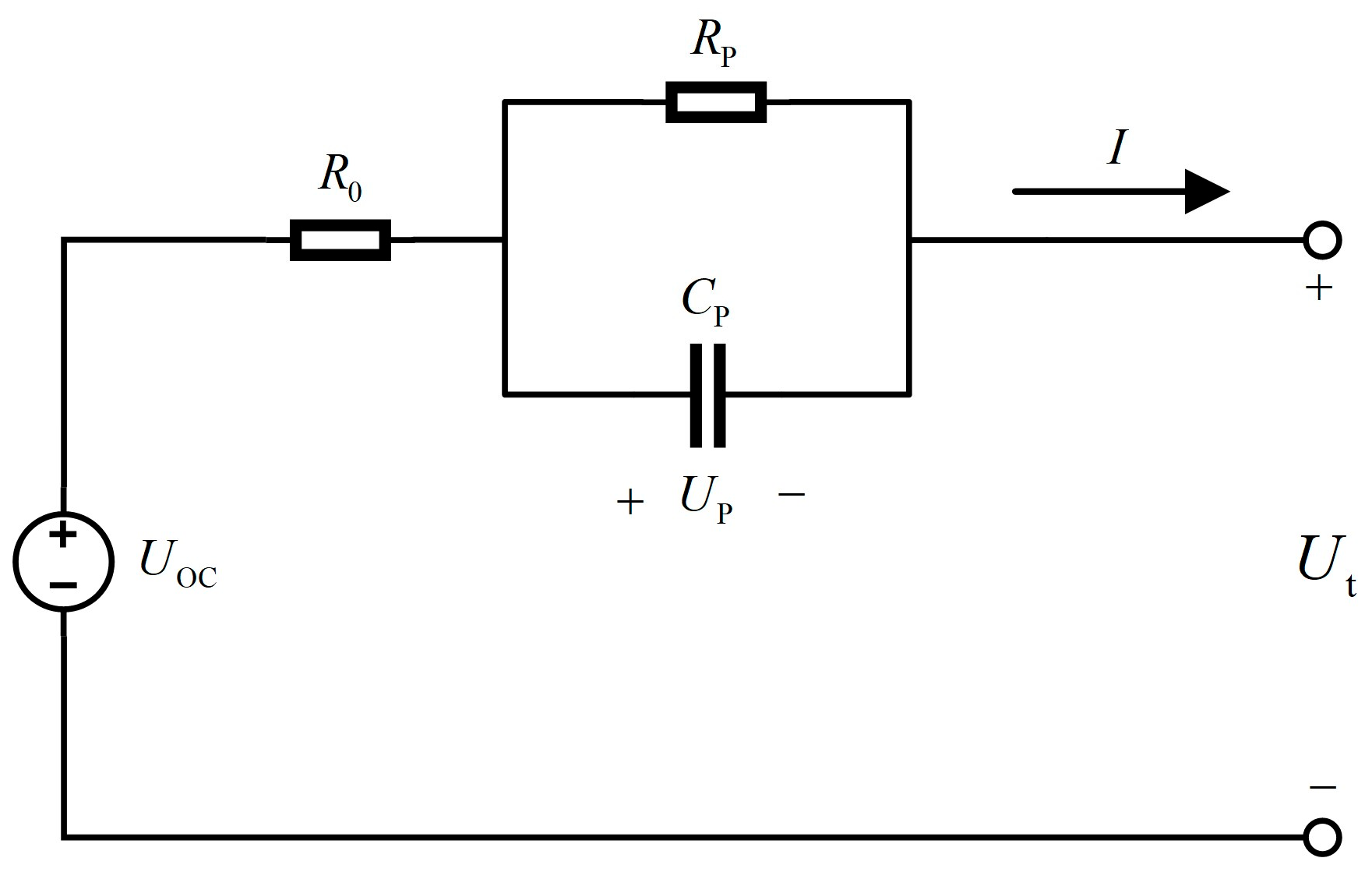
3.1. Battery Model

The equivalent circuit model (ECM) is used to describe the nonlinear characteristics of a battery through circuit components such as resistors and capacitors [26]. Typical ECMs include the Rint model, Thevenin model [27], and dual polarization model [28]. The Thevenin model was selected for battery modeling because it accurately represents the polarization effect of batteries and requires a moderate computational cost [29]. Its circuit structure is shown in Figure 3.

In Figure 3, $R_{\mathrm{p}}$ represents the polarization resistance, $C_{\mathrm{p}}$ represents the polarization capacitance, $U_{\mathrm{p}}$ represents the polarization voltage, $U_{\mathrm{OC}}$ denotes the open-circuit voltage, $R_0$ denotes the ohmic internal resistance, $I$ is the current, and $U_{\mathrm{t}}$ is the terminal voltage. According to Kirchhoff’s law, the circuit equations for the model are described as follows:

$$\begin{array}{l}{\displaystyle \frac{d{U}_{\mathrm{p}}}{dt}}={\displaystyle \frac{I}{C_{\mathrm{p}}}}-{\displaystyle \frac{U_{\mathrm{p}}}{R_{\mathrm{p}}{C}_{\mathrm{p}}}},\\ U_{\mathrm{t}}=U_{\mathrm{oc}}-U_{\mathrm{p}}-I{R}_0.\end{array}$$

(1)

By choosing $SOC$ and $U_{\mathrm{p}}$ as the system state variables, the state space equations for the Thevenin equivalent circuit model can be obtained as follows:

$$\begin{array}{l}\left[\begin{array}{c}SO{C}_k\\ U_{\mathrm{p},k}\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& e^{-{\displaystyle \frac{T}{\tau }}}\end{array}\right]\left[\begin{array}{c}SO{C}_{k-1}\\ U_{\mathrm{p},k-1}\end{array}\right]+\left[\begin{array}{c}-{\displaystyle \frac{\eta T}{C_{\mathrm{N}}}}\\ R_{\mathrm{p}}(1-e^{-{\displaystyle \frac{T}{\tau }}})\end{array}\right]I_{k-1},\\ U_{\mathrm{t},k}=U_{\mathrm{OC},k}-I_k{R}_0-U_{\mathrm{p},k}.\end{array}$$

(2)

where $\tau =C_{\mathrm{p}}$, $k$ represents the moment, $\eta$ denotes the charge and discharge efficiency, $C_{\mathrm{N}}$ represents the battery capacity, and $T$ represents the sampling time.

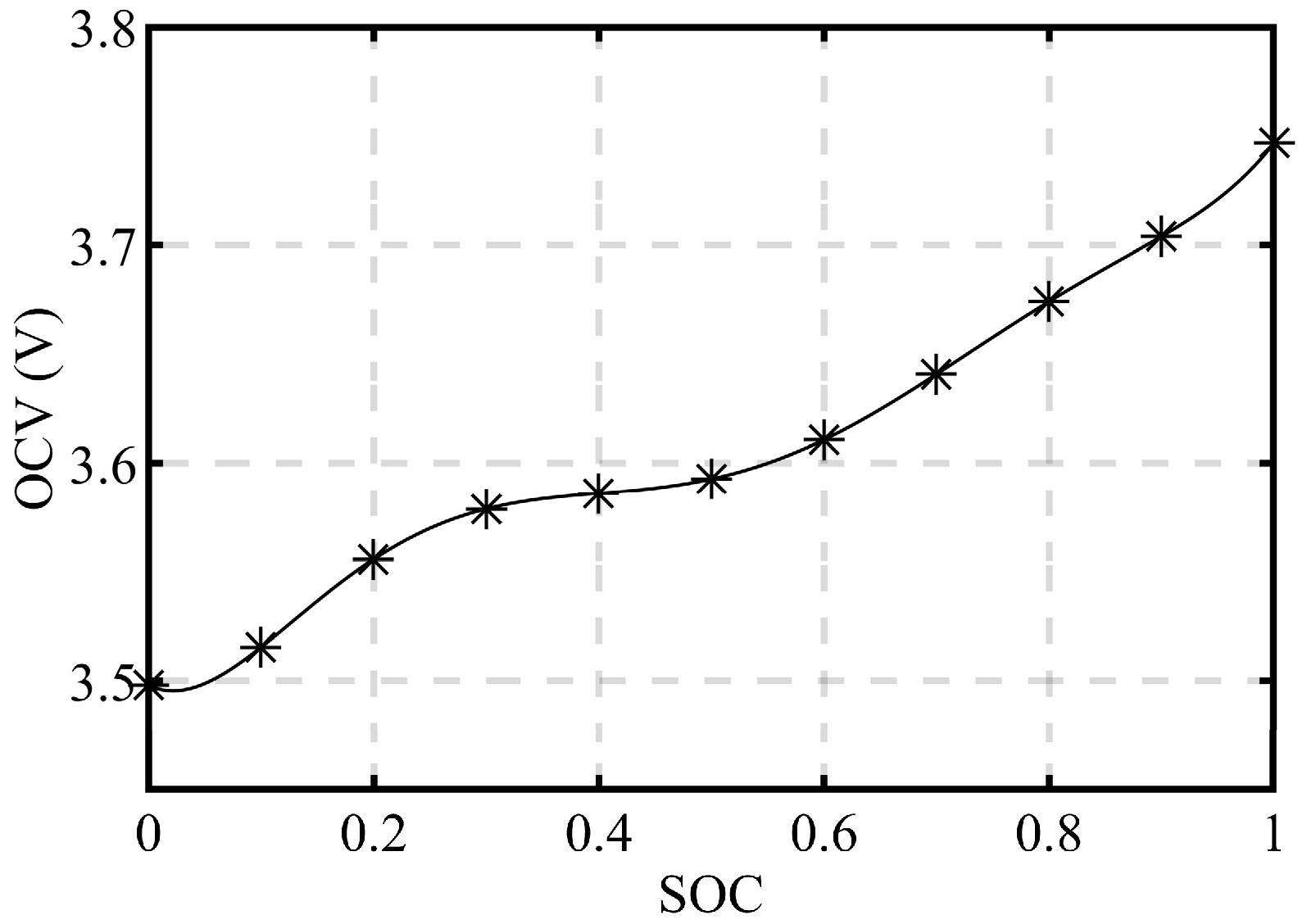
3.2. Parameter Identification

The OCV, as a critical parameter in the ECM of batteries, exhibits a highly nonlinear relationship with the SOC [30]. The precision of the OCV-SOC curve fitting plays a crucial role in determining the accuracy of parameter identification and SOC estimation.

The HPPC test was employed to conduct charge and discharge cycles on the battery at currents of 1 A, 2 A, 4 A, and 6 A, respectively. In the middle of each cycle, ten percent of the rated capacity was discharged at a constant current of 1 A for a total of ten cycles. The terminal voltage was measured after each cycle and sufficient resting, at which point the terminal voltage could be approximately equal to the OCV. Then, the linear relationship between the OCV and SOC was obtained through sixth-order polynomial fitting, and the OCV-SOC fitting curve is shown in Figure 4. The fitted equation for the OCV and SOC is as follows:

$$\begin{array}{l}OCV=26.88SO{C}^6+-85.69SO{C}^5+102.67SO{C}^4\\ -55.97SO{C}^3+13.10SO{C}^2-0.49SO{C}^1+3.59.\end{array}$$

(3)

Accurate model parameters are crucial for SOC estimation. PSO is favored because of its simplicity, ease of implementation, rapid convergence, and minimal parameter regulation required compared to other common offline parameter identification methods based on optimization algorithms [31]. Thus, it was used to identify R₀, R_p, and C_p in the battery model.

PSO is designed to imitate the collaborative behavior of birds in a flock searching for food [32]. In the pursuit of the optimal solution, each bird is modeled as a particle that updates its velocity and position according to its own best-known location and the best-known location of the entire population. By continually updating their velocities and positions, particles move toward the optimal solution and ultimately find the target solution. The identification of Thevenin model parameters was carried out using PSO in conjunction with HPPC test data obtained from the battery, with the identified model parameters shown in

Table 2. Parameters of the Thevenin model.

SOC (100%)	R0 (Ω)	Rp (Ω)	$\mathit{\tau }$
100	0.0429	0.0127	18.8830
90	0.0432	0.0198	25.1113
80	0.0435	0.0200	26.4768
70	0.0427	0.0200	24.7980
60	0.0433	0.0199	35.9415
50	0.0433	0.0160	28.5256
40	0.0436	0.0170	30.2397
30	0.0437	0.0160	25.9252
20	0.0455	0.0200	30.5394
10	0.0653	0.0200	47.8707

.

4. Method for SOC Estimation

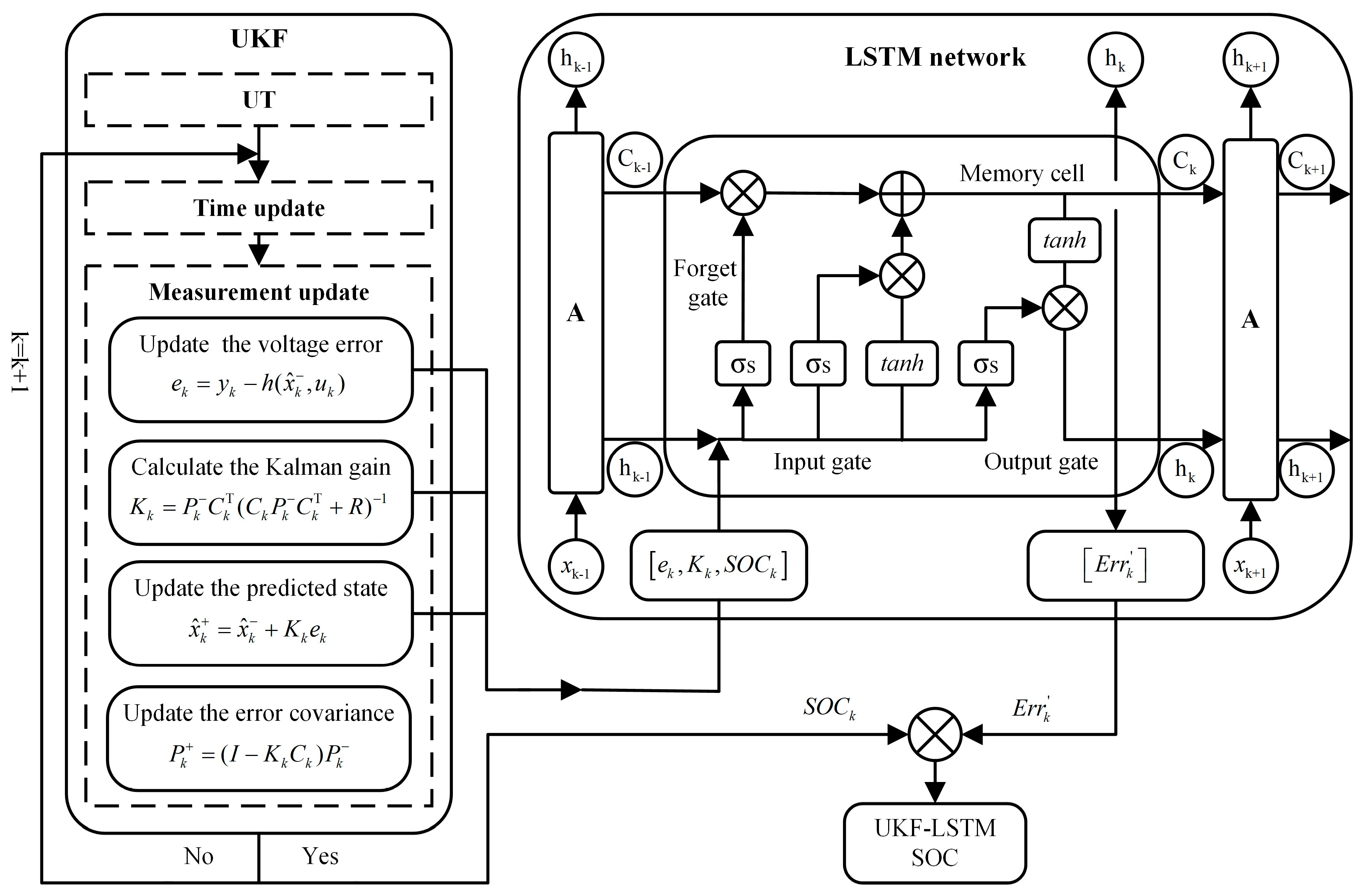
4.1. The UKF Method

The UKF employs the UT to substitute the linearization process of the Taylor expansion in nonlinear systems, thereby avoiding the introduction of linear errors. The approach also removes the necessity to compute the complex Jacobian matrix for the system equations, effectively reducing the computational load and minimizing state estimation errors [33]. The equation of the nonlinear system of the battery, considering the impact of noise, can be expressed in the following form:

$$\left\{\begin{array}{l}{x}_{k+1}=f(x_k,u_k)+{\omega }_k\\ y_k=h(x_k,u_k)+v_k\end{array}\right..$$

(4)

where $f$ and $h$ represent the state and observation equations of the nonlinear system, respectively, $x$ denotes the state vector of the system with $x_{k+1}$ equal to $\left[{SOC}_k, U_{\mathrm{p},k}\right]$, $y$ denotes the observation vector of the system with $y_k$ equal to $U_{\mathrm{t},k}$, $u$ represents the input vector with $u_k$ equal to $I_k$, ${\omega }_k$ is the process noise with the covariance $Q$, and $v_k$ is the observation noise with the covariance $R$. It is assumed that both ${\omega }_k$ and $v_k$ are Gaussian white noises and are independent of each other.

The UKF approximates the real system using the UT [34]. The UT, as a numerical sampling method, involves identifying a minimal set of Sigma points to estimate the mean and covariance of the state variables after undergoing a nonlinear transformation. Subsequently, the system equations are mapped to generate new Sigma points which are then used to obtain the transformed mean and covariance. The steps of the UT are as follows:

(1) Compute the Sigma sampling points:

$$\left\{\begin{array}{l}{x}^{(0)}=\overline{x},i=0\\ x^{(i)}=\overline{x}+{(\sqrt{(n+\lambda )P})}_i,i=1\sim n\\ x^{(i)}=\overline{x}-{(\sqrt{(n+\lambda )P})}_i,i=n+1-2n\end{array}\right..$$

(5)

(2) Compute the weights corresponding to the Sigma sampling points:

$$\left\{\begin{array}{l}{{\omega }_m}^{(0)}={\displaystyle \frac{\lambda }{n+\lambda }}\\ {{\omega }_c}^{(0)}={\displaystyle \frac{\lambda }{n+\lambda }}+(1-{\alpha }^2+\beta )\\ {{\omega }_m}^{(i)}={{\omega }_c}^{(i)}={\displaystyle \frac{\lambda }{2(n+\lambda )}},i=1\sim 2n\end{array}\right..$$

(6)

where $\stackrel{-}{x}$ and $P$ represent the mean and covariance, respectively. $i$ denotes the serial number of the sampling point; $n$ is the dimension of the state; ${\omega }_m$ is the weight of the mean; ${\omega }_c$ is the weight assigned to the covariance; $\lambda$ is a scaling factor intended to reduce the overall prediction error and complies with parameters $\lambda ={\alpha }^2(n+{\rm K})-n$ and ${\rm K}=3-n$; ${\rm K}$ is a parameter to be determined, and it is often set to 0 to ensure that $(n+\lambda )P$ represents a semi-positive definite matrix; $\alpha$ is a coefficient that controls the state of the sampling point distribution, ranging from 0 to 1; and $\beta$ is a parameter to be determined, required to be greater than or equal to 0, used to integrate the effects of higher-order terms.

4.2. The LSTM Network Method

Temporal relationships are crucial in battery test data. Unlike the traditional BP network, which completely ignores the impact of temporal relationships on data modeling, the recurrent neural network (RNN) incorporates the memory cell to preserve historical information, thereby enhancing the forecasting accuracy of time series data [35]. As a variant of the RNN, the LSTM network was proposed by Hochreiter et al. [36]. It is specifically designed to address the issue of long-term dependencies. The network can be trained to retain information over extended periods and possesses specific memory functions. It primarily consists of the memory cell, forget gate, input gate, and output gate. The input gate regulates the incoming information of the neuron at a specific moment. The output gate simultaneously manages the output information of the neuron; the forget gate allows the model to choose whether to discard or retain old information upon the introduction of new data. By controlling the memory cell through the forget gate and input gate, issues such as gradient vanishing and explosion can be efficiently avoided, and the ability of the neural network to extract time series relationships can be enhanced [37]. The computation of the LSTM network with the time step k is as follows:

$$\left\{\begin{array}{l}{c}_k=f_k{c}_{k-1}+i_k\tanh (W_c{x}_k+U_c{h}_{k-1}+b_c)\\ f_k={\sigma }_g(W_f{x}_k+U_f{h}_{k-1}+b_f)\\ i_k={\sigma }_g(W_i{x}_k+U_i{h}_{k-1}+b_i)\\ o_k={\sigma }_g(W_o{x}_k+U_o{h}_{k-1}+b_o)\\ h_k=\tanh (c_k)o_k\end{array}\right..$$

(7)

where $k$ is the current moments and $k-1$ denotes the previous moments. The variables $i_k$, $f_k$, $o_k$, and $c_k$ represent the outputs of the input gate, forget gate, output gate, and cell state update, respectively; $W_f$, $W_i$, $W_c$, and $W_o$ are the input weights corresponding to these four components, respectively; $U_f$, $U_i$, $U_c$, and $U_o$ are the output weights corresponding to these components, respectively; $b_f$, $b_i$, $b_c$, and $b_o$ are the biases corresponding to these states, respectively; $x_k$ and $h_k$ represent the input vectors and the outputs of the hidden layer, respectively; and ${\sigma }_g$ and $\tanh$ are the activation functions used.

4.3. Improving the UKF Method Using LSTM Network

The UKF, based on Bayesian theory and the UT, exhibits good applicability in battery SOC estimation. However, it also faces challenges with unstable estimation results and greater errors. This instability arises because the UT cannot fully replicate actual data distributions, and the process and observation noises in the UKF additionally compromise the results, leading to uncertain SOC estimates. Moreover, the UKF demands high precision in battery modeling, yet the identified model parameters do not accurately represent the battery during SOC estimation, resulting in some errors. Given these issues, it is challenging to achieve accurate SOC estimation using only a model-based UKF in actual operation.

The LSTM network, recognized for its potent learning and mapping capabilities, is particularly effective in processing time series data and addressing long-term dependency issues. Considering that the UKF is prone to estimation errors due to inherent defects, noise introduction and model inaccuracy, an LSTM network is leveraged for offline training to compensate for these shortcomings in the UKF. Consequently, the LSTM network can correct estimation errors of the UKF, enhancing its SOC estimation accuracy.

The implementation process of the UKF-LSTM joint method is as follows:

(1) The SOC pre-estimation using UKF:

UKF obtains the Kalman gain ($K_k$) by measuring and predicting the covariance and realizes the state estimation by dynamically adjusting the weight using the $K_k$ and combining the error of the terminal voltage ($e_k$). Considering that the $K_k$ and $e_k$ can extensively represent the characteristics and distribution of the entire error prediction data set, and the UKF estimation result (${SOC}_k$) can also directly affect the error. Therefore, following the principle of neural network sample selection with small similarity between parameters, $K_k$, $e_k$, and ${SOC}_k$ are selected as the input, and the state estimation error (${Err}_k$) is used as the output to train the LSTM network.

Based on the analysis above, firstly, PSO is utilized to obtain the parameters of the Thevenin model, obtaining $R_0$, $R_{\mathrm{p}}$, and $C_{\mathrm{p}}$ based on data collected from the battery HPPC test. Secondly, the HPPC test data are input into the UKF and executed, with the $K_k$, $e_k$, and ${SOC}_k$ being recorded at each moment of the UKF calculation process, and the SOC estimation error of the UKF is obtained.

(2) Training the LSTM network:

Firstly, to prevent the large difference in data scale in the data set, the following formula is used to standardize the data set.

$$Z={\displaystyle \frac{x-\overline{X}}{S}}.$$

(8)

where $\stackrel{-}{X}$ and $S$ are the mean and standard deviation of the entire training data set, respectively, and $x$ is the original value. The test data set is scaled using the same $\stackrel{-}{X}$ and $S$ values as the training data set.

Secondly, to enhance the computational efficiency of the LSTM network, the hidden layer is configured as a single layer after weighing the network depth and computational efficiency. The hidden layer comprises 500 units; the initial learning rate is configured to 0.0008 after several adjustments. Additionally, a strategy of gradual decay in the learning rate is implemented, where the learning rate is reduced by a decay factor of 0.5 every 20 training cycles; the batch size is set to 120, given the computational efficiency and the size of the data set; and the maximum number of iterations for constructing the network is capped at 80 for the construction of the network. The input features are defined as $K_k$, $e_k$, and ${SOC}_k$, and the output feature is ${Err}_k$. To accurately identify the difference between the forecasted and actual values during the forward transfer process and thus control the size of the weight gradient in the network, the root mean square error (RMSE) is employed as the loss function of the LSTM network.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N{[Er{r}_k-{Err}_k^{’}]}^2}}.$$

(9)

where $N$ is the length of time, the ${Err}_k$ and ${Err}_k^{’}$ are the input error and prediction error at the moment $k$, respectively.

Finally, the feature parameters under the HPPC test are used as the training data set for the LSTM network. The LSTM network, which is constructed and trained using the aforementioned data set, is employed to correct the SOC estimation discrepancies for the UKF.

(3) Building the joint algorithm for error compensation:

Firstly, the test data set is selected, and the corresponding $K_k$, $e_k$, ${SOC}_k$, and ${Err}_k$ are calculated during the SOC estimation operation of the UKF. Secondly, the feature parameters are input into the LSTM network that has been successfully trained, and the SOC estimation error of the UKF is predicted. Lastly, the optimal SOC estimation is obtained after error compensation by the LSTM network. The framework of the combined UKF-LSTM algorithm is shown in Figure 5.

5. Results and Discussions

5.1. Verification of Parameter Identification

The accuracy of parameter identification was validated using UDDS test data. Results obtained from PSO were applied to the Thevenin model to predict terminal voltage values. These predicted voltages were then compared and analyzed with the measured values to validate the accuracy of the identification results. The terminal voltage error for the UDDS test is illustrated in Figure 6 to verify the parameter identification results. As depicted in Figure 6, considerable error fluctuations were observed at the beginning of each charge and discharge cycle, attributed to the polarization effect in lithium batteries. Notably, there were rises in the error at the end of the working condition charge and discharge, particularly after 12,626 s, due to the chemical instability caused by the low capacity of the LIB. The remaining sections of the terminal voltage error were maintained within 40 mV. The mean absolute error (MAE) and RMSE for the terminal voltage were 19.8 mV and 19.6 mV, respectively. The validation results demonstrate that PSO effectively identified model parameters, and the Thevenin model simulated the characteristics of the LIB well.

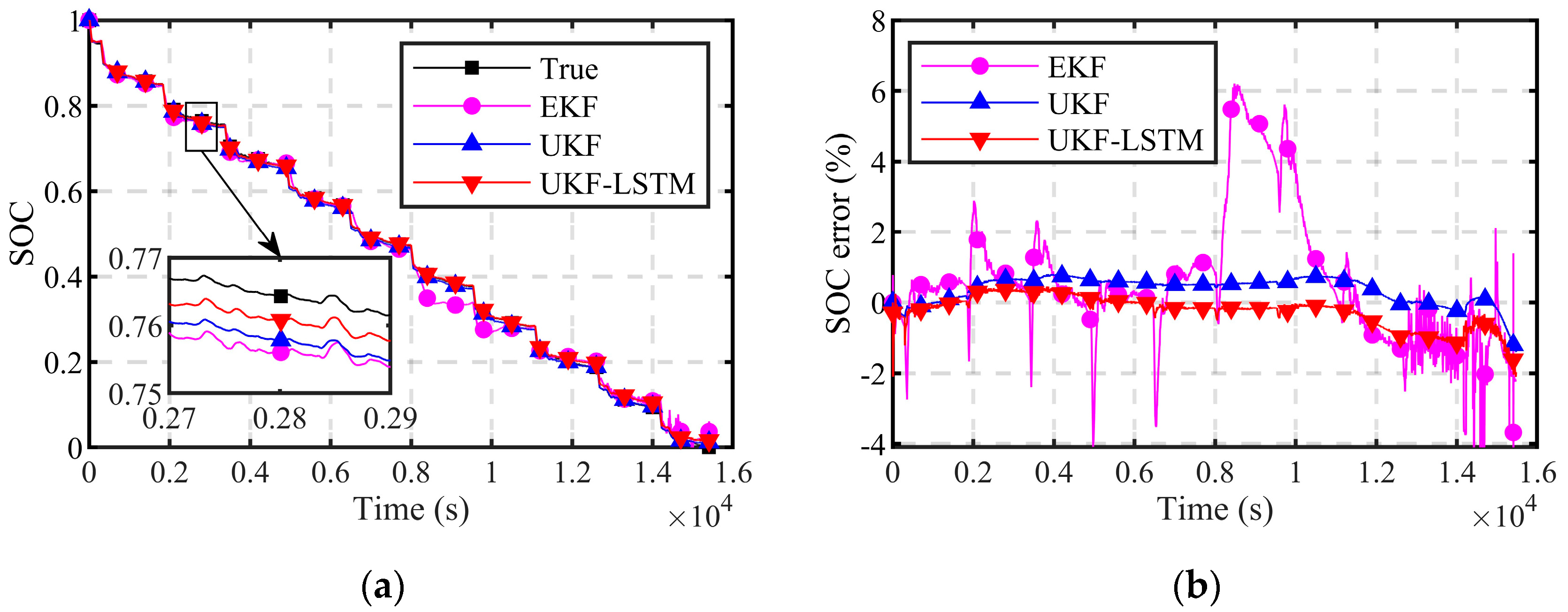
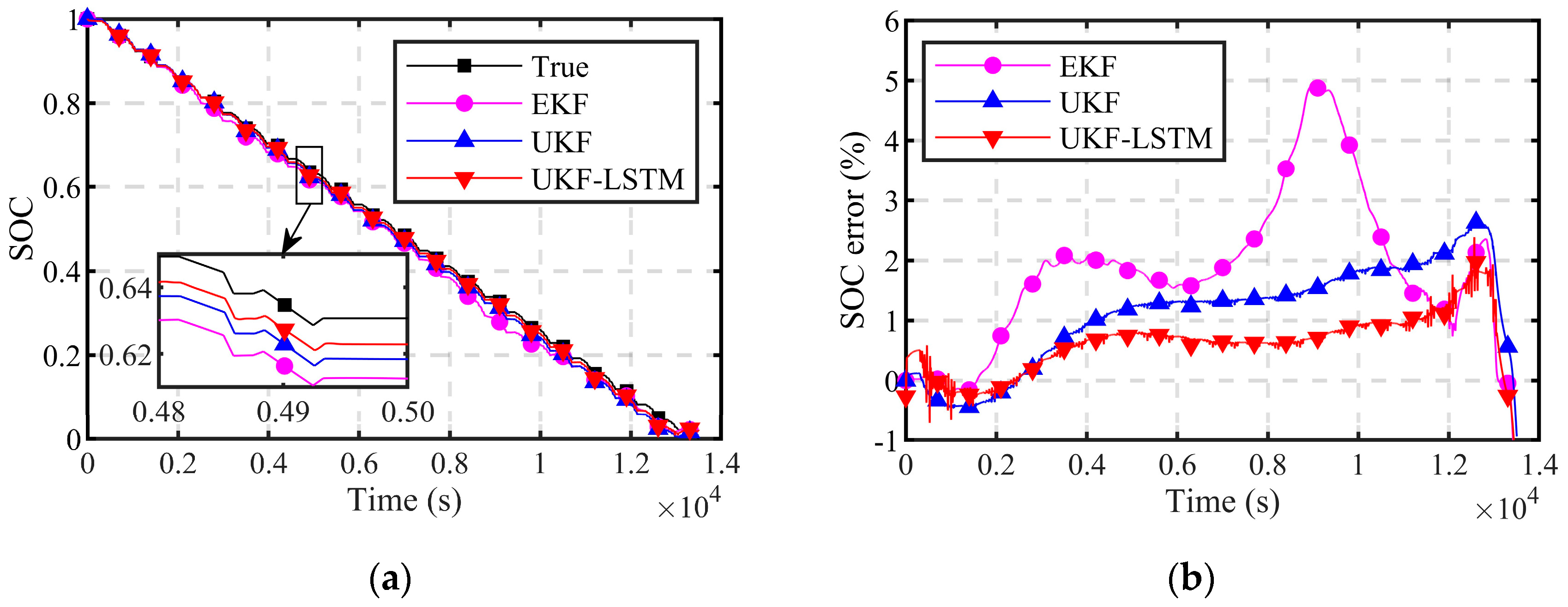
5.2. Analysis of SOC Estimation Results

To evaluate the effectiveness of the algorithm proposed in this study, 15,476 valid data sets from the UDDS test were individually input into the EKF, UKF, and UKF-LSTM algorithms. The SOC estimation outcomes for three algorithms from the UDDS test are shown in Figure 7. As observed from Figure 7b, the error curve trends of the UKF and UKF-LSTM algorithms are quite similar, both exhibiting some error fluctuations. However, the fluctuations of the proposed algorithm are notably smaller. Among these algorithms, the difference between the SOC estimates derived from the EKF and the true values was more significant. This discrepancy is attributed to the drastic chemical reactions of the lithium battery under frequent and high discharge rates during the UDDS test, rendering the EKF unable to complete accurate SOC estimation. In comparison to the EKF, the UKF demonstrated higher accuracy in estimating the SOC. This enhancement arose because the UT used in the UKF does not require the neglect of higher-order terms, thereby providing greater computational accuracy for nonlinear systems. Compared to the first two algorithms, the UKF-LSTM yielded the lowest SOC estimation errors, and its error variation range was also smaller. This improvement was due to the LSTM network effectively mitigating the errors of the UKF, significantly enhancing SOC estimation accuracy.

To thoroughly assess the effectiveness of the joint algorithm, the MAE and RMSE of various SOC estimation algorithms were computed. From the data provided in

Table 3. SOC estimation error statistical analysis for the UDDS test.

Methods	MAE (%)	RMSE (%)
EKF	1.3469	0.5568
UKF	0.4480	0.3588
UKF-LSTM	0.3628	0.2404

, it was concluded that the MAE and RMSE of the UKF-LSTM decreased by 0.9841% and 0.3164%, respectively, compared to the EKF. Compared to those of the UKF, the MAE and RMSE of the UKF-LSTM decreased by 0.0852% and 0.1184%, respectively. The computational results indicate that the algorithm proposed in this study attained superior SOC estimation accuracy compared to conventional methods in the UDDS test.

To rigorously evaluate the robustness and generalization capacity of the proposed algorithm, a total of 13,500 valid data sets derived from the DST were employed for validation. Figure 8 depicts the estimated SOC values of the three algorithms assessed in the DST. The true value of the SOC was calculated by the Coulomb counting method. As depicted in Figure 8a, the SOC estimation result of the UKF-LSTM fluctuated within a narrow range around the true value, and its curve-fitting effect is noticeably superior to that of the EKF and UKF, fully demonstrating the error correction capability of the LSTM network. As evident from the estimation error comparison graph in Figure 8b, unlike the error curve of the EKF, the UKF and UKF-LSTM exhibit roughly the same trend. At the beginning of discharge, the error of UKF was very small, so the error compensation effect of the neural network was not prominent. However, as the discharge deepened, the UKF showed substantial error fluctuations under the DST, while the fluctuations of the UKF-LSTM were considerably smaller. The error curves of both UKF and the proposed algorithm tend to rise in the middle and late stages of discharge, but the UKF-LSTM maintained a smaller error and exhibited higher estimation accuracy.

The SOC estimation errors of the three algorithms were calculated from the DST. They can be analyzed from the data provided in

Table 4. SOC estimation error statistical analysis for the DST.

Methods	MAE (%)	RMSE (%)
EKF	1.8460	1.8027
UKF	1.2085	1.1068
UKF-LSTM	0.6841	0.6132

. Compared to the EKF, the UKF-LSTM exhibited a reduction in the MAE by 0.9841% and in the RMSE by 0.3164%, respectively. Furthermore, compared to the UKF, the UKF-LSTM demonstrated a decrease in the MAE by 0.0852% and in the RMSE by 0.1184%, respectively. Under the DST conditions, the proposed algorithm demonstrated superior SOC estimation accuracy compared to conventional Kalman filter algorithms.

6. Conclusions

As a classical KF algorithm, the UKF is widely utilized in estimating the SOC of LIBs. To enhance the precision of SOC estimation using the UKF, an innovative UKF-LSTM error compensation algorithm utilizing the LSTM network was introduced. The precision and robustness of SOC estimation using the proposed method were validated through different experiments.

(1)

In this study, the Thevenin model was used to characterize the battery. The unknown parameters of the battery model were obtained by the PSO algorithm, and the model accuracy was verified using the UDDS test. The validation results demonstrate that PSO could accurately identify the model parameters, and the Thevenin model could effectively characterize the battery.

(2)

A joint UKF-LSTM algorithm is proposed, which utilizes an LSTM network to correct the estimation error of the UKF. The LSTM network is trained using feature parameters that affect the UKF estimation error. Then, the LSTM network is employed to reduce the error of the UKF, thereby improving its SOC estimation performance.

(3)

The HPPC test data were used for training, while experimental data from the UDDS tests and DSTs were employed for validation. The results indicate that the RMSE of the UKF-LSTM could be controlled under 0.6132% under both validation conditions. Compared to that of the UKF, the RMSE of the proposed algorithm decreased by 0.1184% and 0.4936% in the UDDS tests and DSTs, respectively. In summary, the UKF-LSTM exhibited high accuracy and robustness in the SOC estimation, thus ensuring the reliability of SOC estimates.

In future studies, the impact of parameters such as temperature and cycle aging on SOC estimation will be considered. Moreover, the experimental samples will be expanded to include various types of lithium-ion batteries to enhance the generalization of the proposed method.