Comprehensive Modeling of SiC Inverter Driven Form Wound Motor Coil for Insights on Coil Insulation Stress
Abstract
:1. Introduction
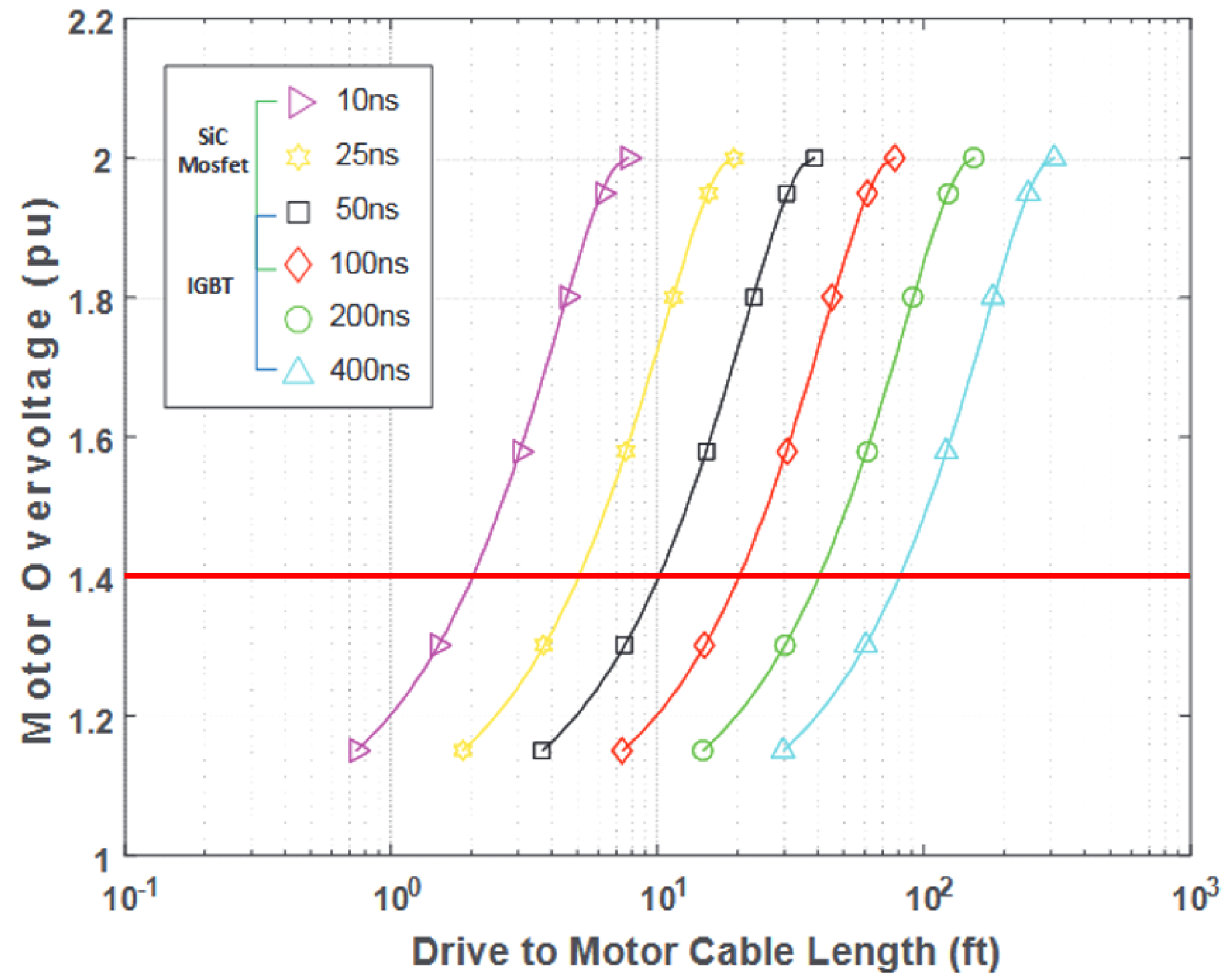
2. Motor Overvoltage and Reflected Wave Phenomenon
3. FEA Modeling of Motor Coil System
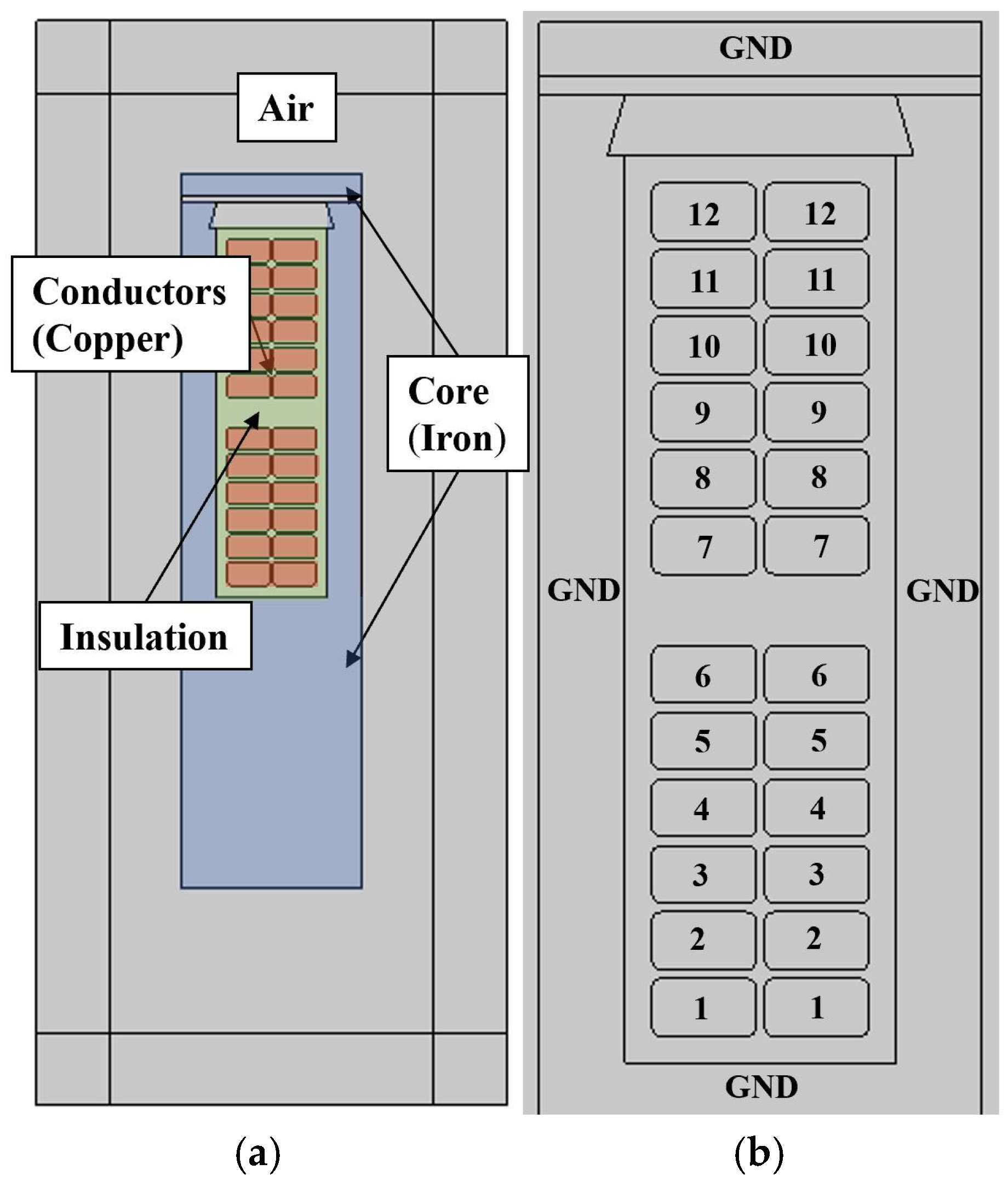
3.1. Geometric Setup of FEA
3.2. Selection of Model Depth
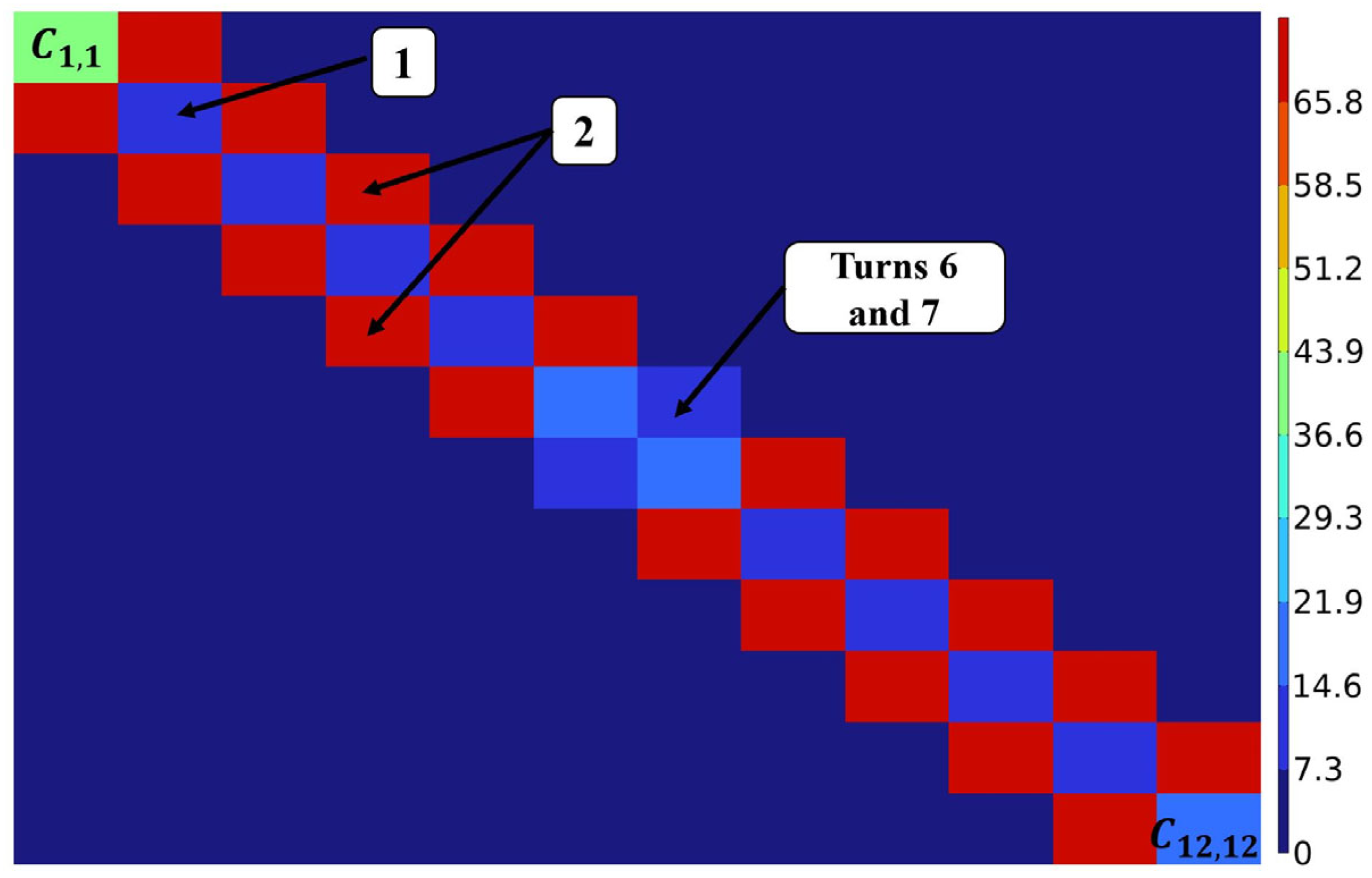
3.3. Calculation of Capacitances
3.4. Calculation of Frequency Dependent Resistance and Inductance
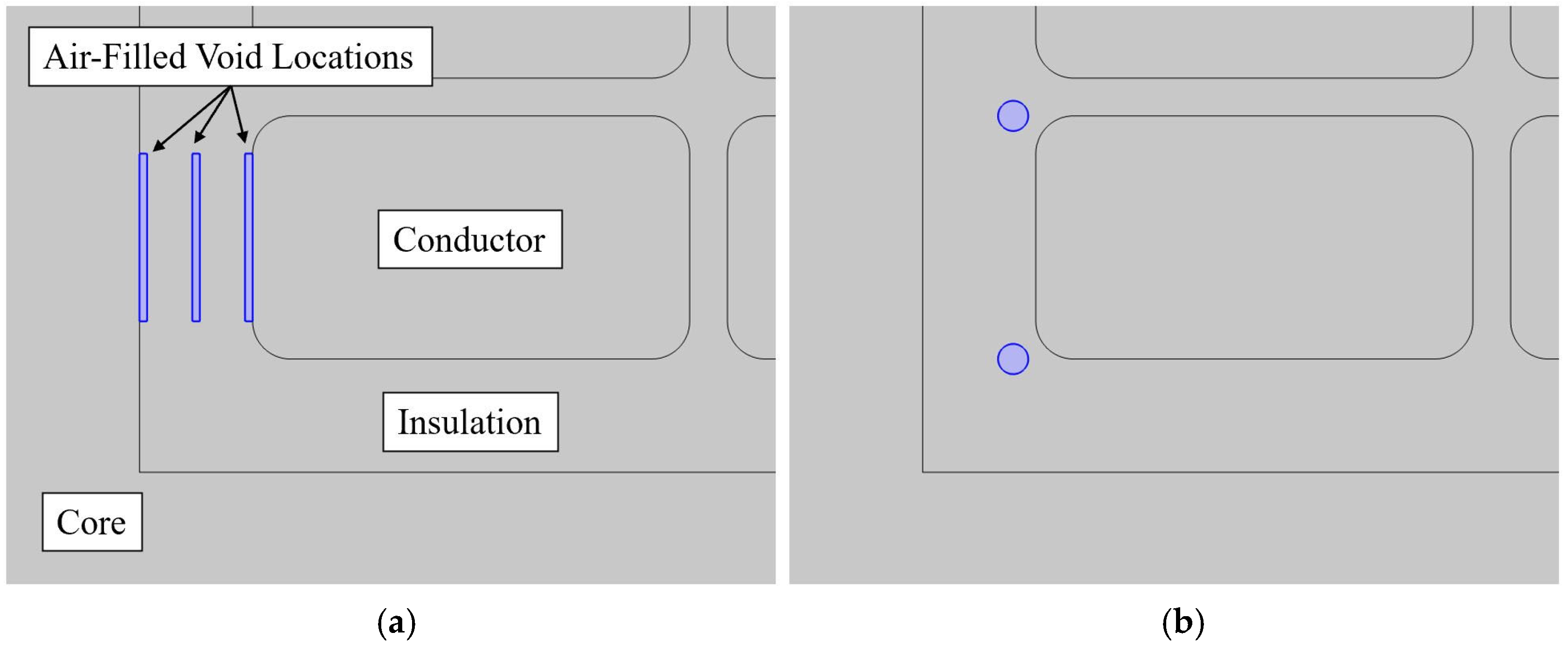
3.5. Modeling of Voids and Delaminations
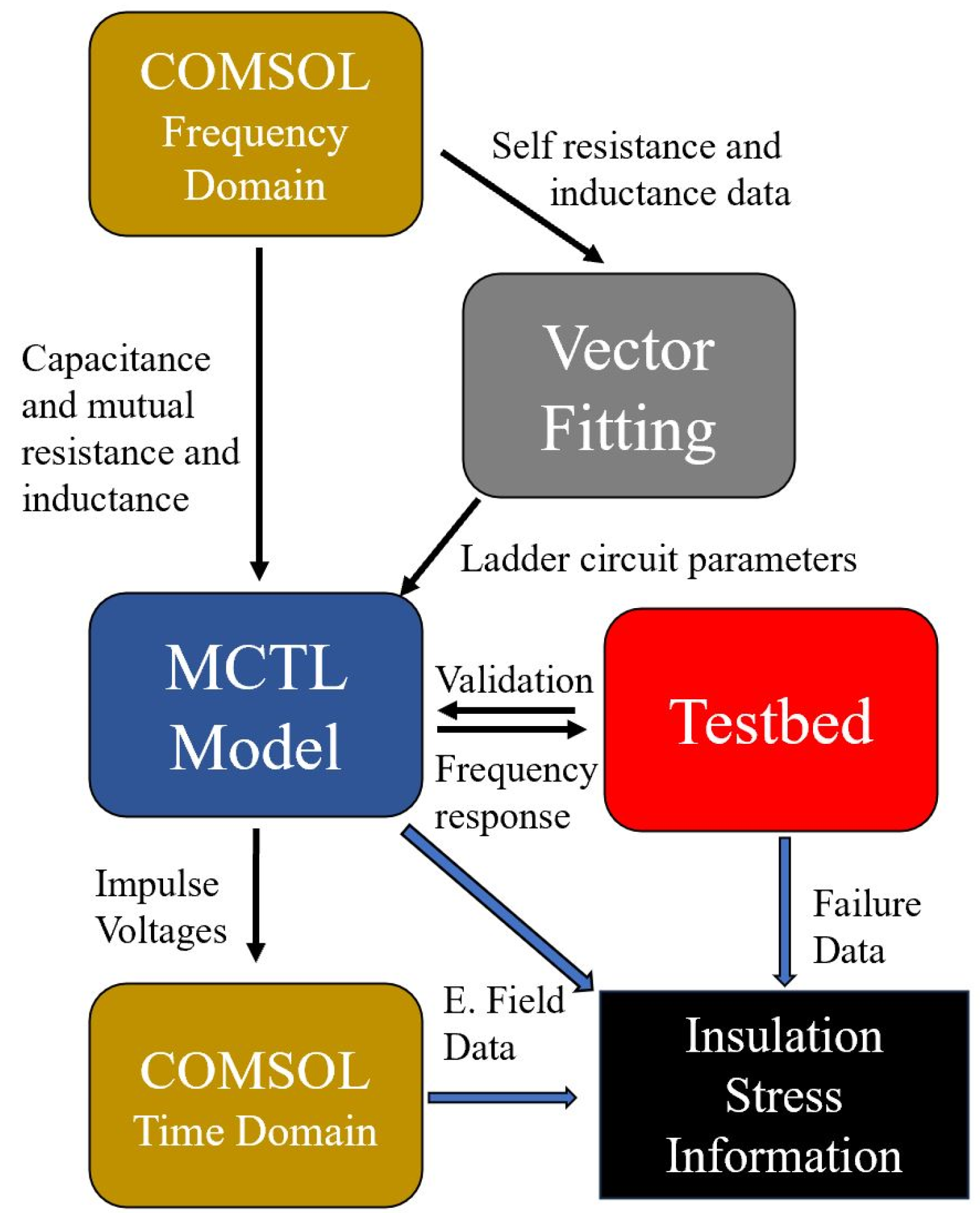
4. MCTL Model of Coil Electrical Behavior
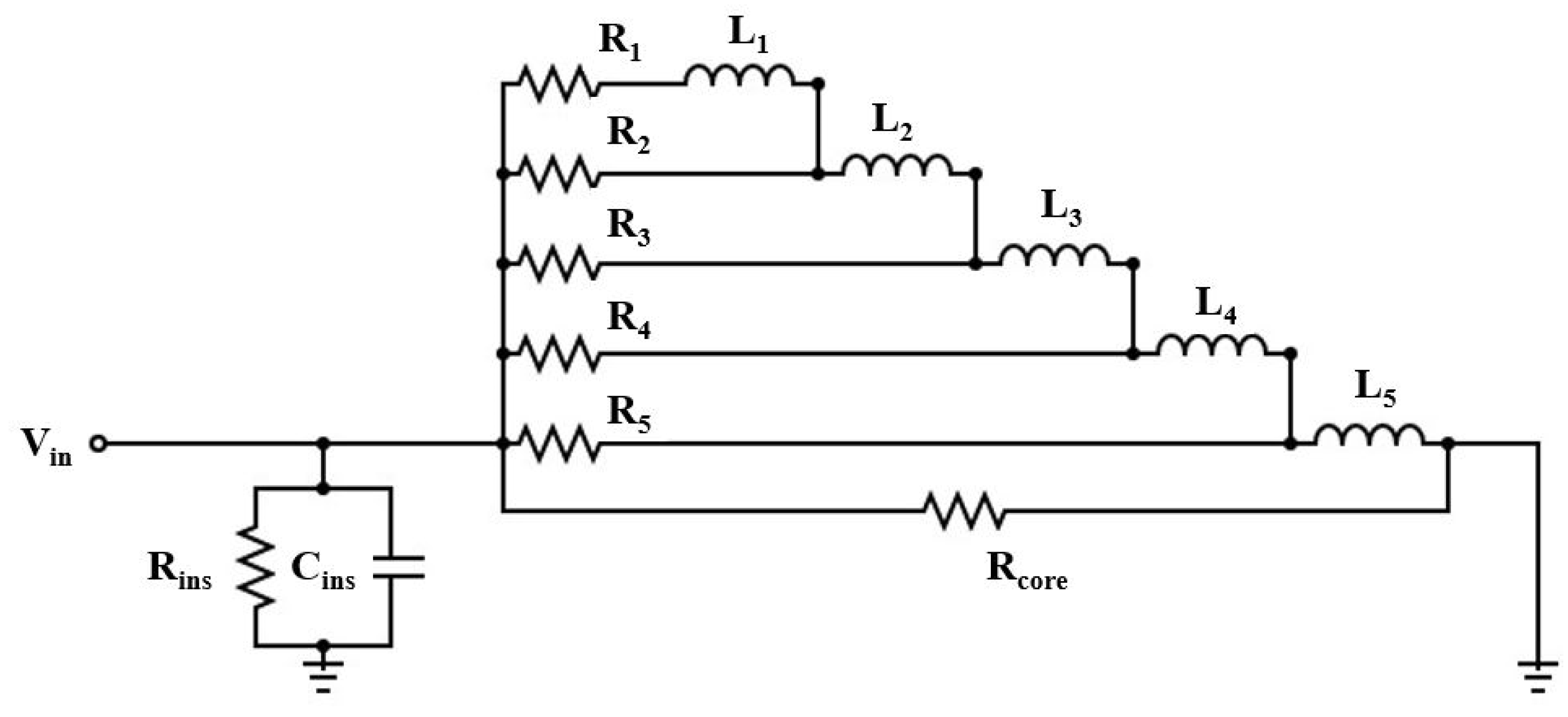
4.1. The Use of Ladder Circuits for Representing the Frequency Dependent Coil Behaviors
4.2. Calculations of Ladder Circuit Parameters
4.3. Ladder Circuit Implementation
4.4. FEA Modeling of Voltage Distributions in Time
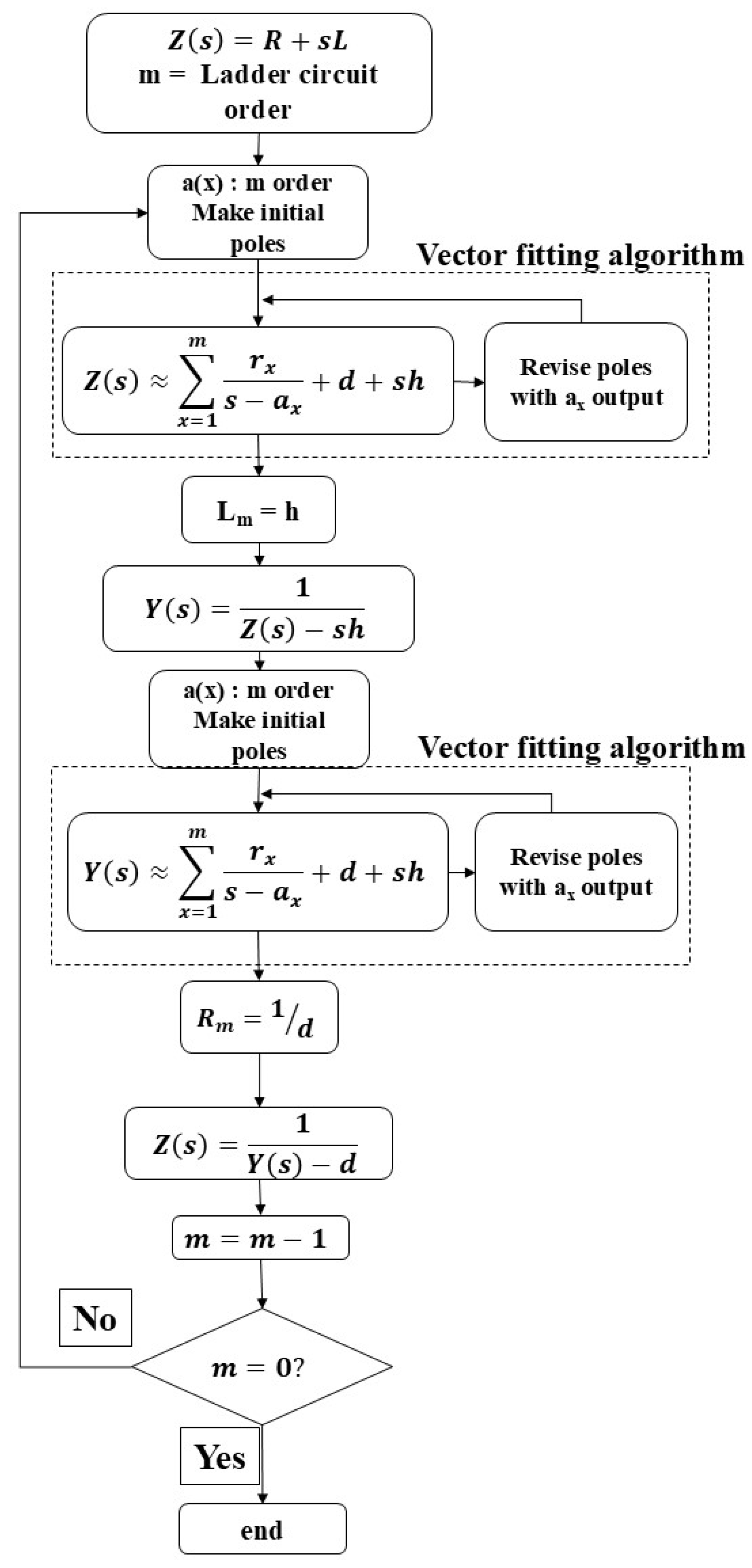
4.5. Analytical Modeling of Ladder Circuit Impedance
5. Experimental Setup
5.1. Testbed
5.2. ETFE Method
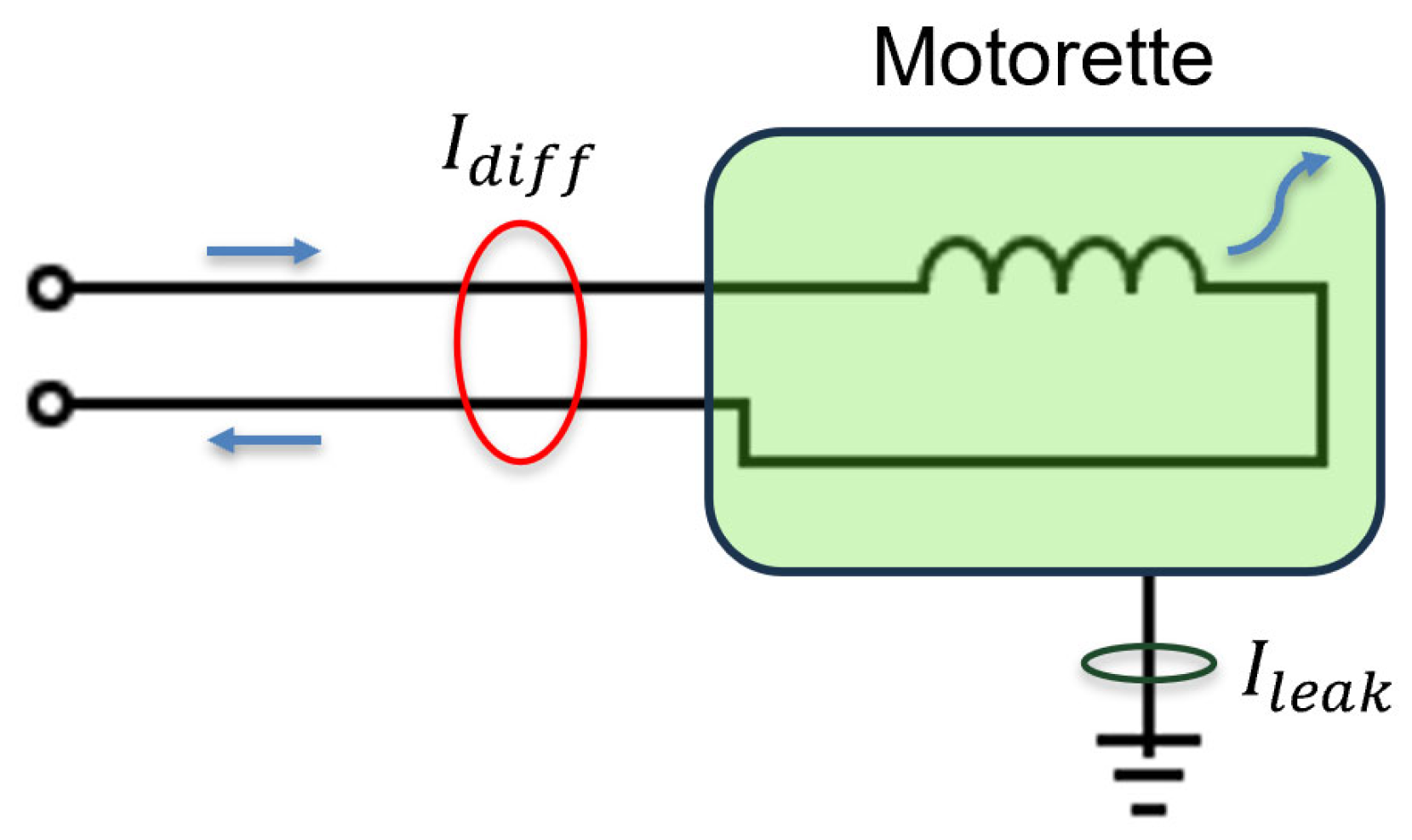
5.3. SOH Monitoring Techniques
5.4. Experimental Design
6. Results
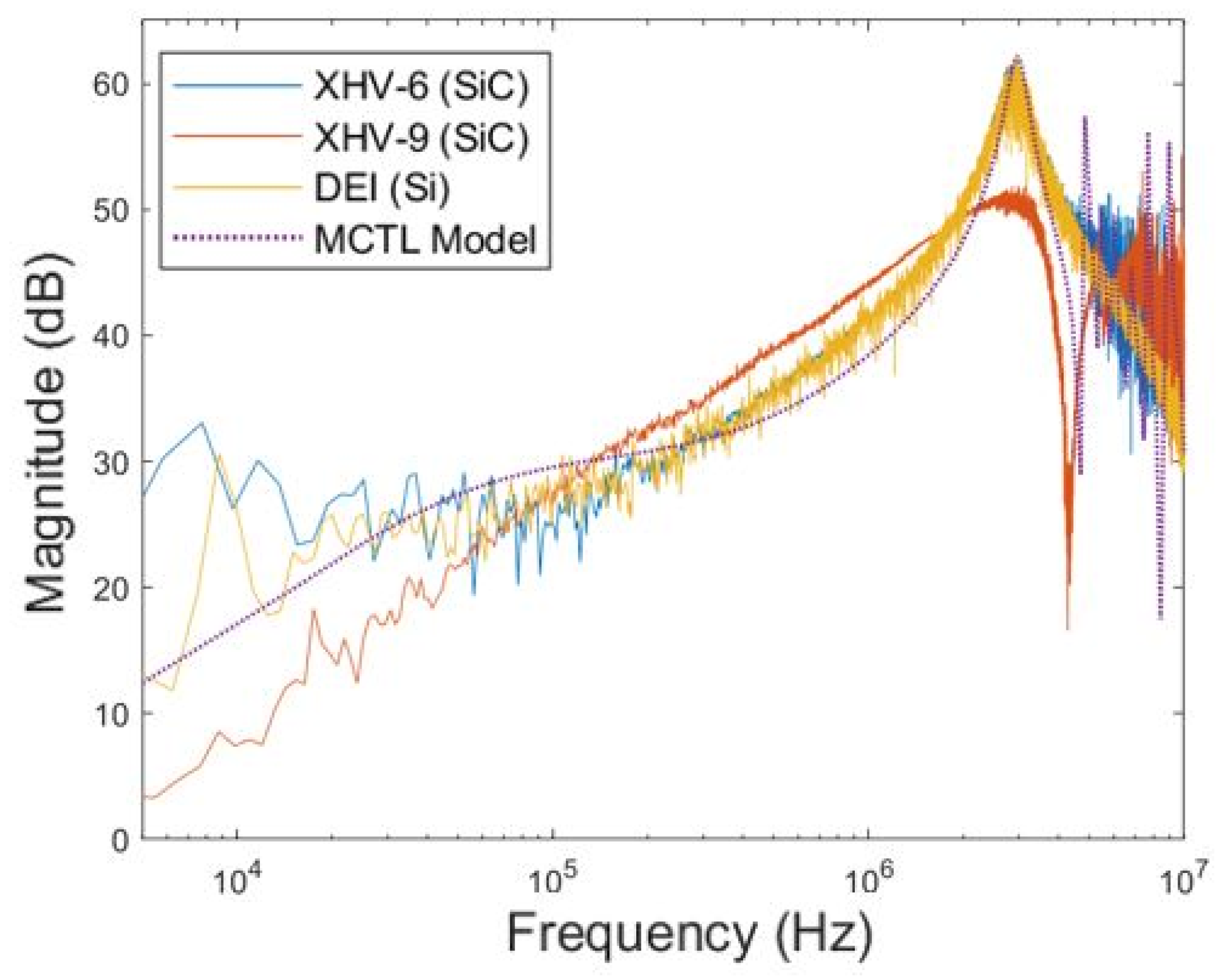
6.1. Model Validation Using Impedance Response
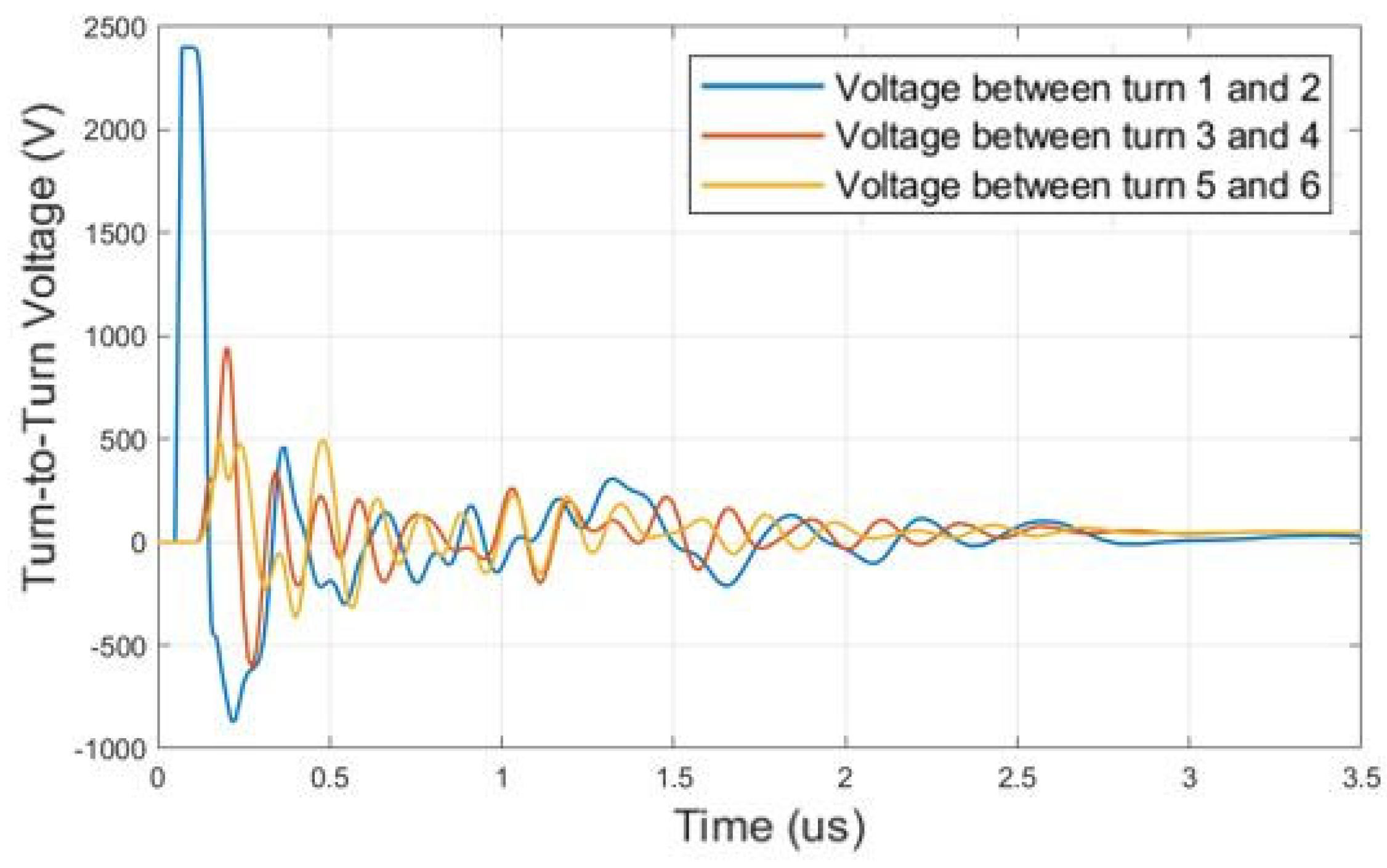
6.2. Simulation of the Overvoltage Phenominom and Voltage Distribution of the Coils
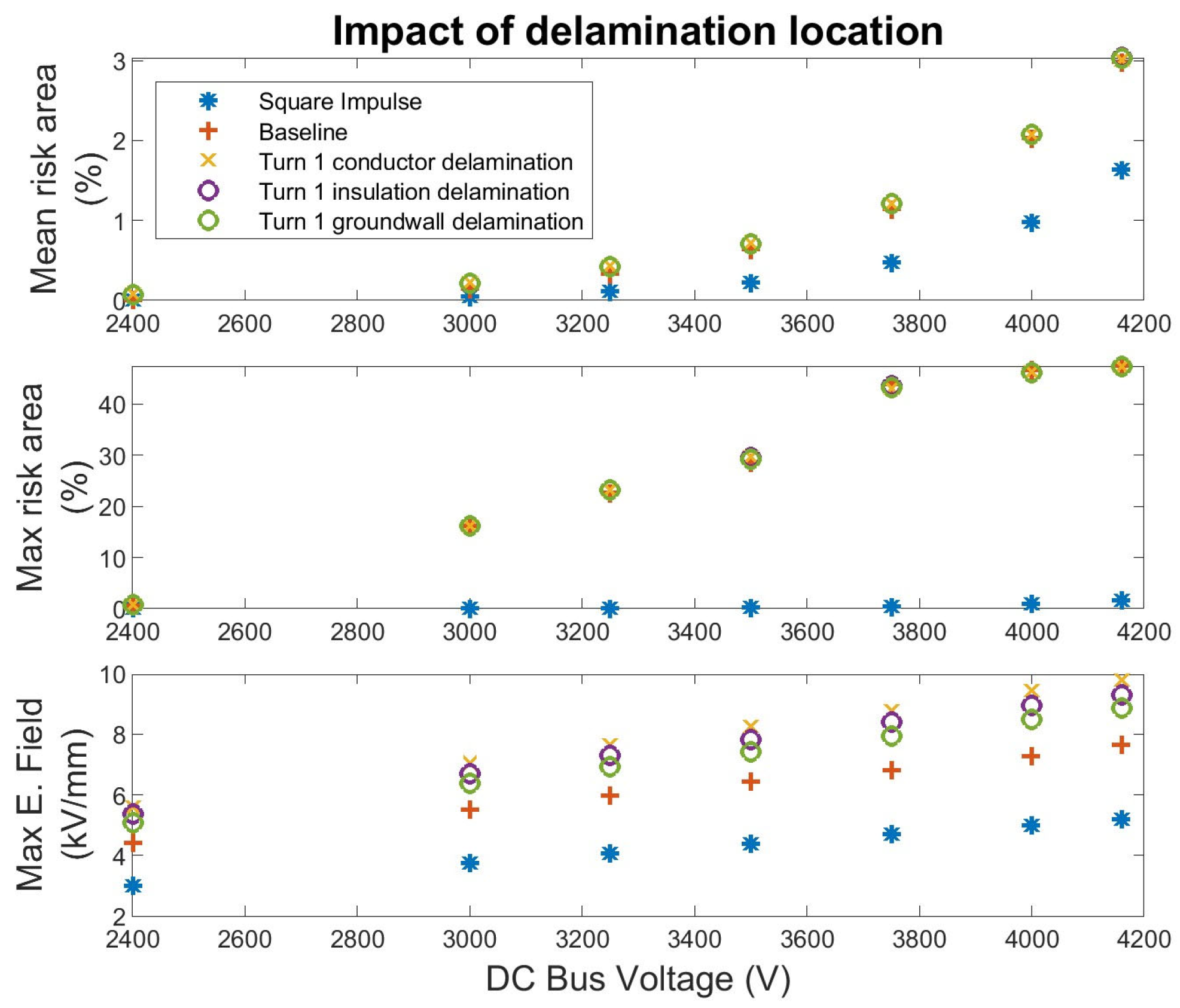
6.3. Modeling the Impact of Delaminations on Electrical Stress
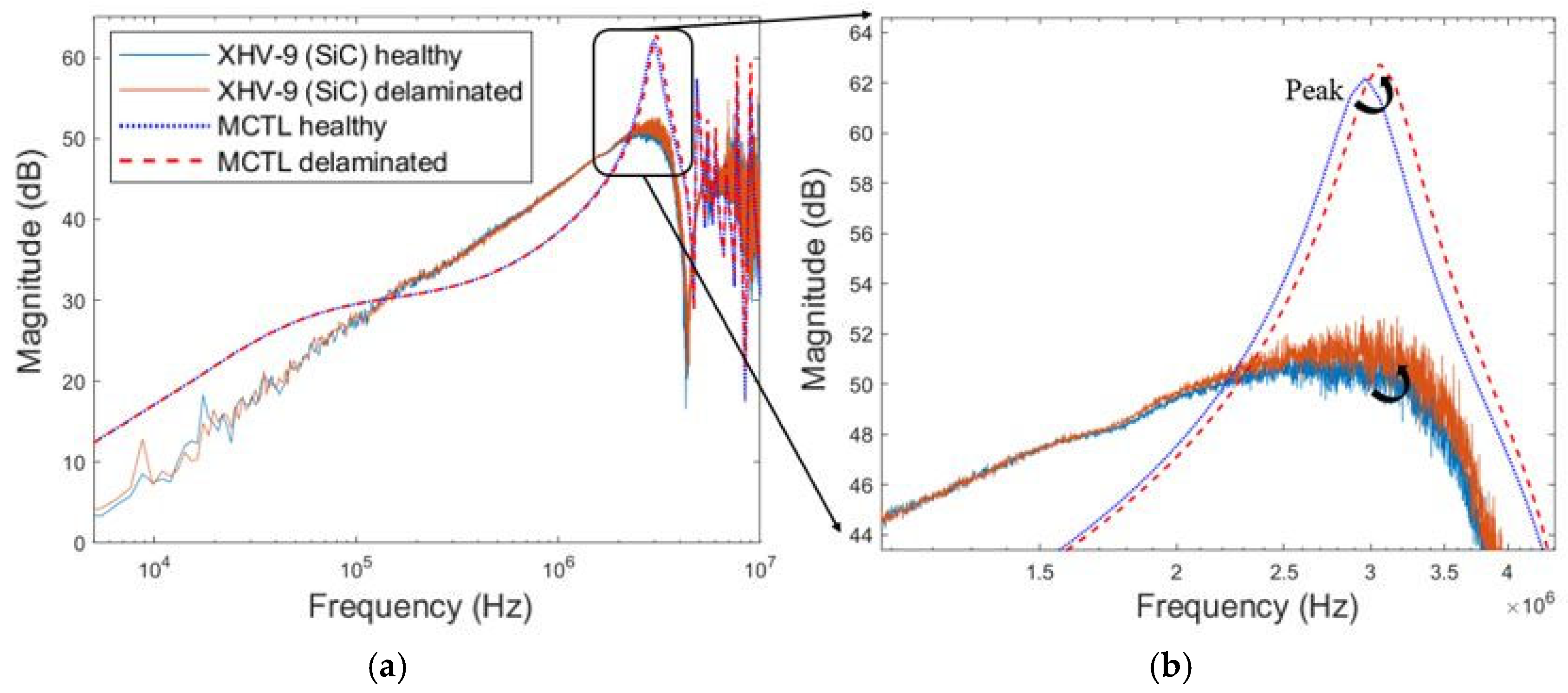
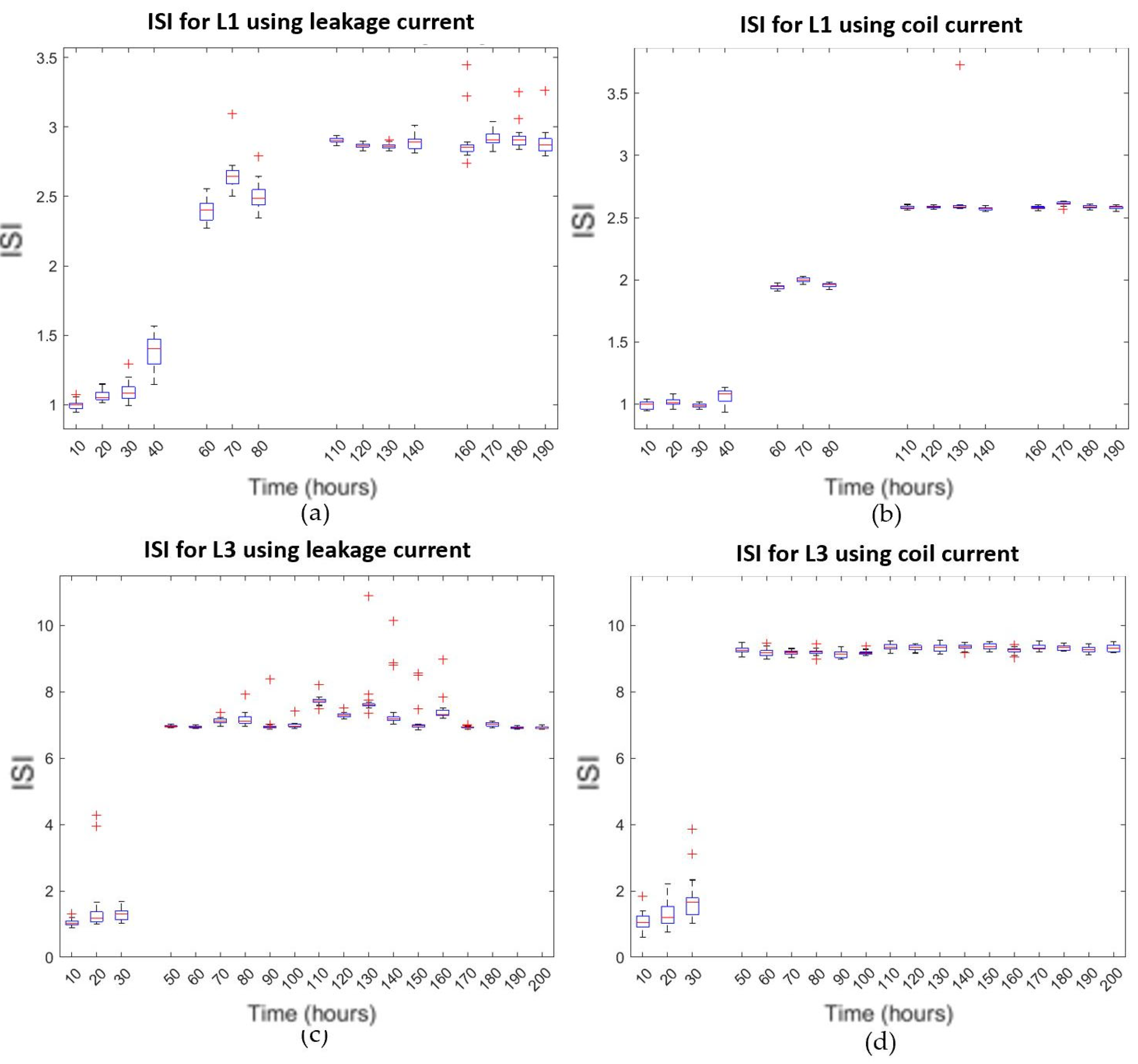
6.4. Results of SoH Tracking with Aged Coils
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Petri, T.; Keller, M.; Parspour, N. The Insulation Resilience of Inverter-Fed Low Voltage Traction Machines: Review, Challenges, and Opportunities. IEEE Access 2022, 10, 104023–104049. [Google Scholar] [CrossRef]
- Lee, W.; Li, S.; Han, D.; Sarlioglu, B.; Minav, T.; Pietola, M. A Review of Integrated Motor Drive and Wide-Bandgap Power Electronics for High-Performance Electro-Hydrostatic Actuators. IEEE Trans. Transp. Electrif. 2018, 4, 684–693. [Google Scholar] [CrossRef]
- Zoeller, C.; Vogelsberger, M.; Fasching, R.; Grubelnik, W.; Wolbank, T. Evaluation and Current-Response-Based Identification of Insulation Degradation for High Utilized Electrical Machines in Railway Application. IEEE Trans. Ind. Appl. 2017, 53, 2679–2689. [Google Scholar] [CrossRef]
- Ding, R.; Dou, Z.; Qi, Y.; Mei, W.; Liu, G. Analysis on characteristic of 3.3-kV full SiC device and railway traction converter design. IET Power Electron. 2022, 15, 978–988. [Google Scholar] [CrossRef]
- Pietrini, G.; Barater, D.; Franceschini, G.; Mancinelli, P.; Cavallin, A. An open problem for More Electrical Aircraft (MEA): How insulation systems of actuators can be qualified? In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Khan, Q.; Refaat, S.; Abu-Rub, H.; Toliyat, H. Partial Discharge Modeling of Internal Discharge in Electrical Machine Stator Winding. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020. [Google Scholar]
- Kaufhold, M.; Auinger, H.; Berth, M.; Speck, J.; Eberhardt, M. Electrical stress and failure mechanism of the winding insulation in PWM-inverter-fed low-voltage induction motors. IEEE Trans. Ind. Electron. 2000, 47, 396–402. [Google Scholar] [CrossRef]
- Xiong, H.; Liu, R.; Hu, B.; You, H.; Wei, Z.; Zhang, J.; Wang, J. The Ohio State University Partial Discharge Detection Platform for Electric Machine Windings Driven by PWM Voltage Excitation. In Proceedings of the 2019 IEEE Electrical Insulation Conference (EIC), Calgary, AB, Canada, 16–19 June 2019; pp. 517–520. [Google Scholar]
- D’Amato, D.; Loncarski, J.; Monopoli, V.; Cupertino, F.; Di Noia, L.; Del Pizzo, A. Impact of PWM Voltage Waveforms in High-Speed Drives: A Survey on High-Frequency Motor Models and Partial Discharge Phenomenon. Energies 2022, 15, 1406. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X.; Zhang, Y.; Bo, H.; Liang, Z. Comparison of Different Simulating Calculation Methods for Electric Fields Along the Stator End-winding of HV Rotating Machine. In Proceedings of the 2020 IEEE Electrical Insulation Conference (EIC), Knoxville, TN, USA, 22 June–3 July 2020; pp. 448–451. [Google Scholar]
- Liu, P.; Liu, X.; Zhang, Y.; Hu, B.; Liang, Z. Electric Field Analysis of Stress Grading System Delamination in the Stator End-winding of High Voltage Rotating Machine. In Proceedings of the 2021 IEEE Electrical Insulation Conference (EIC), Denver, CO, USA, 7–28 June 2021; pp. 420–423. [Google Scholar]
- Ma, Z.; Zhou, C.; Hepburn, D.; Cowan, K. FEM Simulation of Electrical Stresses Within Motor Stator Windings for Online PD Localization. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials, Sydney, NSW, Australia, 19–22 July 2015; pp. 668–671. [Google Scholar]
- Pauli, F.; Kilper, M.; Driendl, N.; Hameyer, K. Modeling of the Partial Discharge Process Between the Winding and the Stator of Low Voltage Machines for Traction Applications. IEEE Trans. Energy Convers. 2021, 36, 2310–2318. [Google Scholar] [CrossRef]
- Zhou, X.; Giangrande, P.; Ji, Y.; Zhao, W.; Ijaz, S.; Galea, M. Insulation for Rotating Low-Voltage Electrical Machines: Degradation, Lifetime Modeling, and Accelerated Aging Tests. Energies 2024, 17, 1987. [Google Scholar] [CrossRef]
- Barzkar, A.; Ghassemi, M. Precise Evaluation of Repetitive Transient Overvoltages in Motor Windings in Wide-Bandgap Drive Systems. Vehicles 2022, 4, 697–726. [Google Scholar] [CrossRef]
- Kilper, M.; Naumoski, H.; Hameyer, K. About the Modelling of Effects caused by Fast Switching Semiconductors operating Low Voltage Electrical Machines. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; pp. 219–224. [Google Scholar]
- Sundeep, S.; Wang, J.; Griffo, A. Holistic Modeling of High-Frequency Behavior of Inverter-Fed Machine Winding, Considering Mutual Couplings in Time Domain. IEEE Trans. Ind. Appl. 2021, 57, 6044–6057. [Google Scholar] [CrossRef]
- Sundeep, S.; Wang, J.; Griffo, A.; Alvarez-Gonzalez, F. Antiresonance Phenomenon and Peak Voltage Stress Within PWM Inverter Fed Stator Winding. IEEE Trans. Ind. Electron. 2021, 68, 11826–11836. [Google Scholar] [CrossRef]
- Kelly, B.; Zhang, J.; Chen, L. Bar-Wound Machine Voltage Stress: A Method for 2D FE Modeling and Testing. In Proceedings of the 2021 Thirty-Sixth Annual IEEE Applied Power Electronics Conference AND Exposition (APEC 2021), Phoenix, AZ, USA, 14–17 June 2021; pp. 1688–1693. [Google Scholar]
- Xiong, H.; Louie, A.; Liu, R.; Zhang, J.; von Jouanne, A. Finite Element Analysis Modeling and Experimental Verification of Reflected Wave Phenomena in Variable Speed Machine Drive Cables. In Proceedings of the 2017 IEEE International Electric Machines And Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Perisse, F.; Werynski, P.; Roger, D. A new method for ac machine turn insulation diagnostic based on high frequency resonances. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1308–1315. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J.; Leonardi, F.; Munoz, A.; Degner, M. Investigation of Surge Voltage Propagation in Inverter-Driven Electric Machine Windings. IEEE Trans. Ind. Electron. 2023, 70, 9811–9822. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, W.; Gao, C.; Wang, S.; Qiu, J.; Zhu, J.; Guo, Y. Analysis of Inter-Turn Insulation of High Voltage Electrical Machine by Using Multi-Conductor Transmission Line Model. IEEE Trans. Magn. 2013, 49, 1905–1908. [Google Scholar] [CrossRef]
- Krings, A.; Paulsson, G.; Sahlén, F.; Holmgren, B. Experimental Investigation of the Voltage Distribution in Form Wound Windings of Large AC Machines due to Fast Transients. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1700–1706. [Google Scholar]
- Melfi, M.; Sung, J.; Bell, S.; Skibinski, G. Effect of surge voltage risetime on the insulation of low voltage machines fed by PWM converters. In Proceedings of the IAS ‘97—Conference Record of the 1997 Ieee Industry Applications Conference/Thirty-Second IAS Annual Meeting, VOLS 1–3, New Orleans, LA, USA, 5–9 October 1997; pp. 239–246. [Google Scholar]
- Yi, P.; Murthy, P.; Wei, L. Performance Evaluation of SiC MOSFETs with Long Power Cable and Induction Motor. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Friedel, S. How to Calculate a Capacitance Matrix in COMSOL Multiphysics. COMSOL: COMSOL Blog, 2017. Available online: https://www.comsol.com/blogs/how-to-calculate-a-capacitance-matrix-in-comsol-multiphysics (accessed on 1 May 2024).
- COMSOL. Self-Inductance and Mutual Inductance Between Single Conductors. In Application Gallery; COMSOL: Göttingen, Germany; Available online: https://www.comsol.com/model/self-inductance-and-mutual-inductance-between-single-conductors-12653 (accessed on 1 May 2024).
- Borghei, M.; Ghassemi, M.; Kordi, B.; Gill, P.; Oliver, D. A Finite Element Analysis Model for Internal Partial Discharges in an Air-Filled, Cylindrical Cavity inside Solid Dielectric. In Proceedings of the 2021 IEEE Electrical Insulation Conference (EIC), Denver, CO, USA, 7–28 June 2021; pp. 260–263. [Google Scholar]
- Hornak, J.; Trnka, P. Defects of Electrical Insulation Systems with Focus on FEM Modeling. In Proceedings of the 2017 6th International Youth Conference On Energy (IYCE), Budapest, Hungary, 21–24 June 2017. [Google Scholar]
- Otake, Y.; Umemoto, T.; Suga, K.; Yoshimura, M.; Tsurimoto, T.; Hasegawa, H.; Isoya, H.; Ebato, T.; Inoue, N.; Yano, T. Influence of Defect Size on Insulation Deterioration of Epoxy Resins with Voids. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 52–57. [Google Scholar] [CrossRef]
- Magdun, O.; Blatt, S.; Binder, A. Calculation of Stator Winding Parameters to Predict the Voltage Distributions in Inverter Fed AC Machines. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics FOR Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 447–453. [Google Scholar]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Mota, D.D.S. Estimating the Frequency Response of an Excitation System and Synchronous Generator: Sinusoidal Disturbances Versus Empirical Transfer Function Estimate. Power Energy Technol. Syst. 2018, 5, 27–34. [Google Scholar] [CrossRef]
- Saathoff, E.; Shaw, S.; Leeb, S. Line Impedance Estimation. IEEE Trans. Instrum. Meas. 2021, 70, 6501810. [Google Scholar] [CrossRef]
- Babel, A.; Strangas, E. Condition-Based Monitoring and Prognostic Health Management of Electric Machine Stator Winding Insulation. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1855–1861. [Google Scholar]
- Torkaman, H.; Karimi, F. Measurement variations of insulation resistance/polarization index during utilizing time in HV electrical machines—A survey. Measurement 2015, 59, 21–29. [Google Scholar] [CrossRef]
- Gandhi, A.; Corrigan, T.; Parsa, L. Recent Advances in Modeling and Online Detection of Stator Interturn Faults in Electrical Motors. IEEE Trans. Ind. Electron. 2011, 58, 1564–1575. [Google Scholar] [CrossRef]
- Patel, A.; Lai, C.; Iyer, K. A Novel Approach towards Detection and Classification of Electric Machines’ Stator Winding Insulation Degradation using Wavelet Decomposition. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference, IEMDC, San Francisco, CA, USA, 15–18 May 2023. [Google Scholar]
- Yang, J.; Cho, J.; Lee, S.; Yoo, J.; Kim, H. An advanced stator winding insulation quality assessment technique for inverter-fed machines. IEEE Trans. Ind. Appl. 2008, 44, 555–564. [Google Scholar] [CrossRef]
- Zheng, D.; Lu, G.; Qu, J.; Zhang, Y.; Zhang, P. Comparative Study of Neutral-Voltage-Based and Leakage-Current-Based Online Condition Monitoring Methods for Stator Insulation of Inverter-Fed Machines. IEEE Trans. Ind. Electron. 2024, 71, 16664–16674. [Google Scholar] [CrossRef]
- Montero, E.; Vogelsberger, M.; Wolbank, T. Tracking Insulation Degradation of Railway Traction Induction Motors using High-Frequency Differential Current. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition ECCE, Phoenix, AZ, USA, 20–24 October 2024. [Google Scholar]
- Younsi, K.; Neti, P.; Shah, M.; Zhou, J.; Krahn, J.; Weeber, K.; Whitefield, C. On-line Capacitance and Dissipation Factor Monitoring of AC Stator Insulation. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1441–1452. [Google Scholar] [CrossRef]
- Zhang, P.; Younsi, K.; Neti, P. A Novel Online Stator Ground-Wall Insulation Monitoring Scheme for Inverter-Fed AC Motors. IEEE Trans. Ind. Appl. 2015, 51, 2201–2207. [Google Scholar] [CrossRef]
- Tsyokhla, I.; Griffo, A.; Wang, J. On-Line Monitoring of Winding Insulation Health using High Frequency Common Mode Voltage from PWM. In Proceedings of the 2015 IEEE INTERNATIONAL ELECTRIC MACHINES & DRIVES CONFERENCE (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1433–1439. [Google Scholar]
- Zhang, P.; Neti, P.; Younsi, K. Online Monitoring of Capacitance and Dissipation Factor of Motor Stator Winding Insulation during Accelerated Life Testing. In Proceedings of the 2018 Ieee Energy Conversion Congress And Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3267–3271. [Google Scholar]
- Nussbaumer, P.; Vogelsberger, M.; Wolbank, T. Exploitation of Induction Machine’s High-Frequency Behavior for Online Insulation Monitoring. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 579–585. [Google Scholar]
- Saeed, M.; Fernández, D.; Guerrero, J.; Díaz, I.; Briz, F. Insulation Condition Assessment in Inverter-Fed Motors Using the High-Frequency Common Mode Current: A Case Study. Energies 2024, 17, 470. [Google Scholar] [CrossRef]
- Tsyokhla, I.; Griffo, A.; Wang, J. Online Condition Monitoring for Diagnosis and Prognosis of Insulation Degradation of Inverter-Fed Machines. IEEE Trans. Ind. Electron. 2019, 66, 8126–8135. [Google Scholar] [CrossRef]
- Mentlík, V.; Trnka, P.; Svoboda, M.; Hornak, J.; Totzauer, P.; Harvánek, L. Aging Phenomena of Paper-Oil Insulating System under Different Voltage Stress. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials, Sydney, NSW, Australia, 19–22 July 2015; pp. 548–551. [Google Scholar]








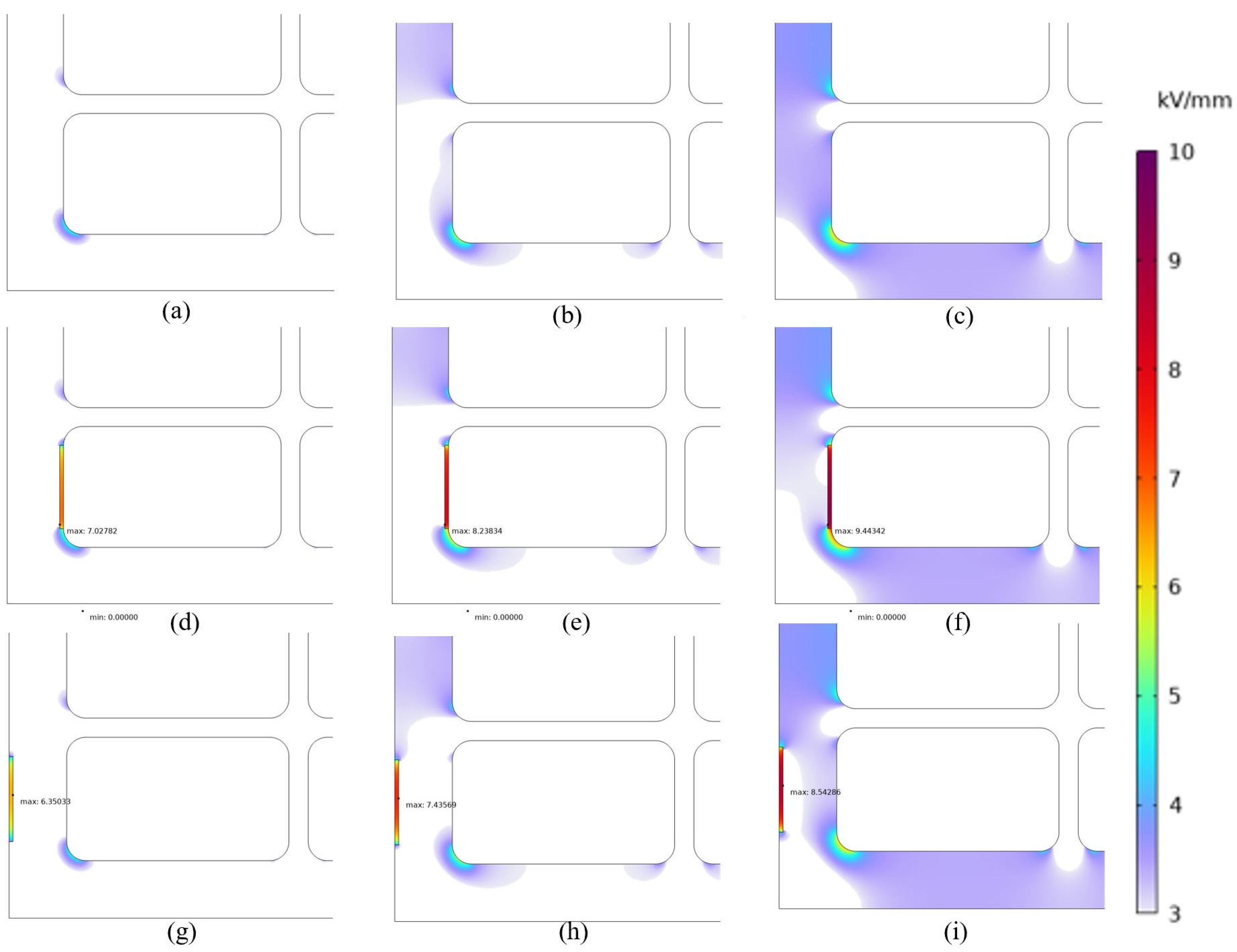
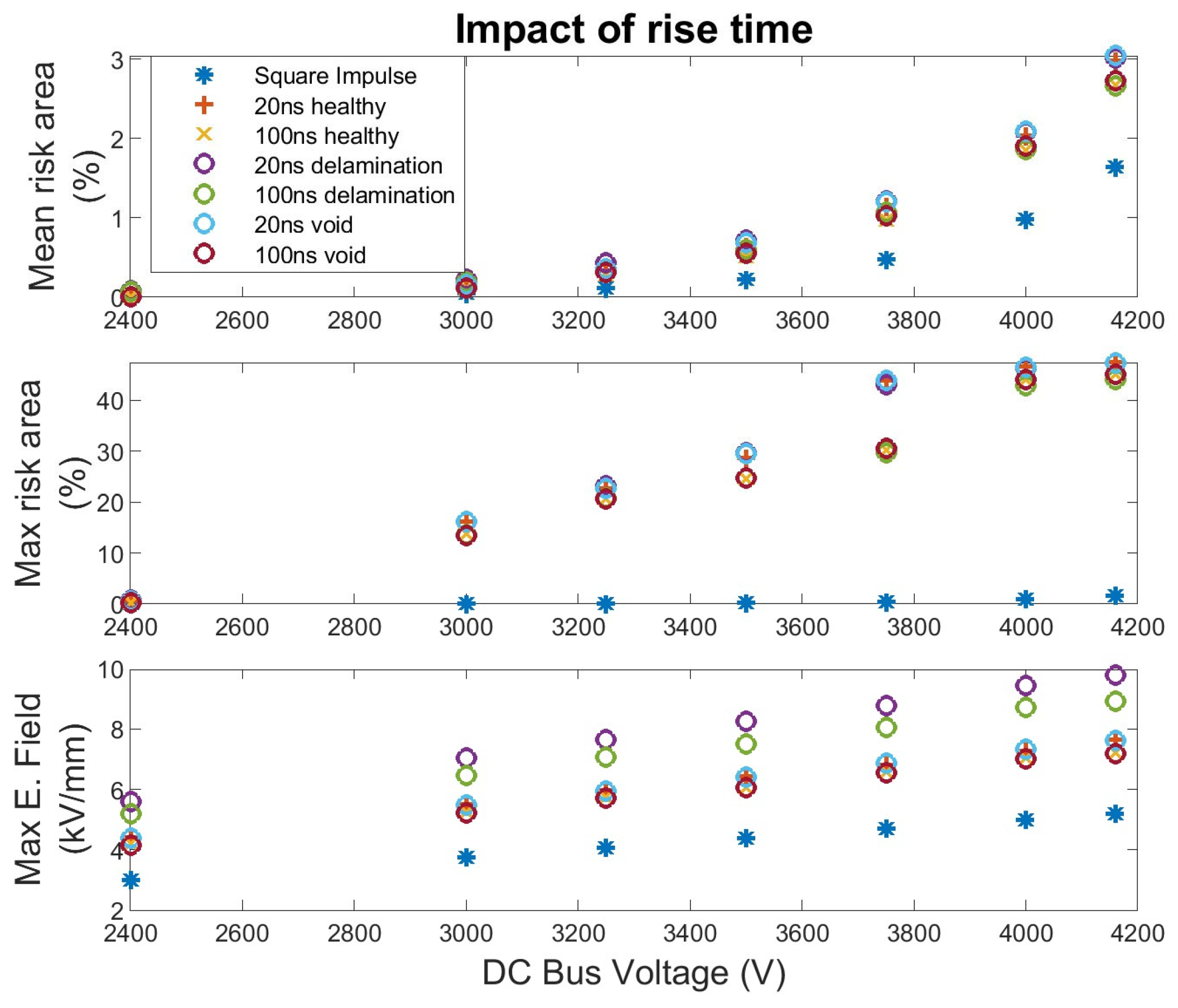

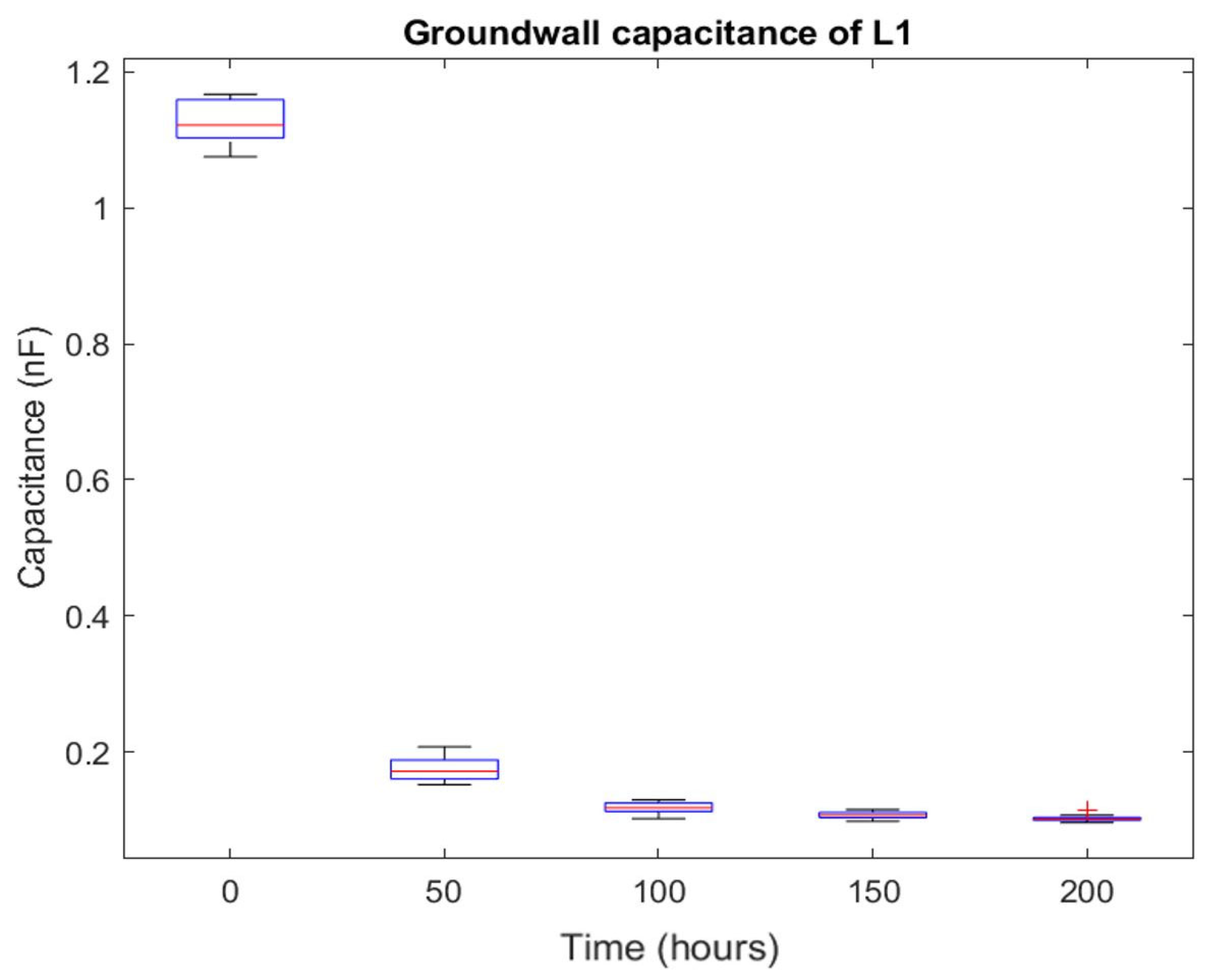
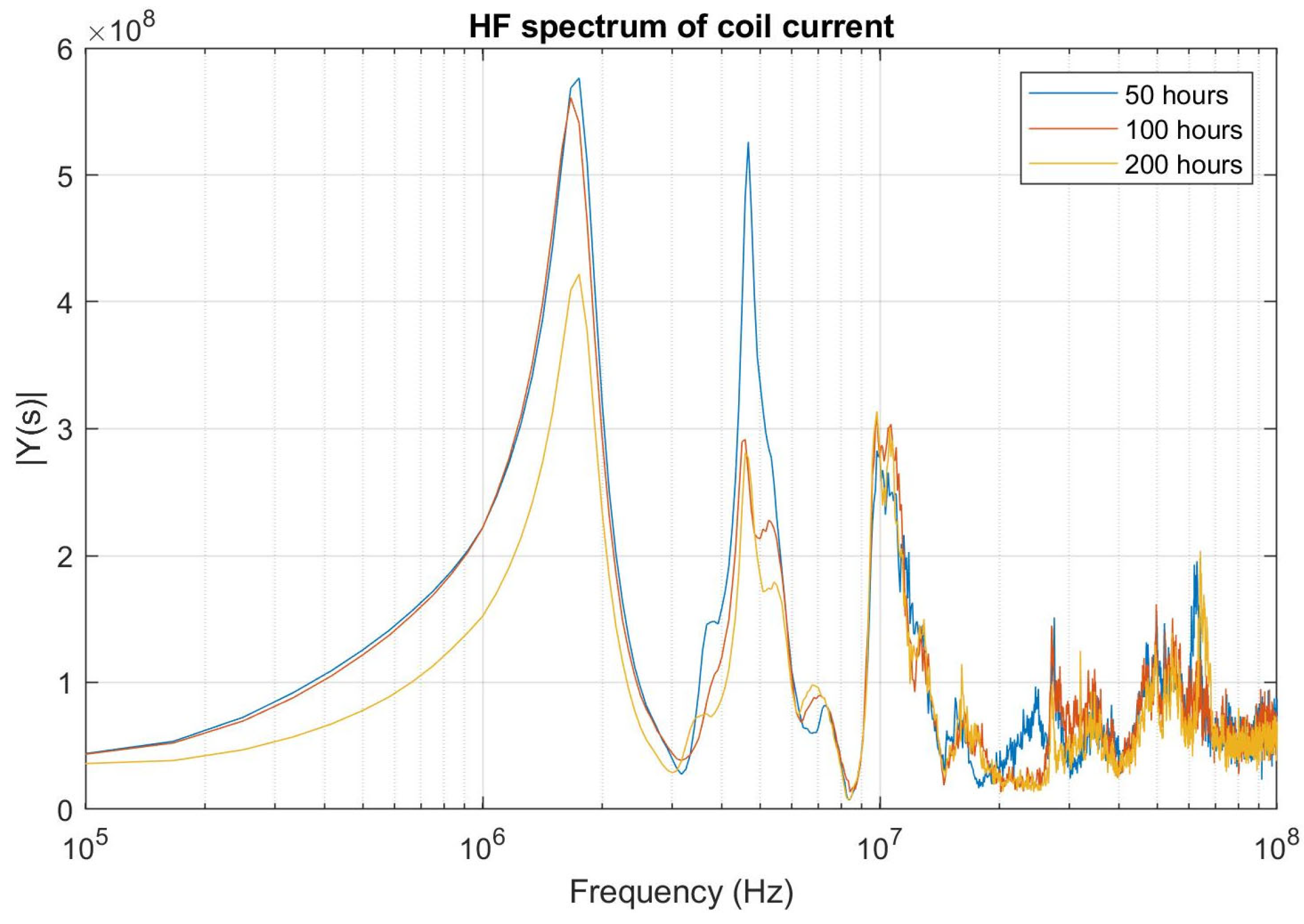
| Mesh Setting | Mesh Elements | Turn 2 Self Capacitance (pF) | Turn 1 to Turn 2 Mutual Capacitance (pF) |
|---|---|---|---|
| Fine | 29,056 | 14.087659 | 68.322529 |
| Extra Fine | 37,498 | 14.087642 | 68.322302 |
| Extremely Fine | 81,692 | 14.087610 | 68.321973 |
| Capacitive Pair | FEA Capacitance (pF) | Analytical Capacitance (pF) |
|---|---|---|
| Turn 1–2 | 68.3 | 67.7 |
| Turn 2-Gnd | 14.1 | 12.5 |
| Turn 2–4 | 0.0008 | 0.0008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirizzotti, B.; Agamloh, E.; von Jouanne, A.; Yokochi, A. Comprehensive Modeling of SiC Inverter Driven Form Wound Motor Coil for Insights on Coil Insulation Stress. Energies 2025, 18, 1262. https://doi.org/10.3390/en18051262
Sirizzotti B, Agamloh E, von Jouanne A, Yokochi A. Comprehensive Modeling of SiC Inverter Driven Form Wound Motor Coil for Insights on Coil Insulation Stress. Energies. 2025; 18(5):1262. https://doi.org/10.3390/en18051262
Chicago/Turabian StyleSirizzotti, Benjamin, Emmanuel Agamloh, Annette von Jouanne, and Alex Yokochi. 2025. "Comprehensive Modeling of SiC Inverter Driven Form Wound Motor Coil for Insights on Coil Insulation Stress" Energies 18, no. 5: 1262. https://doi.org/10.3390/en18051262
APA StyleSirizzotti, B., Agamloh, E., von Jouanne, A., & Yokochi, A. (2025). Comprehensive Modeling of SiC Inverter Driven Form Wound Motor Coil for Insights on Coil Insulation Stress. Energies, 18(5), 1262. https://doi.org/10.3390/en18051262






