Numerical Study of the Effect of Winglets with Multiple Sweep Angles on Wind Turbine Blade Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Turbine Blade and Winglet Geometry
2.2. Computational Methods
- Fundamental equations
- 2.
- Computational domain, mesh, and boundary condition
3. Results
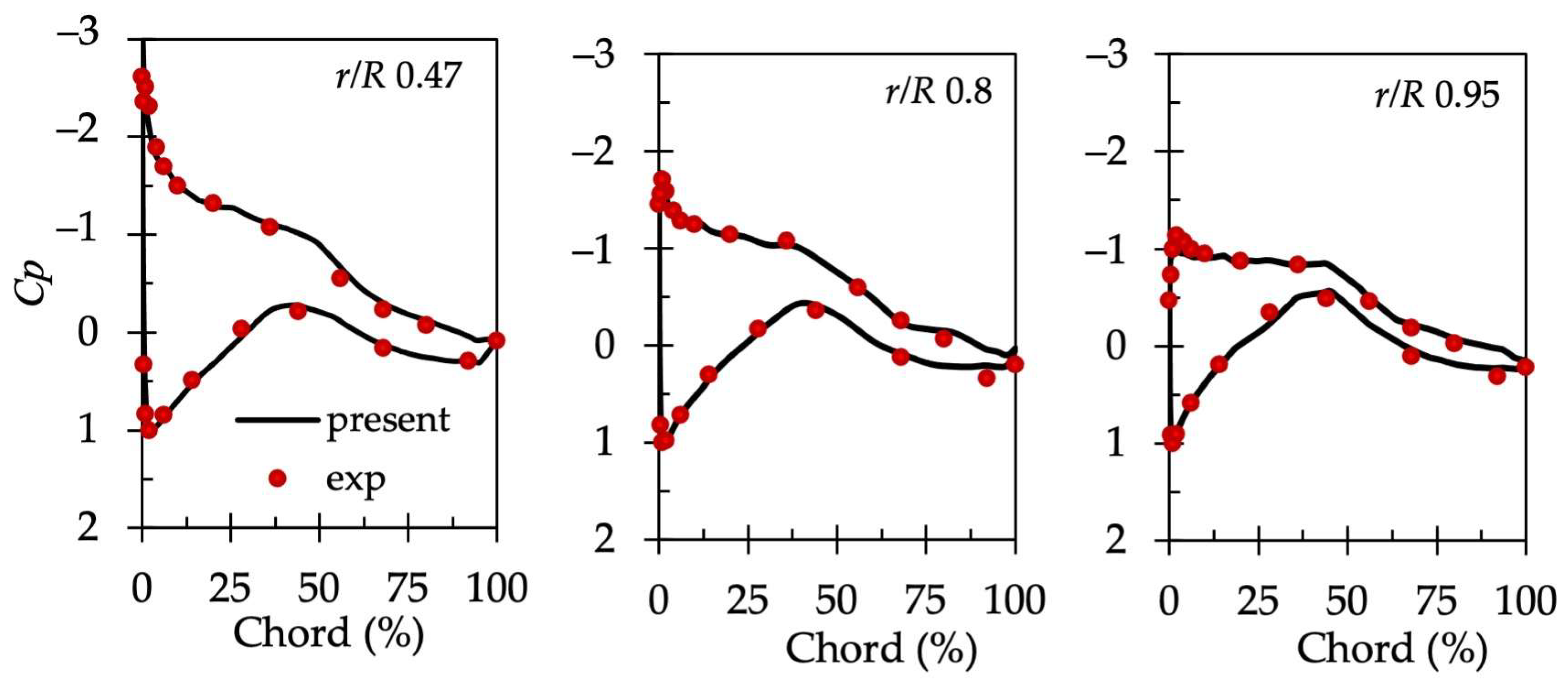
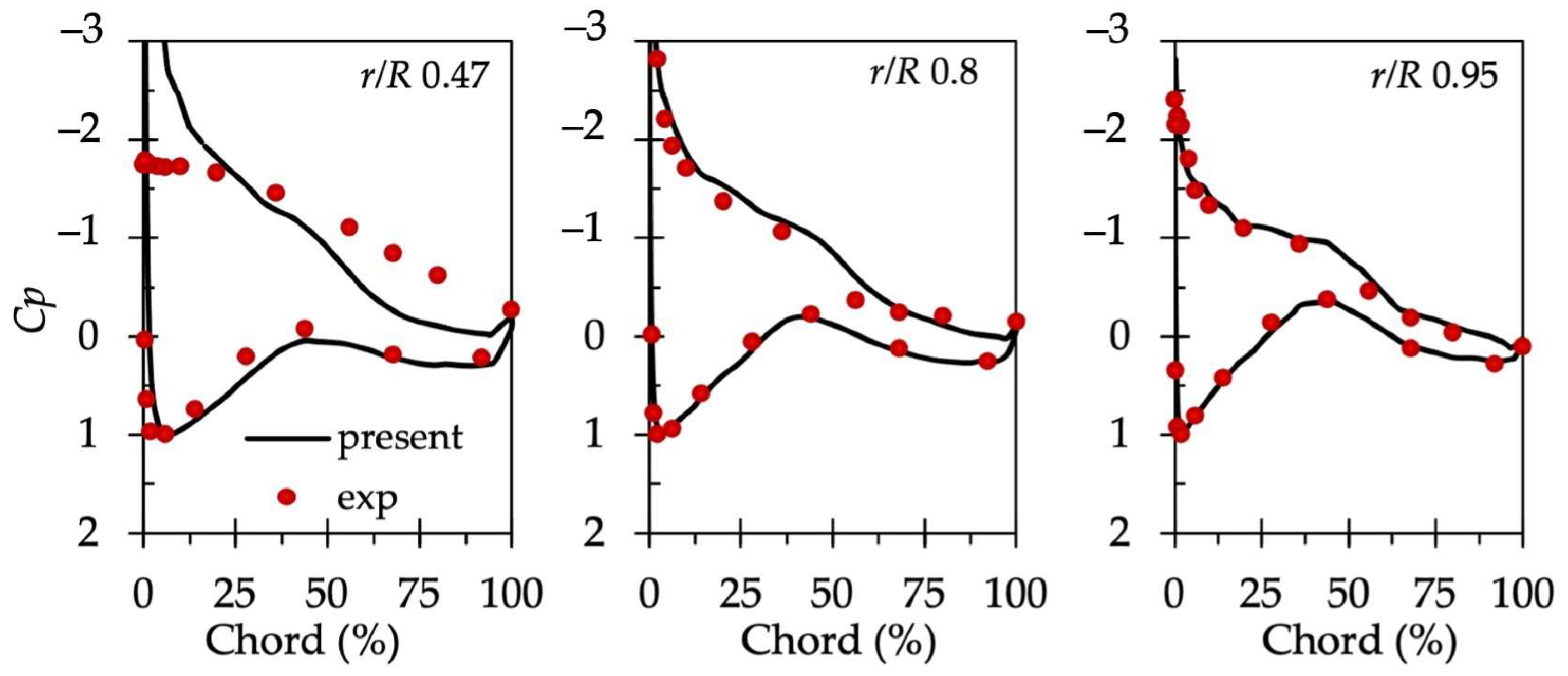
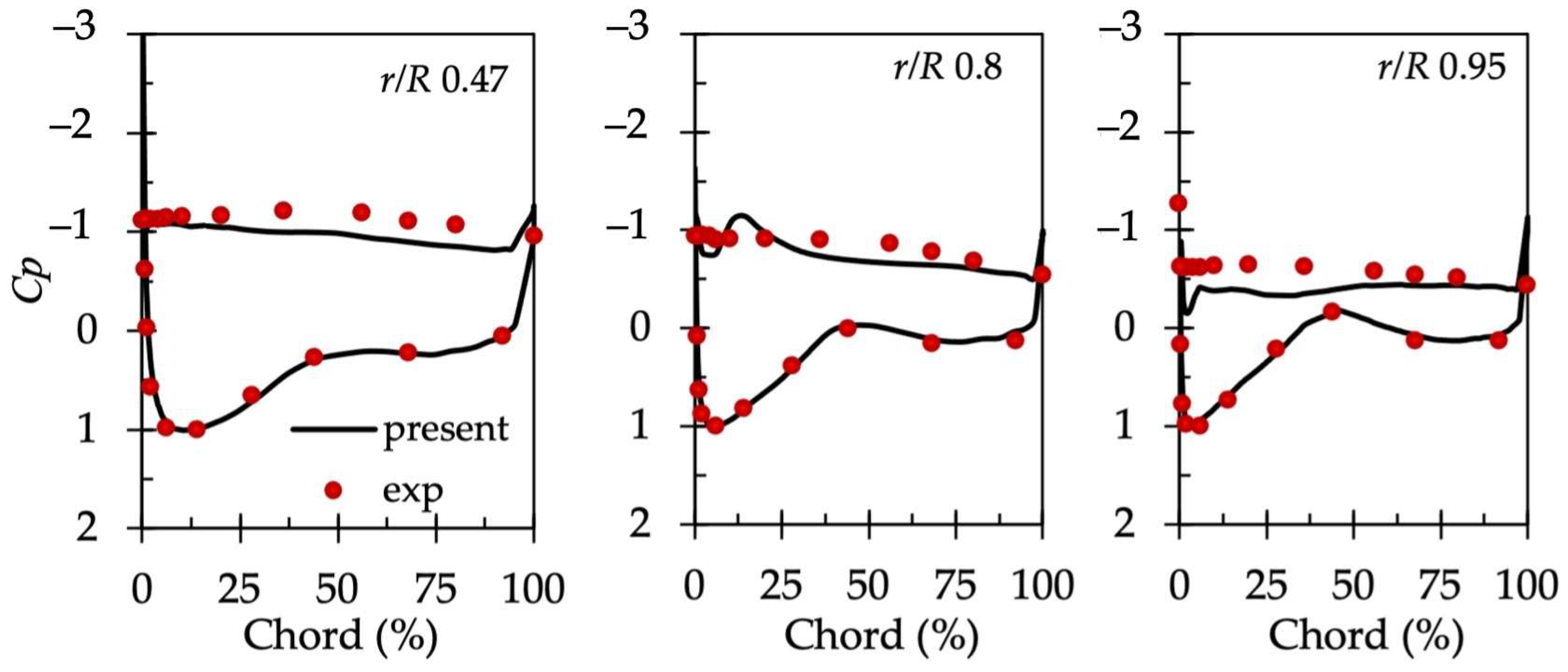
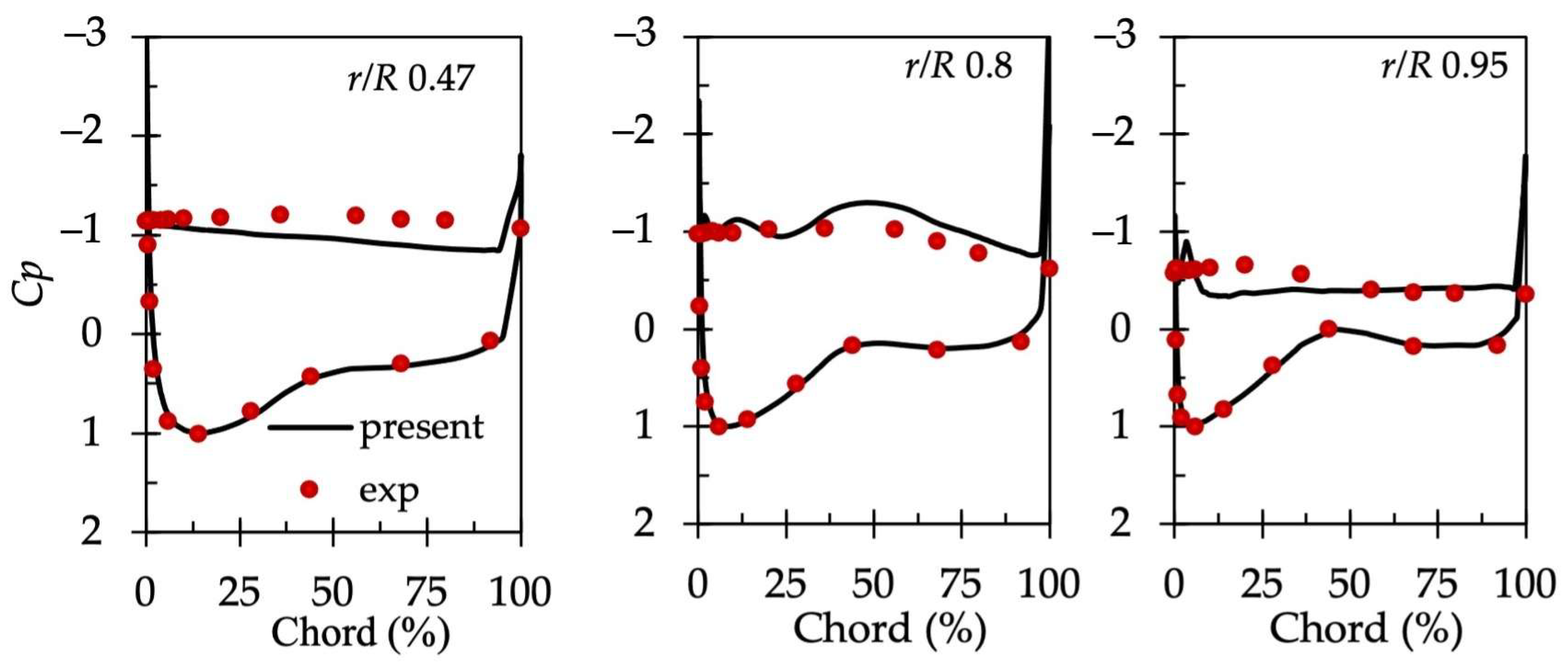
3.1. Validation of Computational Method
3.2. Single-Swept Configuration
3.3. Multi-Swept Configuration
- 1.
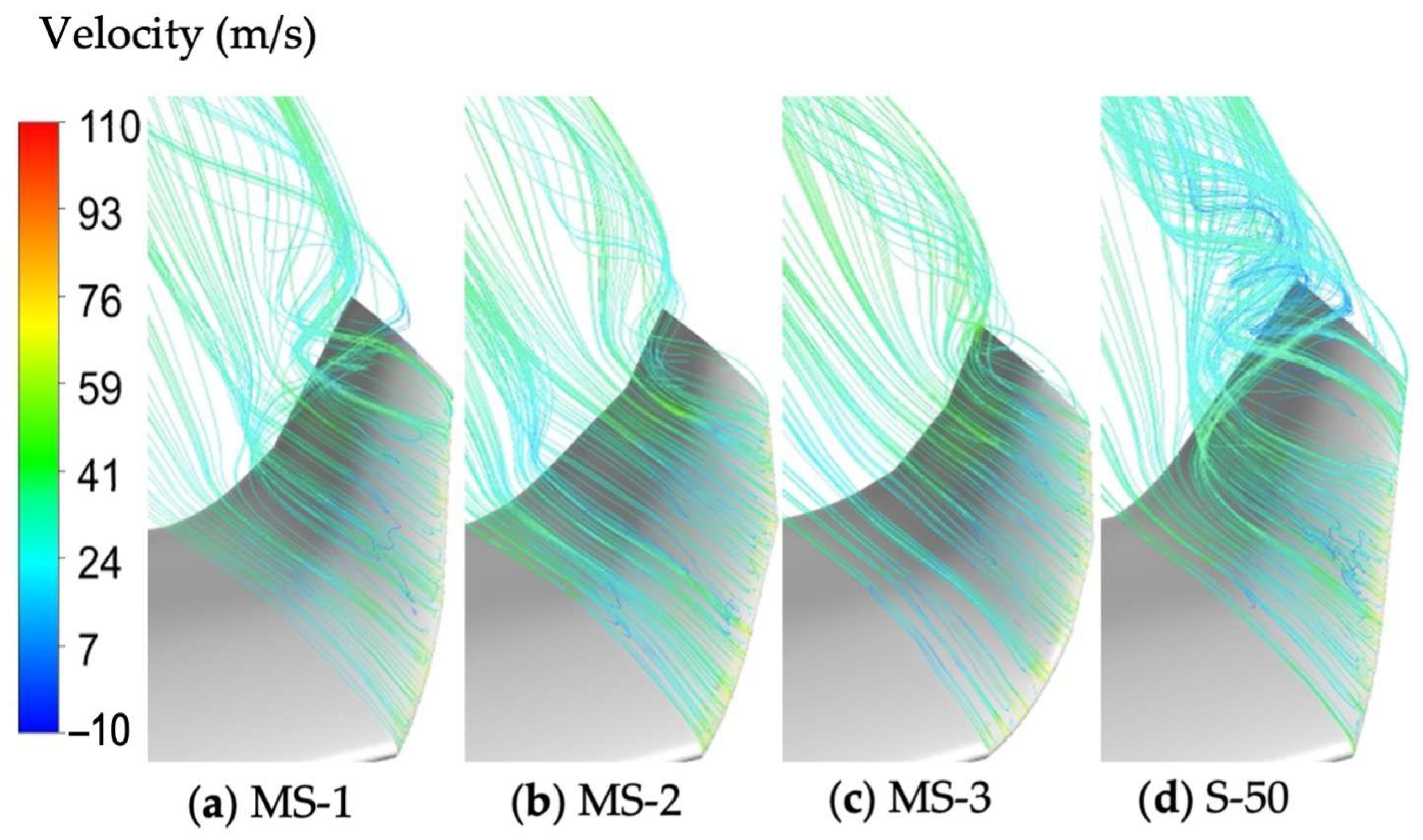
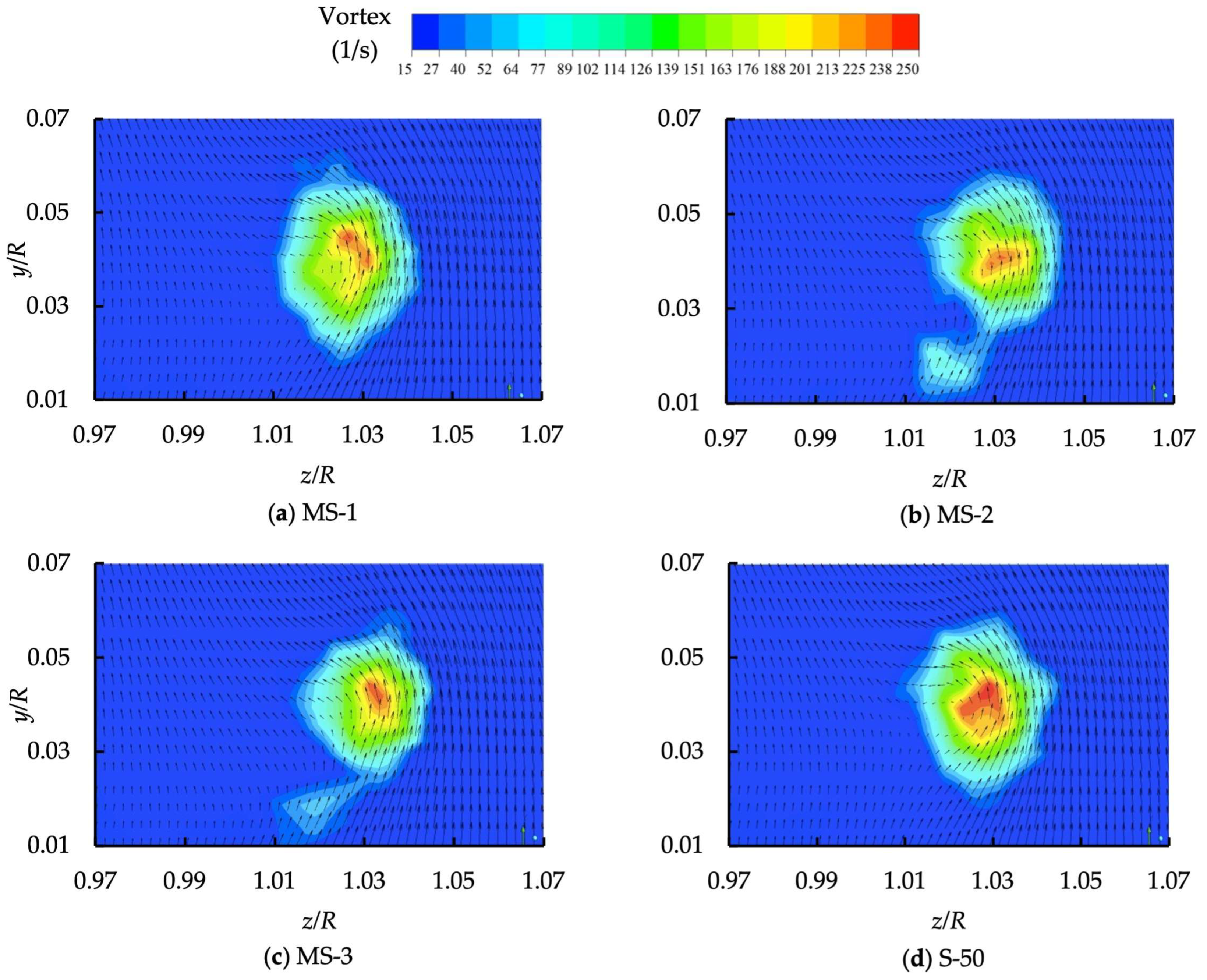
- Flow near winglet and tip vortices
- 2.
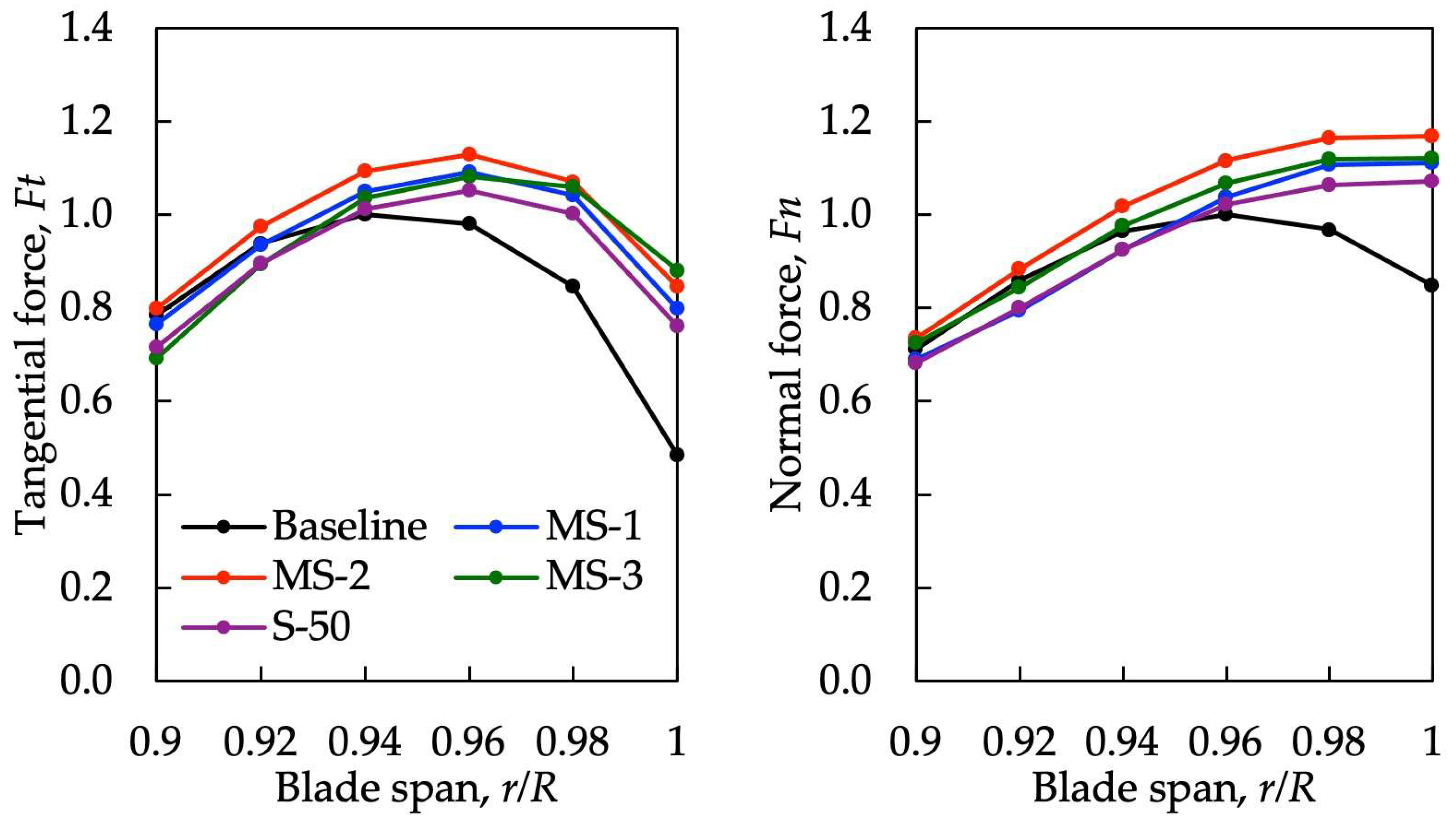
- Tangential and normal forces
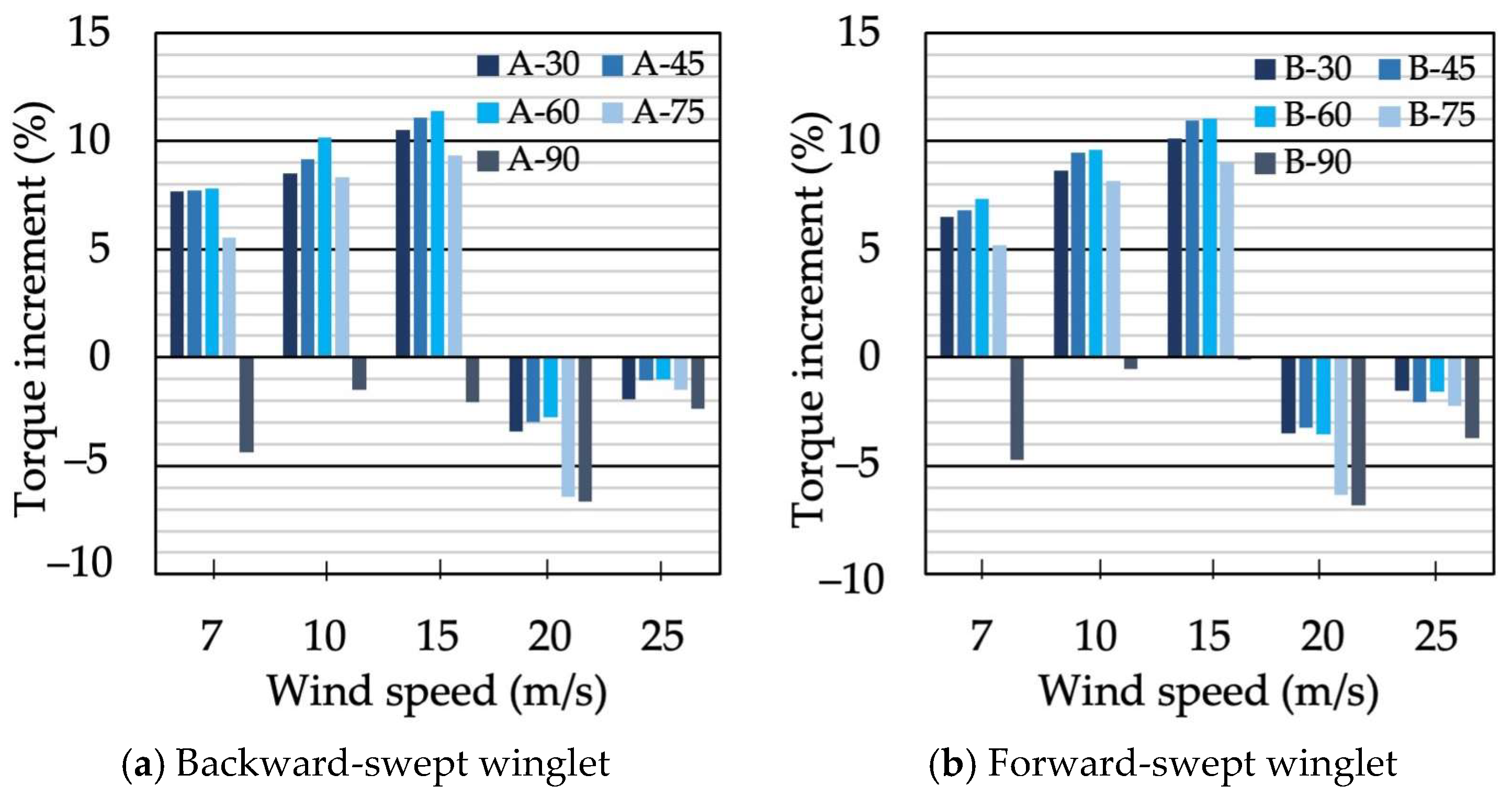
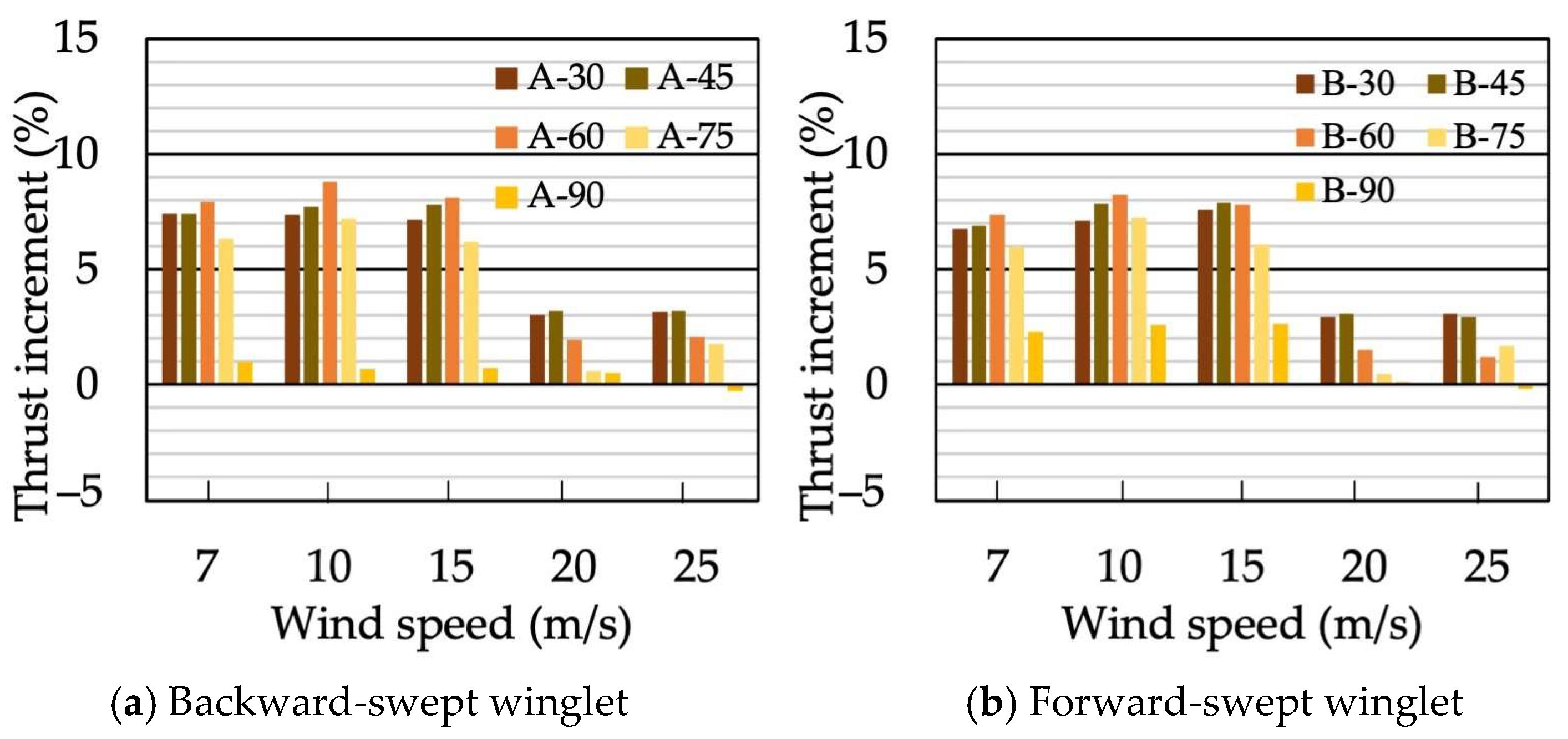
- 3.
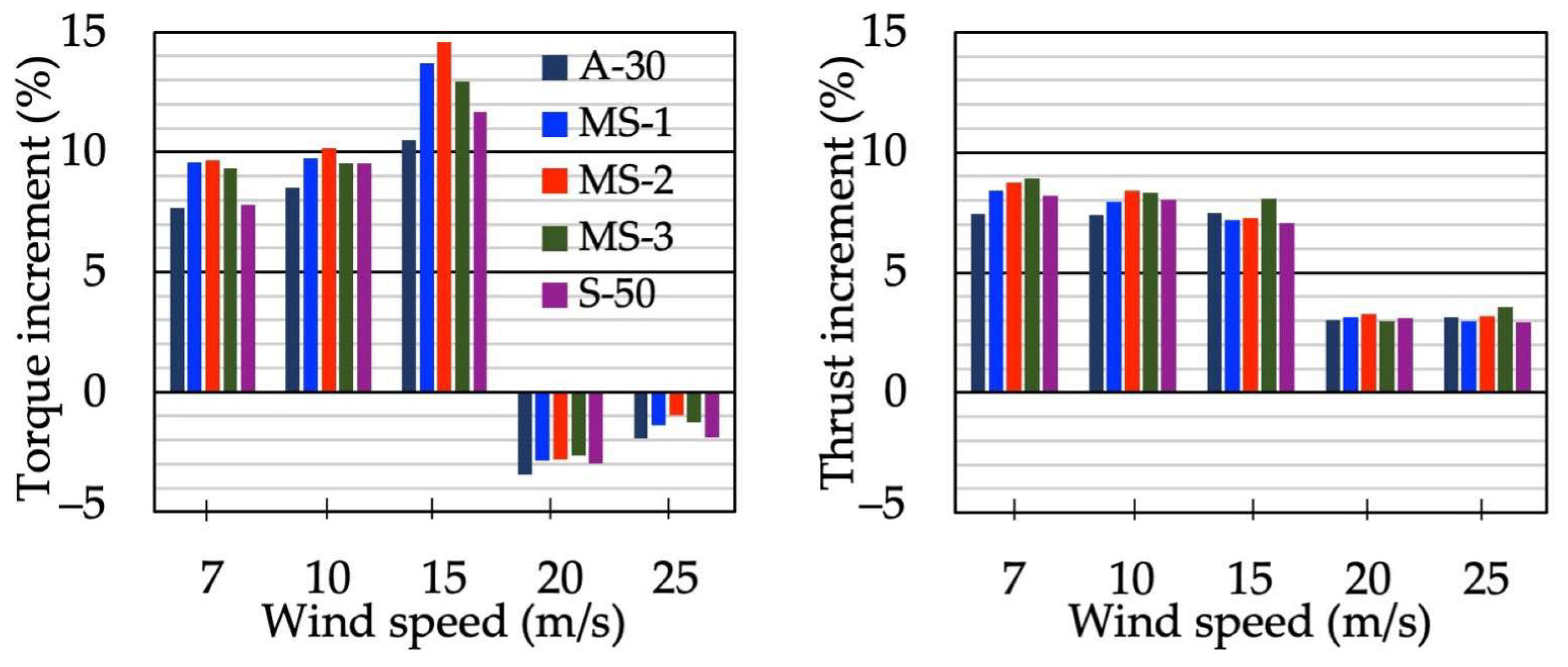
- Torque and thrust increment
- 4.
- Power and power coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Micallef, D.; Akay, B.; Ferreira, C.S.; Sant, T.; Bussel, G.V. The origins of a wind turbine tip vortex. J. Phys. Conf. Ser. 2014, 555, 012074. [Google Scholar] [CrossRef]
- Arumugam, P.; Ramalingam, V.; Bhaganagar, K. A pathway towards sustainable development of small capacity horizontal axis wind turbines—Identification of influencing design parameters & their role on performance analysis. Susain. Energy Technol. Assess. 2021, 44, 101019. [Google Scholar]
- Sun, Z.; Chen, J.; Shen, W.Z.; Zhu, W.J. Improved blade element momentum theory for wind turbine aerodynamic computations. Renew. Energy 2016, 96, 824–831. [Google Scholar] [CrossRef]
- Chattot, J.-J. Effects of blade tip modifications on wind turbine performance using vortex model. Comput. Fluids. 2009, 38, 1405–1410. [Google Scholar] [CrossRef]
- Zhao, T.; Shin, B. An application of upwind difference scheme with preconditioned numerical fluxes to gas-liquid two-phase flows. Fluids 2025, 10, 38. [Google Scholar] [CrossRef]
- Zheng, G.; Xu, P.; Wang, T.; Yan, Q. Study on the bubble collapse characteristics and heat transfer mechanism of the microchannel reactor. Processes 2025, 13, 281. [Google Scholar] [CrossRef]
- Madsen, M.H.; Zahle, F.; Horcas, S.G.; Barlas, T.K.; Sørensen, N.N. CFD-based curved tip shape design for wind turbine blades. Wind Energy Sci. 2022, 7, 1471–1501. [Google Scholar] [CrossRef]
- Wardhana, B.K.; Shin, B. Numerical Investigation of the Effect of Winglet Configurations with Multiple Cant Angles on the Aerodynamic Performance of Wind Turbine Blade. Int. J. Sustain. Energy 2024, 43, 2403486. [Google Scholar] [CrossRef]
- Sy, M.S.; Abuan, B.E.; Danao, L.A.M. Aerodynamic investigation of a horizontal axis wind turbine with split winglet using computational fluid dynamics. Energies 2020, 13, 4983. [Google Scholar] [CrossRef]
- Farhan, A.; Hassanpour, A.; Burns, A. Numerical study of effect of winglet planform and airfoil on a horizontal axis wind turbine performance. Renew. Energy 2019, 131, 1255–1273. [Google Scholar] [CrossRef]
- Jiang, R.; Zhao, Z.; Liu, H.; Wang, T.; Chen, M.; Feng, J.; Wang, D. Numerical study on the influence of vortex generators on wind turbine aerodynamic performance considering rotational effect. Renew. Energy 2022, 186, 730–741. [Google Scholar] [CrossRef]
- Dejene, G.; Ramayya, V.; Bekele, A. Investigation of NREL Phase VI wind turbine blade with different winglet configuration for performance augmentation. Int. J. Sustain. Energy 2024, 43, 2321622. [Google Scholar] [CrossRef]
- Garcia-Ribeiro, D.; Flores-Mezarina, J.A.; Bravo-Mosquera, P.D. Parametric CFD analysis of the taper ratio effects of a winglet on the performance of a Horizontal Axis Wind Turbine. Sustain. Energy Technol. Assess. 2021, 47, 101489. [Google Scholar] [CrossRef]
- Aju, E.J.; Suresh, D.B.; Jin, Y. The influence of winglet pitching on the performance of a model wind turbine: Aerodynamic loads, rotating speed, and wake statistics. Energies 2020, 13, 5199. [Google Scholar] [CrossRef]
- Zhu, B.; Sun, X.; Wang, Y. Performance characteristics of a horizontal axis turbine with fusion winglet. Energy 2017, 120, 431–440. [Google Scholar] [CrossRef]
- Ferrer, E.; Munduate, X. Wind turbine blade tip comparison using CFD. J. Phys. Conf. Ser. 2007, 75, 012005. [Google Scholar] [CrossRef]
- Hansen, T.H.; Mühle, F. Winglet optimization for a model-scale wind turbine. Wind Energy 2018, 21, 634–649. [Google Scholar] [CrossRef]
- Hand, M.M.; Simms, D.A.; Fingersh, L.J. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- Butterfield, C.P.; Musial, W.P.; Simms, D.A. Combined Experiment Phase I: Final Report; National Renewable Energy Laboratory: Golden, CO, USA, 1992. [Google Scholar]
- Menter, F.R. Two-equations eddy-viscocity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassesment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The calculation of low-Reynolds-number-phenomena with a two-equation model of turbulence. Int. J. Heat Mass Trans. 1973, 16, 1119–1130. [Google Scholar] [CrossRef]
- Sedighi, H.; Akbarzadeh, P.; Salavatipour, A. Aerodynamic performance enhancement of horizontal axis wind turbines by dimples on blades: Numerical investigation. Energy 2020, 195, 117056. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent 14.0 User’s Guide; ANSYS: Canonsburg, PA, USA, 2010. [Google Scholar]
- Moshfeghi, M.; Shams, S.; Hur, N. Aerodynamic performance enhancement analysis of horizontal axis wind turbines using a passive flow control method via split blade. J. Wind Eng. Ind. Aerodyn. 2017, 167, 148–159. [Google Scholar] [CrossRef]
- Zhang, Z.; Kuang, L.; Han, Z.; Zhou, D.; Zhao, Y.; Bao, Y.; Duan, L.; Tu, J.; Chen, Y.; Chen, M. Comparative analysis of bent and basic winglets on performance improvement of horizontal axis wind turbines. Energy 2023, 281, 128252. [Google Scholar] [CrossRef]
- Amiri, M.M.; Shadman, M.; Estefen, S.F. URANS simulations of horizontal axis wind turbine under stall condition using Reynolds stress turbulence models. Energy 2020, 213, 118766. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renew. Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Elfarra, M.A.; Sezer-Uzol, N.; Akmandor, I.S. NREL VI rotor blade: Numerical investigation and winglet design and optimization using CFD. Wind Energy 2014, 17, 605–626. [Google Scholar] [CrossRef]
- Huang, S.; Qiu, H.; Wang, Y. Aerodynamic performance of horizontal axis wind turbine with application of dolphin head-shape and lever movement of skeleton bionic airfoils. Energy Convers. Manag. 2022, 267, 115803. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.; Kiendl, J.; Benson, D. A computational procedure for prebending of wind turbine blades. Int. J. Numer. Methods Eng. 2012, 89, 323–336. [Google Scholar] [CrossRef]









| Configuration | Sweep Angle (°) | Cant Angle (°) |
|---|---|---|
| A-30 | 25 | 30 |
| A-45 | 25 | 45 |
| A-60 | 25 | 60 |
| A-75 | 25 | 75 |
| A-90 | 25 | 90 |
| B-30 | −25 | 30 |
| B-45 | −25 | 45 |
| B-60 | −25 | 60 |
| B-75 | −25 | 75 |
| B-90 | −25 | 90 |
| Configuration | Sweep Angle (°) | Cant Angle (°) |
|---|---|---|
| S-0 | 0 | 30 |
| S-25/A-30 | 25 | 30 |
| S-50 | 50 | 30 |
| S-60 | 60 | 30 |
| Configuration | Sweep | Sweep Angle (°) | Cant Angle (°) |
|---|---|---|---|
| MS-1 | 1st (root–0.5 span) | 40 | 30 |
| 2nd (0.5 span–tip) | 50 | ||
| MS-2 | 1st (root–0.75 span) | 40 | 30 |
| 2nd (0.75 span–tip) | 60 | ||
| MS-3 | 1st (root–0.5 span) | 20 | 30 |
| 2nd (0.5 span–0.75 span) | 40 | ||
| 3rd (0.75 span–tip) | 60 | ||
| S-50 | 1st (root–tip) | 50 | 30 |
| Pitch angle | 3° |
| Flap and yaw angles | 0° |
| Rotating direction | Counter-clockwise (upstream view) |
| Rotational speed | 72 rpm |
| Wind speed | 7, 10, 15, 20, 25 m/s |
| Inlet | Inlet velocity Turbulent kinetic energy = 1 m2/s2 Specific dissipation rate = 1 s−1 |
| Outlet | Atmospheric pressure Turbulent kinetic energy = 1 m2/s2 Specific dissipation rate = 1 s−1 |
| Blade | No-slip and moving wall |
| Periodic | Rotational periodic boundary |
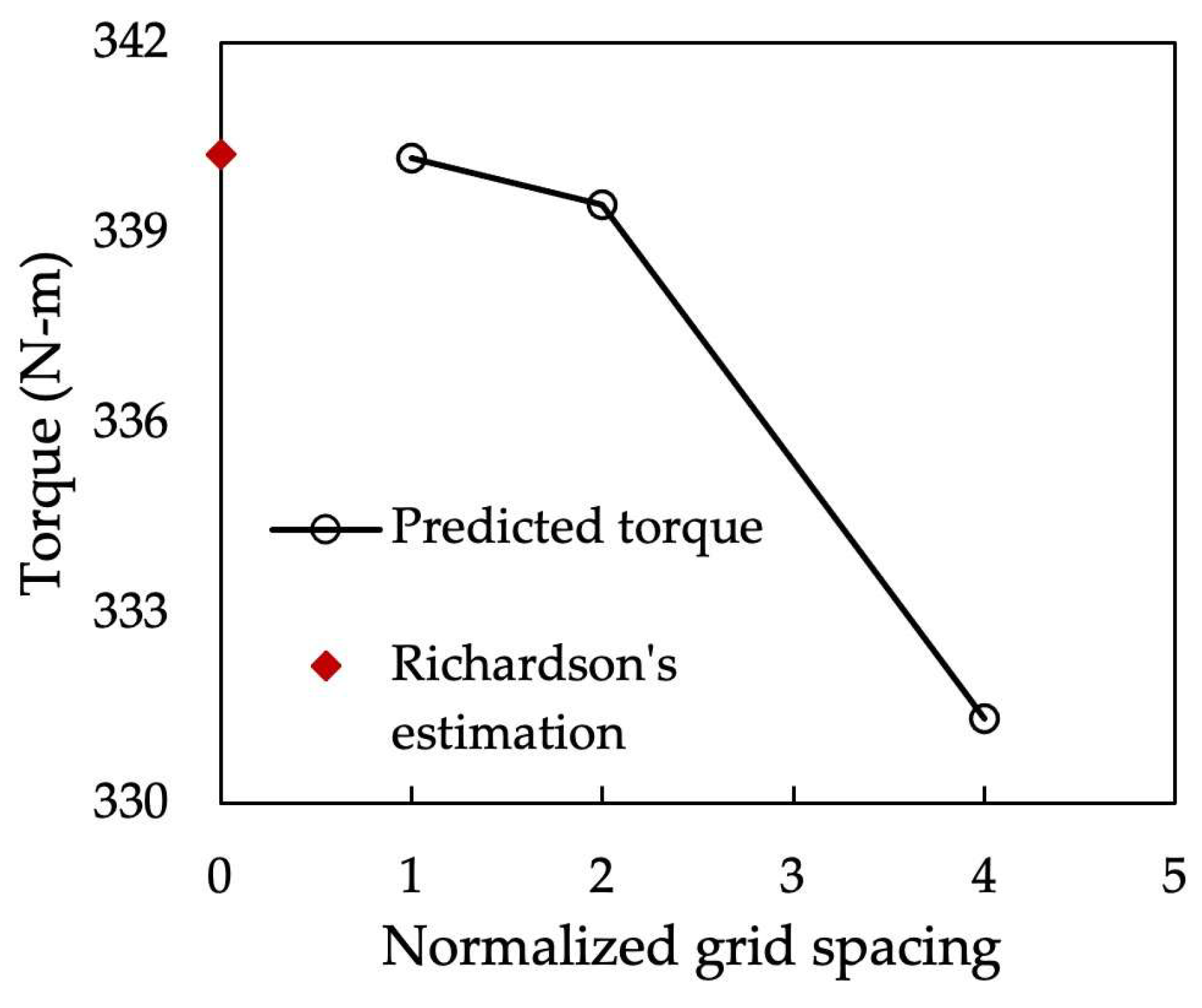
| Mesh Cells | Torque N-m | |
|---|---|---|
| Fine | 3,605,446 | 340.1 |
| Medium | 2,751,754 | 339.4 |
| Coarse | 1,879,628 | 331.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardhana, B.K.; Shin, B. Numerical Study of the Effect of Winglets with Multiple Sweep Angles on Wind Turbine Blade Performance. Energies 2025, 18, 1292. https://doi.org/10.3390/en18051292
Wardhana BK, Shin B. Numerical Study of the Effect of Winglets with Multiple Sweep Angles on Wind Turbine Blade Performance. Energies. 2025; 18(5):1292. https://doi.org/10.3390/en18051292
Chicago/Turabian StyleWardhana, Bayu K., and Byeongrog Shin. 2025. "Numerical Study of the Effect of Winglets with Multiple Sweep Angles on Wind Turbine Blade Performance" Energies 18, no. 5: 1292. https://doi.org/10.3390/en18051292
APA StyleWardhana, B. K., & Shin, B. (2025). Numerical Study of the Effect of Winglets with Multiple Sweep Angles on Wind Turbine Blade Performance. Energies, 18(5), 1292. https://doi.org/10.3390/en18051292






