A Long-Range, High-Efficiency Resonant Wireless Power Transfer via Imaginary Turn Ratio Air Voltage Transformer

Abstract

This paper presents a resonant wireless power transfer method that leverages a 90-degree voltage phase shift between the transmitting and receiving coils to enhance efficiency and maximize power transfer. When the resonant coupling is achieved, the secondary coil with an adjustable capacitor forms a tuned LC circuit. If the primary coil is driven at the resonant frequency of both the primary and secondary sides, the system can transmit 250W of power between the coils over a distance of 50 cm. Using a single power transmitting unit (PTU) board with multiple paralleled gallium nitride high-electron-mobility transistors (GaN HEMTs), the system achieves a maximum power transfer efficiency of 88%, highlighting the effectiveness of the design in high-efficiency, long-distance wireless power transmission. The key to the success of high-power, high-efficiency RWPT is in exhibiting the imaginary turn ratio presented on the air transformer. The imaginary turn ratio can realize the negative impedance conversion that converts the positive resistance on the power-receiving unit into a negative one, and thus, the damping of the resonance oscillation becomes negative and positively encourages more power to be delivered to the power-receiving unit (PRU) load. This paper derives the theory of the imaginary turn ratio and demonstrates the implementation of the RWPT system that exhibits the imaginary turn ratio effect.

1. Introduction

In recent years, wireless power transfer (WPT) has gained substantial attention in fields such as portable electronic devices [1], implanted biomedical devices [2,3,4], electric vehicles (EVs) [5], and unmanned aerial vehicles (UAVs) [6]. In addition, an integrated wireless/fast charger solution for public transit vehicles was also proposed [7]. Variations in transmission distance and energy efficiency are among the most important concerns in these applications.

Among the various WPT systems, the non-radiative inductive power transfer (IPT) technique is widely utilized in short-range applications due to its convenience and safety [8]. Inductive charging is two halves of the inductive coupling interface consisting of the primary and secondary of a two-part transformer [9,10]. In a previous study [11], the relationship between the quality factor of resonance and the coupling factor was noted. However, a notable limitation of an inductive coupling-based WPT is that the transfer distance is significantly less than the diameter of the transmitter or receiver coils, thereby restricting its applicability in certain scenarios.

Long-range wireless power transfer can also benefit from parity-time symmetry-based inductively coupled prototypes [12], which play a crucial role in enhancing long-range wireless power transfer efficiency and stability. This resonance enhances magnetic coupling, allowing efficient energy transfer over longer distances and reducing sensitivity to coil misalignment. Resonant wireless power transfer (RWPT) enables power to be transferred via oscillating magnetic fields that exchange energy between the resonant coils, effectively extending the transfer range beyond the near-field limitations of IPT [13]. Comprehensive overviews of resonant circuits for WPT systems, which address key issues such as zero-voltage switching, zero-voltage derivative switching, and total harmonic distortion, are provided in [14], while classifications, applications, trends, advantages, and disadvantages of RWPT are discussed in [15,16].

Many studies have demonstrated utilizing gallium nitride high-electron-mobility transistors (GaN HEMTs) as switching components to improve their power efficiency in MHz frequency bands [17,18,19,20,21]. However, discussions on efficient wireless non-radiative mid-range energy transfer have been scarce because, in the mid-range magnetic field (also known as the reactive near field or Fresnel region), the relationship between the strengths of the electric (E) and magnetic (H) fields is often too complex to predict and is difficult to measure. In addition, the electromagnetic flux linkage due to coil misalignment reduces the coupling coefficient and mutual inductance, leading to power loss in the system [22].

A theoretical analysis of the RWPT [23] demonstrated that by designing electromagnetic resonators [24] that suffer a minimal loss due to radiation and absorption and have a near field with mid-range extent, for instance, with a fraction of the coil diameter (D) range, the mid-range efficient RWPT is possible. The reason is that if the power transmitting unit (PTU) and power-receiving unit (PRU) are tuned to have the same frequency and they are apart by within a fraction of a wavelength, their near fields are coupled by means of the evanescent wave coupling.

The challenge of resonant wireless power transfer (RWPT) lies in balancing three key factors: long-range transmission, high power delivered to the load (PDL), and high-power transfer efficiency (PTE) to enable its application in industrial products such as EV chargers. The comparisons must account for wired chargers, which currently operate in the 10–100 kW range with efficiencies of 90% or higher over meter-scale distances. This paper presents a possible configuration to achieve the target specification, except that the power delivered to the load (PDL) depends on the number of parallel high-breakdown voltage GaN HEMTs. Negative impedance also significantly improves impedance matching for wideband electroacoustic transduction. Digital non-Foster electronics enhance the bandwidth by over five times, ensuring stability and tenability [25].

This study begins with Section 2, which introduces the basic elements of the RWPT system. A key feature is the addition of a back iron behind the PTU, enhancing the coupling coefficient through open/short circuit testing. In Section 3, we derived the relationship between the quality factor and the coupling coefficient to achieve an imaginary turn ratio in the air voltage transformer. By specially arranging the PTU and PRU structures, the impedance of the DC storage system is converted into a negative impedance, leading to free oscillation and a negative damping effect. The high frequency switch using depletion-mode (D-mode) GaN HEMT is also introduced. In Section 4, we demonstrated the effect of an imaginary turn ratio in the RWPT system and the effect of negative impedance. Another feature of this paper is the use of parallel GaN HEMTs under the class-E amplifier topology and its zero-voltage switching (ZVS) condition to enhance power transfer. The switching loss is minimal, allowing an efficiency of 88% for 250 W of PDL over a 50 cm coil separation.

2. GaN HEMT-Based Class-E Resonant Wireless Power Transfer

As shown in Figure 1, the proposed RWPT system includes four basic elements: air transformer, back iron, PTU resonator circuit, and PRU resonator circuit. It is connected to a wave-clipper rectifier that trims the peak of the received voltage and converts the trimmed voltage into energy stored in a DC storage unit, such as a battery.

There are three geometric factors—namely, the distance of power delivery distance d, the PTU/PRU coil diameter D, and the back iron distance to PTU coil b, as indicated in Figure 1—which are important specifications to the RWPT. These geometric factors could be adjusted in other scenarios; however, in this research, they are fixed at d = 50 cm and D = 72 cm, while the back iron distance b is left to be determined. The goals of the proposed RWPT are high power and high efficiency. In order to achieve the goals, the necessary actions include:

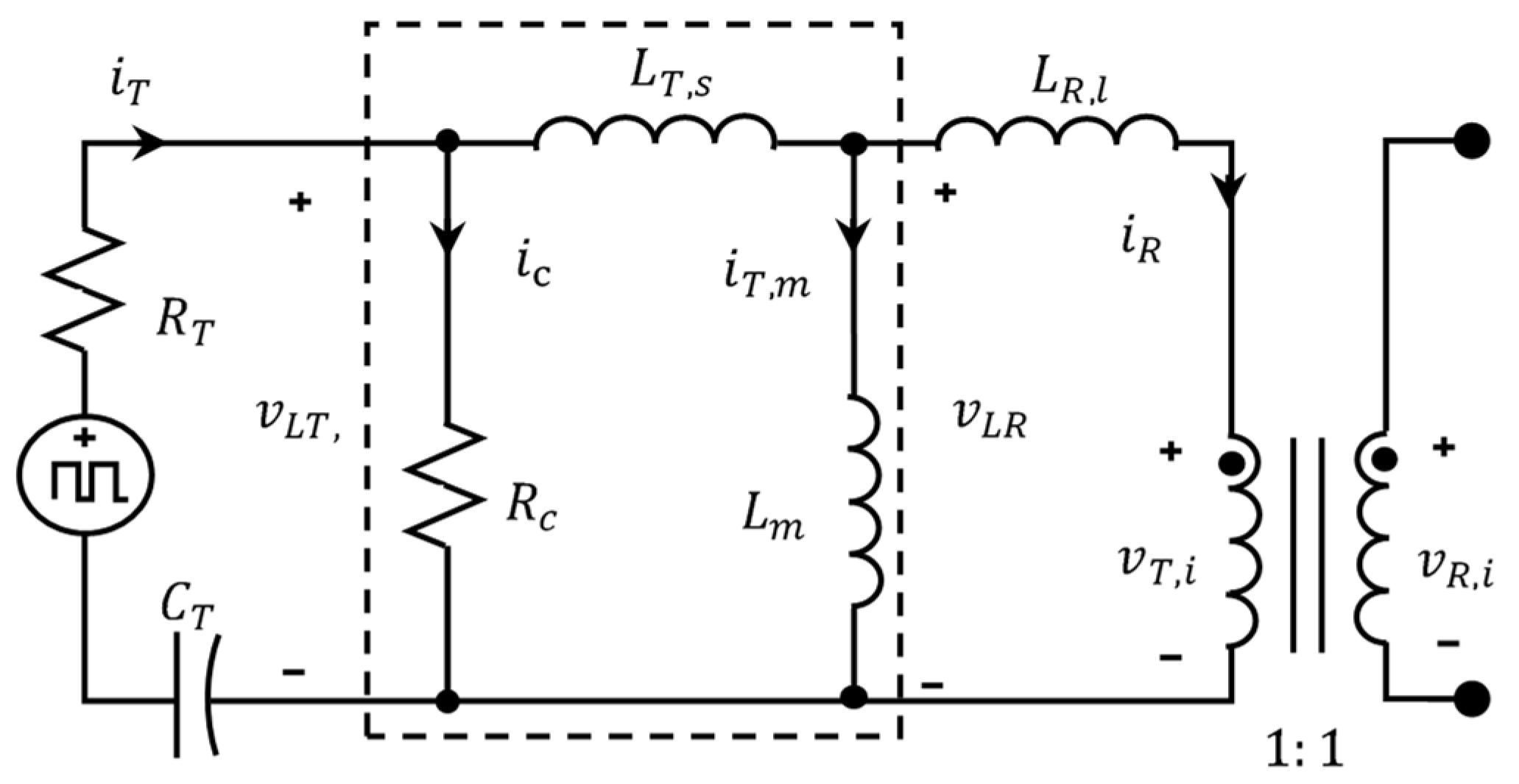
• Tuning the adjustable capacitor to make the ratio between two coil voltages ${\mathrm{v}}_{\mathrm{L}\mathrm{R}}$ and ${\mathrm{v}}_{\mathrm{L}\mathrm{T}}$ an imaginary number, i.e., ${\displaystyle \frac{{\mathrm{v}}_{\mathrm{L}\mathrm{R}}}{{\mathrm{v}}_{\mathrm{L}\mathrm{T}}}}=\mathrm{j}\left|{\displaystyle \frac{{\mathrm{v}}_{\mathrm{L}\mathrm{R}}}{{\mathrm{v}}_{\mathrm{L}\mathrm{T}}}}\right|$.
  Due to the imaginary turn ratio, the impedance of the DC storage system is converted into a negative impedance. The equivalent transformer circuit, which includes this negative impedance, exhibits free oscillation or even a negative damping effect. As a result, the oscillating current increases when the DC storage system is connected to the PRU resonator circuit, thereby maximizing power transfer.
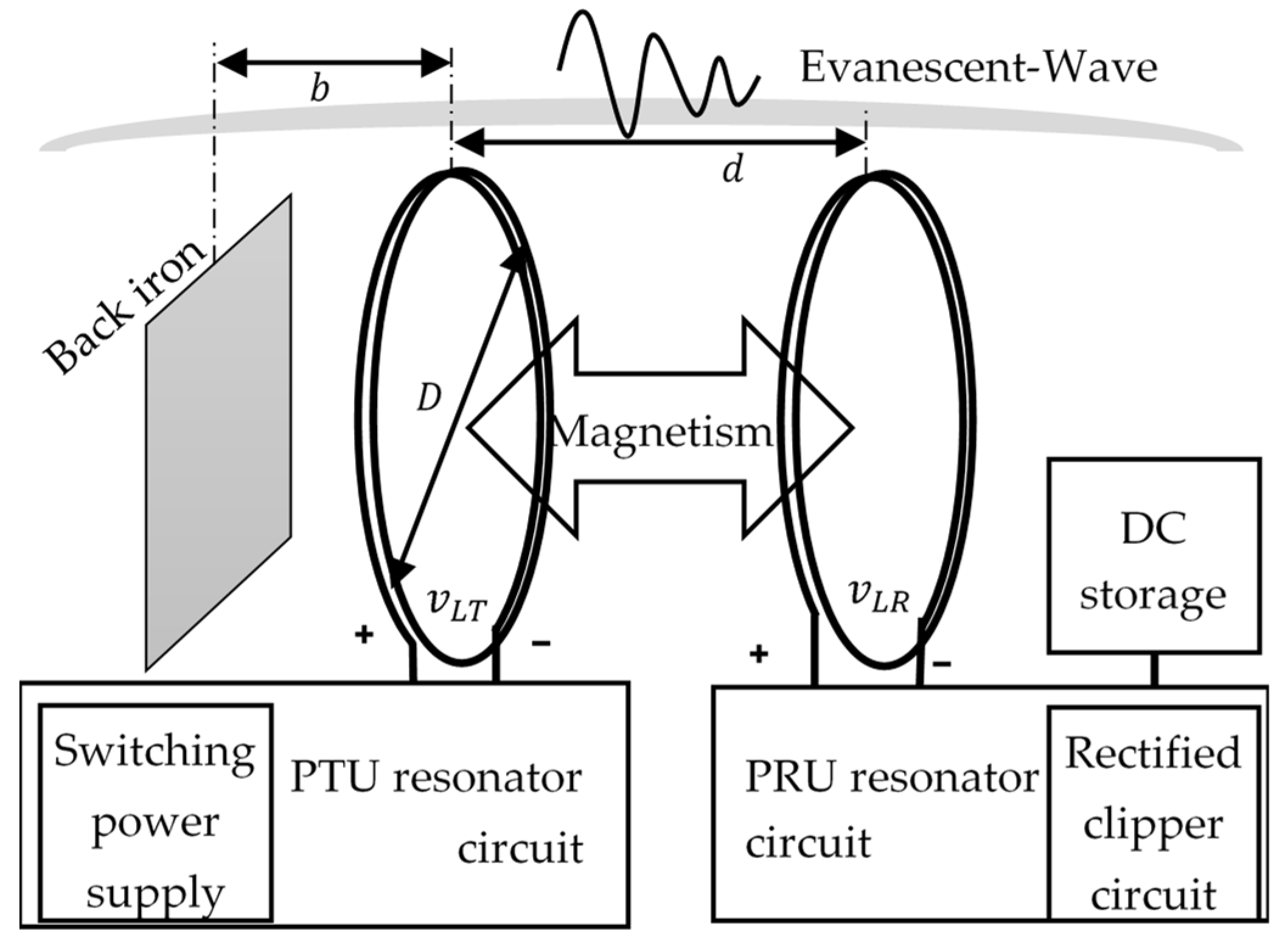
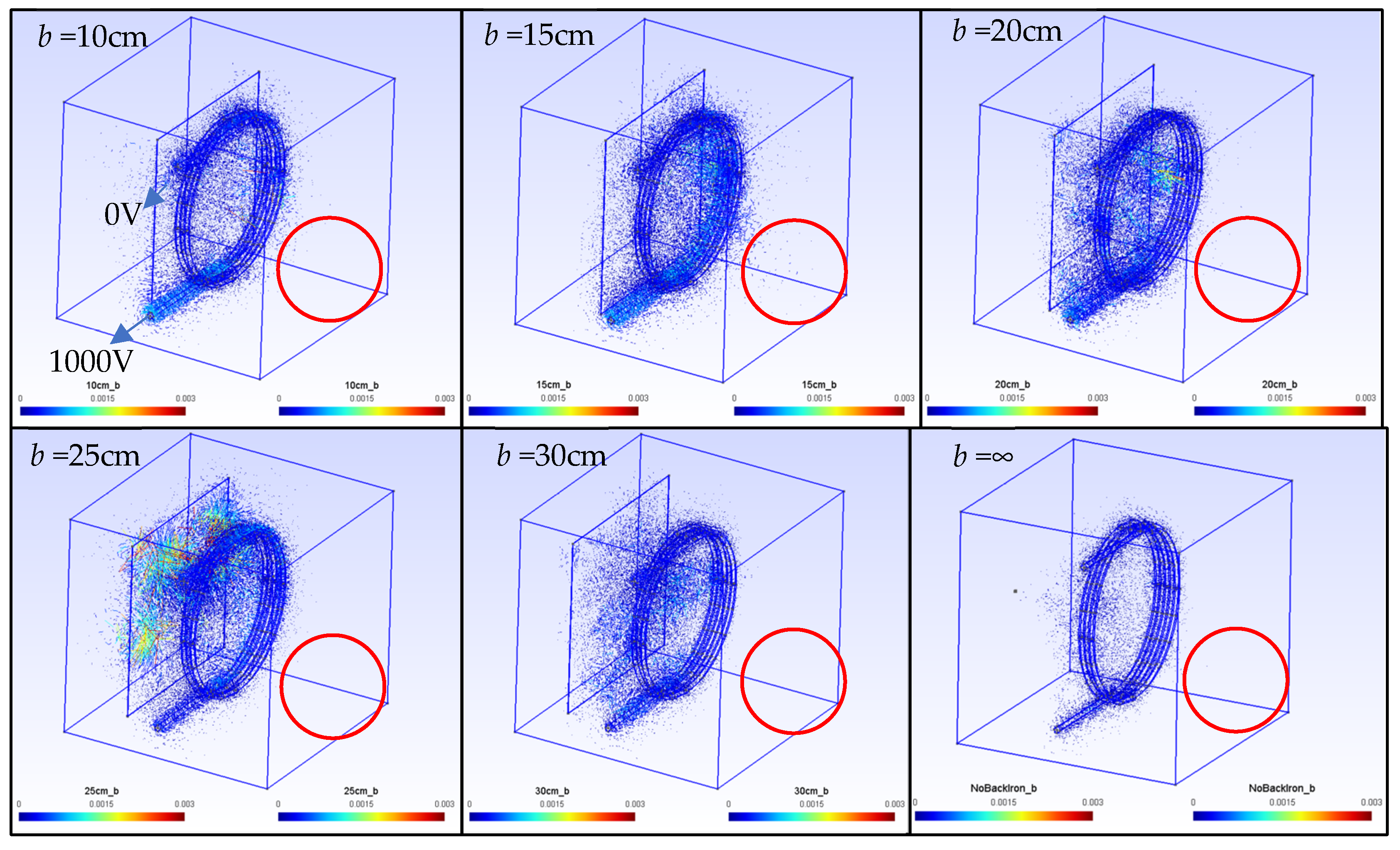
• The back iron distance should be adjusted to balance both high PTE and high PDL.
• The switching frequency and duty cycle of the switching power supply must be controlled to maximize the PTE.

Open Circuit and Short Circuit Test of the PTU Resonator

During the open circuit and short circuit tests, we removed the PRU resonator circuit from the RWPT system, as shown in Figure 2, and replaced it with a voltage meter and ammeter. The back iron is a steel plate on the back of the PTU coil that forms the return path of flux between the PTU coil and PRU coil within the free space. It increases the magnetic flux and, therefore, the current transfer from the PTU to the PRU. The flux ratio of the mutual flux to the primary flux is known as the coupling coefficient k. In the resonance case, the flux ratio changes, and the mutual flux increases. In addition to the flux ratio changes, the evanescent wave effect that occurred on the surface of the back iron, as well as the environment metal structure, may also enhance the magnetic coupling. We need to determine the optimal back iron distance to simultaneously achieve a high coupling coefficient k and high PTE.

The power loss of the PTU is subjected to the coil loss (including the switching loss) and core loss (including the evanescent wave effect). It is assumed that the coil loss is related to the current magnitude and the $P_{core}$ is associated with the coil voltage as follows.

$$\begin{array}{cc} & P_{in}=P_{coil}+P_{core} \\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}& \\ & P_{coil}=I_T^2·R_T, P_{core}=I_c^2·R_c\end{array}$$

(1)

$R_c$ denotes the loss due to the evanescent waves in the vicinity of the PTU and PRU. The root mean square (RMS) current relations are derived from Ohm’s law as follows.

$$\begin{array}{cc} & I_T=I_c+I_{T,m}+I_R\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}& \\ & I_c={\displaystyle \frac{V_{LT,o}}{R_{c }\left(b\right)}}, I_{T,m}={\displaystyle \frac{V_{T,i}+I_R\omega L_{R,l}}{\omega L_m}}\end{array}$$

(2)

Subjected to the open circuit test with the conditions that $I_R=0$, $V_{T,i,o}=V_{R,o}$, the coupling coefficient can be obtained as follows.

$$k={\displaystyle \frac{V_{R,o}}{V_{LT,o}}}$$

(3)

The inductance of the PTU coil is calculated as follows, providing the assumption that the core resistance is $R_c\gg \omega L_T$.

$$L_T={\displaystyle \frac{V_{LT,o}}{\omega I_{T,o}}}$$

(4)

It is found that the coupling coefficient k, i.e., the flux ratio, increases due to the presence of back iron. The PTU inductance $L_T$ is decreased due to the presence of back iron. It is also observed that the primary flux also increases due to the presence of back iron.

$${\displaystyle \frac{\varphi \left(b\right)}{\varphi (\infty )}}={\displaystyle \frac{V_{LT,o}\left(b\right)}{k{V}_{LT,o}(\infty )}}$$

(5)

The effect of back iron on the coupling coefficient, inductance, and magnetic flux gains are schematically shown in Figure 3 and Figure 4. The results show that the primary flux can be tripled, and the coupling coefficient k can be enhanced by 40% due to the presence of back iron.

Comparing the open circuit and short circuit test results, we assume that the core resistance $R_c\left(b\right)$ and the coil resistance $R_T$ remained under the same back iron distance $b$.

$$R_c\left(b\right)={\displaystyle \frac{I_{T,s}^2{V}_{LT,o}^2-I_{T,o}^2{V}_{LT,s}^2}{I_{T,s}^2{P}_{in,o}-I_{T,o}^2{P}_{in,s}}}$$

(6)

$$R_T={\displaystyle \frac{P_{in,o}-\frac{V_{LT,o}^2}{R_c\left(b\right)}}{I_{T,o}^2}}$$

(7)

The result of the resistance calculation is shown in Figure 5. It is shown that the modeled coil resistance $R_T$, which shall include the switching loss and the connector loss remaining nearly constant with or without the back iron. On the other hand, when the back iron becomes too close to the PTU coil (below 20 cm in this study), the core resistance has a rapid drop, which may induce a large core loss due to the eddy current flowing on the back iron.

The FEM analysis was performed using the Sparselizard finite element C++ library [26]. The graphical output was generated using Gmsh(version 4.11.1) [27], which is a three-dimensional finite element mesh generator. The back iron and PTU coil were configured with the same geometric dimensions and the same material used in the experiments. In Figure 6, the rectangular box represents the domain of the FEM analysis, and the coils are subjected to an input voltage of 1 kV. The tiny vectors indicate the magnetic flux directions, whose colors ranged from blue to red indicate the flux density B. The red circles located on the corners FEM domains indicate the flux density in the flux linkage direction toward the PRU. Comparing the analytical results, the flux density exhibits a peak intensity at a back iron distance of $b=$ 25 cm. However, the flux starts to appear inside the red circle when the back iron distance $b\le$ 15 cm. We chose $b=$ 15 cm in the RWPT experiment because it yields the largest flux linkage from the PTU to PRU. When the back iron is absent from behind the PTU coil (i.e., $b=\mathrm{\infty }$), the flux density becomes very low; this result is consistent with the experiments, as shown in Figure 4. The maximum flux density distance $b=$ 25 cm is the highest permeability, which induces less core loss and is also consistent with the highest core loss resistance result shown in Figure 5.

3. Mathematical Modeling of Resonant Wireless Power Transfer

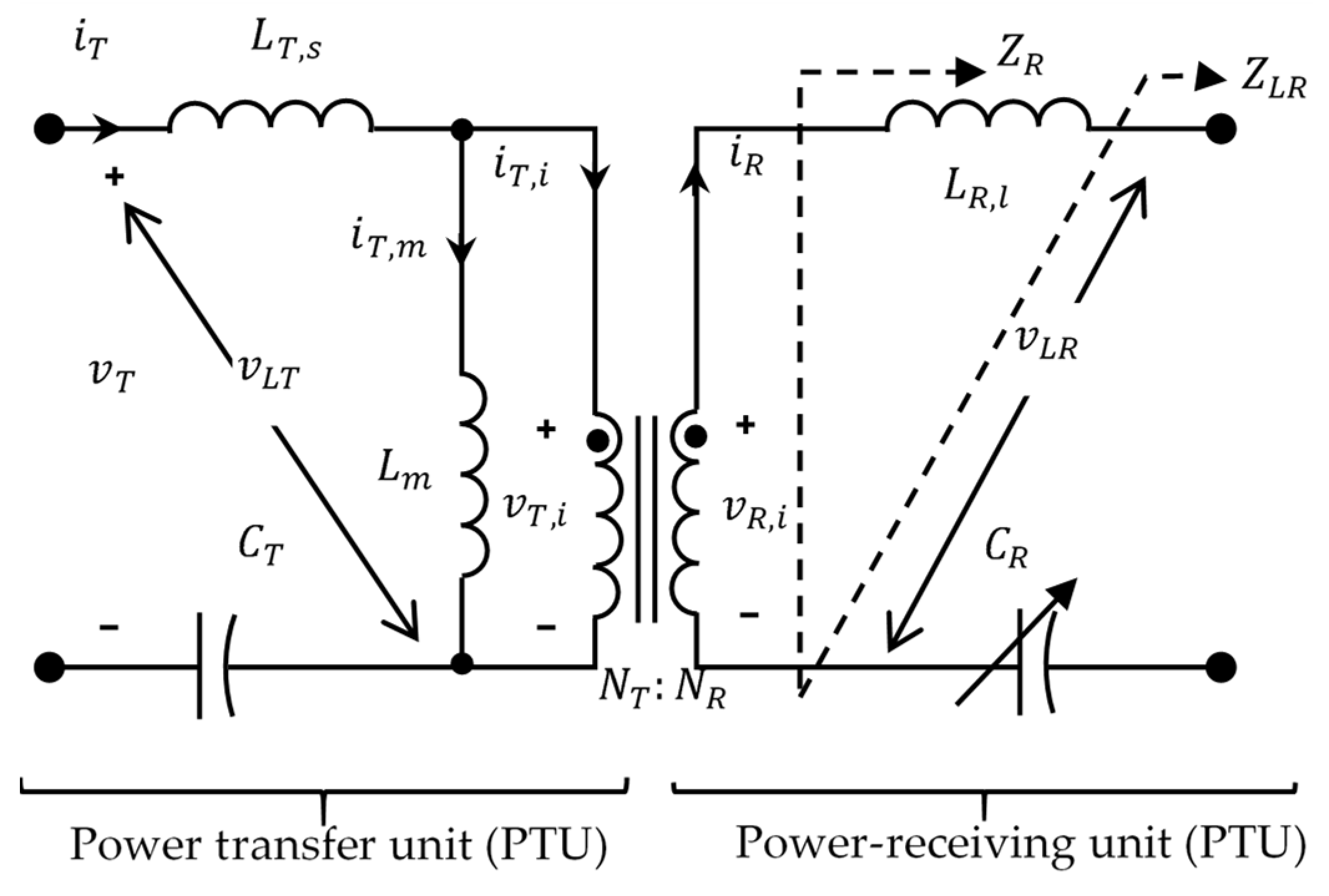
3.1. Imaginary Turn Ratio Conditions

The term “turn ratio” is mathematically defined as the ratio of the coil turning on opposite sides of a transformer, which is a real rational number. The voltage ratio measured from two sides of the transformer usually follows the “turn ratio”. In an air transformer, the voltage across two sides of the air transformer presents a 90-degree phase shift; equivalently, the voltage sees the turn ratio as an imaginary number. In the transformer’s equivalent circuit, which transfers the PRU impedance to the PTU side, the positive resistance of the PRU is converted into a negative resistance. When the turn ratio of the ideal transformer is an imaginary number, the ideal transformer in the equivalent circuit behaves as a negative impedance converter (NIC).

In this section, we analyze the RWPT circuit and provide proof of the existence of the imaginary turn ratio transformer effect. Without loss of generality, we ignored the core resistance $R_c$ from the circuit analysis according to Thevenin’s equivalent circuit theory as shown in Figure 7.

The mutual inductance $L_m$ is related to the transfer voltage $v_{T,i}$ by the equation as follows:

$$v_{T,i}=L_m{\displaystyle \frac{d{i}_{T,m}}{dt}}=N_T{\displaystyle \frac{d{\varphi }_m}{dt}}=a{v}_{R,i}$$

(8)

The overall inductance of the PTU has three parts consisting of leakage inductance, self-inductance, and mutual inductance. When the leakage inductances of the PTU are ignored, the ratio between the mutual inductance, $L_m=k{L}_T$, and the total inductance is known as the coupling coefficient k and can be written in the inductance ratio as follows:

$$k={\displaystyle \frac{L_m}{L_T}}={\displaystyle \frac{L_m}{L_{T,s}+L_m}}$$

(9)

$L_{T,s}=\left(1-k\right)L_T$ denotes the self-inductance of the PTU. The total flux $\varphi$ generated from the PTU consists of the magnetization flux ${\varphi }_m$, the transformer-induced flux ${\varphi }_i$, and the self-induction flux ${\varphi }_s$. The transformer-induced flux ${\varphi }_i$ shall be canceled out due to the coexistence of $i_{T,i}$, and $i_R$ in the magnetic field, as follows:

$${\varphi }_i={\displaystyle \frac{L_m}{N_T}}{i}_{T,i}={{\displaystyle \frac{L_m}{a{N}_T}}i}_R$$

(10)

The current $i_R$ flowing through the inductor of the PRU is a function of the turn ratio $a=N_T/N_R$ of $i_{T,i}$. The voltage output $v_T$ of the PTU resonant generator is derived from (8) to (10) and $i_T=i_{T,i}+i_{T,m}$ as follows:

$$v_T={\displaystyle \frac{1}{C_T}}\int i_{T}dt+L_{T,s}{\displaystyle \frac{d{i}_T}{dt}}+L_m{\displaystyle \frac{d{i}_{T,m}}{dt}}$$

(11)

Subjected to the wave-clipper rectifier and the battery $V_B$ impedance denoted by $Z_R$, and with the turn ratio $a$ being unity, the voltage $v_T$ can be expressed using the Laplace transform as follows:

$$V_T\left(s\right)=\left({\displaystyle \frac{{{\omega }_T}^2}{k{s}^2}}+{\displaystyle \frac{1}{C_T{Z}_R\left(s\right)s}}+{\displaystyle \frac{\left(1-k\right)s}{Z_R\left(s\right)}}{L}_T+{\displaystyle \frac{1}{k}}\right)V_{R,i}\left(s\right)$$

(12)

${\omega }_T=\sqrt{1/L_T{C}_T}$ denotes the resonant frequency of the PTU. The transfer function between the input $V_T\left(s\right)$ and $V_R\left(s\right)$ is then derived as follows:

$${\displaystyle \frac{V_{R,i}\left(s\right)}{V_T\left(s\right)}}={\displaystyle \frac{s^{2}k{C}_T{Z}_R\left(s\right)}{\left(s^2+{{\omega }_T}^2\right)C_T{Z}_R\left(s\right)+ks\left(s^2{L}_T{C}_T\left(1-k\right)+1\right)}}$$

(13)

When the excitation frequency ${\omega }_0$ is identical to the series resonant frequency ${\omega }_R=\sqrt{1/L_{R,l}{C}_R}$ of $Z_R\left(s\right)$, we will obtain a pure resistive circuit $Z_R\left(j{\omega }_R\right)=R_R$. The resistance $R_R$is an equivalent series resistance of the PRU resonator circuit. The transfer function can be simplified as follows:

$${\displaystyle \frac{V_{R,i}\left(s\right)}{V_T\left(s\right)}}\approx {\displaystyle \frac{s}{s^2+{{\omega }_T}^2}}·{\displaystyle \frac{1}{\left(\frac{1}{ks}+\frac{1}{{{\omega }_T}^2{R}_R{C}_T}\right)}}$$

(14)

The above equation shows a sinusoidal relation between the voltage output $v_T$ from the switching power supply and the receiving voltage $v_{R,i}$ on the PRU. Resonance occurs when the switching frequency ${\omega }_0$ of $V_T\left(s\right)$ matches the resonant frequency ${\omega }_T$ and ${\omega }_R$ of the LC tanks of the PTU and PRU. In the resonance condition, the transformer output voltage is derived as follows:

$$\begin{gathered} V_{LT}\left(s\right)=\left({\displaystyle \frac{\left(1-k\right)s{L}_T}{Z_R\left(s\right)}}+{\displaystyle \frac{1}{k}}\right){\displaystyle \frac{Z_R\left(s\right)}{Z_{LR}\left(s\right)}} \\ {V}_{LR}\left(s\right)={\displaystyle \frac{k\left(1-k\right)s{L}_T+Z_R\left(s\right)}{k{Z}_{LR}\left(s\right)}}{V}_{LR}\left(s\right) \end{gathered}$$

(15)

In the state of resonance on the PRU, when ${\omega }_0={\omega }_T={\omega }_R$, we have a circuit relation as follows:

$$Z_{LR}\left(j{\omega }_0\right)=R_R-j{\displaystyle \frac{1}{{\omega }_R{C}_R}}=R_R-j{\omega }_T{L}_T$$

(16)

The voltage transfer function between coils is then written as

$$V_{LT}\left(s\right)={\displaystyle \frac{k\left(1-k\right)j{Q}_s+1}{k\left(1-j{Q}_s\right)}}{V}_{LR}\left(s\right)$$

(17)

$Q_s={\omega }_T{L}_T/R_R$ is the series resonance quality factor. For weak coupling, i.e., the small coefficient $k$, when with a large series resonance, the voltage gain from $V_{LT}$ to $V_{LR}$ is derived as follows.

$${\displaystyle \frac{V_{LR}\left(j{\omega }_1\right)}{V_{LT}\left(j{\omega }_1\right)}}=\left\{\begin{array}{cc}k& Q_s\ll 1/k\\ -j{\displaystyle \frac{1}{Q_s}}& Q_s\approx \sqrt{1/k}\\ -1& Q_s\gg 1/k\end{array}\right.$$

(18)

From the equation above, it can be observed that the imaginary turn ratio can be obtained when three conditions are satisfied simultaneously, as follows:

(1)

The switching frequency ${\omega }_o$ matches the resonant frequency of the PTU’s LC tank, i.e., ${\omega }_o={\omega }_T.$

(2)

The adjustable capacitor $C_R$ shall set the resonant frequency ${\omega }_R$ in the PRU to match the resonant frequency of the PTU’s LC tank, i.e., ${\omega }_R={\omega }_T.$

(3)

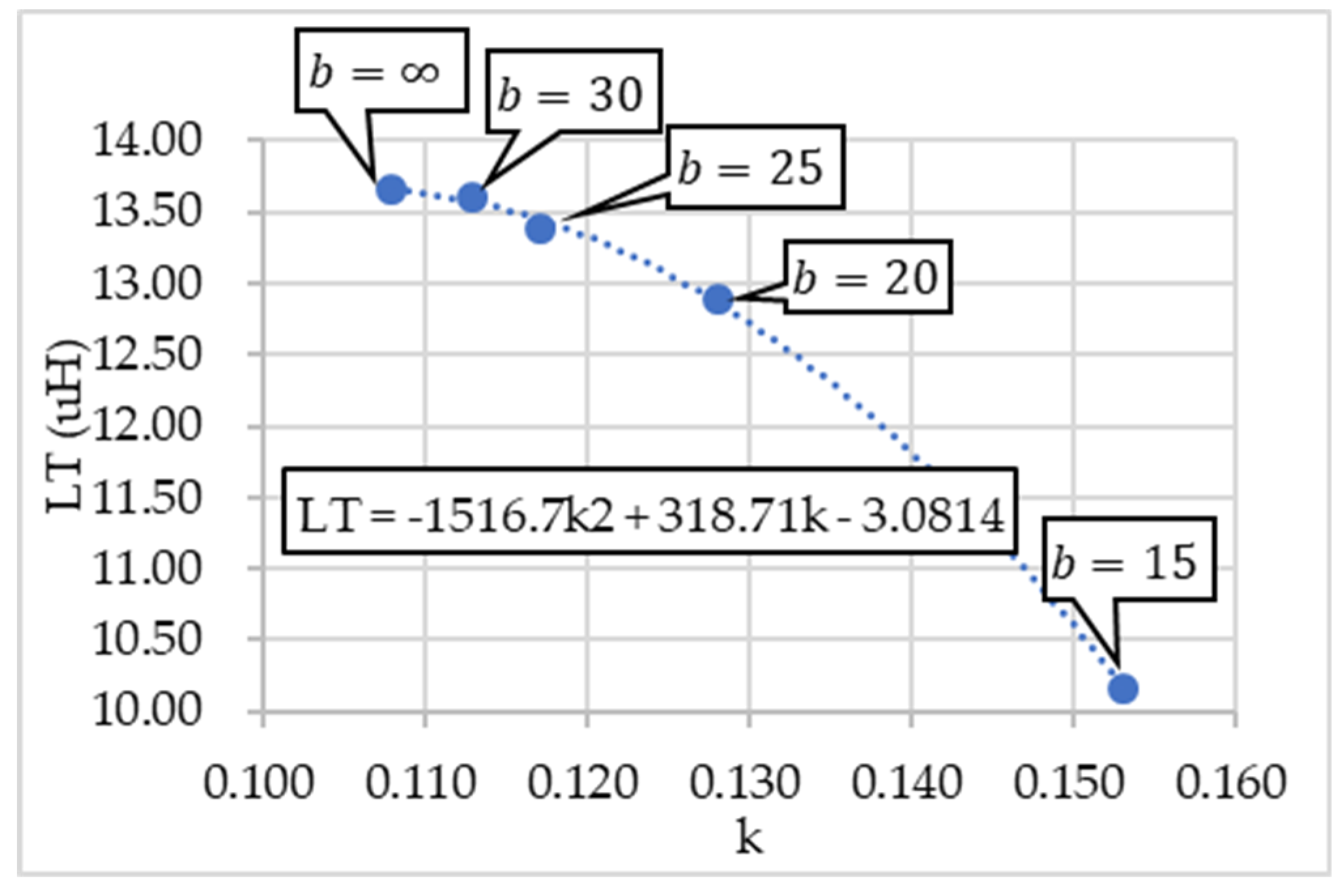
The back iron shall be placed at a distance $b$ to yield the condition that $Q_s\approx \sqrt{1/k}.$

When the aforementioned imaginary turn ratio condition is achieved, there is a ${90}^{°}$ phase difference between the waveforms of $v_{LT}$ to $v_{LR}$. The phase difference between $v_{LT}$ and $v_{LR}$ can be stabilized using a phase-locked loop (PLL) circuit when the mechanically adjustable capacitor is replaced by a tuning diode. In electronics, the tuning diode can be a varicap diode designed to utilize the voltage-dependent capacitance of a reverse-biased p–n junction.

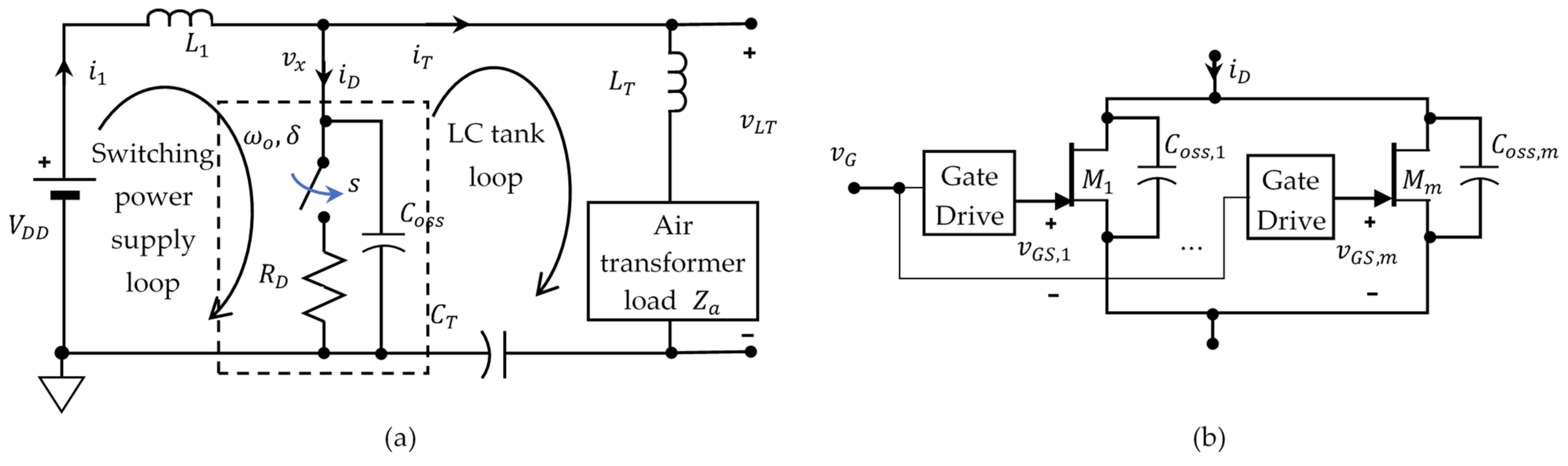
3.2. PTU Resonator with Class-E Amplifier Using Parallel GaN HEMT

The PTU resonator that is based on the class-E amplifier topology, as shown in Figure 8, was introduced in a previous study [18], which consists of two current loops, namely the switching power supply loop and the LC tank loop. In the switching power supply loop, the current governing equation can be written as follows:

$$\begin{array}{cc} & L_1{\displaystyle \frac{d{i}_1}{dt}}=V_{DD}-v_x\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}& \\ & v_x=\left\{\begin{array}{cc}{i}_D{R}_D\approx 0, & s=\mathrm{O}\mathrm{N}\\ V_x\sin \left(\alpha {\omega }_{T}t\right),& s=\mathrm{O}\mathrm{F}\mathrm{F}\end{array}\right.\end{array}$$

(19)

The drain-source voltage of the switch $v_x$ is derived in [18], the peak voltage of which can be 4 to 6 times the input voltage $V_{DD}$. The frequency scaling factor $\alpha$ is a function of the output parasitic capacitance $C_{oss}$ of the switch $s$. In the LC tank loop, the current governing equation can be written as follows:

$$\begin{array}{cc} & L_T{\displaystyle \frac{d^2{i}_T}{d{t}^2}}+Z_a{\displaystyle \frac{d{i}_T}{dt}}+{\displaystyle \frac{1}{C_x}}{i}_T={{\displaystyle \frac{d}{dt}}v}_x\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}& \\ & C_x=\left\{\begin{array}{cc}{C}_T, & s=\mathrm{O}\mathrm{N}\\ {\displaystyle \frac{C_T{C}_{oss}}{C_T+C_{oss}}},& s=\mathrm{O}\mathrm{F}\mathrm{F}\end{array}\right.\end{array}$$

(20)

The air transformer load $Z_a$ is a resistive loading, which is from the parallel loading to the series loading under the resonance condition [17] as follows:

$$Z_a={\displaystyle \frac{1}{R_R}}{\displaystyle \frac{L_R}{C_R}}$$

(21)

The second order O.D.E of (20) exhibits two different resonant frequencies during the switch-on and switch-off times. The resonant frequency is ${\omega }_T$ when the switch is on, and the frequency becomes $\alpha {\omega }_T$ when the switch is off.

$$\alpha =\sqrt{{\displaystyle \frac{1}{L_T\left(\frac{C_T{C}_{oss}}{C_T+C_{oss}}\right)}}}/\sqrt{{\displaystyle \frac{1}{L_T{C}_T}}}=\sqrt{1+{\displaystyle \frac{C_T}{C_{oss}}}}>1$$

(22)

Large frequency variations between the switch-on and switch-off times can disrupt the resonance of the LC tank. Therefore, a GaN transistor, whose $C_{oss}$ is reduced to only 20% in its on-state, is preferable for use in class-E amplifier applications. To increase the PDL, we need to enhance the current-handling capability of the switch. The common strategy is to parallel multiple GaN HEMTs, as supported by (22), since a larger $C_{oss}$ reduces the resonant frequency variation. However, using too many GaN HEMTs in parallel can result in a large lumped $C_{iss}$, which is detrimental to the switching speed. The solution is to use independent gate drives for each GaN HEMT, which can maintain the same switching speed.

The standard voltage and current waveforms are shown in Figure 9. Since the frequency factor $\alpha >1,$ the turn-off time shall be set shorter than the turn-on time; that is, the duty $\delta$ of the switching shall always be greater than 0.5. To achieve the ZVS, the duty shall be set to match the frequency factor as follows:

$$\delta ={\displaystyle \frac{\alpha }{1+\alpha }}$$

(23)

To achieve the zero-current switching (ZCS) and minimizing the switching loss, the switching frequency ${\omega }_o$ must be adjusted. However, deviation of ${\omega }_o$ from the resonant frequency of the LC tank ${\omega }_T$ can degrade the PDL. We must always monitor and balance the trade-off between the PTE and PDL during the power supply switching control.

The parallel GaN HEMT configuration enables a higher current flow through the PTU coil, thereby increasing the PDL. On the other hand, the GaN HEMTs must be properly sorted to ensure similar $C_{iss}$ and $C_{oss}$, guaranteeing synchronized switching. In our experience, the power transfer process will be terminated if any of the parallel D-mode GaN HEMTs malfunctions. This is because the class-E amplifier, as shown in Figure 8a, remains $v_x=0$, resulting in no excitation to the subsequent LC tank when the switch $s$ remains permanently on.

3.3. D-Mode GaN HEMT Characteristics

The present study employed D-mode GaN HEMTs. The newly developed GaN transistor is designed and fabricated by the Compound Semiconductor Device Laboratory (CSDL) at the National Yang Ming Chiao Tung University. The fabricated D-mode GaN HEMTs are packaged in a 5 × 6 Power Quad Flat No-Lead (PQFN) package form, with an on-resistance, $R_{D,on}$, of 250 mΩ, a threshold voltage ($V_{th}$) of approximately −8 V, the continuous drain current ($I_d$) of up to 10 A, and a drain-to-source breakdown voltage ($V_{BD}$) exceeding 1 kV. In addition, a Cu lead frame is utilized in this package to ensure thermal dissipation capabilities. This PQFN GaN HEMT package could provide minimized stray inductance and enhanced thermal dissipation at a higher operating power level, making it a suitable option for the high-power RWPT system.

In RWPT applications, the GaN HEMT is utilized for its key characteristics: high switching frequency, high breakdown voltage, and low parasitic capacitance. The power delivery distance is a function of microwave frequency, and the microwave can propagate longer distances that are subjected to a high switching frequency. The capability of a high switching frequency is granted by the low input parasitic capacitance $C_{iss}$ of the GaN HEMT. In a class-E amplifier, the transistor’s blocking voltage is typically 3 to 5 times the input voltage $V_{DD}$ [21], and the transistor must have a breakdown voltage of 600V in order to allow $V_{DD}=100\mathrm{V}$ for a high PDL. Low output parasitic capacitance, $C_{oss}$, produces low switching loss. The actual parameters of the NCTU 20mm D-mode GaN HEMT are provided in

Table 1. Key parameters in the experiments.

Symbol	Description	Unit	Value
$L_1$	Class-E Inductor	μH	47
$L_T, L_R$	PTU, PRU Coil Inductance	μH	10
$C_T$	PTU Capacitor	pF	680
$C_R$	Tuning Capacitor	pF	200~1000
$D$	PTU/PRU Coil Diameter	cm	72
$C_{P+},C_{P-}$	Voltage-divider Capacitor	nF	3
$C_{c+}, C_{c-}$	Low-pass LC Filter Capacitor	μF	1
$L_{B+}, L_{B-}$	Low-pass LC Filter Inductor	μH	2
Gate Driver	UCC27614DR	30 V, 10 A
$D_{2+},D_{1-}{D}_{2-},D_{1+}$	STPSC4H065B-TR	650 V, 4 A
Battery	NCR18650B	45s2p, 180 V/6.8 Ah
$C_{oss}$	GaN HEMT Output Capacitance	pF	$V_{DS}$
			0 V	600 V
			31	17
$C_{iss}$	GaN HEMT Input Capacitance	pF	46	31
$C_{rss}$	GaN HEMT Feedback Capacitance	pF	23	8
$V_{th}$	GaN HEMT Gate Turn-on Voltage	V	−9
$V_{GS}$	GaN HEMT Maximum	V	10~−30
$R_{D,on}$	GaN HEMT On-Resistance	m$\mathsf{\Omega }$	900
$V_{BD}$	GaN HEMT Breakdown Voltage	V	600
$i_{D,cont.}$	GaN HEMT Continuous Drain Current	A	3

.

3.4. PRU Resonator with Rectified Clipper Circuit

A PRU module for battery charging, proposed in a previous study [16], utilized a half-bridge rectifier topology. In this paper, we propose a full-bridge topology circuit, referred to as the rectified clipper, for battery charging, as illustrated in Figure 10, which consists of the following:

• Tuning Capacitor $C_R$: This capacitor is adjusted to achieve the imaginary turn ratio condition indicated in (18).
• Rectified capacitive voltage divider: This consists of two voltage-divider capacitors, $C_{P+}$ and $C_{P-},$ and two bypass diodes, $D_{P+}$ and $D_{P-}$, which subdivide the resonant voltage. Using the bypass diodes, the capacitor voltages of $C_{P+}$ and $C_{P-}$ are rectified into unipolar voltages.
• Diode-clipping circuit: This circuit consists of a diode and a second-order low-pass LC filter, which transfers the energy from $C_{P+}$ and $C_{P-}$ when their voltage reaches their peaks.

The voltage applied to the PRU resonator is sinusoidal and exhibits a ${90}^{\mathrm{o}}$ phase shift relative to the input voltage when the imaginary turn ratio condition is achieved.

$$v_{LR}=V_{LR,max}\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{o}t+{\displaystyle \frac{\pi }{2}})$$

(24)

As shown in Figure 10, when $v_{LR}>0$, two current loops are formed: the first consists of the current $i_R$, which flows through two capacitors from $C_{P+}$ to $C_R$, and the second consists of the current $i_B$, which flows from $C_{P+}$ to battery $V_B$. The capacitive voltage divider redistributes its capacitor charges when the first current loop is activated, and the voltage across $C_{P+}$ is derived as follows.

$$v_{LR}=V_{LR,max}\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{o}t+{\displaystyle \frac{\pi }{2}})$$

(25)

The second current loop is activated when the capacitor voltage $v_{CP+}$ exceeds $V_B$. The inductor $L_{B+}$ acts as a current buffer, absorbing the voltage difference between $v_{CP+}$ and $V_B$, which directs the current to the battery when the capacitor voltage $v_{CP+}$ is below $V_B$.

The key point is that the PRU resonator presents a nearly pure capacitive load, forming an LC tank together with the PRU coil. However, this capacitive loading circuit has an equivalent capacitance when the capacitance of $C_{P+}$ and $C_{P-}$ is much higher than the capacitance of $C_R$.

4. Circuit Simulation and Experiments

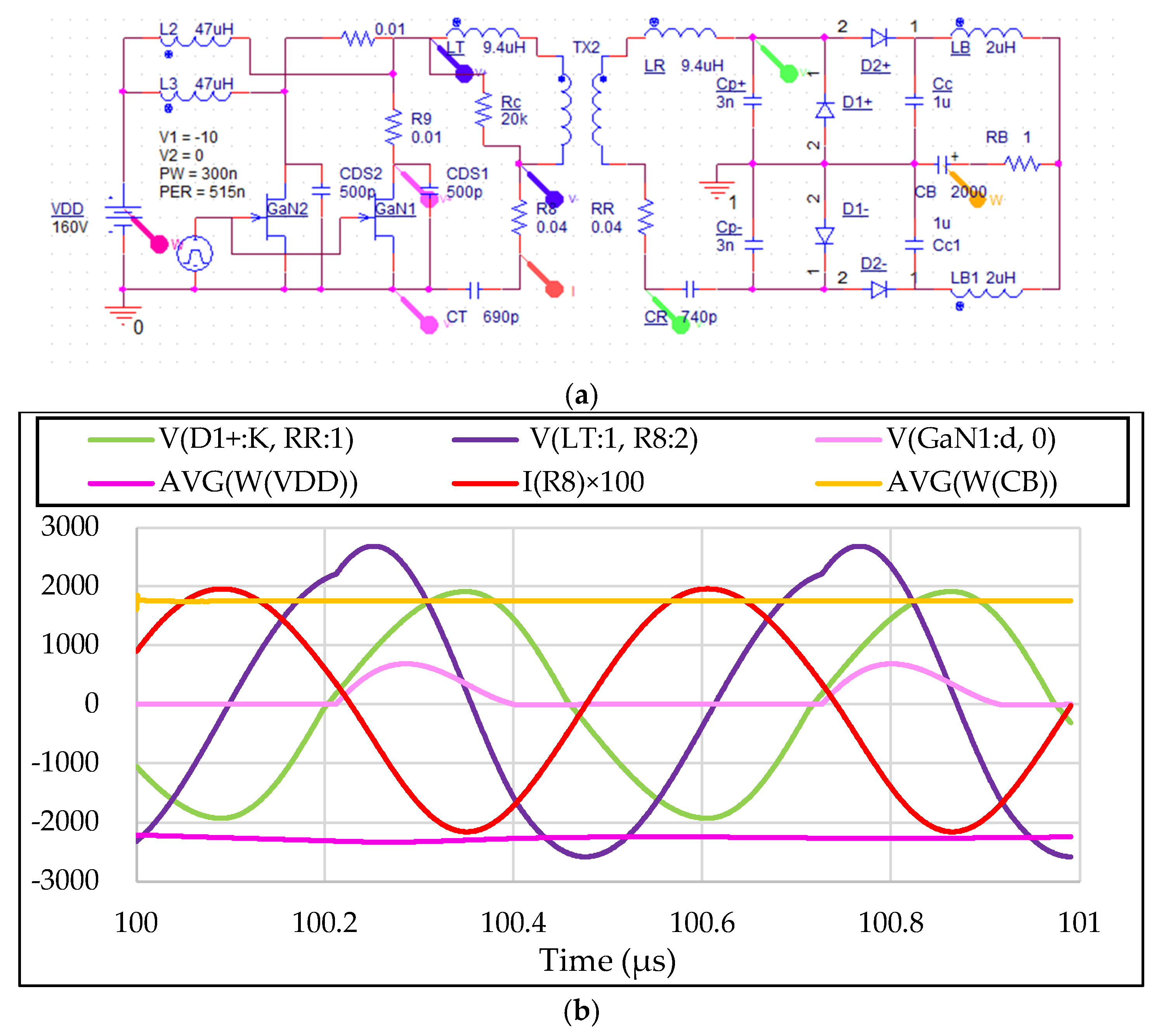
4.1. Simulation

In the OrCAD SPICE circuit simulation shown in Figure 11a, the transformer in the circuit is modeled as an ideal transformer with a core resistance of $R_c=20 \mathrm{k}\mathsf{\Omega }$. The switching power supply employs parallel GaN HEMTs. The switching frequency is set to be 1.94 MHz (=1/515 ns), and the duty is set to be 0.58 (=300 ns/515 ns) according to (22) that $C_T/C_{oss}=690 \mathrm{p}\mathrm{F}/1000 \mathrm{p}\mathrm{F}$. The simulation results are provided in Figure 11b. The resonant frequency of the LC tank can be calculated by substituting $L_T=9.4 \mathrm{u}\mathrm{H}+1 \mathrm{u}\mathrm{H}=10.4 \mathrm{u}\mathrm{H}$ (coupling coefficient $k=1)$ and $C_T=690 \mathrm{p}\mathrm{F}$ into (12) as ${\omega }_T=2 \mathrm{M}\mathrm{H}\mathrm{z}.$ According to the simulation results shown in Figure 11b, the drain-source voltage $v_x$ (purple trace) has the peak denoted by $V_x=750 \mathrm{V},$ being 4.6 times the DC voltage $V_{DD}=160 \mathrm{V}$. The PTU voltage $v_{LT}$ (blue trace) is of two frequencies in the individual turn-on and turn-off periods of time. The PRU voltage $v_{LR}$ (green trace) is a 90-degree phase shift from $v_{LT}$. The battery receiving power $i_B$ (orange trace) is 1.8 kW. The input power (pink trace) is 2150 W; thus, the input current $i_1$ is 13.4 A. The power transfer efficiency, according to the simulation, is 84%. The current $i_T$ on the PTU coil (red trace) exhibits a sinusoidal waveform with a peak current of 20 A. This is 1.5 times the input current, calculated as 20/13.4 = 1.5.

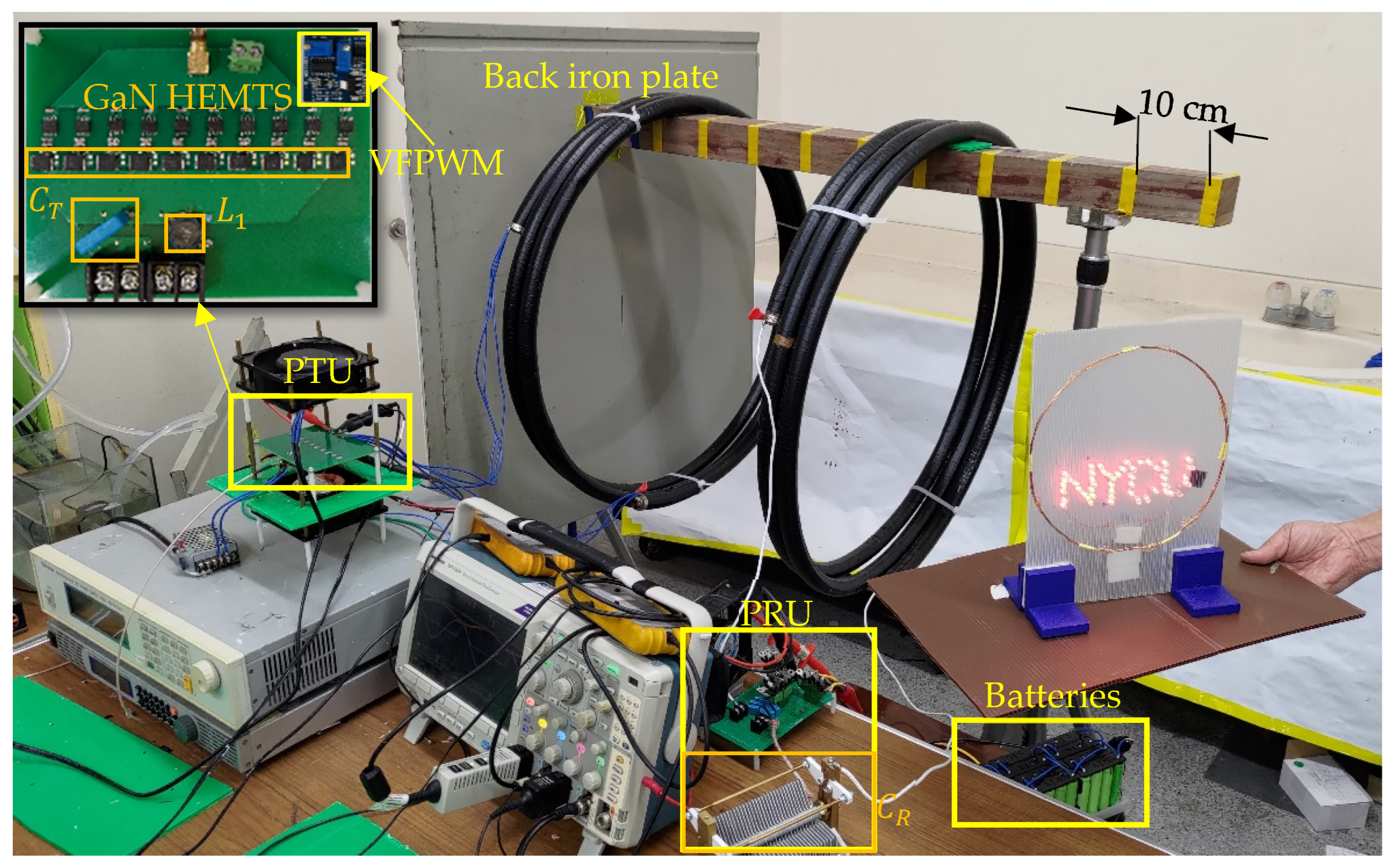
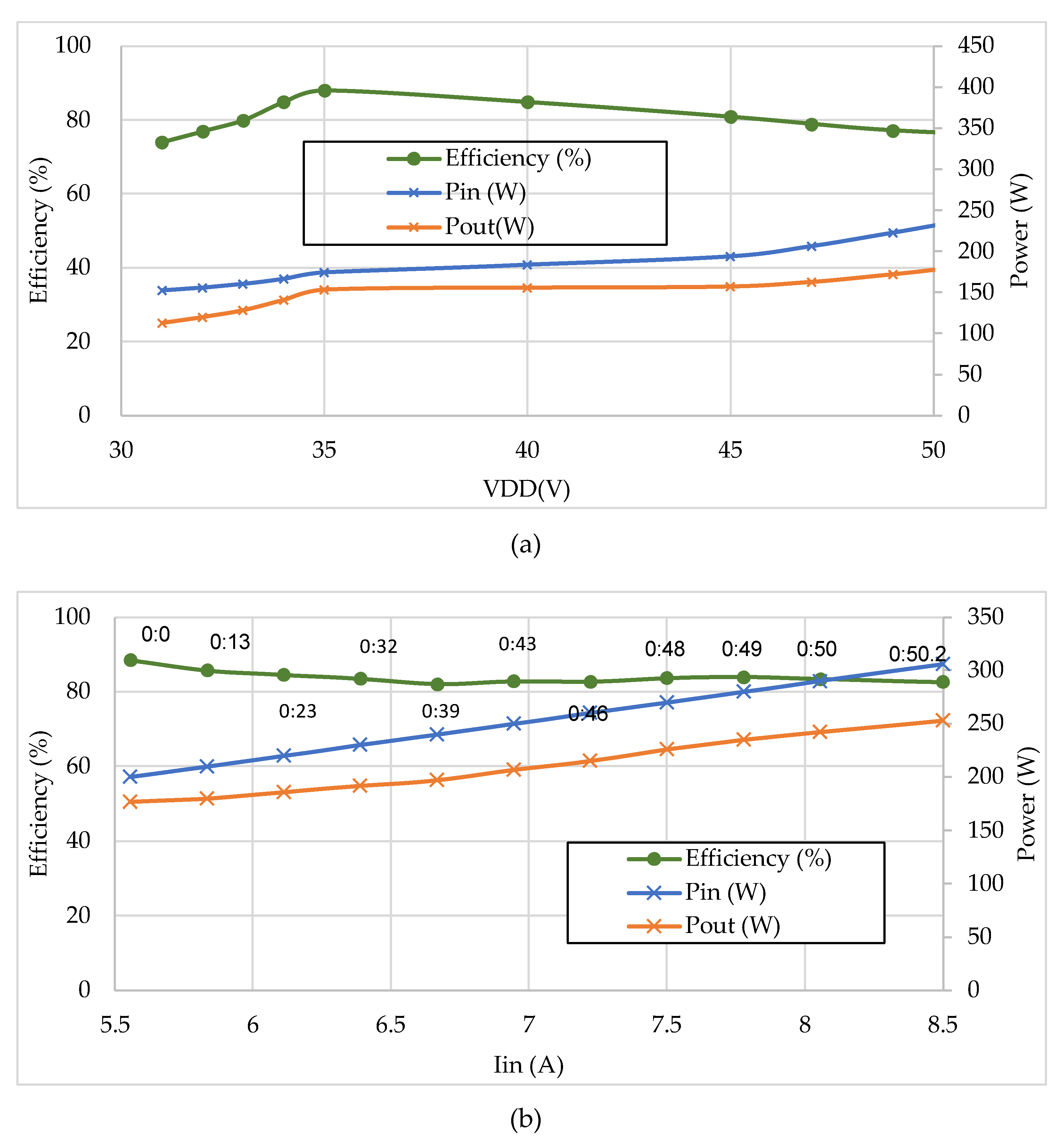
4.2. Experiment

The experiment, as shown in Figure 12, was implemented with three major modules. The PTU board was designed with multiple paralleled D-mode GaN HEMTs, as shown in Figure 8. The gate drives are individual charge-pump drivers [17] driven by the same switching signal. The PRU board was designed with multiple high breakdown voltage SiC diodes, inductors, and capacitors, as shown in Figure 10. The adjustable capacitor $C_R$ was manually tuned to achieve the imaginary turn ratio condition. The air transformer, supported by a wooden bar, consists of a pair of coils spaced 50 cm apart.

Table 1 lists the key parameters of the RWPT system. Figure 12 illustrates the system in operation, showing an LED receiver connected to the output of the air transformer. The other wireless LED receiver lights up while the battery is being charged. Figure 13a depicts the waveforms of the system when $V_{DD}=30 \mathrm{V}$, which shows that the PRU voltage $v_{LR}$ (green trace) is at a 90-degree phase shift from the PTU voltage $v_{LT}$ (cyan trace). $V_x$ is 180 V, which is 6 times the DC voltage $V_{DD}$; the input current $i_1$ is 4 A when the peak current of $i_T=6 A,$ which is coherent with the simulation that the maximum current flowing through the GaN HEMT transistors is 1.5 times the input current reading from the power supply. Figure 13b depicts the current $i_B$ waveform (blue trace) and the voltage waveform of $v_B$, the battery, and the average battery voltage is 210 V, which shows a nearly constant current charging for lithium battery charging.

Several steps were taken to achieve the imaginary turn ratio condition, where the coil voltages on the PTU and PRU coils are in a 90-degree phase shift. In the beginning, we tuned the switching frequency ${\mathsf{\omega }}_{\mathrm{o}}$ on the PTU side, and simultaneously, we adjusted $C_R$ to achieve the 90-degree phase shift. We then adjusted the duty of the PWM to obtain ZVS and ZCS conditions to reduce the switching loss, as shown in Figure 13a. Once these conditions were met, we shifted the differential probe from measuring the PRU coil to measuring the battery voltage, as shown in Figure 13b. The battery voltage is a function of its state-of-charge (SOC), which increases along the experiment time. We found that the differential probe can affect the imaginary turn ratio condition because there exists a 3 pF capacitance in the differential probe. Therefore, we needed to change the current probe position from the PTU coil current measurement to the battery charging current position. After adjusting the capacitance $C_R$ on the PRU side again to achieve the maximum battery charging current, we also verified the satisfaction of the imaginary turn ratio condition due to the presence of the NIC effect inducing a higher charging current.

Figure 14a illustrates the relationship between the output power and the calculated efficiency of the system, as the DC voltage $V_{DD}$ is varied. It highlights that the maximum efficiency of 88% is achieved when the DC input voltage $V_{DD}$ is approximately 35 V. Figure 14b was obtained when we established the DC input voltage $V_{DD}$ as 36 V and waited for approximately 50 s, when both the power input and power output began to grow simultaneously due to the negative impedance converter (NIC) effect of the circuit. The input current $I_{in}$ from the power supply (=$I_i$) started to surge after 10 s since the power supply turned on, and the power surge was in the pace of nearly exponential time. The time tag corresponding to each data point is specified. We recorded the data until the power supply reached the current limit of 8.5 A. It was discovered that the power efficiency can be sustained at a nearly constant level, 83%, and the output power will surge from 177 W to 253 W. After 50 s, the power supply will automatically reduce its voltage to 30 V, and the output power reduces to 215 W under a constant current of 8.5 A.

4.3. Power Loss Analysis

Although the GaN HEMT switches are designed to operate under ZVS conditions, a certain amount of switching loss still occurs. This loss arises because the switches do not achieve ZCS during their transitions. Specifically, when the switches are turned on or off, residual current flows through them, resulting in energy dissipation. The ZVS in the switching control can be achieved by adjusting the duty cycle of the PWM input. The first derivative of the drain-source voltage, labeled as $v_x$ in this study, being zero, implies the ZCS condition in the GaN HEMT switch. The switching loss is a multiplication of the voltage and the current. While the ZCS condition was not considered in the theoretical derivations shown in Figure 9 nor achieved in the analysis shown in Figure 11, it was successfully realized in the experiment, as shown in Figure 13a,b, which was necessary to reduce switching loss.

The power loss is mainly due to the core loss (including back iron), the coil resistance, the equivalent series resistance (ESR) loss of the capacitors, the resistance on the PCB circuit board, and the on-resistance and switching loss of the GaN HEMTS. The definitions of power losses are listed in

Table 2. Description of power losses.

Power Losses	Definition
$P_{coreloss}$	The power loss on the back iron and the surrounding due to the eddy current and evanescent wave effect.
$P_{GaN RDon}$	The power loss on a GaN HEMT during the on-state due to transistor on-resistance.
$P_{GaN switching}$	The power loss on a GaN HEMT while ZVS and ZCS is not achieved.
$P_{coil}$	The power loss on the PTU due to $R_T$, including the coil resistance, the ESR loss of the capacitors, and the resistance on the PCB circuit board during the on-state. The on-resistance of the GaN HEMTs is subtracted from $R_T$ since we already have $P_{GaN RDon}$.

. The total power loss, as shown in Figure 14b at an input current of 8.5 A, was 53 W. According to the air transformer model developed from open/short circuit tests, as shown in Figure 5, we estimated that the core loss from the $v_{LT,max}=720 \mathrm{V}$ and $R_c=23.5 \mathrm{k}\mathsf{\Omega }$ is $P_{coreloss}=1/2·{720 \mathrm{V}}^2/23.5 \mathrm{k}\mathsf{\Omega }=11 \mathrm{W}$. The on-resistance loss of the GaN HEMTs is $P_{GaNRDon}={\left(I_{T,max}/2\right)}^2{R}_{D,on}\delta =6 \mathrm{W}$. The switching loss of the GaN HEMTs evaluated from the typical equation is $P_{GaNswitching}=1/6\left(I_{T,max}{V}_{x,off}{t_{rise}f}_s\right)=8.4 \mathrm{W}$. The coil resistance and the ESR loss of the capacitors can be calculated according to the $R_T=1.12 \mathsf{\Omega }$ obtained from the open/short circuit tests, as shown in Figure 5, which is $P_{coil}={\left(I_{T,max}/2\right)}^2\left(R_T-R_{D,on}\right)\delta =23 \mathrm{W}$. The total known power loss is the sum of $P_{coreloss}+P_{GaNRDon}+P_{GaNswitching}+P_{coil}=48.4 \mathrm{W}$. The power loss budget is shown in Figure 15. A certain amount of power loss is attributed to the evanescent wave effect, which accounts for a portion of the remaining 9% loss. This occurs when part of the input power leaks into the surrounding environment; however, the loss is relatively insignificant in comparison to other factors.

Since the resonant wavelength is much larger than the coils, the field can avoid extraneous objects in the vicinity, and thus, this mid-range power-transfer scheme will not be blocked by obstacles. By utilizing in particular, the magnetic field to achieve the coupling, this method can be safe since magnetic fields interact weakly with living organisms [23].

5. Discussion

The electromagnetics in the Fresnel field induces evanescent waves propagating along the metal–dielectric interface of the surroundings. When Faraday’s law of induction dominates the near field, which involves the magnetization current and its loss, the Maxwell equation of electromagnetics can propagate waves with voltage changes with no current loss in the far field. The mid-range electromagnetics mechanism remains unclear today. Simplifying the energy transfer complexity problem, we focused only on studying the coupling coefficient of magnetism in the H-field. Several hypotheses and corresponding experiments were conducted to clarify the validity of RWPT.

(1)

The Steinmetz model of a transformer was modified for an air-core transformer. The core loss resistor was moved from the magnetization branch to the input port of the air transformer. Therefore, the core loss was not directly associated with the magnetization current; instead, the core loss was associated with the input sinusoidal voltage. Therefore, the loss from the evanescent wave, a function of both the E-field and H-field, can also be included in account of the core loss.

(2)

Open circuit and short circuit tests were conducted to experimentally estimate the core loss resistance in the modified Steinmetz model. The back iron can also be a waveguide to guide the electromagnetic wave propagating in the direction of the PRU.

(3)

Correlating the resonant quality factor with the coupling coefficient can introduce an “imaginary turn ratio”, which brings the RWPT to a very low damping ratio in the equivalent circuit. When the voltage presented on two sides of the air transformer has a 90-degree phase shift, the positive load resistance on the PRU side is converted into a negative resistance, i.e., the square of the imaginary turn ratio is negative, and moves into its equivalent circuit.

(4)

The rectification circuit on the PRU must not interfere with resonance. Therefore, the charges on the PRU side were conveyed to the battery only during the period of time when the capacitor was fully charged.

The back iron serves two main purposes: shortening the mean path length of the magnetic flux in the PTU coil and reflecting microwaves toward the PRU. There were experiments conducted to locate an extra back iron on the back of PRU; however, the result is discouraging, i.e., adding an extra back iron significantly weakened both the PDL and PTE. Based on these experiments, we concluded that adding back iron to the PTU shortens the mean path length of the magnetic flux, thereby enhancing the H-field and improving flux linkage, as observed in the analysis shown in Figure 6. The coupling coefficient increases as the back iron distance is 15 cm in this study. However, the back iron can also increase the leakage flux or the self-inductance, which suppresses the flux linkage. The eddy current loss in the back iron is modeled as a core loss resistor, as shown in Figure 2. According to the experiments shown in Figure 5, the core loss, including the eddy current and hysteresis loss, is not a monotonic function of the back iron distance, and the core loss is indeed related to the flux density changes, as shown in Figure 6.

Comparisons with prior artwork are listed in

Table 3. Comparison to prior artwork.

	Frequency	Type	Coil Gap	PTE	PDL	FOM
Unit	MHz		mm	%	W
WiTricity [28]	0.085	IWPT	N/A	93	11,000	N/A
R. Bosshard et al. [29]	0.1	IWPT	52	97	5000	2.52 × 107
O. Knecht et al. [30]	0.8	IWPT	20	96	30	5.76 × 104
This study	2	RWPT	500	88	250	1.10 × 107
L. Gu et al. [31]	6.78	RWPT	19	95	1000	1.81 × 106
M. Liu et al. [32]	6.78	RWPT	40	84	20	6.72 × 104
J. Li and D. Costinett [33]	6.78	RWPT	N/A	85	10	N/A
J. M. Arteaga et al. [34]	6.78	RWPT	110	88	50	4.84 × 105
L. Gu and J. Rivas-Davila [35]	6.78	RWPT	55	96	1700	8.98 × 106
K. Surakitbovorn and J. Rivas [36]	13.56	RWPT	15	90	300	4.05 × 105

. If we define the Figure of Merit (FOM) as the multiplication of three factors, including the distance (coil gap), efficiency (PTE), and power (PDL), this work has the highest FOM in the RWPT category and the longest distance of all. The FOM in this study with 10 parallel GaN HEMT devices and more parallel GaN HEMT devices with independent gate drives in a single PTU board can also improve the FOM.

We are actively preventing instability; otherwise, the energy transfer control would become unstable. When instability is presented in the energy transfer, the current can surge [19], damaging the GaN HEMT switch. Additionally, the dynamic $R_{on}$ of the GaN HEMT is a function of temperature, or more specifically, a function of current. When the current surged, the $R_{on}$ of the GaN HEMT will increase to add more resistance to the LC tank and, therefore, automatically feedback the current rating to increase the damping ratio. The coupling coefficient changes when the coils are moved, which can disrupt the imaginary turn ratio condition and increase the damping ratio. Therefore, stability can be ensured when the PRU coil is moving.

Capacitor size plays a crucial role in RWPT. A larger capacitor allows more charge to be transferred to the PRU. The PDL is a function of capacitance and switching frequency as follows:

$$\mathrm{P}\mathrm{D}\mathrm{L}=a_1\omega C_T$$

(26)

The constant $a_1$ represents parameters such as the charge transfer rate and input voltage. It can also be derived as follows: inductance is limited by the PDL, while the higher the frequency is, the smaller the inductor shall be.

$$\omega L_T=\sqrt{{\displaystyle \frac{L_T}{C_T}}}={\left({\displaystyle \frac{a_1}{\mathrm{P}\mathrm{D}\mathrm{L}}}\right)}^2$$

(27)

Therefore, $\omega L_T$ remains constant under a constant PDL. When $R_c$ (core resistance) is verified to be much greater than $\omega L_T$ in 2 MHz, as shown in Figure 5, the condition will be true for all frequency spectra, for example, 13.56 MHz.

6. Conclusions

In our study, the resonant wavelength of 150 m at 2 MHz is significantly larger than the dimensions of the PTU and PRU coils. This ensures that the electromagnetic field can bypass extraneous objects in the vicinity, making the mid-range power transfer scheme robust against potential obstructions. The reactive near-field operation can also ensure safety, as magnetic fields have minimal interaction with living organisms. In this study, we derived the resonant conditions necessary to achieve the imaginary turn ratio in the air transformer. Utilizing the imaginary turn ratio, the positive resistance of the power-receiving unit was effectively transformed into a negative resistance. Based on the power loss calculations obtained from the experiment, future efforts will focus on exploring new materials that can reduce coil resistance and the ESR of the capacitors. Additionally, we aim to develop high breakdown voltage, high-power density D-mode GaN HEMTs, which will enhance both power transfer efficiency and the overall power transfer rate, i.e., higher than 250 W per PTU board. These improvements will contribute to achieving even more efficiency, higher than the 88% reported in this study, for RWPT systems.