Interaction Mechanism and Oscillation Characteristics of Grid-Connected Concentrating Solar Power–Battery Energy Storage System–Wind Hybrid Energy System
Abstract
1. Introduction
2. System Description and Small-Signal Modeling
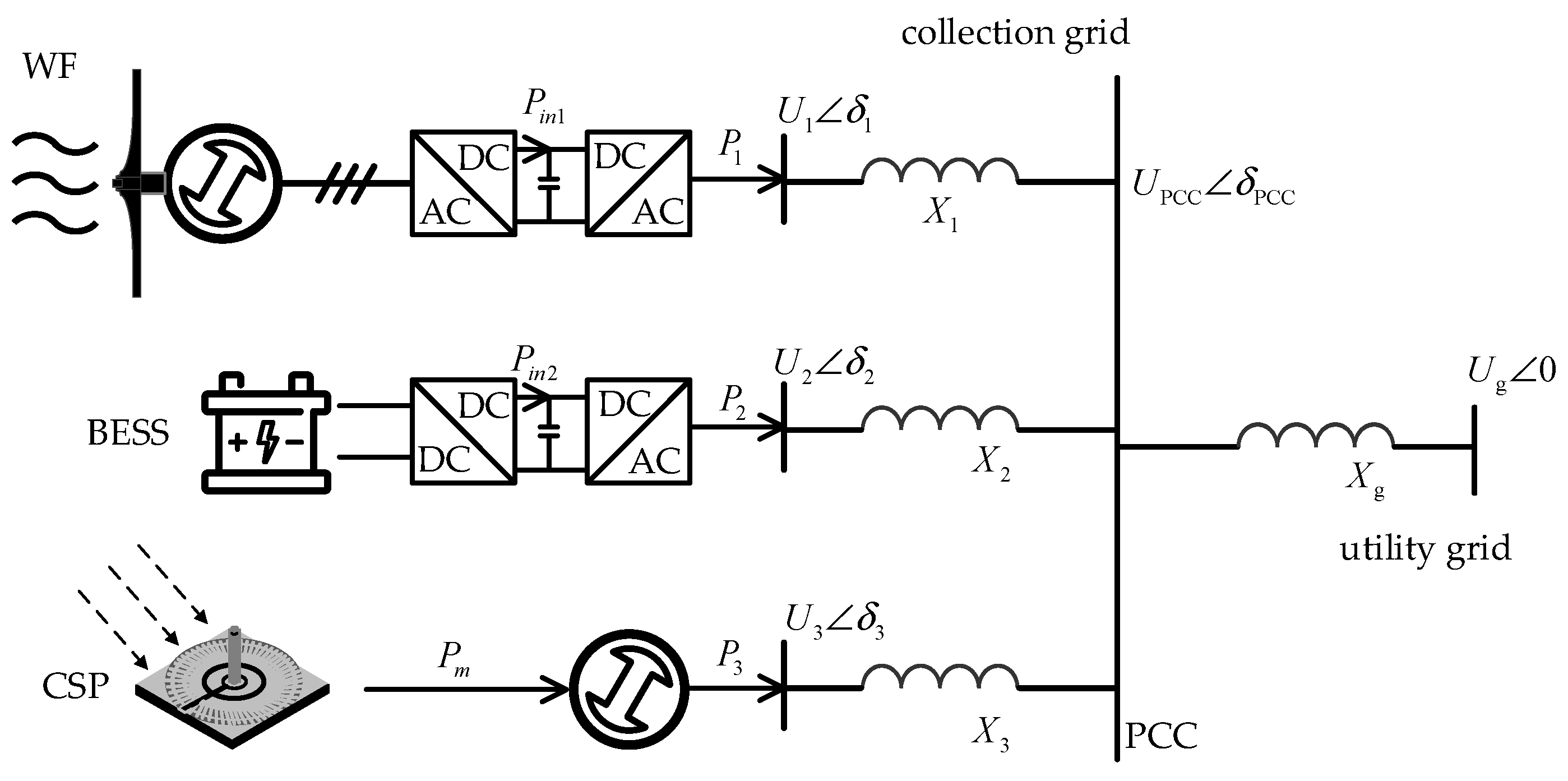
2.1. System Description
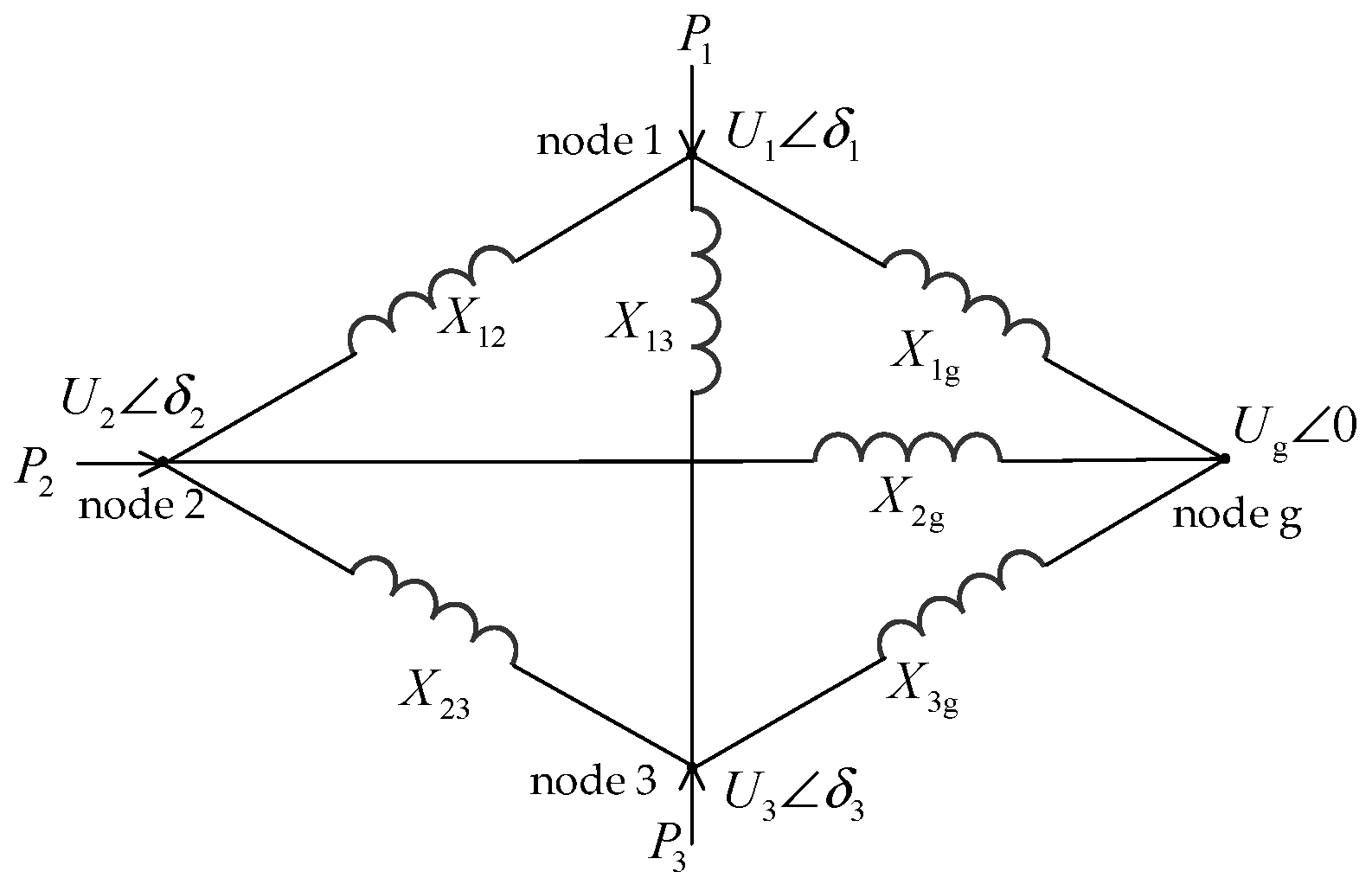
2.2. Collection Grid Coupling Model
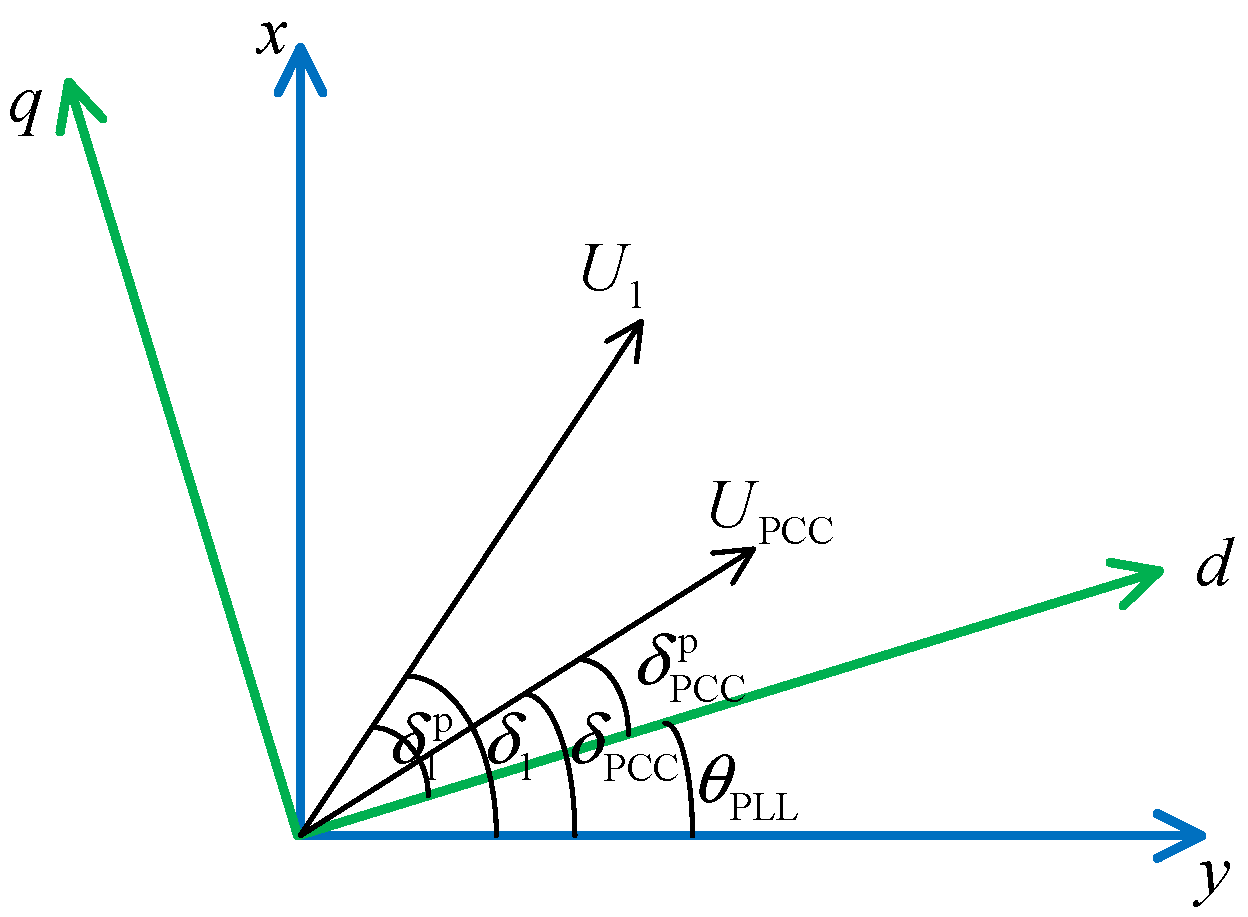
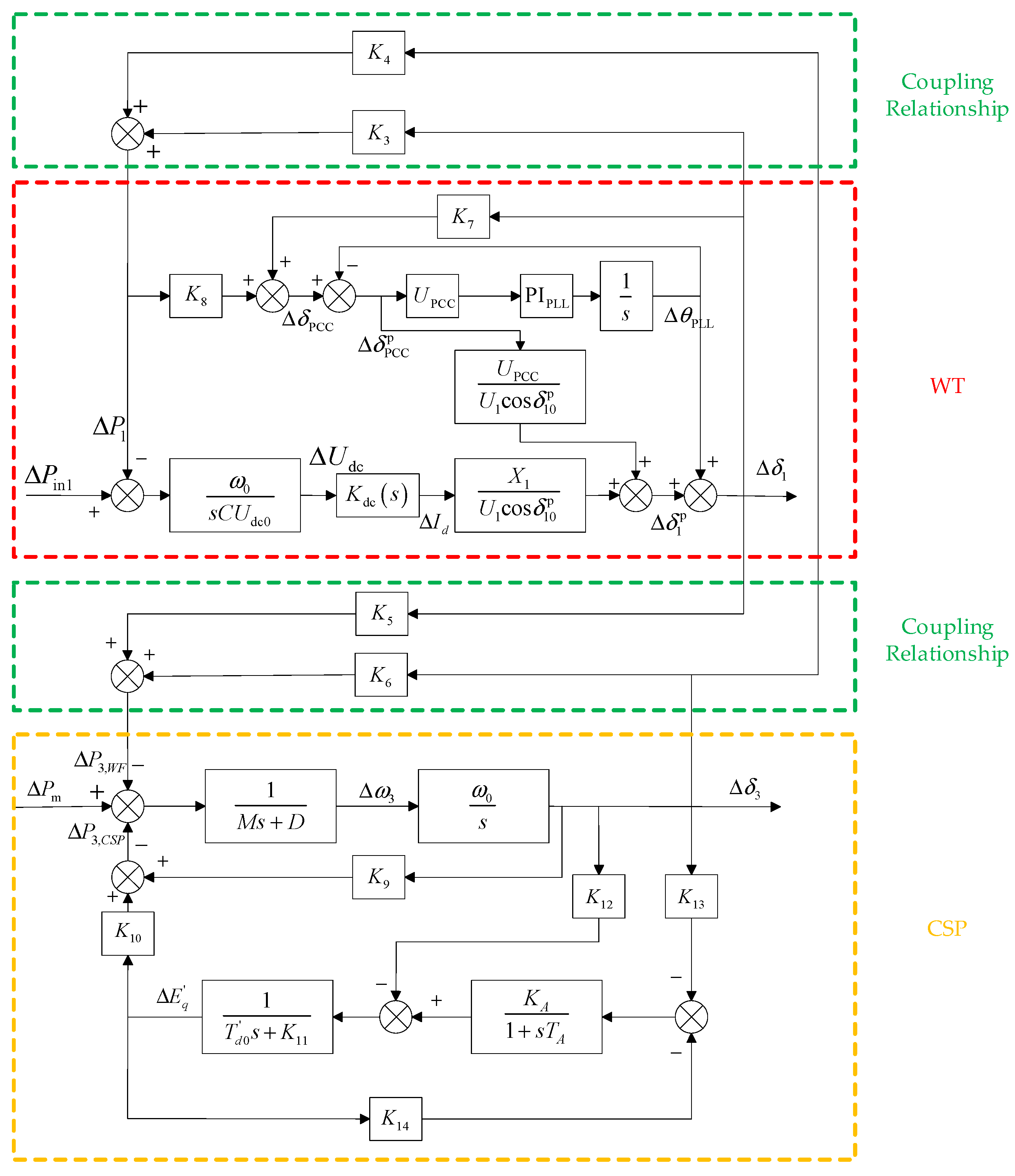
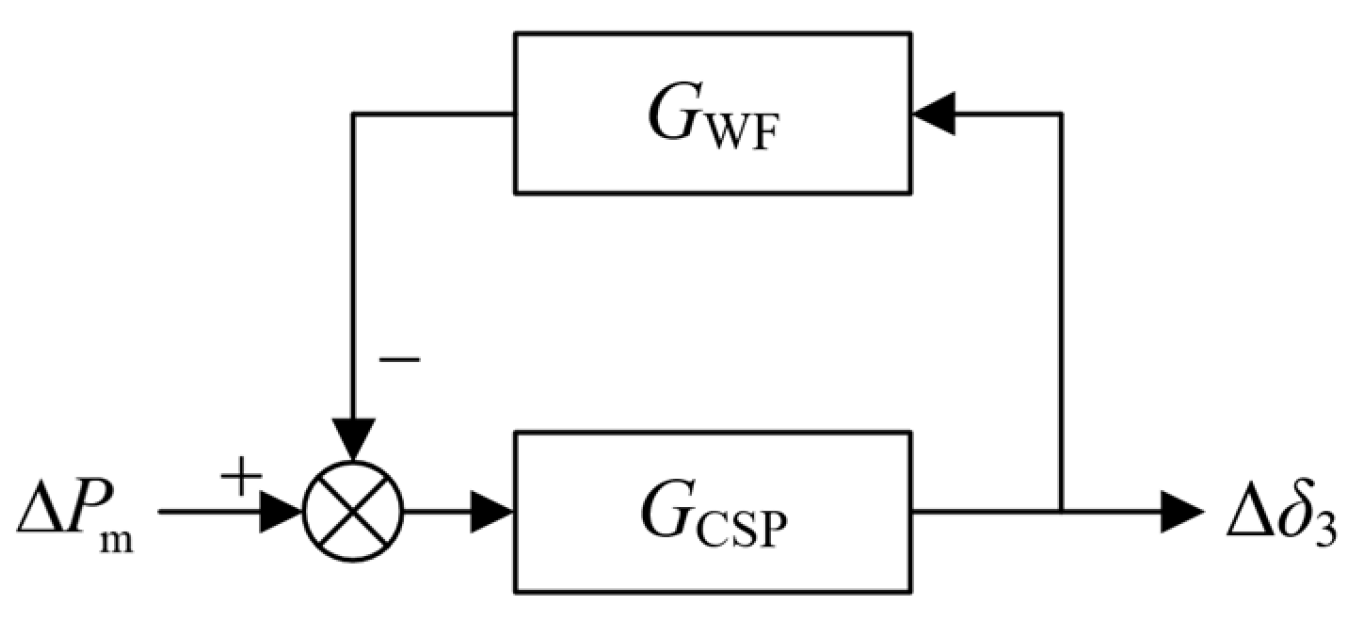
2.3. Small-Signal Model of Wind Farm
2.4. Small-Signal Model of CSP
3. Sub-Synchronous Oscillation in Hybrid Energy System
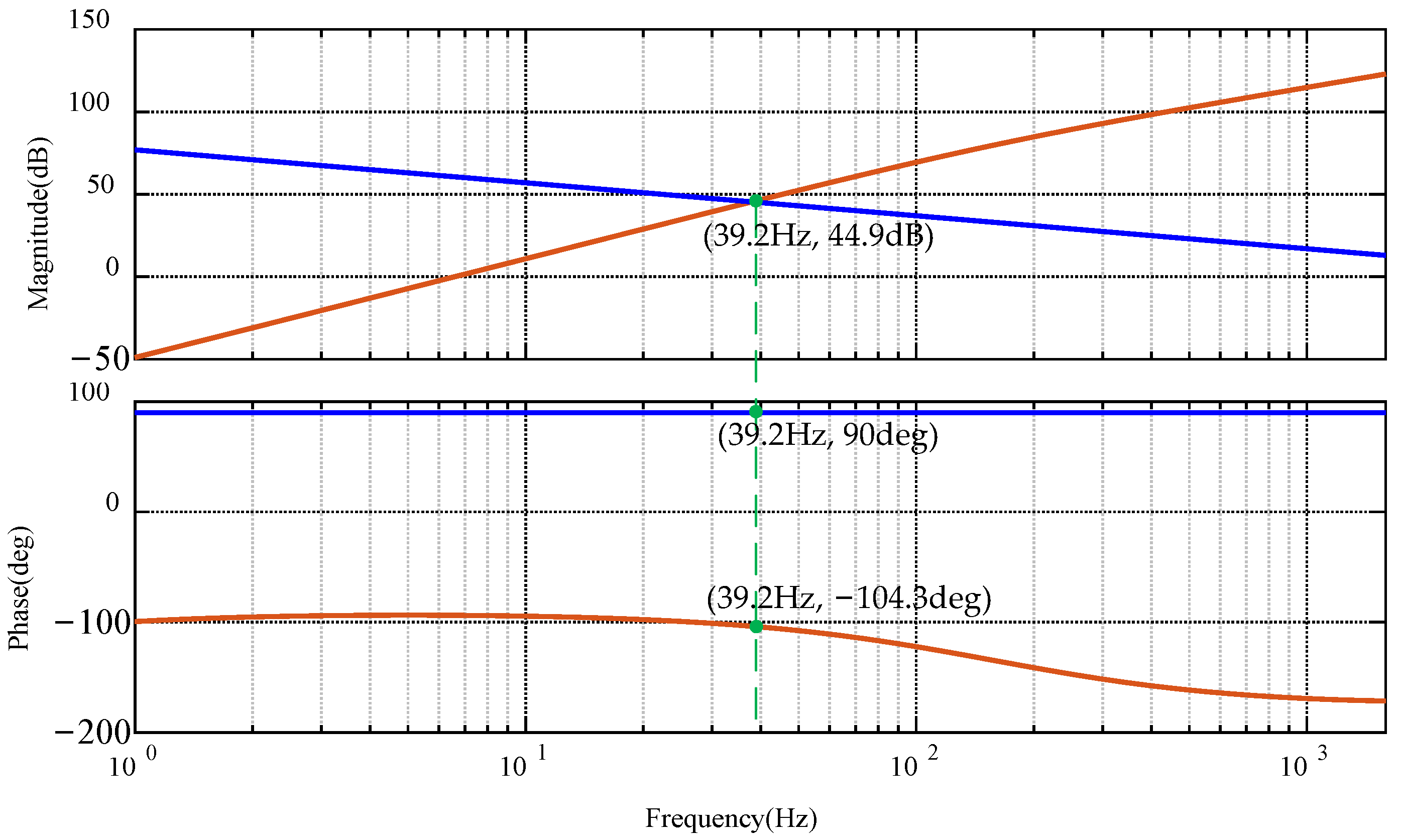
3.1. Instability Analysis
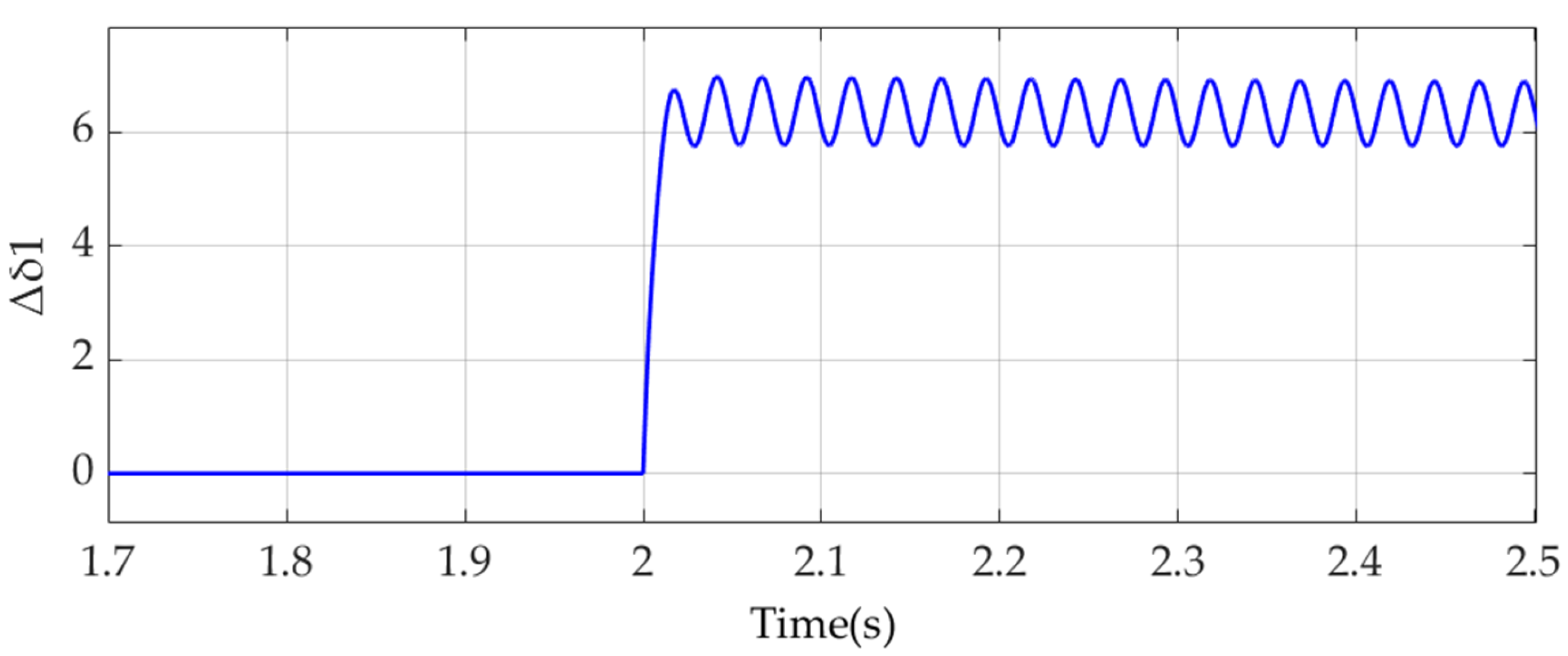
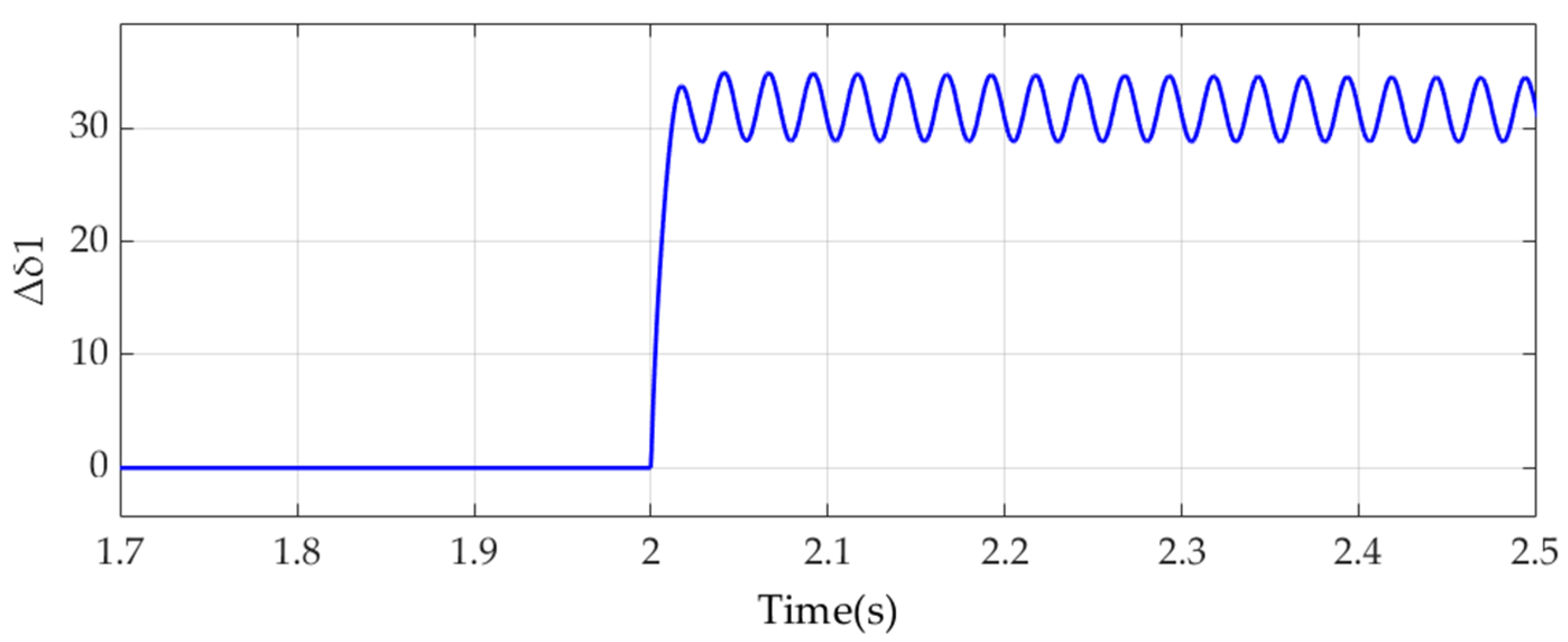
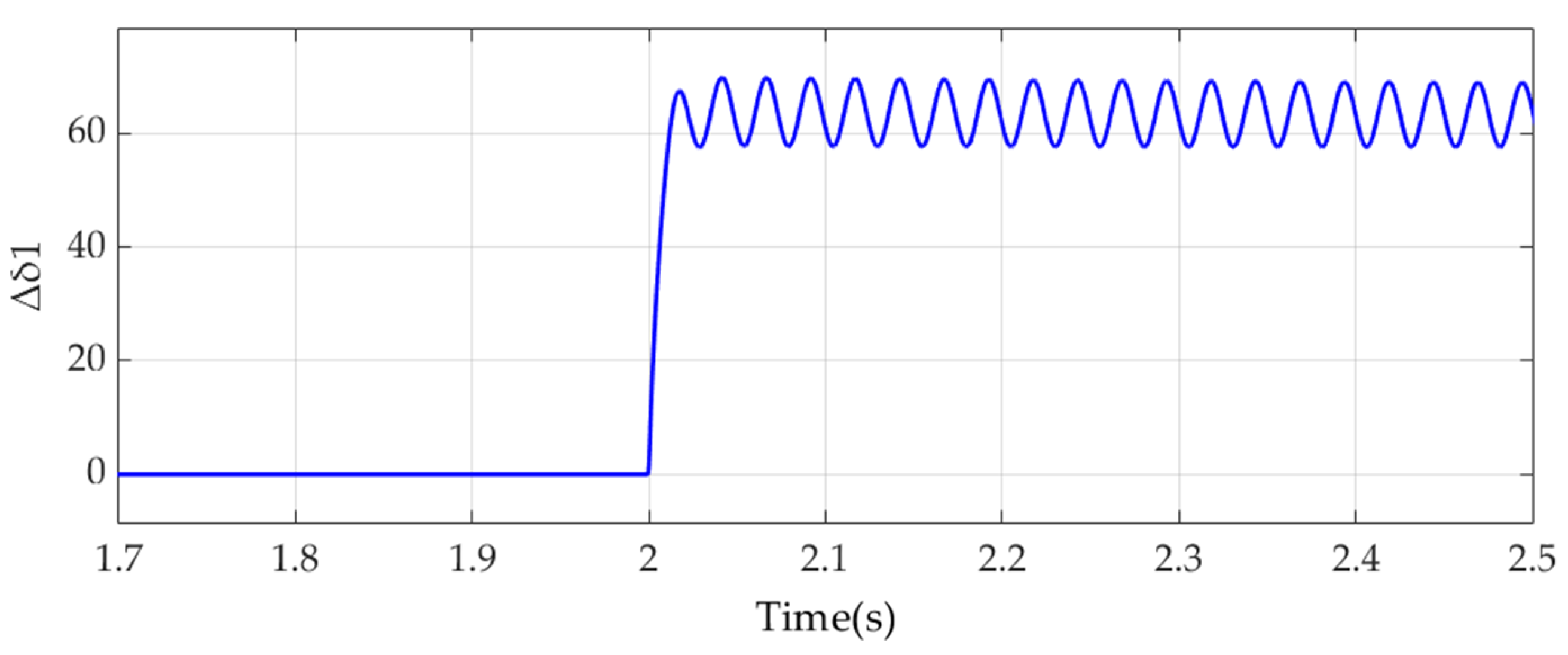
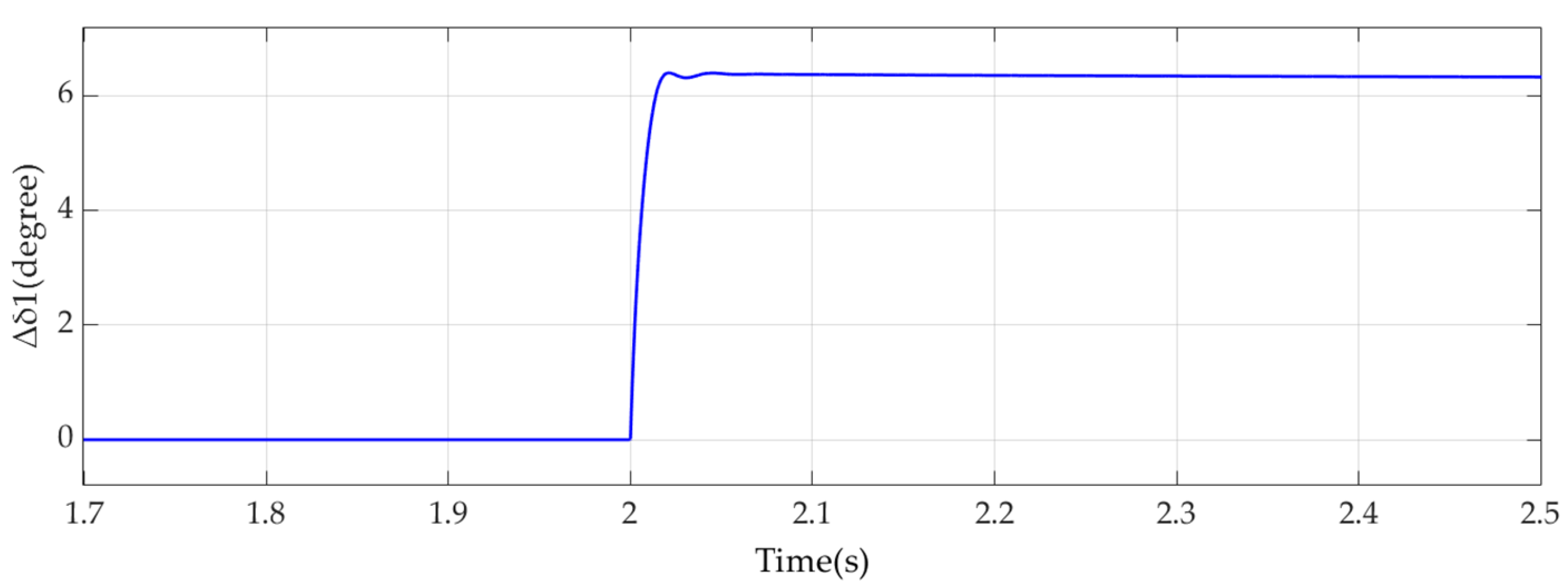
3.2. Time-Domain Simulation Verification
4. Method for Enhancing Stability of Hybrid Energy System
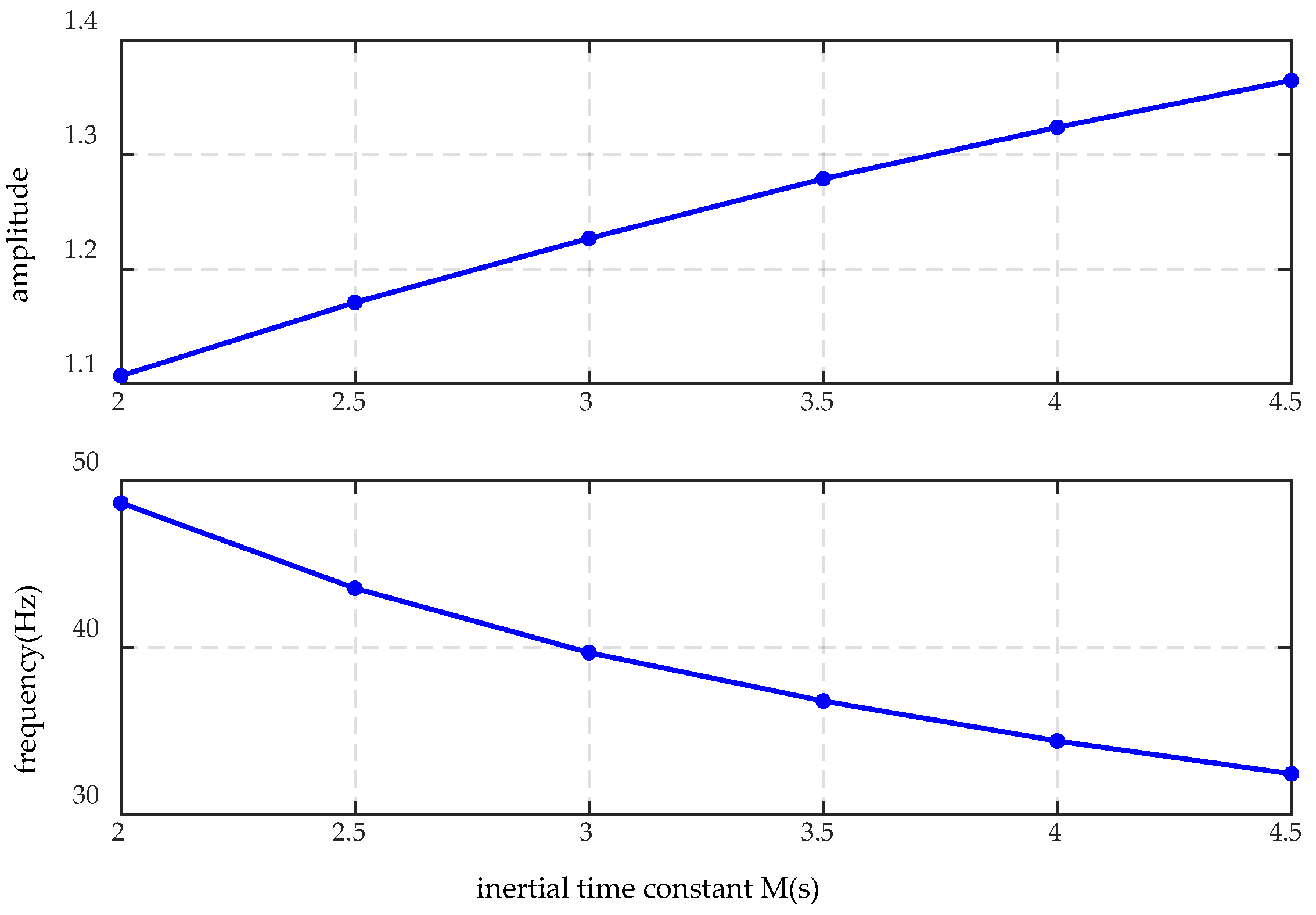
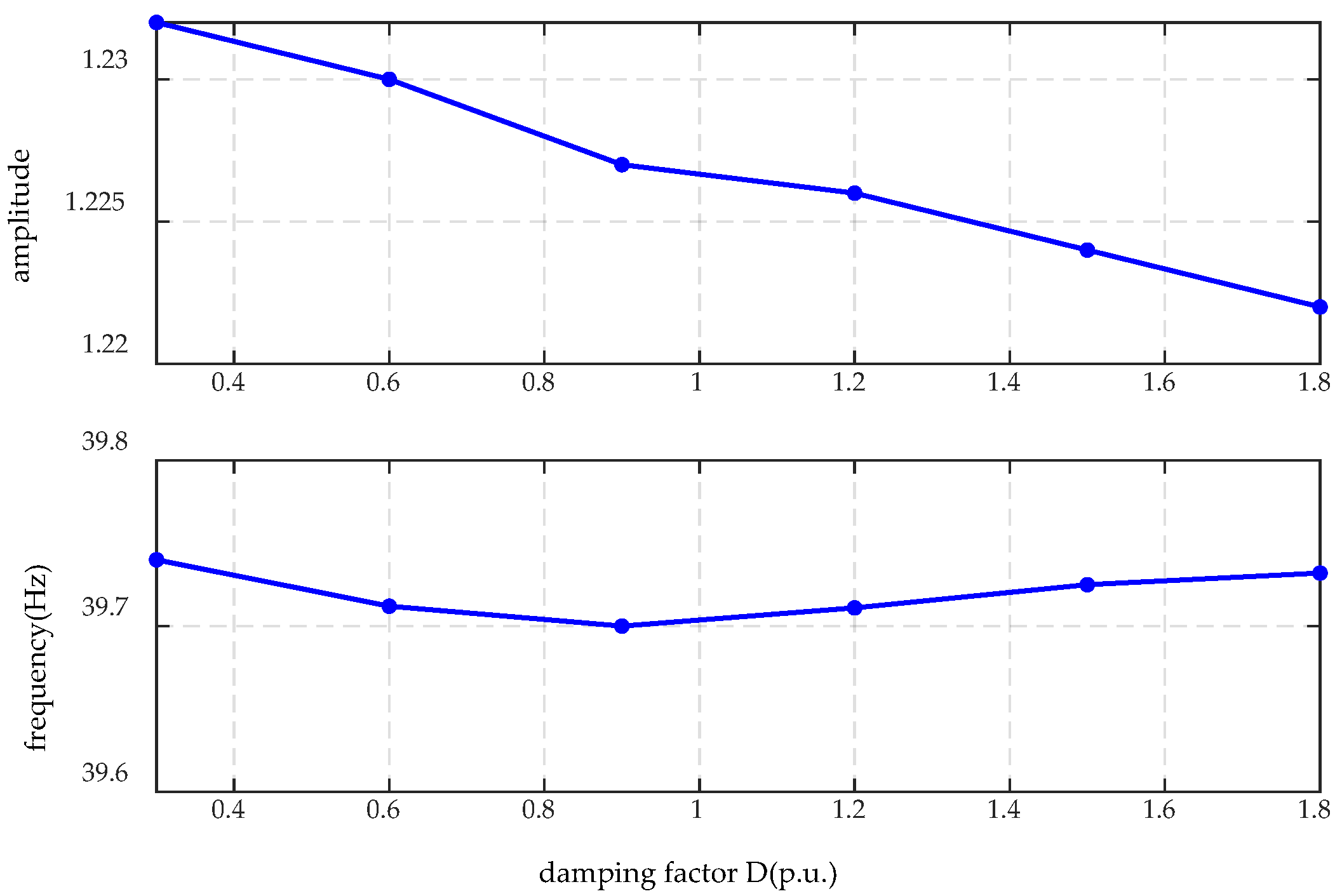
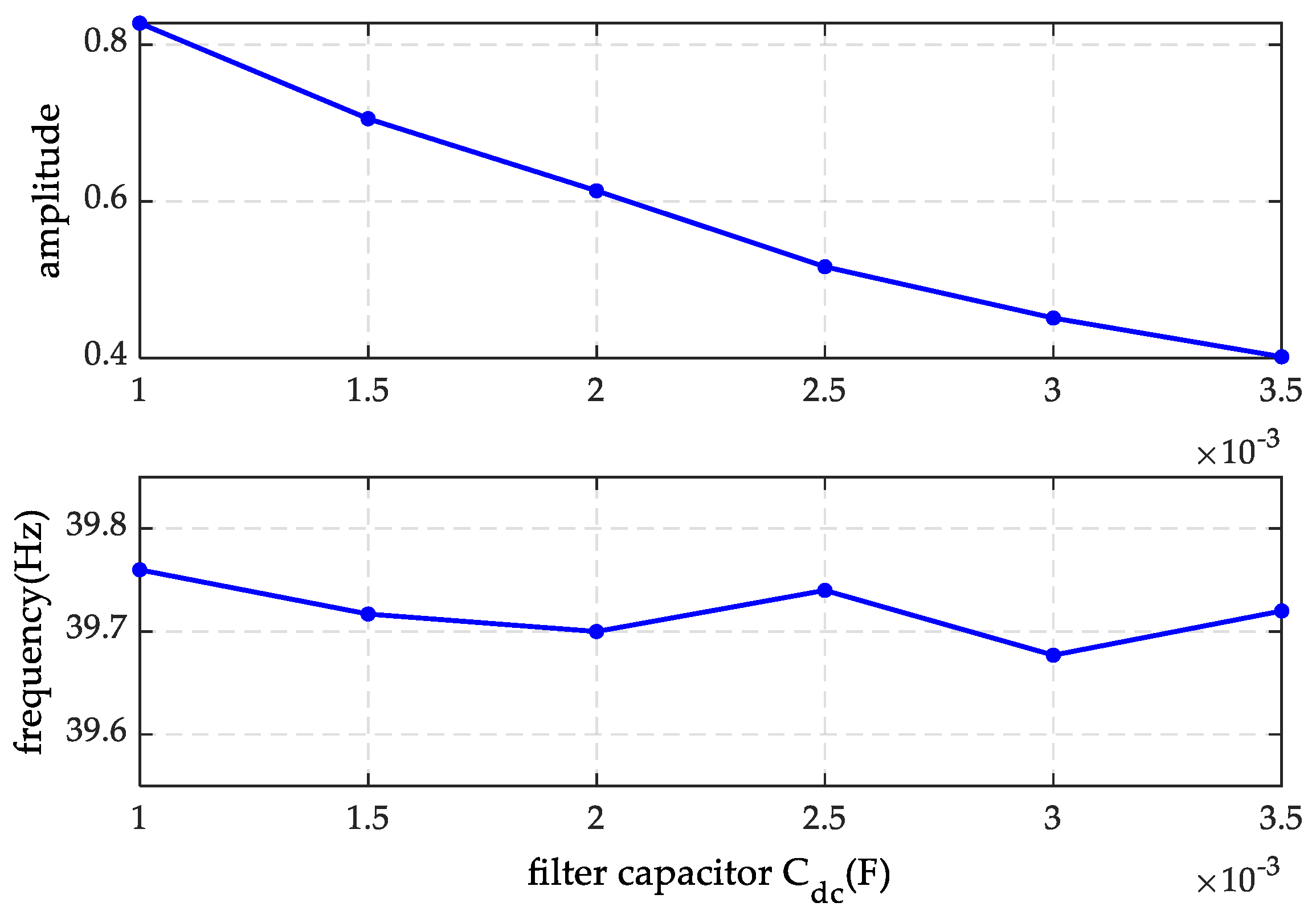
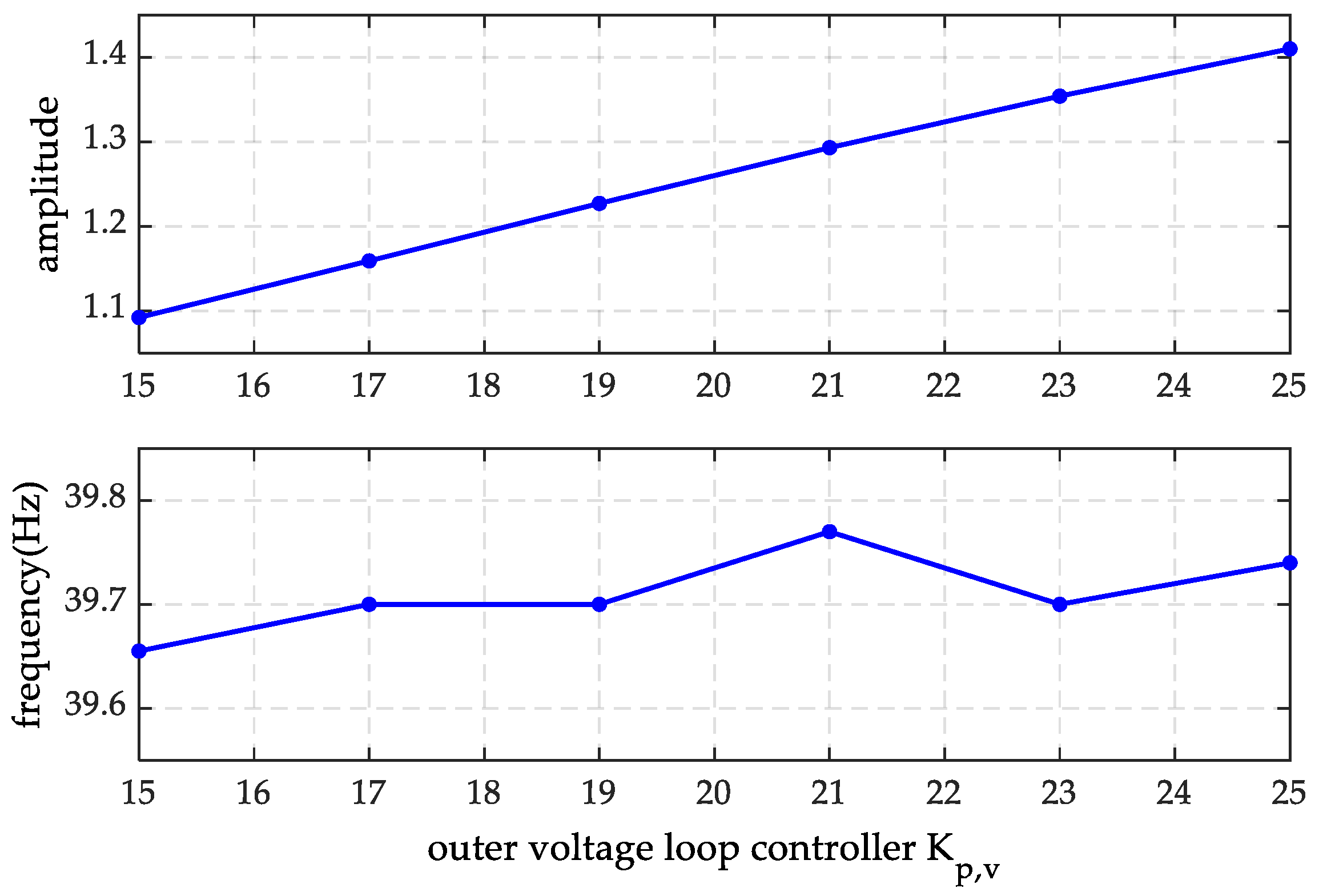
4.1. Impact of System Parameters on Sub-Synchronous Oscillation
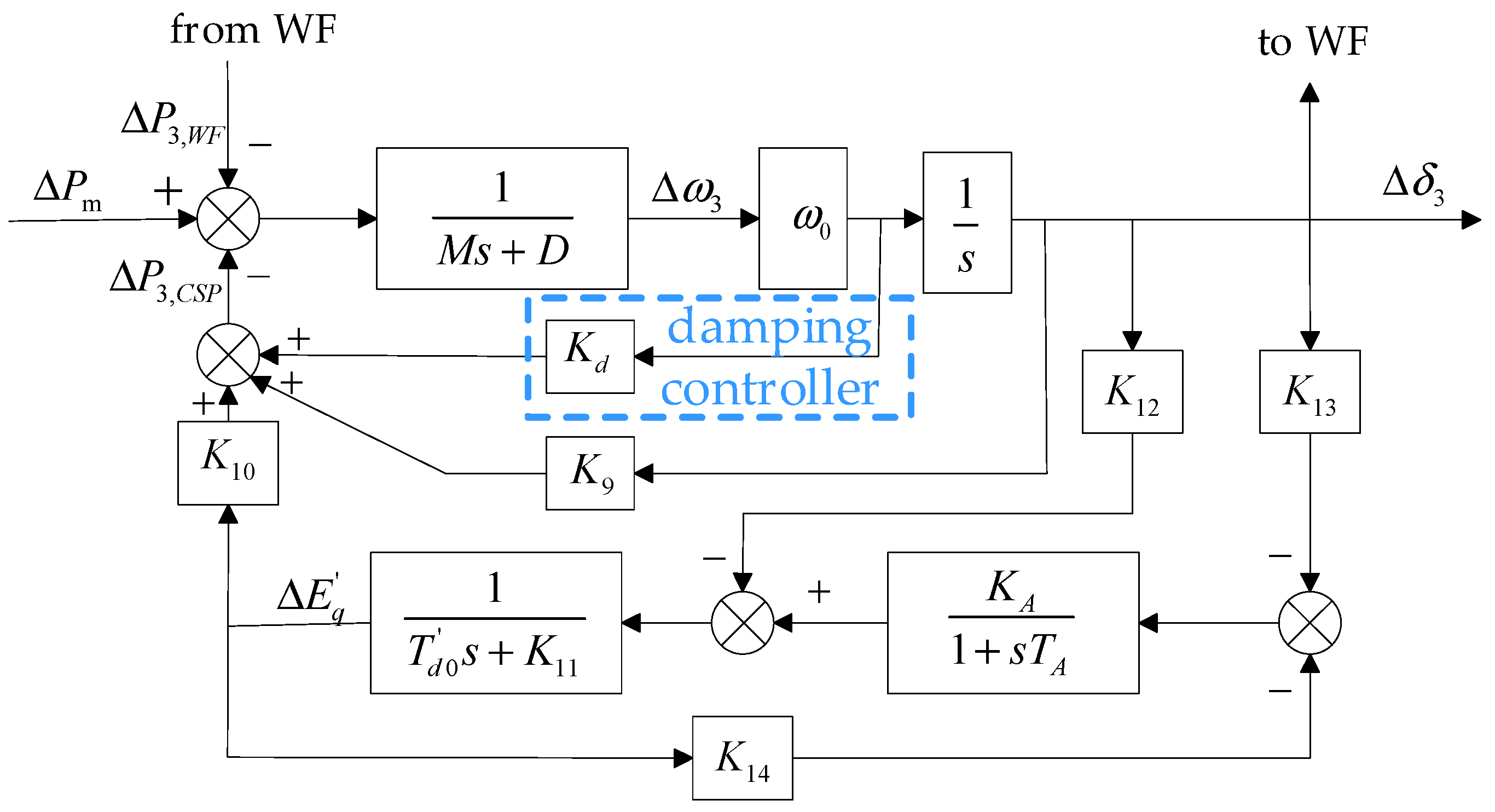
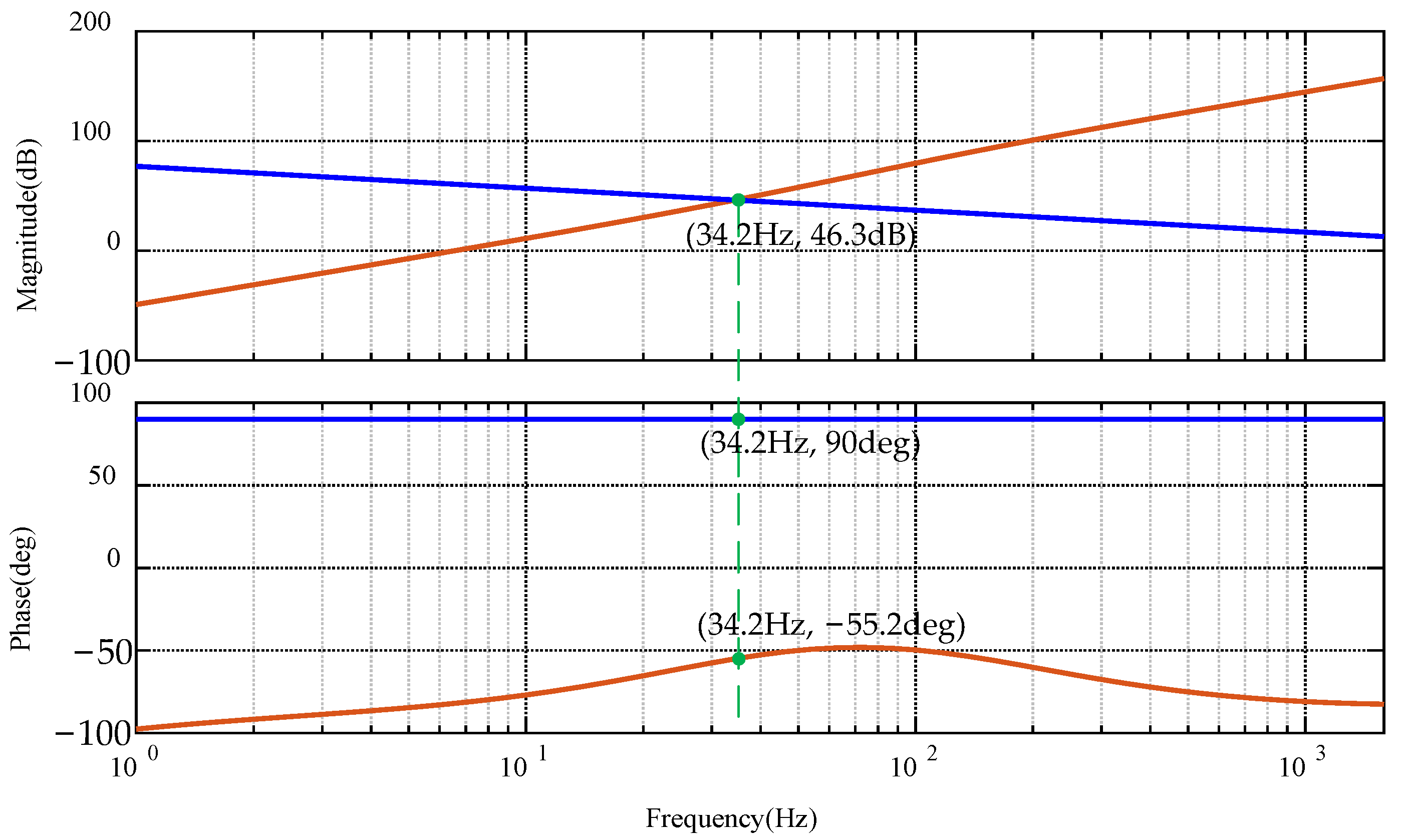
4.2. Design of Damping Controller and Its Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Chen, W.; Wang, P.; Li, K.; Zou, R.; Tian, S.; Yu, H. Forced subsynchronous oscillations of turbine-generators excited by interharmonics from bundled offshore wind farms. IEEE Trans. Power Syst. 2024, 39, 5416–5430. [Google Scholar] [CrossRef]
- Chen, B.; Liu, T.; Liu, X.; He, C.; Nan, L.; Wu, L. Distributionally robust coordinated expansion planning for generation, transmission, and demand side resources considering the benefits of concentrating solar power plants. IEEE Trans. Power Syst. 2023, 38, 1205–1218. [Google Scholar] [CrossRef]
- Du, E.; Zhang, N.; Hodge, B.; Wang, Q.; Kang, C.; Kroposki, B. The role of concentrating solar power toward high renewable energy penetrated power systems. IEEE Trans. Power Syst. 2018, 33, 6630–6641. [Google Scholar] [CrossRef]
- Camm, E.H.; Williams, S.E. Solar Power Plant Design and Interconnection. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 21 April 2011. [Google Scholar]
- Zhang, Z.; Zhao, X. Coordinated power oscillation damping from a VSC-HVDC grid integrated with offshore wind farms: Using capacitors energy. IEEE Trans. Sustain. Energy 2023, 14, 751–762. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, Q. New perspectives and systematic approaches for analyzing negative damping-induced sustained oscillation. IEEE Trans. Power Electron. 2024, 39, 361–373. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, X.; Fu, L.; Edrah, M. Stability and dynamic analysis of the PMSG-based WECS with torsional oscillation and power oscillation damping capabilities. IEEE Trans. Sustain. Energy 2022, 13, 2196–2210. [Google Scholar] [CrossRef]
- Gurung, N.; Bhattarai, R.; Kamalasadan, S. Optimal oscillation damping controller design for large-scale wind integrated power grid. IEEE Trans. Ind. Appl. 2020, 56, 4225–4235. [Google Scholar] [CrossRef]
- Yan, C.; Yao, W.; Wen, J. Impact of active frequency support control of photovoltaic on PLL-based photovoltaic of wind-photovoltaic-thermal coupling system. IEEE Trans. Power Syst. 2023, 38, 4788–4799. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, X. Modelling and analysis of frequency-responsive wind turbine involved in power system ultra-low frequency oscillation. IEEE Trans. Sustain. Energy 2022, 13, 844–855. [Google Scholar] [CrossRef]
- Luo, Q.; Ariyur, K.B.; Mathur, A.K. Control-oriented concentrated solar power plant model. IEEE Trans. Control. Syst. Technol. 2016, 24, 623–635. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Y.; Xiao, X. Concentrated solar power plant modeling for power system studies. IEEE Trans. Power Syst. 2024, 39, 4252–4263. [Google Scholar] [CrossRef]
- Zhai, W.; Jia, Q.; Yan, G. Analysis of sub synchronous oscillation characteristics from a direct drive wind farm based on the complex torque coefficient method. CSEE J. Power Energy Syst. 2024, 11, 1–10. [Google Scholar]
- Yan, G.; Wang, Z.; Zhao, Y.; Wang, Y.; Peng, J.; Wang, D. Analysis and suppression of sub-synchronous oscillation of photovoltaic power generation based on damping torque method. IEEE Trans. Ind. Appl. 2024, 60, 5074–5083. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Li, Y. Torque Analysis of a Power System Integrated with PMSG-based Wind Farm for Low-Frequency Oscillation Mitigation. In Proceedings of the 2022 IEEE International Conference on Power Systems and Electrical Technology (PSET), Aalborg, Denmark, 13–15 October 2022. [Google Scholar]
- Xue, T.; Lyu, J.; Wang, H.; Cai, X. A complete impedance model of a PMSG-based wind energy conversion system and its effect on the stability analysis of MMC-HVDC connected offshore wind farms. IEEE Trans. Energy Convers. 2021, 36, 3449–3461. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Zhao, H.; Yang, F. Comprehensive impedance analysis of DFIG-based wind farms considering dynamic couplings. IEEE Trans. Power Electron. 2025, 40, 2259–2272. [Google Scholar] [CrossRef]
- Li, L.; Wu, H.; Geng, X. Impedance Modeling and Stability Analysis of Wind Farm through HVDC Transmission System Considering Commutation Overlap Characteristic. In Proceedings of the 2024 7th International Conference on Power and Energy Applications (ICPEA), Taiyuan, China, 18–20 October 2024. [Google Scholar]
- Zhan, Y.; Xie, X.; Liu, H.; Liu, H.; Li, Y. Frequency-domain modal analysis of the oscillatory stability of power systems with high-penetration renewables. IEEE Trans. Sustain. Energy 2019, 10, 1534–1543. [Google Scholar] [CrossRef]
- Han, Y.; Sun, H.; Huang, B.; Qin, S. Discrete-time domain modal analysis of oscillatory stability of renewables integrated power systems. IEEE Trans. Power Deliv. 2022, 37, 4248–4260. [Google Scholar] [CrossRef]
- Xu, Y.; Gu, Z.; Sun, K. Characterization of subsynchronous oscillation with wind farms using describing function and generalized Nyquist criterion. IEEE Trans. Power Syst. 2020, 35, 2783–2793. [Google Scholar] [CrossRef]
- Lin, G.; Liu, J.; Wang, P.; Rehtanz, C.; Li, Y.; Wang, S. Low-frequency oscillation analysis of virtual-inertia-controlled DC microgrids based on multi-timescale impedance model. IEEE Trans. Sustain. Energy 2022, 13, 1536–1552. [Google Scholar] [CrossRef]
- Xia, S.; Luo, X.; Chan, K.W.; Zhou, M.; Li, G. Probabilistic transient stability constrained optimal power flow for power systems with multiple correlated uncertain wind generations. IEEE Trans. Sustain. Energy 2016, 7, 1133–1144. [Google Scholar] [CrossRef]
- Bakhshizadeh, M.K.; Ghosh, S.; Kocewiak, Ł.; Yang, G. Improved reduced-order model for PLL instability investigations. IEEE Access 2023, 11, 72400–72408. [Google Scholar] [CrossRef]
- Pang, B.; Nian, H. Collaborative control and allocation method of RSC and GSC for DFIG system to suppress high-frequency resonance and harmonics. IEEE Trans. Ind. Electron. 2020, 67, 10509–10519. [Google Scholar] [CrossRef]
- Kundur, P.S.; Malik, O.P. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 2022. [Google Scholar]
- Zhang, Q.; He, J.; Xu, Y.; Hong, Z.; Chen, Y.; Strunz, K. Average-value modeling of direct-driven PMSG-based wind energy conversion systems. IEEE Trans. Energy Convers. 2022, 37, 264–273. [Google Scholar] [CrossRef]
- Nuzzo, S.; Galea, M.; Gerada, C.; Brown, N. Analysis, modeling, and design considerations for the excitation systems of synchronous generators. IEEE Trans. Ind. Electron. 2018, 65, 2996–3007. [Google Scholar] [CrossRef]


| Parameter | Values |
|---|---|
| Outer-voltage loop controller kp,v, ki,v | 19, 48 |
| Filter capacitor Cdc (F) | 0.002 |
| Nominal value of the DC-link Udc0 (V) | 5400 |
| PLL controller kpPLL, kiPLL | 180, 3200 |
| Parameter | Values |
|---|---|
| Rotor inertia time constant M (s) | 3 |
| Damping coefficient D | 0.9 |
| Synchronous speed ω0 (p.u.) | 1 |
| Initial frequency f0 (p.u.) | 1 |
| Excitation winding time constant T′d0 (s) | 0.01 |
| Voltage regulator KA, TA | 0.1, 0.01 |
| Line reactance Xt (p.u.) | 0.0109 |
| d-axis transient reactance X′d (p.u.) | 0.253 |
| d-axis and q-axis self-inductance reactance Xd, Xq (p.u.) | 2.04, 1.94 |
| Initial value of the q-axis transient electromotive force E′q0 | 1000 |
| Parameter | Values |
|---|---|
| External grid voltage Ug (p.u.) | 110 |
| Impedance between the PCC point and the external grid Xg (p.u.) | 0.0248 |
| Impedance between the output port and the PCC points X1, X2, and X3 (p.u.) | 0.0385, 0.0385, 0.0385 |
| Initial voltage at the PCC point UPCC0 (p.u.), δPCC0 (rad) | 110.02, 0.0175 |
| Voltage at the wind turbine output port U10 (p.u.), δ10 (rad) | 110.03, 0.0333 |
| Voltage at the energy storage system output port U20 (p.u.), δ20 (rad) | 110.02, 0.0223 |
| Voltage at the CSP output port U30 (p.u.), δ30 (rad) | 110.02, 0.0237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Fu, G.; Wang, X.; Lu, G.; Song, R.; Sun, H.; Xue, Z.; Xu, Y.; Kou, P. Interaction Mechanism and Oscillation Characteristics of Grid-Connected Concentrating Solar Power–Battery Energy Storage System–Wind Hybrid Energy System. Energies 2025, 18, 1339. https://doi.org/10.3390/en18061339
Cai S, Fu G, Wang X, Lu G, Song R, Sun H, Xue Z, Xu Y, Kou P. Interaction Mechanism and Oscillation Characteristics of Grid-Connected Concentrating Solar Power–Battery Energy Storage System–Wind Hybrid Energy System. Energies. 2025; 18(6):1339. https://doi.org/10.3390/en18061339
Chicago/Turabian StyleCai, Shengliang, Guobin Fu, Xuebin Wang, Guoqiang Lu, Rui Song, Haibin Sun, Zhihang Xue, Yangsunnan Xu, and Peng Kou. 2025. "Interaction Mechanism and Oscillation Characteristics of Grid-Connected Concentrating Solar Power–Battery Energy Storage System–Wind Hybrid Energy System" Energies 18, no. 6: 1339. https://doi.org/10.3390/en18061339
APA StyleCai, S., Fu, G., Wang, X., Lu, G., Song, R., Sun, H., Xue, Z., Xu, Y., & Kou, P. (2025). Interaction Mechanism and Oscillation Characteristics of Grid-Connected Concentrating Solar Power–Battery Energy Storage System–Wind Hybrid Energy System. Energies, 18(6), 1339. https://doi.org/10.3390/en18061339





