Parametric Forecast of Solar Energy over Time by Applying Machine Learning Techniques: Systematic Review
Abstract
1. Introduction
- ○
- ○
- ○
2. Methods
2.1. Method Used
2.2. Inclusion and Exclusion Criteria
2.3. Sources of Information and Materials
2.4. Selection and Data Gathering
2.5. Informational Data Items
2.6. Measures of Bias and Effect
2.7. Bias Evaluation
2.8. Search Methodology
2.9. Data Synthesis
2.10. Solar Energy Data Collection and Processing
2.11. Evaluation and Effects of the Fuel Sources Currently in Use
2.12. Synthesis Methods
2.13. Research and Data Validation
2.14. Extraction and Correction of Raw Data
2.15. Parametric Estimation of Total Solar Energy
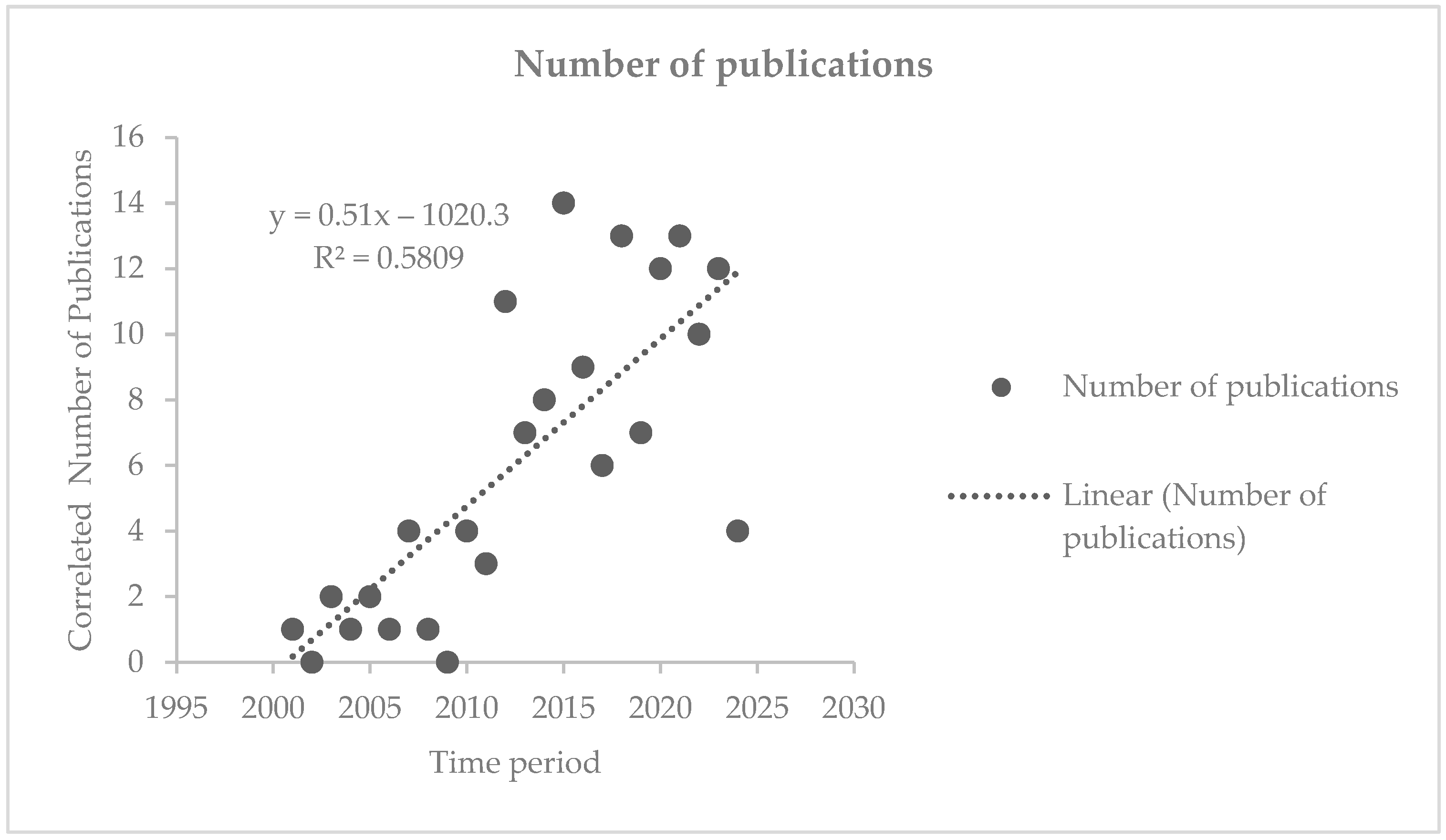
3. Results of Forecasting Solar Energy and Analysis of Systematic Bibliographic Sources
3.1. Parametric Forecasting of Solar Energy
3.1.1. Spectral Distribution Histograms for Days
3.1.2. Autocorrelation and Partial-Autocorrelation Function
3.1.3. Comparison Between Forecasted, Measured, and Theoretical Solar Energy
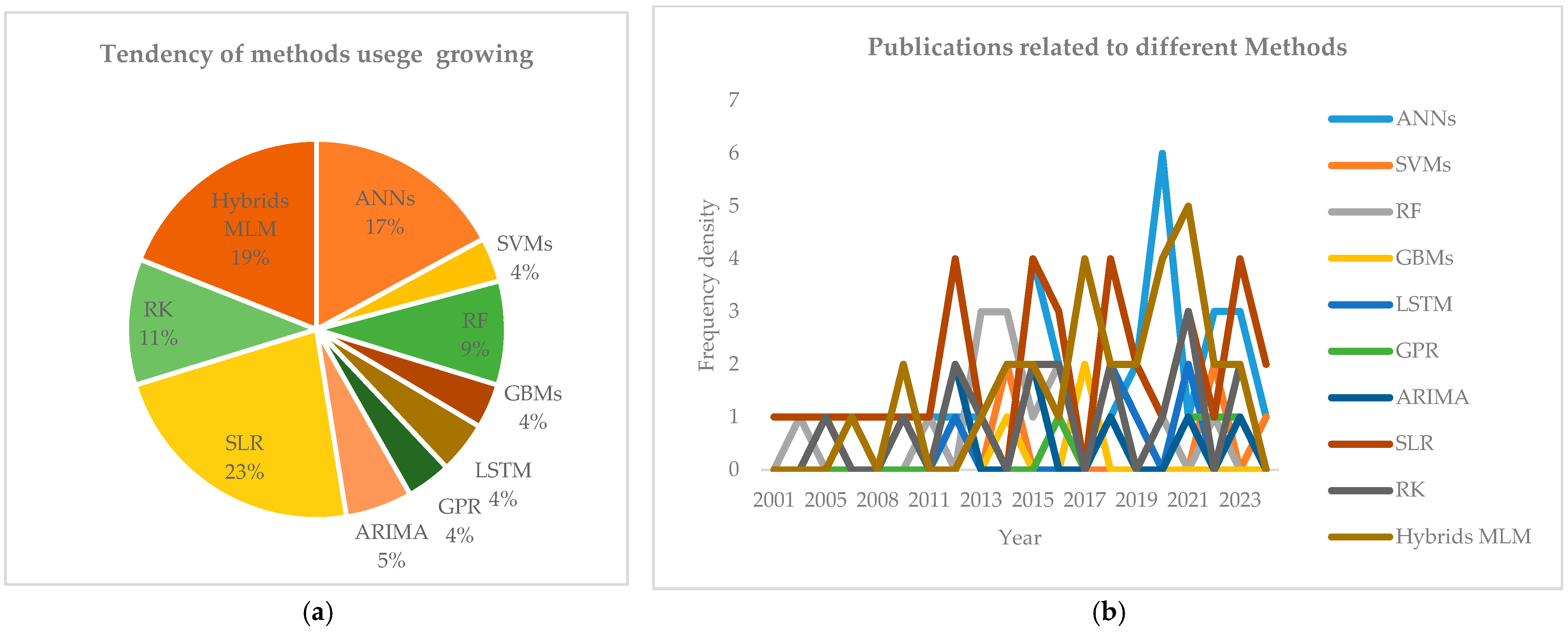
3.2. Analysis of Systematic Bibliographic Data Sources
3.2.1. Every Technique for Forecasting Worldwide Horizontal Radiation
Artificial Neural Network (ANN) Model
Support Vector Machine (SVM) Model
Random Forest (RF) Model
Gradient-Boosting Machine (GBM) Model
Long Short-Term Memory (LSTM) Network Model
Gaussian Process Regression (GPR) Model
Autoregressive Integrated Moving Average (ARIMA) Model
Simple Linear Regression (SLR) Model
Regression Kriging (RK) Model
Hybrid Machine Learning Models
Analyzing the Sample Bibliographies and the Data Sources Gathered
4. A Discussion of Machine Learning Techniques for Parameterizing Solar Energy
5. Summary and Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hossain, R.; Ooa, A.M.T.; Alia, A.B.M.S. Historical Weather Data Supported Hybrid Renewable Energy Forecasting using Artificial Neural Network (ANN). Energy Procedia 2012, 14, 1035–1040. [Google Scholar] [CrossRef]
- Babar, B.; Luppino, L.T.; Boström, T.; Anfinsen, S.N. Random forest regression for improved mapping of solar irradiance at high latitudes. Sol. Energy 2020, 198, 81–92. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Tsai, S.-B.; Xue, Y.; Zhang, J.; Chen, Q.; Liu, Y.; Zhou, J.; Dong, W. Models for forecasting growth trends in renewable energy. Renew. Sustain. Energy Rev. 2017, 77, 1169–1178. [Google Scholar] [CrossRef]
- Tracking SDG 7—The Energy Progress Report 2023. Available online: https://cdn.who.int/media/docs/default-source/air-pollution-documents/air-quality-and-health/sdg7-report2023-full-report_web.pdf?sfvrsn=669e8626_3&download=true (accessed on 16 December 2023).
- Mucomole, F.V.; Silva, C.A.S.; Magaia, L.L. Regressive and Spatio-Temporal Accessibility of Variability in Solar Energy on a Short Scale Measurement in the Southern and Mid Region of Mozambique. Energies 2024, 17, 2613. [Google Scholar] [CrossRef]
- Benghanem, M.; Joraid, A.A. A multiple correlation between different solar parameters in Medina, Saudi Arabia. Renew. Energy 2007, 32, 2424–2435. [Google Scholar] [CrossRef]
- Ohtake, H.; Shimose, K.; Fonseca, J.G.D.S.; Takashima, T.; Oozeki, T.; Yamada, Y. Accuracy of the solar irradiance forecasts of the Japan Meteorological Agency mesoscale model for the Kanto region, Japan. Sol. Energy 2013, 98, 138–152. [Google Scholar] [CrossRef]
- Mohanty, S.; Patra, P.K.; Sahoo, S.S.; Mohanty, A. Forecasting of solar energy with application for a growing economy like India: Survey and implication. Renew. Sustain. Energy Rev. 2017, 78, 539–553. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, X.; She, K. Forecasting Japan’s Solar Energy Consumption Using a Novel Incomplete Gamma Grey Model. Sustainability 2019, 11, 5921. [Google Scholar] [CrossRef]
- Ramirez-Vergara, J.; Bosman, L.B.; Leon-Salas, W.D.; Wollega, E. Ambient temperature and solar irradiance forecasting prediction horizon sensitivity analysis. Mach. Learn. Appl. 2021, 6, 100128. [Google Scholar] [CrossRef]
- Sward, J.A.; Ault, T.R.; Zhang, K.M. Genetic algorithm selection of the weather research and forecasting model physics to support wind and solar energy integration. Energy 2022, 254, 124367. [Google Scholar] [CrossRef]
- Funk, P.A.; Larson, D.L. Parametric model of solar cooker performance. Sol. Energy 1998, 62, 63–68. [Google Scholar] [CrossRef]
- Sahin, G.; Isik, G.; van Sark, W.G.J.H.M. Predictive modeling of PV solar power plant efficiency considering weather conditions: A comparative analysis of artificial neural networks and multiple linear regression. Energy Rep. 2023, 10, 2837–2849. [Google Scholar] [CrossRef]
- Duf, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Jawaid, F.; NazirJunejo, K. Predicting daily mean solar power using machine learning regression techniques. In Proceedings of the 2016 Sixth International Conference on Innovative Computing Technology (INTECH), Dublin, Ireland, 24–26 August 2016; pp. 355–360. [Google Scholar] [CrossRef]
- Litjens, G.B.M.A.; Kausika, B.B.; Worrell, E.; van Sark, W.G.J.H.M. A spatio-temporal city-scale assessment of residential photovoltaic power integration scenarios. Sol. Energy 2018, 174, 1185–1197. [Google Scholar] [CrossRef]
- Zhang, J.; Hodge, B.-M.; Lu, S.; Hamann, H.F.; Lehman, B.; Simmons, J.; Campos, E.; Banunarayanan, V.; Black, J.; Tedesco, J. Baseline and target values for regional and point PV power forecasts: Toward improved solar forecasting. Sol. Energy 2015, 122, 804–819. [Google Scholar] [CrossRef]
- Dyson, M.E.H.; Borgeson, S.D.; Tabone, M.D.; Callaway, D.S. Using smart meter data to estimate demand response potential, with application to solar energy integration. Energy Policy 2014, 73, 607–619. [Google Scholar] [CrossRef]
- Jebli, I.; Belouadha, F.-Z.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by pearson correlation using machine learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- Jung, Y.; Lee, H.; Kim, J.; Cho, Y.; Kim, J.; Lee, Y.G. Spatio-Temporal Characteristics in the Clearness Index Derived from Global Solar Radiation Observations in Korea. Atmosphere 2016, 7, 55. [Google Scholar] [CrossRef]
- Kaur, A.; Nonnenmacher, L.; Pedro, H.T.C.; Coimbra, C.F.M. Benefits of solar forecasting for energy imbalance markets. Renew. Energy 2016, 86, 819–830. [Google Scholar] [CrossRef]
- Zhang, J.; Florita, A.; Hodge, B.-M.; Lu, S.; Hamann, H.F.; Banunarayanan, V.; Brockway, A.M. A suite of metrics for assessing the performance of solar power forecasting. Sol. Energy 2015, 111, 157–175. [Google Scholar] [CrossRef]
- Wenham, S.R.; Green, M.A.; Watt, M.E.; Corkish, R.; Sproul, A. (Eds.) Applied Photovoltaics, 3rd ed.; Routledge: London, UK, 2011. [Google Scholar] [CrossRef]
- Mucomole, F.V.; Silva, C.A.S.; Magaia, L.L. Temporal Variability of Solar Energy Availability in the Conditions of the Southern Region of Mozambique. Am. J. Energy Nat. Resour. 2023, 2, 27–50. [Google Scholar] [CrossRef]
- Energy Access Situation in Mozambique—Energypedia. Available online: https://energypedia.info/wiki/Situa%C3%A7%C3%A3o_de_Acesso_%C3%A0_Energia_em_Mo%C3%A7ambique (accessed on 15 December 2023).
- Yousif, J.H.; Al-Balushi, H.A.; Kazem, H.A.; Chaichan, M.T. Analysis and forecasting of weather conditions in Oman for renewable energy applications. Case Stud. Therm. Eng. 2019, 13, 100355. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Adedeji, P.A.; Akinlabi, S.A.; Madushele, N.; Olatunji, O.O. Neuro-fuzzy resource forecast in site suitability assessment for wind and solar energy: A mini review. J. Clean. Prod. 2020, 269, 122104. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Inman, R.H.; Coimbra, C.F.M. 4—Mathematical methods for optimized solar forecasting. In Renewable Energy Forecasting; Kariniotakis, G., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2017; pp. 111–152. [Google Scholar] [CrossRef]
- Choi, M.; Rachunok, B.; Nateghi, R. Short-term solar irradiance forecasting using convolutional neural networks and cloud imagery. Environ. Res. Lett. 2021, 16, 044045. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. Artificial neural network forecast of monthly mean daily global solar radiation of selected locations based on time series and month number. J. Clean. Prod. 2019, 216, 1–13. [Google Scholar] [CrossRef]
- Lauret, P.; Lorenz, E.; David, M. Solar Forecasting in a Challenging Insular Context. Atmosphere 2016, 7, 18. [Google Scholar] [CrossRef]
- Wen, H.; Du, Y.; Chen, X.; Lim, E.G.; Wen, H.; Yan, K. A regional solar forecasting approach using generative adversarial networks with solar irradiance maps. Renew. Energy 2023, 216, 119043. [Google Scholar] [CrossRef]
- Breitkreuz, H.; Schroedter-Homscheidt, M.; Holzer-Popp, T.; Dech, S. Short-Range Direct and Diffuse Irradiance Forecasts for Solar Energy Applications Based on Aerosol Chemical Transport and Numerical Weather Modeling. J. Appl. Meteorol. Climatol. 2009, 48, 1766–1779. [Google Scholar] [CrossRef]
- Boland, J.; David, M.; Lauret, P. Short term solar radiation forecasting: Island versus continental sites. Energy 2016, 113, 186–192. [Google Scholar] [CrossRef]
- Blaga, R.; Sabadus, A.; Stefu, N.; Dughir, C.; Paulescu, M.; Badescu, V. A current perspective on the accuracy of incoming solar energy forecasting. Prog. Energy Combust. Sci. 2019, 70, 119–144. [Google Scholar] [CrossRef]
- Nam, S.; Hur, J. A hybrid spatio-temporal forecasting of solar generating resources for grid integration. Energy 2019, 177, 503–510. [Google Scholar] [CrossRef]
- Kumler, A.; Xie, Y.; Zhang, Y. A New Approach for Short-Term Solar Radiation Forecasting Using the Estimation of Cloud Fraction and Cloud Albedo; NREL: Golden, CO, USA, 2018. [Google Scholar] [CrossRef]
- Aler, R.; Martín, R.; Valls, J.M.; Galván, I.M. A Study of Machine Learning Techniques for Daily Solar Energy Forecasting Using Numerical Weather Models. In Intelligent Distributed Computing VIII; Camacho, D., Braubach, L., Venticinque, S., Badica, C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 269–278. [Google Scholar]
- Dhillon, S.; Madhu, C.; Kaur, D.; Singh, S. A Solar Energy Forecast Model Using Neural Networks: Application for Prediction of Power for Wireless Sensor Networks in Precision Agriculture. Wirel. Pers. Commun. 2020, 112, 2741–2760. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Zink, R.; Dorner, W.; Stoeglehner, G. Spatio-temporal modeling of roof-top photovoltaic panels for improved technical potential assessment and electricity peak load offsetting at the municipal scale. Comput. Environ. Urban Syst. 2015, 52, 58–69. [Google Scholar] [CrossRef]
- Saffaripour, M.H.; Mehrabian, M.A.; Bazargan, H. Predicting solar radiation fluxes for solar energy system applications. Int. J. Environ. Sci. Technol. 2013, 10, 761–768. [Google Scholar] [CrossRef]
- McCandless, T.; Jiménez, P.A. Examining the Potential of a Random Forest Derived Cloud Mask from GOES-R Satellites to Improve Solar Irradiance Forecasting. Energies 2020, 13, 1671. [Google Scholar] [CrossRef] [PubMed]
- Anuradha, K.; Erlapally, D.; Karuna, G.; Srilakshmi, V.; Adilakshmi, K. Analysis of Solar Power Generation Forecasting Using Machine Learning Techniques. E3S Web Conf. 2021, 309, 01163. [Google Scholar] [CrossRef]
- Zagouras, A.; Pedro, H.T.C.; Coimbra, C.F.M. On the role of lagged exogenous variables and spatio–temporal correlations in improving the accuracy of solar forecasting methods. Renew. Energy 2015, 78, 203–218. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S. An ultra-fast way of searching weather analogs for renewable energy forecasting. Sol. Energy 2019, 185, 255–261. [Google Scholar] [CrossRef]
- Arumugham, D.R.; Rajendran, P. Modelling global solar irradiance for any location on earth through regression analysis using high-resolution data. Renew. Energy 2021, 180, 1114–1123. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive modelling for solar thermal energy systems: A comparison of support vector regression, random forest, extra trees and regression trees. J. Clean. Prod. 2018, 203, 810–821. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A. Scatterometer Backscatter Uncertainty Due to Wind Variability. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3356–3362. [Google Scholar] [CrossRef]
- Cerralbo, P.; Grifoll, M.; Moré, J.; Bravo, M.; Sairouní Afif, A.; Espino, M. Wind variability in a coastal area (Alfacs Bay, Ebro River delta). Adv. Sci. Res. 2015, 12, 11–21. [Google Scholar] [CrossRef]
- Munkhammar, J. Very short-term probabilistic and scenario-based forecasting of solar irradiance using Markov-chain mixture distribution modeling. Sol. Energy Adv. 2024, 4, 100057. [Google Scholar] [CrossRef]
- Kumar, D. Hyper-temporal variability analysis of solar insolation with respect to local seasons. Remote Sens. Appl. Soc. Environ. 2019, 15, 100241. [Google Scholar] [CrossRef]
- Hoff, T.E.; Perez, R. Quantifying PV power Output Variability. Sol. Energy 2010, 84, 1782–1793. [Google Scholar] [CrossRef]
- Mucomole, F.V.; Silva, C.S.A.; Magaia, L.L. Quantifying the Variability of Solar Energy Fluctuations at High–Frequencies through Short-Scale Measurements in the East–Channel of Mozambique Conditions. Am. J. Energy Nat. Resour. 2024, 3, 21–40. [Google Scholar] [CrossRef]
- Paulescu, M.; Paulescu, E. Short-term forecasting of solar irradiance. Renew. Energy 2019, 143, 985–994. [Google Scholar] [CrossRef]
- Gutierrez-Corea, F.-V.; Manso-Callejo, M.-A.; Moreno-Regidor, M.-P.; Velasco-Gómez, J. Spatial Estimation of Sub-Hour Global Horizontal Irradiance Based on Official Observations and Remote Sensors. Sensors 2014, 14, 6758–6787. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Gong, W.; Hu, B.; Lin, A.; Li, H.; Zou, L. Modeling and analysis of the spatiotemporal variations of photosynthetically active radiation in China during 1961–2012. Renew. Sustain. Energy Rev. 2015, 49, 1019–1032. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Syst. Rev. 2021, 10, 89. [Google Scholar] [CrossRef] [PubMed]
- FUNAE (National Energy Fund of Mozambique) [Online]. 2023. Available online: https://funae.co.mz/ (accessed on 30 April 2023).
- INAM (National Meteorology Institute of Mozambique) [Online]. 2024. Available online: https://www.inam.gov.mz/index.php/pt/ (accessed on 5 May 2023).
- AERONET (Aerosol Robotic Network) [Online]. 2024. Available online: https://aeronet.gsfc.nasa.gov/ (accessed on 12 February 2023).
- Smith, C.J.; Bright, J.M.; Crook, R. Cloud cover effect of clear-sky index distributions and differences between human and automatic cloud observations. Sol. Energy 2017, 144, 10–21. [Google Scholar] [CrossRef]
- Kurniadi, A.P.; Aimon, H.; Salim, Z.; Ragimun, R.; Sonjaya, A.; Setiawan, S.; Siagian, V.; Nasution, L.Z.; Nurhidajat, R.; Mutaqin, M.; et al. Analysis of Existing and Forecasting for Coal and Solar Energy Consumption on Climate Change in Asia Pacific: New Evidence for Sustainable Development Goals. Int. J. Energy Econ. Policy 2024, 14, 352–359. [Google Scholar] [CrossRef]
- Renkema, Y.; Visser, L.; AlSkaif, T. Enhancing the reliability of probabilistic PV power forecasts using conformal prediction. Sol. Energy Adv. 2024, 4, 100059. [Google Scholar] [CrossRef]
- Arslan, H.; Baltaci, H.; Akkoyunlu, B.O.; Karanfil, S.; Tayanc, M. Wind speed variability and wind power potential over Turkey: Case studies for Çanakkale and İstanbul. Renew. Energy 2020, 145, 1020–1032. [Google Scholar] [CrossRef]
- Vindel, J.M.; Valenzuela, R.X.; Navarro, A.A.; Polo, J. Temporal and spatial variability analysis of the solar radiation in a region affected by the intertropical convergence zone. Meteorol. Appl. 2020, 27, e1824. [Google Scholar] [CrossRef]
- Klein, S.A.; Cooper, P.I.; Freeman, T.L.; Beekman, D.M.; Beckman, W.A.; Duffie, J.A. A method of simulation of solar processes and its application. Sol. Energy 1975, 17, 29–37. [Google Scholar] [CrossRef]
- Charles, R.G.; Davies, M.L.; Douglas, P.; Hallin, I.L.; Mabbett, I. Sustainable energy storage for solar home systems in rural Sub-Saharan Africa—A comparative examination of lifecycle aspects of battery technologies for circular economy, with emphasis on the South African context. Energy 2019, 166, 1207–1215. [Google Scholar] [CrossRef]
- Puga-Gil, D.; Astray, G.; Barreiro, E.; Gálvez, J.F.; Mejuto, J.C. Global Solar Irradiation Modelling and Prediction Using Machine Learning Models for Their Potential Use in Renewable Energy Applications. Mathematics 2022, 10, 4746. [Google Scholar] [CrossRef]
- Lichtenwoehrer, P.; Abart-Heriszt, L.; Kretschmer, F.; Suppan, F.; Stoeglehner, G.; Neugebauer, G. Evaluating Spatial Interdependencies of Sector Coupling Using Spatiotemporal Modelling. Energies 2021, 14, 1256. [Google Scholar] [CrossRef]
- Ghayekhloo, M.; Ghofrani, M.; Menhaj, M.B.; Azimi, R. A novel clustering approach for short-term solar radiation forecasting. Sol. Energy 2015, 122, 1371–1383. [Google Scholar] [CrossRef]
- Ibrahim, S.; Daut, I.; Irwan, Y.M.; Irwanto, M.; Gomesh, N.; Farhana, Z. Linear Regression Model in Estimating Solar Radiation in Perlis. Energy Procedia 2012, 18, 1402–1412. [Google Scholar] [CrossRef]
- Twidell, J.; Weir, T. Renewable Energy Resources, 3rd ed.; Routledge: London, UK, 2015. [Google Scholar] [CrossRef]
- Mei, L.L.; Xue, Y.; Kokhanovsky, A.A.; von Hoyningen-Huene, W.; de Leeuw, G.; Burrows, J.P. Retrieval of aerosol optical depth over land surfaces from AVHRR data. Atmos. Meas. Techol. 2014, 7, 2411–2420. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, H.; Zheng, F. Aerosol Optical Depth Retrieval over East Asia Using Himawari-8/AHI Data. Remote Sens. 2018, 10, 137. [Google Scholar] [CrossRef]
- Mishra, M.K. Retrieval of Aerosol Optical Depth From INSAT-3D Imager Over Asian Landmass and Adjoining Ocean: Retrieval Uncertainty and Validation. J. Geophys. Res. Atmos. 2018, 123, 5484–5508. [Google Scholar] [CrossRef]
- Levy, R.C.; Munchak, L.A.; Mattoo, S.; Patadia, F.; Remer, L.A.; Holz, R.E. Towards a long-term global aerosol optical depth record: Applying a consistent aerosol retrieval algorithm to MODIS and VIIRS-observed reflectance. Atmos. Meas. Technol. 2015, 8, 4083–4110. [Google Scholar] [CrossRef]
- Zhang, H.; Lyapustin, A.; Wang, Y.; Kondragunta, S.; Laszlo, I.; Ciren, P.; Hoff, R.M. A multi-angle aerosol optical depth retrieval algorithm for geostationary satellite data over the United States. Atmos. Chem. Phys. 2011, 11, 11977–11991. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Gupta, P.; Levy, R.C.; Mattoo, S.; Remer, L.A.; Munchak, L.A. A surface reflectance scheme for retrieving aerosol optical depth over urban surfaces in MODIS Dark Target retrieval algorithm. Atmos. Meas. Technol. 2016, 9, 3293–3308. [Google Scholar] [CrossRef]
- Sun, L.; Wei, J.; Bilal, M.; Tian, X.; Jia, C.; Guo, Y.; Mi, X. Aerosol Optical Depth Retrieval over Bright Areas Using Landsat 8 OLI Images. Remote Sens. 2016, 8, 23. [Google Scholar] [CrossRef]
- Krishnan, N.; Kumar, K.R.; Inda, C.S. How solar radiation forecasting impacts the utilization of solar energy: A critical review. J. Clean. Prod. 2023, 388, 135860. [Google Scholar] [CrossRef]
- Tian, X.; Liu, S.; Sun, L.; Liu, Q. Retrieval of Aerosol Optical Depth in the Arid or Semiarid Region of Northern Xinjiang, China. Remote Sens. 2018, 10, 197. [Google Scholar] [CrossRef]
- Gopinathan, K.K. A simple method for predicting global solar radiation on a horizontal surface. Sol. Wind Technol. 1988, 5, 581–583. [Google Scholar] [CrossRef]
- Badescu, V.; Budea, S. How significant is the stability of the radiative regime when the best operation of solar DHW systems is evaluated? Renew. Energy 2016, 88, 346–358. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, S.; Qian, Y. Big data analysis of solar energy fluctuation characteristics and integration of wind-photovoltaic to hydrogen system. In Computer Aided Chemical Engineering; Kokossis, A.C., Georgiadis, M.C., Pistikopoulos, E., Eds.; 33 European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2023; Volume 52, pp. 3103–3109. [Google Scholar] [CrossRef]
- Kómar, L.; Kocifaj, M. Uncertainty of daylight illuminance on vertical building façades when determined from sky scanner data: A numerical study. Sol. Energy 2014, 110, 15–21. [Google Scholar] [CrossRef]
- Mustafa, M.; Malik, M.O.F. Factors Hindering Solar Photovoltaic System Implementation in Buildings and Infrastructure Projects: Analysis through a Multiple Linear Regression Model and Rule-Based Decision Support System. Buildings 2023, 13, 1786. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A.; Khoshnevisan, B.; Saboohi, H. A comparative study between fuzzy linear regression and support vector regression for global solar radiation prediction in Iran. Sol. Energy 2014, 109, 135–143. [Google Scholar] [CrossRef]
- Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression: Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Jogunuri, S.; Ft, J.; Stonier, A.A.; Peter, G.; Jayaraj, J.; Ganji, V. Random Forest machine learning algorithm based seasonal multi-step ahead short-term solar photovoltaic power output forecasting. In IET Renewable Power Generation; Wiley: Hoboken, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Perveen, G.; Rizwan, M.; Goel, N.; Anand, P. Artificial neural network models for global solar energy and photovoltaic power forecasting over India. Energy Sources Part Recovery Util. Environ. Eff. 2020, 47, 864–889. [Google Scholar] [CrossRef]
- Wu, J.; Niu, Z.; Li, X.; Huang, L.; Nielsen, P.S.; Liu, X. Understanding multi-scale spatiotemporal energy consumption data: A visual analysis approach. Energy 2023, 263, 125939. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar Irradiance Forecasting Using Deep Neural Networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Ayet, A.; Tandeo, P. Nowcasting solar irradiance using an analog method and geostationary satellite images. Sol. Energy 2018, 164, 301–315. [Google Scholar] [CrossRef]
- Barhmi, K.; Heynen, C.; Golroodbari, S.; van Sark, W. A Review of Solar Forecasting Techniques and the Role of Artificial Intelligence. Solar 2024, 4, 99–135. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Golabi, M.R. Modeling and predicting the electricity production in hydropower using conjunction of wavelet transform, long short-term memory and random forest models. Renew. Energy 2021, 170, 1367–1381. [Google Scholar] [CrossRef]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015; Available online: http://neuralnetworksanddeeplearning.com (accessed on 12 June 2024).
- Pizarroso, J.; Portela, J.; Muñoz, A. NeuralSens: Sensitivity Analysis of Neural Networks. J. Stat. Softw. 2022, 102, 1–36. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. Neural Networks in R Using the Stuttgart Neural Network Simulator: RSNNS. J. Stat. Softw. 2012, 46, 1–26. [Google Scholar] [CrossRef]
- Beck, M.W. NeuralNetTools: Visualization and Analysis Tools for Neural Networks. J. Stat. Softw. 2018, 85, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Tso, G.K.F.; Yau, K.K.W. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Amrouche, B.; Le Pivert, X. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Dahmani, K.; Notton, G.; Voyant, C.; Dizene, R.; Nivet, M.L.; Paoli, C.; Tamas, W. Multilayer Perceptron approach for estimating 5-min and hourly horizontal global irradiation from exogenous meteorological data in locations without solar measurements. Renew. Energy 2016, 90, 267–282. [Google Scholar] [CrossRef]
- Sridharan, M. Generalized Regression Neural Network Model Based Estimation of Global Solar Energy Using Meteorological Parameters. Ann. Data Sci. 2023, 10, 1107–1125. [Google Scholar] [CrossRef]
- Flocas, A.A. Estimation and prediction of global solar radiation over Greece. Sol. Energy 1980, 24, 63–70. [Google Scholar] [CrossRef]
- Panamtash, H.; Zhou, Q.; Hong, T.; Qu, Z.; Davis, K.O. A copula-based Bayesian method for probabilistic solar power forecasting. Sol. Energy 2020, 196, 336–345. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef]
- Kuo, P.-H.; Huang, C.-J. A Green Energy Application in Energy Management Systems by an Artificial Intelligence-Based Solar Radiation Forecasting Model. Energies 2018, 11, 819. [Google Scholar] [CrossRef]
- Mathiesen, P.; Collier, C.; Kleissl, J. A high-resolution, cloud-assimilating numerical weather prediction model for solar irradiance forecasting. Sol. Energy 2013, 92, 47–61. [Google Scholar] [CrossRef]
- Devaraj, J.; Madurai Elavarasan, R.; Shafiullah, G.; Jamal, T.; Khan, I. A holistic review on energy forecasting using big data and deep learning models. Int. J. Energy Res. 2021, 45, 13489–13530. [Google Scholar] [CrossRef]
- Ramsami, P.; Oree, V. A hybrid method for forecasting the energy output of photovoltaic systems. Energy Convers. Manag. 2015, 95, 406–413. [Google Scholar] [CrossRef]
- Gupta, S.; Katta, A.R.; Baldaniya, Y.; Kumar, R. Hybrid Random Forest and Particle Swarm Optimization Algorithm for Solar Radiation Prediction. In Proceedings of the 2020 IEEE 5th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 30–31 October 2020; pp. 302–307. [Google Scholar] [CrossRef]
- Travieso-González, C.M.; Cabrera-Quintero, F.; Piñán-Roescher, A.; Celada-Bernal, S. A Review and Evaluation of the State of Art in Image-Based Solar Energy Forecasting: The Methodology and Technology Used. Appl. Sci. 2024, 14, 5605. [Google Scholar] [CrossRef]
- Erdener, B.C.; Feng, C.; Doubleday, K.; Florita, A.; Hodge, B.-M. A review of behind-the-meter solar forecasting. Renew. Sustain. Energy Rev. 2022, 160, 112224. [Google Scholar] [CrossRef]
- Sharma, A.; Kakkar, A. A review on solar forecasting and power management approaches for energy-harvesting wireless sensor networks. Int. J. Commun. Syst. 2020, 33, e4366. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, Y.; Xia, X.; Shi, G. Validation of GFS day-ahead solar irradiance forecasts in China. arXiv 2020, arXiv:2007.01639. [Google Scholar]
- Hill, A.; Massey, A.; Mandallaz, D. The R Package forestinventory: Design-Based Global and Small Area Estimations for Multiphase Forest Inventories. J. Stat. Softw. 2021, 97, 1–40. [Google Scholar] [CrossRef]
- Kuiper, R.M.; Hoijtink, H. A Fortran 90 Program for the Generalized Order-Restricted Information Criterion. J. Stat. Softw. 2013, 54, 1–19. [Google Scholar] [CrossRef]
- Fu, C.-L.; Cheng, H.-Y. Predicting solar irradiance with all-sky image features via regression. Sol. Energy 2013, 97, 537–550. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Reconciling solar forecasts: Sequential reconciliation. Sol. Energy 2019, 179, 391–397. [Google Scholar] [CrossRef]
- Kühn, M.; Nakaten, N.; Streibel, M.; Kempka, T. CO2 Geological Storage and Utilization for a Carbon Neutral “Power-to-gas-to-power” Cycle to Even Out Fluctuations of Renewable Energy Provision. Energy Procedia 2014, 63, 8044–8049. [Google Scholar] [CrossRef]
- Zwane, N.; Tazvinga, H.; Botai, C.; Murambadoro, M.; Botai, J.; de Wit, J.; Mabasa, B.; Daniel, S.; Mabhaudhi, T. A Bibliometric Analysis of Solar Energy Forecasting Studies in Africa. Energies 2022, 15, 5520. [Google Scholar] [CrossRef]
- Yang, C.; Xie, L. A novel ARX-based multi-scale spatio-temporal solar power forecast model. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Tawn, R.; Browell, J. A review of very short-term wind and solar power forecasting. Renew. Sustain. Energy Rev. 2022, 153, 111758. [Google Scholar] [CrossRef]
- Smith, P.F.; Ganesh, S.; Liu, P. A comparison of random forest regression and multiple linear regression for prediction in neuroscience. J. Neurosci. Methods 2013, 220, 85–91. [Google Scholar] [CrossRef]
- Liu, D.; Sun, K. Random forest solar power forecast based on classification optimization. Energy 2019, 187, 115940. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Perpiñán, O.; Marcos, J.; Lorenzo, E. Electrical power fluctuations in a network of DC/AC inverters in a large PV plant: Relationship between correlation, distance and time scale. Sol. Energy 2013, 88, 227–241. [Google Scholar] [CrossRef]
- Klima, K.; Apt, J. Geographic smoothing of solar PV: Results from Gujarat. Environ. Res. Lett. 2015, 10, 104001. [Google Scholar] [CrossRef]
- Perez, R.; David, M.; Hoff, T.E.; Jamaly, M.; Kivalov, S.; Kleissl, J.; Lauret, P.; Perez, M. Spatial and Temporal Variability of Solar Energy. Found. Trends® Renew. Energy 2016, 1, 1–44. [Google Scholar] [CrossRef]
- Marcos, J.; Marroyo, L.; Lorenzo, E.; Alvira, D.; Izco, E. Power output fluctuations in large scale pv plants: One year observations with one second resolution and a derived analytic model: Power Output Fluctuations in Large Scale PV plants. Prog. Photovolt. Res. Appl. 2011, 19, 218–227. [Google Scholar] [CrossRef]
- Mills, A. Understanding Variability and Uncertainty of Photovoltaics for Integration with the Electric Power System; LBNL-2855E; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2019; Available online: https://escholarship.org/uc/item/58z9s527 (accessed on 15 May 2023).
- Arias-Castro, E.; Kleissl, J.; Lave, M. A Poisson model for anisotropic solar ramp rate correlations. Sol. Energy 2014, 101, 192–202. [Google Scholar] [CrossRef]
- Halász, G.; Malachi, Y. Solar energy from Negev desert, Israel: Assessment of power fluctuations for future PV fleet. Energy Sustain. Dev. 2014, 21, 20–29. [Google Scholar] [CrossRef]
- Madeh Piryonesi, S.; El-Diraby, T.E. Using Machine Learning to Examine Impact of Type of Performance Indicator on Flexible Pavement Deterioration Modeling. J. Infrastruct. Syst. 2021, 27, 04021005. [Google Scholar] [CrossRef]
- Didavi, A.B.K.; Agbokpanzo, R.G.; Agbomahena, M. Comparative study of Decision Tree, Random Forest and XGBoost performance in forecasting the power output of a photovoltaic system. In Proceedings of the 2021 4th International Conference on Bio-Engineering for Smart Technologies (BioSMART), Paris/Créteil, France, 8–10 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Grantham, A.; Gel, Y.R.; Boland, J. Nonparametric short-term probabilistic forecasting for solar radiation. Sol. Energy 2016, 133, 465–475. [Google Scholar] [CrossRef]
- Srivastava, R.; Tiwari, A.N.; Giri, V.K. Solar radiation forecasting using MARS, CART, M5, and random forest model: A case study for India. Heliyon 2019, 5, e02692. [Google Scholar] [CrossRef]
- Madanchi, A.; Absalan, M.; Lohmann, G.; Anvari, M.; Reza Rahimi Tabar, M. Strong short-term non-linearity of solar irradiance fluctuations. Sol. Energy 2017, 144, 1–9. [Google Scholar] [CrossRef]
- Woyte, A.; Belmans, R.; Nijs, J. Fluctuations in instantaneous clearness index: Analysis and statistics. Sol. Energy 2007, 81, 195–206. [Google Scholar] [CrossRef]
- Jung, Y.; Jung, J.; Kim, B.; Han, S. Long short-term memory recurrent neural network for modeling temporal patterns in long-term power forecasting for solar PV facilities: Case study of South Korea. J. Clean. Prod. 2020, 250, 119476. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Long short term memory–convolutional neural network based deep hybrid approach for solar irradiance forecasting. Appl. Energy 2021, 295, 117061. [Google Scholar] [CrossRef]
- Kamani, D.; Ardehali, M.M. Long-term forecast of electrical energy consumption with considerations for solar and wind energy sources. Energy 2023, 268, 126617. [Google Scholar] [CrossRef]
- Sopian, K.; Othman, M.Y.H. Estimates of monthly average daily global solar radiation in Malaysia. Renew. Energy 1992, 2, 319–325. [Google Scholar] [CrossRef]
- Kayima, P.; Semakula, H.M.; Wasswa, H.; Mugagga, F.; Mukwaya, P.I. Analysis of the socio-economic benefits of on-grid hybrid solar energy system on Bugala island in Uganda. Energy Sustain. Dev. 2023, 77, 101332. [Google Scholar] [CrossRef]
- Stevović, I.; Mirjanić, D.; Stevović, S. Possibilities for wider investment in solar energy implementation. Energy 2019, 180, 495–510. [Google Scholar] [CrossRef]
- Alkasassbeh, M. Hybrid One-Step Block Fourth Derivative Method for the Direct Solution of Third Order Initial Value Problems of Ordinary Differential Equations. Int. J. Pure Appl. Math. 2018, 119, 207–224. Available online: https://www.academia.edu/79478316/Hybrid_One_Step_Block_Fourth_Derivative_Method_for_the_Direct_Solution_of_Third_Order_Initial_Value_Problems_of_Ordinary_Differential_Equations (accessed on 7 July 2024).
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. [Google Scholar] [CrossRef]
- Kurtgoz, Y.; Deniz, E. Chapter 1.8—Comparison of ANN, Regression Analysis, and ANFIS Models in Estimation of Global Solar Radiation for Different Climatological Locations. In Exergetic, Energetic and Environmental Dimensions; Dincer, I., Colpan, C.O., Kizilkan, O., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 133–148. [Google Scholar] [CrossRef]
- Kumar, D.S.; Maharjan, S.; Albert; Srinivasan, D. Ramp-rate limiting strategies to alleviate the impact of PV power ramping on voltage fluctuations using energy storage systems. Sol. Energy 2022, 234, 377–386. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Said, Y.; Alanazi, A. AI-based solar energy forecasting for smart grid integration. Neural Comput. Appl. 2023, 35, 8625–8634. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Trabea, A.A. Estimation of horizontal diffuse solar radiation in Egypt. Energy Convers. Manag. 2003, 44, 2471–2482. [Google Scholar] [CrossRef]
- Vijayakumar, G.; Kummert, M.; Klein, S.A.; Beckman, W.A. Analysis of short-term solar radiation data. Sol. Energy 2005, 79, 495–504. [Google Scholar] [CrossRef]
- Awachie, I.R.N.; Okeke, C.E. Measurement of solar energy radiation at Nsukka and the determination of the regression coefficients. Energy Convers. Manag. 1988, 28, 295–302. [Google Scholar] [CrossRef]
- Lee, J.C.Y.; Fields, M.J.; Lundquist, J.K. Assessing variability of wind speed: Comparison and validation of 27 methodologies. Wind Energy Sci. 2018, 3, 845–868. [Google Scholar] [CrossRef]
- Unterberger, V.; Lichtenegger, K.; Kaisermayer, V.; Gölles, M.; Horn, M. An adaptive short-term forecasting method for the energy yield of flat-plate solar collector systems. Appl. Energy 2021, 293, 116891. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef]
- Kurtz, B.; Mejia, F.; Kleissl, J. A virtual sky imager testbed for solar energy forecasting. Sol. Energy 2017, 158, 753–759. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, G.N. Estimation of convective mass transfer in solar distillation systems. Sol. Energy 1996, 57, 459–464. [Google Scholar] [CrossRef]
- Teke, A.; Yıldırım, H.B.; Çelik, Ö. Evaluation and performance comparison of different models for the estimation of solar radiation. Renew. Sustain. Energy Rev. 2015, 50, 1097–1107. [Google Scholar] [CrossRef]
- Park, J.-S.; Katagi, T.; Yamamoto, S.; Hashimoto, T. Operation control of photovoltaic/diesel hybrid generating system considering fluctuation of solar radiation. Sol. Energy Mater. Sol. Cells 2001, 67, 535–542. [Google Scholar] [CrossRef]
- Stetz, T.; Von Appen, J.; Niedermeyer, F.; Scheibner, G.; Sikora, R.; Braun, M. Twilight of the Grids: The Impact of Distributed Solar on Germany?s Energy Transition. IEEE Power Energy Mag. 2015, 13, 50–61. [Google Scholar] [CrossRef]
- Suri, M.; Huld, T.; Dunlop, E.; Albuisson, M.; Lefèvre, M.; Wald, L. Uncertainties in solar electricity yield prediction from fluctuation of solar radiation. In Proceedings of the 22nd European Photovoltaic Solar Energy Conference, Milan, Italy, 3–7 September 2007. [Google Scholar]
- Jerez, S.; Tobin, I.; Turco, M.; Jiménez-Guerrero, P.; Vautard, R.; Montávez, J.P. Future changes, or lack thereof, in the temporal variability of the combined wind-plus-solar power production in Europe. Renew. Energy 2019, 139, 251–260. [Google Scholar] [CrossRef]
- Trapero, J.R.; Kourentzes, N.; Martin, A. Short-term solar irradiation forecasting based on Dynamic Harmonic Regression. Energy 2015, 84, 289–295. [Google Scholar] [CrossRef]
- Akuffo, F.O.; Brew-Hammond, A. The frequency distribution of daily global irradiation at Kumasi. Sol. Energy 1993, 50, 145–154. [Google Scholar] [CrossRef]
- Tiba, C.; Ramalho, R.D.; de Souza, J.L.; da Silva, M.A.D.A. Variabilidade da Irradiação Solar em Escala de Minuto no Estado de Alagoas. An. Congr. Bras. De Energ. Sol. CBENS 2016, 1–7. [Google Scholar] [CrossRef]
- Sha, A.; Aiello, M. Topological considerations on peer-to-peer energy exchange and distributed energy generation in the smart grid. Energy Inform. 2020, 3, 8. [Google Scholar] [CrossRef]
- Koudouris, G.; Dimitriadis, P.; Iliopoulou, T.; Mamassis, N.; Koutsoyiannis, D. A stochastic model for the hourly solar radiation process for application in renewable resources management. Adv. Geosci. 2018, 45, 139–145. [Google Scholar] [CrossRef]
- Lam, J.C.; Li, D.H.W. Regression Analysis of Solar Radiation and Sunshine Duration. Archit. Sci. Rev. 1996, 39, 15–23. [Google Scholar] [CrossRef]
- Thaker, J.; Höller, R. A Comparative Study of Time Series Forecasting of Solar Energy Based on Irradiance Classification. Energies 2022, 15, 2837. [Google Scholar] [CrossRef]
- Mucomole, F.V.; Silva, C.A.S.; Magaia, L.L. A Systematic Review on the Accessibility of Spatial and Temporal Variability of Solar Energy Availability on a Short Scale Measurement. Am. J. Energy Nat. Resour. 2024, 3, 60–85. [Google Scholar] [CrossRef]
- Hao, W.; Zhang, H.; Liu, S.; Lai, Y. Design and prediction method of dual working medium solar energy drying system. Appl. Therm. Eng. 2021, 195, 117153. [Google Scholar] [CrossRef]
- Nakayama, K.; Tsuji, M.; Chantana, J.; Kawano, Y.; Nishimura, T.; Hishikawa, Y.; Minemoto, T. Description of short circuit current of outdoor photovoltaic modules by multiple regression analysis under various solar irradiance levels. Renew. Energy 2020, 147, 895–902. [Google Scholar] [CrossRef]
- Younis, S.M.; El-Shakweer, M.H.; El-danasary, M.M.; Gharieb, A.A.; Mourad, R.I. Effect of some factors on water distillation by solar energy. Misr J. Agric. Eng. 2010, 27, 586–599. [Google Scholar] [CrossRef]
- Midilli, A.; Kucuk, H. Mathematical modeling of thin layer drying of pistachio by using solar energy. Energy Convers. Manag. 2003, 44, 1111–1122. [Google Scholar] [CrossRef]
- Lauka, D.; Pakere, I.; Blumberga, D. First solar power plant in Latvia. Analysis of operational data. Energy Procedia 2018, 147, 162–165. [Google Scholar] [CrossRef]
- Li, H.; Jia, H.; Zhong, K.; Zhai, Z. Analysis of factors influencing actual absorption of solar energy by building walls. Energy 2021, 215, 118988. [Google Scholar] [CrossRef]
- Ma, C.; Rogers, A.A.; Kragt, M.E.; Zhang, F.; Polyakov, M.; Gibson, F.; Chalak, M.; Pandit, R.; Tapsuwan, S. Consumers’ willingness to pay for renewable energy: A meta-regression analysis. Resour. Energy Econ. 2015, 42, 93–109. [Google Scholar] [CrossRef]
- Guta, D.D. Determinants of household adoption of solar energy technology in rural Ethiopia. J. Clean. Prod. 2018, 204, 193–204. [Google Scholar] [CrossRef]
- Abdul-Wahab, S.A.; Bakheit, C.S.; Al-Alawi, S.M. Principal component and multiple regression analysis in modelling of ground-level ozone and factors affecting its concentrations. Environ. Model. Softw. 2005, 20, 1263–1271. [Google Scholar] [CrossRef]
- Jamei, M.; Ahmadianfar, I.; Olumegbon, I.A.; Karbasi, M.; Asadi, A. On the assessment of specific heat capacity of nanofluids for solar energy applications: Application of Gaussian process regression (GPR) approach. J. Energy Storage 2021, 33, 102067. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Verma, T.; Tiwana, A.P.S.; Reddy, C.C.; Arora, V.; Devanand, P. Data Analysis to Generate Models Based on Neural Network and Regression for Solar Power Generation Forecasting. In Proceedings of the 2016 7th International Conference on Intelligent Systems, Modelling and Simulation (ISMS), Bangkok, Thailand, 25–27 January 2016; pp. 97–100. [Google Scholar] [CrossRef]
- Alizamir, M.; Kim, S.; Kisi, O.; Zounemat-Kermani, M. A comparative study of several machine learning based non-linear regression methods in estimating solar radiation: Case studies of the USA and Turkey regions. Energy 2020, 197, 117239. [Google Scholar] [CrossRef]
- Rapti, A.S. Atmospheric transparency, atmospheric turbidity and climatic parameters. Sol. Energy 2000, 69, 99–111. [Google Scholar] [CrossRef]
- Salmanoğlu, F.; ÇetiN, N.S. An Approach on Developing a Dynamic Wind-Solar Map for Tracking Electricity Production Potential and Energy Harvest. Gazi Univ. J. Sci. Part Eng. Innov. 2022, 9, 62–78. [Google Scholar] [CrossRef]
- Gomes, C.C.C.; Torres, I.C.; Tiba, C. Taxas de rampas de irradiância e potência. In CIES2020-XVII Congresso Ibérico e XIII Congresso Ibero-Americano de Energia Solar; LNEG—Laboratório Nacional de Energia e Geologia: Lisboa, Portugal, 2020; pp. 927–934. [Google Scholar] [CrossRef]
- Siebentritt, S. What limits the efficiency of chalcopyrite solar cells? Sol. Energy Mater. Sol. Cells 2011, 95, 1471–1476. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. A Novel Approach for Ramp-Rate Control of Solar PV Using Energy Storage to Mitigate Output Fluctuations Caused by Cloud Passing. IEEE Trans. Energy Convers. 2014, 29, 507–518. [Google Scholar] [CrossRef]
- Hofer, T.; Madlener, R. Locational (In)Efficiency of Renewable Energy Feed-In into the Electricity Grid: A Spatial Regression Analysis. Energy J. 2021, 42, 171–196. [Google Scholar] [CrossRef]
- Güçlü, Y.S.; Dabanlı, İ.; Şişman, E.; Şen, Z. HARmonic–LINear (HarLin) model for solar irradiation estimation. Renew. Energy 2015, 81, 209–218. [Google Scholar] [CrossRef]
- Quoc Hung, D.; Mishra, Y. Voltage fluctuation mitigation: Fast allocation and daily local control of DSTATCOMs to increase solar energy harvest. IET Renew. Power Gener. 2019, 13, 2558–2568. [Google Scholar] [CrossRef]
- Kawasaki, N.; Oozeki, T.; Otani, K.; Kurokawa, K. An evaluation method of the fluctuation characteristics of photovoltaic systems by using frequency analysis. Sol. Energy Mater. Sol. Cells 2006, 90, 3356–3363. [Google Scholar] [CrossRef]
- de Freitas Viscondi, G.; Alves-Souza, S.N. A Systematic Literature Review on big data for solar photovoltaic electricity generation forecasting. Sustain. Energy Technol. Assess. 2019, 31, 54–63. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J.; Nazarko, Ł.; Rabayah, H.S.; Abendeh, R.M.; Alawneh, R. ARIMA Models in Solar Radiation Forecasting in Different Geographic Locations. Energies 2023, 16, 5029. [Google Scholar] [CrossRef]
- Lee, J.; Hsu, N.C.; Bettenhausen, C.; Sayer, A.M. Retrieval of aerosol optical depth under thin cirrus from MODIS: Application to an ocean algorithm. J. Geophys. Res. Atmos. 2013, 118, 10111–10124. [Google Scholar] [CrossRef]
- UEM-Eduardo Mondlane University. Department of Physics-Solar Energy Data Source [Online]. 2023. Available online: https://uem.mz/index.php/en/home-english/ (accessed on 9 December 2023).





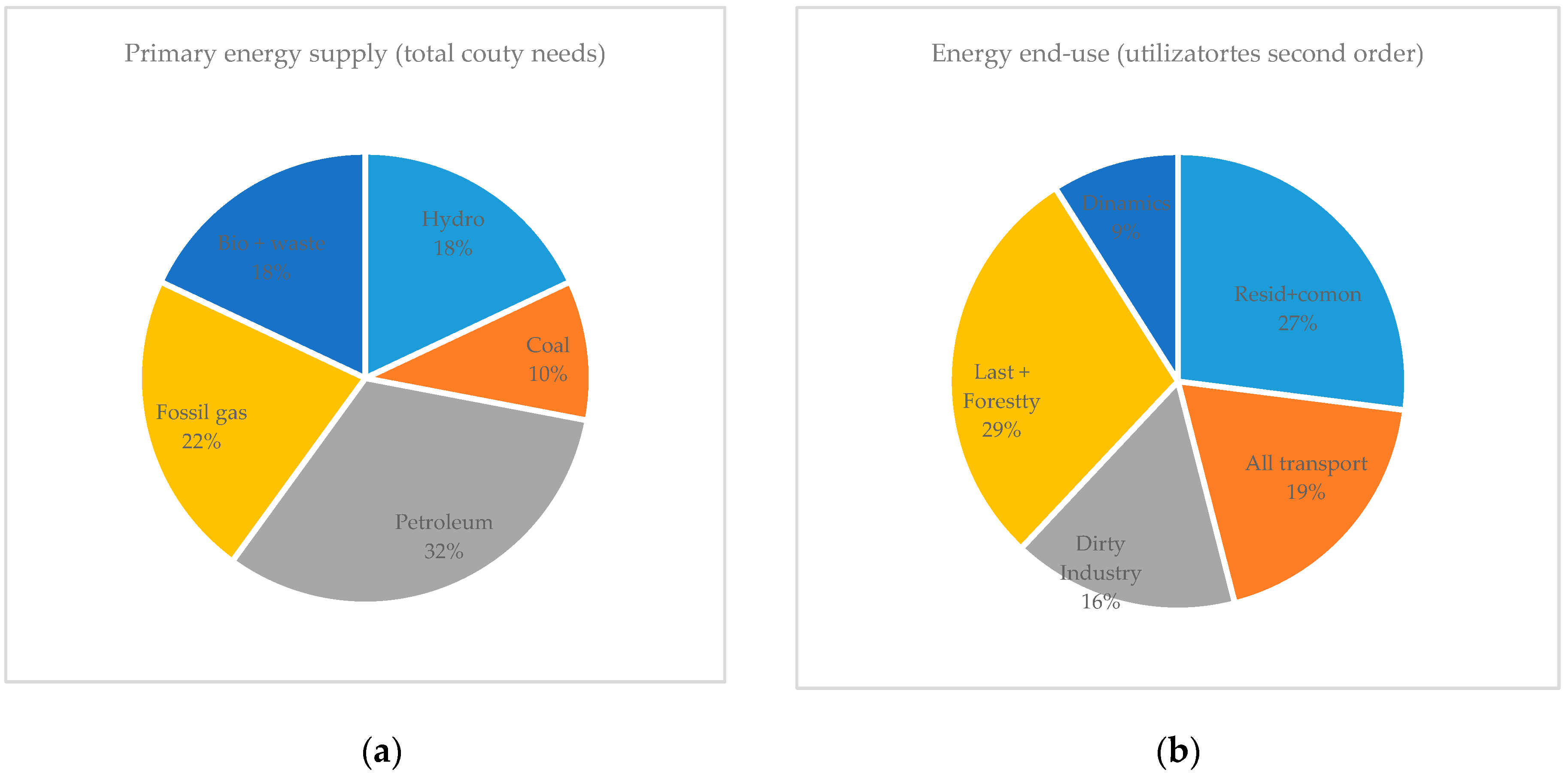




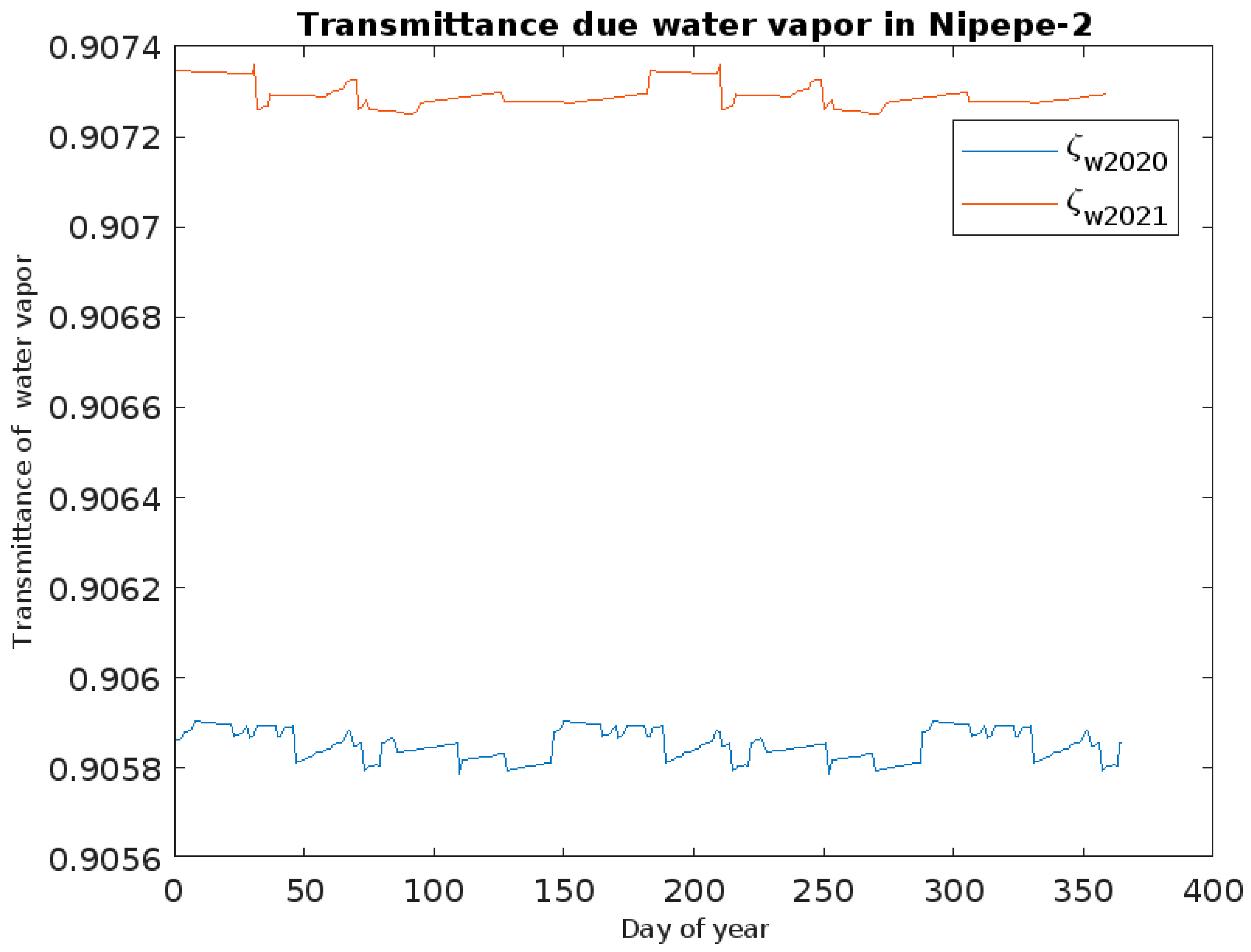

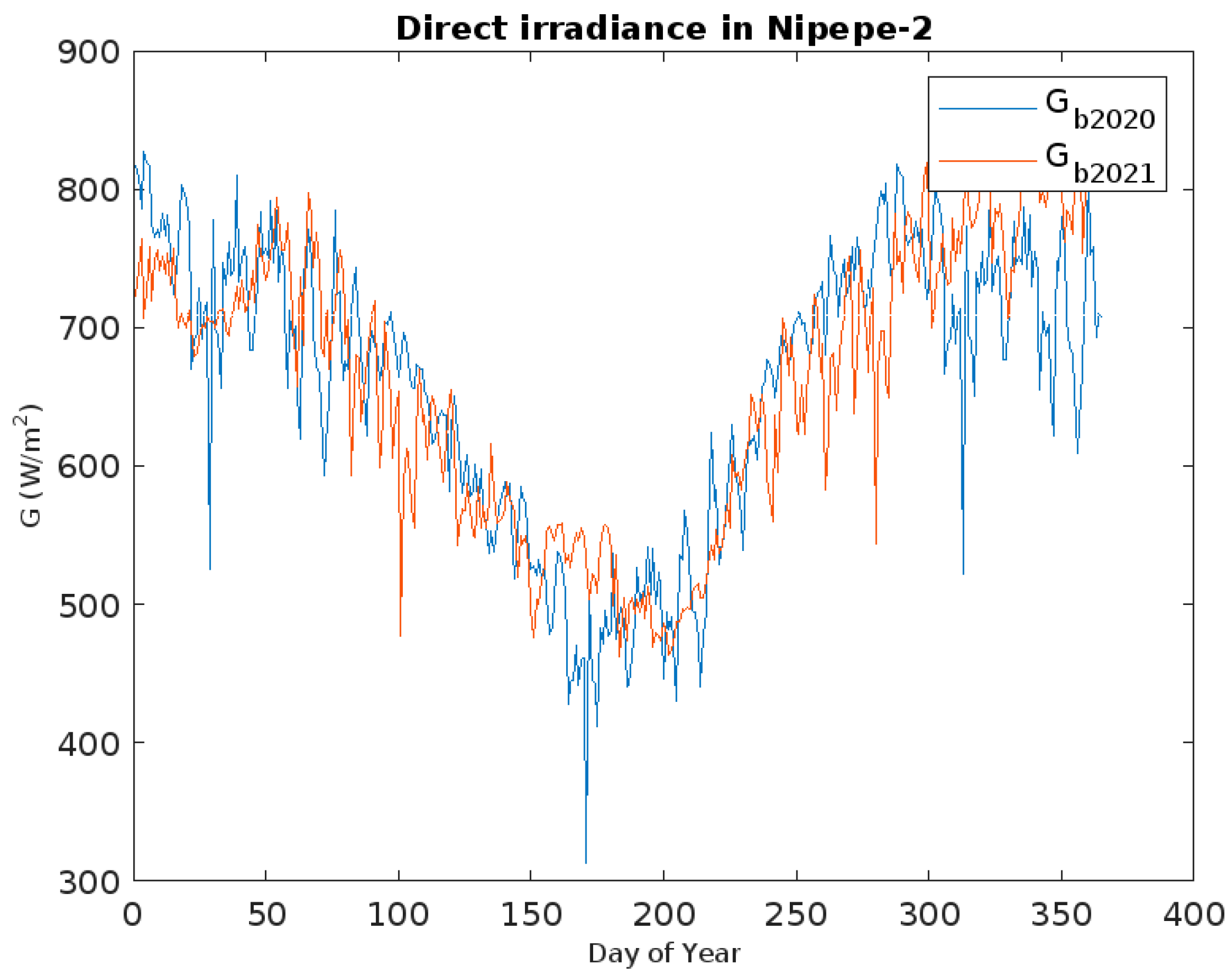
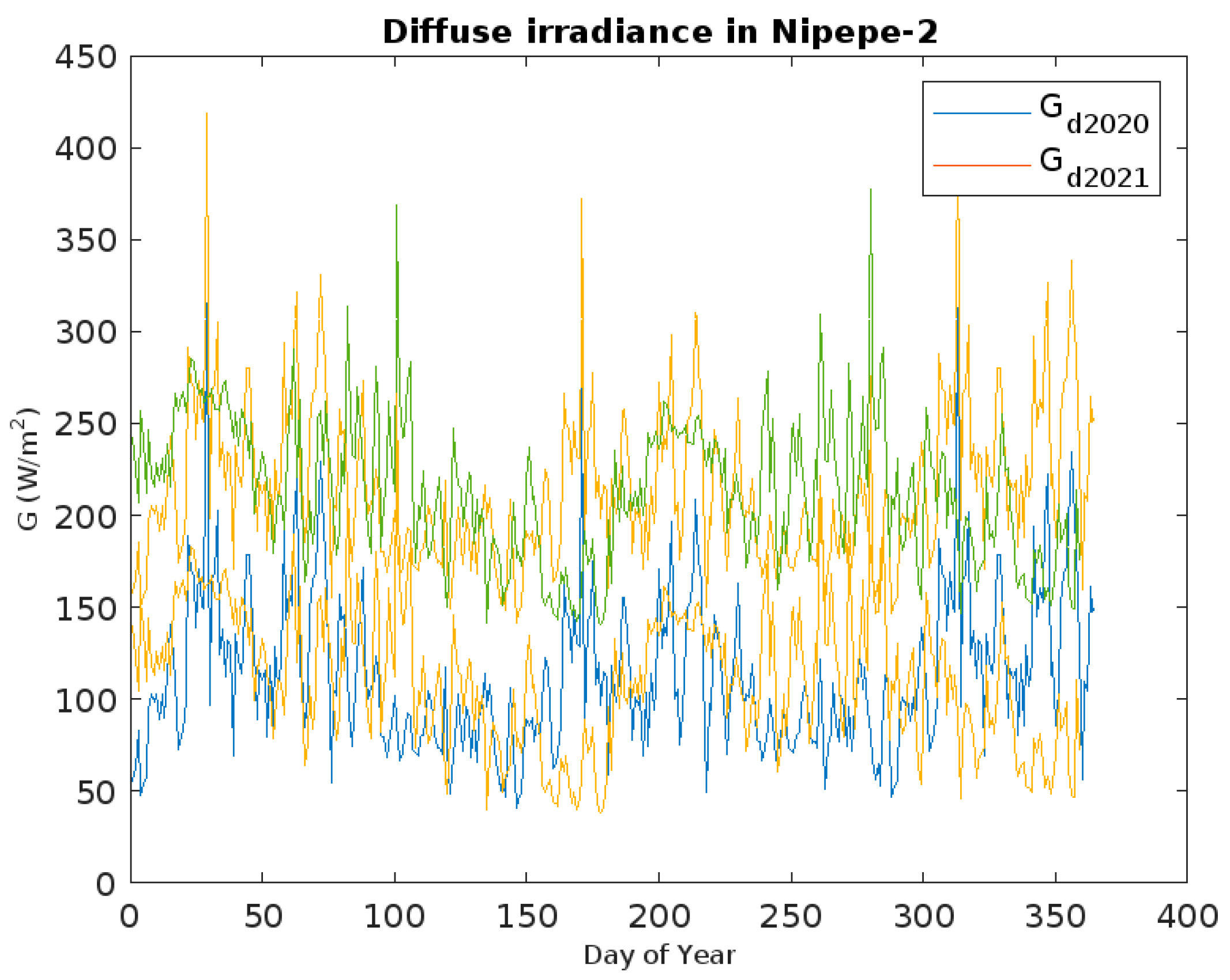




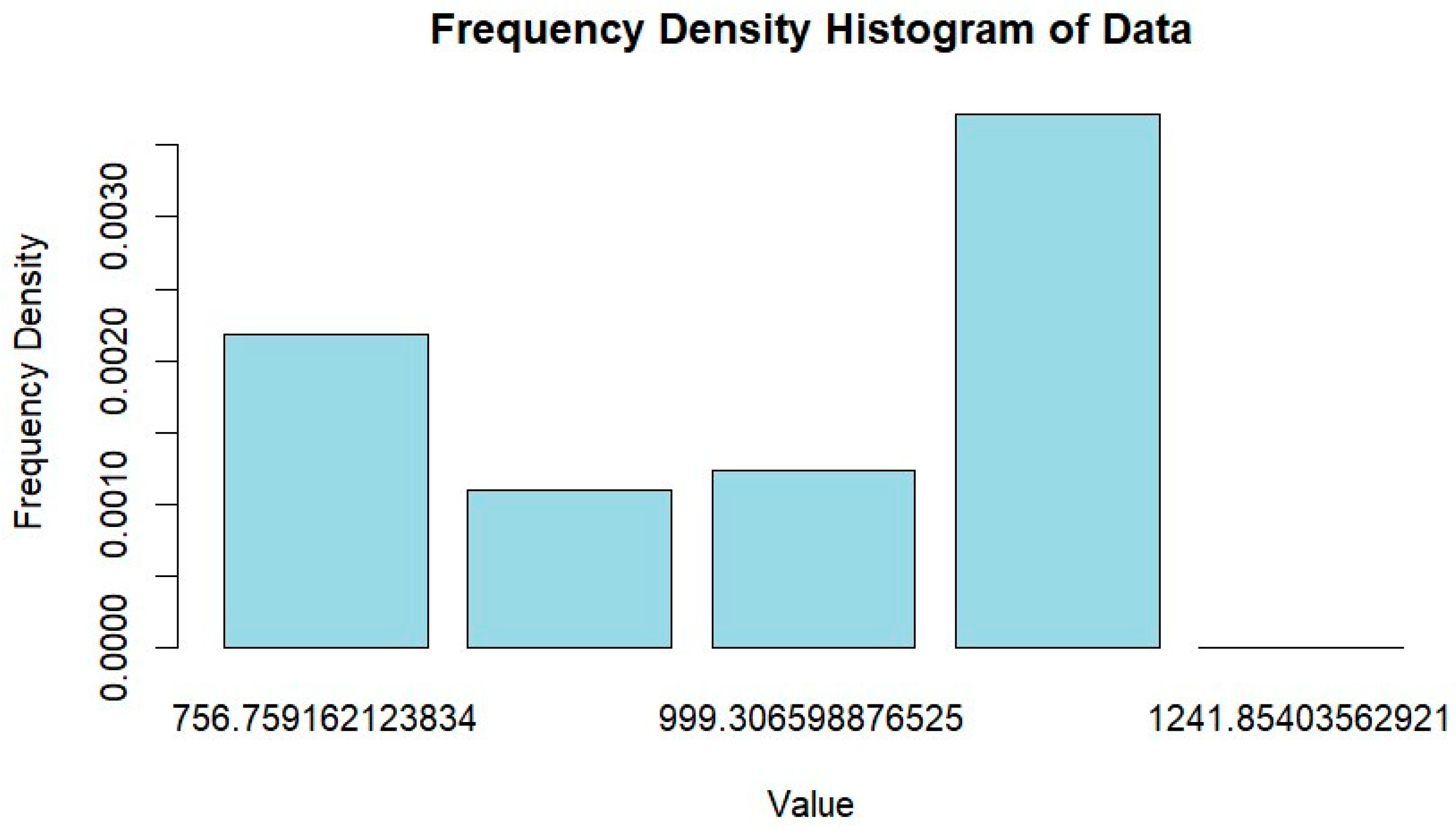
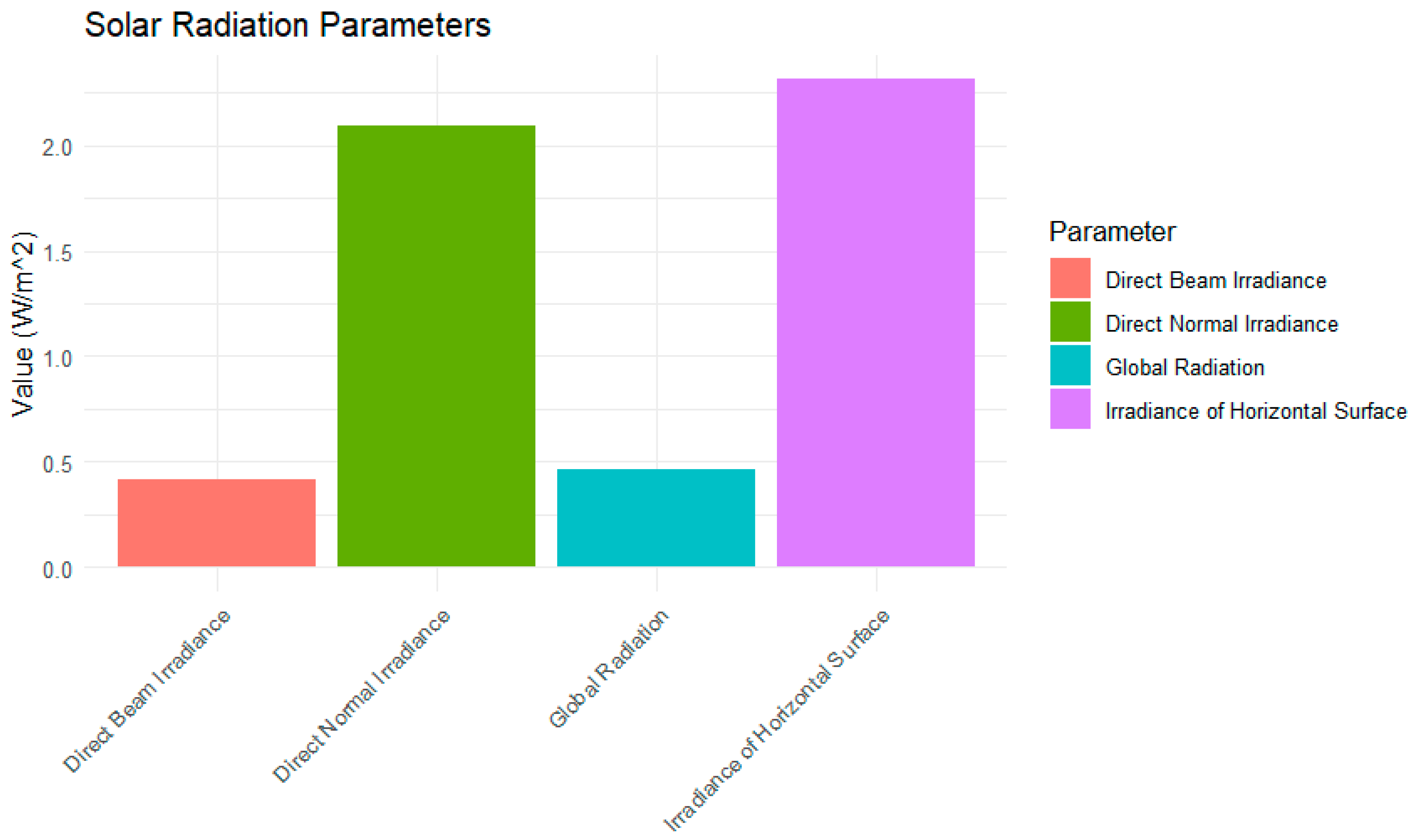

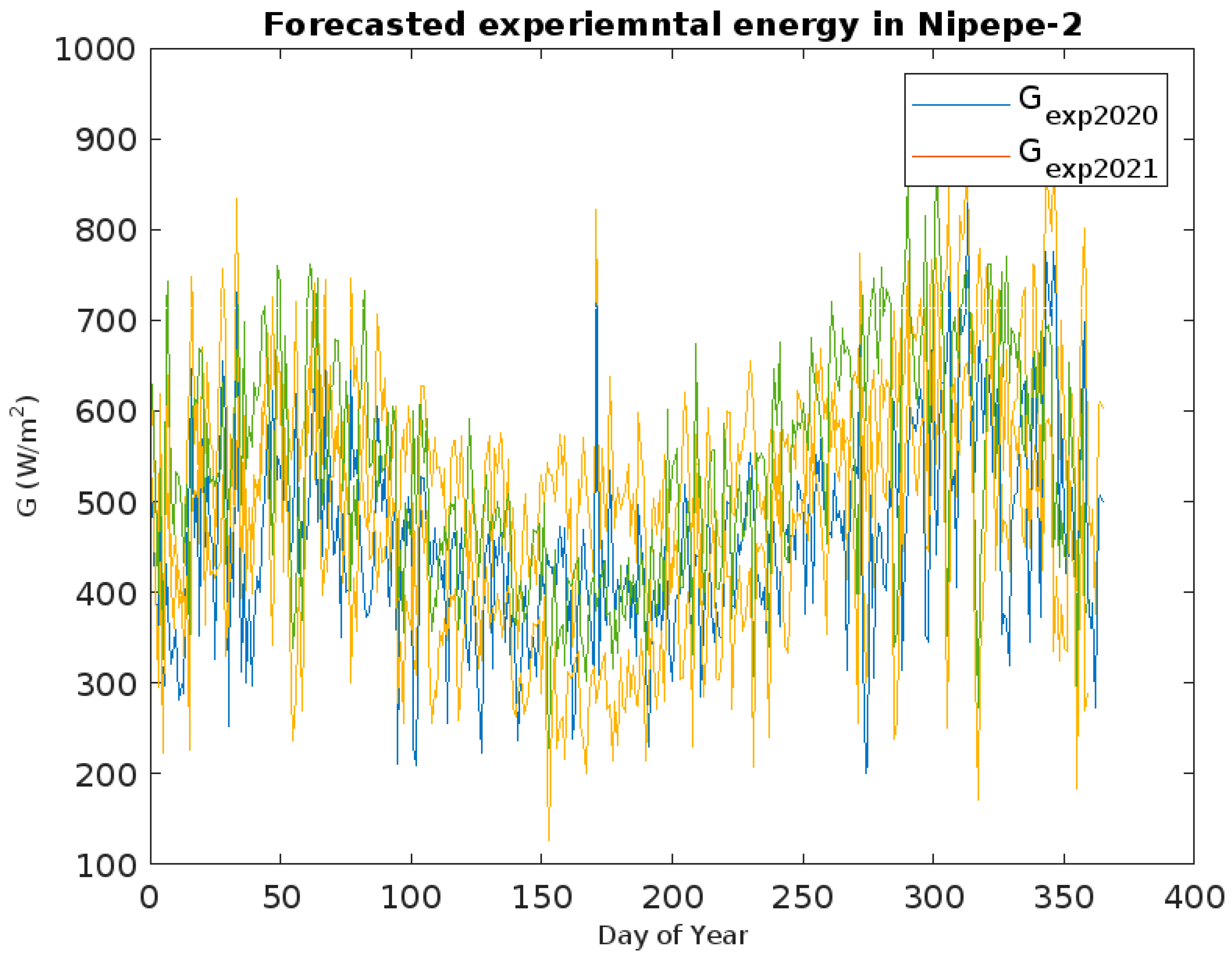
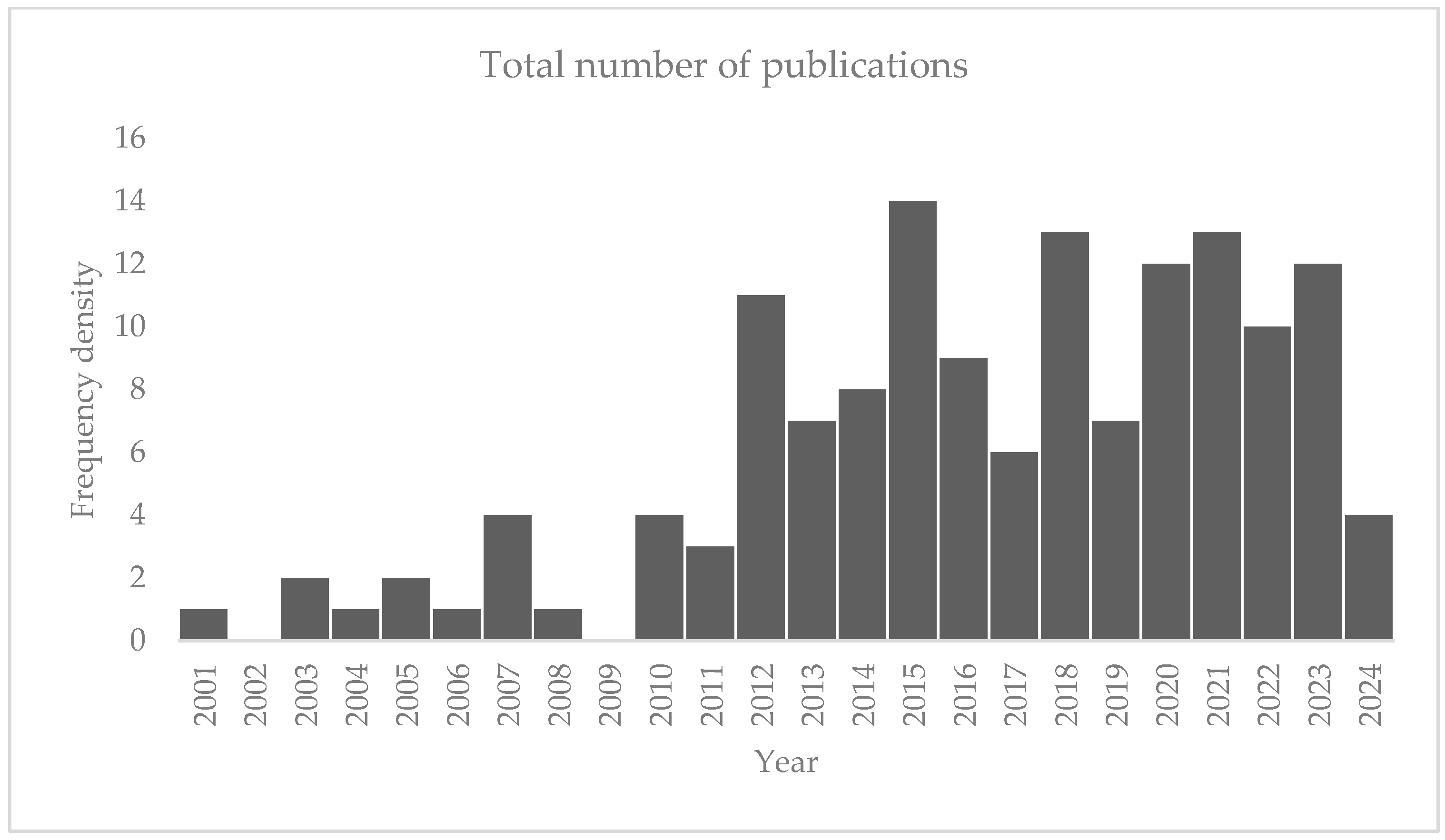

| ID | Station | Province | Tower | Code | Long (X) | Lat (Y) | Altitude | ||
| MZ25 | MZ25_Nipepe | Niassa | TDM | TDM | 35°26′12.82″ E | 13°54′25.93″ S | 60 | ||
| ID | Station | Province | Tower | λ (nm) | Amplitude | Level | Long (X) | Lat (Y) | Altitude |
| 1_A | Niassa | Niassa | AERONET | 400–500 | 4″, 1/24 H | 2.0 | 37.5665 | −12.155 | 510 |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Benghanem & Joraid, 2016) [7] | GHI in sitio | 1 | A multiple correlation between different solar parameters | 653,801 | 0.00028–1 | 2016 | France | Seasoned | Not esteemed |
| (Ramirez-Vergara et al., 2021) [11] | GHI | 24 | Ambient temperature and solar irradiance forecasting | 9,597,012 | 0.00028–1 | 2021 | China | Continental | Not estimated |
| (ousif, et al., 2019) [27] | GHI | 1 | Analysis and forecasting of weather | 522,448 | 0.00028–1 | 2019 | Oman | Continental | Not estimated |
| (Mellit & Pavan, 2010) [32] | GHI in sitio | 24 | A 24-h forecast of solar irradiance using ANN | 2,022,175 | 1 | 2020 | Italy | Continental | Not estimated |
| (Wen et al., 2023) [35] | GHI in sitio | 0.017, 24, 8760 | A regional solar forecasting approach | 5,557,443 | 0.00028–1 | 2023 | China | Continental | 10.93 ± 2.35% |
| (Breitkreuz et al., 2009) [36] | AOD, GHI in sitio | 0.083 | Solar energy forecast basing in different MLM and input | 1,504,228 | 0.00028 | 2007 | Germany | Oceanic temperate | +28 W/m2 (+12%) and (−19 W/m2 or −14%) (on average+9 W/m2 or +2%). |
| (Blaga et al., 2019) [38] | GHI in sitio | 1 | Accuracy of solar energy forecasting | 426,112 | 1 | 2019 | Spain | Mediterranean | Not estimated |
| (Nam & Hur, 2019) [39] | GHI | 1 | Generating resources for grid integration | 1,001,429 | 0.00028–1 | 2019 | Korea | Continental | Not estimated |
| (Kumler et al., 2018) [40] | GHI in sitio, atmospheric | 1 | A Physics-based for Intra-hour forecasting | 6,569,201 | 0.00028–1 | 2018 | USA | Subtropical | Not estimated |
| (Aler et al., 2015) [41] | GHI | 1 | MLM for Daily Solar Energy Forecasting | 5,809,722 | 0.00028–1 | 2015 | Netherlands | Continental | Not estimated |
| (Dhillon et al., 2020) [42] | GHI | 1 | ANN for Prediction of Power for Wireless | 4,422,112 | 0.00028–1 | 2020 | South Africa | Tropical | Not estimated |
| (McCandless & Jiménez, 2020) [45] | GHI in sitio | 0.25 and 3 | A model tree approach to forecasting | 5,010,008 | 1 | 2020 | USA | Subtropical | Not estimated |
| (Wang et al., 2015) [59] | Wind, GHI | 1 | Wind, solar, and electrical load forecasting methods | 2,489,426 | 0.00028–1 | 2022 | China | Continental | Not estimated |
| (Ghayekhloo et al., 2015) [73] | GHI in sitio | 24 | A novel clustering approach for short-term | 2,477,108 | 24 | 2015 | USA | Subtropical | Not estimated |
| (Dahmani et al., 2016) [106] | GHI in situ and Satellite | 1 and 0.083 | Estimating 5-min and hourly GHI | 1,244,167 | 0.083 | 2015 | Algeria | Arid to semi-arid | nRMSE = 13.90%, nRMSE igual a 19.35% e 18.65%. |
| (Sridharan, 2023) [107] | GHI in sitio | 1 | Generalized Regression Neural Network Model | 3,287,000 | 1 | 2023 | India | Monsoon tropical | GRNN, fuzzy logic and ANN are 3.55%, 4.64%, and 5.49% |
| (Flocas, 1980) [108] | GHI in sitio | 1 | Estimation and prediction GHI Greece | 131,957 | 1 | 2012 | Greece | Mediterranean | Not estimated |
| (Panamtash et al., 2020b) [109] | GHI in sitio | 1 | Probabilistic solar power forecasting | 1,356,254 | 0.00028–1 | 2020 | Germany | Oceanic temperate | Not estimated |
| (H. Sun et al., 2016) [110] | GHI in sitio | 1 | A Green Energy Application | 5,255,033 | 24 | 2016 | South Africa | Tropical | Not estimated |
| (Kuo & Huang, 2018) [111] | GHI in sitio | 1 | MLM in Solar PV Energy | 1,106,048 | 0.00028–1 | 208 | Netherlands | Continental | Not estimated |
| (Mathiesen et al., 2013) [112] | GHI in sitio | 1 | A high-resolution, cloud-assimilating | 8,146,426 | 1 | 2013 | USA | Subtropical | Not esteemed |
| (Devaraj et al., 2021) [113] | GHI in sitio | 1 | Energy forecasting using big data | 3,001,569 | 24 | 2021 | USA | Subtropical | Not esteemed |
| (Ramsami & Oree, 2015) [114] | GHI in sitio | 24 | A hybrid method for forecasting the energy | 7,222,109 | 0.00028–1 | 2015 | China | Continental | Not estimated |
| (S. Gupta et al., 2020) [115] | GHI | 1 | Evaluation of solar forecasting technologies | 2,459,000 | 1 | 2020 | India | Subtropical | Not estimated |
| (Travieso-González et al., 2024) [116] | GHI | 1 | Solar energy forecasting using machine learning models | 2,436,008 | 24 | 2024 | Romania | Subtropical | Not estimated |
| (Erdener et al., 2022) [117] | GHI | 24 | A review of behind-the-meter solar forecasting | 6,114,644 | 0.00028–1 | 2022 | USA | Subtropical | Not estimated |
| (Sharma & Kakkar, 2020) [118] | GHI | 1 | Management approaches for energy-harvesting | 723,008 | 1 | 2020 | Germany | Oceanic temperate | Not estimated |
| (Y. Zhang et al., 2011) [119] | GHI | 1 | Validation of GFS day-ahead solar irradiance | 1,897,445 | 24 | 2011 | China | Mediterranean | Not estimated |
| Source | Data Source | Resolution (h) | Contribution | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Gutierrez-Corea et al., 2014) [58] | GHI in sitio and satellite | 0.25 | Spatial estimation of GHI | 506,030 | 1 | 2014 | Spain | Mediterranean | 67% of stations (average ±2STD.) |
| (Barhmi et al., 2024) [98] | GHI | 1 | Solar Forecasting Techniques | 9856 | 0.00028–1 | 2024 | The Netherlands | Continental | Not estimated |
| (Kühn et al., 2014) [124] | GHI (in sitio), wind | 1 | Fluctuations in renewable energy supply | 357,592 | 0.00028–1 | 2014 | Germany | Oceanic temperate | Not esteemed |
| (Zwane et al., 2022) [125] | GHI in sitio | 24 | Solar Energy Forecasting | 8825 | 24 | 2022 | South Africa | Tropical | Not estimated |
| (C. Yang & Xie, 2012) [126] | GHI | 1 | Solar forecasting, its dependence | 285 | 0.00028–1 | 2012 | USA | Subtropical | Not estimated |
| (Tawn & Browell, 2022) [127] | GHI | 1 | Short-term wind, solar forecasting | 84,789 | 0.00028–1 | 2022 | France | Seasoned | Not estimated |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Babar et al., 2020) [2] | GHI in situ and satellite, Cloud, Albedo | 0.083 | Mapping of solar radiation in high latitudes. | 385,207 | 1 | 2020 | Norway | Oceanic, continental, | RMSD—17.9, 27.1 Wm−2; RMSD—16.2; MAD—10.8, |
| (Cerralbo et al., 2015) [52] | GHI (in sitio) | 0.0000028 | Wind variability in a coastal area | 643,801 | 1–24 | 2015 | Alfacs Bay | Seasoned | Not esteemed |
| (Mei et al., 2014) [76] | GHI (in sitio) | 0.0056 | Retrieval of aerosol optical depth | 4,851,699.4 | 1–24 | 2013 | USA | Subtropical | Not esteemed |
| (Zhang et al., 2011) [80] | GHI (in sitio) | 1–24 | A multi-angle aerosol optical depth retrieval | 9,970,610 | 1–24 | 2011 | Canada | Seasoned | Not esteemed |
| (Pedro et al., 2012) [81] | GHI (in sitio) | 0.0000028 | Assessment of forecasting techniques for solar power | 2,057,777 | 1–24 | 2012 | Mexico | Seasoned | Not esteemed |
| (Krishnan et al., 2023) [84] | GHI (in sitio) | 0.17 | Solar radiation forecasting impacts | 885,156 | 1–24 | 2023 | Brazil | Tropical | Not esteemed |
| (Badescu & Budea, 2016) [87] | GHI (in sitio) | 0.017 | Significant is the stability of the radiative regime | 9,597,000 | 1–24 | 2016 | China | Continental | Not esteemed |
| (Perpiñán et al., 2013) [131] | GHI (in sitio) | 0.017 | Urban rooftop PV systems &fluctuation | 17,900,000 | 1–24 | 2014 | Netherlands | Seasoned | Not esteemed |
| (Klima & Apt, 2015) [132] | GHI (in sitio) | 0.0000028 | Geographic solar PV smoothing | 4,851,699 | 124 | 2015 | USA | Subtropical | Not esteemed |
| (Perez et al., 2016) [133] | GHI (in sitio) | 0.000028 | Spatial and Temporal Variability of GHI | 6001.5621 | 124 | 2016 | USA | Subtropical | Not esteemed |
| (Marcos et al., 2011) [134] | GHI (in sitio) | 0.00028 | Power fluctuations: the PV plant/filter | 506,030 | 1–24 | 2022 | Spain | Medi terrain | Not esteemed |
| (Mills, 2011) [135] | GHI (in sitio) | 0.017 | Variability GHI Wide-Area Geographic | 4,851,699 | 1–24 | 2011 | USA | Subtropical | Not esteemed |
| (Arias-Castro et al., 2014) [136] | GHI (in sitio) | 0.017 | Anisotropic solar ramp rate correlations | 4,851,699 | 1–24 | 2014 | USA | Subtropical | Not esteemed |
| (Halász & Malachi, 2014) [137] | GHI (in sitio) | 0.017 | Assessment of PV power fluctuations | 20,720 | 0.017–24 | 2014 | Israel | Temperate a tropical | Not esteemed |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Tsai et al., 2017) [4] | GHI in sitio | 1 | Models for forecasting growth trends in renewable energy | 9,597,000 | 1 | 2017 | China | Continental | NGMB(1,1) highest GM(1,1) |
| (Smith et al., 2013) [128] | GHI (in sitio), wind | 1 | A comparison of random forest regression | 357,592 | 0.00028–1 | 2013 | Germany | Oceanic temperate | Not esteemed |
| (Liu & Sun, 2019) [129] | GHI (in sitio) | 0.00028, 0.083 | Random forest solar power forecast | 18 | 1 | 2019 | USA | Tropical | Not esteemed |
| (Madanchi et al., 2017) [142] | GHI (in sitio) | 0.000028, 0.00028, 0.017 | Strong nonlinearity of GHI fluctuations | 562,500 | 0.0000028–0.017 | 2017 | Several countries | Moderate | Not esteemed |
| (Woyte et al., 2007) [143] | GHI (in sitio) | 0.00139 | Fluctuations in the instant clarity index | 310,500 | 0.0019–24 | 2007 | Belgium, German, Australia | Moderate maritime, moderate | Not esteemed |
| (Kumari & D. Toshniwal, 2021) [145] | GHI (in sitio) | 0.0167 | Long short term memory–convolutional | 4,851,699 | 1–24 | 2021 | USA | Subtropical | Not esteemed |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Sopian & Othman, 1992) [147] | GHI in sitio | 1 | Estimates of monthly and daily GHI Malaysia | 330,803 | 1 | 2012 | Malaysia | Equatorial | Not estimated |
| (Kayima et al., 2023) [148] | GHI (in sitio) | 1 | Socio-economic benefits of on-grid hybrid solar | 241,038 | 1 | 2023 | Uganda | Equatorial, hot and humid | Coef. = 1.73, 1.25, 1.03, increased access ∼1.26–1.77, 1.38 |
| (Stevović et al., 2019) [149] | GHI in sitio | 1 | Possibilities for wider investment in solar | 8,510,000 | 1 | 2019 | 28 EU countries and Serbia | Tropical | Not esteemed |
| (Alkasassbeh, 2018) [150] | GHI | 1 | Taxonomy of wind and solar energy forecasting | 4,851,699 | 24 | 2018 | Saudi Arabia | Tropical | Not estimated |
| (Aslam et al., 2021) [151] | GHI | 1 | Deep learning methods for power load | 4,851,699 | 0.00028–1 | 2021 | Singapore | Humid tropical | Not estimated |
| (Kurtgoz & Deniz, 2018) [152] | GHI | 1 | A virtual sky imager testbed forecasting | 5,891,699 | 8760 | 2018 | USA | Subtropical | Not estimated |
| (Lee et al., 2018.) [159] | GHI and clear sky | 0.083 | Assessing variability of wind speed | 5,852,589 | 0.00028–1 | 2018 | Singapore | Humid tropical | Not estimated |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Ayet & Tandeo, 2018) [97] | GHI Satellite | 6 | Nowcasting solar irradiance | 643,801 | 1–24 | 2018 | France | Seasoned | Not esteemed |
| (Nielsen et al., 2012) [100] | GHI (in sitio), wind | 0.33 | PV Power Fluctuations Neural Networks and Deep Learning | 506,030 | 0.00028–0.33 | 2012 | Spain | Mediterranean | Not esteemed |
| (Pizarroso et al., 2022) [101] | GHI Satellite | 1 | Variability Sensitivity Analysis | 3,287,263 | 1–24 | 2021 | Indian | Monsoon tropical | Not esteemed |
| (D. S. Kumar et al., 2022) [153] | GHI (in sitio) | 1 | PV Ramp Rate Limiting Strategies | 734.3 | 124 | 2022 | Singapore | Humid tropical | Not esteemed |
| (Deo et al., 2016) [154] | GHI | 1 | SVM for forecasting GHI incident | 32,527,263 | 0.00028–1 | 2016 | Australia | Tropical Atlantic | Not estimated |
| (Said & Alanazi, 2023) [155] | GHI | 1 | AI-based solar energy forecasting for grid | 3,287,263 | 0.00028–1 | 2023 | Brazil | Tropical | Not esteemed |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Zhang et al., 2015) [23] | GHI | 1 | A suite of metrics for assessing the performance | 5,833,697.1 | 0.00028–1 | 2015 | Japan | Oceanic temperate | Not estimated |
| (Ramirez Camargo et al., 2015) [43] | GHI | 1 | Forecasting prediction horizon sensitivity a | 5,859,699 | 0.00028–1 | 2015 | USA | Mediterranean | Not estimated |
| (Arslan et al., 2020) [67] | GHI | 1 | Wind speed variability and wind power potential | 5,891,659.4 | 1 | 2020 | France | Seasoned | Not esteemed |
| (El-Sebaii & Trabea, 2003) [156] | GHI in sitio | 1 | Estimation of horizontal diffuse solar radiation | 1,002,001 | 1 | 2023 | Egypt | Tropical | Not esteemed |
| (Vijayakumar et al., 2005) [157] | GHI in sitio | 1 | Analysis of short-term solar radiation data | 4,851,699 | 1 | 2005 | USA | Subtropical | Not esteemed |
| (Awachie & Okeke, 1988) [158] | GHI in sitio and isolation | 1 | Measurement of solar energy radiation | 5545 | 1 | 2012 | Nigeria, Nsukka | Tropical | 0.21 and 0.51 with 0.7% |
| (J. C. Y. Lee et al., 2018) [159] | GHI | 1 | Solar Power Generation Forecast Model | 7,856,698 | 0.00028–1 | 2018 | Brazil | Tropical Atlantic | Not esteemed |
| (Unterberger et al., 2021) [160] | GHI | 1 | Energy yield of flat-plate solar collector systems | 5,871,222.7 | 0.00028–1 | 2021 | Brazil | Tropical Atlantic | Not estimated |
| (Alessandrini et al., 2015) [161] | GHI | 1 | Forecasting daily total solar-radiation | 7,468,698.2 | 0.00028–1 | 2015 | Germany | Oceanic temperate | Not estimated |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error |
|---|---|---|---|---|---|---|---|---|---|
| (Mucomole et al., 2024) [6] | GHI, wind | 1 | Regressive and Spatiotemporal Accessibility | 506,030 | 1–24 | 2024 | Mozambique | Tropical | RMSE 21% |
| (Mucomole et al., 2023a) [25] | GHI in sitio | 0.017 and 0.16 | Temporal Variability of Solar Energy | 801,590 | 0.167 | 2023 | Mozambique | Tropical | RMSE 30% |
| (Qing & Niu, 2018) [28] | GHI (in sitio) | 1 | Hourly day-ahead solar irradiance | 281,748 | 1–24 | 2088 | Brazil | Tropical Atlantic | Not estimated |
| (Hoff & Perez, 2010) [55] | GHI in sitio | 1 | Quantifying PV power Output Variability | 92,644 | 1 | 2010 | USA | Subtropical | Not esteemed |
| (Chen et al., 2023) [88] | GHI (in sitio) wind | 24 | Big data analysis of PV power fluctuation | 9,597,000 | 1–24 | 2023 | China | Continental | Not estimated |
| (S. Kumar & Tiwari, 1996) [163] | GHI in sitio | 1 | Estimation of convective mass transfer in solar | 3,287,015 | 1 | 2012 | India | Monsoon tropical | C = 0.0322; n = 0.4114 for 8 × 106 in an active solar still. |
| (Teke et al., 2015) [164] | GHI in sitio | 1 | Estimation of solar radiation | 83,562 | 1 | 2015 | Turkey | Mediterranean, Continental, Semi-arid | Not esteemed |
| (Park et al., 2001) [165] | GHI (in sitio) | 1 | Hybrid PV System Operation Control | 377,973 | 1–24 | 2001 | Japan | Oceanic temperate | Not estimated |
| (Stetz et al., 2015) [166] | GHI | 1 | The Impact of Solar on Germany’s Energy | 357,592 | 1–24 | 2015 | Germany | Oceanic temperate | Not estimated |
| (Suri et al., 2007) [167] | GHI | 1 | Solar electricity GHI prediction fluctuation | 442,569 | 1–24 | 2007 | France | Seasoned | Not estimated |
| (Jerez et al., 2019) [168] | GHI and wind | 1 | Future temporal variability PV Europe. | 8760 | 1–24 | 2019 | Spain | Mediterranean | Not estimated |
| (Trapero et al., 2015) [169] | GHI (in sitio) | 1 | Short-Term Solar Irradiation Forecast | 506,030 | 1 | 2015 | Spain | Mediterranean | Not estimated |
| (Akuffo & Brew-Hammond, 1993) [170] | GHI (in sitio) | 24 | Establishing frequency distribution | 238,535 | 24 | 2003 | Gana | Tropical | Not estimated |
| (Tiba et al., 2016) [171] | GHI (in sitio) | 0.017–3 | variability of solar irradiation (minute) | 27,843,295 | 0.0167–3 | 2016 | Brazil | Tropical Atlantic | Not estimated |
| (Sha & Aiello, 2020) [172] | GHI (in sitio) | 0.017 | Decentralized Energy Exchange Smart Grid. | 17,900,145 | 1–24 | 2018 | Netherlands | Oceanic temperate | Not estimated |
| (Koudouris et al., 2018) [173] | GHI (in sitio) | 1 | GHI process for renewable manage | 131,957 | 1–24 | 2018 | Greece | Mediterranean | Not estimated |
| (Lam & Li, 1996) [174] | GHI in sitio | 1 | Regression Analysis of Solar Radiation | 9,597,000 | 131,400 | 2011 | China | Continental | Not esteemed |
| (Thaker & Höller, 2022) [175] | GHII | 1 | Time Series Forecasting of Solar Energy | 249,951 | 1 | 2022 | Germany | Oceanic temperate | Not esteemed |
| (Mucomole et al., 2024b) [176] | GHI | 1 | Accessibility of Spatial and Temporal Solar | 281,948 | 1 | 2024 | Mozambique | Tropical | Not estimated |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Error Assumption |
|---|---|---|---|---|---|---|---|---|---|
| (Funk & Larson, 1998) [13] | GHI, temperature and charge | 1 | Parametric model of solar cooker | 4,851,699.4 | 1 | 2012 | USA | Subtropical | Coeficient of heat |
| (Jebli et al., 2021) [20] | DHI | 1 | Prediction of diffuse solar | 9,597,000 | 1 | 2016 | China | Continental | Not esteemed |
| (Jung et al., 2016) [21] | DHI | 1 | Spatiotemporal Characteristics in the Clearness | 6,025,321 | 1 | 2016 | China | Continental | Not esteemed |
| (Adedeji et al., 2020) [29] | GHI in sitio | 1 | Resource forecast in site suitability assessment for wind and solar energy | 3,287,129 | 1 | 2023 | India | Monsoon tropical | GRNN, fuzzy logic and ANN are 3.55%, 4.64%, and 5.49% |
| (Arumugham & Rajendran, 2021) [49] | irradiance, weather and solar angle | 0.17 | Modeling global solar irradiance | 9,597,000 | 0.17 | 2021 | Several locations | Continental | Not estimated |
| (Mustafa & Malik, 2023) [90] | GHI in sitio | 1 | Analysis through a MLR, and Decision Support | 881,913 | 1 | 2023 | Pakistan | Subtropical | Not esteemed |
| (Hao et al., 2021) [177] | GHI in sitio, temperature | 1 | Design and prediction method of dual | 9,597,000 | 1 | 2021 | China | Continental | R2 of 0.98 and 0.94 |
| (Nakayama et al., 2020) [178] | GHI in sitio, PV Power | 1 | Description of short circuit current outdoor | 377,975 | 1 | 2020 | Japan | Temperate oceanic | ≥0.5 kW/m2 (on sunny day) |
| (Younis et al., 2010) [179] | GHI in sitio | 1 | effect of some factors on water distillation b | 1,002,459 | 1 | 2010 | Egypt. | Egypt | 1% significance. |
| (Fu & Cheng, 2013) [122] | GHI in sitio | 0.83 | Predicting solar irradiance | 8,227,114 | 0.83 | 2013 | China | Continental | Not estimated |
| (Gupta, et al., 2016) [82] | GHI, | 1 | A surface reflectance scheme for retrieving AOT | 344,509 | 1 | 2016 | India | Monsoon tropical | Not estimated |
| (Vijayakumar et al., 2016) [83] | GHI in sitio | 1 | Aerosol Optical Depth Retrieval over Bright Areas | 4,851,699.4 | 1 | 2016 | USA | Subtropical | Not esteemed |
| (Midilli & Kucuk, 2003) [180] | GHI in sitio | 1 | Mathematical modeling of thin layer drying | 83,562 | 1 | 2012 | Turkey | Mediterranean, Continental, Semi-arid | Rsfsd = 0.9983, χ2sfsd = 2.697 × 10−5 |
| (Lauka et al., 2018) [181] | GHI in sitio | 1 | First solar power plant in Latvia. | 64,589 | 1 | 2018 | Latvia | cool summers and cold winters | Not esteemed |
| (Li et al., 2021) [182] | GHI (in sitio) | 1 | Influencing actual absorption of solar | 4057.0496 | 1 | 2021 | China | Continental | Not esteemed |
| (Ma et al., 2015) [183] | GHI | 1 | Description of short circuit current | 6,597,230 | 1 | 2015 | India | Monsoon tropical | Not estimated |
| (Guta, 2018) [184] | GHI in sitio | 1 | Solar energy technology in rural | 1,112,009 | 1 | 2018 | Ethiopia | Temperate | Not estimated |
| Source | Data Source | Resolution (h) | Contributions | Area (km2) | Forecast Horizon (h) | Year | Location | Climate | Erro |
|---|---|---|---|---|---|---|---|---|---|
| (Ohtake et. al., 2019) [8] | GHI in sitio, PV | 1 | Accuracy of the solar irradiance forecasts | 585,144 | 1 | 2013 | Japan | Tropical | Not estimated |
| (Mohanty et al., 2017) [9] | GHI in sitio | 1 | Forecasting growing economy | 3,287,596 | 1 | 2017 | India | Monsoon tropical | Not estimated |
| (Sahin et al., 2023) [14] | GHI, power solar | 1 | Predictive ANN and MR | 83,562 | 1 | 2023 | Turkey | Mediterrain, Continental, Semi-arid | Not esteemed |
| (Pedro et al., 2017) [30] | solar, wind, tidal | 1, 2, 3 | Mathematical methods for optimized solar forecasting | 95,592 | 1 | 2017 | USA | Subtropical | Not esteemed |
| (Lauret et al., 2016) [34] | GHI in sitio | 1 | Solar radiation forecasting in an insular | 357,592 | 1 | 2015 | France | Oceanic temperate | Not esteemed |
| (Saffaripour et al., 2013) [44] | GHI in sitio | 1 | Predicting solar radiation fluxes for solar energy | 1,648,896 | 1 | 2013 | Iran | Subtropical and tropical arid high altitude | Not esteemed |
| (Anuradha et al., 2021a) [46] | GHI (in sitio) | 1 | Forecasting Using Machine Learning | 3,287,263 | 1 | 2021 | India | Monsoon tropical | Not esteemed |
| (Ahmad et al., 2018) [50] | GHI in sitio | 1 | Predictive modeling for solar thermal energy | 243,610 | 1 | 2018 | United Kingdom | Temperate oceanic | Not esteemed |
| (Klein et al., 1975) [69] | GHI in sitio, thermal | 1 | Simulation of solar processes and its application | 99,452 | 1 | 2005 | USA | Tropical | Not esteemed |
| (Charles et al., 2019) [70] | GHI in sitio, PV | 0.25 | ustainable energy storage for solar home systems in rural | 8825 | 175,200 | 2019 | Saharan Africa | Tropical | 7 and 17% |
| (Puga-Gil et al., 2022) [71] | GHI in sitio | 0.017 and 0.167 | Global Solar Irradiation Modeling and Prediction | 5,227,080 | 0.167 | 2022 | China | Tropical | Not esteemed |
| (Fahrmeir et al., 2013) [86] | GHI, power solar | 1 | Regression: Models, Methods and Applications | 710,850 | 1 | 2013 | Morocco | Temperate | Not esteemed |
| (Ramedani et al., 2014) [91] | several data tests | 1 | ANN approach on Type II Regression Analysis | 83,562 | 1 | 2014 | Turkey | Mediterranea, Continental, Semi-arid | ANN based in lower error than the OLS based bisector technique |
| (Jogunuri et al., 2007) [93] | GHI in sitio | 1 | Seasonal multi-step ahead short-term solar | 6,599,236 | 1 | 2007 | China | Continental | Not esteemed |
| (Perveen et al., 2013) [94] | GHI in sitio | 1 | Global solar energy and PV power forecasting | 385,207 | 1 | 202 | India | Oceanic, continental, subarctic and alpine | RF (MAE) 10.2; STD. 1.5; Interpolation 21.3; STD. 6.4 (Wm−2) |
| (Wu et al., 2023) [95] | PV data | 1 | Understanding spatiotemporal energy | 7,394,021 | 1–24 | 2023 | China | Continental | Not estimated |
| (Alzahrani et al., 2017) [96] | GHI (in sitio) | 1–24 | Solar Irradiance Forecasting Using Deep Neural Networks | 8,514,876 | 1–24 | 2017 | Brazil | Tropical | Not estimated |
| (Hill et al., 2021) [120] | GHI Satellite | 1 | Design-Based Global and Small Area Estimations for Multiphase Forest Inventories | 506,030 | 1–24 | 2021 | Spain | Mediterranean | Not estimated |
| (Kuipe et al., 2013) [121] | GHI in sitio | 1 | Generalized Order-Restricted Information Criterion | 4,287,289 | 1 | 2013 | India | Monsoon tropical | GRNN, fuzzy logic and ANN are 3.55%, 4.64%, and 5.49% |
| (Kurtgoz & Deniz, 2018) [152] | GHI in sitio | 1 | Estimation of GHI for Different Climatological | 83,562 | 1 | 2018 | Turkey | Mediterranea, Continental and Semi-arid | Not esteemed |
| (Abdul-Wahab et al., 2005) [185] | wind speed, direction, air temperature, GHI | 1 | Gground-level ozone and factors affecting | 309,501 | 1 | 2004 | Oman | Arid and dry desert | Not esteemed |
| (Jamei et al., 2021) [186] | GHI in sitio and nanoparticles | 0.0167 and 1 | Application of Gaussian process regression | 1,648,589 | 1 | 2021 | Iran | Subtropical and tropical arid high altitude | GPR (R = 0.99974, 0.01506 J/kg); (R = 0.99563, 0.06085 J/kg) |
| (Verma et al., 2016) [188] | GHI, cloud cover, temperature, wind speed, rainfall | 1 | Data Analysis to Generate Models Based | 2,567,008 | 1 | 2016 | India | Monsoon tropical | Not estimated |
| (Alizamir et al., 2020) [189] | GHI (in sitio) | 1 | Estimating solar radiation | 1,648,025 | 1 | 2020 | Iran | Subtropical and tropical arid high altitude | Not esteemed |
| (Rapti, 2000) [190] | Climate | 1 | Atmospheric climatic turbidity, transparency | 6,682,023 | 1–24 | 2010 | Greece | Mediterranean | Not estimated |
| (Salmanoğlu & ÇetiN, 2022) [191] | Wind | 1–24 | Harvest wind-Solar PV for Production | 5,682,026 | 1–24 | 2022 | Harvest | Tropical | Not estimated |
| (Gomes et al., 2020) [192] | GHI (in sitio) | 1 | Irradiance and power ramp rates | 8,514,876 | 124 | 2020 | India | Monsoon tropical | Not estimated |
| (Siebentritt, 2011) [193] | GHI (in sitio), wind | 0.0167 | Efficiency imitates chalcopyrite solar cells | 2586 | 124 | 2010 | Luxembourg | Semi-continental | Not estimated |
| (Alam et al., 2014) [194] | GHI (in sitio) | 0.0167 | Solar PV ramp rate control | 7,692,023 | 124 | 2014 | Australia | Hot and dry | Not estimated |
| (Güçlü et al., 2015) [196] | GHI in sitio | 0.00028 | Correlational multidimensional and LR | 861,591 | 1 | 2015 | Germany | Oceanic temperate | Not esteemed |
| (Quoc Hung & Mishra, 2019) [197] | GHI (in sitio) | 0.00028, 0.0167 | Voltage fluctuation | 7,692,023 | 1–24 | 2019 | Australia | Hot and dry | Not esteemed |
| (Kawasaki et al., 2006) [198] | GHI (in sitio) | 0.0000028 | PV fluctuation assessment | 377,973 | 0.00028–0.017 | 2006 | Japan | Oceanic temperate | Not esteemed |
| (de Freitas Viscondi & Alves-Souza, 2019) [199] | GHI | 1 | Big data for solar pv electricity | 489,595 | 1 | 2019 | Brasil | Tropical | Not estimated |
| ANNs | SVMs | RF | GBMs | LSTM | GPR | ARIMA | SLR | RK | Hybrids MLM | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cumulative | 28 | 6 | 14 | 6 | 7 | 6 | 9 | 19 | 17 | 33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mucomole, F.V.; Silva, C.A.S.; Magaia, L.L. Parametric Forecast of Solar Energy over Time by Applying Machine Learning Techniques: Systematic Review. Energies 2025, 18, 1460. https://doi.org/10.3390/en18061460
Mucomole FV, Silva CAS, Magaia LL. Parametric Forecast of Solar Energy over Time by Applying Machine Learning Techniques: Systematic Review. Energies. 2025; 18(6):1460. https://doi.org/10.3390/en18061460
Chicago/Turabian StyleMucomole, Fernando Venâncio, Carlos Augusto Santos Silva, and Lourenço Lázaro Magaia. 2025. "Parametric Forecast of Solar Energy over Time by Applying Machine Learning Techniques: Systematic Review" Energies 18, no. 6: 1460. https://doi.org/10.3390/en18061460
APA StyleMucomole, F. V., Silva, C. A. S., & Magaia, L. L. (2025). Parametric Forecast of Solar Energy over Time by Applying Machine Learning Techniques: Systematic Review. Energies, 18(6), 1460. https://doi.org/10.3390/en18061460







