A Win-Win Coordinated Scheduling Strategy Between Flexible Load Resource Operators and Smart Grid in 5G Era

Abstract

With the rapid expansion of 5G base stations, the increasing energy consumption and fluctuations in power grid loads pose significant challenges to both network operators and grid stability. This paper proposes a coordinated scheduling strategy designed to address these pressing issues by leveraging the flexible load management capabilities of 5G base stations and their potential for inter-regional power demand response within the smart grid framework. This study begins by quantifying the dispatch potential of 5G base stations through a detailed analysis of their load dynamics, particularly under tidal fluctuations, which are critical for understanding the temporal variability of energy consumption. Building on this foundation, dormancy and load transfer strategies are introduced to model the scheduling potential for regional energy storage, enabling more efficient utilization of available resources. To further enhance the optimization of energy distribution, a many-to-many proportional energy-sharing algorithm is developed, which facilitates the aggregation of scheduling capacities across multiple regions. Finally, a comprehensive multi-objective, two-layer collaborative dispatching strategy is proposed, aiming to mitigate grid load volatility and reduce electricity procurement costs for 5G operators. Extensive simulation results demonstrate the effectiveness of this strategy, showing a significant reduction in grid load variance by 37.88% and a notable decrease in operational electricity costs for 5G base stations from CNY 4616.0 to 3024.1. These outcomes highlight the potential of the proposed approach to achieve a win-win scenario, benefiting both base station operators and the smart grid by enhancing energy efficiency and grid stability.

1. Introduction

In recent years, China has emphasized the acceleration of new infrastructure development. As a key component of this “new infrastructure”, the construction of 5G communication base stations is progressing steadily, with the number of base stations expected to reach 8 million by 2025 [1]. Given that the power consumption of 5G base stations is three to four times higher than that of 4G base stations [2,3], and more stations are required to cover the same communication range, the energy consumption issue is particularly prominent [4]. This, in turn, exacerbates the fluctuation of power grid load [5]. In addition, the large-scale integration of renewable energy sources further amplifies grid fluctuations [6]. Therefore, reducing energy consumption and grid volatility while meeting the growing demand for 5G base stations is of significant importance.

To ensure a reliable power supply, 5G base stations are typically equipped with electrochemical energy storage systems as backup power sources. By 2025, the demand for backup batteries in these stations is expected to reach 78.6 GW·h [7]. Given that base station energy storage mostly remains idle and floating charged for long periods, and considering the variation in communication loads across different regions, their dual source-load characteristics and inter-regional collaborative scheduling capabilities can be leveraged as flexible loads for power demand response. Optimizing the base station–grid interactive dispatching strategy can maximize the schedulable potential of 5G base station clusters, improve the utilization of 5G network resources, aid in peak-load shaving and valley-filling for the supply side, and ease the operational pressure on the power grid.

Extensive research exists on the potential of 5G base station energy storage. Reference [8] correlates the lower limit of the state of charge (SOC) of base station energy storage with the station’s load state, constructing a schedulable potential model. Reference [9] designs the backup time for base station energy storage, considering mains reliability, and evaluates schedulable capacity based on communication load and backup time. Reference [10] employs a Markov model approach to enhance communication reliability with minimal repair time. However, most of these studies focus solely on the original transmitting power and do not fully utilize the potential of dormant load transfer, limiting the effective release of base station energy storage regulation potential.

Research on dispatching strategies for base station backup energy storage in grid demand response has also been conducted. Reference [11] establishes an economic dispatch model for the 5G base station light-storage system, considering hourly electricity prices and base station load. Reference [12] proposes an energy storage regulation algorithm based on the upper confidence interval of battery state perception to maximize the weighted difference between regulation benefits and load curve variance. Yet, reference [13] explores transferring excess energy storage from 5G base stations to the grid. However, these studies mostly focus on the base station clusters’ interaction with the grid, neglecting energy flow and regional cooperativity among the clusters. In contrast, reference [14] connects base stations and the power distribution network, while reference [15] proposes an optimal power purchase algorithm based on one-sided matching and introducing a bidirectional preference list for energy storage regulation in 5G distribution network base stations. However, the majority of current studies explore single or few-to-many energy-sharing models, with limited analysis of many-to-many configurations.

In response, this paper proposes an interactive scheduling strategy between base stations and the power grid to maximize the schedulable potential of 5G base station clusters. By considering base station dormancy and communication load transfer, a potential model for 5G base stations is developed, and a many-to-many proportional energy-sharing strategy is proposed to aggregate multi-region schedulable capacities. A multi-objective, two-layer optimization framework is established for the interaction between 5G base station clusters and the power grid, aiming to minimize grid load volatility and power purchase costs for base stations. The strategy layers objectives through interactions between 5G cluster aggregators and the grid. Finally, the proposed model’s effectiveness is verified.

The key innovations of this study include:

• The introduction of load transfer and energy-sharing mechanisms, which significantly expand the schedulable capacity of energy storage systems by enabling flexible resource allocation across multiple regions;
• The development of a many-to-many proportional allocation algorithm, which optimizes energy distribution among 5G base station clusters and enhances the efficiency of multi-region coordination.

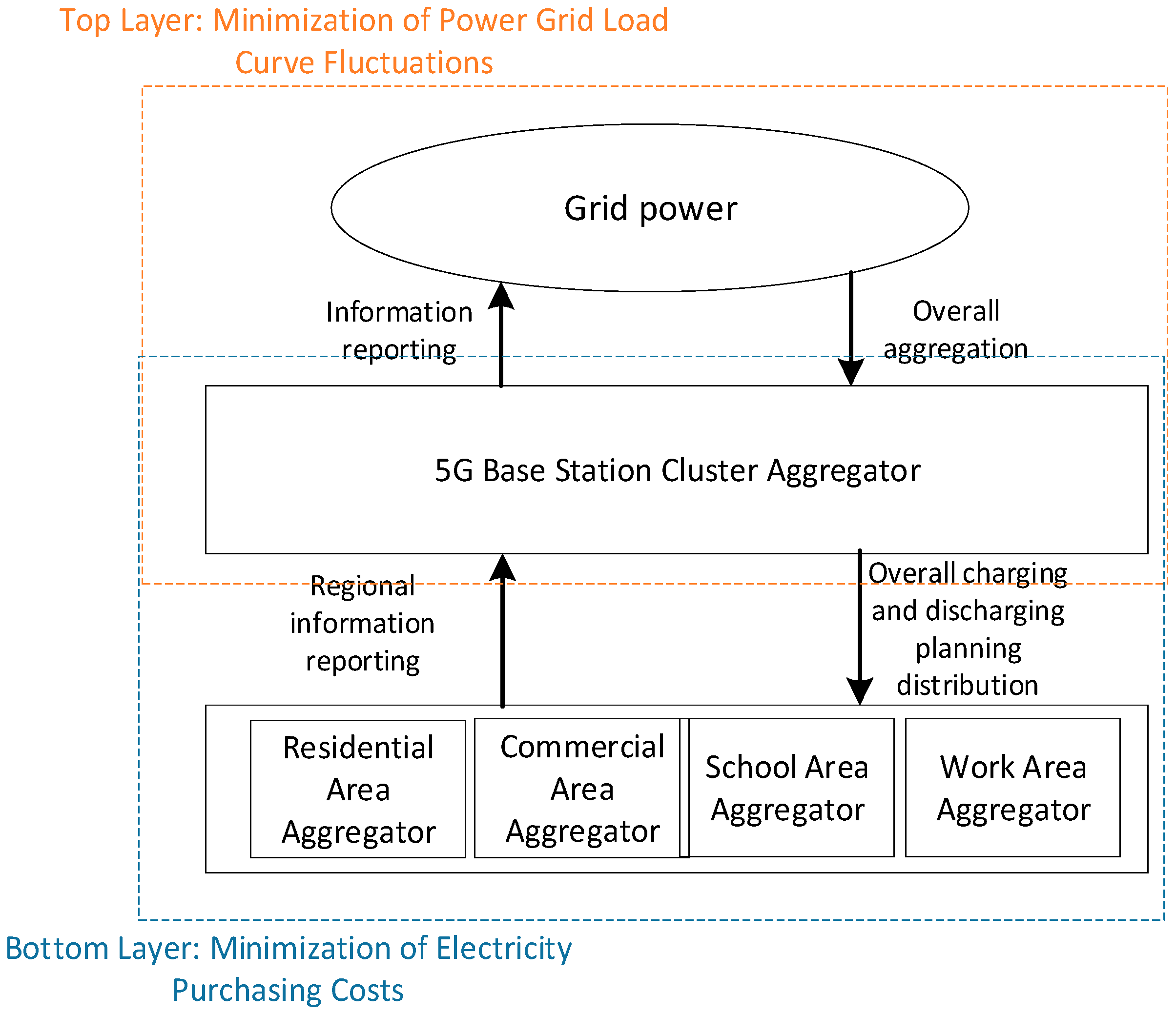
2. Overview of Multi-Objective Two-Layer Optimization Architecture of 5G Base Station Clusters

The interactive dispatching scenario diagram of a 5G base station cluster and power distribution network to maximize the schedulable potential established in this paper is shown in Figure 1.

As shown in Figure 1, the study area in this paper is divided into four functional zones: work, commercial, school, and residential. These zones include entities such as 5G micro and macro base stations, the power distribution network, and 5G cluster aggregator. During interactions between the 5G base stations and the power grid, the backup time is first calculated based on the reliability parameters of each regional distribution network. Load transfer is then performed for micro base stations that meet the criteria. Potential models for individual and regional 5G base stations are established using real-time load and backup time data from the transferred macro base stations. Next, a many-to-many proportional allocation algorithm is used to achieve energy sharing between functional zones, transferring excess power from surplus zones to deficit zones, thereby enhancing the overall dispatchable potential of the 5G base station cluster. Finally, the cluster status information is integrated and uploaded to the power grid. The power grid, after considering its own load and other factors, issues electricity price information and an overall charge and discharge plan to the cluster aggregator. The aggregator then formulates real-time control strategies and issues control instructions to each zone. In each zone, energy storage is charged when there is a demand for power absorption from the grid. When the grid load is heavy, energy storage discharges to alleviate grid pressure, ultimately achieving energy interaction between the base stations and the power grid.

3. Analysis and Modeling of Scheduling Energy Storage Potential for 5G Base Stations

3.1. Analysis of Energy Storage Scheduling Potential of 5G Base Station Based on Spatio-Temporal Tidal Characteristics

This paper examines a 5G base station cluster composed of macro and micro base stations. The macro stations provide extensive coverage with stable signals and possess energy storage, while micro stations enhance local signal quality and network capacity. The active antenna unit (AAU) in 5G base station electrical equipment accounts for nearly 90% of total power consumption, making it the primary energy consumer. The AAU’s power consumption fluctuates with the communication load of the base station, resulting in the overall power consumption of the 5G base station being highly dependent on real-time communication load [16,17]. As user positions and communication behaviors vary over time, the communication load of a base station exhibits a tidal effect. 5G base stations are typically equipped with energy storage batteries sized based on the peak load to prevent power supply interruptions [18]. Due to the pronounced peak and valley characteristics of communication loads, backup energy storage often includes redundant resources, presenting an optimization opportunity. Consequently, 5G base stations, as flexible loads, are well-suited for participating in power grid regulation.

The dense deployment of 5G base stations creates overlapping coverage areas, allowing for load migration while maintaining communication service quality [19]. Given the linear relationship between communication and power load, micro base stations can transfer communication loads to macro stations when dormancy thresholds are met. This transfer increases the real-time power consumption of the macro station, raises its charging upper limit, and expands its schedulable capacity. Thus, load transfer optimizes cluster power consumption, reduces electricity costs, and enhances the energy storage capacity of macro stations, boosting their scheduling potential.

The load curves of 5G base stations in different functional areas show distinct differences and complementarity [20]. Regional aggregation through real-time energy sharing can further enhance overall scheduling potential. High-load functional areas can prioritize energy use from adjacent surplus areas, reducing reliance on power grid purchases and mitigating peak grid loads. This strategy significantly improves the scheduling potential of 5G base station clusters. The construction process of the 5G base station energy storage scheduling potential model is shown in Figure 2.

3.2. Construction of a Scheduling Potential Model for 5G Base Station Units

3.2.1. Energy Storage Backup Time of 5G Base Station

This paper divides the load area into four parts: work, business, school, and residence, which is recorded as a collection $\Pi =\left\{\mathrm{res},\mathrm{com},\mathrm{sch},\mathrm{work}\right\}$. The average power outage time and average power outage times of different functional areas were normalized, and the average backup time of residential areas was taken as the benchmark [21], and the minimum backup power time for energy storage of base stations in different functional areas was obtained:

$$T_{\min }^{j,\mathrm{s}\in \Pi }=T_{\min }^{j,res}{\displaystyle \frac{{\eta }^j{r}^j}{{\eta }^{j,\mathrm{res}}{r}^{j,\mathrm{res}}}}$$

(1)

Therefore, the outage duration on the power distribution network side can be obtained.

3.2.2. The Real-Time Power Consumption of the 5G Base Stations

Load transfer refers to the process of redistributing electrical load from one area or system to another to optimize energy usage, balance grid demand, and enhance operational efficiency. For the 5G macro base station j, the power consumption can be expressed as follows:

$$P_{\mathrm{b}}^{\prime j}(t)=P_{\mathrm{b},\mathrm{s}}^j(t)+{\beta }_j{P}_{\mathrm{b},\mathrm{r}}^{\prime j}(t)$$

(2)

where ${\beta }_j$ is the efficiency coefficient of macro base station j, taken as the reciprocal of the efficiency of the power amplifier; $P_{\mathrm{b},\mathrm{r}}^{\prime j}(t)$ is the transmission power of base station j, which increases with the number of users accessing it [22].

For 5G micro base station i, there are two states of active and dormant in each time period, and its power consumption can be expressed as follows:

$$P_{\mathrm{b}}^i(t)=\left\{\begin{array}{l}{P}_{\mathrm{sleep}}^i,q=1\hfill \\ P_{\mathrm{b},\mathrm{s}}^i(t)+\beta P_{\mathrm{b},\mathrm{r}}^i(t),q=0\hfill \end{array}\right.$$

(3)

where q = 1 indicates that the micro base station i is in sleep mode, and q = 0 indicates that the micro base station i is in active mode. When the dynamic power consumption of the micro base station is less than the sleep threshold, q = 1 is set to 1, otherwise it is set to 0.

When q = 1, the distance between the micro base station i and the nearest macro base station k is calculated, and the product of the load and distance of the micro base station i is calculated:

$$W_i=P_{\mathrm{b},\mathrm{r}}^i(t)\times s_{i,k}$$

(4)

The product of the load transfer to macro base station k is sorted and further classified according to the number of covered Acer stations. The collection of micro-base stations in multi-coverage areas is

$${\Psi }^{\prime }=\left\{i\right|\left|C_i\right|>1\}$$

(5)

For the micro base station with overlapping coverage area of the multi-macro station, the restart probability is low, which reduces the conversion times of the base station state, thus reducing the power consumption more efficiently [23]. Therefore, when the macro station cannot accommodate the transfer load of all micro base stations, these micro base stations in the overlapping coverage area are preferentially dormant. According to the above sorting rules, the set of micro base stations that can be contained is

$$\Psi =\{i|{\displaystyle \sum _k{P}_{\mathrm{b}}^i(t)\le }{P}_{k,\max }\}$$

(6)

Therefore, for the macro base station k after load transfer, the power expression is

$$P_{\mathrm{b}}^k(t)=P_{\mathrm{b},\mathrm{s}}^j(t)+{\beta }_k{P}_{\mathrm{b}}^{\prime k}(t)+{\displaystyle \sum _{i=1}^{i\in \Psi }\frac{P_{\mathrm{b},\mathrm{r}}^i(t)}{{\beta }_i}}$$

(7)

3.2.3. G Base Station Scheduling Capacity Model

The main function of 5G base station energy storage is to serve as a backup power supply to ensure the uninterrupted power supply demand of the base station. Therefore, the base station energy storage only participates in the power dispatch during the normal power supply, and the power supply only for the base station itself when the city power is cut off. Considering the upper and lower limits of charge and discharge of energy storage batteries and the requirements of standby energy storage, the rechargeable and discharging dispatching capacity of a single base station j during time t is

$$E_{\mathrm{c},\lim }^j(t)=(E_{j,\max }-E_j(t))B_j(t)$$

(8)

$$E_{\mathrm{dis},\lim }^j(t)=(E_j(t)-E_{j,\min }-E_{\min }(t))B_j(t)$$

(9)

$$E_{\min }(t)={\displaystyle {\int }_t^{t+T_{\min }^j}{P}_{\mathrm{b}}^j(t)dt}$$

(10)

where $(E_{j,\max }-E_j(t))$ indicates the upper limit of energy storage, and $(E_j(t)-E_{j,\min }-E_{\min }(t))$ indicates the lower limit of the scheduling capacity of energy storage, which is obtained by subtracting the inherent lower limit of the energy storage itself from the maximum capacity, and then further subtracting the standby energy needed to ensure communication reliability; ${\displaystyle {\int }_t^{t+T_{\min }^j}{P}_{\mathrm{b}}^j(t)dt}$ represents the standby energy, which is calculated based on the standby duration and real-time load. $B_j(m)$ is a 0–1 variable, where $B_j(m)=1$ indicates that the grid is supplying power normally and the standby energy of the base station can participate in adjustment, while $B_j(m)=0$ indicates that the grid is failing to supply power and the standby energy of the base station is used to supply power to the base station communication equipment.

According to the rechargeable capacity and discharging scheduling capacity, the maximum charge and discharge power of a single base station j standby energy storage within a scheduling interval is

$$P_{\mathrm{b},\mathrm{c}}^j(t)\le \min \{{\displaystyle \frac{E_{j,\max }-E_j(t)}{{\alpha }_c\Delta t}},P_{\mathrm{c},\max }^j\}{B}_j(t)$$

(11)

$$P_{\mathrm{b},\mathrm{dis}}^j(t)\le \min \{{\displaystyle \frac{E_j(t)-E_{j,\min }-E_{\min }(t){\alpha }_{\mathrm{dis}}}{\Delta t}},P_{\mathrm{dis},\max }^j\}{B}_j(t)$$

(12)

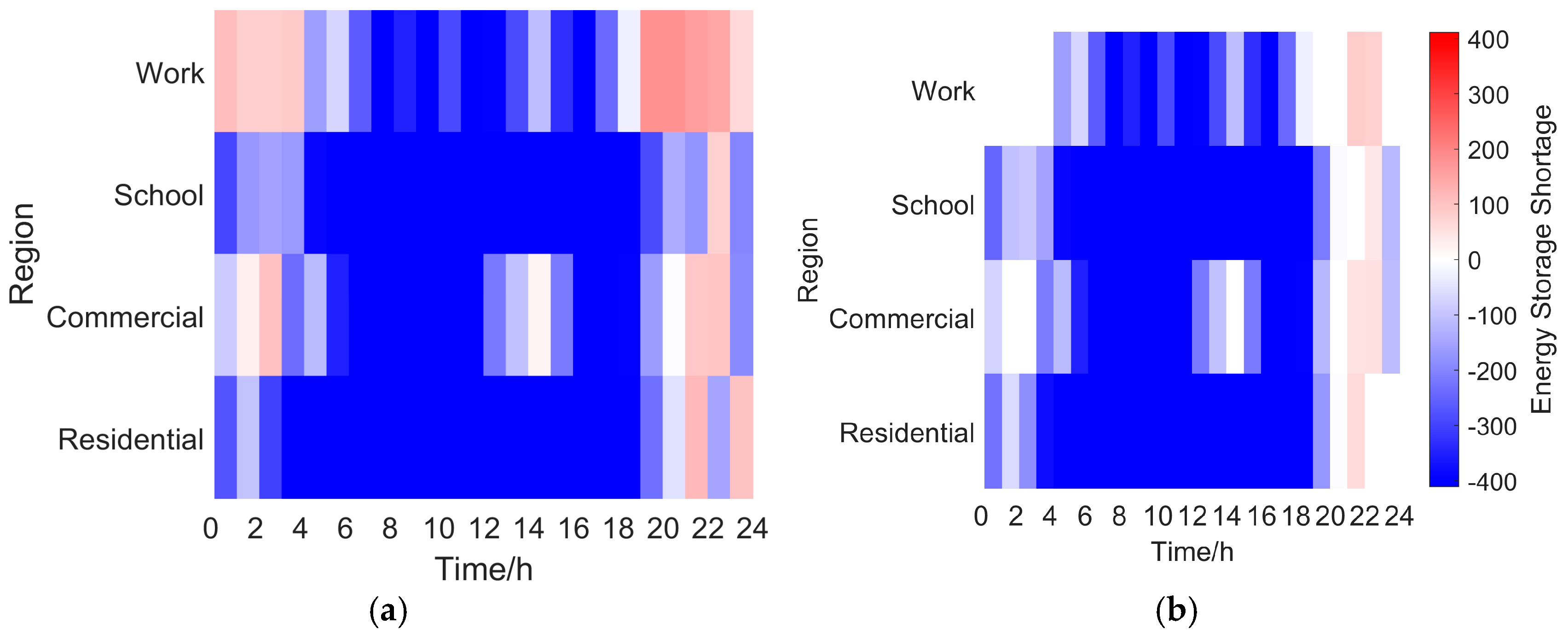
3.3. Construction of the Scheduling Potential Model of 5G Base Station Cluster Based on Energy Sharing

Energy sharing involves the collaborative distribution of surplus energy among multiple nodes or systems to improve resource utilization and enhance overall efficiency in energy management. In the process of participating in the optimal operation of the power grid, the optional regulation modes can be divided into decentralized regulation and aggregate regulation. Because 5G base station energy storage is characterized by large quantity, wide distribution, and small individual capacity, it will bring excessive computing burden and workload [23,24] to the power grid under the decentralized regulation mode. Therefore, this paper will adopt the aggregate regulation mode and introduce regional aggregators as intermediate agents to construct a distributed regulation architecture. Assuming that n is the total number of base stations involved in the aggregation in a certain functional area, and considering the constraints of base station backup energy storage and SOC, the rechargeable and discharging dispatching capacity in a certain functional area is obtained:

$$E_{\mathrm{c},\lim }^m(t)={\displaystyle \sum _{j=1}^n(E_{j,\max }-E_j(t))B_j(t)}$$

(13)

$$E_{\mathrm{dis},\lim }^m(t)={\displaystyle \sum _{j=1}^n(E^j(t)-E_{\min }^j-E_{\min }(t))B_j(t)}$$

(14)

As mentioned in Section 3.1 of this paper, there is a tidal effect in 5G base station load, and there are obvious differences in load peak and trough periods between different regions, which can make full use of this complementary feature for energy sharing. Based on this, this paper puts forward a kind of energy sharing strategy based on multi-to-proportional allocation, namely in each period, through the real-time calculation of surplus power and power shortage, calculate the optimal energy distribution ratio, to ensure the efficient transfer and utilization of energy between different areas, and realize the reasonable distribution and optimization of energy. The specific steps are as follows.

• Determine the energy state: Based on the load and storage conditions of each region, calculate the total power demand and current storage surplus or shortage. Regions where storage capacity cannot cover upcoming standby demands are energy-scarce, while those exceeding standby demands are energy-rich. Energy-rich regions are denoted as ${\theta }^F(t)=\{F_h,F_{h+1,\dots },F_H\}$, and energy-scarce regions are denoted as ${\theta }^D(t)=\{D_g,D_{g+1,\dots },D_G\}$.
• Calculate the total energy surplus and power shortage. Calculate the total surplus energy ${\displaystyle \sum _{h=1}^H{E}_F^h}$ and power shortage ${\displaystyle \sum _{g=1}^G{E}_D^g}$ in each region, and calculate the proportion of energy surplus of each region $r_F^h=E_F^h/{\displaystyle \sum _{h=1}^H{E}_F^h}$ and the proportion of energy shortage of each region $r_d^g=E_D^g/{\displaystyle \sum _{g=1}^G{E}_D^g}$. According to Equation (15), the energy transfer target is obtained as

  $$E_{F\to D}=\min \{{\displaystyle \sum _{h=1}^H{E}_F^h},{\displaystyle \sum _{g=1}^G{E}_D^g}\}$$

  (15)
• Construct the energy transmission matrix. To achieve optimal energy allocation, construct the energy transmission matrix and use the maximum matching rule for selective calculation. First, define the energy transmission matrix: $E=\left[\begin{array}{ccc}{E}_{F_1\to D_1}& \cdots & E_{F_1\to D_G}\\ ⋮& \ddots & ⋮\\ E_{F_H\to D_1}& \cdots & E_{F_H\to D_G}\end{array}\right]$ where $E_{F_h\to D_g}$ represents the transmission energy from the energy-rich region $F_h$ to the energy-scarce region $D_g$. Next, perform a selective calculation: (1) Identify the region $F_{h^{*}}$ with the largest current surplus energy and the region $D_{g^{*}}$ with the largest current energy deficit. (2) Calculate the transferable energy at this moment as $\Delta E=\min \{E_F^{h^{*}},E_D^{g^{*}}\}$. (3) Update the total surplus energy and total deficit energy, and determine whether there are still energy surplus or deficit regions unprocessed. If they exist, return to step (1) and continue with the selective calculation until the energy transfer between all surplus and deficit regions is complete.
• Complete the inter-regional energy transmission. The final energy transfer matrix is the best energy transfer scheme obtained under the maximum value matching principle. After the energy transfer scheme is implemented in each functional area, the updated power is the equilibrium power realized under the scheme, so as to maximize the scheduling potential of the 5G base station cluster. The shared scheduling potential of the 5G base station cluster is expressed as follows:

  $$E_{\mathrm{c},\lim }(t)={\displaystyle \sum _{m=1}^{N_a}(E_{\max }^m-E_{\mathrm{c},\lim }^m(t))B_k(t)}$$

  (16)

  $$E_{\mathrm{dis},\lim }(t)={\displaystyle \sum _{m=1}^{N_a}(E^m-E_{\min }^m(t)-E_{\min }(t))B_k(t)}$$

  (17)

4. Multi-Objective Two-Layer Optimization Scheduling Strategy for 5G Base Station Cluster

Based on the power reduction demand of the 5G base station and the grid side peak load filling demand, on the basis of the cluster aggregation and schedulable capacity model established in Section 3, a multi-objective two-layer optimization architecture of the 5G base station cluster is proposed in Figure 3.

In the top layer, the 5G macro-micro base station integrates the cluster load status information and energy storage status information and uploads it to the superior power grid, participates in the power grid dispatching in the form of cluster aggregator, minimizes the variance of the load curve of the power grid, and obtains the overall charge and discharge plan based on the lower optimization, further dispatching between regions. At this point, with the economy of a single region as the goal, the specific scheduling strategies of each region at different times are solved, respectively, so that each region can complete the charge and discharge action together.

4.1. Interaction Model of 5G Base Station Cluster and Power Grid

The top layer of the 5G base station cluster multi-objective two-layer regulation model is the interaction between the 5G base station cluster aggregator and power purchase and sale. Since this paper takes the power grid as the leader and the 5G base station cluster aggregator as the follower, the power grid peak load filling has a higher priority, so the objective function of the top layer model is to minimize the variance of the power grid load curve:

$$\min f_1={\displaystyle \frac{{\displaystyle \sum _{t=1}^T[P_{\mathrm{load}}(t)}-(P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(t)-P_{\mathrm{B},\mathrm{C}}^{\mathrm{total}}(t))-P_{\mathrm{a}}{]}^2}{T}}$$

(18)

$$P_{\mathrm{a}}={\displaystyle \sum _{t=1}^T[P(t)-(P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(t)-P_{\mathrm{B},\mathrm{C}}^{\mathrm{total}}(t)})]/T$$

(19)

In the top layer, the overall charging and discharge power of the 5G base station cluster and the upper limit of transmission power of the power grid, is as follows:

• Cluster Aggregator energy storage charge and discharge power constraint:

  $$0\le P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(t)\le {\displaystyle \sum _{m=1}^{N_a}{P}_{\mathrm{B},\mathrm{D},\max }^m(t)}$$

  (20)

  $$0\le P_{\mathrm{B},\mathrm{C}}^{\mathrm{total}}(t)\le {\displaystyle \sum _{i=1}^{N_a}{P}_{\mathrm{B},\mathrm{C},\max }^m(t)}$$

  (21)
• Cluster aggregator energy storage energy equation constraint:

  $$E(t)=E_0+{\displaystyle \sum _{l=1}^{t-1}[{\alpha }_c{P}_{\mathrm{B},\mathrm{C}}^{\mathrm{total}}(l)-\frac{P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(l)}{{\alpha }_{\mathrm{dis}}}]\Delta t}$$

  (22)
• Cluster aggregator energy storage SOC constraints:

  $$\max \{{\displaystyle \sum _{m=1}^{N_a}{E}_{\min }^m},{\displaystyle \sum _{m=1}^{N_a}{E}_{\min }^m(t)}\}\le E(t)\le {\displaystyle \sum _{m=1}^{N_a}{E}_{\max }^m}$$

  (23)
• Power constraints on the grid:

  $$P_{\mathrm{grid}}^{\min }\le P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(t)\le P_{\mathrm{grid}}^{\max }$$

  (24)

  $$P_{\mathrm{grid}}^{\min }\le P_{\mathrm{C},\mathrm{D}}^{\mathrm{total}}(t)\le P_{\mathrm{grid}}^{\max }$$

  (25)

4.2. Energy Allocation Optimization Model for Regional Coordination

At each moment at the end of the energy sharing, a cluster aggregator will be on the upper 5G base station cluster and the power grid interaction overall charge and discharge plan area issued, at the same time as using an electricity purchase/electricity dynamic time-sharing double electricity price mechanism, encouraging the 5G base station area cluster in the case of energy surplus to the power grid, a target function for the 5G base station cluster economic cost minimum:

$$\max f_2={\displaystyle \sum _{m=1}^{N_a}{\displaystyle \sum _{t=1}^T(F_1+F_2-C_1)}}$$

(26)

$$F_1=(P_{{\mathrm{B},\mathrm{D}}_{\mathrm{load}}}^m(t)-P_{\mathrm{B},\mathrm{C}}^m(t)){\epsilon }_1(t)$$

(27)

$$F_2=P_{{\mathrm{B},\mathrm{D}}_{\mathrm{sell}}}^m(t){\epsilon }_2(t)$$

(28)

$$C_1={\displaystyle \sum _{j=1}^n{C}_{\mathrm{b}}^j(P_{\mathrm{b},\mathrm{dis}}^j(t)+P_{\mathrm{b},\mathrm{c}}^j(t))}$$

(29)

$$P_{\mathrm{B},\mathrm{D}}^m(t)=P_{{\mathrm{B},\mathrm{D}}_{\mathrm{load}}}^m(t)+P_{{\mathrm{B},\mathrm{D}}_{\mathrm{sell}}}^m(t)$$

(30)

where $F_1$ is the storage revenue of the base station; $F_2$ is the revenue of the sale to grid; $C_1$ is the charge and discharge loss cost of the base station storage.

The specific constraints are provided as follows:

• Regional aggregator energy storage charge and discharge power constraint:

  $$0\le P_{\mathrm{B},\mathrm{D}}^m(t)\le {\displaystyle \sum _{j=1}^n\min \{\frac{E_{j,\max }-E_j(t)}{{\eta }_{\mathrm{c}}\Delta t},P_{\mathrm{c},\max }^j\}}$$

  (31)

  $$0\le P_{\mathrm{B},\mathrm{C}}^m(t)\le {\displaystyle \sum _{j=1}^n\min \{\frac{E_j(t)-E_{j,\min }-E_{\min }(t){\eta }_{\mathrm{dis}}}{\Delta t},P_{\mathrm{dis},\max }^j\}}$$

  (32)
• Regional aggregator energy storage energy equation constraints:

  $$E^m(t)=E_0^m+{\displaystyle \sum _{l=1}^{t-1}[{\alpha }_{\mathrm{c}}{P}_{\mathrm{B},\mathrm{C}}^m(l)-\frac{P_{\mathrm{B},\mathrm{D}}^m(l)}{{\alpha }_{\mathrm{dis}}}]\Delta t}$$

  (33)
• Regional aggregator energy storage SOC constraints:

  $$\max \{{\displaystyle \sum _{j=1}^n{E}_{\min }^j},{\displaystyle \sum _{j=1}^n{E}_{\min }^j(t)}\}\le E^m(t)\le E_{\max }^m$$

  (34)
• Overall charge and discharge power constraint:

  $$P_{\mathrm{B},\mathrm{D}}^{\mathrm{total}}(t)={\displaystyle \sum _{m=1}^{N_a}{P}_{\mathrm{B},\mathrm{D}}^m(t)}$$

  (35)

  $$P_{\mathrm{B},\mathrm{C}}^{\mathrm{total}}(t)={\displaystyle \sum _{m=1}^{N_a}{P}_{\mathrm{B},\mathrm{C}}^m(t)}$$

  (36)
• Charge and discharge state constraint:

  $$P_{\mathrm{B},\mathrm{C}}^m(t)P_{\mathrm{B},\mathrm{D}}^m(t)=0$$

  (37)

5. Example and Analysis

5.1. Basic Data

This paper takes the residential, commercial, school, and working areas in a certain area of 5 km × 5 km as an example. Each functional area is evenly distributed with 10 5G macro base stations, while the entire region is evenly distributed with 200 5G micro base stations. The coverage radius of a macro base station is 500 m. The base station load curve characteristics of each functional area and the grid load curve of the area are set by reference [8]. Each macro base station is equipped with two groups of 48 V/500 Ah lithium iron phosphate cascade batteries as backup energy storage. The rated capacity of the battery is 48 kW·h, the charging and discharging efficiency of energy storage is 0.95, the charging and discharging loss coefficient is 0.14, the upper limit of battery SOC is 0.9, and the lower limit is 0.1. The base station parameters, including load characteristics and energy consumption patterns, are derived from actual traffic measurements in a specific urban area. The simulation is based on the MATLAB 2021a software platform, implemented by YALMIP toolbox programming (version R20230622), and solved by the GUROBI solver (version 12.0). The hardware environment for the simulation includes an AMD Ryzen 7 3800X 8-Core processor @ 3.89 GHz and 16.00 GB RAM sourced from Advanced Micro Devices (AMD), headquartered in Santa Clara, CA, USA, ensuring efficient computation and accurate results. Time-sharing purchase and sale price is used in the model and set according to reference [15].

5.2. Analysis of the Results

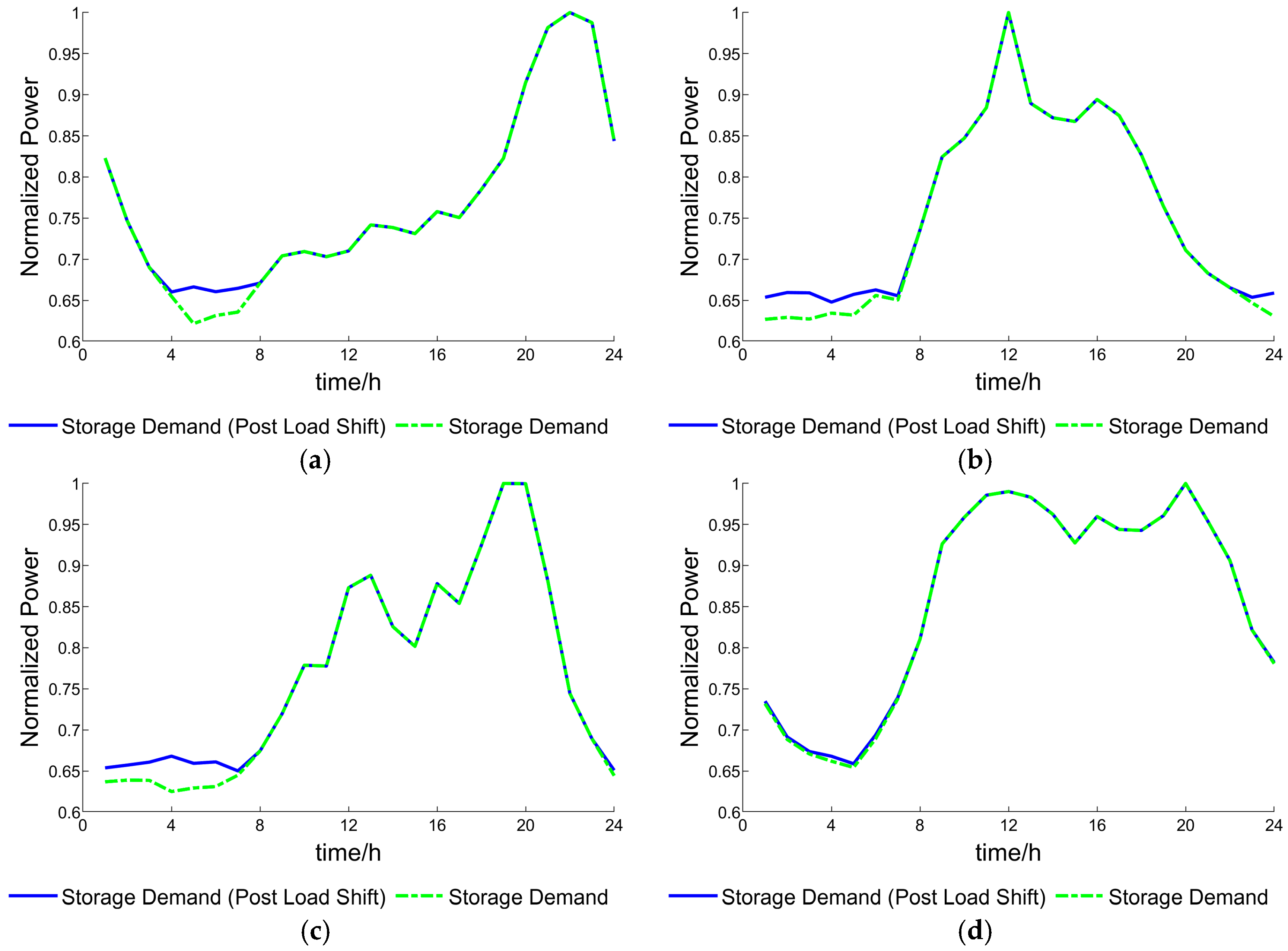
5.2.1. Analysis of Scheduling Potential of Energy Storage in 5G Base Stations

Based on the backup time and real-time load, the initial backup energy storage curve and the backup energy storage curve after load transfer are obtained, as shown in Figure 4.

Figure 4 shows a comparison of the energy storage demand (after load transfer) and the original energy storage demand in different time periods in residential, commercial, school, and working areas. As can be seen from Figure 4, the load trough period of each region is distributed at 0:00–7:00 and 22:00–24:00, which coincides with the grid valley period. Therefore, during this period, each region increases the energy storage demand through load transfer, which can broaden the dispatching capacity of each region in this period, which is conducive to the 5G base station cluster to help the grid side to complete the valley filling.

In this paper, the multi-to-multi energy sharing algorithm is adopted to complete the energy flow from the surplus area to the power shortage area. The energy storage shortage pair in each area before and after the algorithm is used, as shown in Figure 5.

In Figure 5, blue indicates the power surplus and red indicates the power shortage. As can be seen from Figure 5, before the energy sharing of regional energy storage, there is a serious surplus/power shortage in each region. After the energy sharing, the energy storage in each region is balanced and the power shortage is alleviated. This is because under the tidal effect, the load of 5G base stations in different functional areas has staggered peaks. At the same time, due to the complementarity of the schedulable capacity of different regions at the same time, the power shortage areas can be met through energy sharing between regions, and the power purchased from the grid side can be effectively reduced during the peak of the grid load.

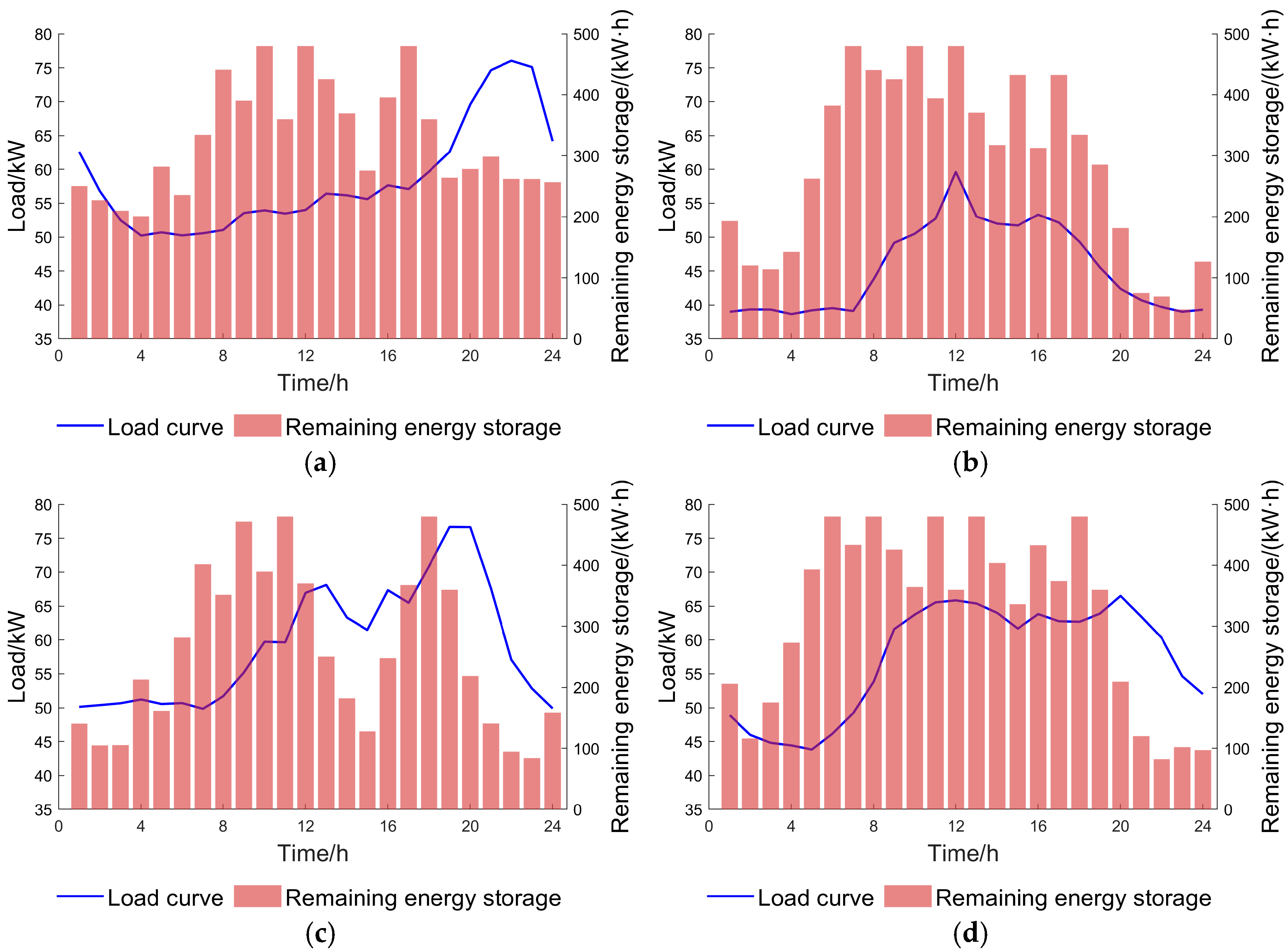
5.2.2. Optimization Scheduling Results of 5G Base Station Clusters

The results of upper-layer optimization scheduling in the multi-objective two-layer optimization model of the 5G base station cluster are shown in Figure 6.

As can be seen from Figure 6, the peak time of the power grid is mainly 12:00–14:00 and 18:00–21:00, and the valley time is mainly 0:00–7:00 and 22:00–24:00. The energy storage of the 5G base station conducts overall discharge at the peak and charge at the valley, which has the effect of peak shifting and valley filling on the power grid curve, leveling the overall load curve, and will not cause new curve fluctuations due to the additional charging and discharge of energy storage.

After the interaction between the 5G base station cluster and the power grid obtains the overall charging and discharge plan, the 5G base station will consider its own economy and distribute the functional areas of the 5G base station. The results of charge and discharge plan allocation for each functional area are shown in Figure 7.

As shown in Figure 7, from 0:00 to 7:00, the optimized overall charge and discharge plan reduces grid load fluctuations, resulting in a rise and then fall in charging. Figure 8 illustrates that, after distributing the overall plan, each region charges according to its own load situation. Between 3:00 and 6:00, the overall charging power peaks, accumulating energy storage to meet grid valley filling demands. During non-peak periods, regions maintain backup energy storage to ensure communication reliability. From 12:00 to 14:00 and 17:00 to 21:00, when the grid peaks, base station energy storage discharges to help with peak load. Significant charge–discharge cooperation is observed due to tidal effects and complementary storage needs. For instance, residential peak load occurs from 19:00 to 24:00, maintaining stable energy storage for backup, while commercial areas discharge to meet peak grid demands. This cooperation ensures balanced dispatching, enhancing flexibility and reliability of the 5G base station system and smoothing the grid load curve.

5.2.3. Comparison Results Under Different Methods

The scheduling results from the multi-objective two-layer optimization model of the 5G base station cluster in this paper are compared with the original power grid load curve, without single-target collaborative scheduling or optimization measures. The results are presented in Figure 8 and

Table 1. Performance of the multi-objective two-level optimization scheduling model.

Scene	Grid Load Curve Variance 105 (kW2·h2)	Power Purchase Cost (RMB)
No optimization	6.81	4616.0
Single-Layer Direct Scheduling Strategy	4.66	3466.2
Multi-Objective Two-Layer Model Scheduling Strategy	4.53	3024.1

.

Figure 8 and Table 1 demonstrate that the multi-objective two-layer dispatching strategy reduces load curve variance by 37.88% compared to the single-target optimization without dispatching, indicating suppressed grid load fluctuations. Power purchase costs decrease from CNY 4616.0 to 3024.1, significantly enhancing the economy of the 5G base station cluster. This improvement is due to regional coordination and energy sharing, where power-deficit areas of 5G base stations prioritize dispatching from surplus areas, reducing grid power purchases during peak times and aiding in grid peak load management while meeting their own needs. Additionally, energy sharing promotes efficient regional energy transmission, reducing grid reliance and minimizing power purchase costs, thus verifying the effectiveness of the 5G base station cluster’s multi-objective two-layer optimization model.

6. Conclusions

Aiming at the problem of 5G base station energy consumption and the problem of power grid load fluctuation, this paper constructs the 5G base station energy storage scheduling potential model of the 5G base station that considers the communication load transfer and base station dormancy, and proposes the multi-objective two-layer cooperative scheduling strategy of the 5G base station cluster considering energy sharing and power grid transaction. The following conclusions can be obtained through an example simulation:

• The proposed method can effectively expand the upper limit of backup energy storage during the trough period. On the one hand, it can better meet the charging demand of the grid side and increase the adjustable range of the Acer station by 35.932 kW; on the other hand, the 5G micro base station enters dormancy when meeting the dormancy threshold, reducing the overall power consumption of the base station side, and the maximum energy-saving efficiency can reach 9.13%;
• The multi-objective and two-layer optimization scheduling model of the 5G base station cluster designed in this paper can well take into account the demand of peak load shifting and valley filling on the power grid side and the economy of the 5G base station side. Using the spatial and temporal complementarity of each functional region, the mechanism of energy sharing and collaborative scheduling optimization among regions is constructed, so that the 5G cluster shows the characteristics of peak discharge and trough charging, and the variance of the power grid load curve is reduced by 37.88%. At the same time, inter-regional coordination can effectively reduce the overall outsourcing power of 5G base station peak time, and obtain benefits through the low charging and high charging of energy storage, reducing the power purchase cost from CNY 4616.0 to 3024.1, realizing a win-win situation between 5G base station operators and the power grid.

In this paper, there are ideal and single energy storage resources, and mobile energy storage [25] represented by electric vehicles are not considered. Meanwhile, the development of 6G communication technology will bring higher bandwidth, lower delay, and stronger network coverage [26], which can further optimize resource allocation and improve network performance. How to combine with cutting-edge communication technology to build a comprehensive optimal scheduling model considering the participation of multiple subjects is the author’s next research focus.