Optimization of Renewable-Based Multi-Energy Systems in Residential Building Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. Framework of the Decision-Making Process
2.2. Building the Case Study
2.3. Multi-Energy Systems Parameters
2.4. Energy Hub Formulation
2.5. Optimization Problem
- Constant parameters include all of the fixed values that are considered to be unchanged when solving the optimization problem.
- Design variables describe the optimization factors for the decision-making process and providing optimal solutions.
- Objective functions formulated by mathematical expressions include design variables and determining the goals of the optimization problem, i.e., the optimization criteria.
- Constraints impose the boundaries or the limitations or the requirements of the design variable in the optimization problem.
- Mathematical techniques define the type of the optimization problem (linear, integer, etc.) and select the appropriate solver for finding the optimal solutions.
2.5.1. Constant Parameters
2.5.2. Design Variables
2.5.3. Objective Functions
- Cost (EUR): The total annual economic costs including systems’ operation and installation, which are set for minimization.
- Ener (kWh): The total annual energy costs including systems’ primary energy consumption and embodied energy, which are set for minimization.
- Envir (kg CO2): The total annual environmental costs including systems’ GHG emission during operation and the embodied emissions, which are set for minimization.
- InstCost (EUR/kW or m2): The installation costs of the systems (Table 5).
- EmbEner (kWh/kW or m2): The embodied energy of the systems (Table 5).
- GHGEm (kg CO2/kW or m2): The embodied GHG emissions of the systems (Table 5).
- OpCost (EUR/kWh): The economic costs resulting from the systems’ operation (Table 4).
- PrEner (-): The primary energy factors for the grid electricity (Table 4).
- OpGHGEm (kg CO2/kWh): The environmental costs, i.e., the GHG emitted during systems operation (Table 4).
- LDi (years): The life duration of the energy systems examined (Table 5).
- Qjdem (kWh): The building energy demand for each energy use (j).
- Pjdem (kW): The power demand for each energy use (j).
- Hsol (kWh/m2): The incident solar irradiation.
- nPV, COPj: The efficiency of the photovoltaic systems and the coefficient of performance of the heat pumps (Table 5).
2.5.4. Constraints
- The design variable defining the participation level of the energy systems should be limited to a lower bound of 0% and an upper bound of 100%.
- The energy demand for each energy use should be fully met by at least one energy system.
- The installation of the heat pump should be considered only when its participation is preferable by the optimization criteria.
2.5.5. Mathematical Techniques
3. Results
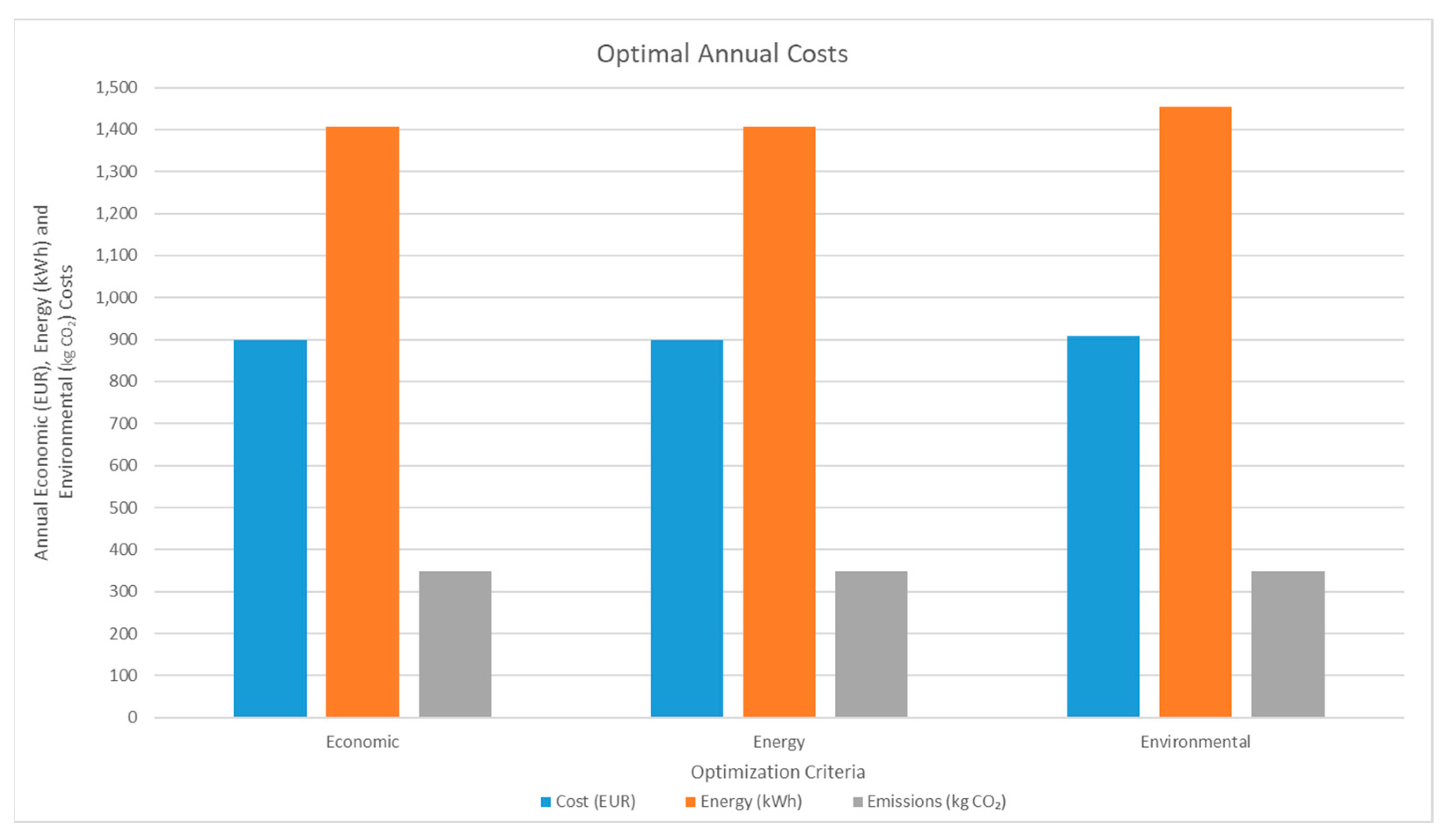
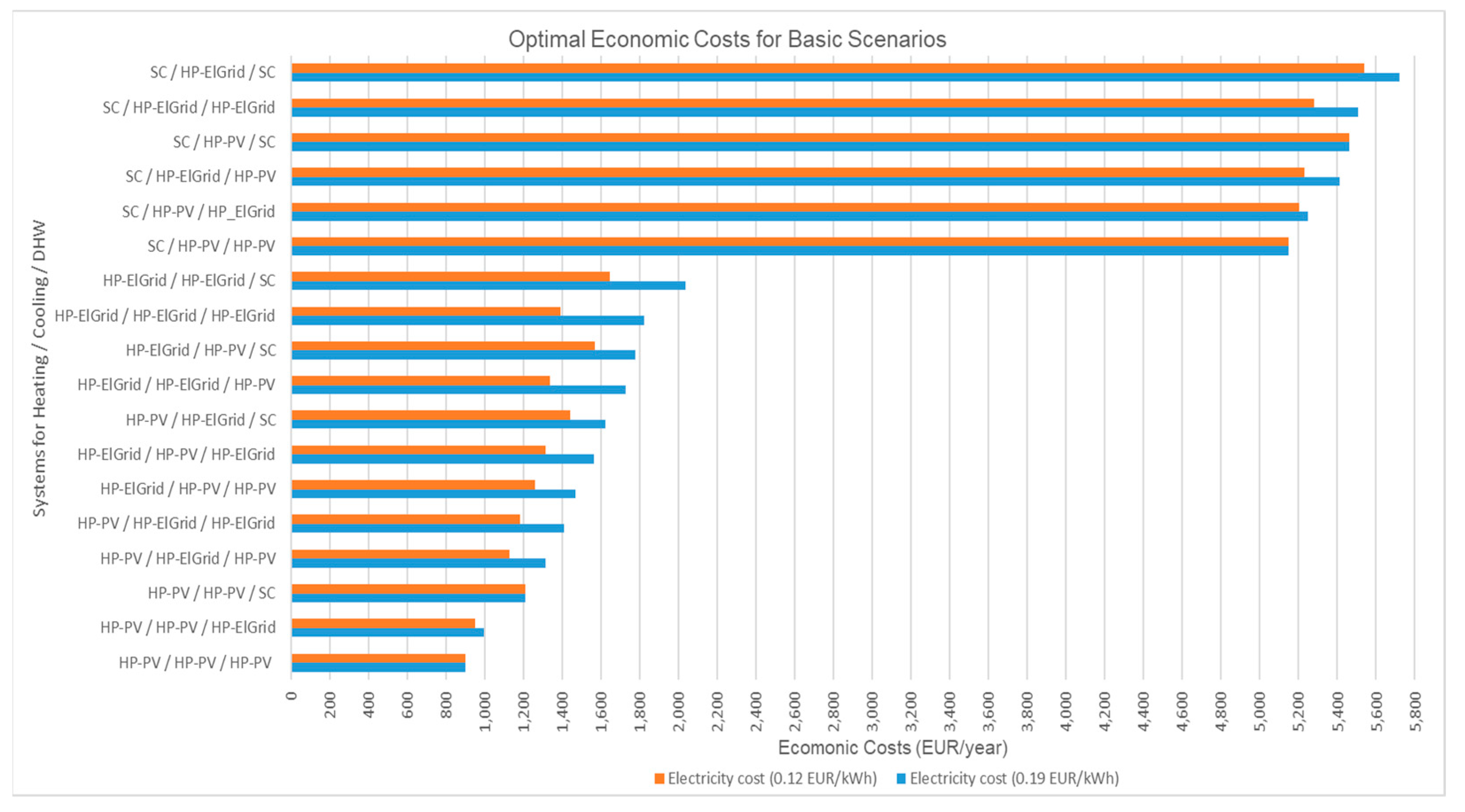
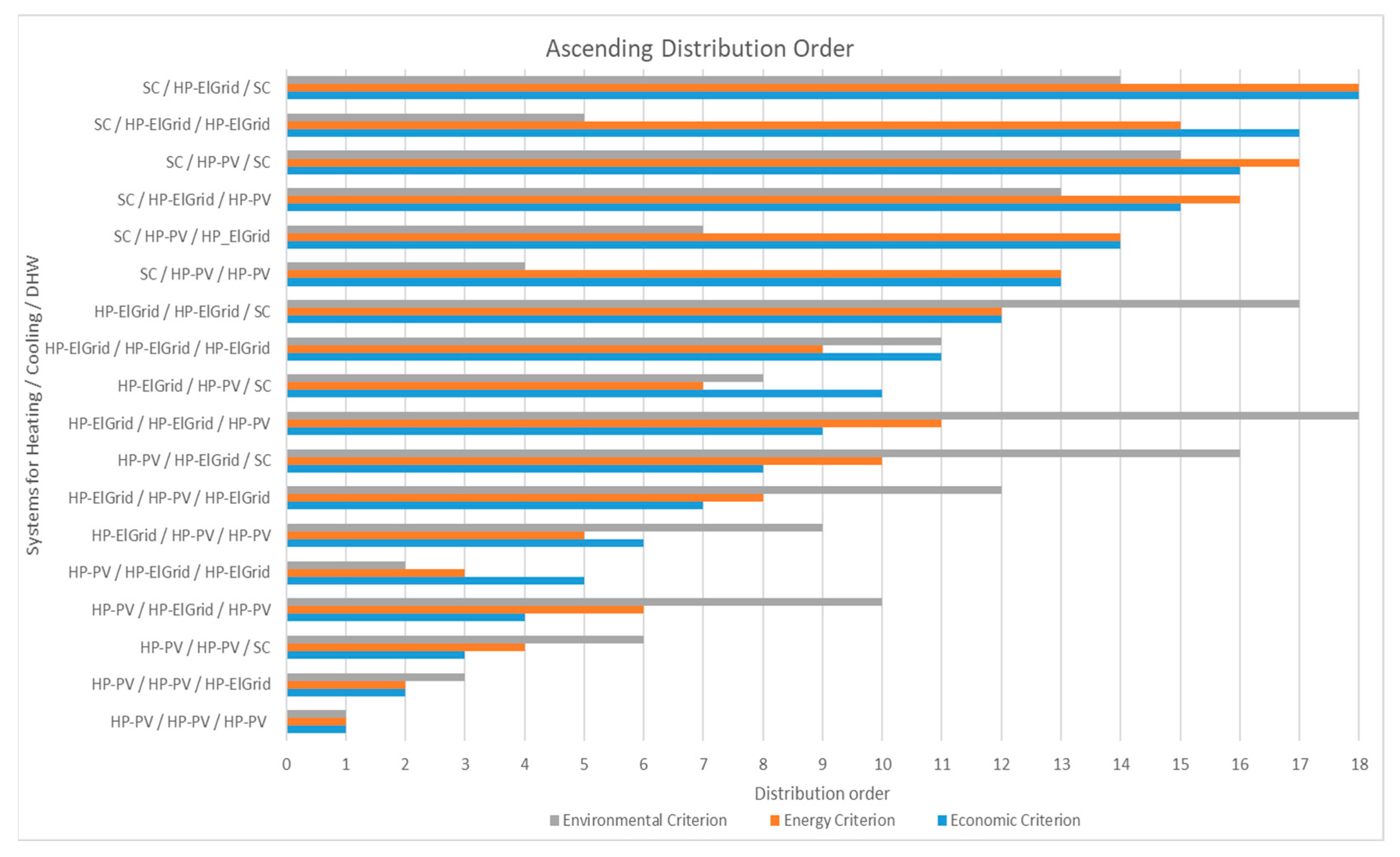
3.1. Optimization Results of the Proposed EH
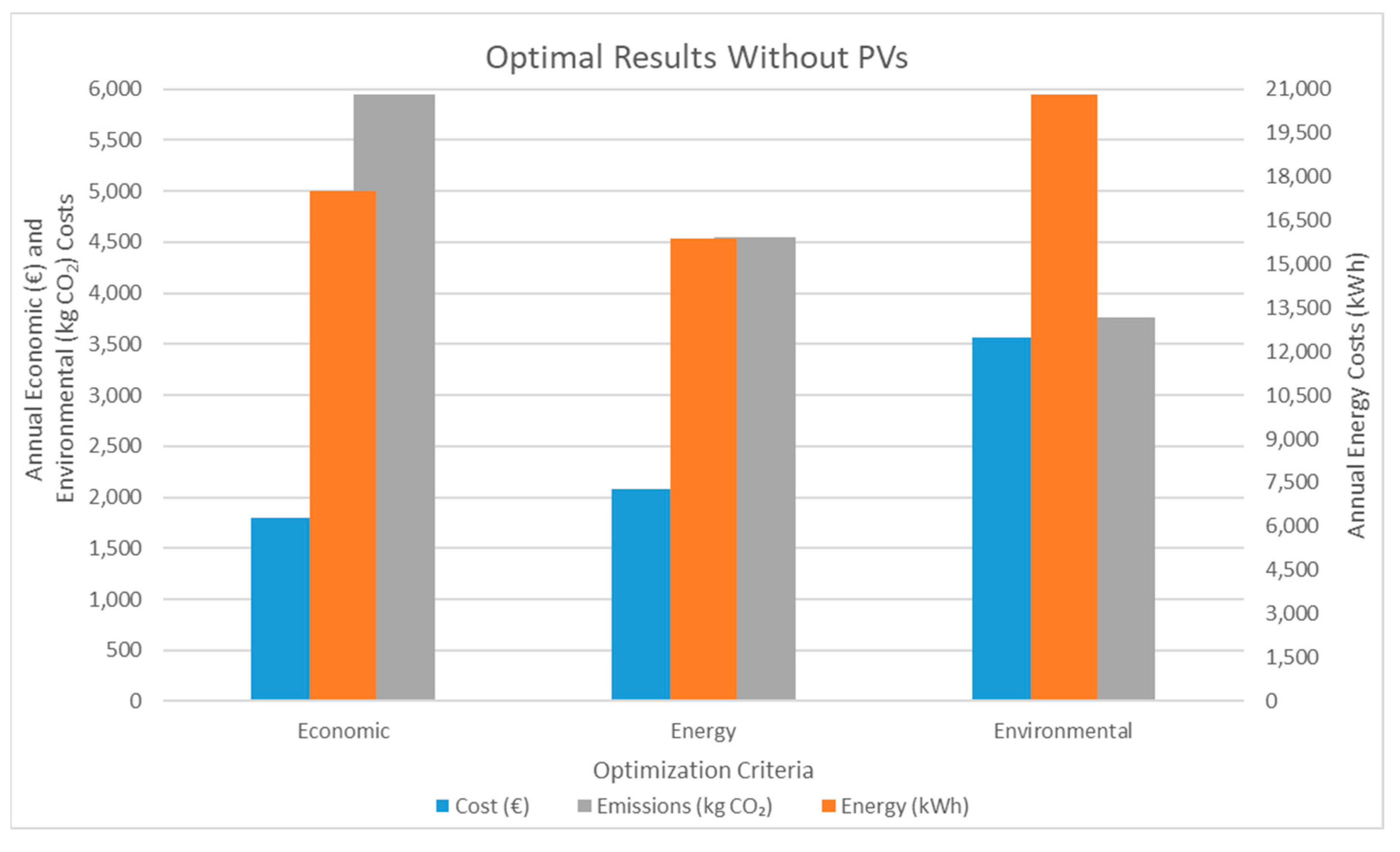
3.2. Optimization Results of the EH Without PVs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EU | European Union |
| GHG | greenhouse gas |
| RES | renewable energy source |
| EED | Energy Efficiency Directive |
| EPBD | Energy Performance of Buildings Directive |
| RED | Renewable Energy Directive |
| GOV | Governance Regulation |
| NECPs | National Energy and Climate Plans |
| NZEB | nearly zero-energy building |
| ZEB | zero-emission building |
| MEPS | Minimum Energy Performance Standards |
| ESM | energy saving measures |
| ESS | energy supply systems |
| EH | energy hub |
| LCA | life cycle assessment |
| GAMS | General Algebraic Modelling System |
| MP | mathematical programming |
| U-values | thermal transmittance coefficients |
| DHW | domestic hot water |
| H | space heating |
| C | space cooling |
| CO2 | carbon dioxide |
| EPD | Environmental Product Declaration |
| CED | cumulative energy demand |
| COP | coefficient of performance |
| EER | energy efficiency ratio |
| ALAMO | Automatic Learning of Algebraic Models |
| RMSE | root mean square error |
| HP | heat pump |
| SC | solar thermal collector |
| PV | photovoltaic system |
| LD | life duration |
References
- International Energy Agency (IEA). World Energy Outlook. Secure Sustainable Together; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Eurostat. Interactive Publications. Shedding Light on Energy in Europe—2024 Edition. Available online: https://ec.europa.eu/eurostat/web/interactive-publications/energy-2024#energy-consumption (accessed on 19 March 2025).
- Hamilton, I.; Kennard, H. 2020 Global Status Report for Buildings and Construction: Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector; United Nations Environment Programme: Nairobi, Kenya, 2020. [Google Scholar]
- Wong, J.K.W.; Li, H. Intelligent building research: A review. Autom. Constr. 2005, 14, 143–159. [Google Scholar] [CrossRef]
- European Commission, Directorate-General for Energy. EU Energy in Figures Statistical Pocketbook 2023. Publications Office of the European Union. 2023. Available online: https://data.europa.eu/doi/10.2833/502436 (accessed on 19 March 2025).
- Eurostat. Energy Statistics—An Overview. 2021. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Energy_statistics_-_an_overview#Primary_energy_production (accessed on 19 March 2025).
- UN Environment and IEA. Towards a Zero-Emission, Efficient, and Resilient Buildings and Construction Sector. Global Status Report 2017. 2017. Available online: www.globalabc.org (accessed on 1 March 2019).
- Rosenow, J.; Cowart, R.; Bayer, E.; Fabbri, M. Assessing the European Union’s Energy Efficiency Policy: Will the Winter Package deliver on “Efficiency First”? Energy Res. Soc. Sci. 2017, 26, 72–79. [Google Scholar] [CrossRef]
- Buildings Performance Institute Europe. 2017. Available online: https://www.bpie.eu/publication/97-of-buildings-in-the-eu-need-to-be-upgraded/ (accessed on 19 March 2025).
- European Environmental Agency (EEA). Greenhouse Gas Emissions from Energy Use in Buildings in Europe. 2024. Available online: https://www.eea.europa.eu/en/analysis/indicators/greenhouse-gas-emissions-from-energy (accessed on 19 March 2025).
- Buildings Performance Institute (BPIE). Deep Renovation: Shifting from Exception to Standard Practice in EU Policy. 2021. Available online: https://www.bpie.eu/wp-content/uploads/2021/11/BPIE_Deep-Renovation-Briefing_Final.pdf (accessed on 19 March 2025).
- International Renewable Energy Agency (IRENA). World Energy Transitions Out-Look. 2022. Available online: https://www.irena.org/Digital-Report/World-Energy-Transitions-Outlook-2022 (accessed on 19 March 2025).
- Buildings Performance Institute (BPIE). Report on the Evolution of the European Regulatory Framework for Buildings Efficiency. 2022. Available online: https://www.bpie.eu/wp-content/uploads/2022/02/rev6_SPIPA_EU.pdf (accessed on 19 March 2025).
- European Union. Directive (EU) 2024/1275 of the European Parliament and of the Council of 24 April 2024 on the Energy Performance of Buildings (Recast). In Official Journal of the European Union; European Union: Brussels, Belgium, 2024. [Google Scholar]
- European Commission. Communication from the Commission to the European parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions the European Green Deal. Brussels. 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2019%3A640%3AFIN (accessed on 19 March 2025).
- European Commission. Commission Welcomes Completion of Key “Fit for 55” Legislation, Putting EU on Track to Exceed 2030 Targets. Brussels. 2023. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_23_4754 (accessed on 19 March 2025).
- European Commission. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions. REPowerEU Plan. Brussels. 2022. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2022%3A230%3AFIN&qid=1653033742483 (accessed on 19 March 2025).
- Zhang, C.; Cui, C.; Zhang, Y.; Yuan, J.; Luo, Y.; Gang, W. A review of renewable energy assessment methods in green building and green neighborhood rating systems. Energy Build. 2019, 195, 68–81. [Google Scholar] [CrossRef]
- Ran, S.; Lyu, W.; Li, X.; Xu, W.; Wang, B. A solar-air source heat pump with thermosiphon to efficiently utilize solar energy. J. Build. Eng. 2020, 31, 101330. [Google Scholar] [CrossRef]
- Nik-Bakht, M.; Panizza, R.O.; Hudon, P.; Chassain, P.Y.; Bashari, M. Economy-energy trade off automation—A decision support system for building design development. J. Build Eng. 2020, 30, 2352–7102. [Google Scholar] [CrossRef]
- Fabrizio, Ε.; Corrado, V.; Filippi, Μ. A model to design and optimize multi-energy systems in buildings at the design concept stage. Renew. Energy 2010, 35, 644–655. [Google Scholar] [CrossRef]
- Kilis, V.; Paschalidis, N.; Ploskas, N.; Panaras, G. Energy Hub Optimization on Residential Building Case. E3S Web Conf. 2023, 436, 01017. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Zhang, C.; Fan, C. Attention-based interpretable neural network for building cooling load prediction. Appl. Energy 2021, 299, 117238. [Google Scholar] [CrossRef]
- Haddad, S.; Synnefa, A.; Marcos, M.Á.P.; Paolini, R.; Delrue, S.; Prasad, D.; Santamouris, M. On the potential of demand-controlled ventilation system to enhance indoor air quality and thermal condition in Australian school classrooms. Energy Build. 2021, 238, 110838. [Google Scholar] [CrossRef]
- Zhang, C.; Gang, W.; Wang, J.; Xu, X.; Du, Q. Numerical and experimental study on the thermal performance improvement of a triple glazed window by utilizing low-grade exhaust air. Energy 2019, 167, 1132–1143. [Google Scholar] [CrossRef]
- D’Agostino, D.; Mazzarella, L. What is a Nearly zero energy building? Overview, implementation and comparison of definitions. J. Build. Eng. 2019, 21, 200–212. [Google Scholar] [CrossRef]
- Harkouss, F.; Fardoun, F.; Biwole, P.H. Multi-objective optimization methodology for net zero energy buildings. J. Build. Eng. 2018, 16, 57–71. [Google Scholar] [CrossRef]
- Longo, S.; Montana, F.; Riva Sanseverino, E. A review on optimization and cost-optimal methodologies in low-energy buildings design and environmental considerations. Sustain. Cities Soc. 2019, 45, 87–104. [Google Scholar] [CrossRef]
- Ferrara, M.; Della Santa, F.; Bilardo, M.; De Gregorio, A.; Mastropietro, A.; Fugacci, U.; Vaccarino, F.; Fabrizio, E. Design optimization of renewable energy systems for NZEBs based on deep residual learning. Renew. Energy 2021, 176, 590–605. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-Timescale Security Evaluation and Regulation of Integrated Electricity and Heating System. IEEE Trans. Smart Grid 2024, 16, 1088–1099. [Google Scholar] [CrossRef]
- Sergi, B.; Pambour, K. An Evaluation of Co-Simulation for Modeling Coupled Natural Gas and Electricity Networks. Energies 2022, 15, 5277. [Google Scholar] [CrossRef]
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Sontag, R.; Lange, A. Cost effectiveness of decentralized energy supply systems taking solar and wind utilization plants into account. Renew. Energy 2003, 28, 1865–1880. [Google Scholar] [CrossRef]
- Zhao, R.; Zheng, W. Efficient operation of combined residential and commercial energy hubs incorporating load management and two-point approximation for uncertainty modeling. Comput. Electr. Eng. 2024, 116, 109197. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X.; Wu, H.; He, Y.; Xu, B.; Ding, M. Energy hub management for integrated energy systems: A multi-objective optimization control strategy based on distributed output and energy conversion characteristics. Energy 2024, 306, 132526. [Google Scholar] [CrossRef]
- Zhai, X.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Wang, P.; Sun, H. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Zeineddine, A.W.; Assi, C. Demand-side management by regulating charging and discharging of the EV ESS and utilizing renewable energy. IEEE Trans. Ind. Inform. 2018, 14, 117–126. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Zheng, X. Stochastic-Weighted Robust Optimization Based Bilayer Operation of a Multi-Energy Building Microgrid Considering Practical Thermal Loads and Battery Degradation. IEEE Trans. Sustain. Energy 2022, 13, 668–682. [Google Scholar] [CrossRef]
- ΤΕΕ 20701-1; Analytical Technical Specifications of Parameters for the Calculation of Buildings’ Energy Performance and the Issuing of Energy Performance Certificate. Technical Directive of the Technical Chamber of Greece (TEE): Athens, Greece, 2017.
- Manoudis, A. Life Cycle Analysis of Energy Systems Used in Residential Buildings. Master’s Thesis, International Hellenic University, Thessaloniki, Greece, 2011. [Google Scholar]
- Longo, S.; Cellura, M.; Guarino, F.; La Rocca, V.; Maniscalco, G.; Morale, M. Embodied energy and environmental impacts of a biomass boiler: A life cycle approach. AIMS Energy 2015, 3, 214–226. [Google Scholar] [CrossRef]
- Frischknecht, R.; Rebitzer, G. The Ecoinvent database system: A comprehensive web based LCA database. J. Clean. Prod. 2005, 13, 1337–1343. [Google Scholar] [CrossRef]
- Cabal, H.; Lechon, Y.; Saez, R. Environmental aspects of integration of decentralized generation into the overall electricity generation system. In EUSUSTEL Task Report; Ministerio de Educación y Ciencia: Madrid, Spain, 2005. [Google Scholar]
- Ochoa, L.; Ries, R.; Matthews, H.S.; Hendrickson, C. Life Cycle Assessment of Residential Buildings. In American Society of Civil Engineers Construction Research Congress; Working Paper; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Mouzeviris, G.; Papakostas, Κ. Comparative Analysis of Air-to-Water and Ground Source Heat Pumps Performances. Int. J. Sustain. Energy 2021, 40, 69–84. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Solar Engineering of Thermal Processes, Photovoltaics and Wind, 5th ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Rosli, M.A.M.; Zaki, D.S.M.; Rahman, F.A.; Sepeai, S.; Nurfaizey, A.H.; Nawam, M. F-chart method for design domestic hot water heating system in Ayer Keroh Melaka. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 59–67. [Google Scholar]
- Wilson, Z.T.; Sahinidis, N.V. The ALAMO approach to machine learning. Comput. Chem. Eng. 2017, 106, 785–795. [Google Scholar] [CrossRef]
- Bilard, M.; Galata, S.; Fabrizio, E. The role of Primary Energy Factors (PEF) for electricity in the evaluation and comparison of building energy performance: An investigation on European nZEBs according to EN 17423:2020. Sustain. Cities Soc. 2019, 87, 104189. [Google Scholar] [CrossRef]
- Balaras, C.A.; Dascalaki, E.G.; Psarra, I.; Cholewa, T. Primary Energy Factors for Electricity Production in Europe. Energies 2023, 16, 93. [Google Scholar] [CrossRef]
- Balaras, C.A.; Dascalaki, E.G.; Patsioti, M.; Droutsa, K.G.; Kontoyiannidis, S.; Cholewa, T. Carbon and Greenhouse Gas Emissions from Electricity Consumption in European Buildings. Buildings 2023, 14, 71. [Google Scholar] [CrossRef]
- Achterberg, T. SCIP: Solving constraint integer programs. Math. Prog. Comp. 2009, 1, 1–41. [Google Scholar] [CrossRef]

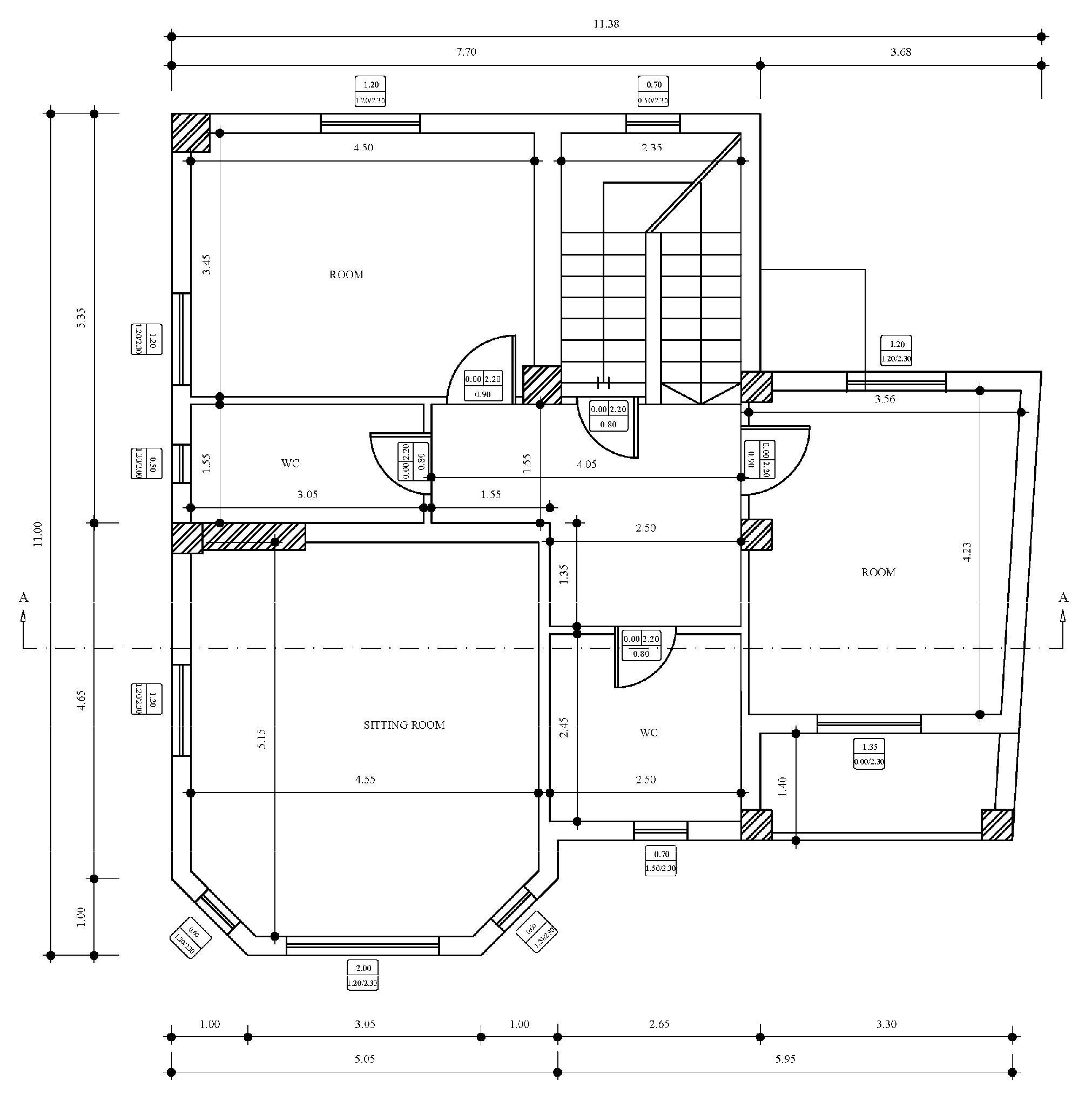

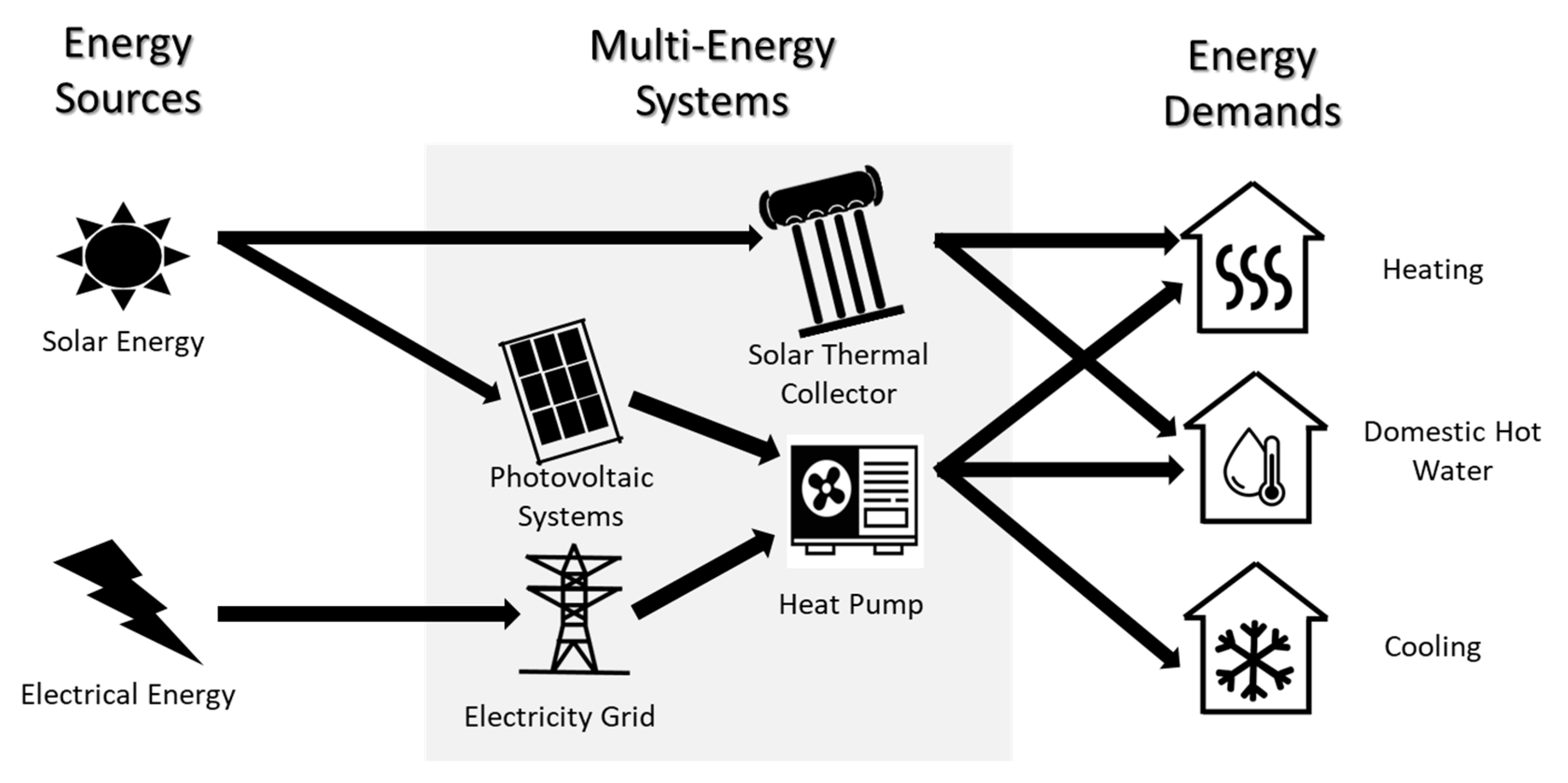
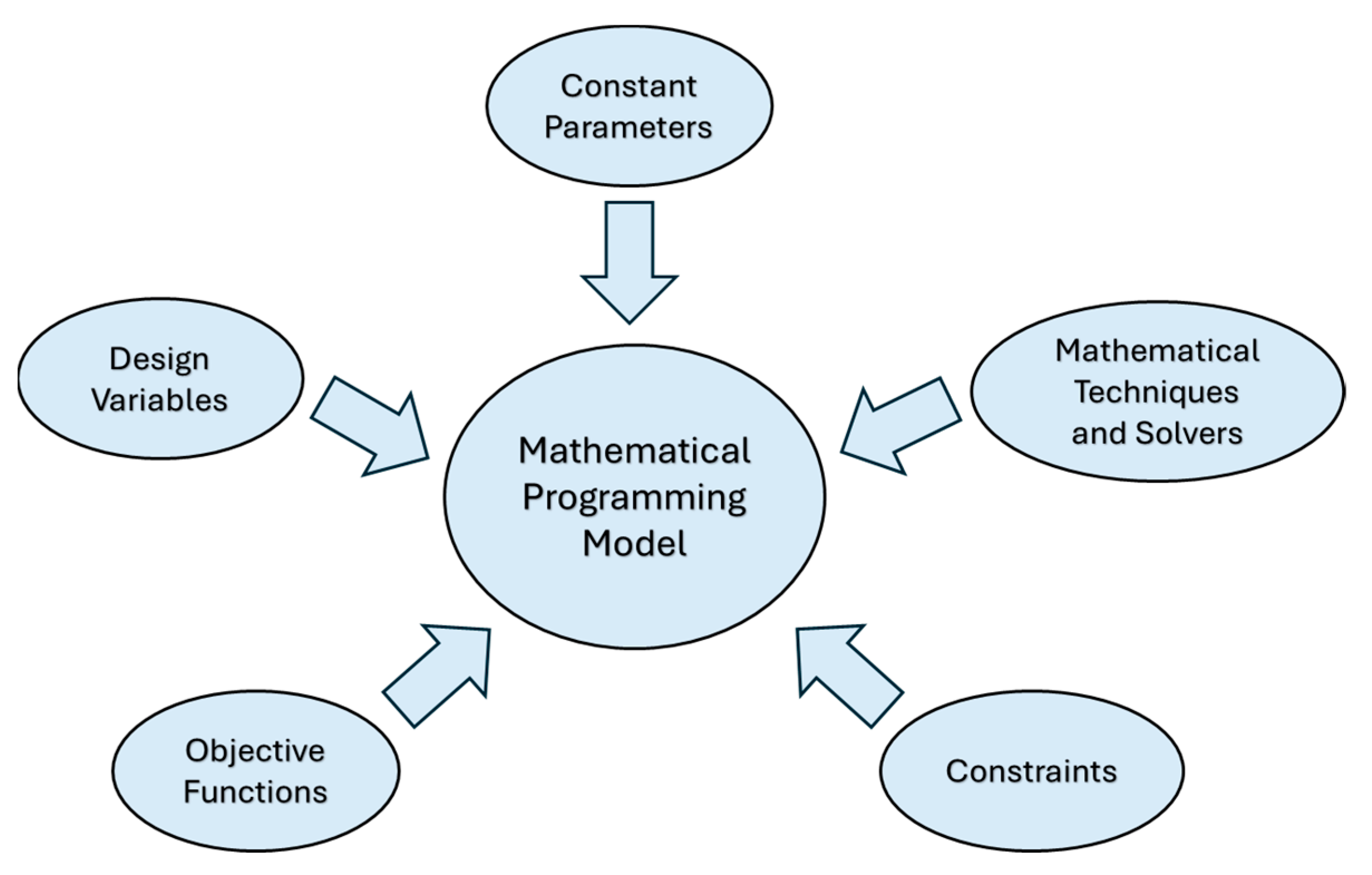
| Geometric Parameters | Values |
|---|---|
| Height (m) | 12 |
| Floor area (m2) | 390.5 |
| Volume (m3) | 1171.5 |
| Façade surface (m2) | 667.5 |
| Window surface (m2) | 41 |
| Components | U-Values (W/m2K) |
|---|---|
| External wall | 0.6 |
| Floor | 0.85 |
| Roof | 0.55 |
| Windows | 2.4 |
| Solar Collector Parameters | Values |
|---|---|
| Thermal performance curve slope—FRUL | 4 W/m2K |
| Thermal performance intercept—FR(τα)n | 0.75 |
| Coefficient for collector location—τα/(τα)n | 0.96 |
| Heat exchanger coefficient—F’R/FR | 0.95 |
| Storage tank volume per collector area—M | 75 L/m2 |
| Energy Sources | Economic Costs (EUR/kWh) | Primary Energy Factors | GHG Emission Coefficients (kg CO2/kWh) |
|---|---|---|---|
| Solar Energy | 0 | 0 | 0 |
| Electrical Energy | 0.12/0.19 | 2.9/2.1/1.8 | 0.989/0.6/0.2 |
| Energy System Parameters | Heat Pump | Solar Collector | Photovoltaic System |
|---|---|---|---|
| Efficiency | 4/4.3 1 | f-chart | 0.2 |
| Life Duration (years) | 25 | 25 | 25 |
| Installation Costs | 600 EUR/kW | 380 EUR/m2 | 250 EUR/m2 |
| Energy Costs | 142 kWh/kW | 103 kWh/m2 | 192.5 kWh/m2 |
| Environmental Costs | 337 kg CO2/kW | 1890 kg CO2/m2 | 1022 kg CO2/m2 |
| Design Variables | Values | Definition |
|---|---|---|
| Non-negative [0,1] | The participation level of the energy systems’ operation | |
| Binary (0 or 1) | The participation of the energy systems’ installation (HP) | |
| i represents the energy systems examined, i.e., heat pump (HP), solar thermal collector (SC) and the photovoltaic system (PV) j represents the energy uses; thus, the building energy demand for space heating (H), cooling (C) and domestic hot water (DHW) | ||
| Optimization Criteria | Economic | Energy | Environmental |
|---|---|---|---|
| Heating | 100% HP-ElGrid | 51.6% HP-ElGrid 48.4% SC (36 m2) | 12.6% HP-ElGrid 87.4% SC (140.5 m2) |
| Cooling | 100% HP-ElGrid | 100% HP-ElGrid | 100% HP-ElGrid |
| DHW | 40% HP-ElGrid 60% SC (2.5 m2) | 18.8% HP-ElGrid 81.2% SC (5.5 m2) | 4.6% HP-ElGrid 95.4% SC (14.5 m2) |
| (a) Economic Criterion | ||||
| Sensitivity Analysis Parameters | Systems | Economic | Energy | Environmental |
| 0.19/2.9/0.989 1 | 27 kW HP-ELGrid 2.5 m2 SC | EUR 1794 | 17,514.5 kWh | 5947.6 kg CO2 |
| 0.19/2.1/0.6 1 | 12,835.3 kWh | 3672.4 kg CO2 | ||
| 0.19/1.8/0.2 1 | 11,080.6 kWh | 1332.7 kg CO2 | ||
| (b) Energy Criterion | ||||
| Sensitivity Analysis Parameters | Systems | Economic | Energy | Environmental |
| 0.19/2.9/0.989 1 | 27 kW HP-ELGrid 41.5 m2 SC | EUR 2082 | 15,870.3 kWh | 4549.9 kg CO2 |
| 0.19/2.1/0.6 1 | 27 kW HP-ELGrid 20 m2 SC | EUR 1892 | 12,293.4 kWh | 3209.8 kg CO2 |
| 0.19/1.8/0.2 1 | 27 kW HP-ELGrid 15.5 m2 SC | EUR 1855 | 10,776.3 kWh | 1243.7 kg CO2 |
| (c) Environmental Criterion | ||||
| Sensitivity Analysis Parameters | Systems | Economic | Energy | Environmental |
| 0.19/2.9/0.989 1 | 27 kW HP-ELGrid 155 m2 SC | EUR 3569 | 20,796.4 kWh | 3766.7 kg CO2 |
| 0.19/2.1/0.6 1 | 27 kW HP-ELGrid 120.5 m2 SC | EUR 3084 | 16,180.6 kWh | 2563.1 kg CO2 |
| 0.19/1.8/0.2 1 | 27 kW HP-ELGrid 49.5 m2 SC | EUR 2172 | 11,448.6 kWh | 1172 kg CO2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilis, V.; Anastasiadis, G.; Ploskas, N.; Panaras, G. Optimization of Renewable-Based Multi-Energy Systems in Residential Building Design. Energies 2025, 18, 1541. https://doi.org/10.3390/en18061541
Kilis V, Anastasiadis G, Ploskas N, Panaras G. Optimization of Renewable-Based Multi-Energy Systems in Residential Building Design. Energies. 2025; 18(6):1541. https://doi.org/10.3390/en18061541
Chicago/Turabian StyleKilis, Vasileios, Georgios Anastasiadis, Nikolaos Ploskas, and Giorgos Panaras. 2025. "Optimization of Renewable-Based Multi-Energy Systems in Residential Building Design" Energies 18, no. 6: 1541. https://doi.org/10.3390/en18061541
APA StyleKilis, V., Anastasiadis, G., Ploskas, N., & Panaras, G. (2025). Optimization of Renewable-Based Multi-Energy Systems in Residential Building Design. Energies, 18(6), 1541. https://doi.org/10.3390/en18061541








