Flow Management in High-Viscosity Oil–Gas Mixing Systems: A Study of Flow Regimes
Abstract
:1. Introduction
2. Physical and Mathematical Model
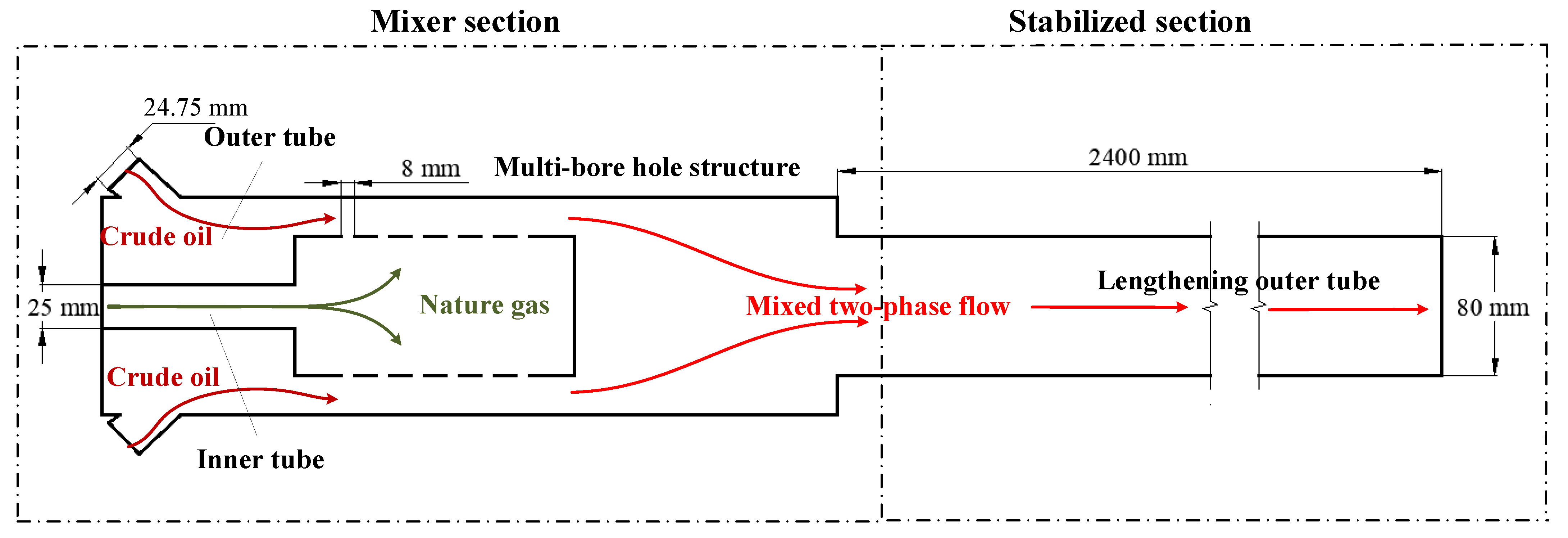
2.1. Physical Model
2.2. Governing Equations
2.3. Physical Parameter Range
2.4. Mesh Independence Verification and Validation Test
3. Results and Discussion
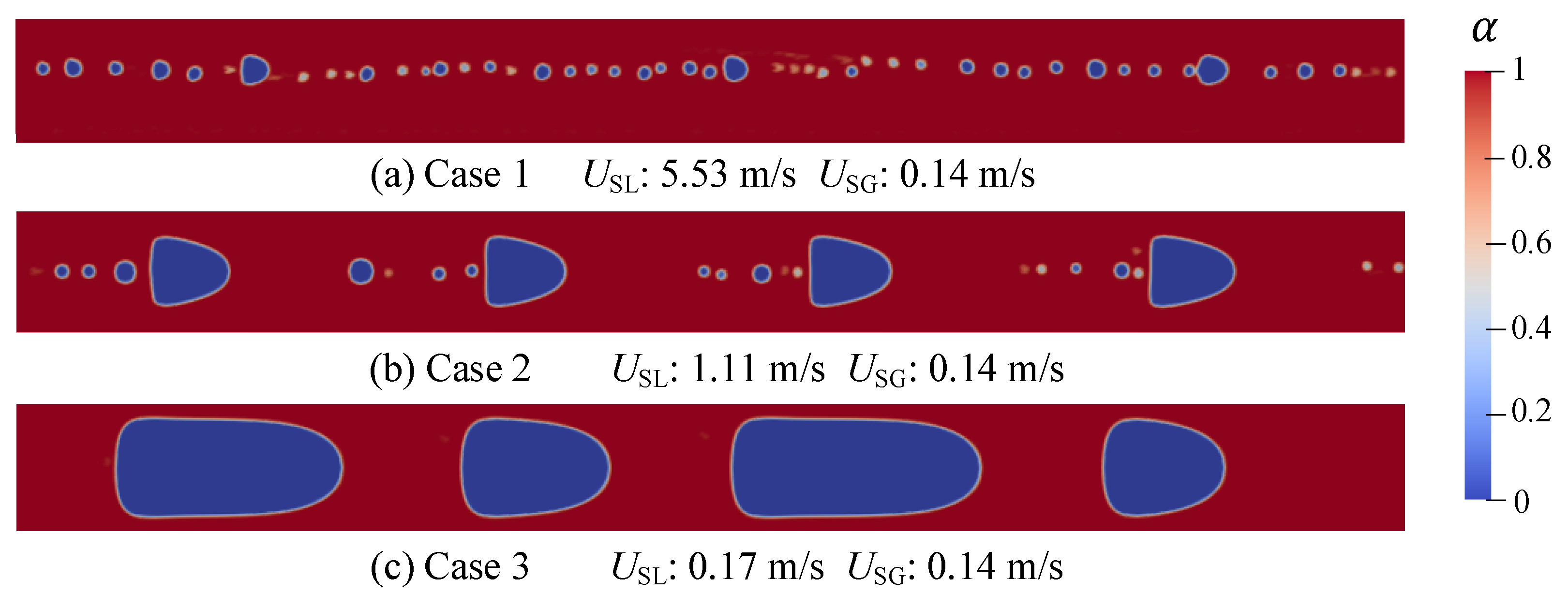
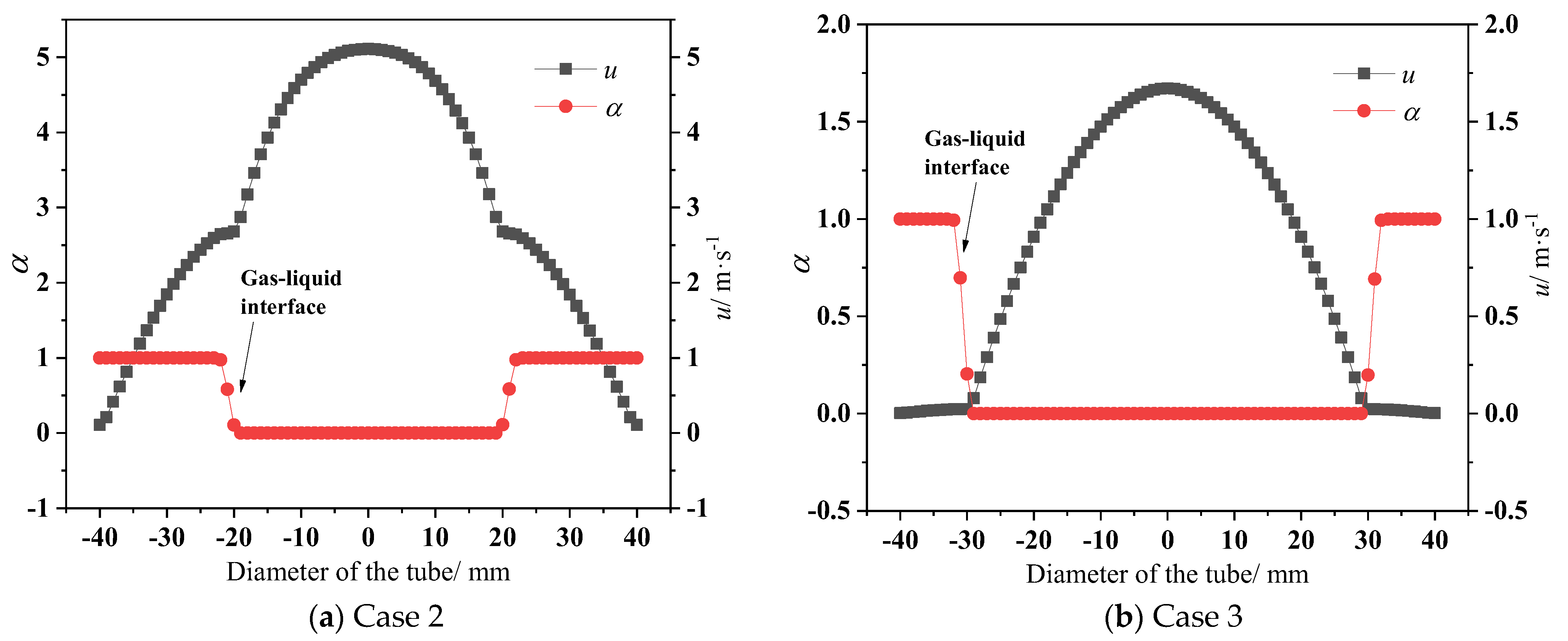
3.1. Bubble Flow and Plug Flow
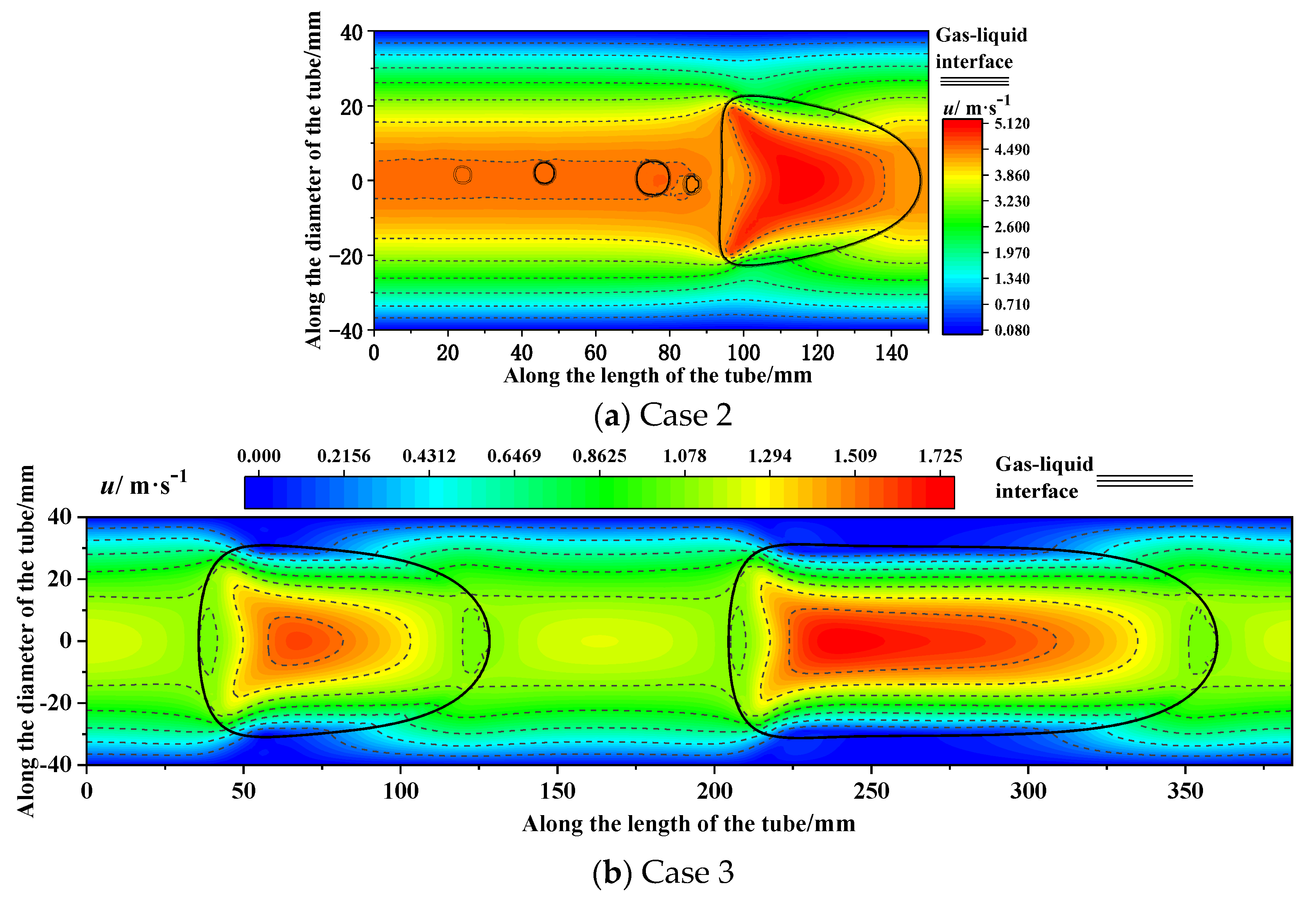
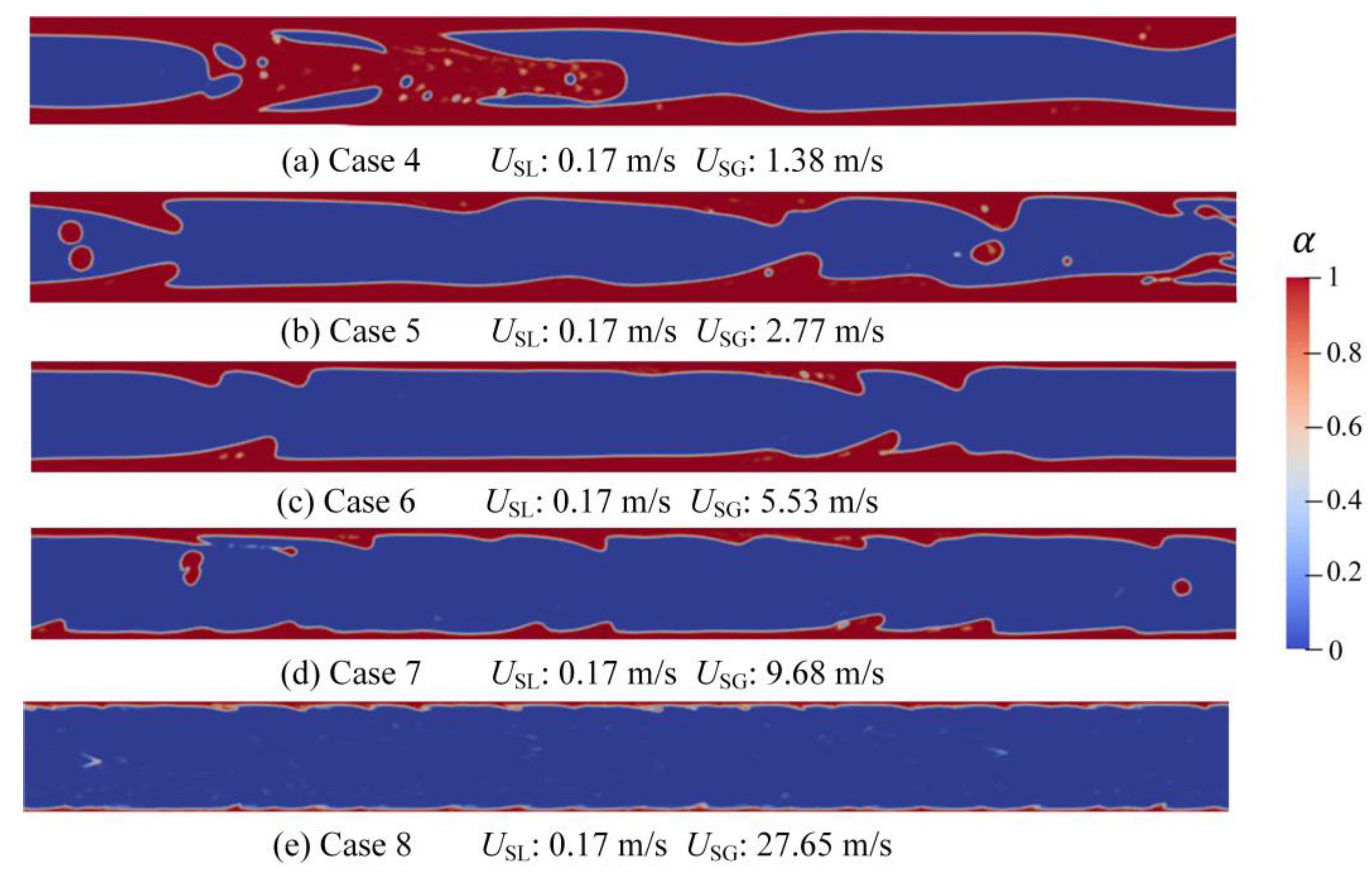
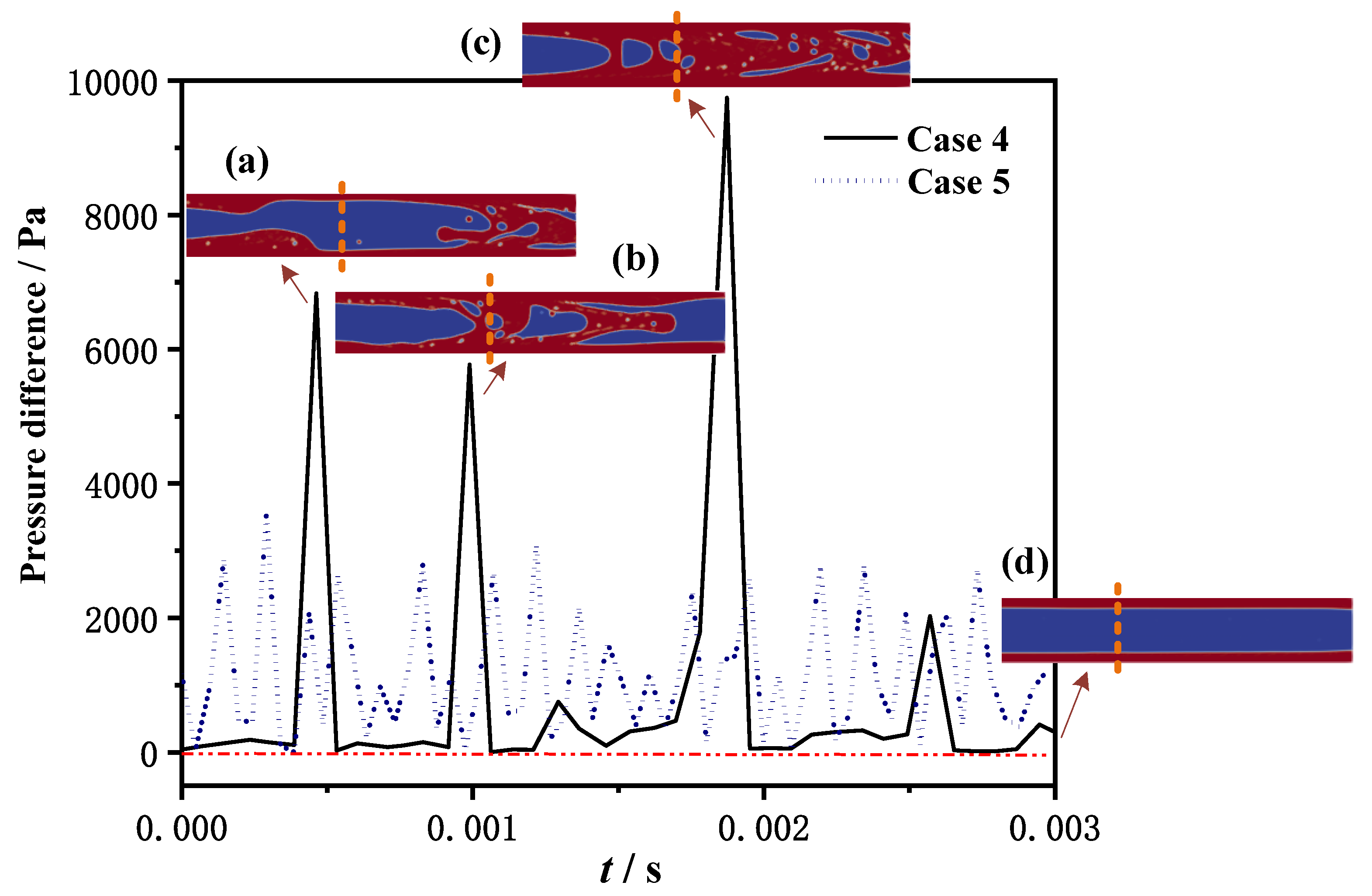
3.2. Slug Flow and Wave Flow
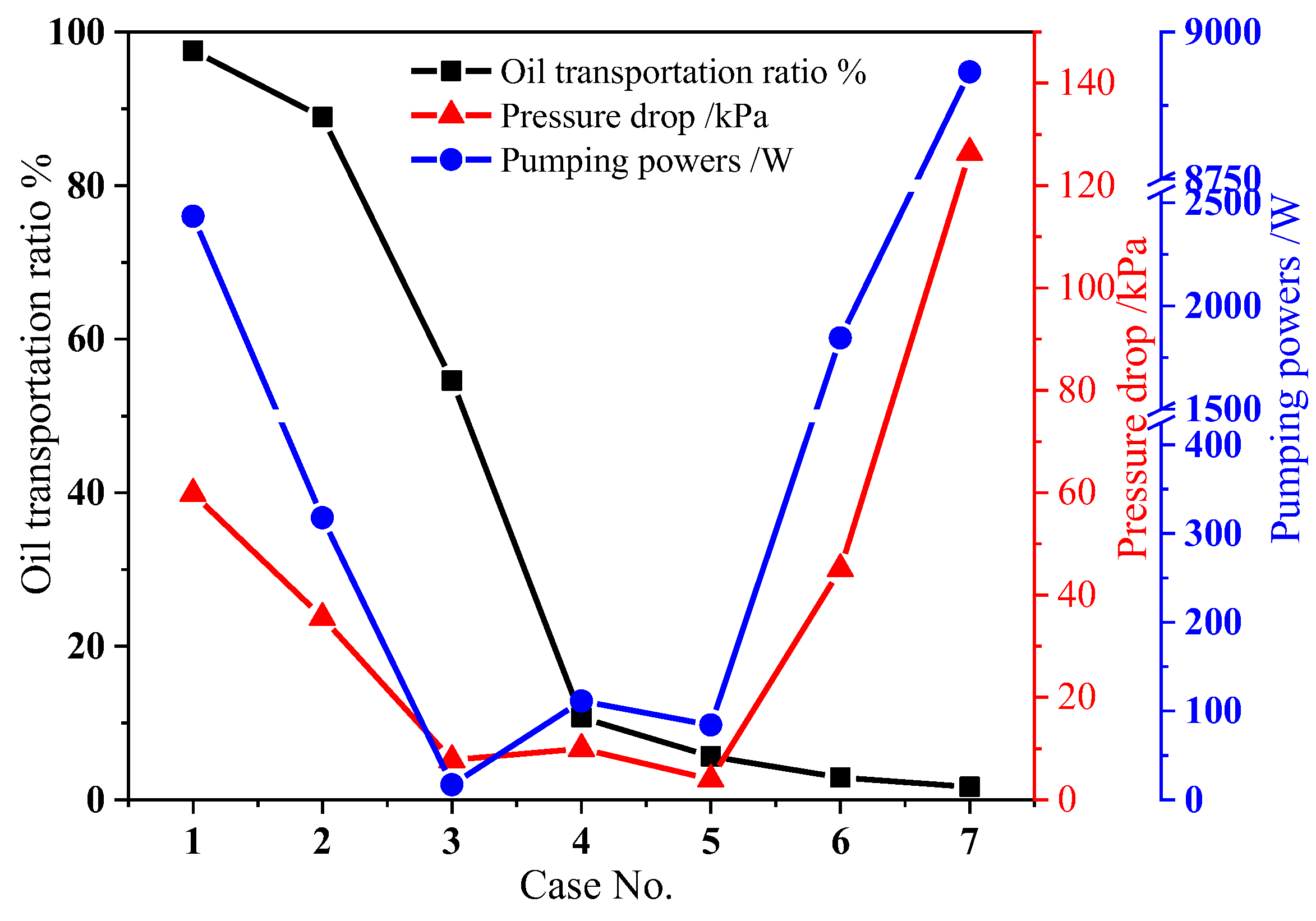
3.3. Energy Consumption Analysis
4. Conclusions
- (a)
- The growth of bubbles within the pipeline was influenced by the interplay of volume fraction, flow velocity, and bubble slip velocity.
- (b)
- In the plug flow, owing to the high viscosity of the oil, the small bubbles formed in the wake remained largely intact, in contrast to the fragmentation seen in air–water two-phase flows.
- (c)
- In the slug flow, the intermittent interaction of liquid with the upper and lower walls resulted in significant pressure fluctuations. This phenomenon should be avoided in practical operations.
- (d)
- The stable annular flow exhibited the lowest pressure drop loss, making it the ideal condition for oil–gas multiphase transport. The plug flow, on the other hand, offered the advantages of high oil transportation rates and low pump power consumption.
5. Future Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khaledi, H.A.; Smith, I.E.; Unander, T.E.; Nossen, J. Investigation of two-phase flow pattern, liquid holdup and pressure drop in viscous oil–gas flow. Int. J. Multiph. Flow 2014, 67, 37–51. [Google Scholar] [CrossRef]
- Otsubo, Y. Hydrogen compression and long-distance transportation: Emerging technologies and applications in the oil and gas industry—A technical review. Energy Convers. Manag. X 2025, 25, 100836. [Google Scholar] [CrossRef]
- Jansen, F.E.; Shoham, O.; Taitel, Y. The elimination of severe slugging—Experiments and modeling. Int. J. Multiph. Flow 1996, 22, 1055–1072. [Google Scholar] [CrossRef]
- Baliño, J.L.; Burr, K.P.; Nemoto, R.H. Modeling and simulation of severe slugging in air–water pipeline–riser systems. Int. J. Multiph. Flow 2010, 36, 643–660. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Q.; Cao, Y.; Huang, B.; Guo, L. Effects of riser height and pipeline length on the transition boundary and frequency of severe slugging in offshore pipelines. Ocean Eng. 2024, 298, 117253. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Q.; Fu, J.; Chang, Y.; Wu, Q.; Guo, L. Study on eliminating severe slugging by manual and automatic choking in long pipeline-riser system. Chem. Eng. Sci. 2024, 292, 119978. [Google Scholar] [CrossRef]
- Baba, Y.D.; Aliyu, A.M.; Archibong, A.E.; Abdulkadir, M.; Lao, L.; Yeung, H. Slug length for high viscosity oil-gas flow in horizontal pipes: Experiments and prediction. J. Pet. Sci. Eng. 2018, 165, 397–411. [Google Scholar] [CrossRef]
- Liu, X.-M.; Zhong, H.-Q.; Li, Y.-C.; Liu, Z.-N.; Wang, Q. Experimental study of flow patterns and pressure drops of heavy oil-water-gas vertical flow. J. Hydrodyn. Ser. B 2014, 26, 646–653. [Google Scholar] [CrossRef]
- Chen, K.; Wang, X.; Peng, H.; Liu, W.; Chen, P.; Wen, L. Study on water fraction of oil–gas–water three-phase flow based on electrical methods. Energy Rep. 2022, 8, 90–98. [Google Scholar] [CrossRef]
- Wang, D.; Jin, N.; Zhai, L.; Ren, Y. Quantitative research of the liquid film characteristics in upward vertical gas, oil and water flows. Chin. J. Chem. Eng. 2023, 54, 67–79. [Google Scholar] [CrossRef]
- Chang, Y.; Xu, Q.; Zou, S.; Zhao, X.; Wu, Q.; Wang, Y.; Thévenin, D.; Guo, L. Experiments and predictions for severe slugging of gas-liquid two-phase flows in a long-distance pipeline-riser system. Ocean Eng. 2024, 301, 117636. [Google Scholar] [CrossRef]
- Li, Z.; Tan, C.; Zhang, S.; Dong, F. Global-local state analysis and monitoring-based velocity measurement of oil–gas–water three-phase flow. Chem. Eng. J. 2024, 497, 154759. [Google Scholar] [CrossRef]
- Abdelsamie, A.; Voß, S.; Berg, P.; Chi, C.; Arens, C.; Thévenin, D.; Janiga, G. Comparing LES and URANS results with a reference DNS of the transitional airflow in a patient-specific larynx geometry during exhalation. Comput. Fluids 2023, 255, 105819. [Google Scholar] [CrossRef]
- Mandhane, J.M.; Gregory, G.A.; Aziz, K. A flow pattern map for gas—Liquid flow in horizontal pipes. Int. J. Multiph. Flow 1974, 1, 537–553. [Google Scholar] [CrossRef]
- Mukherjee, H.; Brill, J.P. Empirical equations to predict flow patterns in two-phase inclined flow. Int. J. Multiph. Flow 1985, 11, 299–315. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for slug frequency during gas-liquid flow in horizontal and near horizontal pipes. Int. J. Multiph. Flow 1977, 3, 585–596. [Google Scholar] [CrossRef]
- Lin, P.Y.; Hanratty, T.J. Prediction of the initiation of slugs with linear stability theory. Int. J. Multiph. Flow 1986, 12, 79–98. [Google Scholar] [CrossRef]
- Shaaban, O.M.; Al-Safran, E.M. Prediction of slug length for high-viscosity oil in gas/liquid horizontal and slightly inclined pipe flows. Geoenergy Sci. Eng. 2023, 221, 211348. [Google Scholar] [CrossRef]
- Padoin, N.; Souza, A.Z.D.; Ropelato, K.; Soares, C. Numerical simulation of isothermal gas−liquid flow patterns in microchannels with varying wettability. Chem. Eng. Res. Des. 2016, 109, 698–706. [Google Scholar] [CrossRef]
- Yan, K.; Che, D. A coupled model for simulation of the gas–liquid two-phase flow with complex flow patterns. Int. J. Multiph. Flow 2010, 36, 333–348. [Google Scholar] [CrossRef]
- Nieves-Remacha, M.J.; Yang, L.; Jensen, K.F. OpenFOAM Computational Fluid Dynamic Simulations of Two-Phase Flow and Mass Transfer in an Advanced-Flow Reactor. Ind. Eng. Chem. Res. 2015, 54, 6649–6659. [Google Scholar] [CrossRef]
- Nagarajan, H.K.; Trujillo, M.F. Quantifying a common inconsistency in RANS-VoF modeling of water and oil core annular flow. Int. J. Multiph. Flow 2024, 181, 105008. [Google Scholar] [CrossRef]
- Li, H.; Pourquié, M.J.B.M.; Ooms, G.; Henkes, R.A.W.M. DNS and RANS for core-annular flow with a turbulent annulus. Int. J. Multiph. Flow 2024, 174, 104733. [Google Scholar] [CrossRef]
- Li, S.; Kang, Y.; Wang, T.; Pan, W.; Li, C.X. Numerical Simulation on Jet Flow Characteristics of Pressure Drop Sleeve of Drain Regulating Valve. Fluid Mach. 2019, 47, 19–26. [Google Scholar] [CrossRef]
- Warren, B.A.; Klausner, J.F. Developing Lengths in Horizontal Two-Phase Bubbly Flow. J. Fluids Eng. 1995, 117, 512–518. [Google Scholar] [CrossRef]
- Salcudean, M.; Groeneveld, D.C.; Leung, L. Effect of flow-obstruction geometry on pressure drops in horizontal air-water flow. Int. J. Multiph. Flow 1983, 9, 73–85. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Bankoff, S.G.; Lee, S.C. A Comparison of Flooding Models for Air-Water and Steam-Water Flow. In Advances in Two-Phase Flow and Heat Transfer; Kakaç, S., Ishii, M., Eds.; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1983; Volume 64, pp. 745–780. [Google Scholar] [CrossRef]
- Weller, H.G. A New Approach to VOF-based Interface Capturing Methods for Incompressible and Compressible Flow. Tech. Rep. 2008, 4, 35. [Google Scholar]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
- Li, H.; Pourquié, M.J.B.M.; Ooms, G.; Henkes, R.A.W.M. Simulation of vertical core-annular flow with a turbulent annulus. Int. J. Multiph. Flow 2023, 167, 104551. [Google Scholar] [CrossRef]
- Li, H.; Pourquié, M.J.B.M.; Ooms, G.; Henkes, R.A.W.M. Simulation of a turbulent annulus with interfacial waves in core-annular pipe flow. Int. J. Multiph. Flow 2022, 154, 104152. [Google Scholar] [CrossRef]
- Feng, G.K.; Wang, X. Oil & Gas Gathering & Transportation; University of Petroleum Press: Dongying, China, 1988; pp. 154–159. [Google Scholar]
- Alameedy, U.; Al-Sarkhi, A.; Abdul-Majeed, G. Comprehensive review of severe slugging phenomena and innovative mitigation techniques in oil and gas systems. Chem. Eng. Res. Des. 2025, 213, 78–94. [Google Scholar] [CrossRef]


| Working Fluid | Viscosity/m2·s−1 | Density/kg·m−3 |
|---|---|---|
| Oil | 3.79 × 10−5 | 845 |
| Natural gas | 1.38 × 10−6 | 8.7 |
| Case No. | Inlet Velocity/m·s−1 | Superficial Velocity/m·s−1 | ||
|---|---|---|---|---|
| Oil | Gas | Oil | Gas | |
| 1 | 28.88 | 1.42 | 5.53 | 0.14 |
| 2 | 5.78 | 1.42 | 1.11 | 0.14 |
| 3 | 0.87 | 1.42 | 0.17 | 0.14 |
| 4 | 0.87 | 14.15 | 0.17 | 1.38 |
| 5 | 0.87 | 28.31 | 0.17 | 2.77 |
| 6 | 0.87 | 56.62 | 0.17 | 5.53 |
| 7 | 0.87 | 99.08 | 0.17 | 9.68 |
| 8 | 0.87 | 283.09 | 0.17 | 27.65 |
| Elements No. | 68,965 | 108,637 | 155,594 | 192,094 |
| Film thickness/mm | 7.68 | 7.96 | 8.16 | 8.16 |
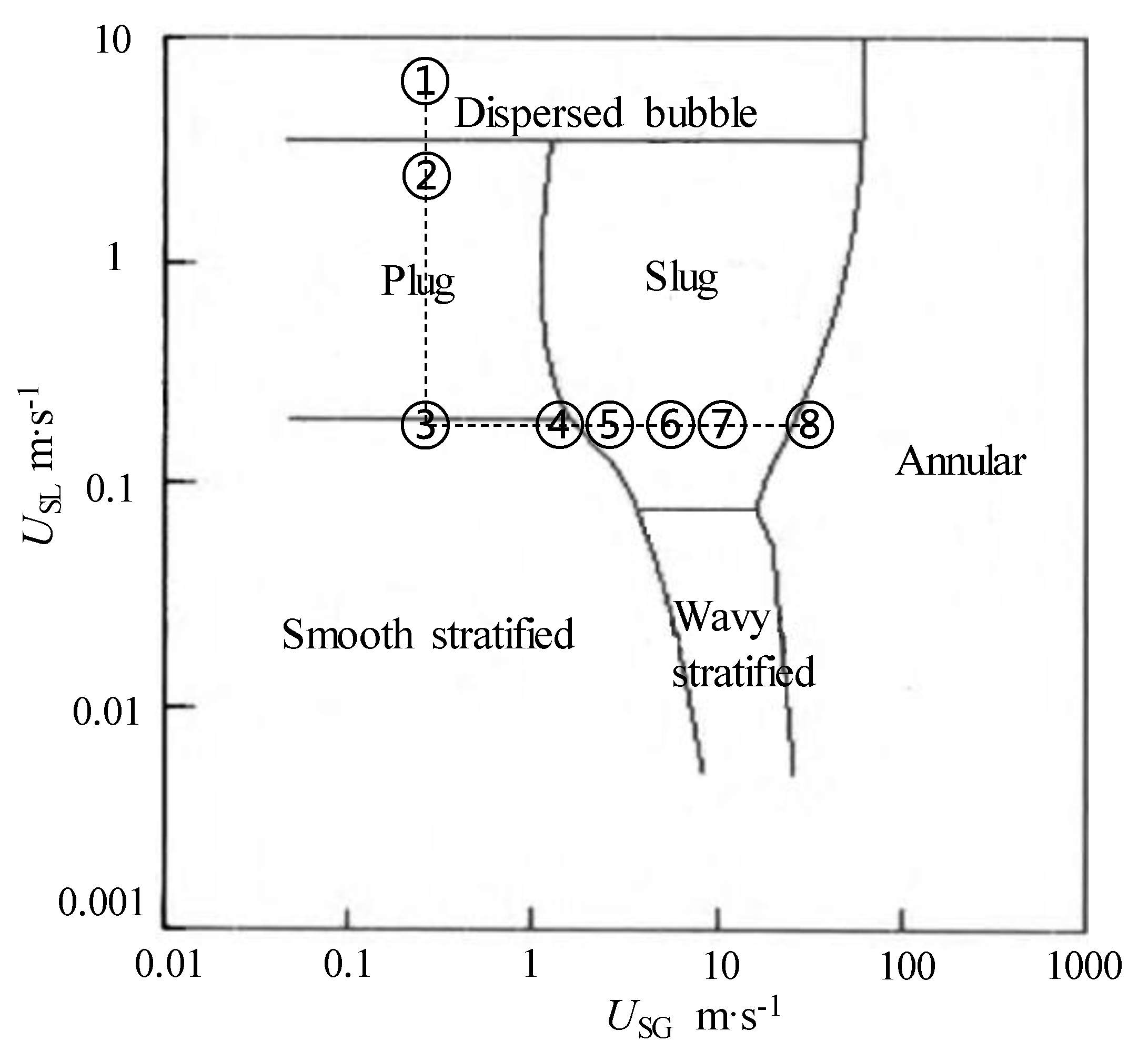
| Case No. | USL/m·s−1 | USG/m·s−1 | OpenFOAM | Bill | Mandhane |
|---|---|---|---|---|---|
| 1 | 5.53 | 0.14 | Bubble | Bubble | Dispersed bubble |
| 2 | 1.11 | 0.14 | Bubble | Bubble | Plug |
| 3 | 0.17 | 0.14 | Plug | Stratified | Plug / Stratified * |
| 4 | 0.17 | 1.38 | Slug | Slug | Plug / Slug / Stratified * |
| 5 | 0.17 | 2.77 | Annular | Slug | Slug |
| 6 | 0.17 | 5.53 | Annular | Slug | Slug |
| 7 | 0.17 | 9.68 | Annular | Annular/Slug | Slug |
| 8 | 0.17 | 27.65 | Annular | Annular | Annular |
| Case No. | H/mm | ul/m·s−1 | ugl/m·s−1 |
|---|---|---|---|
| 2 | 42 | 2.66 | 0.038 |
| 3 | 61 | 0.05 | 0.057 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Li, M.; Wang, Y. Flow Management in High-Viscosity Oil–Gas Mixing Systems: A Study of Flow Regimes. Energies 2025, 18, 1550. https://doi.org/10.3390/en18061550
Tian J, Li M, Wang Y. Flow Management in High-Viscosity Oil–Gas Mixing Systems: A Study of Flow Regimes. Energies. 2025; 18(6):1550. https://doi.org/10.3390/en18061550
Chicago/Turabian StyleTian, Jiaming, Mao Li, and Yueshe Wang. 2025. "Flow Management in High-Viscosity Oil–Gas Mixing Systems: A Study of Flow Regimes" Energies 18, no. 6: 1550. https://doi.org/10.3390/en18061550
APA StyleTian, J., Li, M., & Wang, Y. (2025). Flow Management in High-Viscosity Oil–Gas Mixing Systems: A Study of Flow Regimes. Energies, 18(6), 1550. https://doi.org/10.3390/en18061550







