Fully Distributed Consensus Voltage Restoration Control Based on Dynamic Event-Triggered Mechanisms for Offshore Wind Power Systems
Abstract
:1. Introduction
- (1)
- (2)
- (3)
- Compared to traditional, static event-triggered mechanisms, this paper proposes a dynamic event-triggered control scheme for offshore wind power systems. Unlike existing control approaches, the proposed scheme achieves faster convergence. By analyzing the voltage characteristics of the offshore wind power system, dynamic triggering conditions related to the system state are introduced to effectively reduce the communication burden and simplify system complexity.
2. Modeling Framework
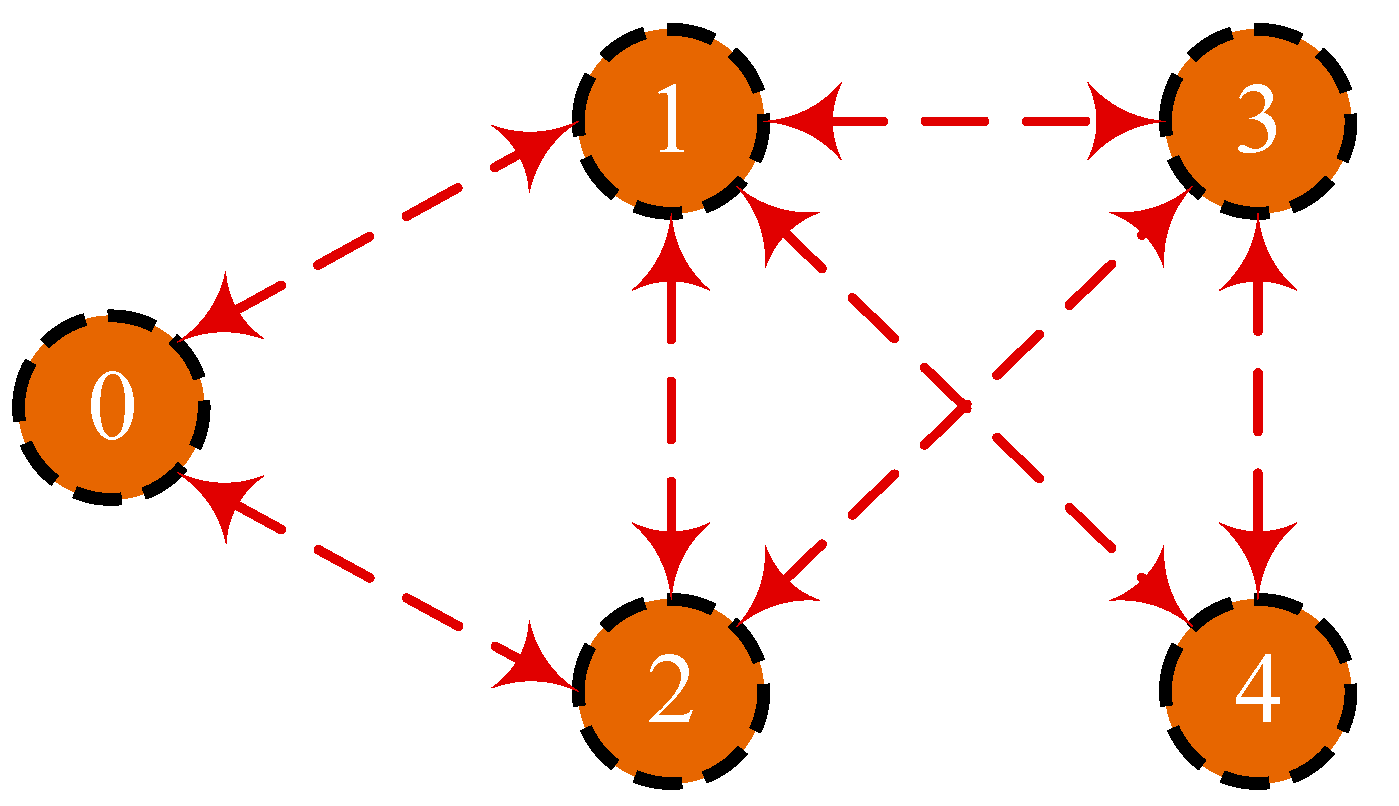
2.1. Graph Theory
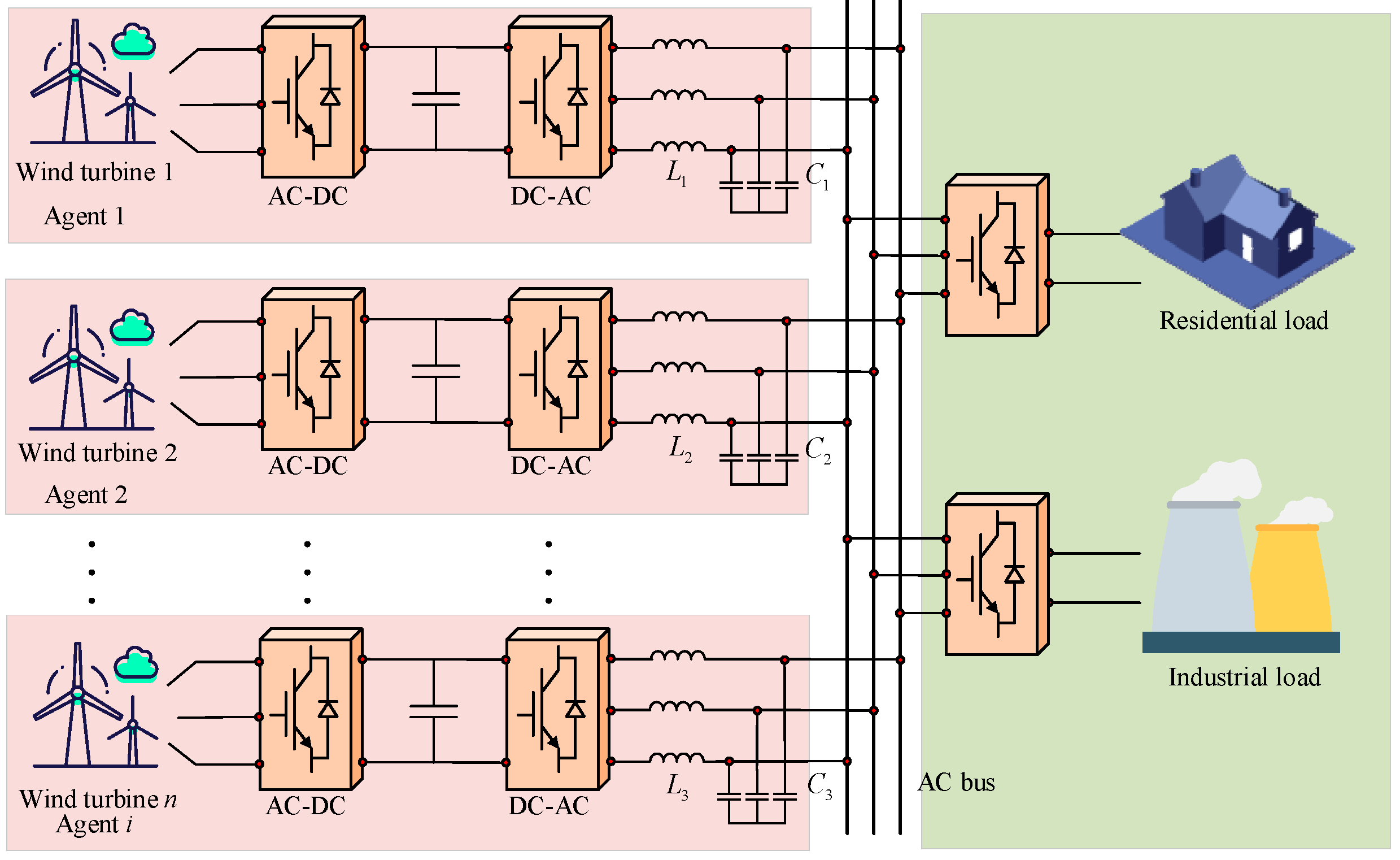
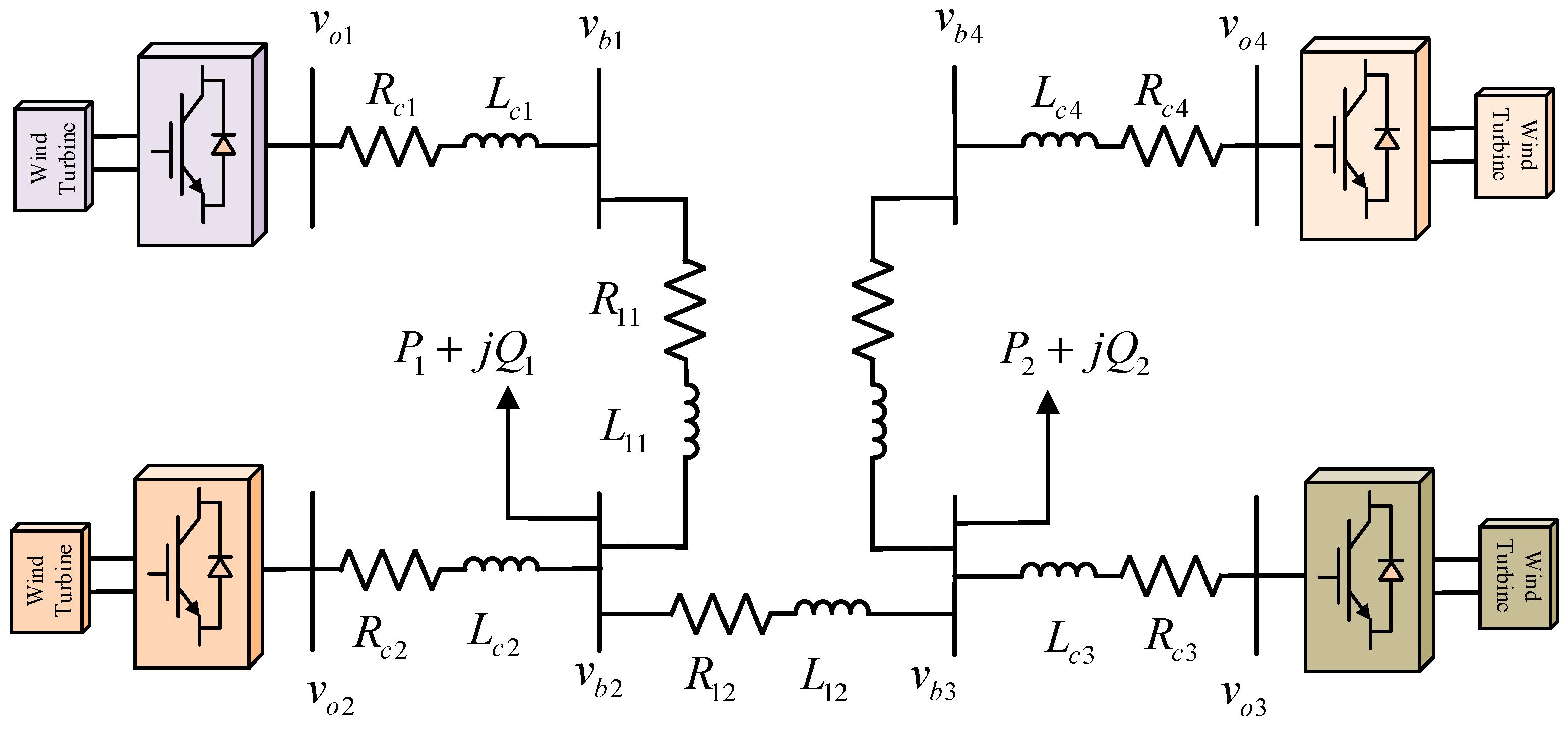
2.2. Structural Modeling of Offshore Wind Power Systems
3. Fully Distributed Secondary Voltage Control Based on Adaptive Dynamic Event-Triggered Mechanisms
3.1. Dynamic Event Trigger Controller Design
3.2. No Zeno Behavior Proof
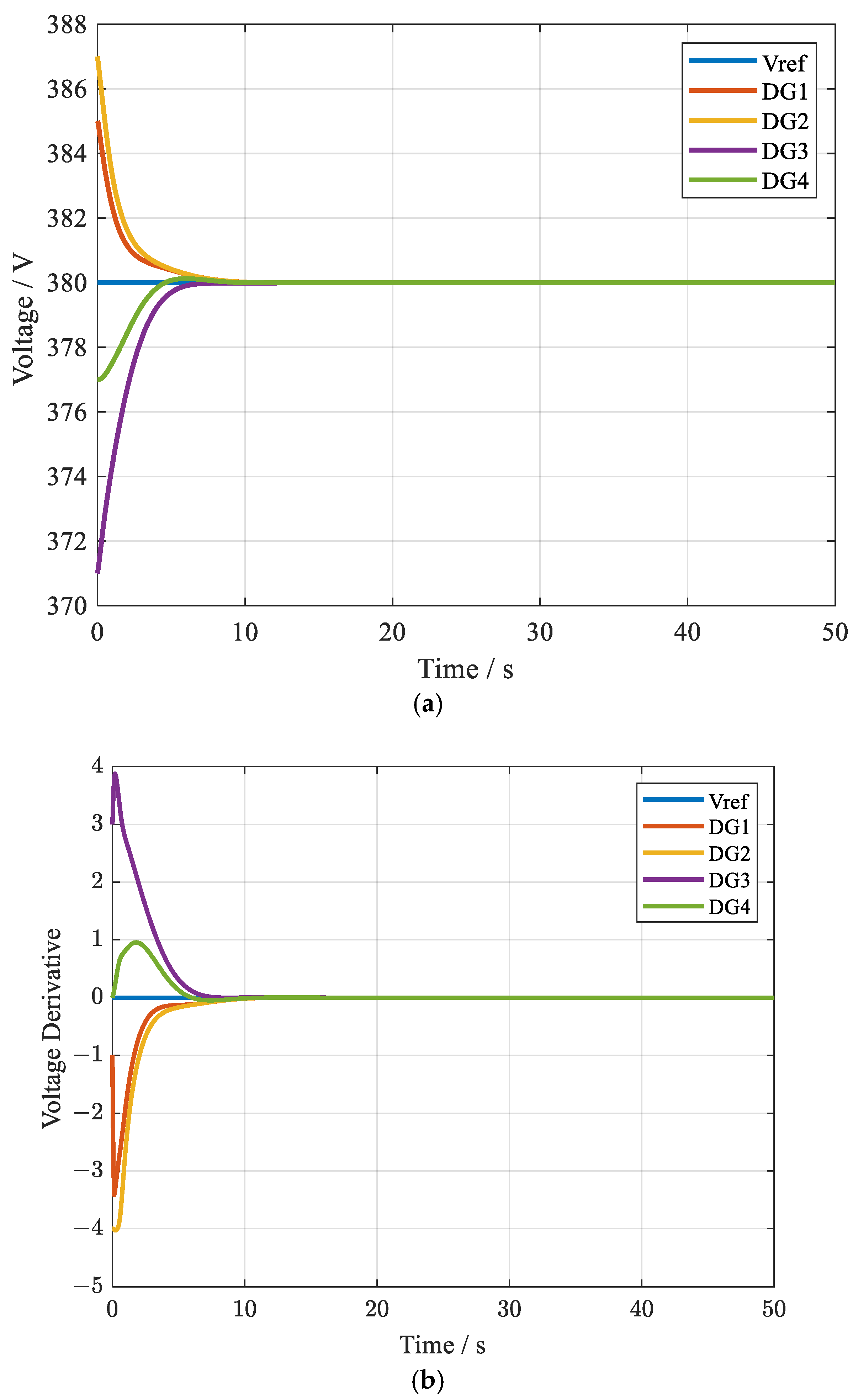
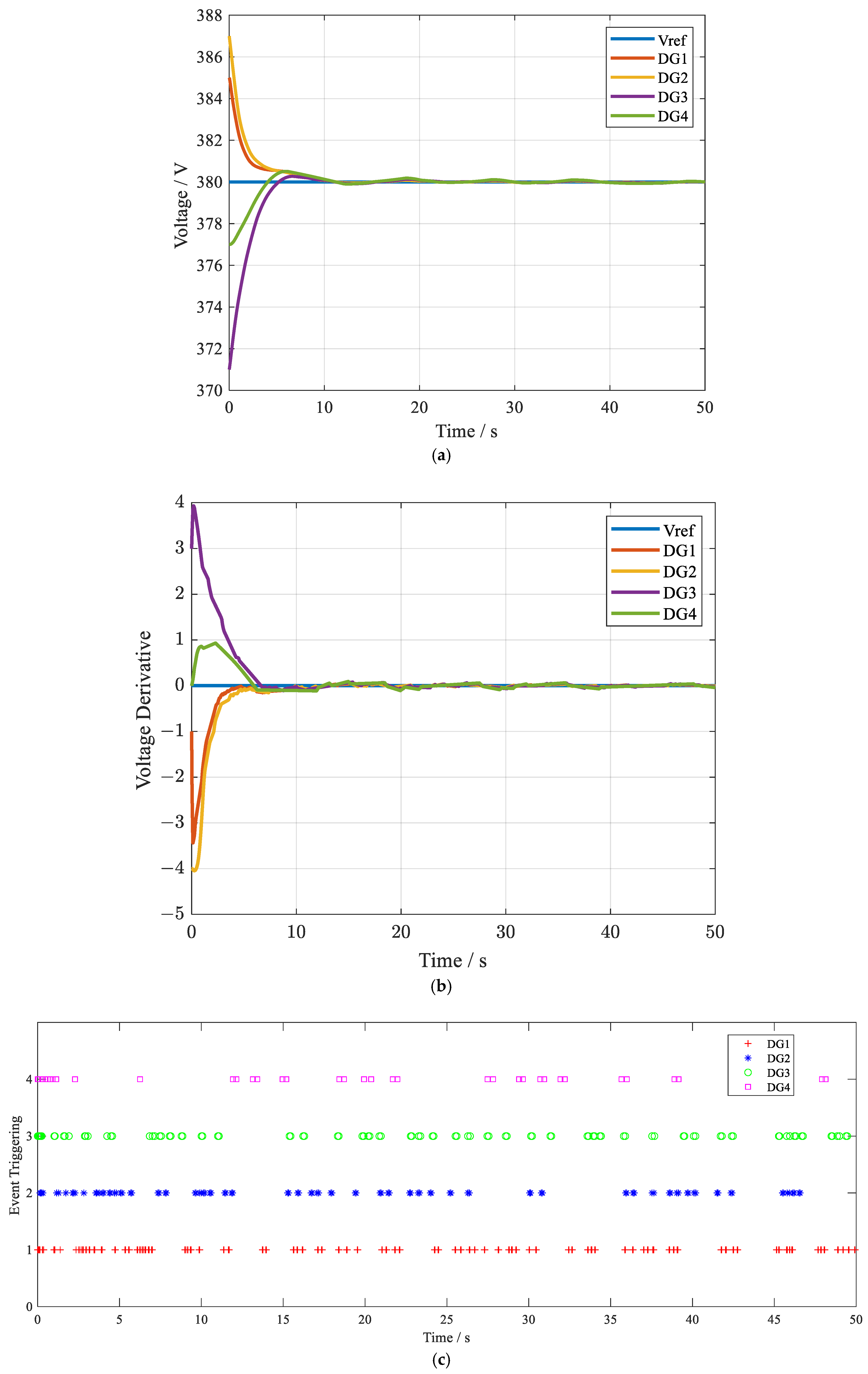
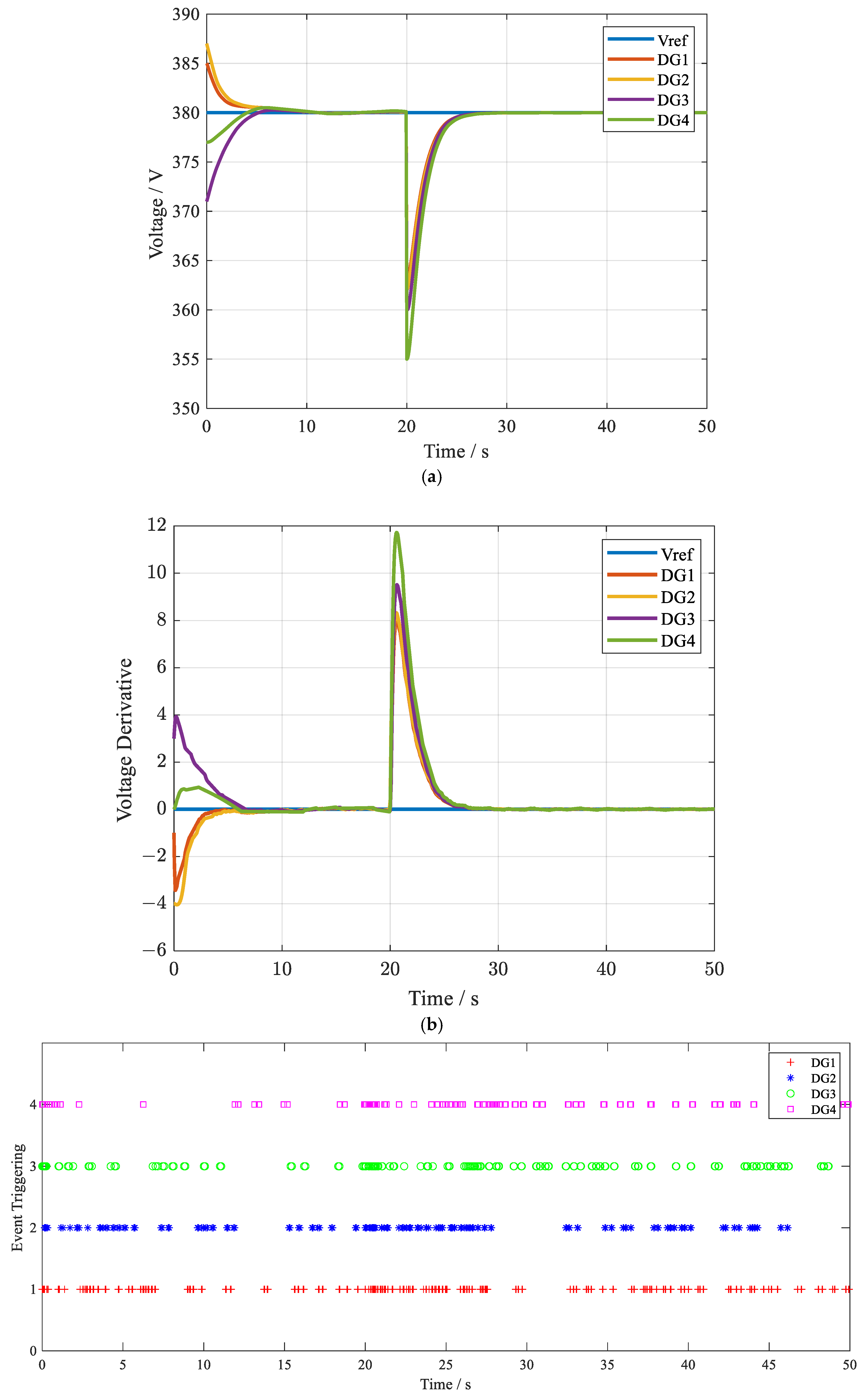
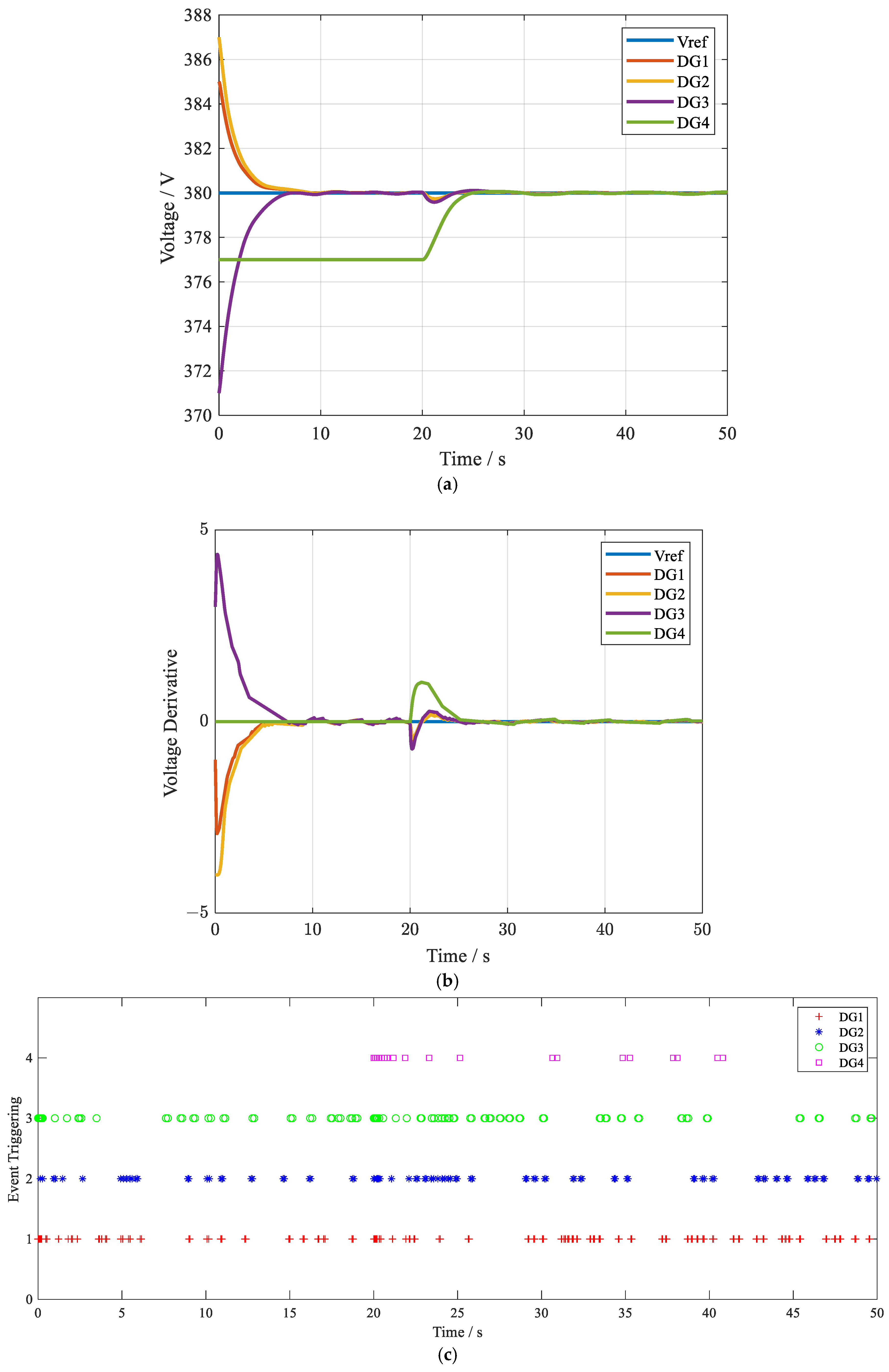
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zuo, K.; Wu, L. A Review of Decentralized and Distributed Control Approaches for Islanded Microgrids: Novel Designs, Current Trends, and Emerging Challenges. Electr. J. 2022, 35, 107–138. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A.; Lewis, F.L. A Multiobjective Distributed Control Framework for offshore wind power systems. IEEE Trans. Ind. Inform. 2014, 3, 1785–1798. [Google Scholar] [CrossRef]
- Leitner, S.; Yazdanian, M.; Mehrizi-Sani, A.; Muetze, A. Small-Signal Stability Analysis of an Inverter-Based Microgrid With Internal Model-Based Controllers. IEEE Trans. Smart Grid 2018, 5, 5393–5402. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi, S.A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 4, 1905–1919. [Google Scholar]
- Wang, R.; Yu, X.; Sun, Q.; Li, D.; Gui, Y.; Wang, P. The Integrated Reference Region Analysis for Parallel DFIGs’ Interfacing Inductors. IEEE Trans. Power Electron. 2024, 39, 7632–7642. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Ma, D.; Hu, X. Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid 2020, 11, 2856–2866. [Google Scholar]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B.; Zhang, H. Event-triggered Voltage Distributed Cooperative Control with Communication Delay. Proc. CSEE 2020, 40, 5426–5435. [Google Scholar]
- Cai, P.; Wen, C. Distributed Secondary Frequency Control for Islanded Microgrids Based on Ratio-Consistent Algorithms. Acta Energiae Solaris Sin. 2020, 10, 74–81. [Google Scholar]
- Kou, L.; Li, Y.; Wu, M.; Rui, T.; Hu, C.; Zhang, Q. Coordinated Control Strategy for Distributed Microgrid Voltage Restoration. Adv. Technol. Electr. Eng. Energy 2018, 5, 65–72. [Google Scholar]
- Yin, X.; Cao, L.; Wang, Y. Multi agent deep reinforcement learning based cooperative voltage control in distribution network. Electrotech. Electr. 2025, 63–71. [Google Scholar]
- Cui, Y.; Zhang, H.; Wang, H. Construction of multi agent information automation fusion model for smart grid. Tech. Autom. Appl. 2025, 44, 110–114. [Google Scholar]
- Zhang, L. Autonomous control method of distributed energy storage system in smart grid based on multi agent consistency theory. High Volt. Appar. 2024, 60, 230–237,258. [Google Scholar]
- Zhu, Y.; Long, Y.; Yu, L. Microgrid voltage control and delay optimization based on consistency algorithm. Transducer Microsyst. Technol. 2020, 9, 42–45. [Google Scholar]
- Yu, H.; Guan, X.; Ruan, P.; Wei, S.; Liu, D. A Study on Multi-Objective Optimization of Microgrids Based on Improved Differential Evolutionary Algorithm. Electr. Age 2019, 9, 51–53. [Google Scholar]
- Liu, X.; Wang, Y.; Xiao, J. Secondary Controland Stability Analysis of Ring-Bus DC Microgrids. Control Theory Appl. 2021, 7, 979–987. [Google Scholar]
- Wang, R.; Sun, Q.; Hu, W.; Li, Y.; Ma, D.; Wang, P. SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 2021, 36, 7866–7879. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Zhang, P.; Gui, Y.; Qin, D.; Wang, P. Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar]
- Yao, D.; Dou, C.; Yue, D.; Zhao, N.; Zhang, T. Event-Triggered Adaptive Consensustracking Control for Nonlinear Switching Multi-Agent Systems. Neurocomputing 2020, 415, 157–164. [Google Scholar]
- Lai, J.; Lu, X.; Yu, X.; Yao, W.; Wen, J.; Cheng, S. Distributed Multi-DER Cooperative Control for Master-Slave-Organized Microgrid Networks With Limited Communication Bandwidth. IEEE Trans. Ind. Inform. 2019, 6, 3443–3456. [Google Scholar] [CrossRef]
- Xie, Y.; Lin, Z. Distributed Event-Triggered Secondary Voltage Control for Microgrids with Time Delay. IEEE Trans. Syst. Man Cybern. Syst. 2019, 8, 1582–1591. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.-L.; Zhang, X.-M.; Ding, D. Dynamic Event-triggered Control and Estimation: A Survey. Int. J. Autom. Comput. 2021, 6, 857–886. [Google Scholar] [CrossRef]
- Han, F.; Lao, X.; Li, J.; Wang, M.; Dong, H. Dynamic Event-Triggered Protocol-Based Distributed Secondary Control for Islanded Microgrids. Int. J. Electr. Power Energy Syst. 2022, 137, 107723. [Google Scholar] [CrossRef]
- Yang, C.; Yao, W.; Fang, J.; Ai, X.; Chen, Z.; Wen, J.; He, H. Dynamic Event-Triggered Robust Secondary Frequency Control for Islanded AC Microgrid. Appl. Energy 2019, 242, 821–836. [Google Scholar] [CrossRef]
- Liang, Y.; Liang, S.; Yu, X.; Lai, X.; Liu, M. Distributed resilient restoration scheduling of transmission and distribution grid with multiple offshore wind farms in typhoon weather. Power Syst. Technol. 2025, 49, 447–458. [Google Scholar]
- Yang, X.; Liu, B.; Liu, Y.; Fu, Z. Automatic generation control strategy with wind energy under aperiodic intermittent control. Control. Decis. 2024, 39, 4027–4036. [Google Scholar]
- Li, H.; Liao, X.; Huang, T.; Zhu, W. Event-Triggering Sampling Based Leader-Following Consensus in Second-Order Multi-Agent Systems. IEEE Trans. Autom. Control 2015, 7, 1998–2003. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Cai, Y.; Sun, S.; Sun, J. Leader-Following Consensus for a Class of Nonlinear Multiagent Systems Under Event-Triggered and Edge-Event Triggered Mechanisms. IEEE Trans. Cybern. 2022, 8, 7643–7654. [Google Scholar] [CrossRef]
- Zhu, W.; Jiang, Z.-P.; Feng, G. Event-Based Consensus of Multi-Agent Systems with General Linear Models. Automatica 2014, 2, 552–558. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed Event-Triggered Control for Multi-Agent Systems. IEEE Trans. Autom. Control 2012, 5, 1291–1297. [Google Scholar] [CrossRef]
- Zou, W.; Ahn, C.K.; Xiang, Z. Event-Triggered Consensus Tracking Control of Stochastic Nonlinear Multiagent Systems. IEEE Syst. J. 2019, 4, 4051–4059. [Google Scholar] [CrossRef]
- Duan, M.-M.; Liu, C.-L.; Liu, F. Event-Triggered Consensus Seeking of Heterogeneous First-Order Agents With Input Delay. IEEE Access 2017, 5, 5215–5223. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, Q.; Zhu, W. Adaptive Event-Based Consensus of Multi-Agent Systems with General Linear Dynamics. J. Syst. Sci. Complex. 2018, 1, 120–129. [Google Scholar] [CrossRef]
- Zhu, W.; Zhou, Q.; Wang, D. Consensus of Linear Multi-Agent Systems Via Adaptive Event-Based Protocols. Neurocomputing 2018, 318, 175–181. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.; Zhou, Q. Leader-Following Consensus of Multi-Agent Systems via Adaptive Event-Based Control. J. Syst. Sci. Complex. 2019, 3, 846–856. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 2, 613–625. [Google Scholar] [CrossRef]
- Abhinav, S.; Schizas, I.D.; Ferrese, F.; Davoudi, A. Optimization-Based AC Microgrid Synchronization. IEEE Trans. Ind. Inform. 2017, 5, 2339–2349. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed Cooperative Secondary Control of Microgrids Using Feedback Linearization. IEEE Trans. Power Syst. 2013, 28, 3462–3470. [Google Scholar] [CrossRef]
- Li, X.; Tang, Y.; Karimi, H.R. Consensus of Multi-Agent Systems Via Fully Distributed Event-Triggered Control. Automatica 2020, 116, 108898. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Han, J.; Zhou, J.; Hu, W.; Zhang, H.; Wang, P. Energy-Management Strategy of Battery Energy Storage Systems in DC Microgrids: A Distributed Dynamic Event-Triggered H∞ Consensus Control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5692–5701. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Cui, G. Distributed cooperative control of islanded microgrid triggered by dynamic events. Control. Theory Appl. 2024, 41, 2335–2344. [Google Scholar]
- Yue, Y.; Tian, T.; Zhao, H. Distributed coordinated control strategy for microgrid based on dynamic event triggering. J. Shaanxi Univ. Sci. Technol. 2024, 42, 138–143. [Google Scholar]

| Year | Paper | Focus |
|---|---|---|
| 2020 | Zhang et al. [7] | Use droop control to maintain voltage stabilization within a certain range |
| 2021 | Liu et al. [15] | Secondary control of a toroidal DC microgrid |
| 2024 | Yang et al. [25] | Automatic power generation strategy with wind energy under nonperiodic intermittent control |
| 2025 | Yin et al. [10] | Cooperative control of voltage zoning in distribution networks based on deep reinforcement learning with multiple intelligences |
| 2025 | Cui et al. [11] | Smart Grid MASs Information Automation Fusion Model Construction |
| 2025 | Zhang et al. [12] | Autonomous Control Method for Distributed Energy Storage System within Smart Grid Based on Multi-Intelligent Body Coherence Theory |
| Notations | Definitions |
|---|---|
| Distributed generations | |
| Multi-agent systems | |
| The number of MASs | |
| 2-norm of vectors (matrices) | |
| The k-th trigger moment of i-th MAS | |
| Real part of the ith eigenvalue | |
| m × n order matrix | |
| The transpose of the matrix | |
| The inverse of the matrix | |
| Column vector | |
| Kronecker product |
| Description | Symbol | Values |
|---|---|---|
| DGi | ||
| Lines | Line 1 & Line 3 | Line 2 |
| RL Loads |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Zeng, Z.; Tian, Y.; Wang, C.; Xiao, J.; Lin, X. Fully Distributed Consensus Voltage Restoration Control Based on Dynamic Event-Triggered Mechanisms for Offshore Wind Power Systems. Energies 2025, 18, 1755. https://doi.org/10.3390/en18071755
Chen D, Zeng Z, Tian Y, Wang C, Xiao J, Lin X. Fully Distributed Consensus Voltage Restoration Control Based on Dynamic Event-Triggered Mechanisms for Offshore Wind Power Systems. Energies. 2025; 18(7):1755. https://doi.org/10.3390/en18071755
Chicago/Turabian StyleChen, Dawei, Zhijie Zeng, Ye Tian, Chenyu Wang, Jun Xiao, and Xiaoqing Lin. 2025. "Fully Distributed Consensus Voltage Restoration Control Based on Dynamic Event-Triggered Mechanisms for Offshore Wind Power Systems" Energies 18, no. 7: 1755. https://doi.org/10.3390/en18071755
APA StyleChen, D., Zeng, Z., Tian, Y., Wang, C., Xiao, J., & Lin, X. (2025). Fully Distributed Consensus Voltage Restoration Control Based on Dynamic Event-Triggered Mechanisms for Offshore Wind Power Systems. Energies, 18(7), 1755. https://doi.org/10.3390/en18071755





