Quantifying the Economic Advantages of Energy Management Systems for Domestic Prosumers with Electric Vehicles
Abstract
1. Introduction
1.1. Relevant Literature
1.2. Motivation and Contribution
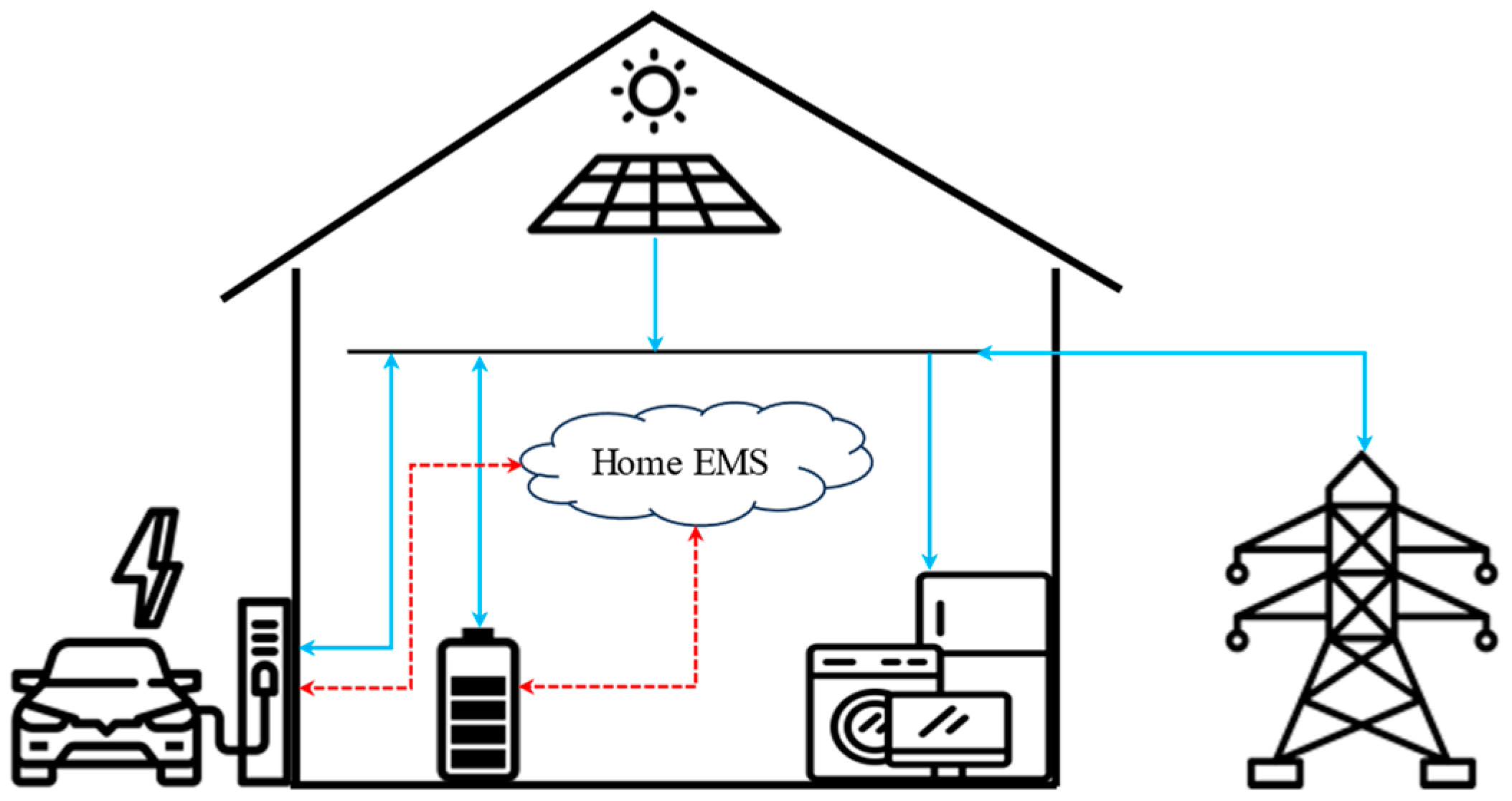
2. EMS Structure and Methodology
- The PV panels, the EV charging station, and the BESS installed in the household with their size/capacity, and technical operational limits;
- The day-ahead hourly forecast and real-time measurements of residential consumption, and ;
- The day-ahead hourly forecast and real-time measurements of PV production, and ;
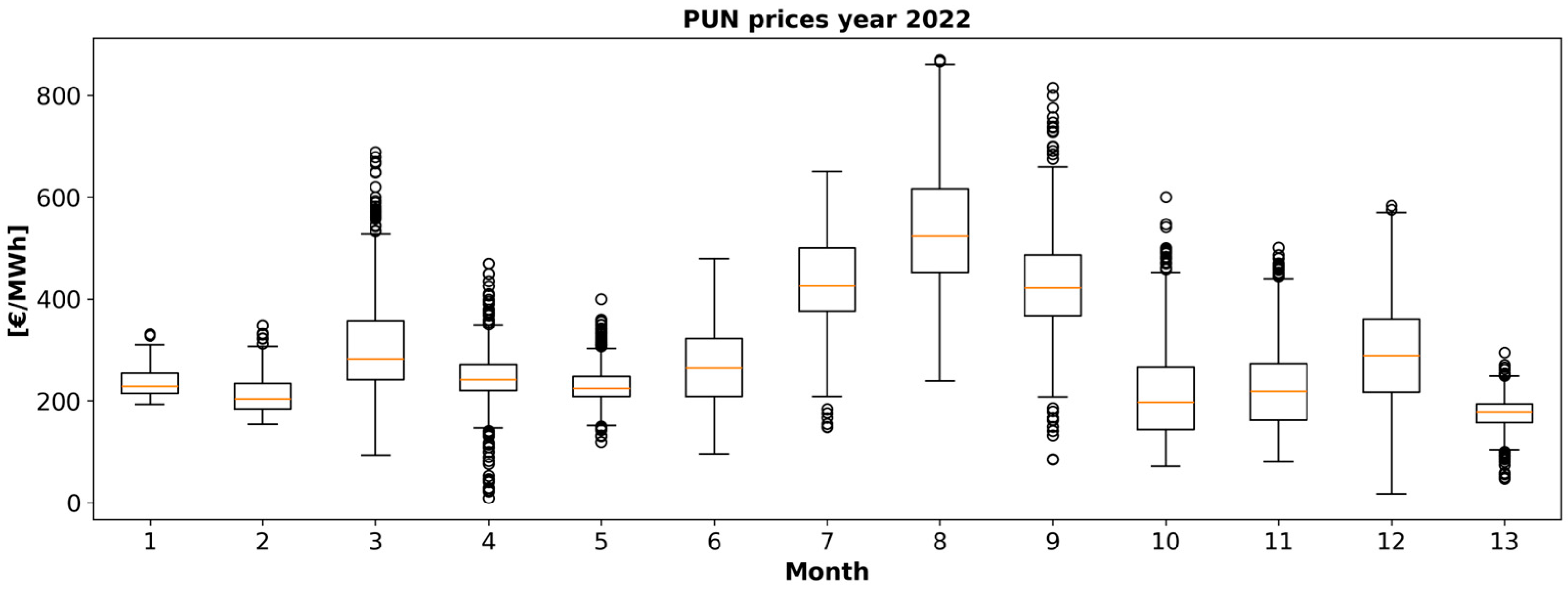
- The forecast of electricity purchase and selling price profiles, ;
- The day-ahead forecast schedule of the electric vehicle usage (in particular, the time periods t in which the EV is at used, = 0, and the expected energy consumption for the trip, ).
- The storage operational constraints;
- The maximum grid import and export limitation;
- The power balance of the house;
- The achievement of a minimum state of charge (SOC) of the EV battery at the time requested by the user.
2.1. Forecasting Module
2.2. First Layer—MILP Mathematical Formulation
- Battery storage: average charging power , discharging power , net power exchange , and state-of-energy for each timestep t;
- Electric vehicle: average charging power , discharging power , net power exchange , and state-of-energy for each timestep t;
- Grid interaction: average power purchased from the grid and power sold back to the grid for each timestep t.
- Storage dynamics: for both the battery and the EV, constraints define charging and discharging power limits as well as the state-of-charge evolution over time;
- Grid constraints: electricity purchased and sold must comply with the contractual limits of the user;
- Power balance: at each timestep, the total electricity generated by non-dispatchable sources, energy discharged from storage, and energy purchased from the grid must always balance the total energy used for storage charging and exports to the grid.
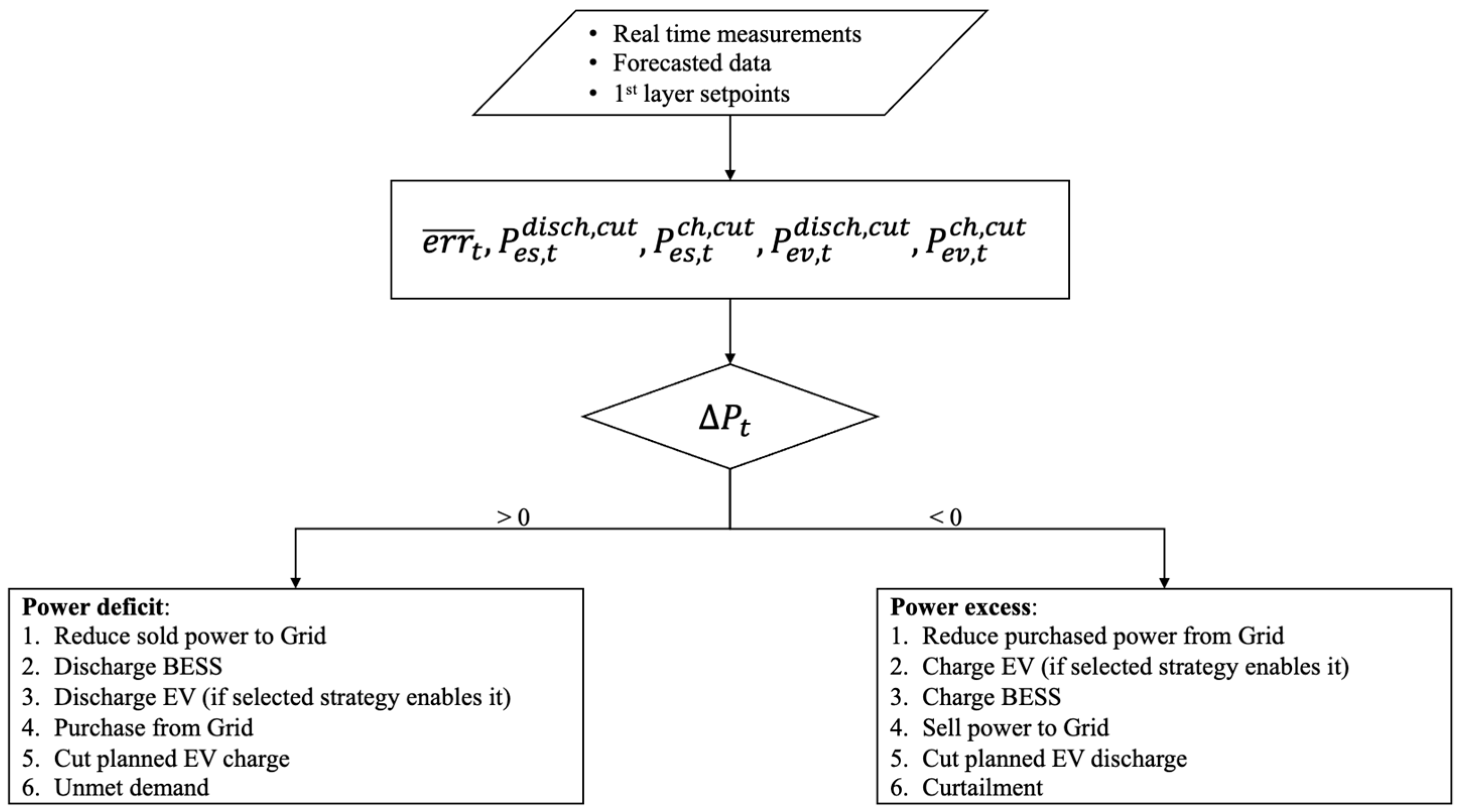
2.3. Second Layer—Heuristic Control
- Reduce grid interaction;
- BESS or EV power supply (different priority according to power deficit/excess and selected strategy);
- Increase grid interaction;
- Additional cut of planned EV setpoint;
- Unmet demand or curtailment.
2.4. Benchmark Algorithm
3. Case Studies
3.1. Key Performance Indicators
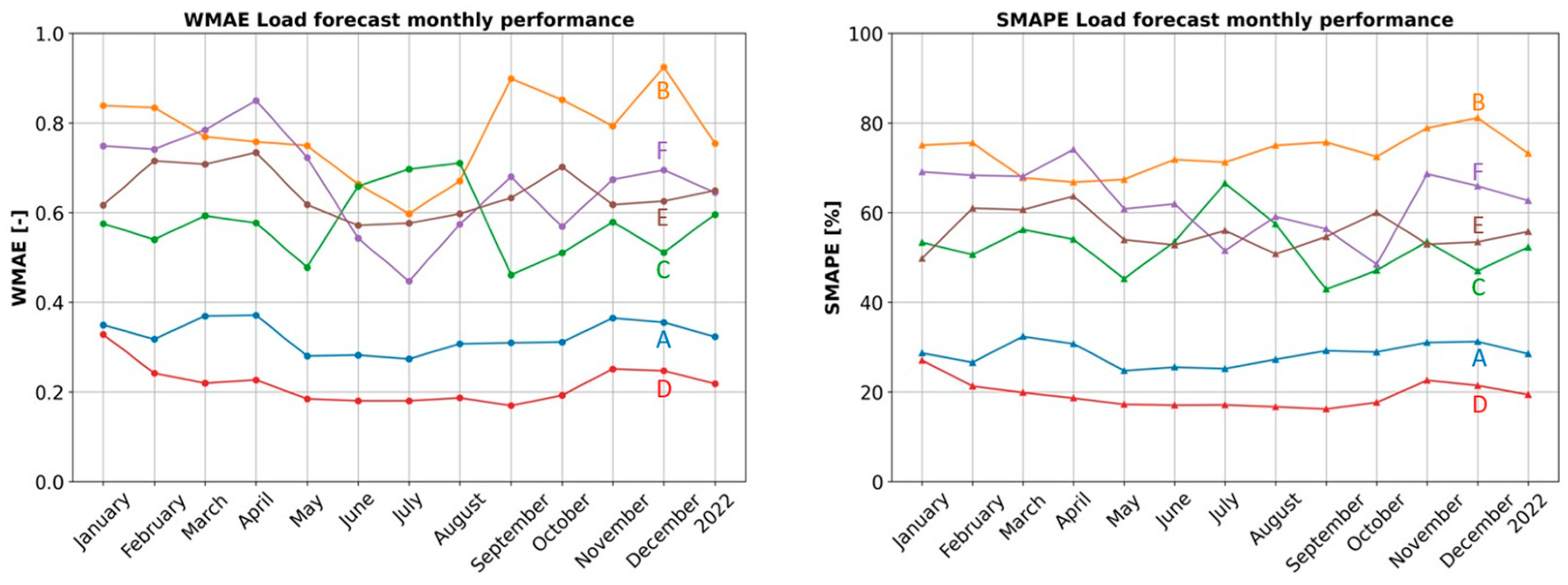
3.1.1. Forecast Module Characterization
3.1.2. Techno-Economic Assessment
3.2. PV Production
3.3. Residential Consumption
3.4. Techno-Economic Parameters
3.5. EV Weekly Commute
4. Results and Discussion
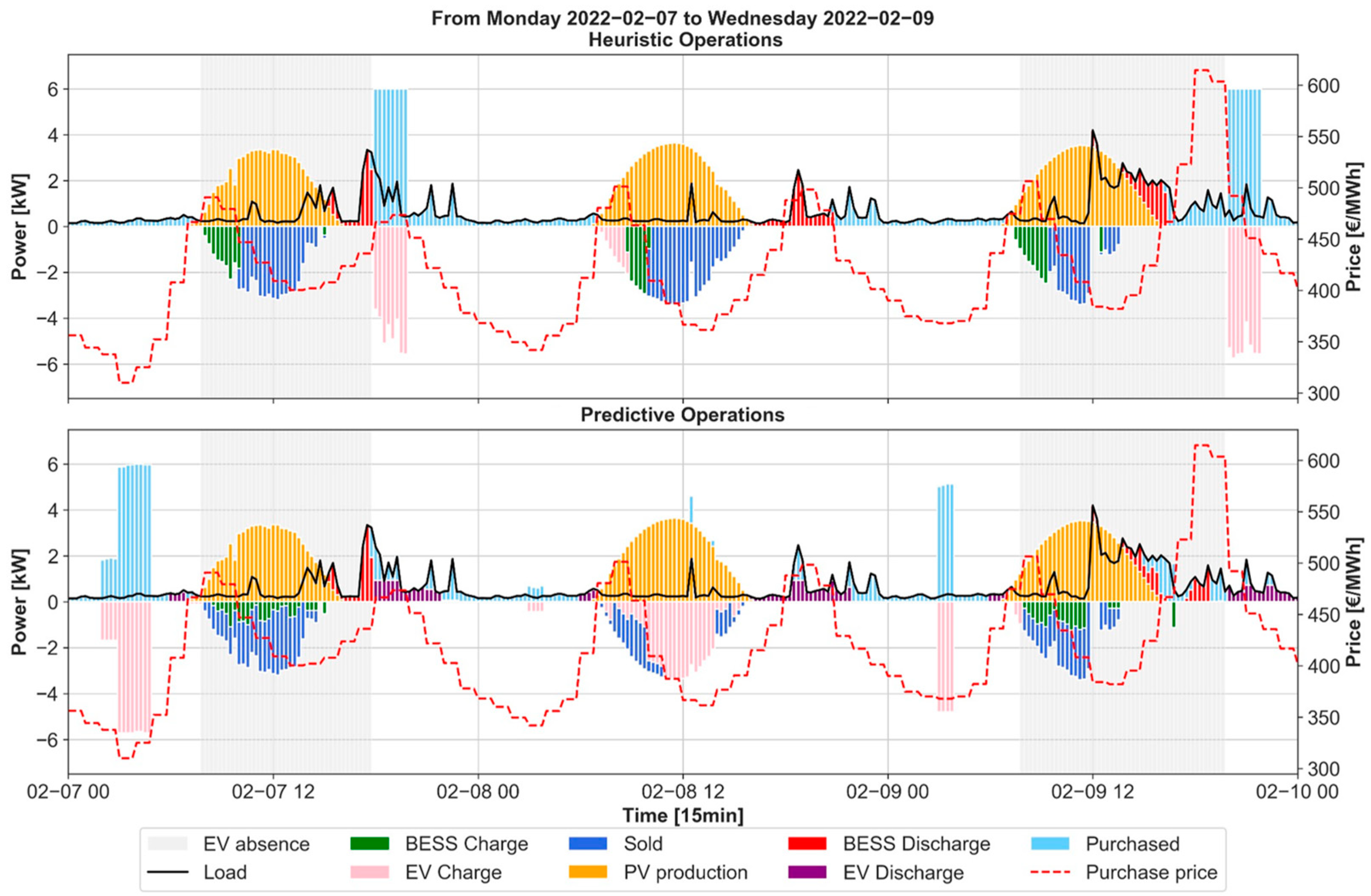
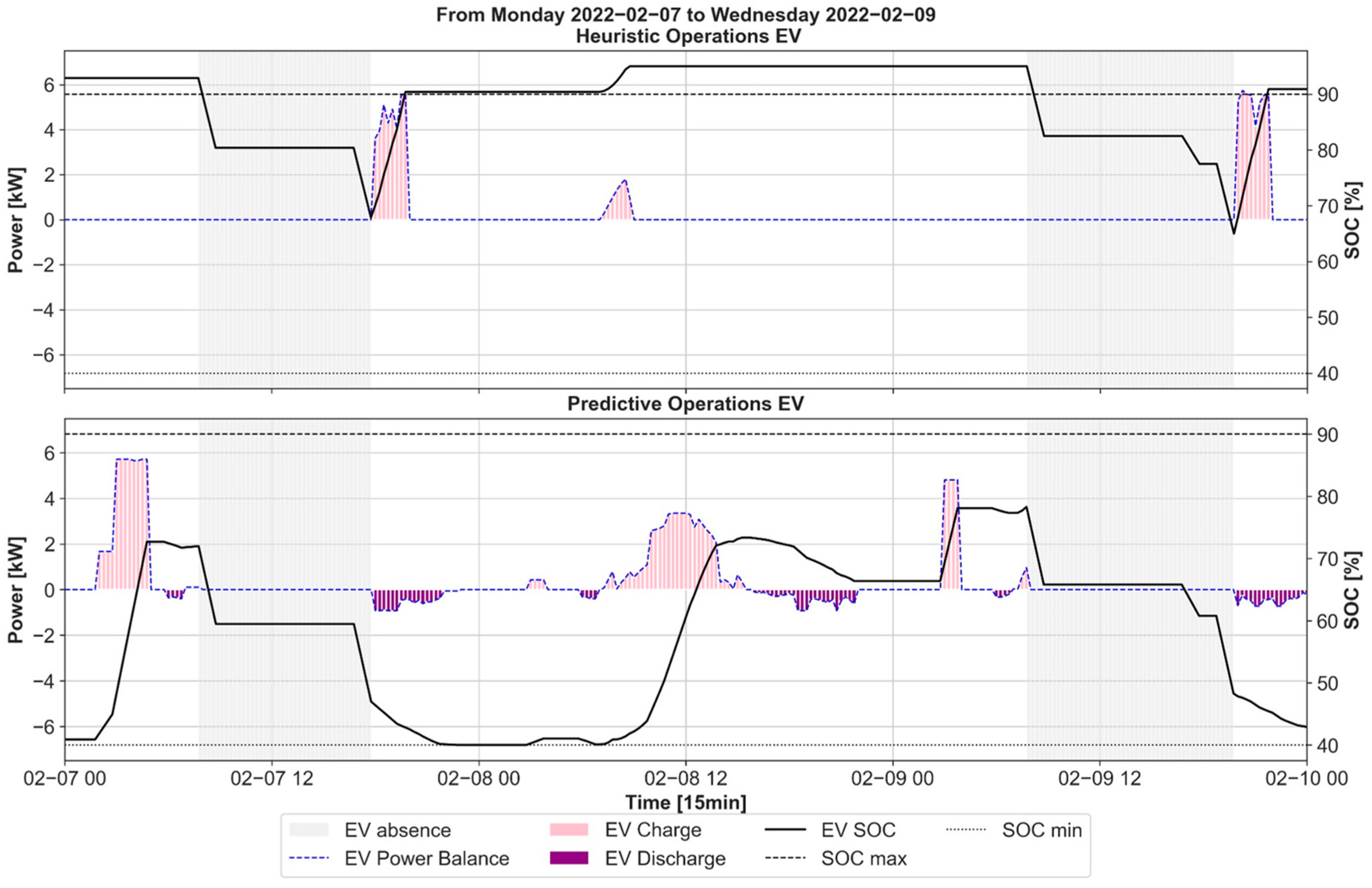
4.1. Predictive vs. Heuristic Management
4.2. Case 0—Reference Without Electric Mobility
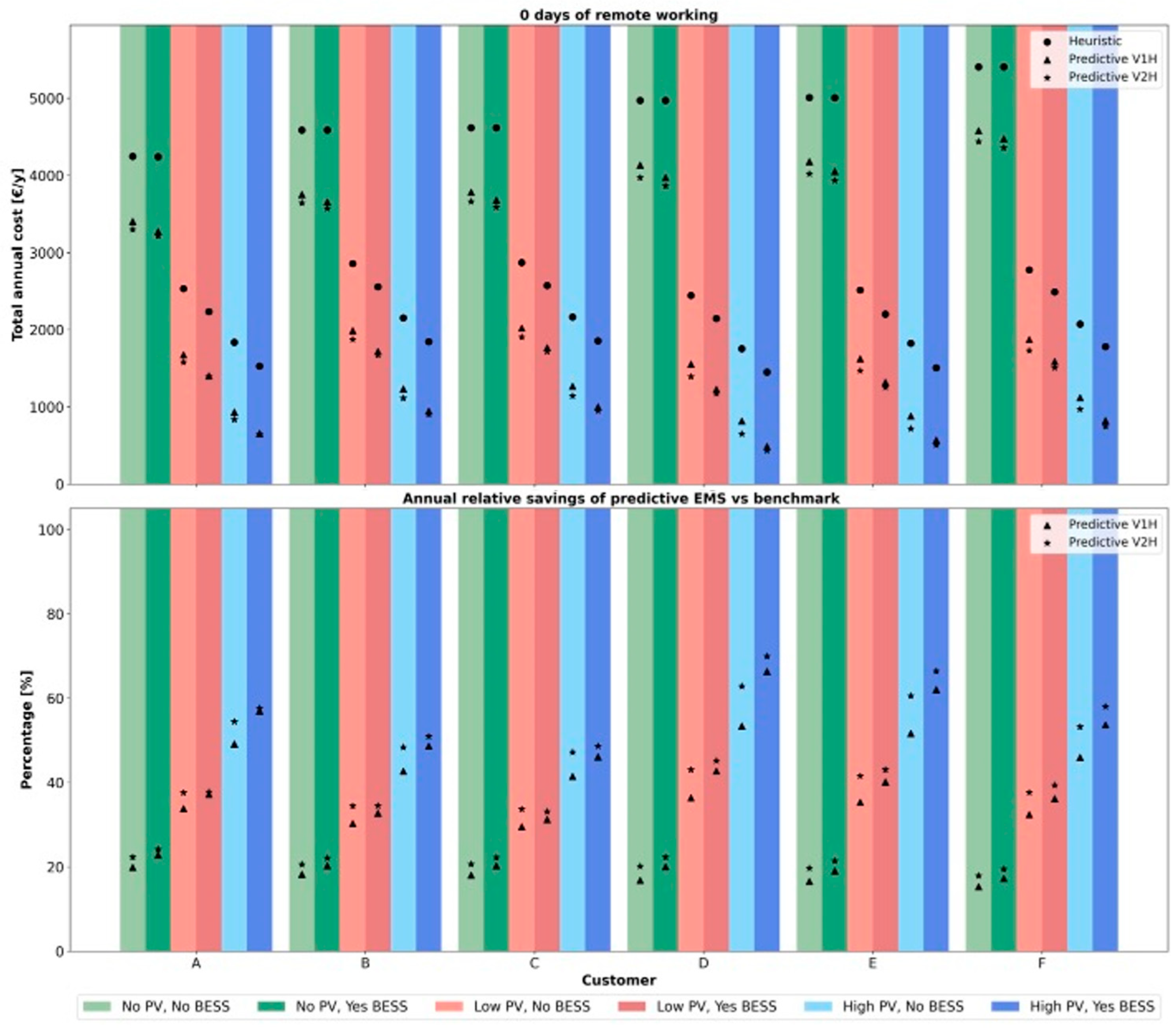
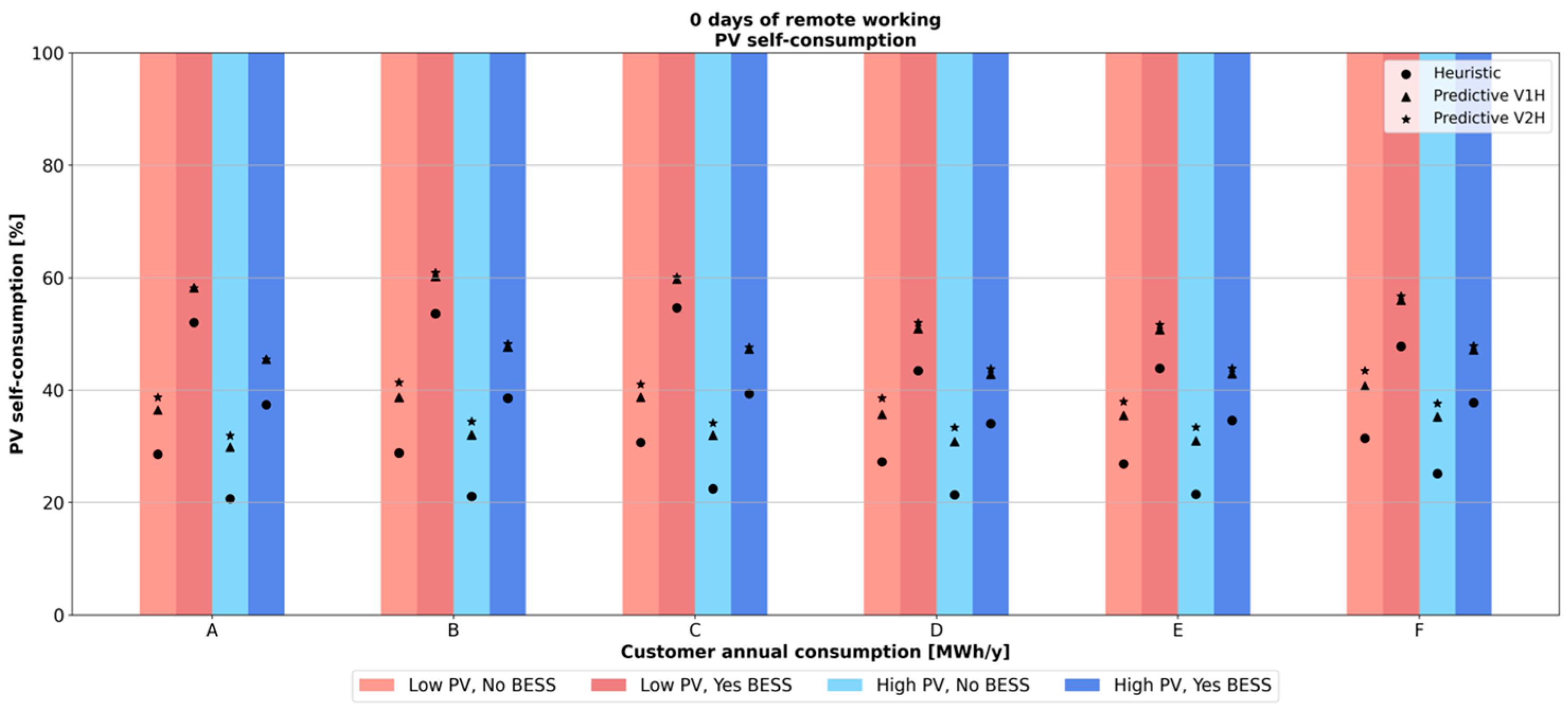
4.3. Case 1—No Days of Remote Working
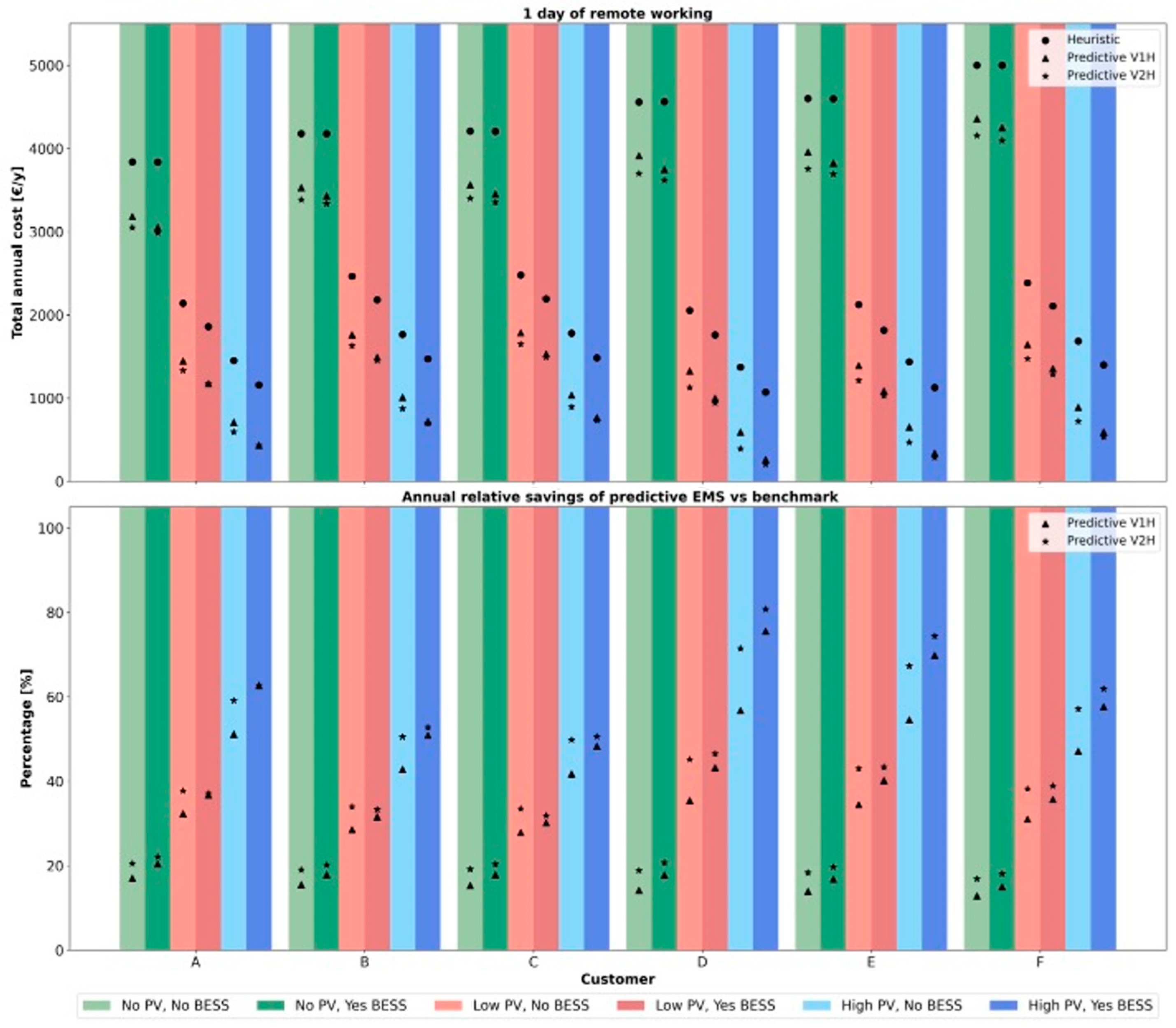
4.4. Case 2—1 Day of Remote Working
4.5. Case 3—2 Days of Remote Working
4.6. Ideal Performance Assessment
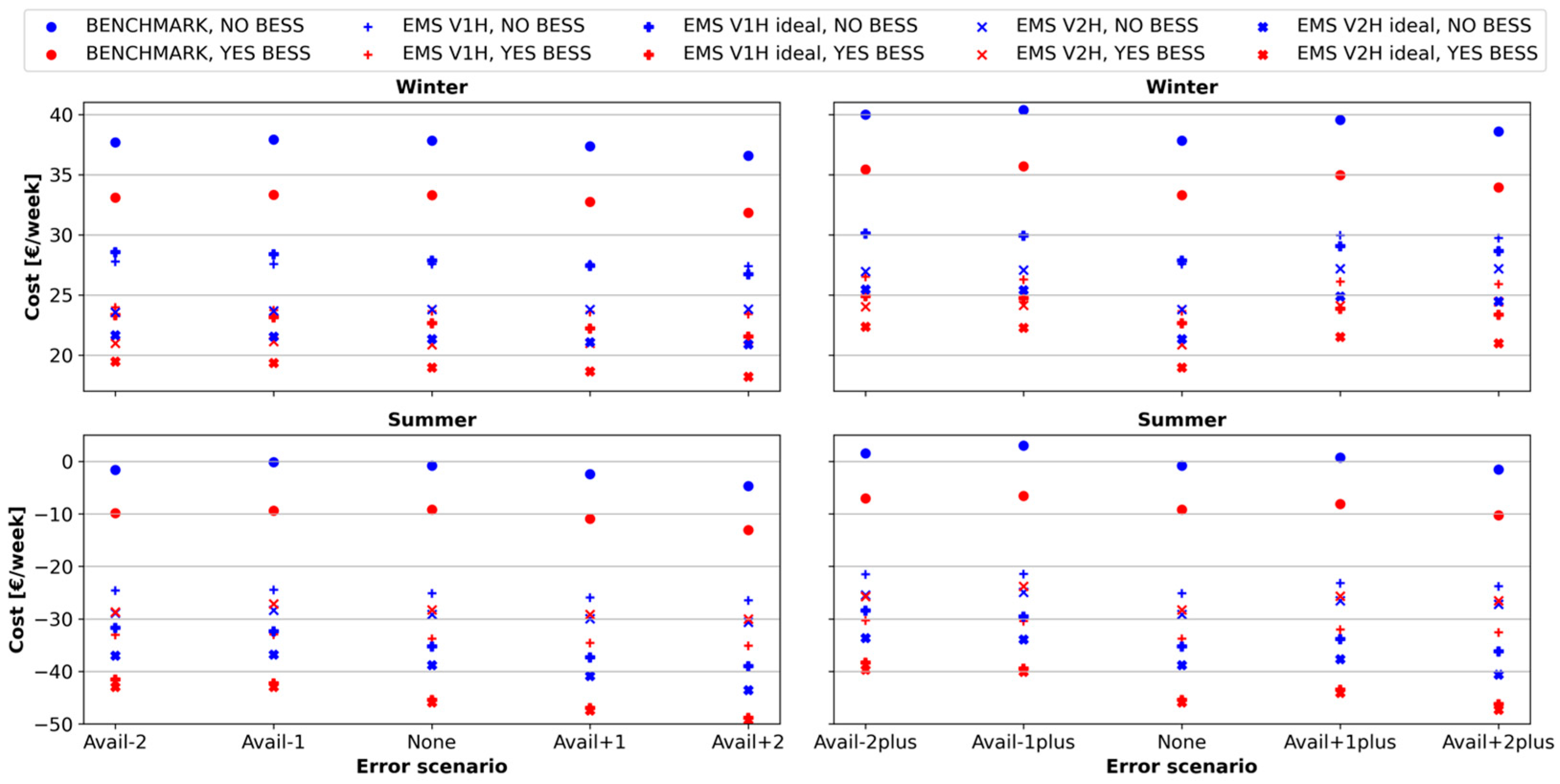
4.7. Impact of EV Usage Forecast Errors
5. Conclusions and Further Developments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AVPF | absolute value of perfect forecast |
| BESS | battery energy storage system |
| CRF | capital recovery factor |
| DAM | day-ahead market |
| DR | demand response |
| EMS | energy management system |
| EV | electric vehicle |
| HEMS | home energy management system |
| IGDT | information-gap decision theory |
| KPI | key performance indicator |
| MAPE | mean absolute percentage error |
| MG | microgrid |
| MILP | mixed-integer linear programming |
| MPC | model predictive control |
| O&M | operation and maintenance |
| OF | objective function |
| OPEX | operational expenditure |
| PUN | Prezzo Unico Nazionale |
| PV | photovoltaic |
| PZ | zonal price |
| RES | renewable energy sources |
| RD | relative difference |
| RS | relative savings |
| RVPF | relative value of perfect forecast |
| SDP | stochastic dynamic programming |
| SH | shrinking horizon |
| SMAPE | symmetric mean absolute percentage error |
| SOC | state of charge |
| SOE | state of energy |
| TC | total cost |
| V1H | unidirectional smart charging |
| V2H | vehicle-to-home |
| WMAE | weighted mean absolute error |
| Sets | |
| Set of energy storage units | |
| Set of electric vehicles | |
| Set of first layer timesteps | |
| Set of second layer timesteps | |
| Continuous variables (valid for both first and second layers) | |
| Parameters | |
| Profile of the electricity purchase price [€/kWh] | |
| Timestep duration of the EMS I layer [hours] | |
| Timestep duration of the EMS II layer [hours] | |
| Profile of the electricity selling price [€/kWh] | |
Appendix A. Case Studies EV Weekly Commute Detail
| Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monday | home | 07:45 | 25 | 08:30 | work | 17:30 | 25 | 18:15 | home | ||||||||
| Tuesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 25 | 18:15 | home | ||||||||
| Wednesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 10 | 17:50 | leisure | 19:30 | 25 | 20:00 | home | ||||
| Thursday | home | 07:45 | 25 | 08:30 | work | 17:30 | 5 | 17:40 | shopping | 18:30 | 23 | 19:00 | home | ||||
| Friday | home | 07:45 | 25 | 08:30 | work | 16:00 | 25 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Saturday | home | 11:00 | 40 | 11:45 | leisure | 16:00 | 40 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Sunday | home |
| Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monday | home | ||||||||||||||||
| Tuesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 25 | 18:15 | home | ||||||||
| Wednesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 10 | 17:50 | leisure | 19:30 | 25 | 20:00 | home | ||||
| Thursday | home | 07:45 | 25 | 08:30 | work | 17:30 | 5 | 17:40 | shopping | 18:30 | 23 | 19:00 | home | ||||
| Friday | home | 07:45 | 25 | 08:30 | work | 16:00 | 25 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Saturday | home | 11:00 | 40 | 11:45 | leisure | 16:00 | 40 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Sunday | home |
| Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monday | home | 07:45 | 25 | 08:30 | work | 17:30 | 25 | 18:15 | home | ||||||||
| Tuesday | home | ||||||||||||||||
| Wednesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 10 | 17:50 | leisure | 19:30 | 25 | 20:00 | home | ||||
| Thursday | home | ||||||||||||||||
| Friday | home | 07:45 | 25 | 08:30 | work | 16:00 | 25 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Saturday | home | 11:00 | 40 | 11:45 | leisure | 16:00 | 40 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Sunday | home |
| Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | End Time | Distance | Start Time | Activity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monday | home | ||||||||||||||||
| Tuesday | home | 07:45 | 25 | 08:30 | work | 17:30 | 25 | 18:15 | home | ||||||||
| Wednesday | home | ||||||||||||||||
| Thursday | home | 07:45 | 25 | 08:30 | work | 17:30 | 5 | 17:40 | shopping | 18:30 | 23 | 19:00 | home | ||||
| Friday | home | ||||||||||||||||
| Saturday | home | 11:00 | 40 | 11:45 | leisure | 16:00 | 40 | 16:45 | home | 19:00 | 10 | 19:10 | leisure | 22:00 | 10 | 22:10 | home |
| Sunday | home |
Appendix B. Economic Analysis Detail
| User | A | B | C | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | No | Low | High | No | Low | High | No | Low | High | ||||||||||
| BESS | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | |
| Case 0 | 1372.4 | 1372.3 | −234.0 | −469.8 | −912.8 | −1147.0 | 1720.7 | 1720.5 | 100.2 | −154.5 | −588.6 | −849.5 | 1749.1 | 1748.9 | 112.1 | −122.1 | −574.7 | −812.1 | |
| 1372.4 | 1229.3 | −234.0 | −507.7 | −912.8 | −1184.5 | 1720.7 | 1612.1 | 100.2 | −172.6 | −588.6 | −870.8 | 1749.1 | 1631.5 | 112.1 | −142.2 | −574.7 | −835.2 | ||
| 0.0% | 10.4% | 0.0% | 8.1% | 0.0% | 3.3% | 0.0% | 6.3% | 0.0% | 11.7% | 0.0% | 2.5% | 0.0% | 6.7% | 0.0% | 16.5% | 0.0% | 2.8% | ||
| Case 1 | 4246.9 | 4240.7 | 2531.1 | 2235.2 | 1837.1 | 1529.5 | 4588.0 | 4587.1 | 2856.7 | 2556.0 | 2153.8 | 1844.2 | 4615.3 | 4615.6 | 2871.2 | 2570.9 | 2165.7 | 1856.2 | |
| 3402.5 | 3273.5 | 1675.0 | 1403.2 | 934.1 | 658.0 | 3751.6 | 3655.5 | 1990.6 | 1718.8 | 1234.7 | 947.1 | 3783.1 | 3679.3 | 2023.0 | 1768.0 | 1267.3 | 1000.2 | ||
| 3300.5 | 3215.8 | 1579.9 | 1391.0 | 836.5 | 647.4 | 3643.1 | 3573.9 | 1874.1 | 1673.4 | 1111.8 | 904.2 | 3662.1 | 3590.2 | 1904.7 | 1720.5 | 1143.4 | 953.2 | ||
| 19.9% | 22.8% | 33.8% | 37.2% | 49.2% | 57.0% | 18.2% | 20.3% | 30.3% | 32.8% | 42.7% | 48.6% | 18.0% | 20.3% | 29.5% | 31.2% | 41.5% | 46.1% | ||
| 22.3% | 24.2% | 37.6% | 37.8% | 54.5% | 57.7% | 20.6% | 22.1% | 34.4% | 34.5% | 48.4% | 51.0% | 20.7% | 22.2% | 33.7% | 33.1% | 47.2% | 48.6% | ||
| Case 2 | 3838.6 | 3836.4 | 2139.4 | 1859.7 | 1451.1 | 1159.7 | 4179.8 | 4180.6 | 2465.1 | 2181.0 | 1764.9 | 1471.4 | 4208.3 | 4207.4 | 2479.0 | 2193.3 | 1779.4 | 1485.1 | |
| 3183.2 | 3051.6 | 1448.0 | 1175.5 | 709.1 | 433.1 | 3532.3 | 3432.1 | 1761.4 | 1492.0 | 1009.1 | 722.5 | 3563.7 | 3454.9 | 1787.6 | 1531.3 | 1036.1 | 767.9 | ||
| 3050.7 | 2988.3 | 1331.7 | 1170.3 | 593.5 | 431.7 | 3385.8 | 3337.1 | 1628.6 | 1454.7 | 873.1 | 695.6 | 3402.4 | 3352.6 | 1648.5 | 1494.3 | 893.0 | 733.7 | ||
| 17.1% | 20.5% | 32.3% | 36.8% | 51.1% | 62.7% | 15.5% | 17.9% | 28.5% | 31.6% | 42.8% | 50.9% | 15.3% | 17.9% | 27.9% | 30.2% | 41.8% | 48.3% | ||
| 20.5% | 22.1% | 37.8% | 37.1% | 59.1% | 62.8% | 19.0% | 20.2% | 33.9% | 33.3% | 50.5% | 52.7% | 19.2% | 20.3% | 33.5% | 31.9% | 49.8% | 50.6% | ||
| Case 3 Nissan Leaf | 3397.8 | 3397.4 | 1694.0 | 1418.5 | 1013.6 | 735.5 | 3742.4 | 3741.2 | 2026.9 | 1750.7 | 1337.9 | 1053.1 | 3768.1 | 3769.2 | 2038.2 | 1768.5 | 1348.8 | 1073.8 | |
| 2843.6 | 2712.1 | 1044.4 | 787.8 | 305.2 | 40.4 | 3190.9 | 3036.1 | 1350.0 | 1042.4 | 597.9 | 271.6 | 3224.2 | 3118.7 | 1389.0 | 1154.5 | 624.8 | 316.5 | ||
| 2706.8 | 2643.3 | 902.2 | 774.5 | 155.5 | 28.6 | 2989.6 | 2915.9 | 1113.0 | 951.8 | 419.6 | 281.9 | 3064.7 | 3011.4 | 1219.6 | 1097.7 | 365.2 | 210.2 | ||
| 16.3% | 20.2% | 38.3% | 44.5% | 69.9% | 94.5% | 14.7% | 18.8% | 33.4% | 40.5% | 55.3% | 74.2% | 14.4% | 17.3% | 31.9% | 34.7% | 53.7% | 70.5% | ||
| 20.3% | 22.2% | 46.7% | 45.4% | 84.7% | 96.1% | 20.1% | 22.1% | 45.1% | 45.6% | 68.6% | 73.2% | 18.7% | 20.1% | 40.2% | 37.9% | 72.9% | 80.4% | ||
| Case 3 Tesla Model S | 4046.5 | 4046.8 | 2186.5 | 1920.0 | 1501.5 | 1222.8 | 4385.5 | 4385.1 | 2504.9 | 2243.4 | 1810.6 | 1533.5 | 4414.7 | 4414.7 | 2526.5 | 2273.8 | 1831.8 | 1560.4 | |
| 3372.1 | 3243.7 | 1534.6 | 1287.5 | 789.5 | 528.2 | 3721.0 | 3626.6 | 1849.0 | 1610.2 | 1087.6 | 816.2 | 3752.9 | 3649.8 | 1881.5 | 1658.1 | 1120.2 | 872.1 | ||
| 3231.8 | 3174.8 | 1397.9 | 1272.7 | 640.7 | 516.0 | 3571.3 | 3524.9 | 1690.3 | 1562.3 | 904.9 | 770.7 | 3588.6 | 3540.5 | 1719.9 | 1600.0 | 939.0 | 815.2 | ||
| 16.7% | 19.8% | 29.8% | 32.9% | 47.4% | 56.8% | 15.2% | 17.3% | 26.2% | 28.2% | 39.9% | 46.8% | 15.0% | 17.3% | 25.5% | 27.1% | 38.8% | 44.1% | ||
| 20.1% | 21.5% | 36.1% | 33.7% | 57.3% | 57.8% | 18.6% | 19.6% | 32.5% | 30.4% | 50.0% | 49.7% | 18.7% | 19.8% | 31.9% | 29.6% | 48.7% | 47.8% | ||
| Case 4 | 2889.4 | 2889.6 | 1202.1 | 937.7 | 524.0 | 259.3 | 3232.6 | 3233.4 | 1539.2 | 1268.4 | 848.7 | 570.9 | 3262.4 | 3261.5 | 1551.1 | 1280.2 | 864.2 | 586.5 | |
| 2464.8 | 2330.5 | 662.0 | 412.6 | −69.0 | −334.7 | 2814.0 | 2712.7 | 977.6 | 730.5 | 233.6 | −40.4 | 2845.0 | 2734.0 | 1000.3 | 772.0 | 259.8 | 4.0 | ||
| 2287.2 | 2254.2 | 497.6 | 406.9 | −241.2 | −331.8 | 2620.9 | 2592.9 | 789.6 | 688.9 | 33.0 | −69.7 | 2633.2 | 2608.3 | 801.9 | 722.5 | 48.0 | −33.5 | ||
| 14.7% | 19.3% | 44.9% | 56.0% | 113.2% | 229.1% | 12.9% | 16.1% | 36.5% | 42.4% | 72.5% | 107.1% | 12.8% | 16.2% | 35.5% | 39.7% | 69.9% | 99.3% | ||
| 20.8% | 22.0% | 58.6% | 56.6% | 146.0% | 227.9% | 18.9% | 19.8% | 48.7% | 45.7% | 96.1% | 112.2% | 19.3% | 20.0% | 48.3% | 43.6% | 94.4% | 105.7% | ||
| User | D | E | F | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | No | Low | High | No | Low | High | No | Low | High | ||||||||||
| BESS | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | |
| Case 0 | 2103.5 | 2103.3 | −303.9 | −588.0 | −978.3 | −1266.6 | 2146.2 | 2146.0 | −235.3 | −516.1 | −918.0 | −1200.0 | 2545.2 | 2545.0 | 24.6 | −229.3 | −668.0 | −927.4 | |
| 2103.5 | 1926.2 | −303.9 | −635.5 | −978.3 | −1309.7 | 2146.2 | 2000.9 | −235.3 | −547.1 | −918.0 | −1228.9 | 2545.2 | 2426.6 | 24.6 | −260.8 | −668.0 | −956.6 | ||
| 0.0% | 8.4% | 0.0% | 8.1% | 0.0% | 3.4% | 0.0% | 6.8% | 0.0% | 6.0% | 0.0% | 2.4% | 0.0% | 4.7% | 0.0% | 13.7% | 0.0% | 3.1% | ||
| Case 1 | 4971.4 | 4970.2 | 2443.0 | 2144.7 | 1753.7 | 1451.7 | 5008.0 | 5006.0 | 2514.0 | 2202.9 | 1823.5 | 1507.7 | 5405.4 | 5406.1 | 2775.0 | 2488.1 | 2072.3 | 1780.7 | |
| 4134.3 | 3972.9 | 1554.5 | 1228.6 | 817.4 | 488.6 | 4178.1 | 4051.8 | 1625.3 | 1318.4 | 881.7 | 572.0 | 4577.9 | 4474.2 | 1875.8 | 1587.5 | 1120.1 | 824.6 | ||
| 3969.9 | 3861.7 | 1391.7 | 1176.0 | 651.8 | 436.5 | 4021.7 | 3934.3 | 1469.3 | 1254.8 | 719.8 | 506.4 | 4437.4 | 4355.4 | 1729.8 | 1508.9 | 969.6 | 747.6 | ||
| 16.8% | 20.1% | 36.4% | 42.7% | 53.4% | 66.3% | 16.6% | 19.1% | 35.4% | 40.2% | 51.6% | 62.1% | 15.3% | 17.2% | 32.4% | 36.2% | 45.9% | 53.7% | ||
| 20.1% | 22.3% | 43.0% | 45.2% | 62.8% | 69.9% | 19.7% | 21.4% | 41.6% | 43.0% | 60.5% | 66.4% | 17.9% | 19.4% | 37.7% | 39.4% | 53.2% | 58.0% | ||
| Case 2 | 4560.5 | 4563.3 | 2055.7 | 1760.0 | 1371.2 | 1072.9 | 4600.5 | 4599.7 | 2125.5 | 1816.5 | 1436.0 | 1125.4 | 5000.7 | 5002.3 | 2384.5 | 2106.1 | 1684.5 | 1399.3 | |
| 3915.1 | 3750.7 | 1327.1 | 999.0 | 593.1 | 262.3 | 3958.9 | 3827.1 | 1393.1 | 1086.5 | 652.7 | 339.4 | 4358.6 | 4251.3 | 1644.3 | 1354.8 | 890.3 | 593.0 | ||
| 3699.6 | 3620.4 | 1126.9 | 941.8 | 391.5 | 206.2 | 3756.0 | 3693.9 | 1211.7 | 1030.0 | 469.6 | 288.3 | 4156.1 | 4097.8 | 1473.8 | 1286.7 | 722.4 | 533.4 | ||
| 14.2% | 17.8% | 35.4% | 43.2% | 56.7% | 75.6% | 13.9% | 16.8% | 34.5% | 40.2% | 54.6% | 69.8% | 12.8% | 15.0% | 31.0% | 35.7% | 47.1% | 57.6% | ||
| 18.9% | 20.7% | 45.2% | 46.5% | 71.5% | 80.8% | 18.4% | 19.7% | 43.0% | 43.3% | 67.3% | 74.4% | 16.9% | 18.1% | 38.2% | 38.9% | 57.1% | 61.9% | ||
| Case 3 Nissan Leaf | 4125.3 | 4124.5 | 1616.6 | 1337.0 | 937.4 | 655.2 | 4165.1 | 4164.4 | 1693.5 | 1395.0 | 1009.2 | 706.5 | 4562.4 | 4563.5 | 1949.8 | 1688.8 | 1254.6 | 989.0 | |
| 3575.4 | 3411.2 | 923.4 | 606.2 | 192.3 | −133.6 | 3619.2 | 3492.1 | 986.2 | 693.3 | 247.3 | −51.6 | 4016.3 | 3834.9 | 1245.6 | 972.3 | 493.6 | 208.4 | ||
| 3353.6 | 3273.8 | 624.3 | 458.9 | −63.9 | −211.9 | 3422.7 | 3358.4 | 757.3 | 613.4 | 9.0 | −133.4 | 3725.2 | 3634.7 | 922.9 | 740.0 | 268.2 | 117.7 | ||
| 13.3% | 17.3% | 42.9% | 54.7% | 79.5% | 120.4% | 13.1% | 16.1% | 41.8% | 50.3% | 75.5% | 107.3% | 12.0% | 16.0% | 36.1% | 42.4% | 60.7% | 78.9% | ||
| 18.7% | 20.6% | 61.4% | 65.7% | 106.8% | 132.3% | 17.8% | 19.4% | 55.3% | 56.0% | 99.1% | 118.9% | 18.4% | 20.4% | 52.7% | 56.2% | 78.6% | 88.1% | ||
| Case 3 Tesla Model S | 4767.4 | 4768.8 | 2112.7 | 1816.6 | 1434.6 | 1133.0 | 4806.4 | 4806.3 | 2169.9 | 1877.3 | 1484.3 | 1184.6 | 5205.0 | 5205.0 | 2424.7 | 2157.3 | 1731.5 | 1461.9 | |
| 4104.3 | 3944.0 | 1410.4 | 1097.7 | 673.2 | 352.8 | 4148.4 | 4023.8 | 1473.5 | 1187.2 | 729.7 | 431.6 | 4548.2 | 4445.3 | 1736.5 | 1466.8 | 975.9 | 695.2 | ||
| 3878.6 | 3804.9 | 1163.0 | 1018.0 | 417.5 | 272.1 | 3947.7 | 3890.1 | 1248.9 | 1104.9 | 494.8 | 350.6 | 4331.9 | 4275.6 | 1519.7 | 1372.3 | 751.4 | 601.6 | ||
| 13.9% | 17.3% | 33.2% | 39.6% | 53.1% | 68.9% | 13.7% | 16.3% | 32.1% | 36.8% | 50.8% | 63.6% | 12.6% | 14.6% | 28.4% | 32.0% | 43.6% | 52.4% | ||
| 18.6% | 20.2% | 45.0% | 44.0% | 70.9% | 76.0% | 17.9% | 19.1% | 42.4% | 41.1% | 66.7% | 70.4% | 16.8% | 17.9% | 37.3% | 36.4% | 56.6% | 58.8% | ||
| Case 4 | 3615.5 | 3617.4 | 1131.0 | 847.9 | 452.6 | 165.7 | 3655.4 | 3655.3 | 1198.6 | 906.0 | 515.3 | 220.1 | 4052.9 | 4053.0 | 1459.9 | 1193.4 | 766.0 | 491.3 | |
| 3196.4 | 3028.9 | 553.0 | 233.5 | −173.7 | −499.2 | 3240.3 | 3106.3 | 613.0 | 319.5 | −120.6 | −421.2 | 3640.3 | 3530.8 | 861.6 | 593.3 | 118.8 | −161.8 | ||
| 2913.6 | 2867.4 | 259.9 | 153.9 | −472.8 | −578.1 | 2980.9 | 2948.6 | 350.9 | 252.4 | −386.1 | −482.5 | 3361.7 | 3328.0 | 613.3 | 507.6 | −129.7 | −236.2 | ||
| 11.6% | 16.3% | 51.1% | 72.5% | 138.4% | 401.2% | 11.4% | 15.0% | 48.9% | 64.7% | 123.4% | 291.4% | 10.2% | 12.9% | 41.0% | 50.3% | 84.5% | 132.9% | ||
| 19.4% | 20.7% | 77.0% | 81.9% | 204.5% | 448.8% | 18.5% | 19.3% | 70.7% | 72.1% | 174.9% | 319.2% | 17.1% | 17.9% | 58.0% | 57.5% | 116.9% | 148.1% | ||
| User | A | B | C | D | E | F | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | No | Low | High | No | Low | High | No | Low | High | No | Low | High | No | Low | High | No | Low | High | |
| Case 0 | 960.3 | 1836.6 | 1823.6 | 728.6 | 1830.4 | 1893.6 | 789.1 | 1706.4 | 1748.0 | 1189.4 | 2225.0 | 2223.8 | 975.1 | 2091.9 | 2086.2 | 795.6 | 1915.0 | 1936.3 | |
| Case 1 | 865.5 | 1823.7 | 1852.3 | 645.0 | 1824.0 | 1930.2 | 696.5 | 1710.8 | 1792.3 | 1083.0 | 2186.6 | 2206.7 | 847.9 | 2059.2 | 2078.0 | 696.0 | 1934.3 | 1982.8 | |
| 568.4 | 1267.7 | 1268.6 | 464.0 | 1346.5 | 1393.0 | 482.3 | 1235.8 | 1276.2 | 726.4 | 1447.5 | 1444.4 | 586.5 | 1439.1 | 1431.9 | 550.2 | 1482.2 | 1489.7 | ||
| Case 2 | 883.6 | 1828.8 | 1851.8 | 672.6 | 1808.0 | 1922.6 | 730.5 | 1720.4 | 1799.8 | 1103.3 | 2201.5 | 2219.7 | 884.3 | 2057.6 | 2101.8 | 719.9 | 1942.0 | 1995.1 | |
| 418.8 | 1083.2 | 1086.1 | 326.7 | 1166.9 | 1190.9 | 333.7 | 1035.1 | 1068.7 | 531.2 | 1241.7 | 1242.8 | 416.8 | 1219.2 | 1216.5 | 391.4 | 1255.2 | 1268.2 | ||
| Case 3 Nissan Leaf | 882.7 | 1722.2 | 1776.9 | 1038.6 | 2064.1 | 2189.2 | 707.8 | 1573.9 | 2068.3 | 1102.3 | 2128.8 | 2187.2 | 852.6 | 1965.5 | 2005.7 | 1217.2 | 1833.6 | 1913.9 | |
| 426.4 | 856.7 | 851.8 | 494.6 | 1081.6 | 924.3 | 357.9 | 818.0 | 1040.2 | 535.5 | 1109.9 | 993.6 | 431.1 | 965.9 | 956.0 | 607.2 | 1227.5 | 1010.1 | ||
| Case 3 Tesla Model S | 862.0 | 1658.0 | 1753.1 | 633.5 | 1602.7 | 1821.6 | 691.8 | 1498.8 | 1664.4 | 1076.1 | 2098.6 | 2149.9 | 836.3 | 1921.2 | 2000.0 | 690.4 | 1810.0 | 1883.3 | |
| 382.2 | 840.5 | 836.3 | 311.4 | 859.2 | 900.3 | 322.5 | 804.7 | 830.5 | 494.8 | 972.7 | 975.0 | 386.6 | 965.9 | 967.6 | 378.2 | 989.2 | 1005.3 | ||
| Case 4 | 901.2 | 1673.5 | 1783.3 | 679.9 | 1658.1 | 1838.8 | 745.0 | 1532.0 | 1716.7 | 1123.9 | 2143.8 | 2184.4 | 899.0 | 1969.0 | 2016.7 | 734.5 | 1800.1 | 1882.3 | |
| 221.6 | 608.9 | 607.9 | 188.2 | 675.3 | 689.0 | 167.4 | 532.7 | 546.9 | 310.1 | 711.5 | 706.3 | 216.6 | 661.4 | 646.6 | 226.6 | 709.3 | 714.2 | ||
| Ideal EMS | 882.7 | 1722.2 | 1776.9 | 649.6 | 1694.6 | 1850.1 | 707.8 | 1573.9 | 1696.8 | 1102.3 | 2128.8 | 2187.2 | 852.6 | 1965.5 | 2005.7 | 708.4 | 1833.6 | 1913.9 | |
| 426.4 | 856.7 | 851.8 | 345.9 | 867.9 | 924.3 | 357.9 | 818.0 | 849.7 | 535.5 | 995.5 | 993.6 | 431.1 | 965.9 | 956.0 | 413.9 | 1003.5 | 1010.1 | ||
| User | A | B | C | D | E | F | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV | Low | High | Low | High | Low | High | Low | High | Low | High | Low | High | |||||||||||||
| BESS | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | |
| Case 1 | 29% | 52% | 21% | 37% | 29% | 54% | 21% | 39% | 31% | 55% | 22% | 39% | 27% | 43% | 21% | 34% | 27% | 44% | 21% | 35% | 31% | 48% | 25% | 38% | |
| 36% | 58% | 30% | 46% | 39% | 60% | 32% | 48% | 39% | 60% | 32% | 47% | 36% | 51% | 31% | 43% | 35% | 51% | 31% | 43% | 41% | 56% | 35% | 47% | ||
| 39% | 58% | 32% | 45% | 41% | 61% | 34% | 48% | 41% | 60% | 34% | 48% | 39% | 52% | 33% | 44% | 38% | 52% | 33% | 44% | 43% | 57% | 38% | 48% | ||
| Case 2 | 28% | 51% | 20% | 37% | 28% | 52% | 20% | 38% | 30% | 54% | 22% | 38% | 26% | 43% | 21% | 34% | 26% | 43% | 21% | 34% | 31% | 47% | 25% | 37% | |
| 36% | 58% | 29% | 45% | 38% | 60% | 31% | 47% | 39% | 60% | 32% | 47% | 35% | 50% | 30% | 42% | 35% | 50% | 31% | 42% | 40% | 55% | 35% | 46% | ||
| 41% | 57% | 33% | 44% | 43% | 60% | 35% | 47% | 44% | 60% | 35% | 47% | 41% | 52% | 35% | 44% | 40% | 52% | 35% | 43% | 45% | 56% | 38% | 47% | ||
| Case 3 Nissan Leaf | 29% | 52% | 20% | 37% | 28% | 52% | 20% | 37% | 30% | 53% | 22% | 38% | 27% | 43% | 21% | 33% | 27% | 43% | 21% | 34% | 31% | 47% | 25% | 37% | |
| 45% | 64% | 35% | 50% | 47% | 66% | 37% | 51% | 47% | 66% | 37% | 51% | 41% | 56% | 35% | 46% | 42% | 56% | 35% | 47% | 46% | 60% | 39% | 50% | ||
| 51% | 64% | 41% | 49% | 55% | 68% | 43% | 52% | 54% | 66% | 44% | 53% | 50% | 59% | 41% | 48% | 49% | 58% | 42% | 48% | 53% | 62% | 44% | 51% | ||
| Case 3 Tesla Model S | 40% | 62% | 28% | 44% | 41% | 62% | 29% | 45% | 42% | 62% | 30% | 45% | 35% | 50% | 27% | 39% | 35% | 51% | 28% | 40% | 40% | 55% | 31% | 43% | |
| 49% | 67% | 38% | 53% | 51% | 69% | 41% | 55% | 51% | 68% | 41% | 54% | 44% | 58% | 37% | 48% | 45% | 58% | 38% | 49% | 49% | 62% | 42% | 52% | ||
| 54% | 67% | 43% | 52% | 57% | 69% | 46% | 55% | 56% | 69% | 46% | 55% | 52% | 60% | 44% | 50% | 51% | 60% | 44% | 50% | 55% | 63% | 47% | 53% | ||
| Case 4 | 28% | 50% | 19% | 35% | 27% | 50% | 20% | 36% | 29% | 52% | 21% | 37% | 26% | 42% | 20% | 33% | 26% | 42% | 20% | 33% | 30% | 46% | 24% | 36% | |
| 44% | 62% | 34% | 48% | 46% | 64% | 36% | 50% | 46% | 64% | 36% | 49% | 40% | 54% | 33% | 44% | 40% | 54% | 34% | 45% | 45% | 58% | 38% | 48% | ||
| 51% | 61% | 40% | 47% | 55% | 64% | 43% | 49% | 55% | 64% | 43% | 49% | 50% | 56% | 41% | 47% | 49% | 56% | 41% | 46% | 53% | 59% | 44% | 49% | ||
| User | PV | BESS | |||||
|---|---|---|---|---|---|---|---|
| A | No | No | 3397.8 | 2843.6 | 2842.8 | 2706.8 | 2684.4 |
| Yes | 3397.4 | 2712.1 | 2690.1 | 2643.3 | 2616.2 | ||
| Low | No | 1694.0 | 1044.4 | 1028.3 | 902.2 | 856.7 | |
| Yes | 1418.5 | 787.8 | 740.3 | 774.5 | 714.2 | ||
| High | No | 1013.6 | 305.2 | 288.4 | 155.5 | 105.7 | |
| Yes | 735.5 | 40.4 | −13.9 | 28.6 | −39.4 | ||
| B | No | No | 3742.4 | 3192.6 | 3190.9 | 3047.5 | 2989.6 |
| Yes | 3741.2 | 3095.8 | 3036.1 | 2995.9 | 2915.9 | ||
| Low | No | 2026.9 | 1356.0 | 1350.0 | 1185.4 | 1113.0 | |
| Yes | 1750.7 | 1103.4 | 1042.4 | 1056.0 | 951.8 | ||
| High | No | 1337.9 | 602.4 | 597.9 | 419.6 | 344.1 | |
| Yes | 1053.1 | 326.7 | 271.6 | 281.9 | 181.2 | ||
| C | No | No | 3768.1 | 3224.2 | 3220.3 | 3064.7 | 3003.1 |
| Yes | 3769.2 | 3118.7 | 3068.8 | 3011.4 | 2934.7 | ||
| Low | No | 2038.2 | 1389.0 | 1376.4 | 1219.6 | 1139.5 | |
| Yes | 1768.5 | 1154.5 | 1087.5 | 1097.7 | 990.2 | ||
| High | No | 1348.8 | 635.5 | 624.8 | 451.9 | 365.2 | |
| Yes | 1073.8 | 382.6 | 316.5 | 325.3 | 210.2 | ||
| D | No | No | 4125.3 | 3575.4 | 3574.6 | 3353.6 | 3331.5 |
| Yes | 4124.5 | 3411.2 | 3391.2 | 3273.8 | 3246.0 | ||
| Low | No | 1616.6 | 923.4 | 909.3 | 675.4 | 624.3 | |
| Yes | 1337.0 | 606.2 | 555.3 | 527.0 | 458.9 | ||
| High | No | 937.4 | 192.3 | 177.1 | −63.9 | −119.2 | |
| Yes | 655.2 | −133.6 | −187.6 | −211.9 | −286.7 | ||
| E | No | No | 4165.1 | 3619.2 | 3617.1 | 3422.7 | 3356.7 |
| Yes | 4164.4 | 3492.1 | 3424.4 | 3358.4 | 3270.8 | ||
| Low | No | 1693.5 | 986.2 | 980.4 | 757.3 | 665.2 | |
| Yes | 1395.0 | 693.3 | 614.8 | 613.4 | 492.6 | ||
| High | No | 1009.2 | 247.3 | 241.0 | 9.0 | −86.7 | |
| Yes | 706.5 | −51.6 | −132.6 | −133.4 | −259.4 | ||
| F | No | No | 4562.4 | 4019.1 | 4016.3 | 3809.0 | 3725.2 |
| Yes | 4563.5 | 3913.6 | 3834.9 | 3747.3 | 3634.7 | ||
| Low | No | 1949.8 | 1245.6 | 1234.4 | 1029.5 | 922.9 | |
| Yes | 1688.8 | 972.3 | 885.3 | 880.0 | 740.0 | ||
| High | No | 1254.6 | 493.6 | 484.1 | 268.2 | 165.3 | |
| Yes | 989.0 | 208.4 | 126.2 | 117.7 | −18.6 |
| Season | Configuration | None | Avail−2 | Avail−1 | Avail+1 | Avail+2 | Avail−2 Plus | Avail−1 Plus | Avail+1 Plus | Avail+2 Plus | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Winter | NO BESS | 37.82 | 37.68 | 37.92 | 37.37 | 36.57 | 40.00 | 40.37 | 39.56 | 38.60 | |
| 27.56 | 27.76 | 27.57 | 27.57 | 27.39 | 30.16 | 29.97 | 29.96 | 29.74 | |||
| 27.85 | 28.55 | 28.37 | 27.41 | 26.71 | 30.10 | 29.93 | 29.05 | 28.66 | |||
| 23.80 | 23.55 | 23.68 | 23.80 | 23.82 | 26.94 | 27.05 | 27.19 | 27.18 | |||
| 21.33 | 21.64 | 21.54 | 21.08 | 20.90 | 25.46 | 25.41 | 24.88 | 24.47 | |||
| −1% | −3% | −3% | 1% | 3% | 0% | 0% | 3% | 4% | |||
| 12% | 9% | 10% | 13% | 14% | 6% | 6% | 9% | 11% | |||
| YES BESS | 33.30 | 33.09 | 33.34 | 32.74 | 31.84 | 35.44 | 35.69 | 34.97 | 33.94 | ||
| 23.65 | 23.98 | 23.73 | 23.60 | 23.43 | 26.51 | 26.26 | 26.11 | 25.88 | |||
| 22.65 | 23.32 | 23.15 | 22.21 | 21.54 | 24.90 | 24.73 | 23.85 | 23.36 | |||
| 20.87 | 20.98 | 21.12 | 20.98 | 21.30 | 24.01 | 24.16 | 24.13 | 24.44 | |||
| 18.96 | 19.46 | 19.36 | 18.64 | 18.20 | 22.36 | 22.26 | 21.52 | 21.00 | |||
| 4% | 3% | 3% | 6% | 9% | 6% | 6% | 9% | 11% | |||
| 10% | 8% | 9% | 13% | 17% | 7% | 9% | 12% | 16% | |||
| Summer | NO BESS | −0.83 | −1.60 | −0.12 | −2.41 | −4.68 | 1.56 | 3.04 | 0.75 | −1.52 | |
| −25.13 | −24.58 | −24.43 | −25.96 | −26.49 | −21.53 | −21.47 | −23.17 | −23.81 | |||
| −35.27 | −31.69 | −32.34 | −37.31 | −38.98 | −28.42 | −29.58 | −33.81 | −36.18 | |||
| −29.12 | −28.87 | −28.35 | −29.94 | −30.59 | −25.45 | −24.94 | −26.52 | −27.17 | |||
| −38.81 | −36.96 | −36.78 | −40.85 | −43.54 | −33.61 | −33.92 | −37.67 | −40.58 | |||
| 29% | 22% | 24% | 30% | 32% | 24% | 27% | 31% | 34% | |||
| 25% | 22% | 23% | 27% | 30% | 24% | 26% | 30% | 33% | |||
| YES BESS | −9.18 | −9.83 | −9.38 | −10.90 | −13.04 | −7.04 | −6.59 | −8.12 | −10.25 | ||
| −33.75 | −33.01 | −32.96 | −34.57 | −35.12 | −30.28 | −30.41 | −32.04 | −32.59 | |||
| −45.44 | −41.57 | −42.28 | −46.95 | −48.85 | −38.33 | −39.48 | −43.50 | −46.26 | |||
| −28.30 | −28.65 | −27.12 | −29.15 | −30.05 | −25.73 | −23.77 | −25.69 | −26.56 | |||
| −45.89 | −42.95 | −42.97 | −47.41 | −50.14 | −39.69 | −40.06 | −44.07 | −47.33 | |||
| 26% | 21% | 22% | 26% | 28% | 21% | 23% | 26% | 30% | |||
| 38% | 33% | 37% | 39% | 40% | 35% | 41% | 42% | 44% |
References
- European Commission EU Solar Energy Strategy. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2022%3A221%3AFIN&qid=1653034500503 (accessed on 25 September 2023).
- SolarPower Europe Annual Rooftop and Utility Scale Installations in the EU. Available online: https://www.solarpowereurope.org/advocacy/solar-saves/fact-figures/annual-rooftop-and-utility-scale-installations-in-the-eu (accessed on 21 November 2023).
- European Automobile Manufacturers’ Association ACEA EU New Car Registrations June 2023. Available online: https://www.acea.auto/pc-registrations/new-car-registrations-17-8-in-june-battery-electric-15-1-market-share/ (accessed on 25 September 2023).
- European Commission Smart Grids and Meters. Available online: https://energy.ec.europa.eu/topics/markets-and-consumers/smart-grids-and-meters_en (accessed on 14 November 2023).
- European Commission EU Strategy on Energy System Integration. Available online: https://energy.ec.europa.eu/topics/energy-systems-integration/eu-strategy-energy-system-integration_en (accessed on 14 November 2023).
- Ministero dell’Ambiente e della Sicurezza Energetica. Piano Nazionale Integrato per l’Energia e per Il Clima—2023; Ministero dell’Ambiente e della Sicurezza: Rome, Italy, 2023. [Google Scholar]
- Ministero dello Sviluppo Economico; Ministero dell’Ambiente e della Tutela del Territorio e del Mare; Ministero delle Infrastrutture e dei Trasporti. Piano Nazionale Integrato per l’Energia e per Il Clima; Rome, Italy. 2019. Available online: https://energy.ec.europa.eu/system/files/2020-01/it_final_necp_main_it_0.pdf (accessed on 16 February 2025).
- Beaudin, M.; Zareipour, H. Home Energy Management Systems: A Review of Modelling and Complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Battula, A.R.; Vuddanti, S.; Salkuti, S.R. Review of Energy Management System Approaches in Microgrids. Energies 2021, 14, 5459. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Yin, X.; Moura, S.J. Stochastic Optimal Energy Management of Smart Home with PEV Energy Storage. IEEE Trans. Smart Grid 2018, 9, 2065–2075. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Moura, S.; Yin, X.; Pickert, V. Stochastic Control of Smart Home Energy Management with Plug-in Electric Vehicle Battery Energy Storage and Photovoltaic Array. J. Power Sources 2016, 333, 203–212. [Google Scholar] [CrossRef]
- Shin, M.; Choi, D.-H.; Kim, J. Cooperative Management for PV/ESS-Enabled Electric Vehicle Charging Stations: A Multiagent Deep Reinforcement Learning Approach. IEEE Trans. Ind. Inform. 2020, 16, 3493–3503. [Google Scholar] [CrossRef]
- Wi, Y.-M.; Lee, J.-U.; Joo, S.-K. Electric Vehicle Charging Method for Smart Homes/Buildings with a Photovoltaic System. IEEE Trans. Consum. Electron. 2013, 59, 323–328. [Google Scholar] [CrossRef]
- Erdinc, O. Economic Impacts of Small-Scale Own Generating and Storage Units, and Electric Vehicles under Different Demand Response Strategies for Smart Households. Appl. Energy 2014, 126, 142–150. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinç, O.; Bakirtzis, A.G.; Catalão, J.P.S. Optimal Household Appliances Scheduling Under Day-Ahead Pricing and Load-Shaping Demand Response Strategies. IEEE Trans. Ind. Inf. 2015, 11, 1509–1519. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; León-Japa, R.S.; Jurado, F. Optimal Electrification of Off-Grid Smart Homes Considering Flexible Demand and Vehicle-to-Home Capabilities. Appl. Energy 2021, 298, 117184. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Pappi, I.N.; Catalão, J.P.S.; Erdinc, O. Optimal Operation of Smart Houses by a Real-Time Rolling Horizon Algorithm. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 16 July 2016; pp. 1–5. [Google Scholar]
- Erdinc, O.; Paterakis, N.G.; Pappi, I.N.; Bakirtzis, A.G.; Catalão, J.P.S. A New Perspective for Sizing of Distributed Generation and Energy Storage for Smart Households under Demand Response. Appl. Energy 2015, 143, 26–37. [Google Scholar] [CrossRef]
- Pilotti, L.; Moretti, L.; Martelli, E.; Manzolini, G. Optimal E-Fleet Charging Station Design with V2G Capability. Sustain. Energy Grids Netw. 2023, 36, 101220. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Gurung, S.; Jurado, F. Efficient Solution of Many-Objective Home Energy Management Systems. Int. J. Electr. Power Energy Syst. 2022, 136, 107666. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Hasanien, H.M.; Kamel, S.; Turky, R.A.; Jurado, F.; Elkadeem, M.R. Multiobjective Home Energy Management Systems in Nearly-Zero Energy Buildings under Uncertainties Considering Vehicle-to-Home: A Novel Lexicographic-Based Stochastic-Information Gap Decision Theory Approach. Electr. Power Syst. Res. 2023, 214, 108946. [Google Scholar] [CrossRef]
- Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Economic and Environmental Scheduling of Smart Homes with Microgrid: DER Operation and Electrical Tasks. Energy Convers. Manag. 2016, 110, 113–124. [Google Scholar] [CrossRef]
- Erdinç, F.G. Rolling Horizon Optimization Based Real-Time Energy Management of a Residential Neighborhood Considering PV and ESS Usage Fairness. Appl. Energy 2023, 344, 121275. [Google Scholar] [CrossRef]
- Thomas, D.; Deblecker, O.; Ioakimidis, C.S. Optimal Operation of an Energy Management System for a Grid-Connected Smart Building Considering Photovoltaics’ Uncertainty and Stochastic Electric Vehicles’ Driving Schedule. Appl. Energy 2018, 210, 1188–1206. [Google Scholar] [CrossRef]
- Meng, L.; Sanseverino, E.R.; Luna, A.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Microgrid Supervisory Controllers and Energy Management Systems: A Literature Review. Renew. Sustain. Energy Rev. 2016, 60, 1263–1273. [Google Scholar] [CrossRef]
- Moretti, L.; Polimeni, S.; Meraldi, L.; Raboni, P.; Leva, S.; Manzolini, G. Assessing the Impact of a Two-Layer Predictive Dispatch Algorithm on Design and Operation of off-Grid Hybrid Microgrids. Renew. Energy 2019, 143, 1439–1453. [Google Scholar] [CrossRef]
- Esmaeel Nezhad, A.; Rahimnejad, A.; Nardelli, P.H.J.; Gadsden, S.A.; Sahoo, S.; Ghanavati, F. A Shrinking Horizon Model Predictive Controller for Daily Scheduling of Home Energy Management Systems. IEEE Access 2022, 10, 29716–29730. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy Management of Microgrid in Grid-Connected and Stand-Alone Modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Fusco, A.; Gioffré, D.; Leva, S.; Manzolini, G.; Martelli, E.; Moretti, L. Predictive Energy Management System for a PV-BESS System Bidding on Day-Ahead and Intra-Day Electricity Markets. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–6. [Google Scholar]
- Shapiro, A. On Complexity of Multistage Stochastic Programs. Oper. Res. Lett. 2006, 34, 1–8. [Google Scholar] [CrossRef]
- Kim, M.; Park, T.; Jeong, J.; Kim, H. Stochastic Optimization of Home Energy Management System Using Clustered Quantile Scenario Reduction. Appl. Energy 2023, 349, 121555. [Google Scholar] [CrossRef]
- Castelli, A.F.; Moretti, L.; Manzolini, G.; Martelli, E. Robust Optimization of Seasonal, Day-Ahead and Real Time Operation of Aggregated Energy Systems. Int. J. Electr. Power Energy Syst. 2023, 152, 109190. [Google Scholar] [CrossRef]
- Moretti, L.; Martelli, E.; Manzolini, G. An Efficient Robust Optimization Model for the Unit Commitment and Dispatch of Multi-Energy Systems and Microgrids. Appl. Energy 2020, 261, 113859. [Google Scholar] [CrossRef]
- Gestore Servizi Energetici (GSE). Ritiro Dedicato; GSE: Roma, Italy, 2023; Available online: https://www.gse.it/servizi-per-te/fotovoltaico/ritiro-dedicato (accessed on 12 October 2023).
- Gestore Mercati Energetici (GME). Vademecum Della Borsa Elettrica; GME: Roma, Italy, 2009. [Google Scholar]
- Imani, M.H.; Bompard, E.; Colella, P.; Huang, T. Forecasting Electricity Price in Different Time Horizons: An Application to the Italian Electricity Market. IEEE Trans. Ind. Appl. 2021, 57, 5726–5736. [Google Scholar] [CrossRef]
- Gestore Mercati Energetici (GME). Statistiche; GME: Roma, Italy, 2023; Available online: https://www.mercatoelettrico.org/It/download/DatiStorici.aspx (accessed on 23 October 2023).
- Melhem, F.Y.; Grunder, O.; Hammoudan, Z.; Moubayed, N. Energy Management in Electrical Smart Grid Environment Using Robust Optimization Algorithm. IEEE Trans. Ind. Appl. 2018, 54, 2714–2726. [Google Scholar] [CrossRef]
- Boynuegri, A.R.; Yagcitekin, B.; Baysal, M.; Karakas, A.; Uzunoglu, M. Energy Management Algorithm for Smart Home with Renewable Energy Sources. In Proceedings of the International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 December 2013; pp. 1753–1758. [Google Scholar]
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.-P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python, 3rd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2021; Volume 67. [Google Scholar]
- Hart, W.; Watson, J.-P.; Woodruff, D.; Watson, J.-P. Pyomo: Modeling and Solving Mathematical Programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- The Leader in Decision Intelligence Technology-Gurobi Optimization. Gurobi Optimizer Reference Manual; The Leader in Decision Intelligence Technology-Gurobi Optimization: Beaverton, OR, USA, 2021. [Google Scholar]
- Gestore dei Servizi Energetici (GSE). Rapporto Statistico—Solare Fotovoltaico 2022; GSE: Roma, Italy, 2023. [Google Scholar]
- Niu, S.; Zhao, Q.; Chen, H.; Niu, S.; Jian, L. Noncooperative Metal Object Detection Using Pole-to-Pole EM Distribution Characteristics for Wireless EV Charger Employing DD Coils. IEEE Trans. Ind. Electron. 2024, 71, 6335–6344. [Google Scholar] [CrossRef]






| User | <3 MWh/y | >3 MWh/y | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV size | No PV = 0 kW | Low PV = 3 kW | High PV = 4.5 kW | No PV = 0 kW | Low PV = 4.5 kW | High PV = 6 kW | ||||||||||||||||||
| BESS | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | ||||||||||||
| EV | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H | V1H | V2H |
| User | Annual Energy Consumption [MWh/y] | WMAE [-] | SMAPE [%] | |
|---|---|---|---|---|
| Low consumption | A | 2.23 | 0.32 | 28.5% |
| B | 2.55 | 0.75 | 73.2% | |
| C | 2.63 | 0.6 | 52.3% | |
| High consumption | D | 3.43 | 0.22 | 19.4% |
| E | 3.56 | 0.65 | 55.7% | |
| F | 3.85 | 0.65 | 62.6% |
| Battery | Nissan Leaf | Tesla Model S | |
|---|---|---|---|
| 5 kWh | 40 kWh | 100 kWh | |
| On-road specific consumption | - | 0.200 kWh/km | 0.270 kWh/km |
| Nominal charge/discharge power | 4.6 kW | 7.4 kW | 7.4 kW |
| Charge/discharge efficiency | 94% | 97% | 97% |
| Self-discharge | 0.05%/h | 0%/h | 0%/h |
| 80% | 90% | 90% | |
| 20% | 40% | 40% | |
| Throughput cost | 30 €/MWh | 40 €/MWh | 40 €/MWh |
| (BESS lifetime) | 10 y | - | - |
| (discount rate) | 8% | - | - |
| Yearly Mileage [km] | Days of Remote Working Per Week | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | |
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 19,986 | 0 | W | W | W | W | W | L | H |
| Case 2 | 17,386 | 1 | RW | W | W | W | W | L | H |
| Case 3 | 14,630 | 2 | W | RW | W | RW | W | L | H |
| Case 4 | 10,556 | 3 | RW | W | RW | W | RW | L | H |
| User | PV | BESS | ||||
|---|---|---|---|---|---|---|
| A | No | No | 0.8 | 0.0% | 22.4 | 0.7% |
| Yes | 22.0 | 0.6% | 27.1 | 0.8% | ||
| Low | No | 16.2 | 1.0% | 45.5 | 2.7% | |
| Yes | 47.5 | 3.3% | 60.3 | 4.3% | ||
| High | No | 16.7 | 1.7% | 49.8 | 4.9% | |
| Yes | 54.2 | 7.4% | 67.9 | 9.2% | ||
| B | No | No | 1.7 | 0.0% | 57.9 | 1.5% |
| Yes | 59.7 | 1.6% | 80.0 | 2.1% | ||
| Low | No | 6.0 | 0.3% | 72.3 | 3.6% | |
| Yes | 61.1 | 3.5% | 104.2 | 6.0% | ||
| High | No | 4.5 | 0.3% | 75.6 | 5.6% | |
| Yes | 55.1 | 5.2% | 100.7 | 9.6% | ||
| C | No | No | 3.9 | 0.1% | 61.6 | 1.6% |
| Yes | 50.0 | 1.3% | 76.7 | 2.0% | ||
| Low | No | 12.6 | 0.6% | 80.2 | 3.9% | |
| Yes | 67.0 | 3.8% | 107.5 | 6.1% | ||
| High | No | 10.7 | 0.8% | 86.7 | 6.4% | |
| Yes | 66.1 | 6.2% | 115.1 | 10.7% | ||
| D | No | No | 0.8 | 0.0% | 22.1 | 0.5% |
| Yes | 19.9 | 0.5% | 27.8 | 0.7% | ||
| Low | No | 14.1 | 0.9% | 51.1 | 3.2% | |
| Yes | 50.9 | 3.8% | 68.2 | 5.1% | ||
| High | No | 15.2 | 1.6% | 55.4 | 5.9% | |
| Yes | 54.0 | 8.2% | 74.7 | 11.4% | ||
| E | No | No | 2.1 | 0.1% | 66.0 | 1.6% |
| Yes | 67.7 | 1.6% | 87.6 | 2.1% | ||
| Low | No | 5.8 | 0.3% | 92.1 | 5.4% | |
| Yes | 78.5 | 5.6% | 120.8 | 8.7% | ||
| High | No | 6.4 | 0.6% | 95.8 | 9.5% | |
| Yes | 81.1 | 11.5% | 125.9 | 17.8% | ||
| F | No | No | 2.8 | 0.1% | 83.8 | 1.8% |
| Yes | 78.7 | 1.7% | 112.6 | 2.5% | ||
| Low | No | 11.2 | 0.6% | 106.6 | 5.5% | |
| Yes | 87.0 | 5.2% | 140.0 | 8.3% | ||
| High | No | 9.5 | 0.8% | 102.9 | 8.2% | |
| Yes | 82.2 | 8.3% | 136.3 | 13.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gioffrè, D.; Manzolini, G.; Leva, S.; Jaboeuf, R.; Tosco, P.; Martelli, E. Quantifying the Economic Advantages of Energy Management Systems for Domestic Prosumers with Electric Vehicles. Energies 2025, 18, 1774. https://doi.org/10.3390/en18071774
Gioffrè D, Manzolini G, Leva S, Jaboeuf R, Tosco P, Martelli E. Quantifying the Economic Advantages of Energy Management Systems for Domestic Prosumers with Electric Vehicles. Energies. 2025; 18(7):1774. https://doi.org/10.3390/en18071774
Chicago/Turabian StyleGioffrè, Domenico, Giampaolo Manzolini, Sonia Leva, Rémi Jaboeuf, Paolo Tosco, and Emanuele Martelli. 2025. "Quantifying the Economic Advantages of Energy Management Systems for Domestic Prosumers with Electric Vehicles" Energies 18, no. 7: 1774. https://doi.org/10.3390/en18071774
APA StyleGioffrè, D., Manzolini, G., Leva, S., Jaboeuf, R., Tosco, P., & Martelli, E. (2025). Quantifying the Economic Advantages of Energy Management Systems for Domestic Prosumers with Electric Vehicles. Energies, 18(7), 1774. https://doi.org/10.3390/en18071774









