A Multi-Condition-Based Junction Temperature Estimation Technology for Double-Sided Cooled Insulated-Gate Bipolar Transistor Modules
Abstract
:1. Introduction
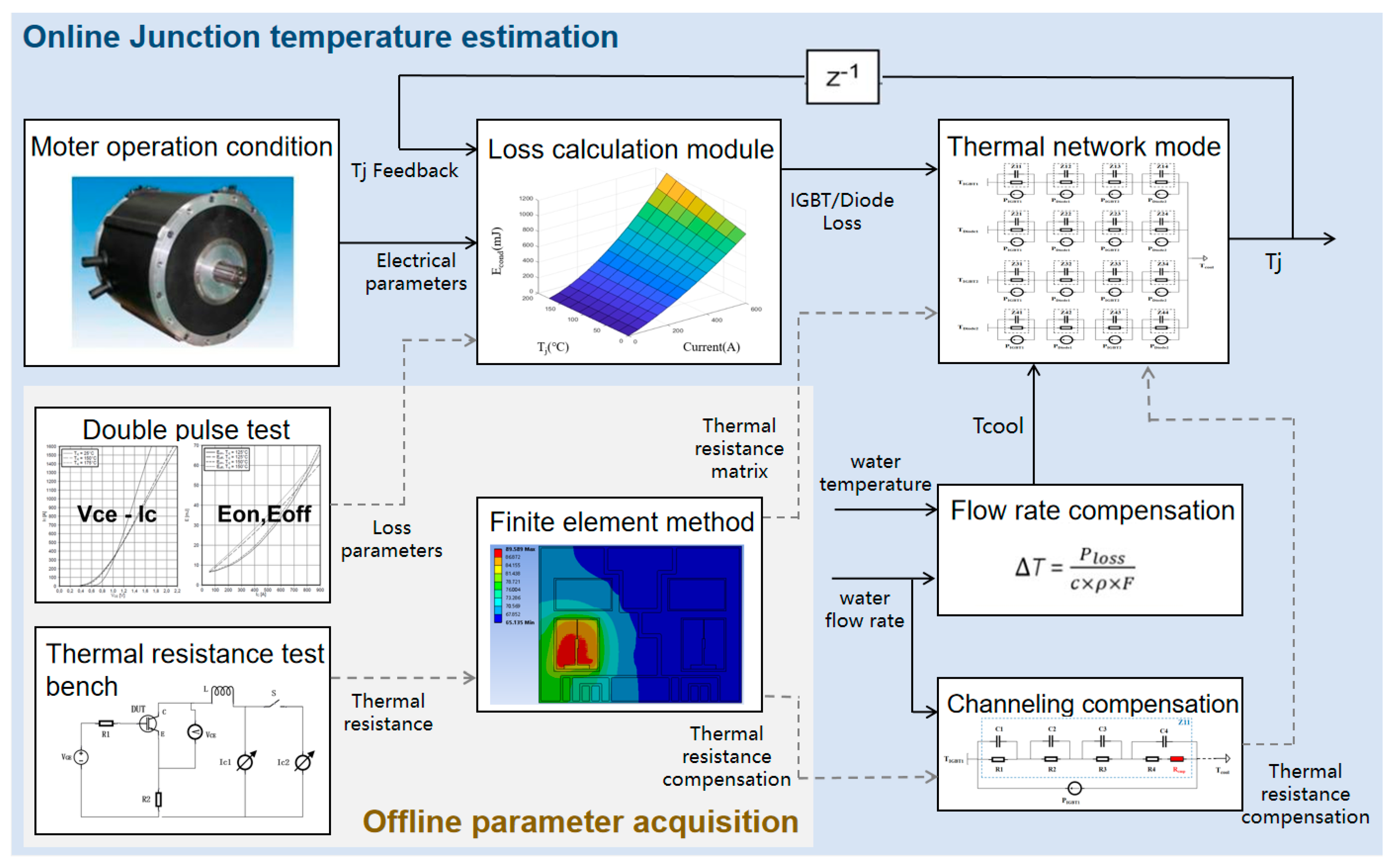
2. System Model Construction
2.1. IGBT Power Loss Model
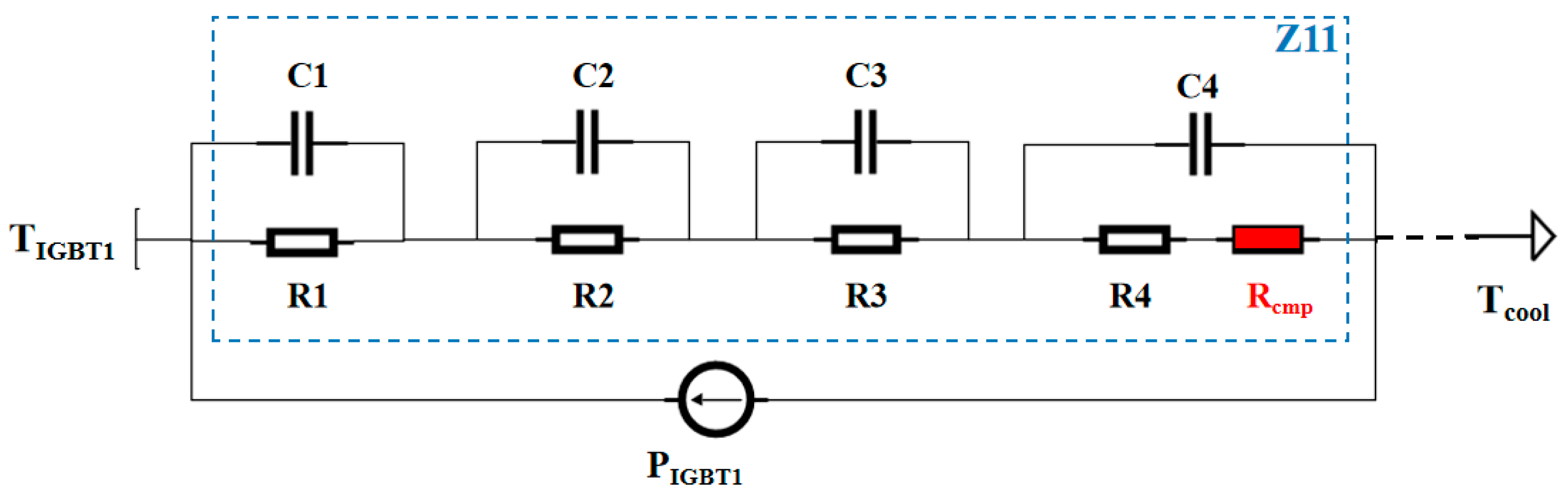
2.2. Thermal Network Model
2.3. Model Optimization Considering Cooling Conditions
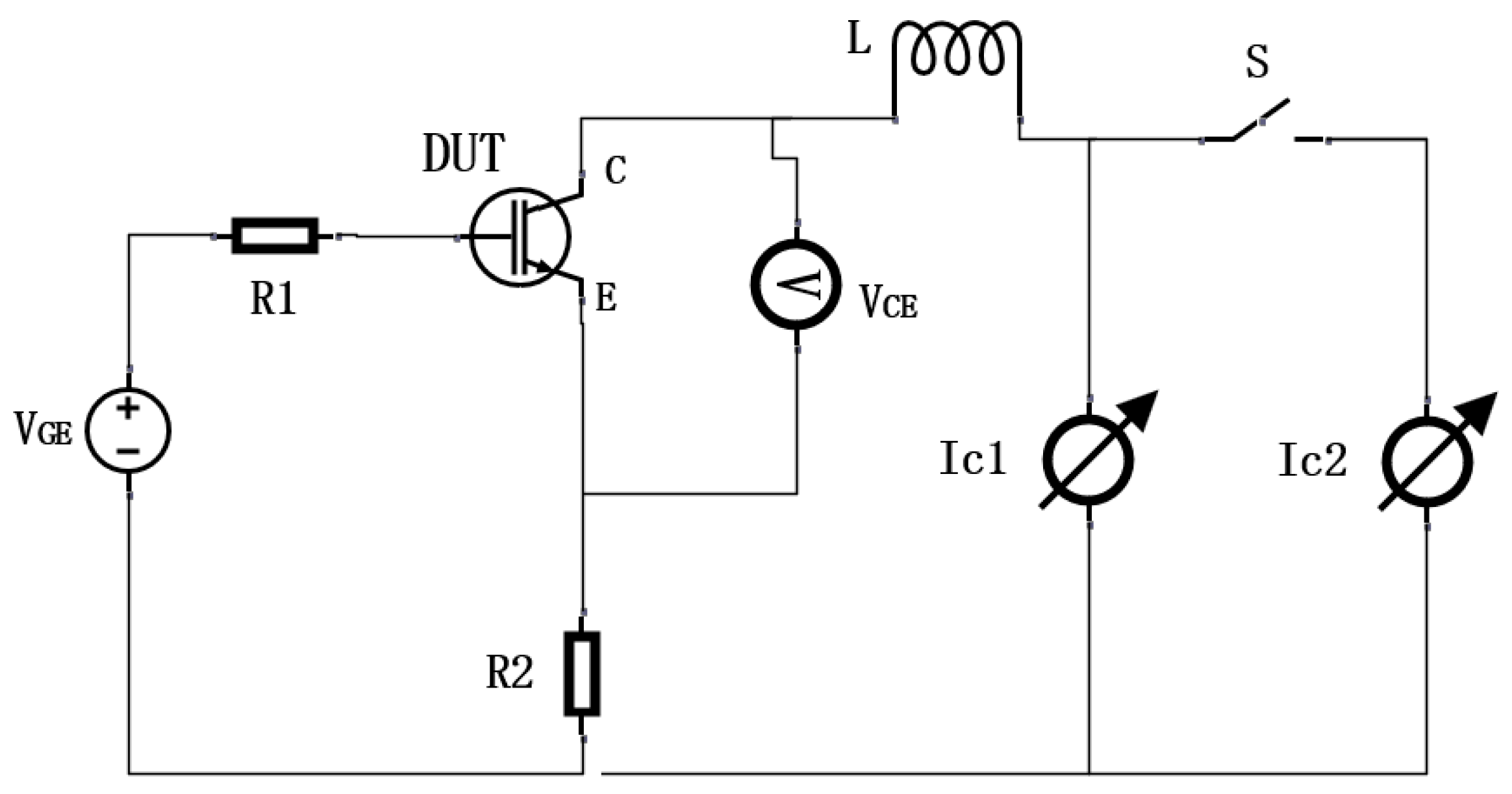
3. Parameter Acquisition and Experimental Verification
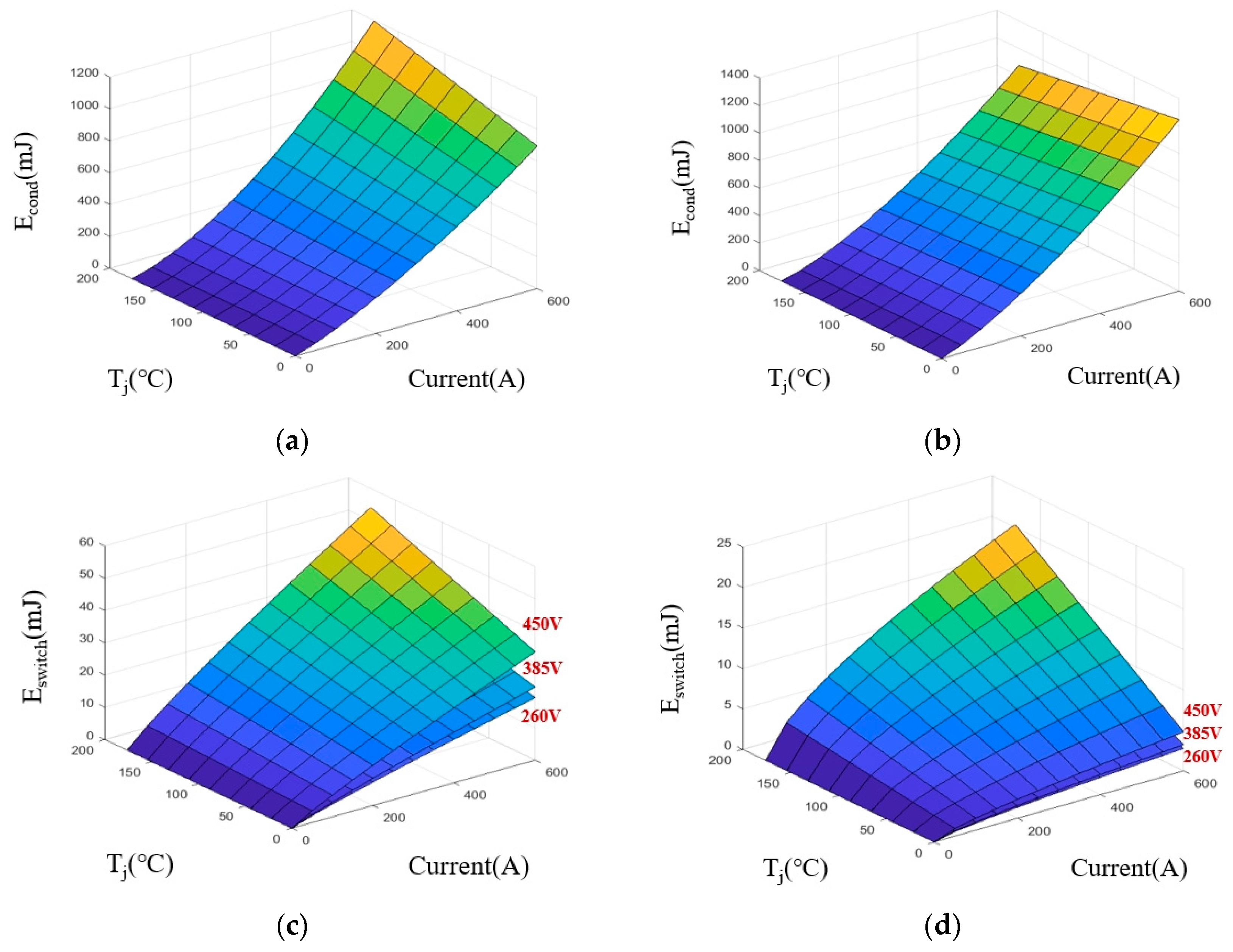
3.1. Loss Parameter Acquisition
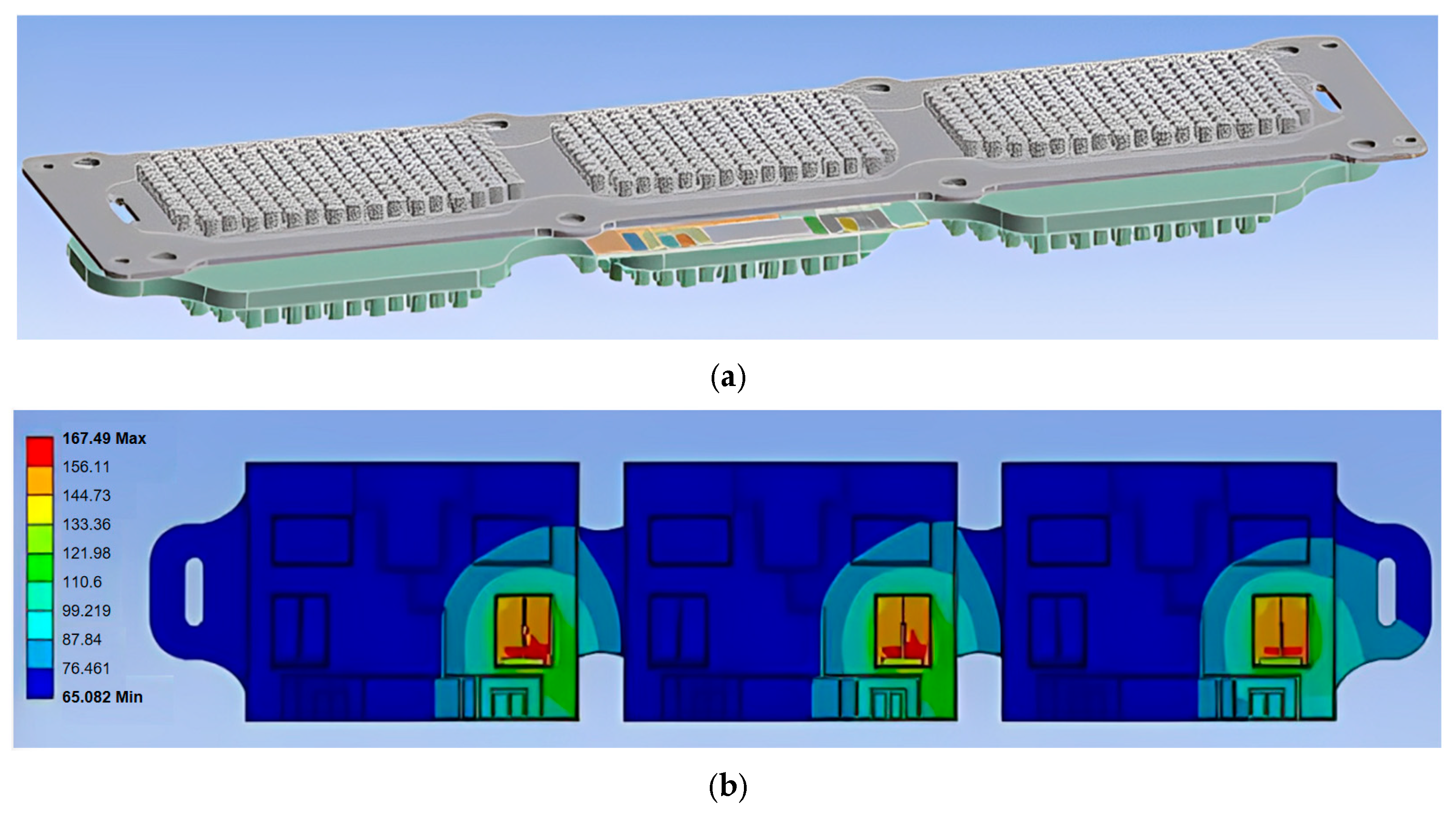
3.2. Obtain Thermal Resistance Parameters Using the Finite Element Method
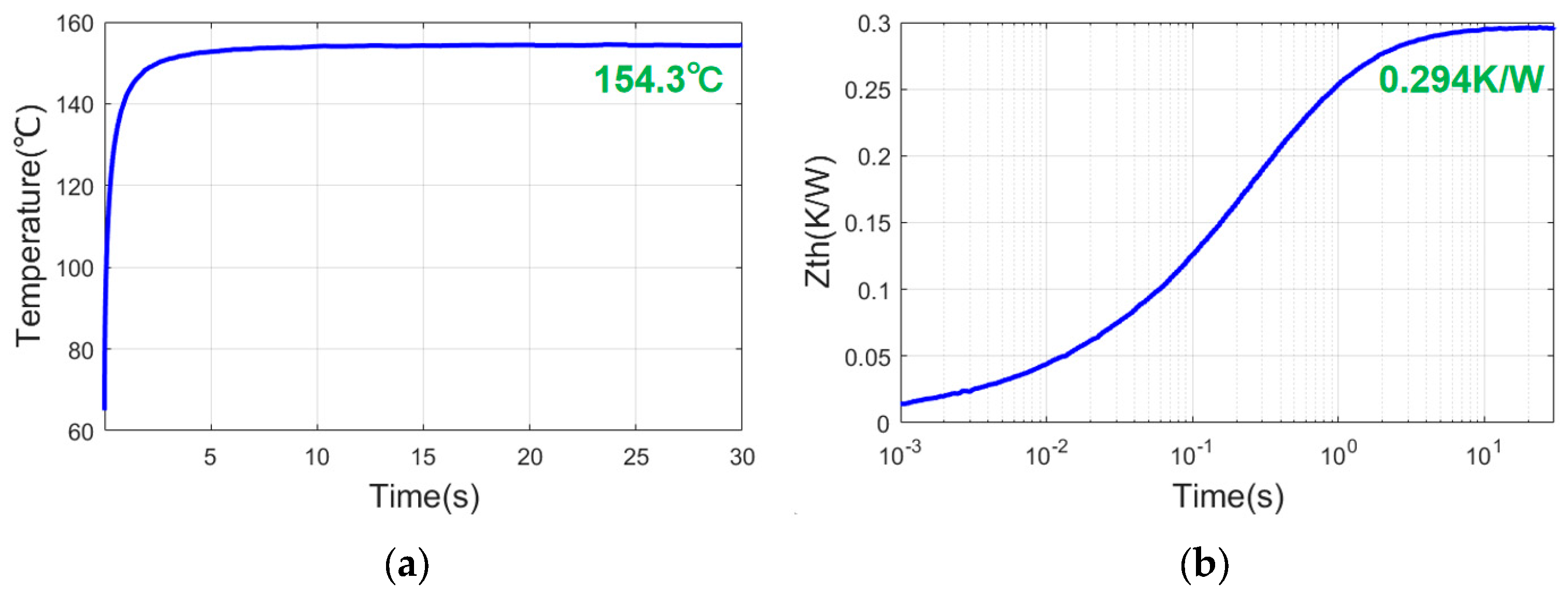
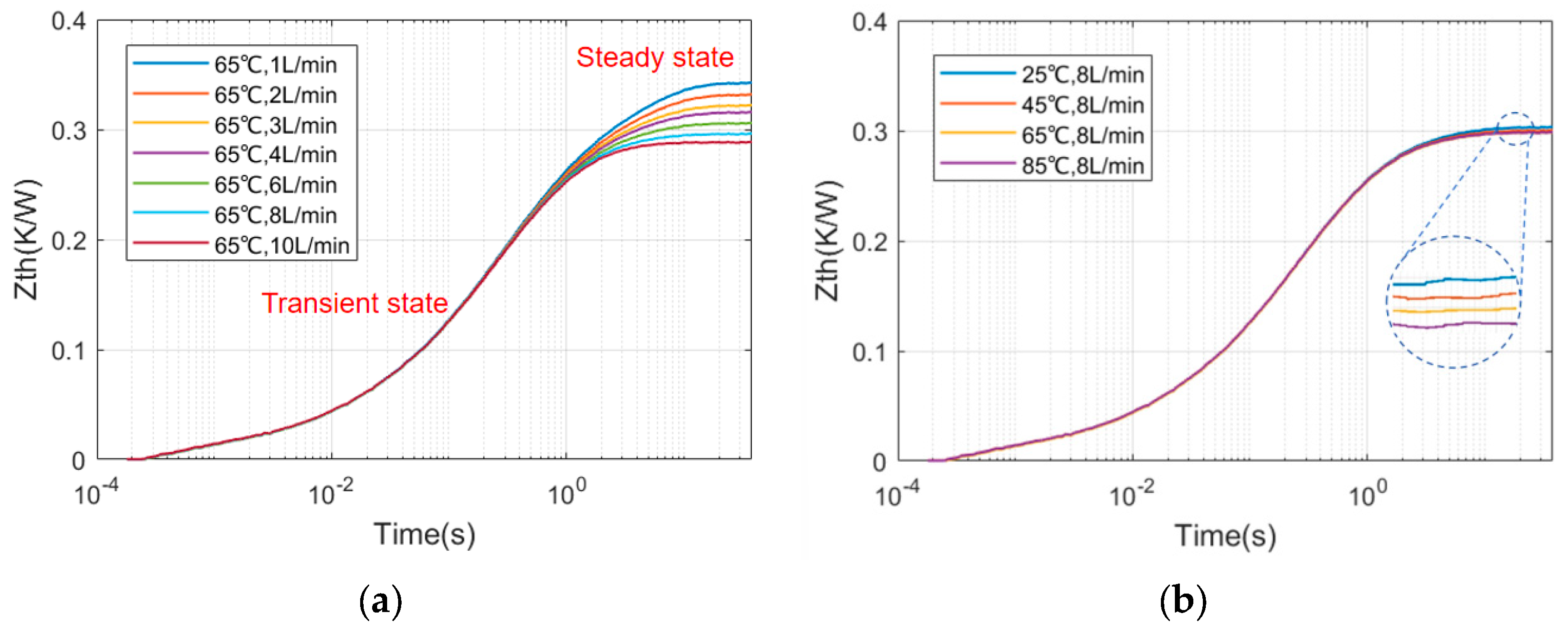
3.3. Thermal Resistance Test Platform Modified Thermal Model
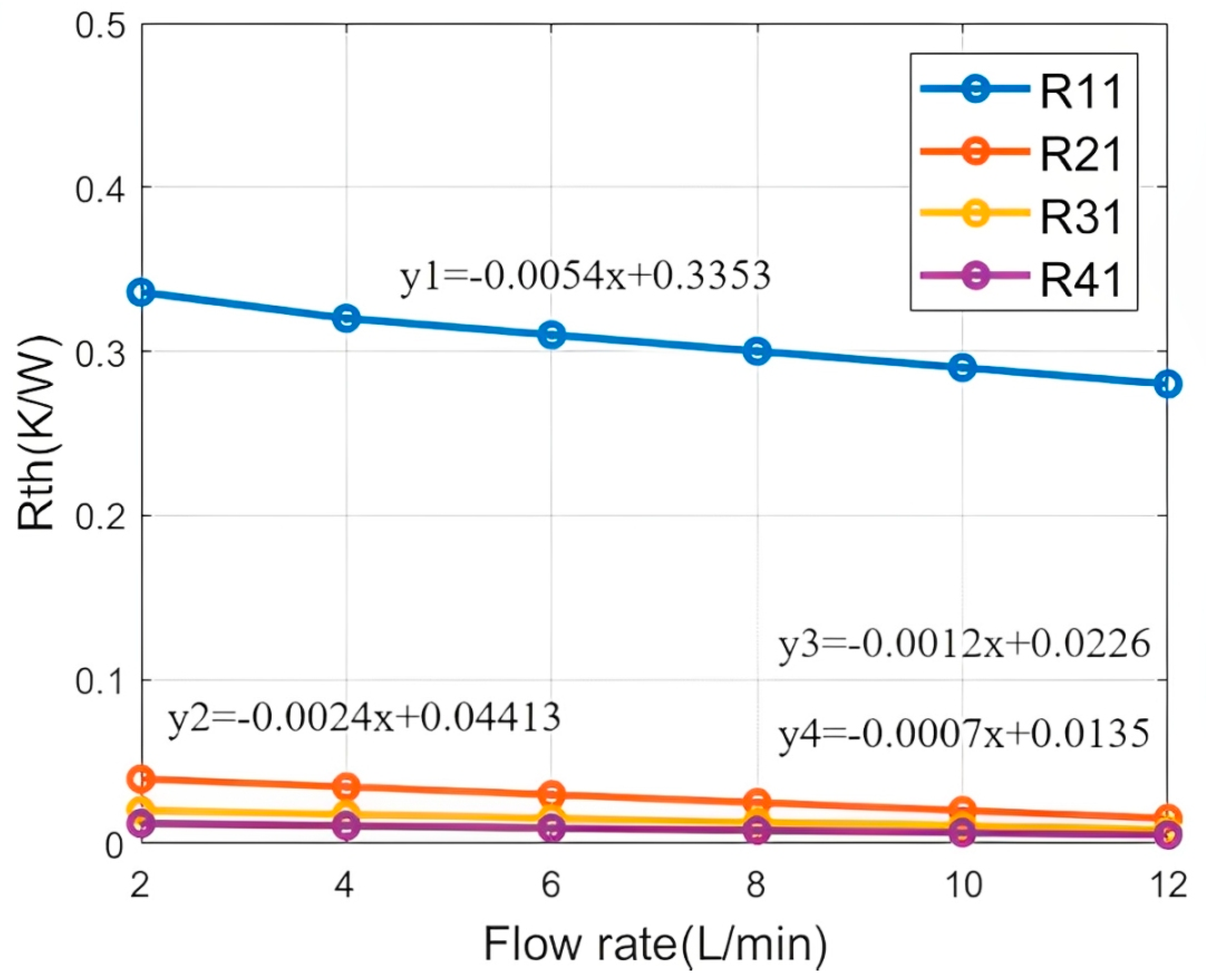
3.4. Cooling Condition-Based Thermal Resistance Parameters Compensation
3.5. Bench-Top Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Loss of IGBT | J | |
| Loss of Diode | J | |
| Thermal impedance response of the j-th chip to the i-th chip | K/W | |
| Junction temperature of chip i | °C | |
| Temperature rise of chip i | °C | |
| Temperature rise of chip i caused by chip j | °C | |
| The n-th order component of the temperature rise caused by chip j to chip i | °C | |
| Temperature rise compensation value of the j-th chip to the i-th chip | °C | |
| The n-th order thermal resistance value in | K/W | |
| The n-th order time constant value in | s | |
| The resistance compensation value for the 4th order thermal resistance in | K/W |
References
- Ning, P.; Wen, X. A Double-Sided Cooling Package Design with Pinfin. In Proceedings of the PCIM Asia 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 27–29 June 2017; pp. 1–7. [Google Scholar]
- Zhou, F.; Zhou, Y.; Fan, T.; Dede, E.M. Double-Side Manifold Micro-Channel Cold Plate for High Power Density Composite DC-DC Converter. In Proceedings of the 2023 22nd IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, M.; Coppola, A.; Alvi, M.; Anwar, M. Comprehensive Review and State of Development of Double-Sided Cooled Package Technology for Automotive Power Modules. IEEE Open J. Power Electron. 2022, 3, 271–289. [Google Scholar] [CrossRef]
- Pai, A.P.; Ebli, M.; Simmet, T.; Lis, A.; Beninger-Bina, M. Characteristics of a SiC MOSFET-based Double Side Cooled High Performance Power Module for Automotive Traction Inverter Applications. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 831–836. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, Y.; Zheng, L.; Du, X.; Wang, J.; Ren, H.; Peng, Y. Online Noninvasive Technique for Condition Monitoring of Cooling System in Urban Rail Vehicles. IEEE Trans. Ind. Electron. 2023, 70, 12762–12772. [Google Scholar] [CrossRef]
- Fernández, M.; Perpiñà, X.; Vellvehi, M.; Aviñó-Salvadó, O.; Llorente, S.; Jordà, X. Power Losses and Current Distribution Studies by Infrared Thermal Imaging in Soft- and Hard-Switched IGBTs Under Resonant Load. IEEE Trans. Power Electron. 2020, 35, 5221–5237. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, L.; Tan, K.; Ji, B.; Zhang, X.; Chai, W.; Cui, X. IGBT Junction Temperature Estimation Using a Dynamic TSEP Independent of Wire Bonding Faults. IEEE Trans. Power Electron. 2023, 38, 5323–5334. [Google Scholar] [CrossRef]
- Guo, W.; Ma, M.; Wang, H.; Chen, Q.; Wang, H.; Song, Q.; Chen, W. Decoupling Compact Thermal Model in Multichip IGBT Modules: A Methodology Based on Concepts of Positive and Negative Mutual Thermal Coupling. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 5476–5492. [Google Scholar] [CrossRef]
- Wang, Z.; Qiao, W.; Qu, L. A Real-Time Adaptive IGBT Thermal Model Based on an Effective Heat Propagation Path Concept. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3936–3946. [Google Scholar] [CrossRef]
- Wang, H.; Qiao, W.; Qu, L. A Thermal Network Model for Multichip Power Modules Enabling to Characterize the Thermal Coupling Effects. IEEE Trans. Power Electron. 2024, 39, 6225–6245. [Google Scholar] [CrossRef]
- Bruckner, T.; Bernet, S. Estimation and measurement of junction temperatures in a three-level voltage source converter. In Proceedings of the 40th IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 106–114. [Google Scholar] [CrossRef]
- Chai, X.; Ning, P.; Cao, H.; Zheng, D.; Li, H.; Huang, Y.; Kang, Y. Online Junction Temperature Measurement of Double-sided Cooling IGBT Power Module through On-state Voltage with High Current. Chin. J. Electr. Eng. 2022, 8, 104–112. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, F.; Wang, F. Junction Temperature Measurement of IGBTs Using Short-Circuit Current as a Temperature-Sensitive Electrical Parameter for Converter Prototype Evaluation. IEEE Trans. Ind. Electron. 2015, 62, 3419–3429. [Google Scholar] [CrossRef]
- Avenas, Y.; Dupont, L.; Khatir, Z. Temperature Measurement of Power Semiconductor Devices by Thermo-Sensitive Electrical Parameters—A Review. IEEE Trans. Power Electron. 2012, 27, 3081–3092. [Google Scholar] [CrossRef]
- Tang, T.; Song, W.; Yang, K.; Chen, J. A Junction Temperature Online Monitoring Method for IGBTs Based on Turn-off Delay Time. IEEE Trans. Ind. Appl. 2023, 59, 6399–6411. [Google Scholar] [CrossRef]
- Arya, A.; Chanekar, A.; Deshmukh, P.; Verma, A.; Anand, S. Accurate Online Junction Temperature Estimation of IGBT Using Inflection Point Based Updated I–V Characteristics. IEEE Trans. Power Electron. 2021, 36, 9826–9836. [Google Scholar] [CrossRef]
- Yun, C.-S.; Malberti, P.; Ciappa, M.; Fichtner, W. Thermal component model for electrothermal analysis of IGBT module systems. IEEE Trans. Adv. Packag. 2001, 24, 401–406. [Google Scholar] [CrossRef]
- van der Broeck, C.H.; Lorenz, R.D.; De Doncker, R.W. Monitoring 3-D Temperature Distributions and Device Losses in Power Electronic Modules. IEEE Trans. Power Electron. 2019, 34, 7983–7995. [Google Scholar] [CrossRef]
- Schweitzer, D.; Chen, L. Heat spreading revisited—Effective heat spreading angle. In Proceedings of the 2015 31st Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 15–19 March 2015; pp. 88–94. [Google Scholar] [CrossRef]
- Feng, X.-Y.; Bai, F.; Ding, H.; Tao, W.-Q. An improved POD-Galerkin method for rapid prediction of three-dimensional temperature field for an IGBT module. Int. Commun. Heat Mass Transf. 2024, 152, 107241. [Google Scholar] [CrossRef]
- Baliga, B.J. Analytical Modeling of IGBTs: Challenges and Solutions. IEEE Trans. Electron Devices 2013, 60, 535–543. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X.; Yu, Y.; Zheng, S.; Sun, P.; Tai, H.-M. Thermal Parameter Monitoring of IGBT Module Using Junction Temperature Cooling Curves. IEEE Trans. Ind. Electron. 2019, 66, 8148–8160. [Google Scholar] [CrossRef]
- Bahman, A.S.; Ma, K.; Blaabjerg, F. General 3D lumped thermal model with various boundary conditions for high power IGBT modules. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 261–268. [Google Scholar] [CrossRef]
- Górecki, K.; Górecki, P. SPICE-Aided Nonlinear Electrothermal Modeling of an IGBT Module. Electronics 2023, 12, 4588. [Google Scholar] [CrossRef]
- Yang, X.; Heng, K.; Dai, X.; Wu, X.; Liu, G. A Temperature-Dependent Cauer Model Simulation of IGBT Module With Analytical Thermal Impedance Characterization. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3055–3065. [Google Scholar] [CrossRef]
- Lu, Y.; Xiang, E.; Jin, Y.; Luo, H.; Yang, H.; Li, W.; Zhao, R. A 3-D Temperature-Dependent Thermal Model of IGBT Modules for Electric Vehicle Application Considering Various Boundary Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 5463–5475. [Google Scholar] [CrossRef]
- Akbari, M.; Bahman, A.S.; Bina, M.T.; Eskandari, B.; Iannuzzo, F.; Blaabjerg, F. A Multi-Layer RC Thermal Model for Power Modules Adaptable to Different Operating Conditions and Aging. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. P.1–P.10. [Google Scholar]
- Heng, K.; Yang, X.; Wu, X.; Ye, J. A 3-D Thermal Network Model for Monitoring of IGBT Modules. IEEE Trans. Electron Devices 2023, 70, 653–661. [Google Scholar] [CrossRef]
- Liu, L.; Bao, M.; Zhang, L.; Fan, X.; Tang, D. Power Loss Calculation Method for IGBT in Converter Valve Based on Inverse Heat Transfer Problem. In Proceedings of the 2021 IEEE 2nd China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 15–17 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Mandray, S.; Guichon, J.-M.; Schanen, J.-L.; Guyennet, M.M.; Dienot, J.-M. Electromagnetic Considerations for Designing Double-Sided Power Modules. IEEE Trans. Ind. Appl. 2009, 45, 871–879. [Google Scholar] [CrossRef]
- Guo, C.; Cui, S.; Tsai, W.; Liu, Y.; Ding, J.; Li, J.; Chen, Z.; Li, Y.; Pan, S.; Feng, S. Measuring Double-Sided Thermal Resistance of Press-Pack IGBT Modules Based on Ratio of Double-Sided Heat Dissipation. IEEE Trans. Electron Devices 2023, 70, 1776–1781. [Google Scholar] [CrossRef]
- Chen, J.; Deng, E.; Zhang, Y.; Huang, Y. Junction-to-Case Thermal Resistance Measurement and Analysis of Press-Pack IGBTs Under Double-Side Cooling Condition. IEEE Trans. Power Electron. 2022, 37, 8543–8553. [Google Scholar] [CrossRef]
- Zhang, X.; Tong, X.; Lv, C.; Du, S.; Chen, K.; Wu, K.; Li, J. A 3-D Thermal Network Model for IGBT Modules Considering Temperature Dependence of Heat Dissipation and Thermal Coupling. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 4906–4910. [Google Scholar] [CrossRef]
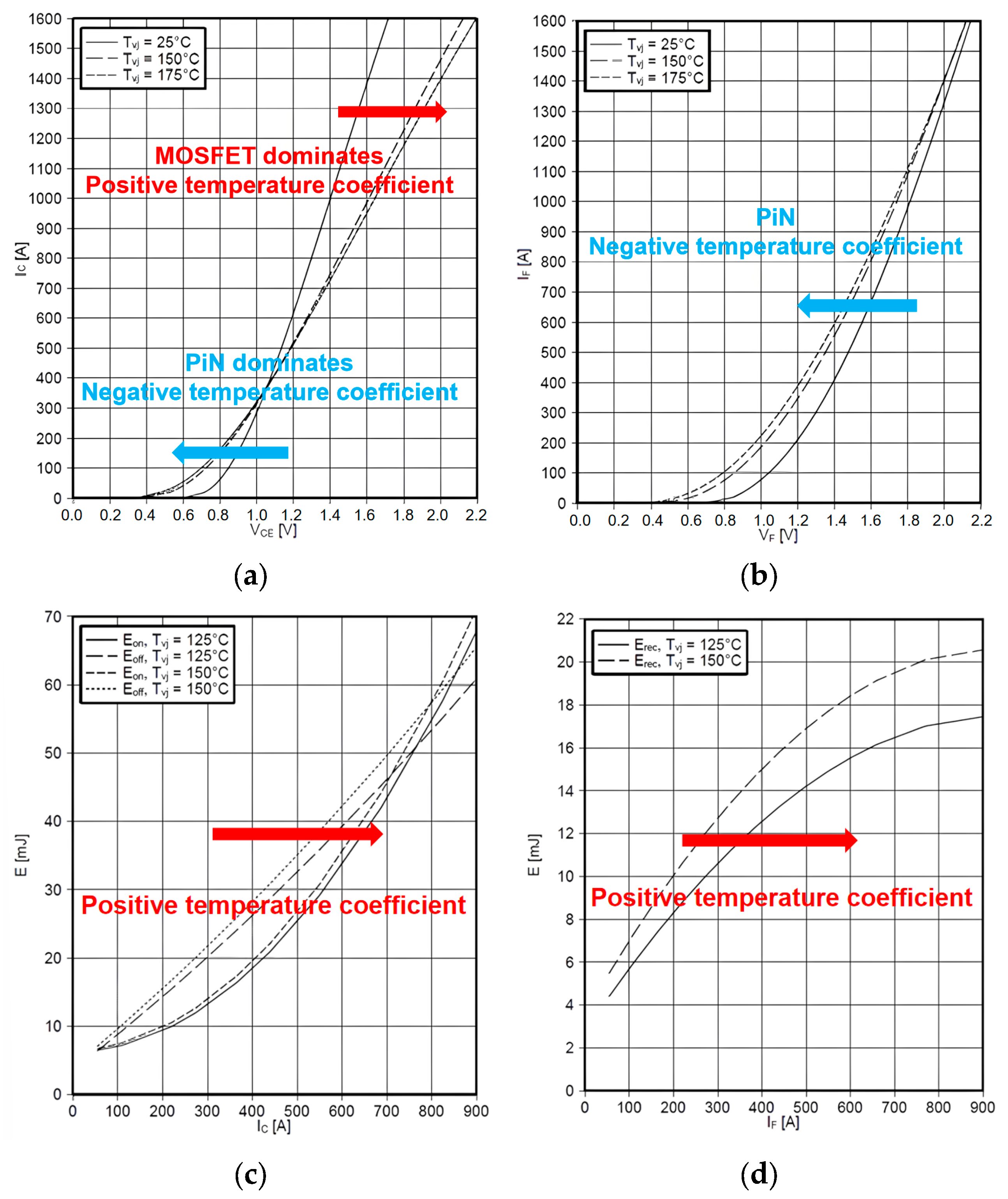
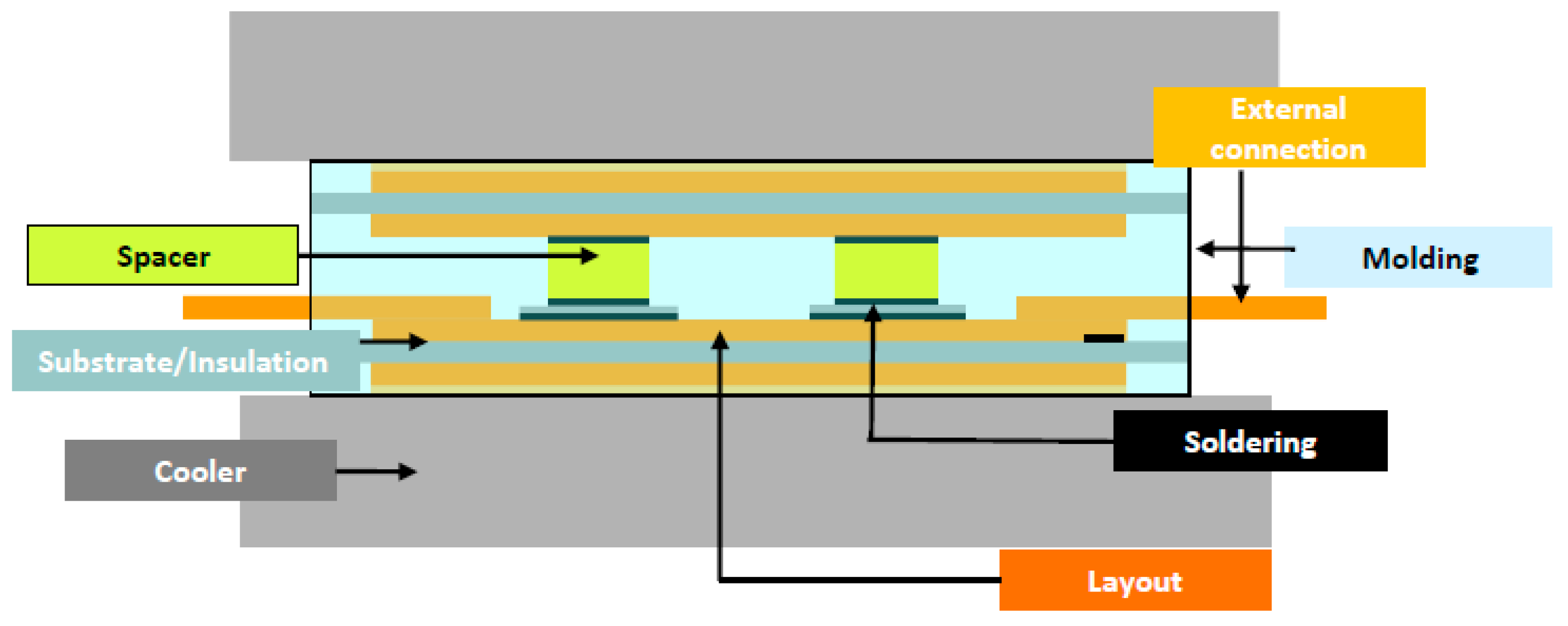

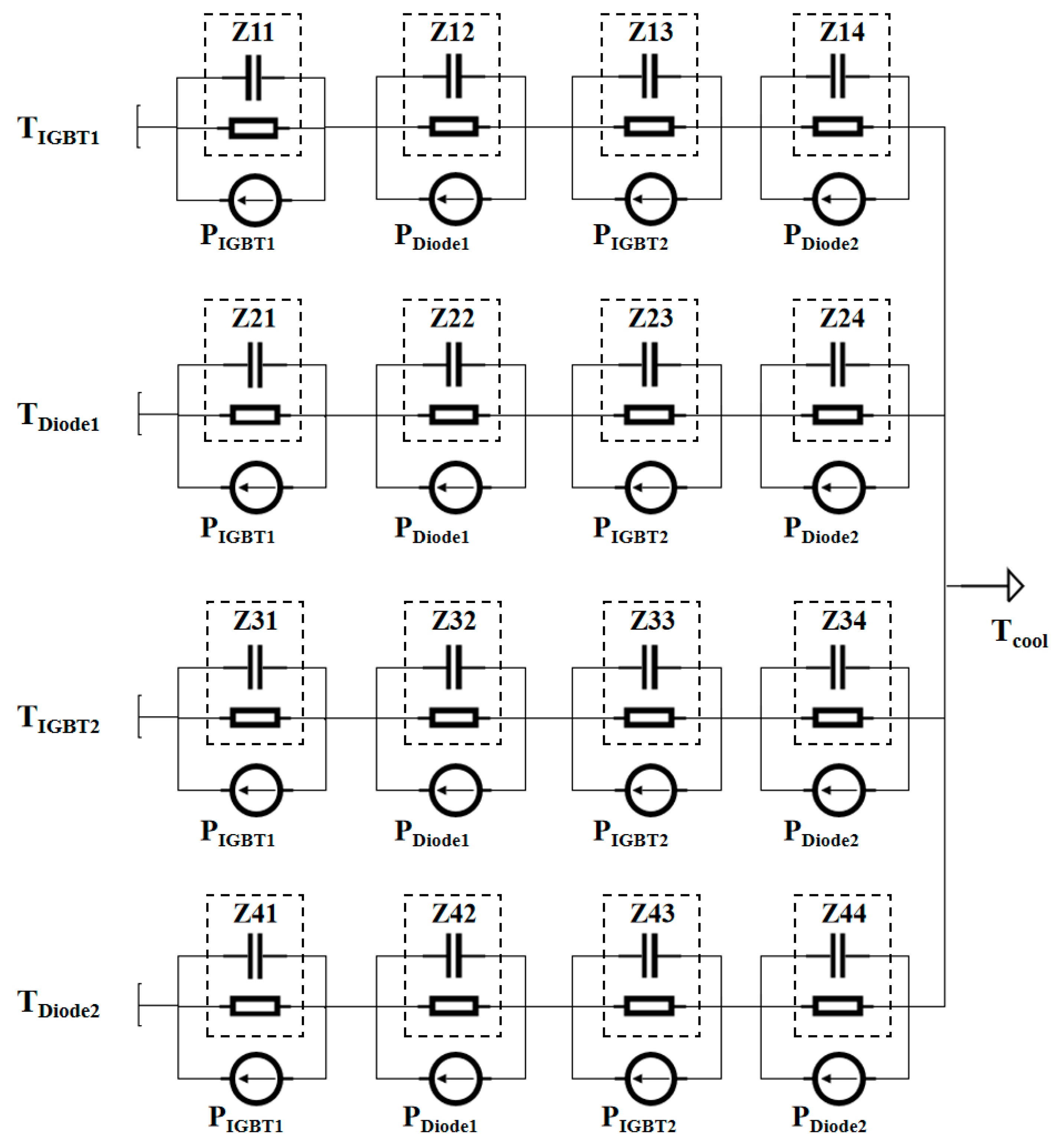
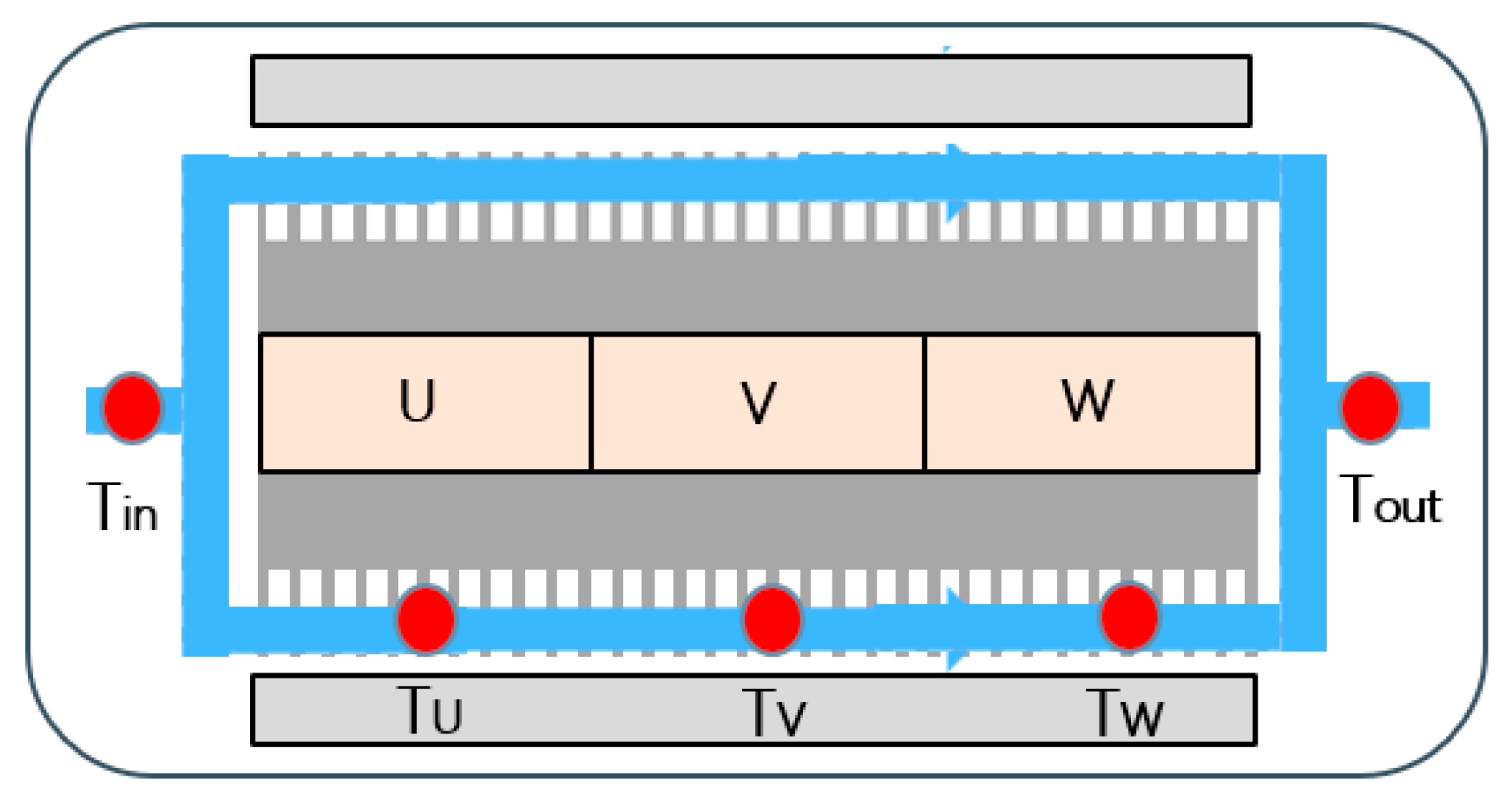




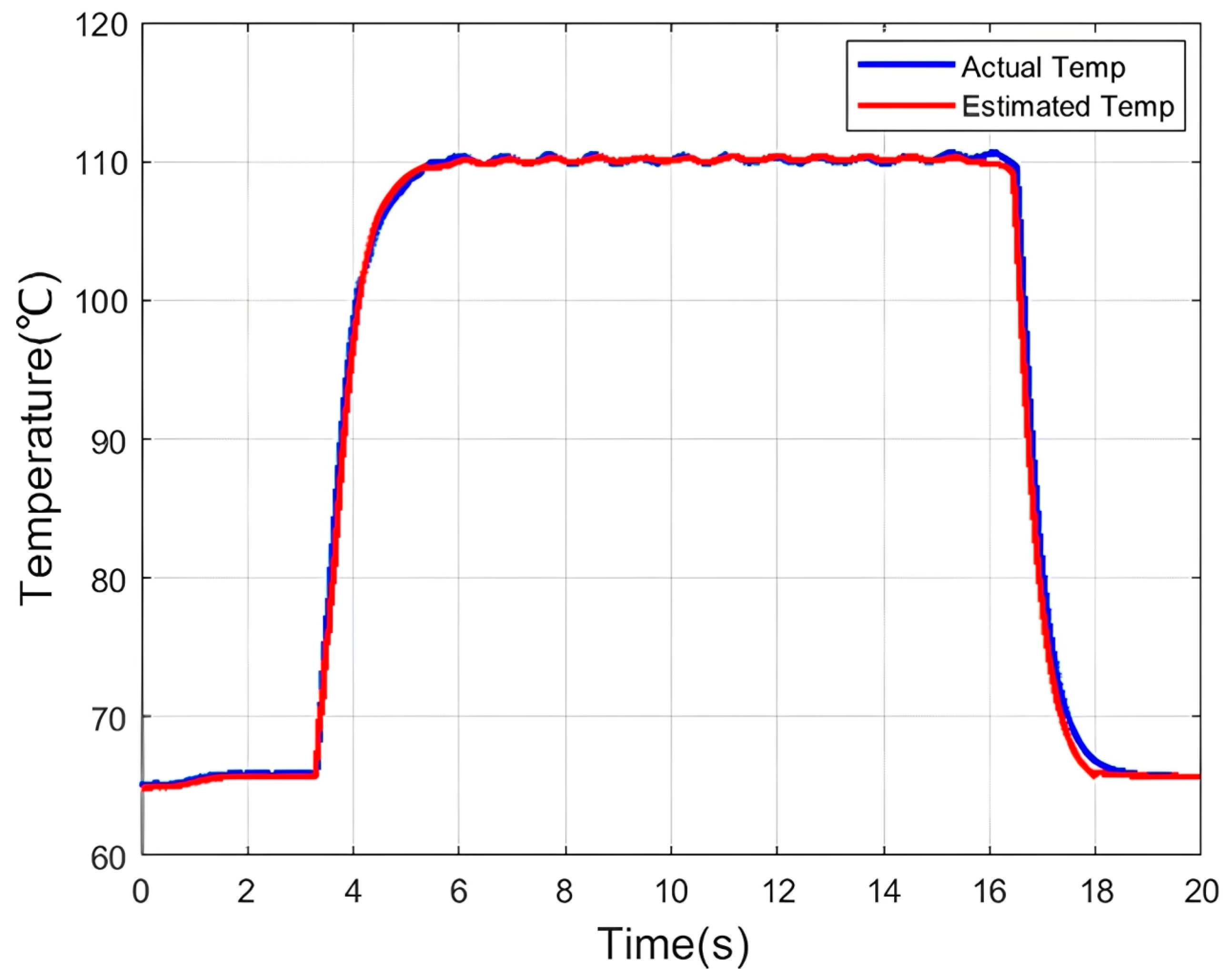
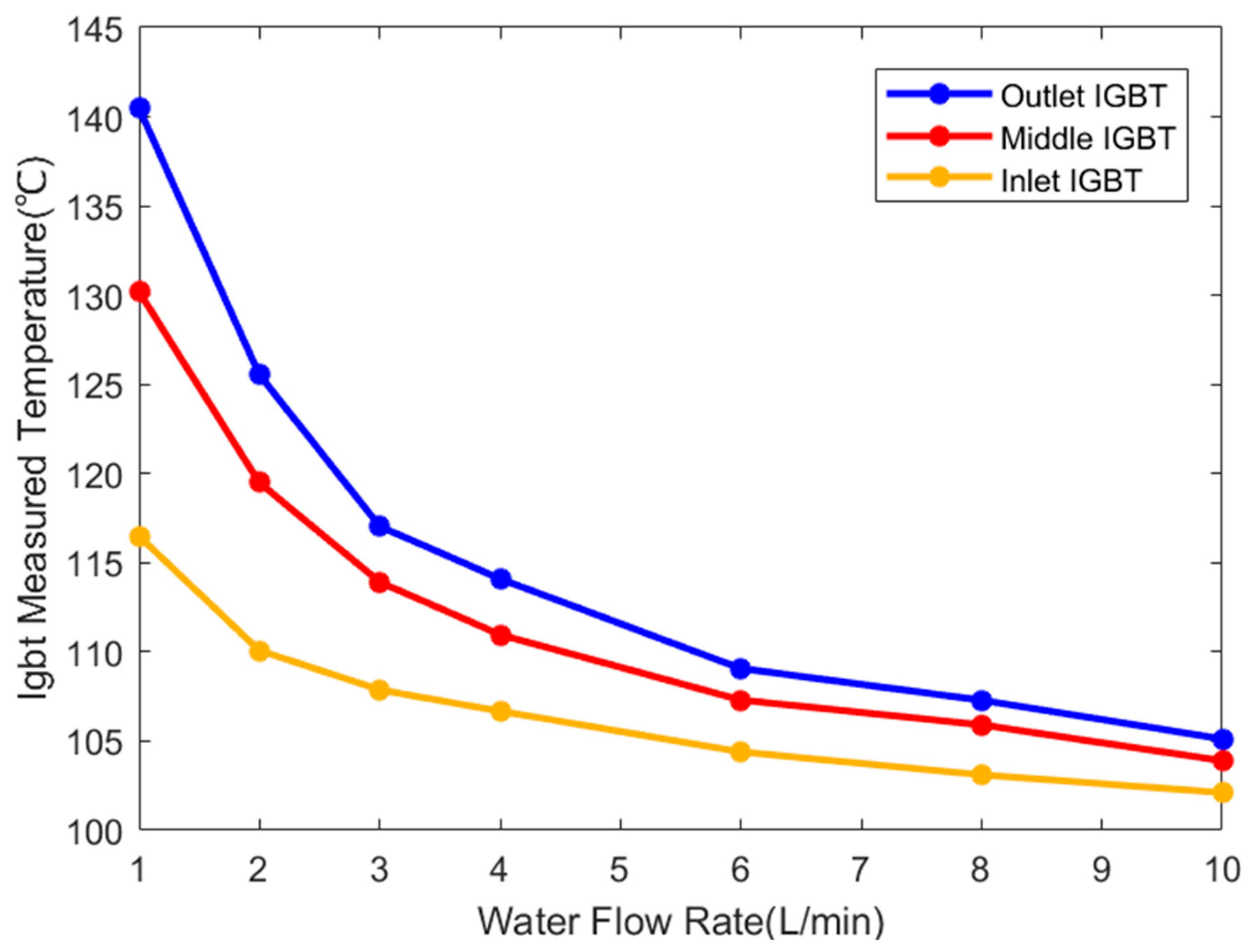
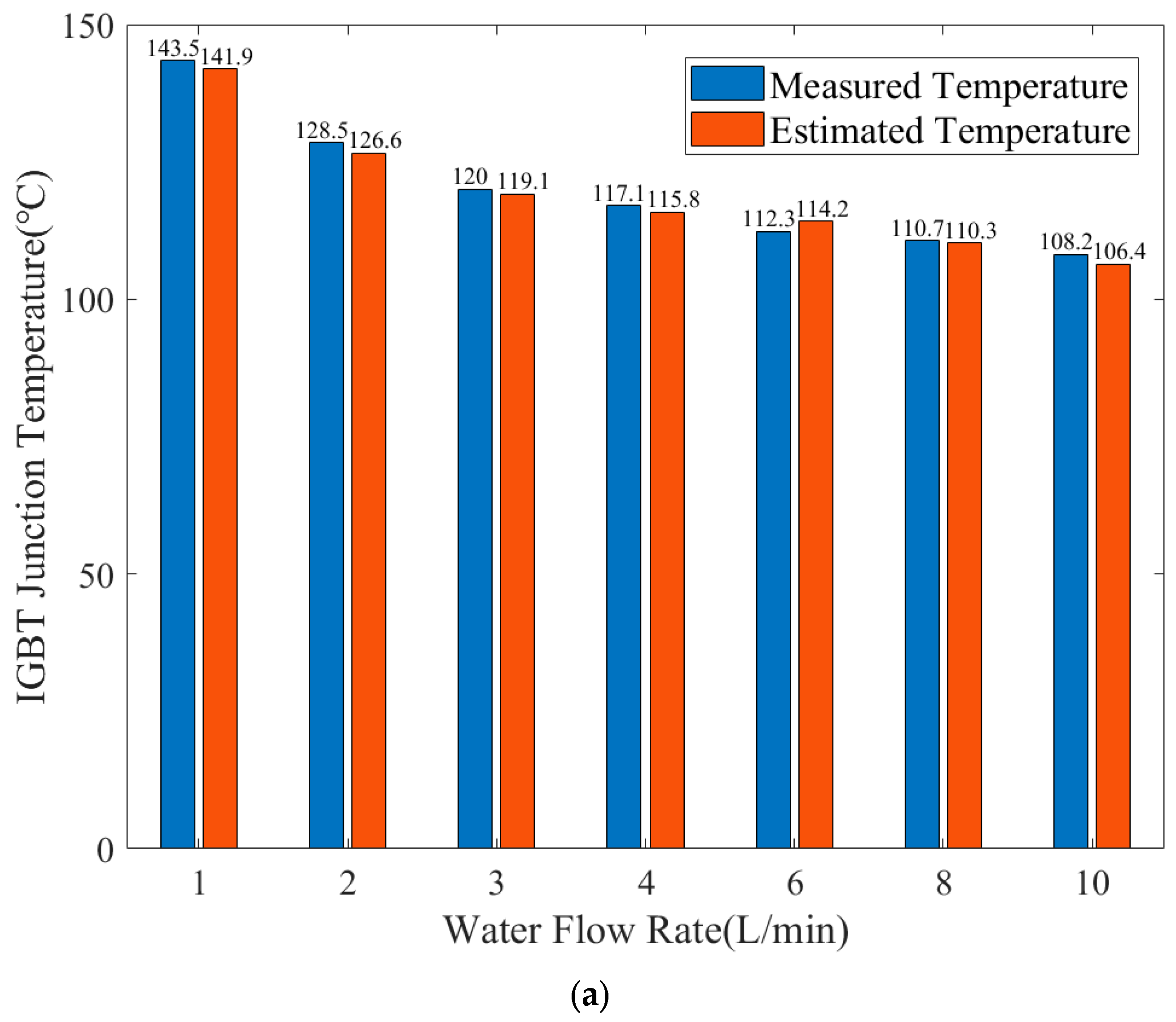
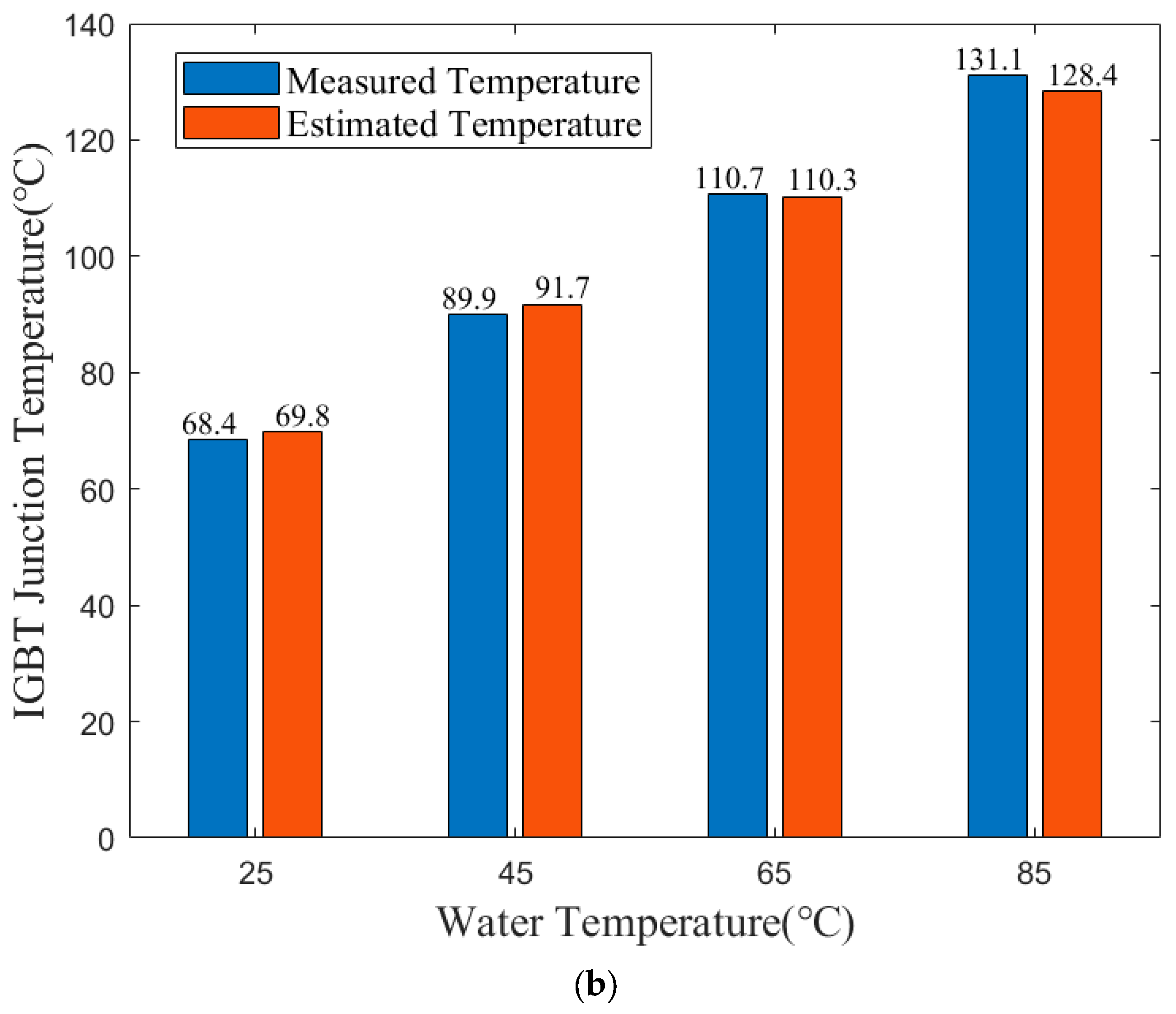
| Layer | Material | Thickness (mm) | Density (g/cm3) | Thermal Conductivity (W/m*K) | Specific Heat (J/g*K) |
|---|---|---|---|---|---|
| Outer_baseplate | Al3003 | \ | 2.74 | 160 | 0.893 |
| Outer_TIM | TIM | 0.15 | 2.70 | 2.2 | 0.800 |
| Outer_Cu1 | Cu | 0.40 | 8.96 | 380 | 0.381 |
| Outer_Ceramic | ZTA | 0.32 | 4.00 | 20 | 0.720 |
| Outer_Cu2 | Cu | 0.30 | 8.96 | 380 | 0.381 |
| Spacer_solder1 | SnSb5 | 0.10 | 7.40 | 55 | 0.230 |
| Spacer | WCu | 2.32 | 15.5 | 200 | 0.170 |
| Spacer_solder2 | SnSb5 | 0.10 | 7.40 | 55 | 0.230 |
| Chip | Si | 0.08 | 2.33 | 98.9 | 0.741 |
| Chip_solder | SnSb5 | 0.1 | 7.40 | 55 | 0.230 |
| Inner_Cu2 | Cu | 0.30 | 8.96 | 380 | 0.381 |
| Inner_Ceramic | ZTA | 0.32 | 4.00 | 20 | 0.720 |
| Inner_Cu1 | Cu | 0.40 | 8.96 | 380 | 0.381 |
| Inner_TIM | TIM | 0.15 | 2.70 | 2.2 | 0.800 |
| Inner_baseplate | Al6063 | \ | 2.72 | 200 | 0.896 |
| Al6061 | \ | 2.72 | 155 | 0.896 |
| Top IGBT | Top Diode | Bot IGBT | Bot Diode | |||||
|---|---|---|---|---|---|---|---|---|
| Top IGBT | Rth | τ | Rth | τ | Rth | τ | Rth | τ |
| 0.03845 | 0.00145 | 4.3 × 10−7 | 0.01 | 4.32 × 10−7 | 0.009 | 3.5 × 10−6 | 0.009 | |
| 0.07424 | 0.03788 | 7 × 10−13 | 0.1 | 3.9 × 10−10 | 0.1 | 3.8 × 10−9 | 0.099 | |
| 0.0678 | 0.2306 | 0.006412 | 0.2228 | 0.001734 | 1 | 0.001429 | 1 | |
| 0.1126 | 1 | 0.04212 | 1.532 | 0.004806 | 3.427 | 0.003774 | 3.278 | |
| Top Diode | Rth | τ | Rth | τ | Rth | τ | Rth | τ |
| 9.6 × 10−7 | 0.009 | 0.01875 | 0.00165 | 5.42 × 10−7 | 0.009 | 4.51 × 10−6 | 0.009 | |
| 9 × 10−12 | 0.099 | 0.05987 | 0.04122 | 4.2 × 10−10 | 0.099 | 3.84 × 10−9 | 0.1 | |
| 0.05146 | 0.214 | 0.05789 | 0.2106 | 0.002834 | 1 | 0.002697 | 1 | |
| 0.00668 | 1.689 | 0.1014 | 1 | 0.003786 | 3.326 | 0.004884 | 3.297 | |
| Bot IGBT | Rth | τ | Rth | τ | Rth | τ | Rth | τ |
| 5.03 × 10−7 | 0.01 | 7.1 × 10−7 | 0.01 | 0.02978 | 0.00201 | 7.8 × 10−12 | 0.009 | |
| 6.4 × 10−11 | 0.1 | 4.6 × 10−13 | 0.1 | 0.07945 | 0.04013 | 4.5 × 10−9 | 0.099 | |
| 0.00198 | 1 | 0.002812 | 1 | 0.06124 | 0.2256 | 0.002189 | 0.1947 | |
| 0.00765 | 3.147 | 0.003179 | 3.332 | 0.1269 | 1 | 0.04134 | 1.624 | |
| Bot Diode | Rth | τ | Rth | τ | Rth | τ | Rth | τ |
| 6.5 × 10−8 | 0.01 | 6.14 × 10−6 | 0.01 | 7.7 × 10−12 | 0.009 | 0.02812 | 0.00171 | |
| 5.6 × 10−11 | 0.1 | 7.4 × 10−11 | 0.1 | 6.34 × 10−9 | 0.099 | 0.06478 | 0.03325 | |
| 0.00151 | 1 | 0.00478 | 1 | 0.001364 | 0.2023 | 0.04215 | 0.2314 | |
| 0.00319 | 3.049 | 0.00115 | 3.198 | 0.004145 | 1.678 | 0.1098 | 1 | |
| Bus Voltage (V) | Load Current (A) | Fundamental Frequency (Hz) | Inverter Loss (J) | Measured Temperature (°C) | Estimated Temperature (°C) | Error (°C) |
|---|---|---|---|---|---|---|
| 385 | 100 | 300 | 567 | 83.97 | 84.31 | 0.34 |
| 385 | 250 | 300 | 1612 | 111.65 | 110.32 | 1.33 |
| 385 | 350 | 300 | 2889 | 147.62 | 149.31 | 1.69 |
| 385 | 350 | 50 | 2896 | 148.32 | 148.89 | 0.57 |
| 260 | 350 | 300 | 1964 | 120.12 | 121.35 | 1.23 |
| 450 | 350 | 300 | 3325 | 160.34 | 158.41 | 1.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Lei, G.; Li, M.; Chang, S.; Wu, S.; Bao, H. A Multi-Condition-Based Junction Temperature Estimation Technology for Double-Sided Cooled Insulated-Gate Bipolar Transistor Modules. Energies 2025, 18, 1785. https://doi.org/10.3390/en18071785
Chen M, Lei G, Li M, Chang S, Wu S, Bao H. A Multi-Condition-Based Junction Temperature Estimation Technology for Double-Sided Cooled Insulated-Gate Bipolar Transistor Modules. Energies. 2025; 18(7):1785. https://doi.org/10.3390/en18071785
Chicago/Turabian StyleChen, Mengfan, Guangyin Lei, Min Li, Shouzhong Chang, Sirui Wu, and Huichuang Bao. 2025. "A Multi-Condition-Based Junction Temperature Estimation Technology for Double-Sided Cooled Insulated-Gate Bipolar Transistor Modules" Energies 18, no. 7: 1785. https://doi.org/10.3390/en18071785
APA StyleChen, M., Lei, G., Li, M., Chang, S., Wu, S., & Bao, H. (2025). A Multi-Condition-Based Junction Temperature Estimation Technology for Double-Sided Cooled Insulated-Gate Bipolar Transistor Modules. Energies, 18(7), 1785. https://doi.org/10.3390/en18071785






