Collaborative Planning of Source–Grid–Load–Storage Considering Wind and Photovoltaic Support Capabilities
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
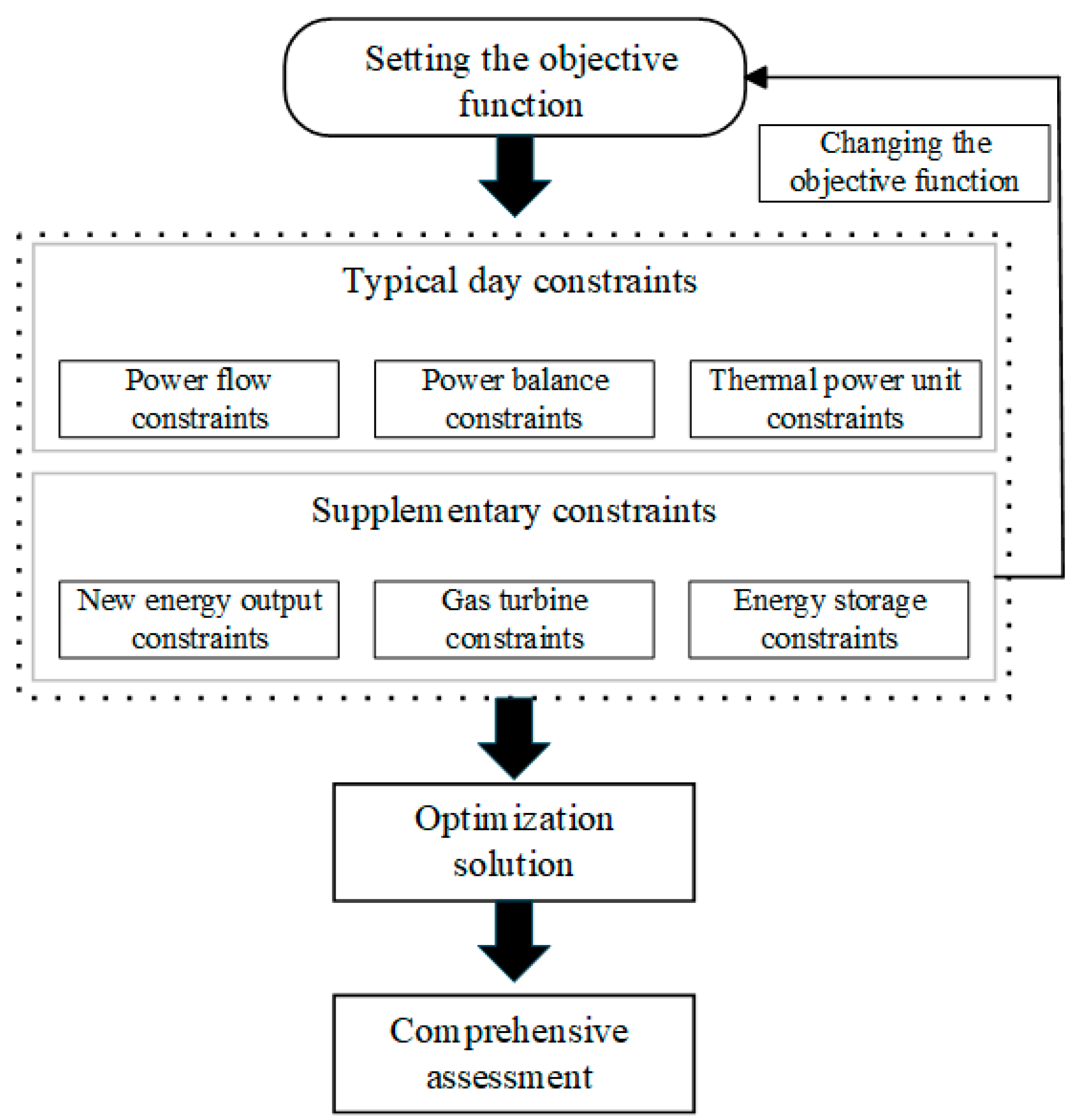
2. A New Power System Planning Framework Considering Multi-Source–Storage Coordinated Deployment
3. Construction of a New Power System Planning Model for Coordinated Deployment of Multiple Sources and Storage Based on Stochastic Difference Equations
3.1. New Energy Output Analysis and Modeling
3.2. Objective Functions
3.3. Typical Day Constraints
4. Multi-Source–Storage Coordinated Deployment Analysis and Modeling
4.1. Gas Turbine Plant Modeling
4.2. Energy Storage Modeling
5. Case Analysis
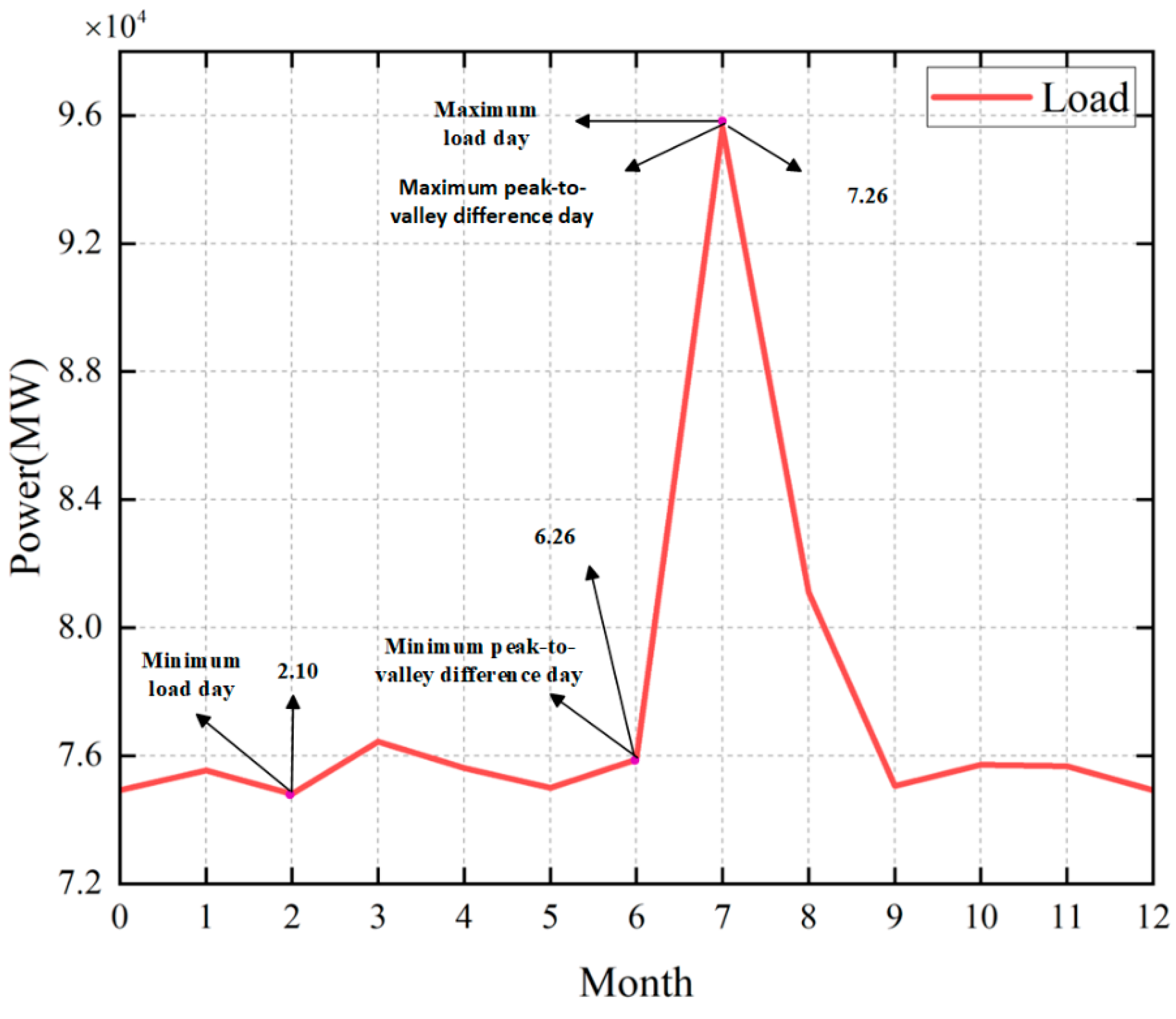
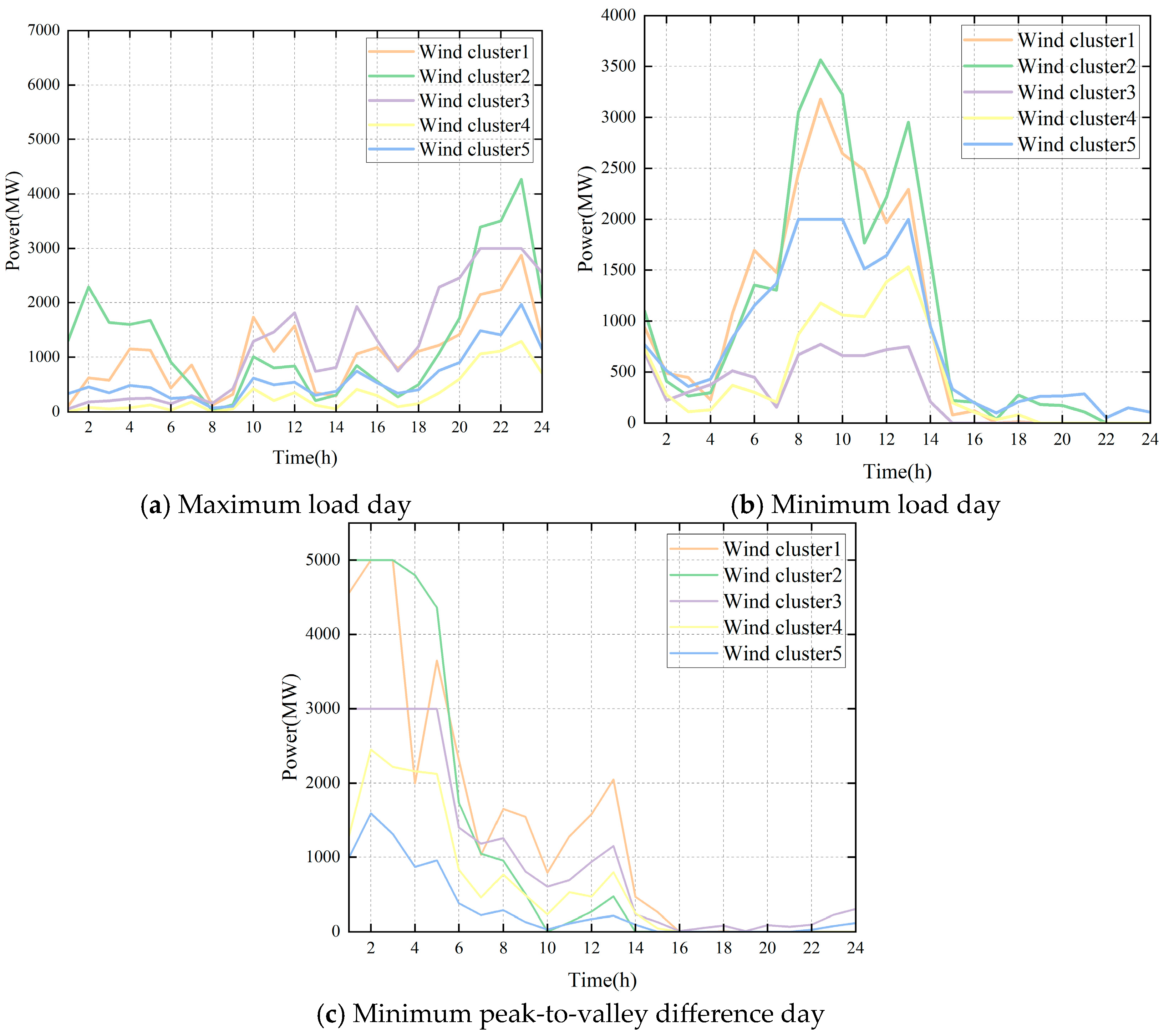
5.1. Data Description and Simulation Setup
5.2. Power Supply-Related Statistics
5.3. Economic Analysis
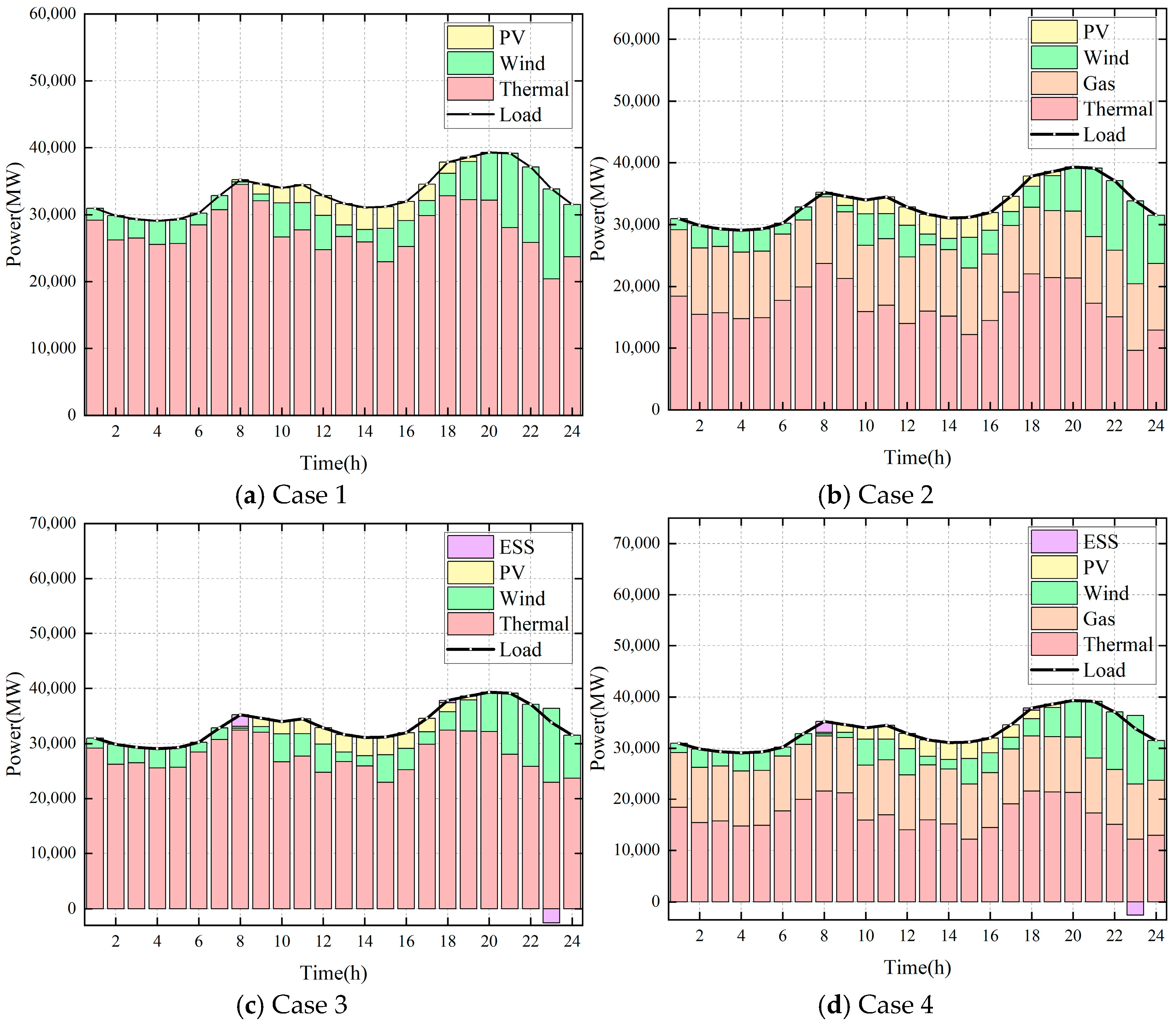
5.4. Supply and Demand Balance Analysis
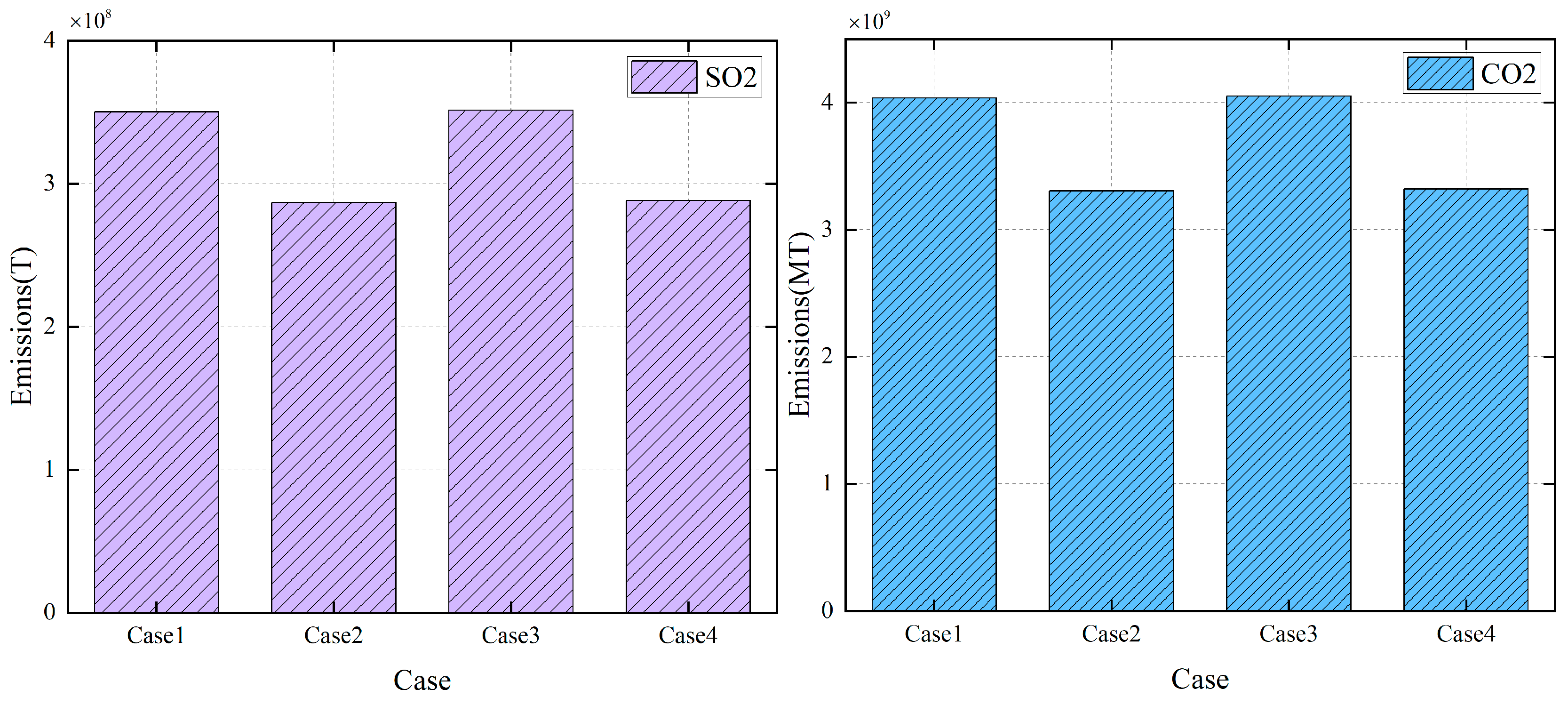
5.5. Environmental Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Autocorrelation coefficient of wind speed series on wind farm | |
| Standard Brownian motion | |
| Gamma function | |
| Wind farm wind speed seasonal factor, m = 1, 2, 3 … 12 | |
| Hourly average wind speed factor of the wind farm during the day, h = 1, 2, … 24 | |
| Wind farm output characteristic curve | |
| Wind farm wake effect coefficient | |
| Photovoltaic output on a typical day | |
| Line power flow between node i and node j | |
| The load of node i | |
| Load shedding amount of node i | |
| Time series within a typical day X | |
| Typical day collection | |
| The number of available wind farm units, for any time t, following the Bernoulli distribution | |
| Cut-in wind speed | |
| Cut-out wind speed | |
| Rated wind speed | |
| Rated output of solar energy | |
| Solar radiation intensity | |
| temperature | |
| Power temperature coefficient of solar panels | |
| Output of thermal power units on a typical day | |
| Wind power output on a typical day | |
| Wind power installed capacity | |
| Photovoltaic installed capacity | |
| Hourly wind power fluctuation curve within a typical day | |
| Hourly photovoltaic fluctuation curve within a typical day | |
| Conversion efficiency of gas turbine | |
| Gas flow rate of gas turbine | |
| Low calorific value of gas from gas turbine | |
| Line loss rate | |
| Gas costs | |
| Thermal power units | |
| Gas turbine | |
| Energy storage | |
| Wind | |
| Photovoltaic | |
| Load shedding |
References
- Numan, M.; Baig, M.F.; Yousif, M. Reliability evaluation of energy storage systems combined with other grid flexibility options: A review. J. Energy Storage 2023, 63, 107022. [Google Scholar]
- Harrouz, A.; Abbes, M.; Colak, I.; Kayisli, K. Smart grid and renewable energy in Algeria. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 1166–1171. [Google Scholar]
- Li, Y.; Liu, H.; Fan, Y.; Tian, X.; Xiao, Y.; Wang, C. Research on the Technology Requirement of Distributed Renewable Energy AC/DC Output System and Network Voltage Coordinated Control. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2369–2372. [Google Scholar]
- Vallée, F.; Brunieau, G.; Pirlot, M.; Deblecker, O.; Lobry, J. Optimal wind clustering methodology for electrical network adequacy studies using non sequential Monte Carlo simulation. In Proceedings of the 2011 International Conference on Clean Electrical Power (ICCEP), Ischia, Italy, 14–16 June 2011; pp. 778–785. [Google Scholar]
- Borges, C.L.T.; Dias, J.A.S. A Model to Represent Correlated Time Series in Reliability Evaluation by Non-Sequential Monte Carlo Simulation. IEEE Trans. Power Syst. 2017, 32, 1511–1519. [Google Scholar] [CrossRef]
- Chen, P.; Pedersen, T.; Bak-Jensen, B.; Chen, Z. ARIMA-Based Time Series Model of Stochastic Wind Power Generation. IEEE Trans. Power Syst. 2010, 25, 667–676. [Google Scholar] [CrossRef]
- Verástegui, F.; Lorca, Á.; Olivares, D.E.; Negrete-Pincetic, M.; Gazmuri, P. An Adaptive Robust Optimization Model for Power Systems Planning With Operational Uncertainty. IEEE Trans. Power Syst. 2019, 34, 4606–4616. [Google Scholar] [CrossRef]
- Liu, C.; Lee, C.; Chen, H.; Mehrotra, S. Stochastic robust mathematical programming model for power system optimization. IEEE Trans. Power Syst. 2015, 31, 821–822. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Suo, X.; Zhao, S.; Ma, Y.; Dong, L. New Energy Wide Area Complementary Planning Method for Multi-Energy Power System. IEEE Access 2021, 9, 157295–157305. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, Y.; Li, H.; Liu, X.; Wen, Y.; Li, W. A Coordinated Planning Method for Micrositing of Tidal Current Turbines and Collector System Optimization in Tidal Current Farms. IEEE Trans. Power Syst. 2019, 34, 292–302. [Google Scholar] [CrossRef]
- Fang, Y.; Han, J.; Du, E.; Jiang, H.; Fang, Y.; Zhang, N.; Kang, C. Electric energy system planning considering chronological renewable generation variability and uncertainty. Appl. Energy 2024, 373, 123961. [Google Scholar] [CrossRef]
- Zhuo, Z.; Zhang, N.; Hou, Q.; Du, E.; Kang, C. Backcasting Technical and Policy Targets for Constructing Low-Carbon Power Systems. IEEE Trans. Power Syst. 2022, 37, 4896–4911. [Google Scholar] [CrossRef]
- Han, P.; Li, P.; Xie, X.; Zhang, J. Coordinated Optimization of Power Rating and Capacity of Battery Storage Energy System with Large-Scale Renewable Energy. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 28–30 October 2022; pp. 189–193. [Google Scholar]
- Wen, Z.; Zhang, X.; Wang, H.; Wang, G.; Wu, T.; Qiu, J. Low-carbon planning for integrated power-gas-hydrogen system with Wasserstein-distance based scenario generation method. Energy 2025, 316, 134388. [Google Scholar] [CrossRef]
- Lai, C.; Kazemtabrizi, B. A novel data-driven tighten-constraint method for wind-hydro hybrid power system to improve day-ahead plan performance in real-time operation. Appl. Energy 2024, 371, 123616. [Google Scholar] [CrossRef]
- Guo, S.; Ren, F.; Wei, Z.; Zhai, X. A multi-objective collaborative planning method for a PV-powered hybrid energy system considering source-load matching. Energy Convers. Manag. 2024, 316, 118848. [Google Scholar] [CrossRef]
- Tian, Y.; Chang, J.; Wang, Y.; Wang, X.; Meng, X.; Guo, A. The capacity planning method for a hydro-wind-PV-battery complementary system considering the characteristics of multi-energy integration into power grid. J. Clean. Prod. 2024, 446, 141292. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, H.; Cheng, H.; Zhang, S.; Zhang, X.; Lu, J. Low-carbon oriented power system expansion planning considering the long-term uncertainties of transition tasks. Energy 2024, 307, 132759. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Z.; Zhou, M.; Wu, Z.; Yuan, B.; Chen, Y.; Li, G. Equalizing multi-temporal scale adequacy for low carbon power systems by co-planning short-term and seasonal energy storage. J. Energy Storage 2024, 84, 111518. [Google Scholar] [CrossRef]
- Wei, H.; Ma, M.; Jiang, H.; Capuder, T.; Teng, F.; Strbac, G.; Zhang, J.; Zhang, N.; Kang, C. Generation and transmission expansion planning incorporating economically feasible heterogeneous demand-side resources. Appl. Energy 2025, 381, 125067. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y. Research on Wind Power Prediction Based on Time Series. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Industrial Design (AIID), Guangzhou, China, 28–30 May 2021; pp. 78–82. [Google Scholar]
- Wang, K.; Zou, J.; Lu, S.; Wang, J.; Zhou, B. Wind Power Output Scene Reconstruction Method Considering Wind Speed Autocorrelation and Source Load Cross-Correlation. In Proceedings of the 2022 5th International Conference on Power and Energy Applications (ICPEA), Guangzhou, China, 18–20 November 2022; pp. 687–692. [Google Scholar]
- Teng, Y.; Xu, J.; Zhang, M.; Liang, W. Study of wind farm power output predicting model based on nonlinear time series. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar]
- Cheng, Y.; Zhang, N.; Lu, Z.; Kang, C. Planning multiple energy systems toward low-carbon society: A decentralized approach. IEEE Trans. Smart Grid 2018, 10, 4859–4869. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, R.; Bi, T. Energy management of distribution-level integrated electric-gas systems with fast frequency reserve. IEEE Trans. Power Syst. 2023, 39, 4208–4223. [Google Scholar] [CrossRef]
- Huang, W.; Du, E.; Capuder, T.; Zhang, X.; Zhang, N.; Strbac, G.; Kang, C. Reliability and vulnerability assessment of multi-energy systems: An energy hub based method. IEEE Trans. Power Syst. 2021, 36, 3948–3959. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, N.; Ge, Y. Energy storage placements for renewable energy fluctuations: A practical study. IEEE Trans. Power Syst. 2022, 38, 4916–4927. [Google Scholar] [CrossRef]





| Number of Units | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| 135 | 120 | 127 | 112 | |
| 0 | 15 | 0 | 15 | |
| 0 | 0 | 8 | 8 | |
| 5 | 5 | 5 | 5 | |
| 5 | 5 | 5 | 5 |
| Cost ( yuan) | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| 1686.78 | 1392.85 | 1685.70 | 1391.25 | |
| 0.00 | 45.88 | 0.00 | 45.00 | |
| 46.80 | 46.80 | 46.80 | 46.80 | |
| 10.40 | 10.40 | 10.40 | 10.40 | |
| 0.00 | 0.00 | 16.00 | 16.00 | |
| 1243.50 | 585.56 | 0.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tian, Z.; Yang, H.; Li, C.; Xu, X.; Zhu, S.; Du, E.; Zhang, N. Collaborative Planning of Source–Grid–Load–Storage Considering Wind and Photovoltaic Support Capabilities. Energies 2025, 18, 2045. https://doi.org/10.3390/en18082045
Wang B, Tian Z, Yang H, Li C, Xu X, Zhu S, Du E, Zhang N. Collaborative Planning of Source–Grid–Load–Storage Considering Wind and Photovoltaic Support Capabilities. Energies. 2025; 18(8):2045. https://doi.org/10.3390/en18082045
Chicago/Turabian StyleWang, Bin, Zengyao Tian, Haotian Yang, Chunshan Li, Xingwei Xu, Shiyu Zhu, Ershun Du, and Ning Zhang. 2025. "Collaborative Planning of Source–Grid–Load–Storage Considering Wind and Photovoltaic Support Capabilities" Energies 18, no. 8: 2045. https://doi.org/10.3390/en18082045
APA StyleWang, B., Tian, Z., Yang, H., Li, C., Xu, X., Zhu, S., Du, E., & Zhang, N. (2025). Collaborative Planning of Source–Grid–Load–Storage Considering Wind and Photovoltaic Support Capabilities. Energies, 18(8), 2045. https://doi.org/10.3390/en18082045







