Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel
Abstract
:1. Introduction
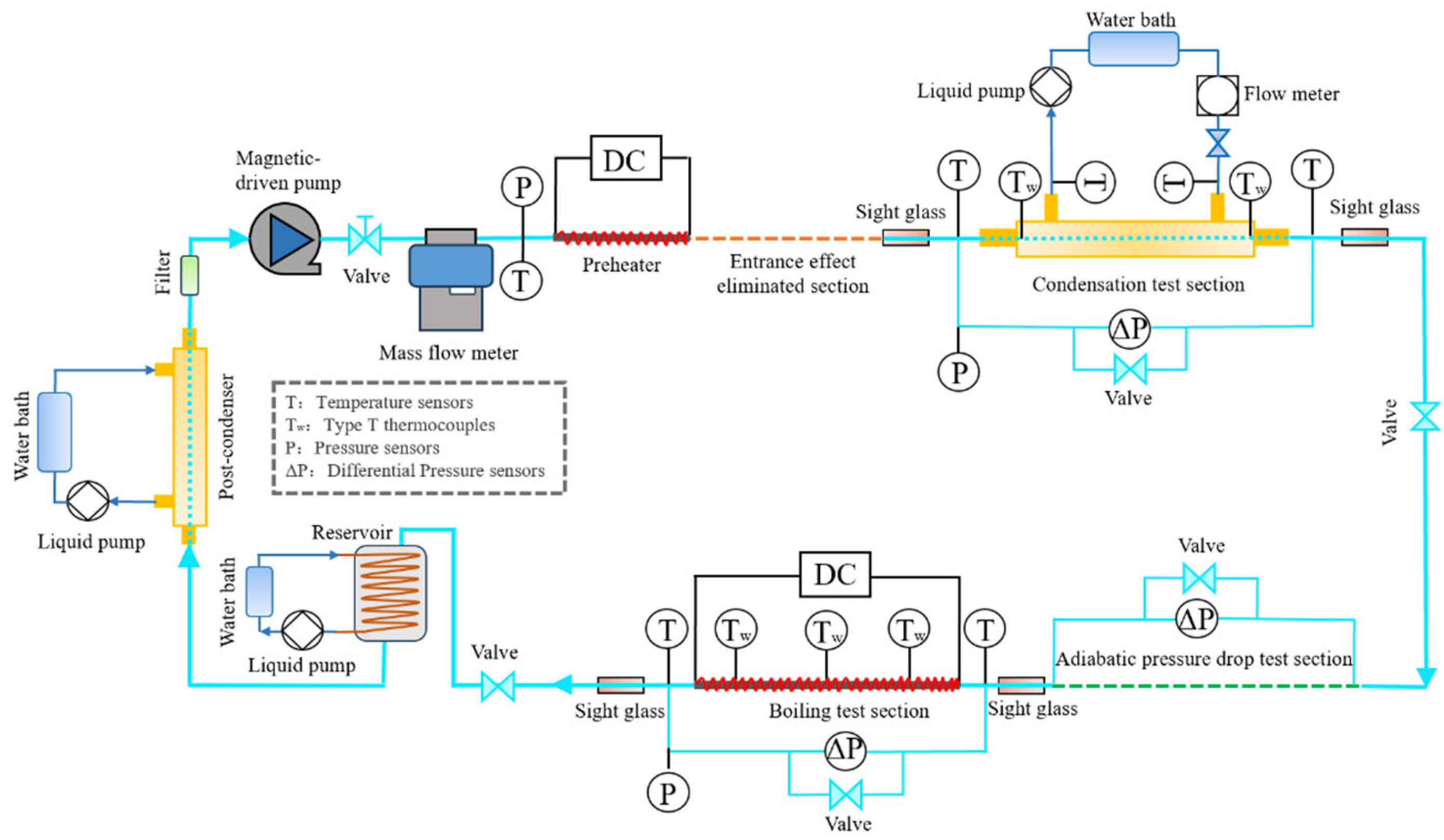
2. Experimental Apparatus
2.1. Experimental System
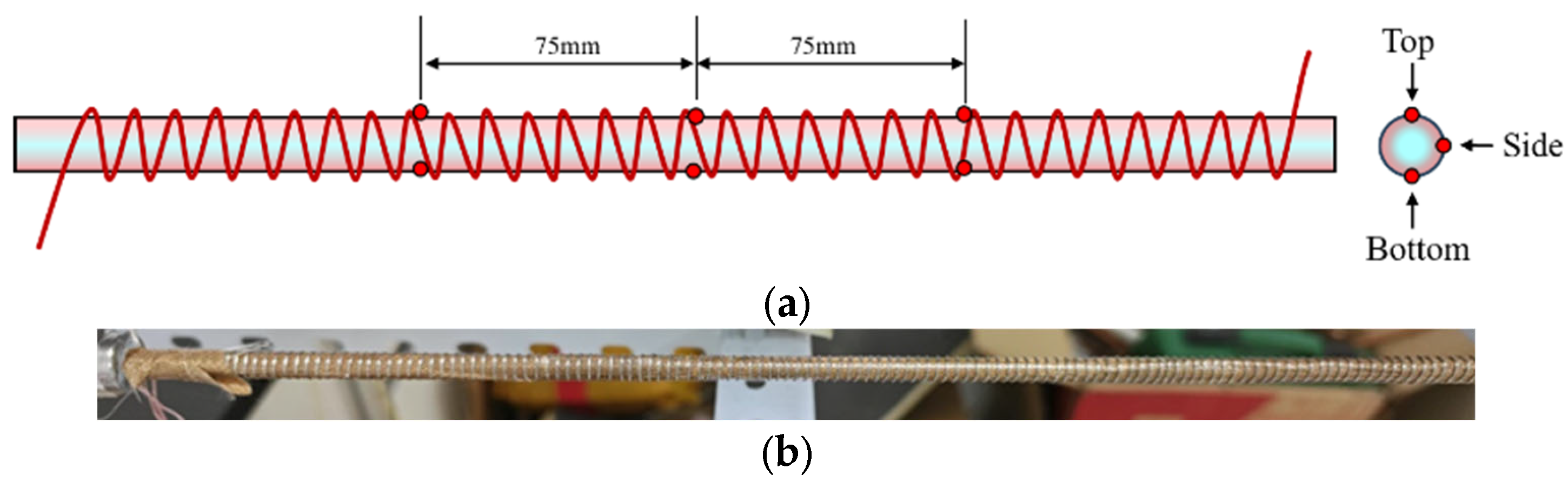
2.2. Test Section
2.3. Data Reduction
2.4. Measurement Uncertainties
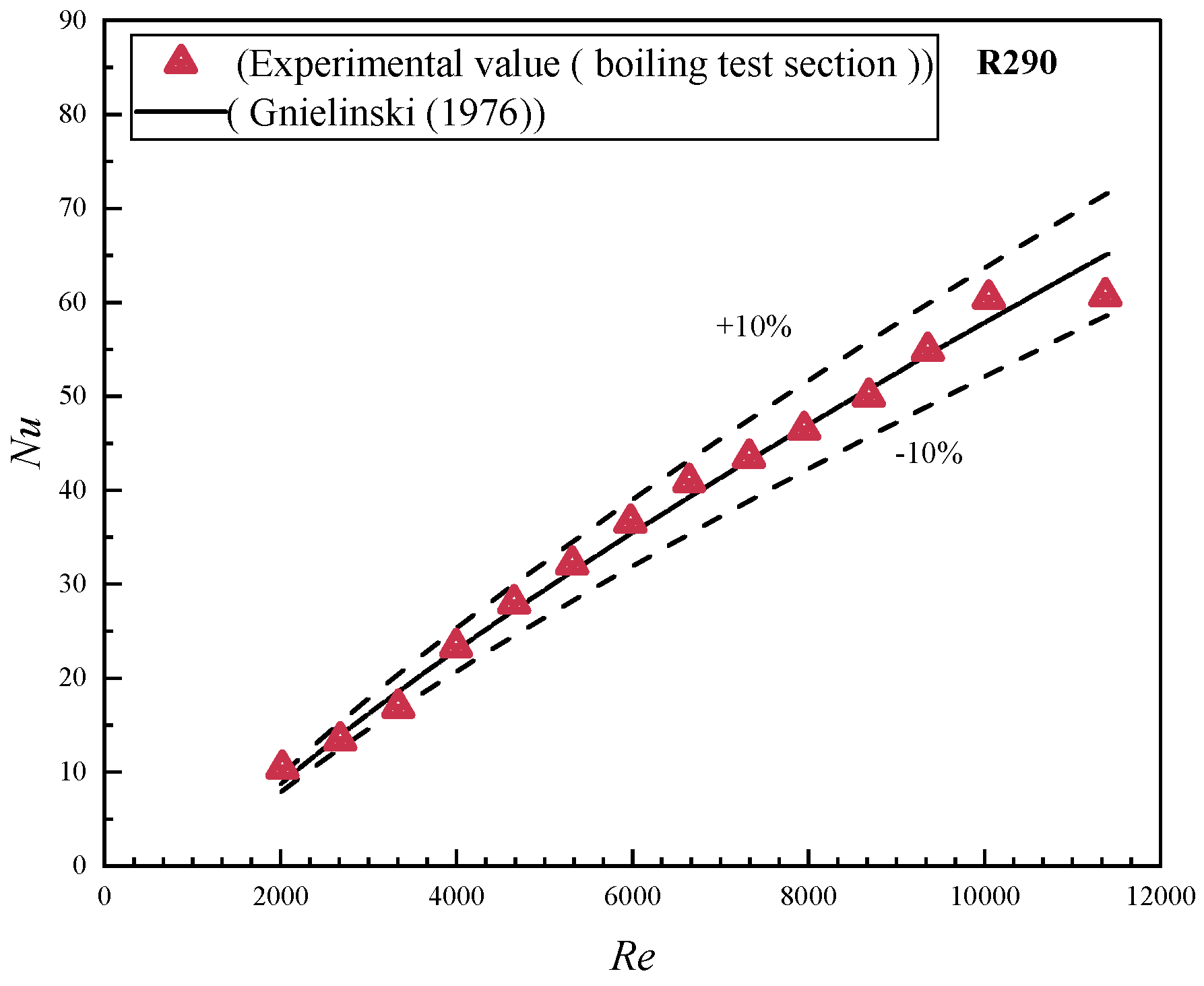
2.5. Single-Phase Verification Experiment
3. Experimental Results for the Boiling Heat Transfer Coefficient
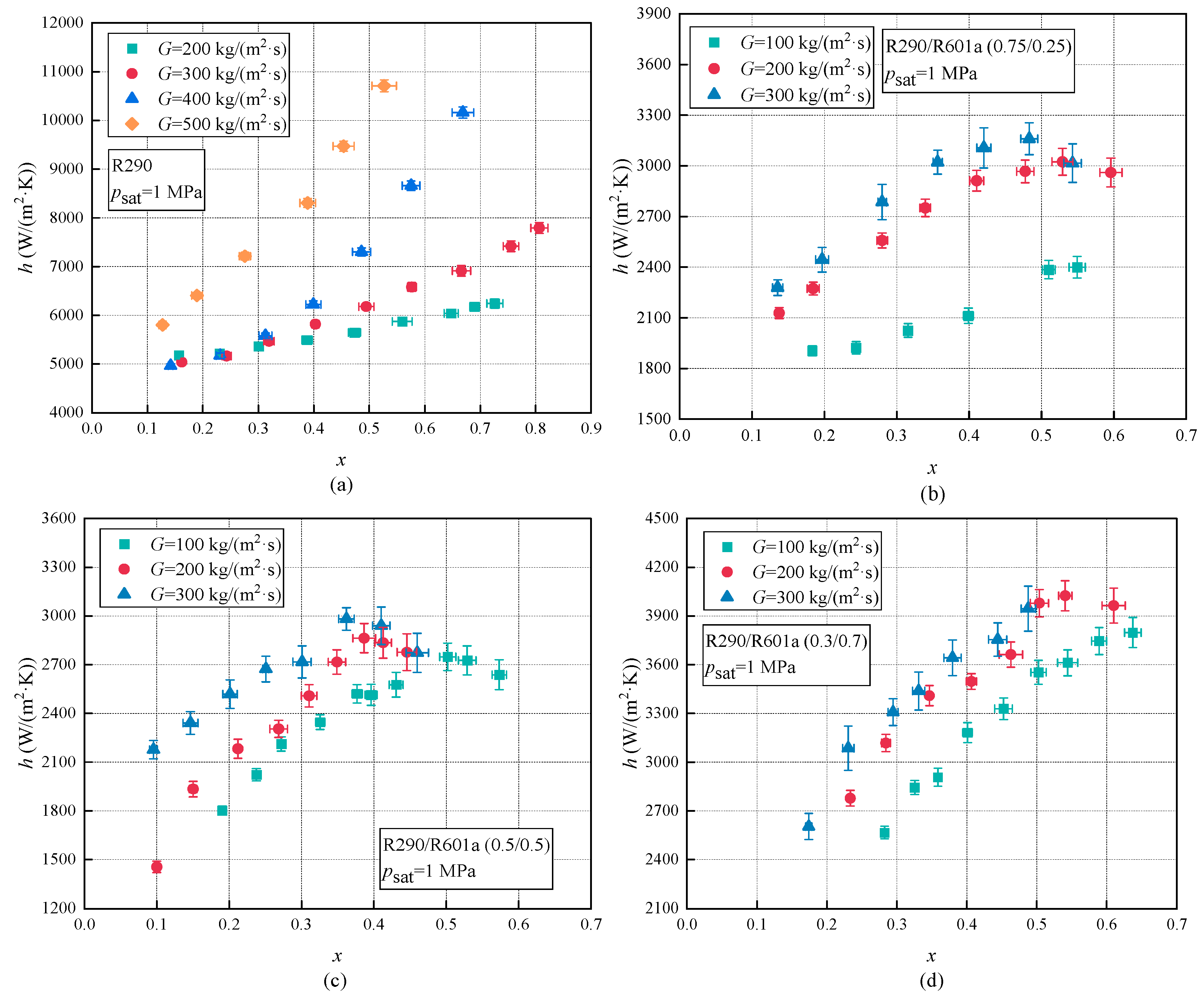
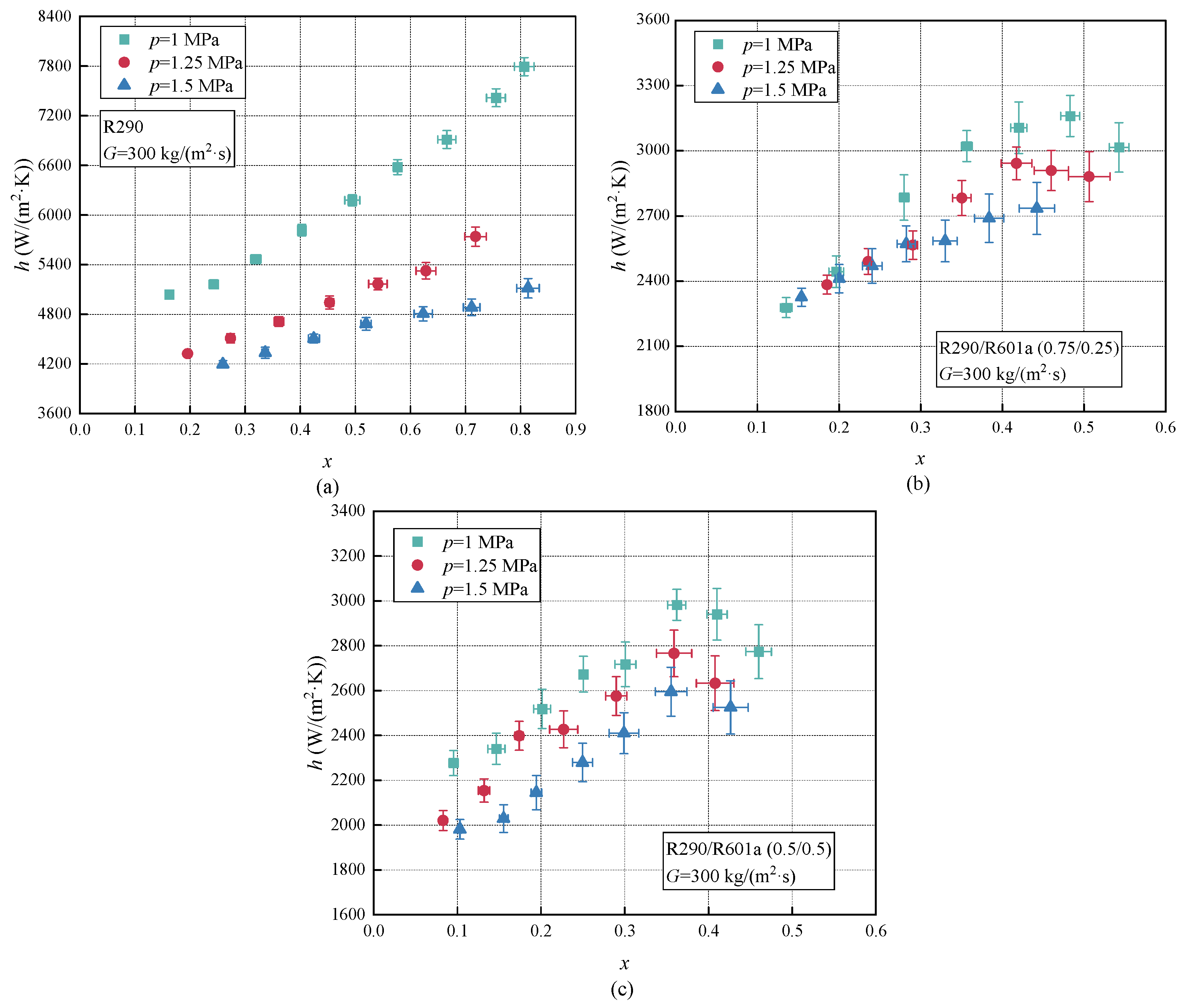
3.1. Effect of Mass Fraction
3.2. Effect of Mass Flux and Vapor Quality
3.3. Effect of Saturation Pressure
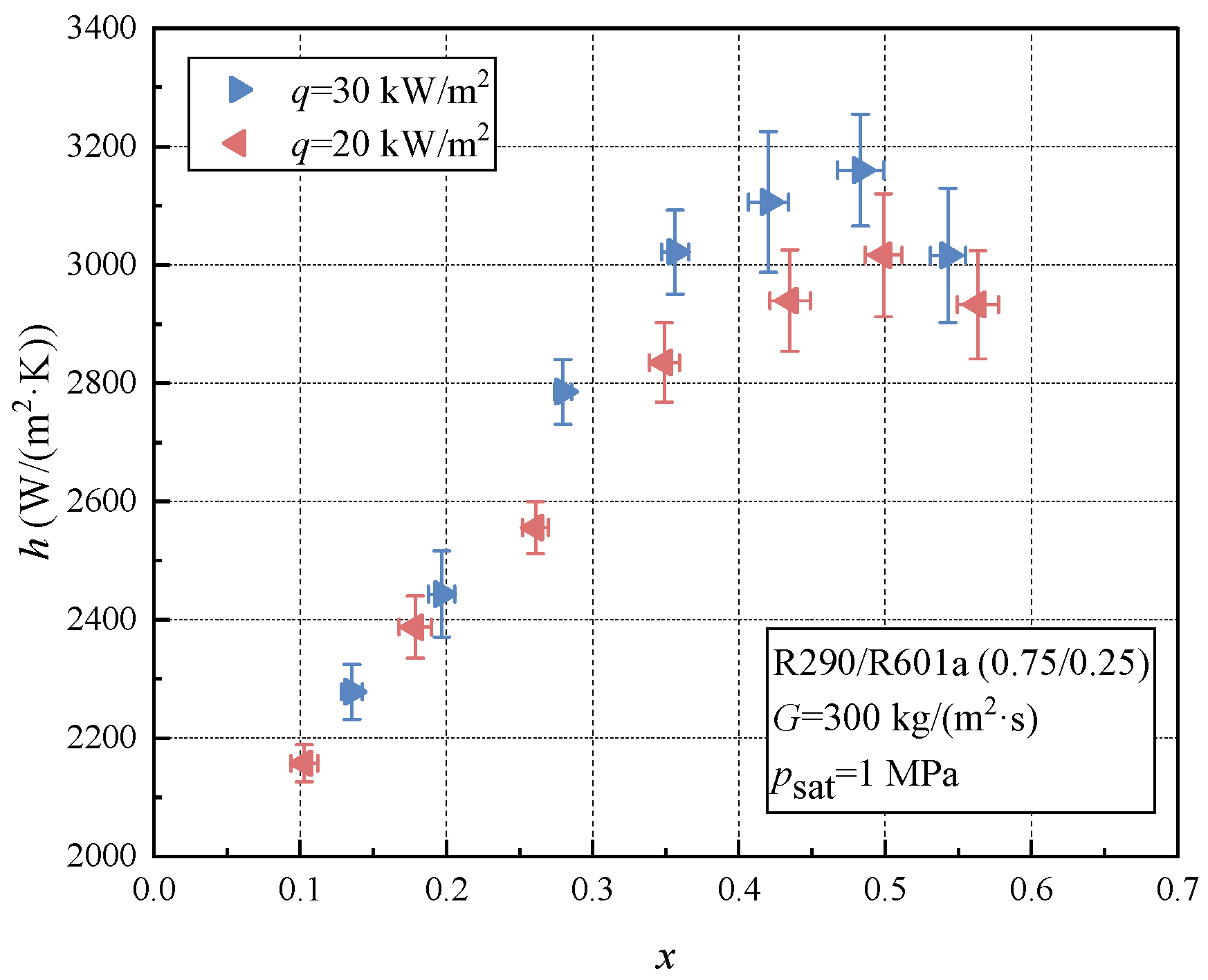
3.4. Effect of Heat Flux
4. Prediction Correlation for the Boiling Heat Transfer Coefficient
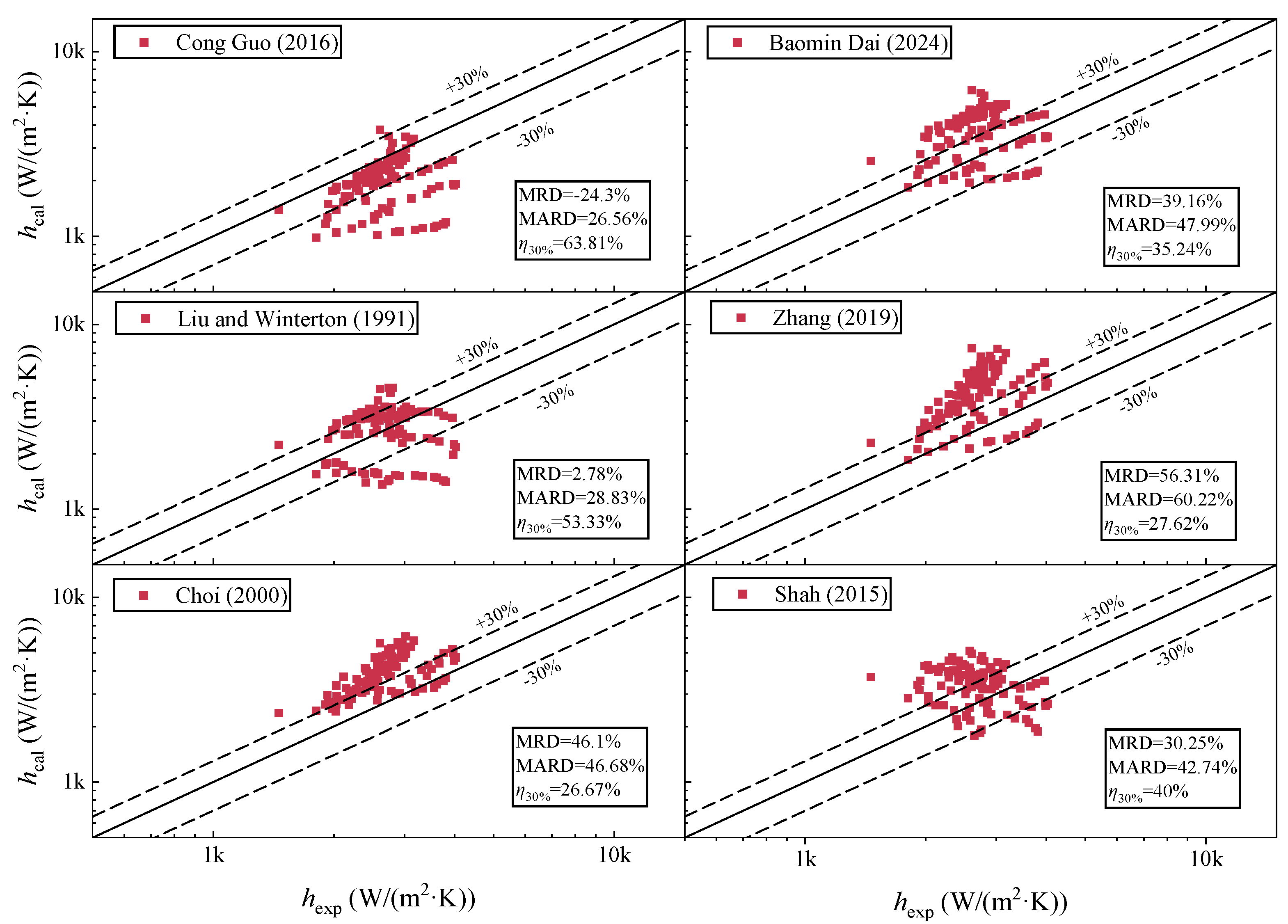
4.1. Study on the Existing Correlation of the Boiling Heat Transfer Coefficient
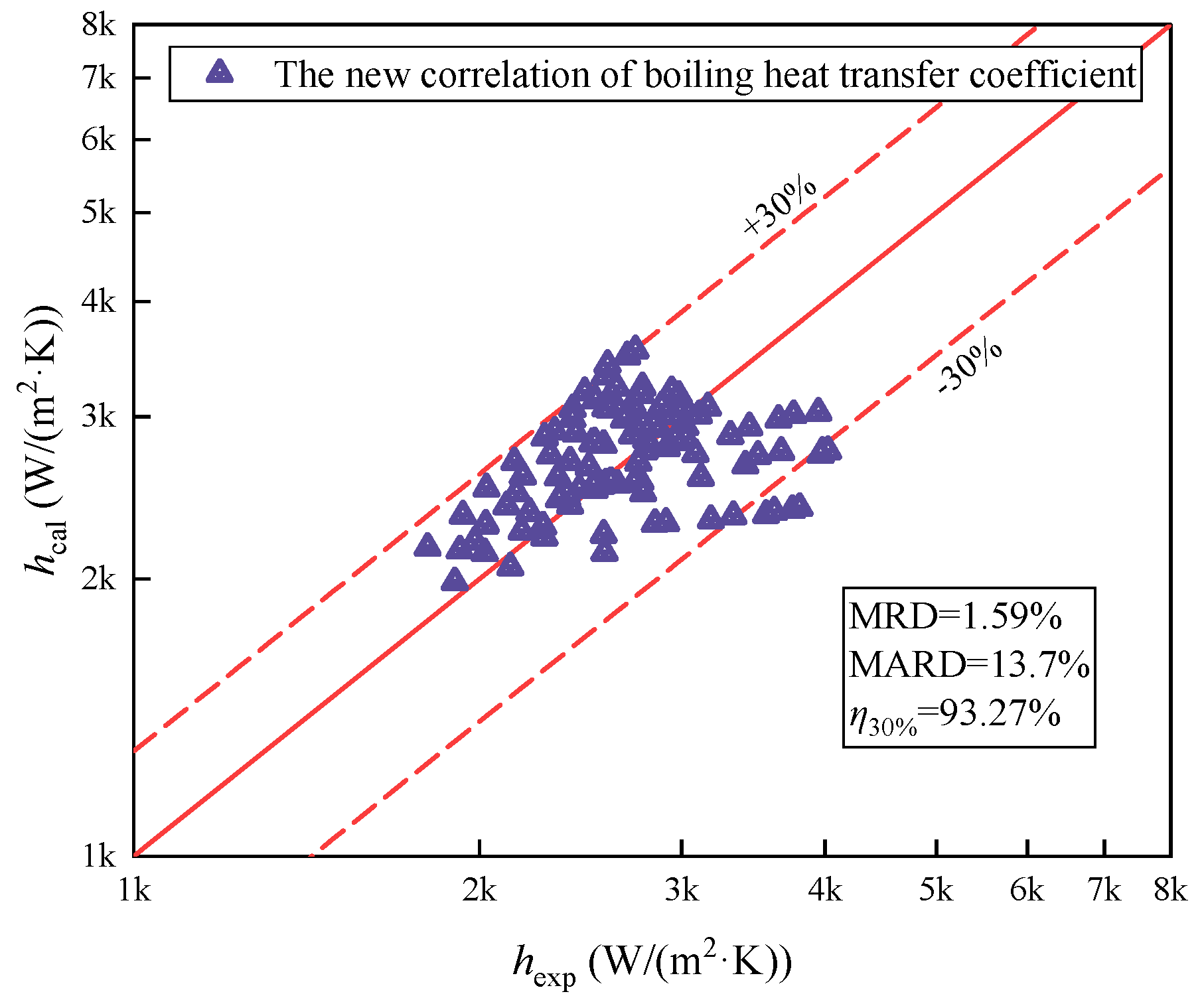
4.2. The Corrected Correlation of the Boiling Heat Transfer Coefficient
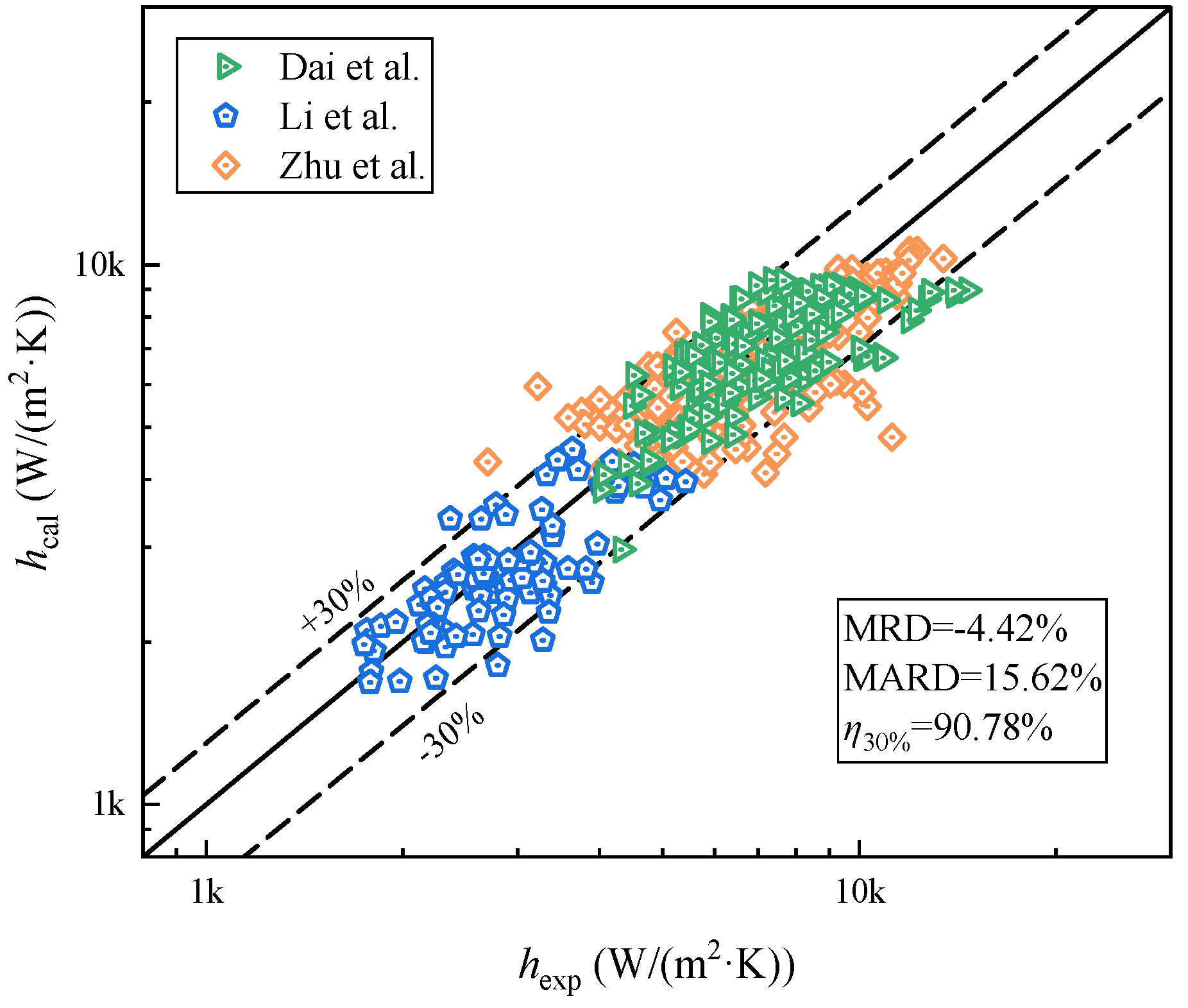
4.3. Evaluation of the New Correlation of the Boiling Heat Transfer Coefficient
5. Conclusions
- The boiling heat transfer coefficient of R290/R601a first decreases and then increases with the decrease in R290 mass fraction, which is mainly affected by thermophysical properties and mass transfer resistance. Due to the thinning of the liquid film during the boiling heat transfer process, there will be a dry-out point. The boiling heat transfer coefficient will first increase and then decrease with the increase in vapor quality. With the increase in mass flux and heat flux, the dry-out point will gradually shift in the direction of low vapor quality. In addition, the boiling heat transfer coefficient will increase with the increase in mass flux and heat flux, and decrease with the increase in saturation pressure.
- The boiling heat transfer experimental data of R290/R601a were compared with the predicted results of six known boiling heat transfer coefficient correlations. The prediction results for the six boiling heat transfer coefficient correlations are lower than expected. Among them, the asymptotic models of Guo et al. [37] and Liu and Winterton [38] have the best prediction effect, and the mean absolute relative deviation is 26.55% and 28.83%.
- Then, the correlation of the mixed boiling heat transfer coefficient is modified, mainly referring to the boiling heat transfer prediction correlation of Zhang et al. [42]. The dimensionless number affecting the boiling heat transfer characteristics of the mixture was subjected to multiple regression and fitted with the experimental data of R290/R601a. The corrected boiling heat transfer correlation has a more accurate prediction ability. The MARD of the model is 13.7%, and 93.27% of the experimental data deviation is within the 30% deviation band. Finally, to verify the applicability of the new boiling heat transfer coefficient correlation, it is necessary to select data from the literature to establish a database. The new correlation of the boiling heat transfer coefficient has a good prediction effect on the database. The MARD is 15.62%, and 90.78% of the experimental data points are within the 30% deviation band.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Bo | boiling number, Bo = q/(GHlv) |
| Cp | specific heat capacity, (J/(kg·K)) |
| Co | convection number, Co = ((1/x) − 1)0.8(ρl − ρv)0.5 |
| di | inner diameter of tube, (mm) |
| do | outer diameter of tube, (mm) |
| de | equivalent diameter, (mm) |
| Fr | Froude number Frv = Gv2/(ρv(ρl − ρv)gdi) |
| g | acceleration of gravity, (m/s2) |
| G | mass flux, (kg/(m2·s)) |
| h | heat transfer coefficient, (W/(m2·K)) |
| hid | The ideal heat transfer coefficient of nucleate boiling |
| H | specified enthalpy, (J/kg) |
| Hlv | latent heat, (J/kg) |
| L | length of test section, (m) |
| m | mass flux, (kg/s) |
| Nu | Nusselt number |
| p | pressure, (MPa) |
| pr | reduced pressure, (MPa) |
| Pr | prandtl number, Prl = Cplμl/λl |
| Re | Reynolds number, Rel = G(1 − x)di/μL; Rev = Gxdi/μv |
| R | single error |
| T | temperature, (K) |
| ΔTm | mean logarithmic temperature, (K) |
| Xinit | mass fraction of more volatile component (R290) |
| XR290 | mass fraction of R290 |
| x | vapor quality |
| xk | factor affecting R |
| z | axial position, (m) |
| Greek symbols | |
| λ | thermal conductivity, (W/(m·K)) |
| μ | viscosity, (Pa·s) |
| ρ | density, (kg/m3) |
| σ | surface tension, (N/m) |
| η | thermal efficiency |
| η30% | percentage of points predicted within a deviation bandwidth of ±30% |
| β | mass transfer coefficient |
| Subscripts | |
| c | cooling water |
| cal | calculated value |
| exp | experimental value |
| g | gravity pressure drop |
| glide | temperature glide |
| i | inner surface |
| in | inlet |
| k | number of thermocouples at section and factors affecting R |
| l | liquid phase |
| o | outer surface |
| out | outlet |
| p | predicted value |
| r | refrigerants |
| t | total |
| test | Boiling test section |
| v | vapor phase |
| w | wall |
| sat | saturation |
| Abbreviations | |
| GEP | Global Warming Potential |
| HCs | hydrocarbons |
| ORC | Organic Rankine Cycle |
| ODP | Ozone Depletion Potential |
| MARD | Mean Absolute Relative Deviation |
| MRD | Mean Relative Deviation |
Appendix A. Thermal Physical Properties of R290/R601a with Different Mass Fractions Under Different Working Conditions
| Xinit | p (MPa) | Tglide (K) | ρl (kg/m3) | ρv (kg/m3) | Hlv (J/kg) × 103 | Cp,l (J/(kg·K)) × 103 | λl (W/(m·K)) × 10−3 | μl (Pa·s) × 10−6 | σ (N/m) × 10−3 |
| 1.00/0 | 1 | 0 | 489.30 | 21.68 | 332.28 | 2.74 | 92.81 | 95.18 | 6.79 |
| 1.25 | 0 | 474.24 | 27.36 | 315.00 | 2.85 | 88.65 | 86.41 | 5.71 | |
| 1.5 | 0 | 460.26 | 33.30 | 298.55 | 2.97 | 85.17 | 79.28 | 4.80 | |
| 0.75/0.25 | 1 | 20.97 | 513.33 | 21.27 | 361.49 | 2.65 | 94.69 | 106.09 | 10.32 |
| 1.25 | 19.89 | 498.22 | 26.81 | 344.60 | 2.75 | 90.46 | 96.18 | 9.01 | |
| 1.5 | 19.68 | 484.25 | 32.5 | 328.33 | 2.86 | 86.93 | 88.17 | 7.88 | |
| 0.50/0.50 | 1 | 31.31 | 528.23 | 22.421 | 368.46 | 2.61 | 93.45 | 113.79 | 8.90 |
| 1.25 | 30.03 | 512.82 | 28.26 | 352.09 | 2.70 | 89.30 | 102.81 | 7.79 | |
| 1.5 | 28.75 | 498.54 | 34.34 | 336.25 | 2.80 | 85.83 | 93.96 | 6.83 | |
| 0.30/0.70 | 1 | 31.81 | 531.32 | 24.15 | 356.45 | 2.62 | 89.85 | 115.02 | 7.51 |
References
- Liu, C.; Gao, T. Off-design performance analysis of basic ORC, ORC using zeotropic mixtures and composition-adjustable ORC under optimal control strategy. Energy 2019, 171, 95–108. [Google Scholar] [CrossRef]
- Bahrami, M.; Pourfayaz, F.; Kasaeian, A. Low global warming potential (GWP) working fluids (WFs) for Organic Rankine Cycle (ORC) applications. Energy Rep. 2022, 8, 2976–2988. [Google Scholar] [CrossRef]
- Sun, H.; Qin, J.; Hung, T.-C.; Huang, H.; Yan, P.; Lin, C.-H. Effect of flow losses in heat exchangers on the performance of organic Rankine cycle. Energy 2019, 172, 391–400. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, R.; Dai, X.; Wang, D.; Ma, Y.; Li, H.; Shi, L. Experimental study of R134a flow boiling in a horizontal tube for evaporator design under typical Organic Rankine Cycle pressures. Int. J. Heat Fluid Flow 2018, 71, 210–219. [Google Scholar] [CrossRef]
- Li, Y.-M.; Wang, C.-C. Investigation of the performance of a transcritical CO2 heat pump system subject to heated water conditions: Perspective from the second law. Appl. Therm. Eng. 2021, 193, 116999. [Google Scholar] [CrossRef]
- Höglund-Isaksson, L.; Purohit, P.; Amann, M.; Bertok, I.; Rafaj, P.; Schöpp, W.; Borken-Kleefeld, J. Cost estimates of the Kigali Amendment to phase-down hydrofluorocarbons. Environ. Sci. Policy 2017, 75, 138–147. [Google Scholar] [CrossRef]
- In, S.; Baek, S.; Jin, L.; Jeong, S. Flow boiling heat transfer of R123/R134a mixture in a microchannel. Exp. Therm. Fluid Sci. 2018, 99, 474–486. [Google Scholar] [CrossRef]
- Bell, I.H.; Domanski, P.A.; McLinden, M.O.; Linteris, G.T. The hunt for nonflammable refrigerant blends to replace R-134a. Int. J. Refrig. 2019, 104, 484–495. [Google Scholar] [CrossRef]
- Li, J.; Song, Q.; Wu, W.; Wang, D.; Jiang, X.; Zhou, S. Energy, exergy, economic and environmental (4E) analysis of zeotropic mixture recuperative heat pump and vapor injection heat pump. Energy 2025, 317, 134681. [Google Scholar] [CrossRef]
- Wu, J.; Sun, S.; Song, Q.; Sun, D.; Wang, D.; Li, J. Energy, exergy, exergoeconomic and environmental (4E) analysis of cascade heat pump, recuperative heat pump and carbon dioxide heat pump with different temperature lifts. Renew. Energy 2023, 207, 407–421. [Google Scholar] [CrossRef]
- Sun, D.; Sun, S.; Song, Q.; Wang, D.; Wang, Y.; Guo, S. Energy, exergy, economic and environmental (4E) analysis of two-stage cascade, Linder-Hampson and reverse Brayton systems in the temperature range from −120 °C to −60 °C. Energy 2023, 283, 129178. [Google Scholar] [CrossRef]
- Moreira, T.A.; Furlan, G.; Oliveira, G.H.d.S.e.; Ribatski, G. Flow boiling and convective condensation of hydrocarbons: A state-of-the-art literature review. Appl. Therm. Eng. 2021, 182, 116129. [Google Scholar] [CrossRef]
- Hsieh, H.-K.; Teng, T.-P. Retrofit assessment of automobile air conditioners using hydrocarbon refrigerants. Appl. Therm. Eng. 2022, 214, 118781. [Google Scholar] [CrossRef]
- Kundu, A.; Kumar, R.; Gupta, A. Comparative experimental study on flow boiling heat transfer characteristics of pure and mixed refrigerants. Int. J. Refrig. 2014, 45, 136–147. [Google Scholar] [CrossRef]
- Diehl de Oliveira, J.; Copetti, J.B.; Cardoso, E.M.; Rodrigues de Souza, R. Flow boiling pressure drop of R-1270 in 1.0 mm tube. Appl. Therm. Eng. 2023, 231, 120885. [Google Scholar] [CrossRef]
- Chen, J.C. A correlation for boiling heat transfer to saturated fluids in convective flow. Ind. Eng. Chem. Process Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef]
- Choi, K.-I.; Pamitran, A.S.; Oh, C.-Y.; Oh, J.-T. Boiling heat transfer of R-22, R-134a, and CO2 in horizontal smooth minichannels. Int. J. Refrig. 2007, 30, 1336–1346. [Google Scholar] [CrossRef]
- Ong, C.L.; Thome, J.R. Flow boiling heat transfer of R134a, R236fa and R245fa in a horizontal 1.030mm circular channel. Exp. Therm. Fluid Sci. 2009, 33, 651–663. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I.J.I.J.o.H.; Transfer, M. Flow boiling heat transfer in two-phase micro-channel heat sinks––I. Experimental investigation and assessment of correlation methods. Int. J. Heat Mass Transf. 2003, 46, 2755–2771. [Google Scholar] [CrossRef]
- Mohammed, S.I.T.; He, G.; Liang, X.; Zhou, S.; Kabeel, A.E.; Sharshir, S.W. Comparative study of flow boiling heat transfer and frictional pressure gradient of a non-azeotropic mixture of R-1270/R-600a, and R-22 in a smooth horizontal tube. Alex. Eng. J. 2020, 59, 4909–4922. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, L.; Xu, Z.; Xia, X.; He, N.; Liu, X.; Han, M. Flow boiling of zeotropic mixture R245fa/R141b inside horizontal smooth tube and microfin tube. Int. J. Therm. Sci. 2022, 176, 107504. [Google Scholar] [CrossRef]
- Pan, L.; Wang, H.; Chen, Q.; Chen, C. Theoretical and experimental study on several refrigerants of moderately high temperature heat pump. Appl. Therm. Eng. 2011, 31, 1886–1893. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Assessment of blends of CO2 with butane and isobutane as working fluids for heat pump applications. Int. J. Therm. Sci. 2009, 48, 1460–1465. [Google Scholar] [CrossRef]
- Liu, M.; Guo, L.; Li, W.; Xu, W.; Zhao, L. Experimental investigation on boiling heat transfer characteristics of R1234yf/R1336mzz(Z) in horizontal flow. Int. J. Refrig. 2024, 159, 344–355. [Google Scholar] [CrossRef]
- Berto, A.; Azzolin, M.; Bortolin, S.; Guzzardi, C.; Del Col, D. Measurements and modelling of R455A and R452B flow boiling heat transfer inside channels. Int. J. Refrig. 2020, 120, 271–284. [Google Scholar] [CrossRef]
- Dai, B.; Wu, T.; Liu, S.; Qi, H.; Zhang, P.; Wang, D.; Wang, X. Flow boiling heat transfer characteristics of zeotropic mixture CO2/R152a with large temperature glide in a 2 mm horizontal tube. Int. J. Heat Mass Transf. 2024, 218, 124779. [Google Scholar] [CrossRef]
- Guo, Q.; Li, M.; Tian, X. Experimental study on flow boiling heat transfer characteristics of R134a, R245fa and R134a/R245fa mixture at high saturation temperatures. Int. J. Therm. Sci. 2020, 150, 106195. [Google Scholar] [CrossRef]
- Dang, C.; Jia, L.; Xu, M.; Huang, Q.; Peng, Q. Experimental study on flow boiling characteristics of pure refrigerant (R134a) and zeotropic mixture (R407C) in a rectangular micro-channel. Int. J. Heat Mass Transf. 2017, 104, 351–361. [Google Scholar] [CrossRef]
- Qi, Z.; Jia, L.; Dang, C.; Zhang, Y. Liquid mass transfer characteristics of zeotropic mixtures of R134a/R245fa during flow boiling in a rectangular channel. Int. J. Heat Mass Transf. 2022, 187, 122551. [Google Scholar] [CrossRef]
- Li, H.; Hrnjak, P. Heat transfer coefficient, pressure gradient, and flow patterns of R1233zd(E) and R1336mzz(Z) evaporating in a microchannel tube. Int. J. Heat Mass Transf. 2022, 182, 121992. [Google Scholar] [CrossRef]
- Song, Q.; Wang, D.; Shen, J.; Zhang, F.; Nie, F.; Zhao, Y.; Gong, M. Experimental and analytical investigation on flow condensation heat transfer of zeotropic mixtures of tetrafluoromethane/ethane. Appl. Therm. Eng. 2021, 197, 117382. [Google Scholar] [CrossRef]
- Wu, J.; Sun, S.; Song, Q.; Wang, D.; Sun, D. Subcritical recuperative air-to-water heat pump with zeotropic mixtures: Comparative and performance assessment. Energy Rep. 2022, 8, 13682–13697. [Google Scholar] [CrossRef]
- El Kadi, K.; Alnaimat, F.; Sherif, S.A. Recent advances in condensation heat transfer in mini and micro channels: A comprehensive review. Appl. Therm. Eng. 2021, 197, 117412. [Google Scholar] [CrossRef]
- Kline, S.J. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flows. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Webb, R.L.; Gupte, N.S. A Critical Review of Correlations for Convective Vaporization in Tubes and Tube Banks. Heat Transf. Eng. 1992, 13, 58–81. [Google Scholar] [CrossRef]
- Guo, C.; Wang, J.; Du, X.; Yang, L. Experimental flow boiling characteristics of R134a/R245fa mixture inside smooth horizontal tube. Appl. Therm. Eng. 2016, 103, 901–908. [Google Scholar] [CrossRef]
- Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat Mass Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
- Zhang, L.; Hihara, E.; Saito, T.; Oh, J.-T. Boiling heat transfer of a ternary refrigerant mixture inside a horizontal smooth tube. Int. J. Heat Mass Transf. 1997, 40, 2009–2017. [Google Scholar] [CrossRef]
- Choi, T.Y.; Kim, Y.J.; Kim, M.S.; Ro, S.T. Evaporation heat transfer of R-32, R-134a, R-32/134a, and R-32/125/134a inside a horizontal smooth tube. Int. J. Heat Mass Transf. 2000, 43, 3651–3660. [Google Scholar] [CrossRef]
- Shah, M.M. A method for predicting heat transfer during boiling of mixtures in plain tubes. Appl. Therm. Eng. 2015, 89, 812–821. [Google Scholar] [CrossRef]
- Zhang, J.; Mondejar, M.E.; Haglind, F. General heat transfer correlations for flow boiling of zeotropic mixtures in horizontal plain tubes. Appl. Therm. Eng. 2019, 150, 824–839. [Google Scholar] [CrossRef]
- Thome, J.R.; Shakir, S. New Correlation for Nucleate Pool Boiling of Aqueous Mixtures; Heat Transfer: Pittsburgh, PA, USA, 1987; pp. 46–57. [Google Scholar]
- Cooper, M.G. Saturation Nucleate Pool Boiling—A Simple Correlation. 1984, pp. 785–793. Available online: https://www.scribd.com/document/502665848/Saturation-Nucleate-Pool-Boiling-A-Simple-Correlation (accessed on 10 March 2024).
- Zhu, Y.; Wu, X.; Wei, Z. Heat transfer characteristics and correlation for CO2/propane mixtures flow evaporation in a smooth mini tube. Appl. Therm. Eng. 2015, 81, 253–261. [Google Scholar] [CrossRef]

| Parameters | Instruments | Range | Uncertainties |
|---|---|---|---|
| Absolute pressure | Baker Hughes Co., UNIK-5000 pressure sensors, US | 0~3 MPa | ±0.04%FS |
| Differential pressure | Baker Hughes Co., UNIK-5000 differential pressure sensors, US | 0~100 kPa | ±0.02%FS |
| Mass flow | RHEONIK Co., RHM-03, Coriolis mass flow meter, Odelzhausen, Germany | 0.038~5 kg/min | ±0.1% |
| Voltage | HSPY Co., DC-regulated power supply, Beijing, China | 0~200 V | ±0.1% |
| Direct current | HSPY Co., DC-regulated power supply, Beijing, China | 0~5 A | ±0.5% |
| Temperature | Ou Chuang Co., T-type thermocouples, Hangzhou, China | −200~260 °C | ±0.2 °C |
| Parameters | Uncertainties |
|---|---|
| Heat flux | ±3.1% |
| Pressure gradient | ±6.25% |
| Vapor quality | ±3.2% |
| Boiling heat transfer coefficient | ±7.49% |
| Parameters | Ranges |
|---|---|
| Inner diameter | 2 mm |
| Mass fractions of R290/R601a mixtures (by mass) | 1/0; 0.75/0.25; 0.5/0.5; 0.3/0.7 |
| Mass flux | 100/200/300/400/500 kg/(m2·s) |
| Saturation pressure | 1/1.25/1.5 MPa |
| Heat flux | 20/30 kW/m2 |
| vapor quality | 0~1 |
| Correlations | MRD (%) | MARD (%) | η30% (%) |
|---|---|---|---|
| Guo et al. [37] | −24.3 | 26.55 | 63.81 |
| Dai et al. [26] | 39.16 | 47.99 | 35.24 |
| Liu and Winterton [38] | 2.78 | 28.83 | 53.33 |
| Zhang et al. [39] | 56.31 | 60.22 | 27.62 |
| Choi et al. [40] | 46.1 | 46.68 | 26.67 |
| Shah et al. [41] | 30.25 | 42.74 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.; Song, Q.; Sun, S.; Zhang, C.; Wang, D. Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel. Energies 2025, 18, 2074. https://doi.org/10.3390/en18082074
Ren C, Song Q, Sun S, Zhang C, Wang D. Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel. Energies. 2025; 18(8):2074. https://doi.org/10.3390/en18082074
Chicago/Turabian StyleRen, Cheng, Qinglu Song, Shoujun Sun, Chuantong Zhang, and Dechang Wang. 2025. "Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel" Energies 18, no. 8: 2074. https://doi.org/10.3390/en18082074
APA StyleRen, C., Song, Q., Sun, S., Zhang, C., & Wang, D. (2025). Experimental Study on Flow Boiling Heat Transfer of Zeotropic Mixture R290/R601a in a Mini-Channel. Energies, 18(8), 2074. https://doi.org/10.3390/en18082074





