Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles
Abstract
:1. Introduction
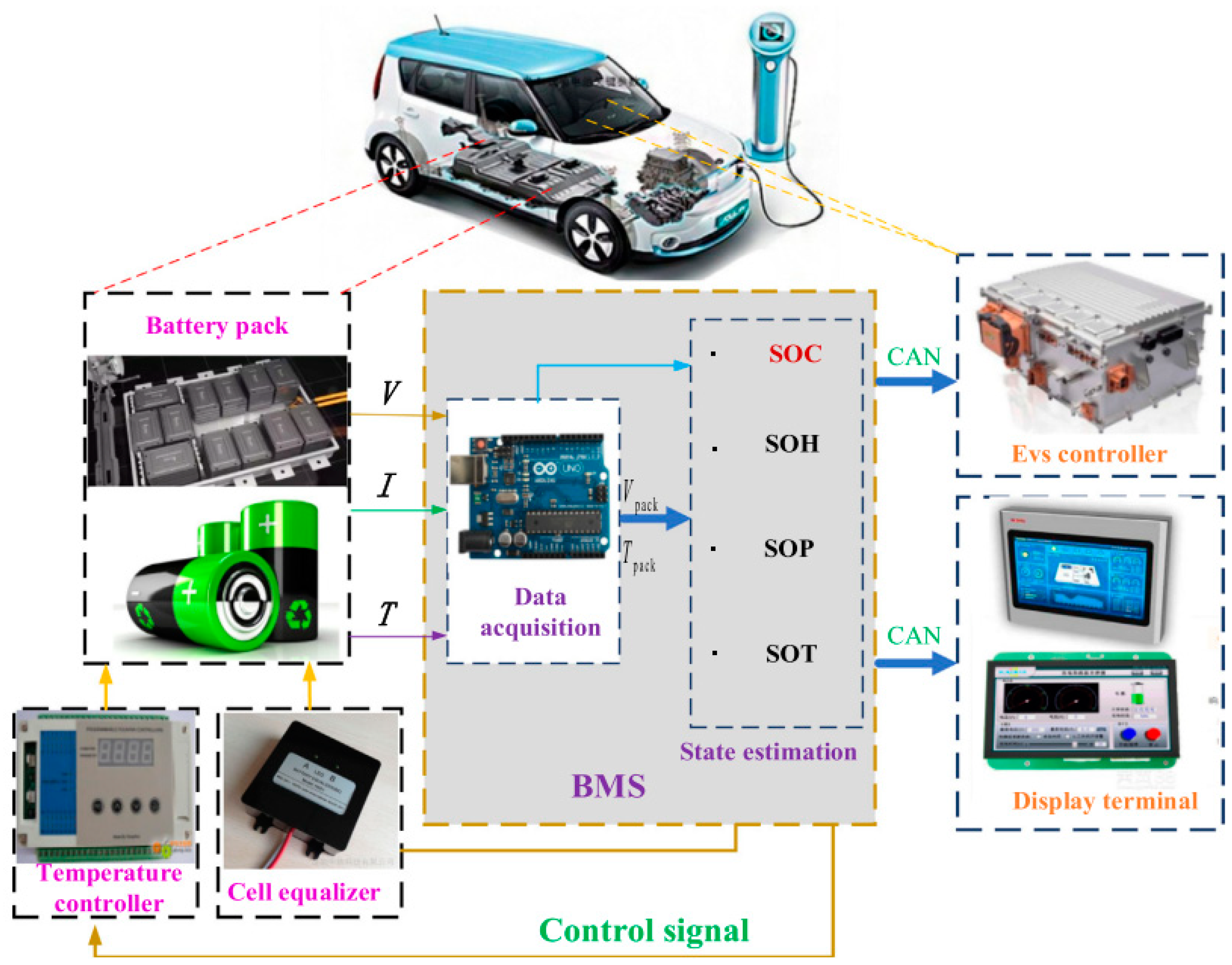
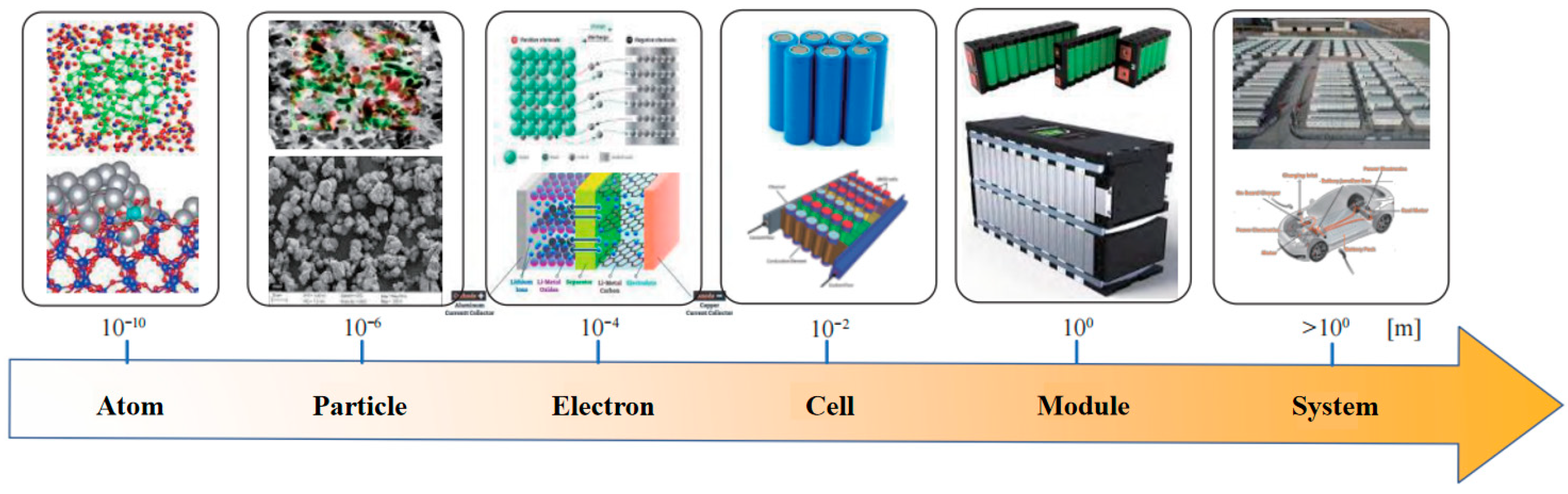
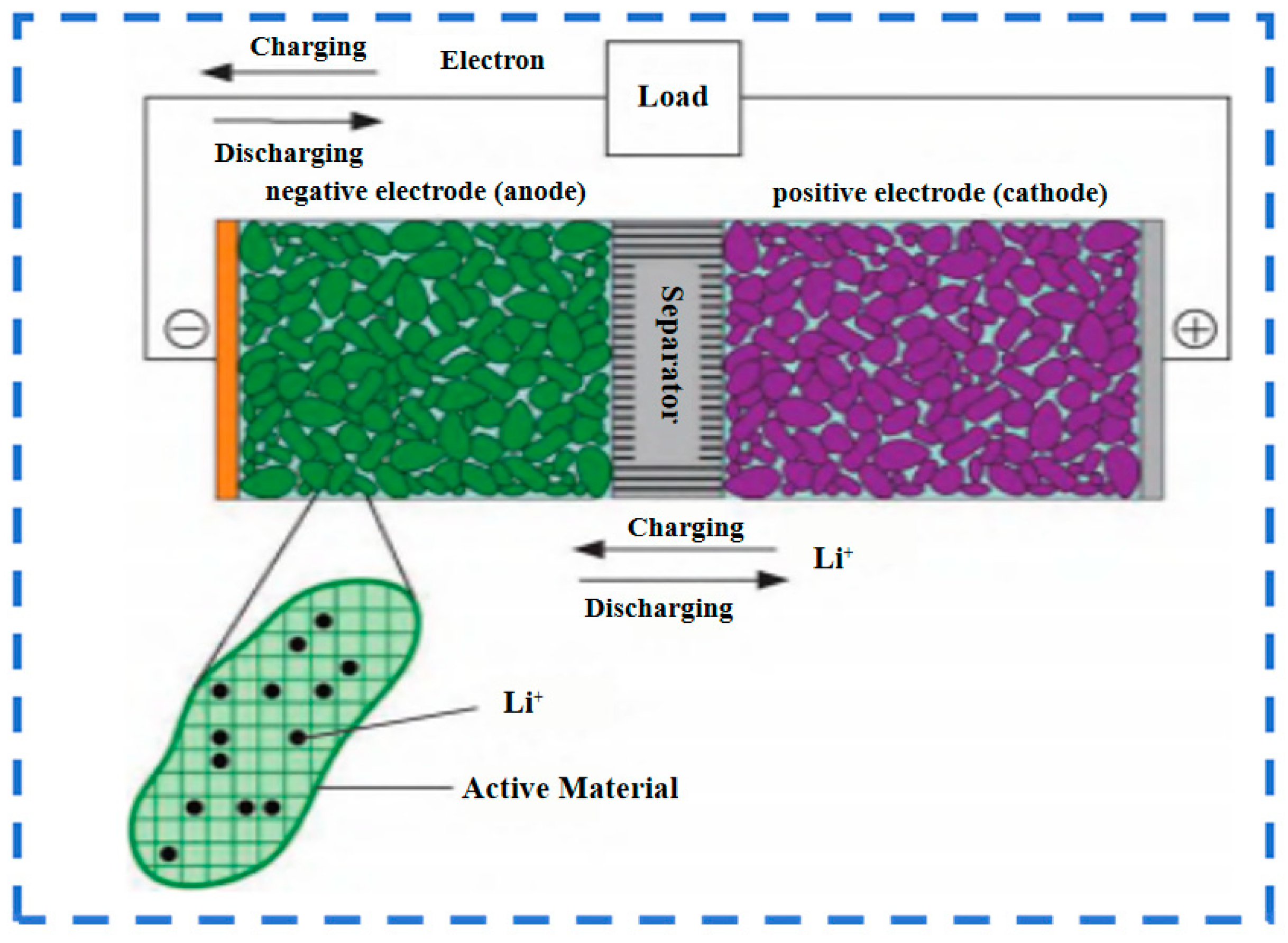
2. Power Batteries
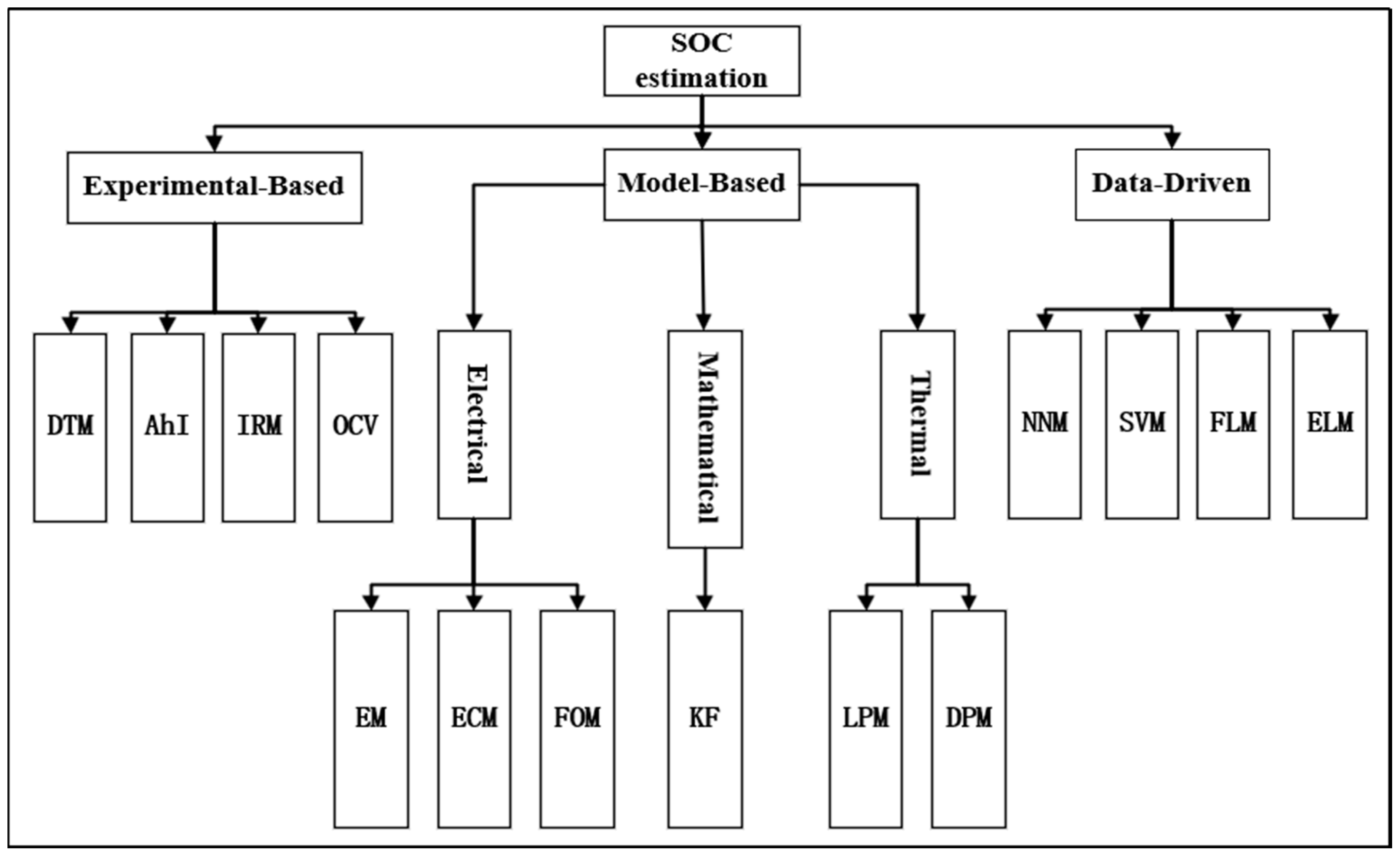
3. SOC Estimation Methodologies for Power Batteries
3.1. Experimental-Based SOC Estimation Methods
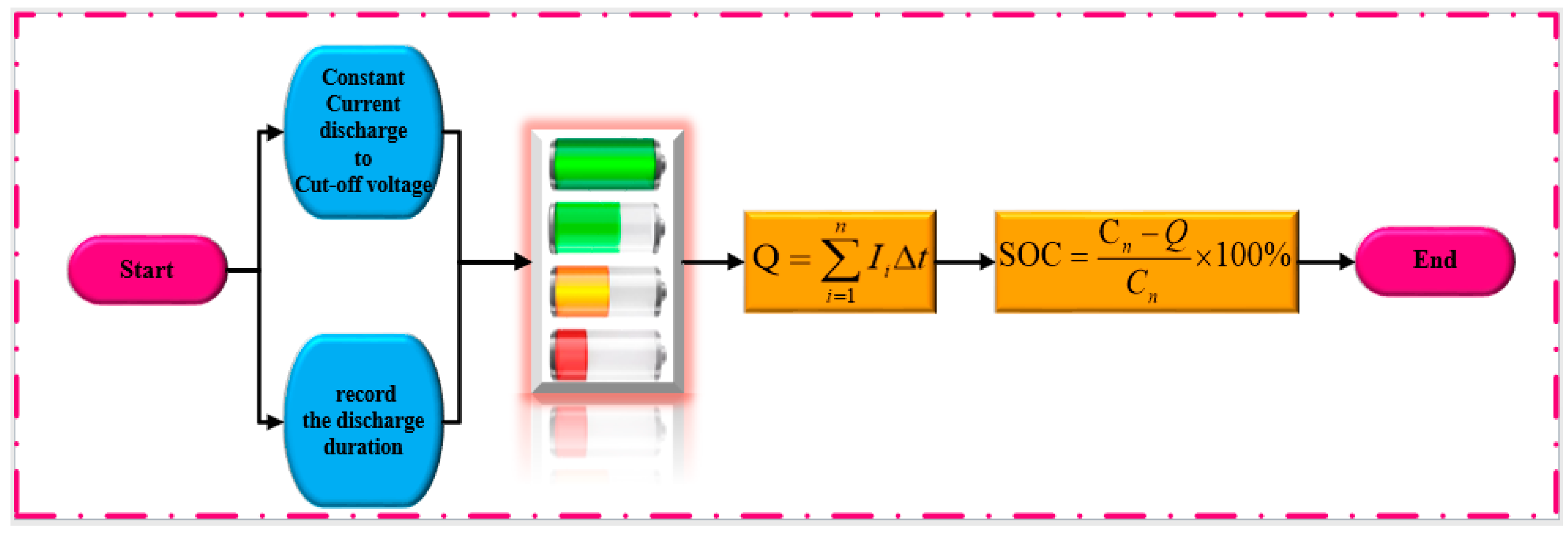
3.1.1. Discharge Test Method
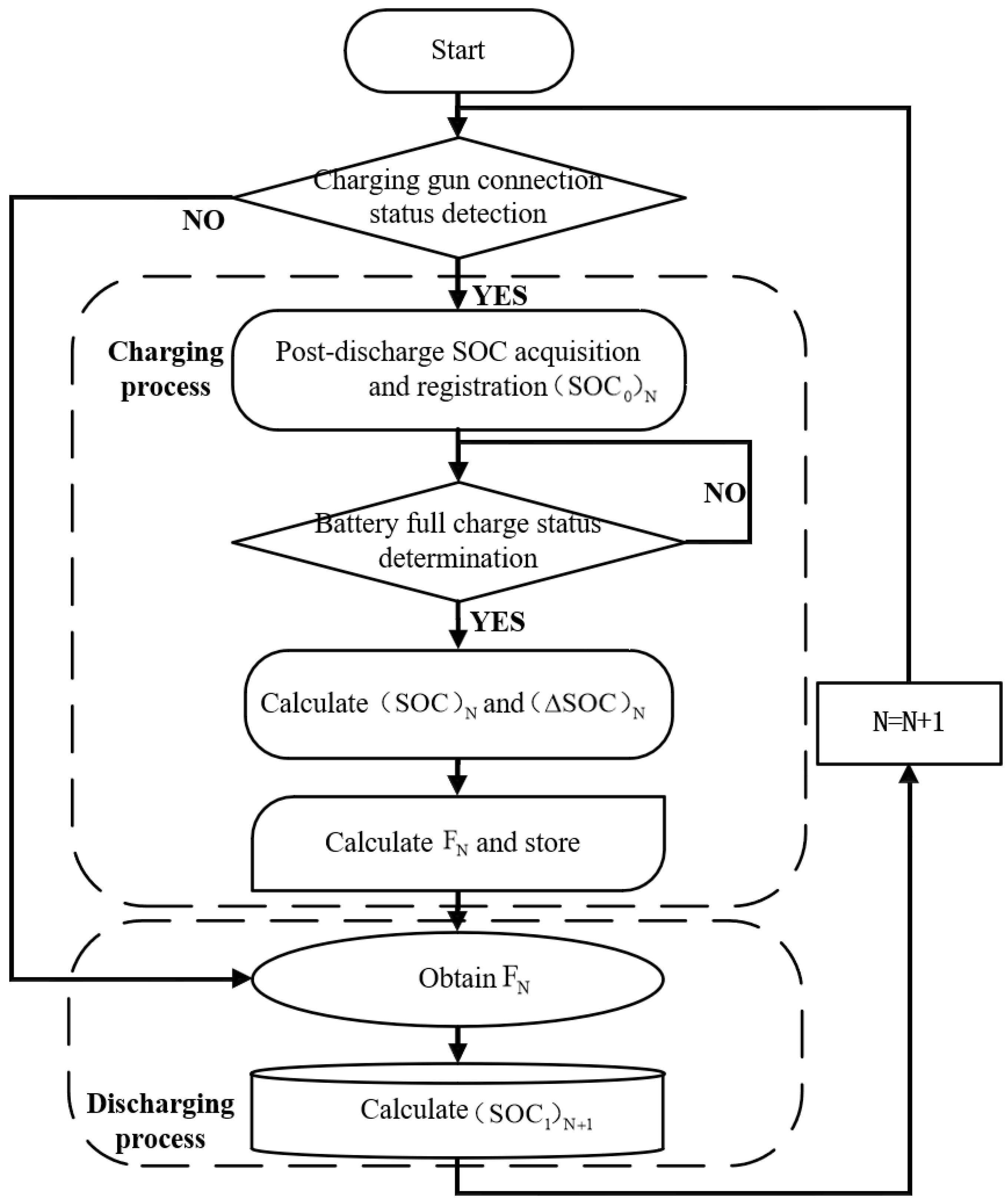
3.1.2. Coulomb Counting Method
3.1.3. Internal Resistance Measurement Method
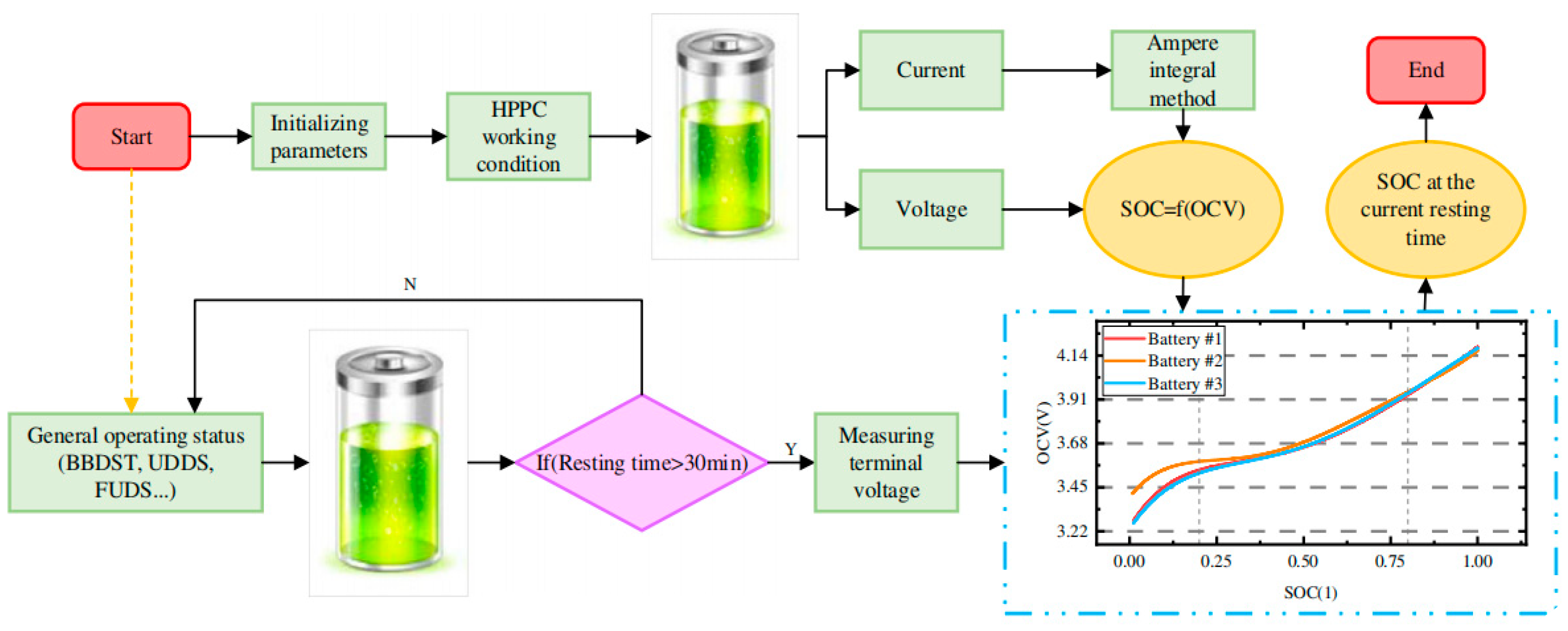
3.1.4. Open-Circuit Voltage Method
3.2. Model-Based SOC Estimation Methods
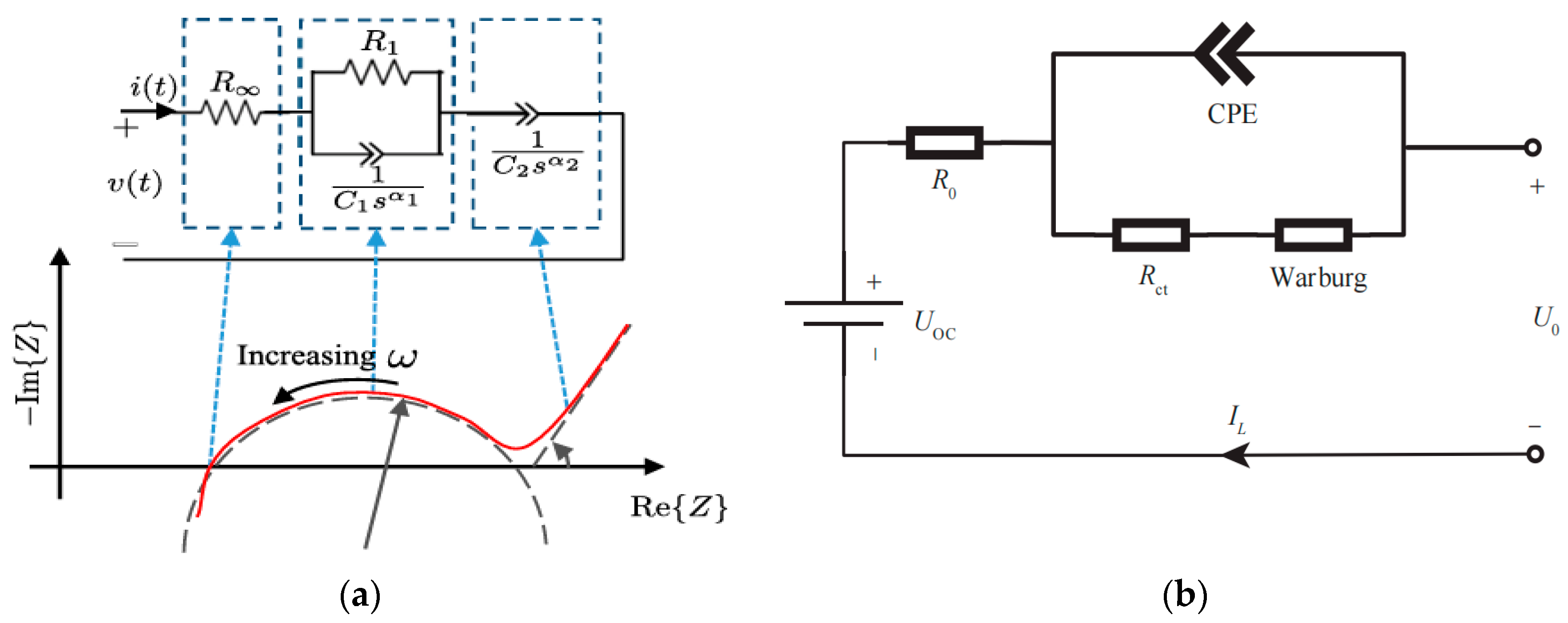
3.2.1. Electrical Models
- (1)
- The P2D model, a classical electrochemical model, accurately reflects complex physicochemical phenomena within batteries by detailing mass transport and charge transfer processes in electrodes and electrolytes [44]. Widely used in lithium-ion battery research, it excels in analyzing ion concentration distributions and potential variations during charge/discharge cycles. However, its reliance on numerous partial differential equations results in high computational costs and stringent resource/time requirements.
- (2)
- The SP model simplifies by treating electrode particles as single entities, focusing on reaction kinetics while ignoring internal concentration gradients [45]. This reduces computational load, making it effective for preliminary design and rapid evaluation where efficiency outweighs precision. However, its oversimplification limits accurate characterization of multiscale phenomena.
- (3)
- The MP model addresses SP’s oversimplification by simulating battery operational states more realistically through interactions between multiple particles and electrode inhomogeneity [46]. It captures both electrode reaction kinetics and internal mass transport/ion concentration distribution. The MP model demonstrates unique advantages in studying high-rate charging/discharging, long-term cycling, and performance under complex environmental conditions. While providing effective tools for analyzing capacity fade mechanisms, thermal management issues, and battery durability, its intermediate complexity between P2D and SP models requires balancing computational accuracy and cost.
3.2.2. Mathematical Models
- (1)
- Kalman Filter (KF): The KF recursively calculates SOC using measurements and state-space models, making it suitable for linear systems. Xu et al. [63] developed a lithium battery SOC estimation method that integrates a Recurrent Cerebellar Model Neural Network (RCMNN) with KF. This approach incorporates recursive units in both associative and weight memory layers. Inputs for the model included voltage, current, and temperature measurements, simulating various charge/discharge scenarios in energy storage systems. Experimental results demonstrated high accuracy and robustness across different conditions.
- (2)
- Extended Kalman Filter (EKF): The EKF extends the KF framework to nonlinear systems through the local linearization of nonlinear functions. However, this linearization can introduce errors. To address this limitation, Tan et al. [64] proposed a Grey Wolf Optimization (GWO)–optimized EKF algorithm, which showed significant reductions in SOC estimation errors and improved accuracy compared to conventional EKF.
- (3)
- Unscented Kalman Filter (UKF): The UKF employs sigma-point sampling to directly handle nonlinearities, providing enhanced accuracy for nonlinear systems, albeit at increased computational costs. Tang et al. [65] developed a hybrid method combining UKF with Variational Bayesian Adaptive UKF (VBAUKF) to reduce process and measurement noise, achieving a precise SOC estimation. Validation under Urban Dynamometer Driving Schedule (UDDS) conditions confirmed SOC estimation errors below 1%, demonstrating the method’s effectiveness.
- (4)
- Cubature Kalman Filter (CKF): The CKF approximates probability density functions using cubature rules, achieving high accuracy and stability for nonlinear systems, though its implementation can be complex. Wu et al. [66] proposed an Improved Maximum Correntropy Adaptive Iterative CKF (IMCC-AICKF) to mitigate instability caused by non-Gaussian noise. Simulations verified that this approach accurately converges to true values with enhanced robustness.
- (5)
- Particle Filter (PF): The PF utilizes Monte Carlo simulations and Bayesian estimation to represent SOC probability distributions through a set of particles, effectively handling arbitrary nonlinear and non-Gaussian systems [67]. However, it suffers from high computational demands and particle degeneracy. Zhang et al. [68] integrated EKF-PF with a second-order Thevenin model to estimate SOC in retired power lithium batteries. Experimental results indicated mean errors below 1.23% and maximum errors under 3.37%, outperforming standard PF approaches.
| Kalman Filter Variant | Advantages | Limitations |
|---|---|---|
| KF [69] | 1. Simple structure 2. High computational efficiency | 1. Inapplicable to nonlinear systems |
| EKF [70] | 1. Effective for linear/weakly nonlinear systems 2. Moderate computational complexity | 1. Poor performance in strong nonlinear systems 2. Sensitivity to initial conditions |
| UKF [71] | 1. Reduced sensitivity to noise/initial conditions 2. Enhanced stability | 1. High computational load 2. Requires optimal sigma-point selection |
| CKF [72] | 1. Accurate state distribution characterization 2. Partial non-Gaussian noise robustness | 1. High computational complexity 2. Demanding hardware resources |
| PF [73] | 1. Handles strong nonlinearities/non-Gaussian noise 2. Low model dependency | 1. Prohibitive computational cost 2. Particle degeneracy issues |
3.2.3. Thermal Model
- (1)
- Lumped Parameter Model: The lumped parameter model is a simplified approach to characterize thermal performance during heat transfer processes. It represents continuously distributed thermal–physical parameters in the system with concentrated parameters. The model assumes instantaneous uniform temperature distribution within the system, neglecting spatial temperature gradients, and treats the entire system or its components as homogeneous “lumped” units with uniform temperature. Based on the law of energy conservation, thermal balance equations are established by analyzing the heat inflow/outflow of the lumped unit and heat storage/variation within the unit, thereby describing the system’s thermal behavior. Zhao et al. [75] proposed an electro-thermal coupled model incorporating temperature effects, which employs discrete identification and UPF-based online parameter identification methods to estimate multiple parameters of the lumped parameter thermal model, with parameter data fitted as continuous environmental functions. As shown in Figure 11, the advantages of this model lie in its simplicity and computational efficiency, enabling the rapid prediction of the system’s overall thermal response trends. This proves particularly valuable for preliminary thermal analysis and estimation. For instance, in scenarios with low temperature accuracy requirements, relatively simple thermal processes, or small-scale systems, the lumped parameter model can provide approximate temperature variation ranges within short timeframes. This assists engineers in rapidly evaluating design feasibility and provides foundational data and conceptual references for subsequent detailed design.
- (2)
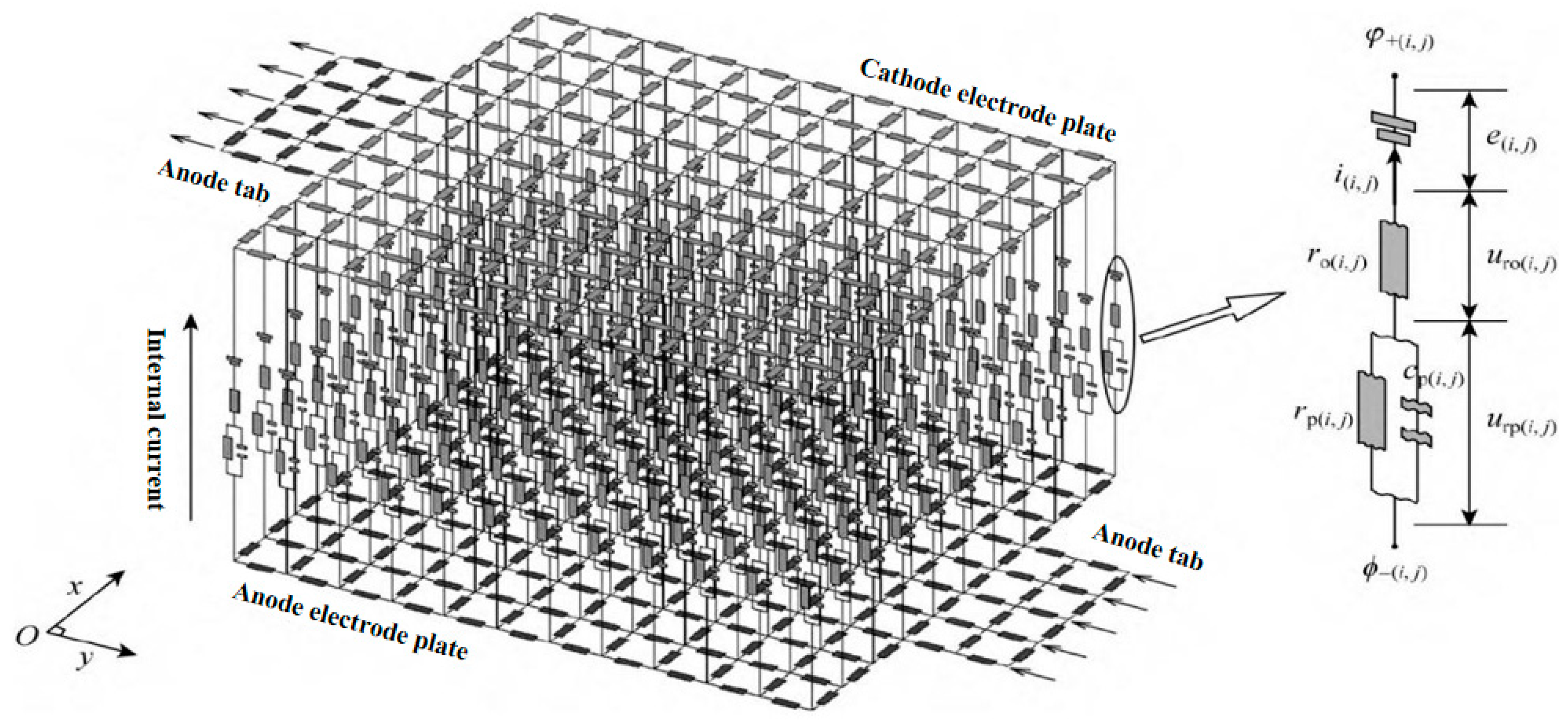
- Distributed Parameter Model: In contrast to lumped parameter models, the distributed parameter model fully considers the continuous spatial variation in internal temperature within objects. The system is divided into numerous micro-units, with thermal balance equations established for each unit. Heat transfer processes in space and time are described through partial differential equations. This unique modeling approach gives distributed parameter models significant advantages in addressing complex heat transfer problems. In battery research, these advantages prove particularly critical. Chen Dafen et al. [76] proposed a construction method for battery distributed parameter equivalent circuit models, with model parameters identified through battery external characteristics. The research process fully leveraged the distributed parameter model’s capability to meticulously characterize heat transfer details. As shown in Figure 12, this model can accurately reconstruct complex temperature distributions within battery systems and reveal detailed heat flow information at different positions. Consequently, it is specifically applicable to scenarios requiring stringent temperature distribution accuracy, involving complex thermal processes and heterogeneous internal heat transfer characteristics, such as battery packs in new energy intelligent connected vehicles and large-scale energy storage battery systems, providing powerful tools for thermal management and performance optimization in these domains.
3.3. Data-Driven SOC Estimation Algorithm
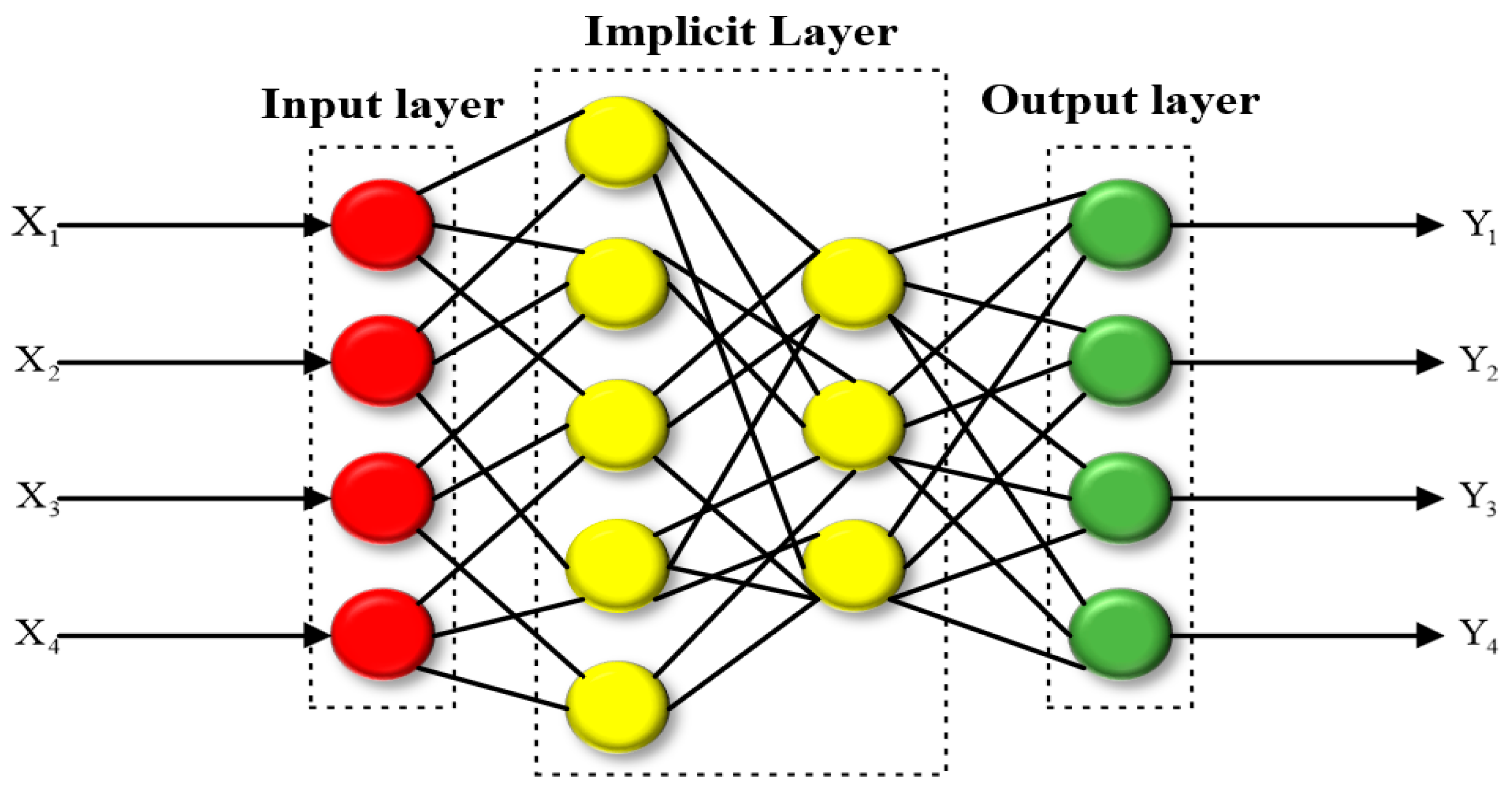
3.3.1. Neural Network Method
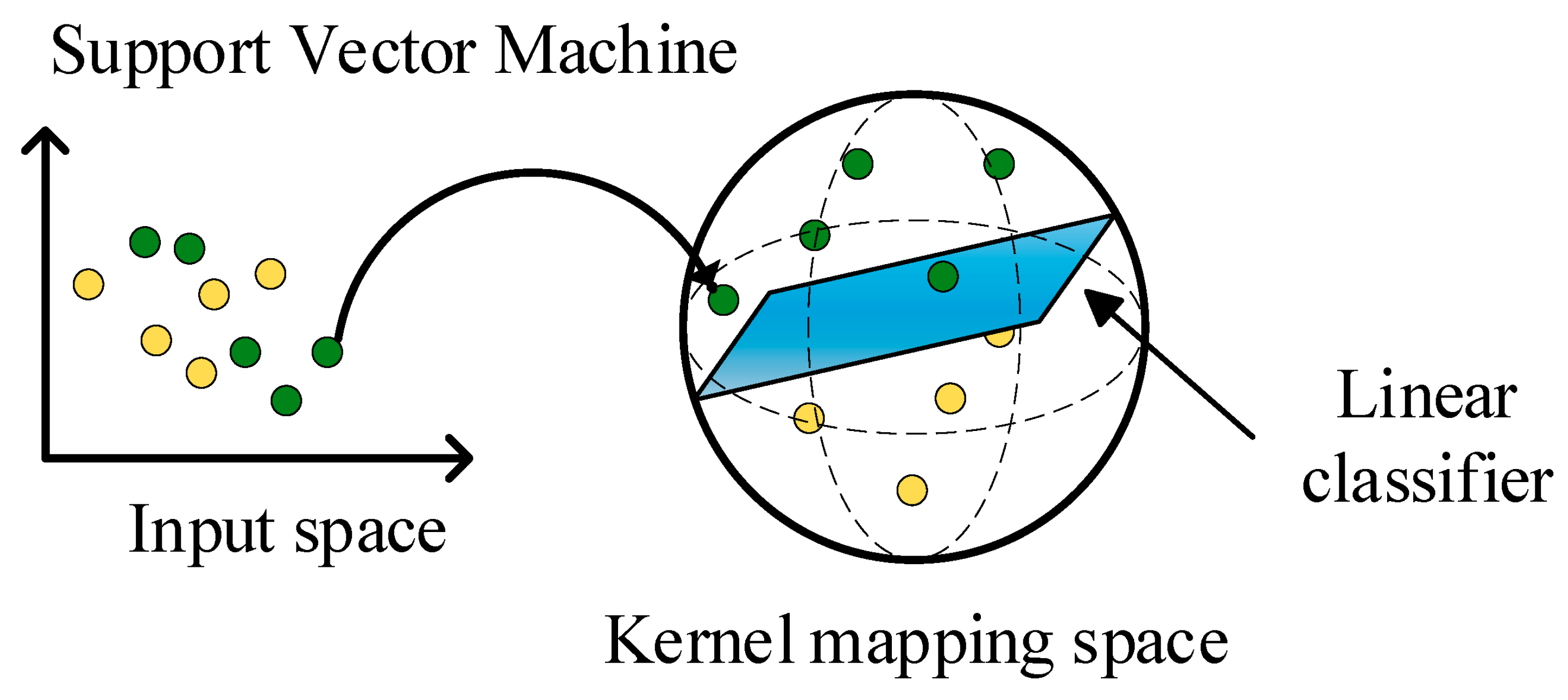
3.3.2. Support Vector Machine
3.3.3. Fuzzy Logic Method
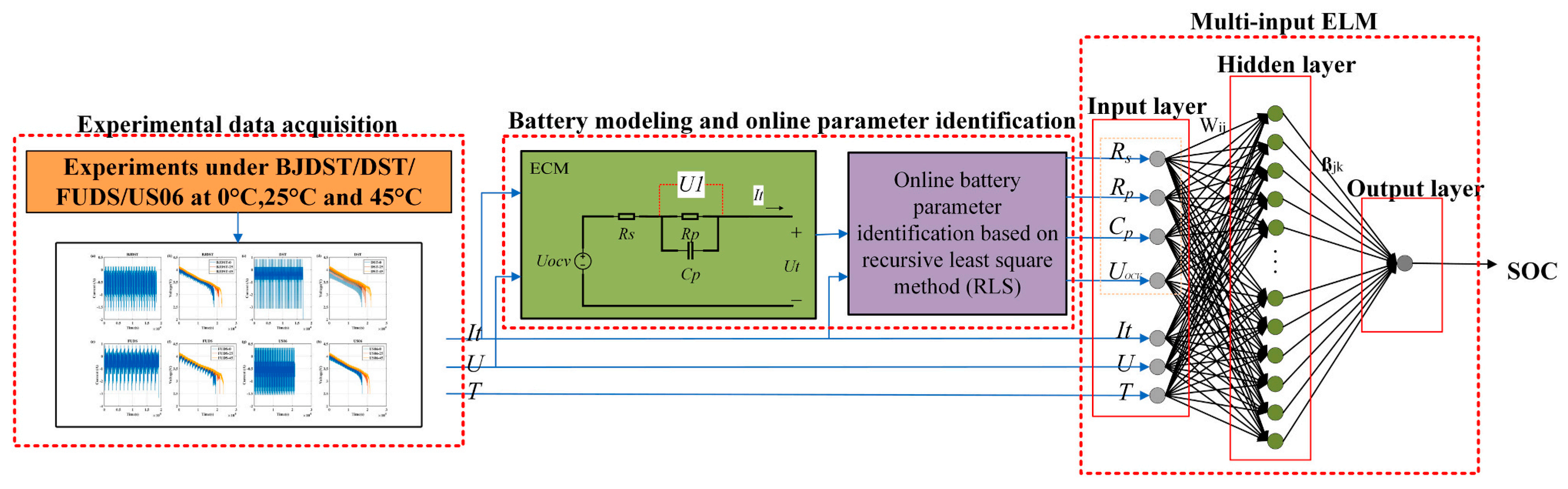
3.3.4. Extreme Learning Machine
3.4. Comparative Analysis of SOC Estimation Methods
4. Industry Frontier Algorithms
5. Conclusions and Perspectives
5.1. Conclusions
- Trade-off between Accuracy and Real-time Performance: SOC estimation requires rapid provision of high-accuracy results to facilitate real-time adjustment of charging strategies. While high-accuracy algorithms, such as Kalman filtering and particle filtering, can deliver precise estimates, they typically demand substantial computational resources, thus restricting their application in resource-constrained embedded systems.
- Balancing Data Quality and Reliability: SOC estimation relies on data from multiple sensors (such as voltage, current, and temperature), which can be significantly affected by external environmental factors. Extreme conditions may degrade sensor performance, resulting in estimation errors. Although multi-sensor collaboration can enhance accuracy, it also adds complexity and cost to the system.
- Adaptability of Models and Algorithms: In practical applications, the diversity of battery types, operating environments, and dynamic states necessitate that SOC estimation models and algorithms exhibit strong adaptability. However, existing SOC estimation solutions each have their strengths and weaknesses, making it challenging to meet all complex requirements.
5.2. Perspectives
- Development of Multi-Fusion Estimation Frameworks: Experimental-based methods demonstrate practical value in specific scenarios but struggle to track SOC dynamics in real time. Model-driven approaches excel in real-time responsiveness, enabling rapid reactions to battery operating states, yet inherently fail to comprehensively reflect internal battery characteristics. Data-driven methods exhibit strong adaptability by automatically adjusting estimation models according to battery properties and operating conditions, but they face challenges such as data collection difficulties, transmission delays, and high storage costs. This highlights the inadequacy of single-method solutions in meeting increasingly stringent BMS requirements. Therefore, creating a multi-fusion estimation framework that enhances universality, robustness, and real-time capability will be a crucial direction for the future.
- Research on Adaptive Algorithms: Investigating adaptive algorithms that can dynamically adjust under varying operating conditions will be vital for addressing the challenges posed by battery performance degradation and environmental changes. Incorporating advanced technologies such as reinforcement learning can further enhance the flexibility and intelligence of these algorithms.
- Optimizing Computational Efficiency:
- (a)
- Parameter Quantization: Reducing the precision of model parameters can decrease storage and computational demands, thereby improving efficiency.
- (b)
- Lightweight Model Compression: Techniques such as pruning and knowledge distillation can simplify model structures and reduce complexity.
- (c)
- Hardware Acceleration: Utilizing specialized hardware accelerators like FPGAs and GPUs can enhance computational performance, ensuring efficient SOC estimation.
- Standardization and Modular Design: Promoting the standardization and modular design of SOC estimation algorithms and models will facilitate flexible deployment across different systems and applications, simplifying the integration process.
- Forward-looking Research and Innovation: Strengthening collaboration between academia and industry to conduct forward-looking research will be essential for exploring new materials, structures, and technologies in battery management. Such innovations could lead to significant advancements in the future of battery management systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Editorial Department. Intelligent Connected Vehicles: Technology Carrying 2024. Intell. Connect. Veh. 2024, 6, 18–23. [Google Scholar]
- Guo, Z. Global Electric Vehicle Market Continues to Expand. People’s Daily, 17 October 2024, International Edition, p. 018. Available online: https://doi.org/10.28655/n.cnki.nrmrb.2024.011541 (accessed on 20 October 2024).
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A Review on the Key Issues for Lithium-Ion Battery Management in Electric Vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Huang, Z.; Zhang, C.; Wei, C. Physics-based battery SOC estimation methods: Recent advances and future perspectives. J. Energy Chem. 2024, 89, 27–40. [Google Scholar] [CrossRef]
- Shu, W. State of Charge Estimation for Lithium-Ion Batteries Using Unscented Kalman Filter; Foshan University of Science and Technology: Foshan, China, 2024. [Google Scholar]
- Zhang, M.; Fan, X. Design of battery management system based on improved ampere-hour integration method. Int. J. Electr. Hybrid Veh. 2022, 14, 1–29. [Google Scholar] [CrossRef]
- Zhu, Y.C. Research on Battery Management System for Mini Fire Trucks Based on Lossless Differential-Coulomb Counting Method; Yancheng Institute of Technology: Yancheng, China, 2024. [Google Scholar]
- Hu, K.; Zhang, B.Z.; Liu, Z.T.; Wang, Y.J.; Zhu, M.F. SOC Estimation Based on Improved Extended Kalman Filter Algorithm. Automot. Pract. Technol. 2023, 48, 6–13. [Google Scholar]
- Wang, S.; Zhang, S.; Wen, S.; Fernandez, C. An accurate state-of-charge estimation of lithium-ion batteries based on improved particle swarm optimization-adaptive square root cubature Kalman filter. J. Power Sources 2024, 624, 235594. [Google Scholar] [CrossRef]
- Fan, K.S. Research on Nonlinear Equivalent Circuit Model Identification of Lithium-Ion Batteries Based on Gaussian Process; Huazhong University of Science and Technology: Wuhan, China, 2023. [Google Scholar]
- Bhattacharya, T.; Ghosh, S. Data driven approach for state-of-charge estimation of lithium-ion cell using stochastic variational Gaussian process. Comput. Electr. Eng. 2024, 120, 109727. [Google Scholar] [CrossRef]
- Hong, J.C.; Pei, J.Q.; Liang, F.W.; Li, M.; Qiu, Y.L.; Zhang, L. Research on SOC Estimation of Real-Vehicle Power Batteries Based on Sparrow Search Optimization-LSTM. J. Southwest Univ. Nat. Sci. Ed. 2024, 46, 41–50. [Google Scholar]
- Zhang, L.; Song, Q.; Li, J. SOC Estimation for Lithium-Ion Batteries Based on the AEKF-SVM Algorithm. Acad. J. Comput. Inf. Sci. 2024, 7, 5. [Google Scholar]
- Baraniak, M.; Płowens, R.; Lota, K.; Bajsert, M.; Lota, G. Novel carbon material with potential application in lead-acid battery technology. Monatshefte Für Chem.-Chem. Mon. 2025, prepublish. 1–7. [Google Scholar] [CrossRef]
- Pulido, Q.F.D.; Covrig, F.C.; Bruchhausen, M. On the Performance of Portable NiMH Batteries of General Use. Batteries 2025, 11, 30. [Google Scholar] [CrossRef]
- Shaari, B.N.; Wani, A.A.; Kamarudin, K.S. Direct Liquid Fuel Cells: Recent Advances and Challenges and the Sustainable Energy Transition; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Li, J.L.; Peng, Y.C.; Wang, X.; Jiang, X.X.; Wang, L. Research Status and Prospects of Lithium-Ion Battery Modeling. Power Gener. Technol. 2024, Online First. 1–15. Available online: http://kns.cnki.net/kcms/detail/33.1405.TK.20240918.1346.004.html (accessed on 8 April 2025).
- Shi, C.; Wang, T.; Liao, X.; Qie, B.; Yang, P.; Chen, M.; Wang, X.; Srinivasan, A.; Cheng, Q.; Ye, Q.; et al. Accordion-like Stretchable Li-ion Batteries with High Energy Density. Energy Storage Mater. 2018, 17, 136–142. [Google Scholar] [CrossRef]
- Li, J.; Li, H. Review on Lithium-Ion Battery State of Charge Estimation Methods. Sci. Technol. Eng. 2022, 22, 2147–2158. [Google Scholar]
- Shrivastava, P.; Naidu, P.A.; Sharma, S.; Panigrahi, B.K.; Garg, A. Review on technological advancement of lithium-ion battery states estimation methods for electric vehicle applications. J. Energy Storage 2023, 64, 107159. [Google Scholar] [CrossRef]
- Gao, W.K. SOC Estimation of Lithium-ion Power Batteries in Alpine Environments; Changchun University of Technology: Changchun, China, 2023. [Google Scholar]
- Liu, Z.C.; Zhang, Y.H.; Wang, J.Q. Review on Advances in SOC Estimation Techniques for Lithium-ion Batteries. Automot. Compon. 2022, 12, 91–95. [Google Scholar]
- Chidambaram, R.K.; Chatterjee, D.; Barman, B.; Das, P.P.; Taler, D.; Taler, J.; Sobota, T. Effect of Regenerative Braking on Battery Life. Energies 2023, 16, 5303. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Guo, T.Z.; Gao, M.Y.; He, Z.W.; Dong, Z.K. A Comprehensive Review of SOC Estimation Methods for Lithium-ion Batteries in Electric Vehicles. J. Electron. Inf. Technol. 2021, 43, 1803–1815. [Google Scholar]
- Ren, G. Introduction of SOC estimation method. IOP Conf. Ser. Earth Environ. Sci. 2021, 687, 012083. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Lu, J.Y.; Long, X.L.; Wei, J.B.; Zhou, R.; Wu, Y.T. Dynamic Identification of Energy Storage Battery Model Parameters. J. Natl. Univ. Def. Technol. 2019, 41, 87–92. [Google Scholar]
- Zhang, Q.Q.; Bai, L.W.; Wang, P. Research Status of State of Charge Estimation for Lithium-ion Power Batteries. Guangdong Chem. Ind. 2024, 51, 48–52. [Google Scholar]
- Lin, C.T.; Chen, Q.S.; Wang, J.P.; Huang, W.H.; Wang, Y.C. SOC Estimation for Electric Vehicle Power Batteries Using Improved Ampere-hour Integral Method. J. Tsinghua Univ. Sci. Technol. 2006, 2, 247–251. [Google Scholar]
- Wang, F. Design of Battery Management System Based on Modified Ampere-Hour Integral Method for SOC Estimation; Hunan University: Changsha, China, 2020. [Google Scholar]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Study of SOC Estimation by the Ampere-Hour Integral Method with Capacity Correction Based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Cui, X.D.; Huang, Y.Q.; Wu, X.M. Comprehensive Review on SOC Estimation Methods and Applications for Lithium Batteries. Electron. Meas. Technol. 2024, 47, 41–59. [Google Scholar]
- Bao, Y.; Dong, W.; Wang, D. Online Internal Resistance Measurement Application in Lithium Ion Battery Capacity and State of Charge Estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Y.; Li, J.; Shen, Y.; Xiao, R.; Ba, T.; Liu, Q. A novel method for constructing the relationships between state of charge and open-circuit voltage of lithium-ion battery under different temperatures with reduced test time. J. Clean. Prod. 2023, 428, 139554. [Google Scholar] [CrossRef]
- Tao, J.; Wang, S.; Cao, W.; Aninakwa, P.T.C.; Guerrero, J.M. A comprehensive review of state-of-charge and state-of-health estimation for lithium-ion battery energy storage systems. Ionics 2024, 30, 5903–5927. [Google Scholar] [CrossRef]
- Wu, G.W. SOC Estimation of Lithium Batteries Based on Adaptive Kalman Filter; Chongqing University of Technology: Chongqing, China, 2022. [Google Scholar]
- Ling, L.Y.; Zhang, H.; Zhang, T.; Yang, C.; Qi, L. SOC Estimation of Lithium Batteries Based on Prediction-rest Open Circuit Voltage Method. J. Power Supply 2025, Online First. 1–10. Available online: http://kns.cnki.net/kcms/detail/12.1420.tm.20240425.1849.028.html (accessed on 8 April 2025).
- Wang, L.X.; Duan, J.D.; Fan, S.G.; Zhao, K. An estimated value compensation method for state of charge estimation of lithium battery based on open circuit voltage change rate. Energy 2024, 313, 134119. [Google Scholar] [CrossRef]
- Ding, Z.T.; Deng, T.; Li, Z.F.; Yin, Y.L. SOC Estimation Method for Lithium-ion Batteries Based on Ampere-hour Integral and Unscented Kalman Filter. China Mech. Eng. 2020, 31, 1823–1830. [Google Scholar]
- Guo, F.; Couto, L.D.; Mulder, G.; Trad, K.; Hu, G.; Capron, O.; Haghverdi, K. A systematic review of electrochemical model-based lithium-ion battery state estimation in battery management systems. J. Energy Storage 2024, 101, 113850. [Google Scholar] [CrossRef]
- Liang, C.C.; Li, H.L.; Chen, Z.; Lin, S.C.; Lin, F.K. Research Progress on Thermogenesis Models of Lithium-Ion Batteries. Qual. Mark. 2023, 13, 16–18. [Google Scholar]
- Dong, Z.W. SOC Estimation of Lithium-ion Batteries Based on Kalman Filter Algorithm; Central South University of Forestry and Technology: Changsha, China, 2024. [Google Scholar]
- Zhang, T. Research on Thermal Runaway and Its Propagation Characteristics and Protection Strategies for Lithium-ion Batteries; Qingdao University: Qingdao, China, 2023. [Google Scholar]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensionalmodels of lithium-Ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Yu, Z.; Tian, Y.; Li, B. A simulation study of Li-ion batteries based on a modified P2Dmodel. J. Power Sources 2024, 618, 234376. [Google Scholar] [CrossRef]
- Ren, L.C.; Zhu, G.R.; Kang, J.Q.; Wang, J.V.; Luo, B.Y.; Chen, C.Y.; Xiang, K. An algorithm for state of charge estimationbased on a single-particle model. J. Energy Storage 2021, 39, 102644. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, F.; Huang, X.D. Research on Multiphysics Modeling and Simulation Technology for All-Solid-State Lithium-ion Batteries. Electron. Devices 2021, 44, 1–6. [Google Scholar]
- Shi, M.Y. Co-simulation of Electrical-Thermal-Aging Coupling and Its Application for Lithium-ion Batteries; Shandong University: Jinan, China, 2021. [Google Scholar]
- Xiong, R.; Li, Z.Y.; Li, H.L.; Wang, J.; Liu, G.F. A novel method for state of charge estimation of lithium-ion batteries at low-temperatures. Appl. Energy 2025, 377, 124514. [Google Scholar] [CrossRef]
- Huang, L.L.; Ren, X.X.; Miao, B.B.; Kong, F.C. SOC Estimation of Lithium-ion Batteries Based on Improved Rint Model. Battery Ind. 2022, 26, 177–180. [Google Scholar]
- Li, H.; Wang, S.L.; Zou, C.Y.; Li, J.C.; Xie, W. SOC Estimation Based on Thevenin Model and Adaptive Kalman Filter. Process Autom. Instrum. 2021, 42, 46–51. [Google Scholar]
- Wang, C.; Xu, M.; Zhang, Q.; Feng, J.; Jiang, R.; Wei, Y.; Liu, Y. Parameters identification of Thevenin model for lithium-ion batteries using self-adaptive Particle Swarm Optimization Differential Evolution algorithm to estimate state of charge. J. Energy Storage 2021, 44, 103244. [Google Scholar] [CrossRef]
- Deng, L. SOC Estimation and Charging Optimization for Power Lithium Batteries Based on Improved PNGV Model; Harbin Institute of Technology: Harbin, China, 2014. [Google Scholar]
- Geng, Y.; Pang, H.; Liu, X. State-of-charge estimation for lithium-ion battery based on PNGV model and particle filter algorithm. J. Power Electron. 2022, 22, 1154–1164. [Google Scholar] [CrossRef]
- Pang, H.; Guo, L.; Wu, L.X.; Jin, J.M.; Liu, K. Improved Dual-Polarization Model Considering Environmental Temperature Effects and SOC Estimation for Lithium-ion Batteries. Trans. China Electrotech. Soc. 2021, 36, 2178–2189. [Google Scholar]
- Wu, T.; Dai, Y. Power Battery SOC Estimation Based on DP Model and Support Vector Regression; Wuhan University of Technology: Wuhan, China, 2022. [Google Scholar]
- Liu, D.; Wang, X.C.; Zhang, M.; Gong, M.X. SOC Estimation of Lithium-ion Batteries in Electric Vehicles Based on N-2RC Model. In Proceedings of the 31st Chinese Control and Decision Conference, Nanchang, China, 3–5 June 2019; Volume 3, p. 6. [Google Scholar]
- Yan, X.W.; Guo, Y.W.; Cui, Y.; Wang, Y.W.; Deng, H.R. Electric Vehicle Battery SOC Estimation based on GNLModel Adaptive Kalman Filter. J. Phys. Conf. Ser. 2018, 1087, 052027. [Google Scholar] [CrossRef]
- Guo, Y.W. Battery SOC Estimation Based on GNL Model and Adaptive Unscented Kalman Filter; North China Electric Power University: Beijing, China, 2019. [Google Scholar]
- Li, L.L.; Tao, Z.S.; Pan, T.L.; Yang, W.L.; Hu, G.Y. Fractional-order Modeling and SOC Estimation Strategy for Lithium Batteries. Energy Storage Sci. Technol. 2023, 12, 544–551. [Google Scholar]
- Antonio, J.L.; Rodríguez, P.I.; Salvador, R. A fractional-order model for calendar aging with dynamic storage conditions. J. Energy Storage 2022, 50, 104537. [Google Scholar]
- Soleymani, T.A.; Mahdi, M.S.A.; Mehrdad, S. Structural identifiability of impedance spectroscopy fractional-order equivalent circuit models with two constant phase elements. Automatica 2022, 144, 110463. [Google Scholar]
- Du, C.Q.; Wu, Z.Y.; Wu, D.M.; Ren, Z. SOC Estimation of Power Batteries Based on KF-EKF Algorithm. J. Wuhan Univ. Technol. 2022, 44, 84–92. [Google Scholar]
- Xu, Z.F.; Li, H.S.; Li, W.Y.; Yu, K. SOC Prediction of Lithium Batteries Using Recurrent Cerebellar Model Neural Network and Kalman Filter. Integr. Intell. Energy 2024, 46, 81–86. [Google Scholar]
- Tan, W.; Jiang, Z.; Liu, Y.; Ren, F. SOC Estimation Method for Lithium Batteries Based on Improved EKF Algorithm. Auto Time 2024, 24, 101–103. [Google Scholar]
- Tang, A.H.; Liu, S.M.; Zou, H.; Chen, Z.M.; Hu, W.X.; Li, Y.H. SOC Estimation Using Variational Bayesian Unscented Kalman Filter. J. Southwest Univ. Nat. Sci. Ed. 2024, 46, 51–59. [Google Scholar]
- Wu, C.L.; Zhao, Y.B.; Ma, Y.; Zhang, Y.; Meng, J.H. SOC Estimation of Lithium-ion Batteries Using Improved Maximum Correntropy Adaptive Iterated Cubature Kalman Filter. J. Xi’an Jiaotong Univ. 2024, 58, 52–64. [Google Scholar]
- Lu, J.L.; Hu, X.H.; Zhang, X.Z.; Wang, Z.; Zhao, Z.H. Dynamic State Estimation of Distribution Network Based on Load Forecasting and Unscented Particle Filter. Proc. CSU-EPSA 2024, 36, 133–140+158. [Google Scholar]
- Zhang, K.R.; Wang, W.Q. SOC Estimation of Retired Power Lithium Batteries Based on EKF-PF Algorithm. Mod. Electron. 2023, 46, 145–150. [Google Scholar]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Andsustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Tang, X.; Huang, H.; Zhong, X.W.; Wang, K.J.; Li, F.; Zhou, Y.H.; Dai, H.F. On-Line Parameter Identification and SOC Estimation for Lithium-Ion Batteries Based on Improved Sage–Husa Adaptive EKF. Energies 2024, 17, 5722. [Google Scholar] [CrossRef]
- Bage, A.N.; Aninakwa, P.T.; Yang, X.; Tu, Q.H. Enhanced moving-step unscented transformed-dual extended Kalman filter for accurate SOC estimation of lithium-ion batteries considering temperature uncertainties. J. Energy Storage 2025, 110, 115340. [Google Scholar] [CrossRef]
- Guo, P.; Ma, W.T.; Yi, D.L.; Liu, X.H.; Wang, X.F.; Dang, L.J. Enhanced square root CKF with mixture correntropy loss for robust state of charge estimation of lithium-ion battery. J. Energy Storage 2023, 73, 108920. [Google Scholar] [CrossRef]
- Li, H.; Qu, Z.; Xu, T.; Wang, Y.; Fan, X.; Jiang, H.; Yuan, C.; Chen, L. SOC estimation based on the gas-liquid dynamics model using particle filter algorithm. Int. J. Energy Res. 2022, 46, 22913–22925. [Google Scholar] [CrossRef]
- Song, L.; Wei, X.Z.; Dai, H.F.; Sun, Z.C. Research Review on Single-cell Thermal Models of Lithium-ion Batteries. Automot. Eng. 2013, 35, 285–291. [Google Scholar]
- Zhao, J.F.; He, F.; Luo, W.D.; Li, Q. SOC Estimation of Power Batteries Based on Electro-thermal Coupling Model. Comput. Simul. 2023, 40, 99–107. [Google Scholar]
- Chen, D.F.; Jiang, J.C.; Wang, Z.G.; Duan, Y.J.; Zhang, Y.R.; Shi, W. Distributed Parameter Equivalent Circuit Model for Power Lithium-ion Batteries. Trans. China Electrotech. Soc. 2013, 28, 169–176. [Google Scholar]
- Chen, J.L. Data-Driven Estimation of SOC and SOH for Lithium-Ion Batteries; Wenzhou University: Wenzhou, China, 2022. [Google Scholar]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2021, 46, 5423–5440. [Google Scholar] [CrossRef]
- Saleem, A.; Batunlu, C.; Direkoglu, C. Precise State-of-Charge Estimation in Electric Vehicle Lithium-Ion Batteries Using a Deep Neural Network. Arab. J. Sci. Eng. 2024, 1–18. [Google Scholar] [CrossRef]
- Ofoegbu, O.E. State of charge (SOC) estimation in electric vehicle (EV) battery management systems using ensemble methods and neural networks. J. Energy Storage 2025, 114, 115833. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Li, Y.; Cao, Y.J.; Wang, Y.X. Improving lightweight state-of-charge estimation of lithium-ion battery using residual network and gated recurrent neural network. J. Energy Storage 2025, 116, 115934. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, X.; Wang, Z. Stat-of-charge estimation for lithium-ion batteries based on recurrent neural network: Current status and perspectives. J. Energy Storage 2025, 112, 115575. [Google Scholar] [CrossRef]
- Wang, W.; Meng, X.D.; Liu, H.; Li, G. A State-of-Charge estimation method of Lithium battery based on BP neural network. J. Phys. Conf. Ser. 2023, 2418, 012118. [Google Scholar]
- Gou, B.; Shen, Y. Hardware-Software Partitioning of Embedded Operating System in the SoC Using a Discrete Hopfield Neural Network Approach. Chin. J. Electron. 2007, 1, 13–17. [Google Scholar]
- Nazim, S.M.; Rahman, M.M.; Joha, I.M.; Jang, Y.M. An RNN-CNN-Based Parallel Hybrid Approach for Battery State of Charge (SoC) Estimation Under Various Temperatures and Discharging Cycle Considering Noisy Conditions. World Electr. Veh. J. 2024, 15, 562. [Google Scholar] [CrossRef]
- Elachhab, A.; Laadissi, E.M.; Tabine, A.; Hajjaji, A. Deep learning and data augmentation for robust battery state of charge estimation in electric vehicles. Electr. Eng. 2024, 1–15. [Google Scholar] [CrossRef]
- Chen, H.M.; Wang, L.Y.; Xu, Y.Y.; Jin, Y.; Chen, X.; Zhang, Q.; Li, S.J.; Liao, C.L.; Wang, L.F.; Wang, L.Y. State of Charge Estimation for Lithium-ion Battery Using Long Short-Term Memory Networks. J. Phys. Conf. Ser. 2024, 2890, 012024. [Google Scholar] [CrossRef]
- Zhang, C.W.; Wang, T.; Wei, M.; Qiao, L.; Lian, G.Q. State of charge estimation for lithium-ion batteries based on gate recurrent unit and unscented Kalman filtering. Ionics 2024, 30, 6951–6967. [Google Scholar] [CrossRef]
- Aaruththiran, M.; Begam, K.M.; Rau, A.V.; Denesh, S. Artificial Neural Networks, Gradient Boosting and Support Vector Machines for electric vehicle battery state estimation:A review. J. Energy Storage 2022, 55, 105384. [Google Scholar]
- Li, J.L.; Peng, Y.C.; Wang, Q.; Liu, H.T. Status and Prospects of Research on Lithium-Ion Battery Parameter Identification. Batteries 2024, 10, 194. [Google Scholar] [CrossRef]
- Yang, C. SOC Estimation and Balanced Control Design for Pure Electric Vehicle Lithium Batteries; Guizhou University: Guizhou, China, 2022. [Google Scholar]
- Yang, Q.X. Remaining Useful Life Prediction Method for Lithium-Ion Batteries Based on Deep Learning; Yantai University: Yantai, China, 2024. [Google Scholar]
- Li, J.B.; Wei, M.; Li, Z.Y.; Ye, M.; Jiao, S.J.; Xu, X.X. Battery State Estimation Using Improved Support Vector Machine Regression. Energy Storage Sci. Technol. 2020, 9, 1200–1205. [Google Scholar]
- Li, X.L.; Sun, Y.K. SOC Prediction of Power Lithium Batteries Based on Modified Fruit Fly Optimization Algorithm Optimized Least Squares Support Vector Machine. J. Nanjing Univ. Nat. Sci. Ed. 2023, 45, 676–681. [Google Scholar]
- Wang, Y.Y.; Li, J.B.; Zhang, F. Battery State Estimation Using Least Squares Support Vector Machine Based on Particle Swarm Optimization. Energy Storage Sci. Technol. 2020, 9, 1153–1158. [Google Scholar]
- Emile, K.V.; Erman, A.; Frank, H.V. Analyzing Differentiable Fuzzy Logic Operators. Artif. Intell. 2022, 302, 103602. [Google Scholar]
- Lin, X.F.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Mi, J.P.; Liu, X.L.; Zhu, D.M.; Chen, L.F.; Li, Y.L. The exploration of the internal homogeneities for a LiFePO4 pouch lithium-ion battery with a 3D electrochemical-thermal coupled model. Next Energy 2024, 4, 100127. [Google Scholar] [CrossRef]
- Wang, B.F.; Wu, Z.; Hou, X.P.; Cheng, Y.; Guo, T.L.; Xiao, H.Z.; Ren, J.W.; Mansor, M.R.A. Fuzzy logic optimized threshold-based energy management strategy for fuel cell hybrid E-bike. Int. J. Hydrog Energy 2024, 63, 123–132. [Google Scholar] [CrossRef]
- Balasubramaniam, P.N.B.R. Fuzzy Logic Controllers and Applications; IntechOpen: London, UK, 2025. [Google Scholar]
- Jing, Z.Y. SOC Prediction and Charging Control Strategy for Automotive Lithium-Ion Batteries; Jilin University: Jilin, China, 2018. [Google Scholar]
- Zhou, B.M.; Zhou, S.; Chen, L.; Xia, J.W. Joint SOC Estimation of Lithium-ion Batteries Based on Fuzzy-EKF Model. Bus Technol. Res. 2021, 43, 20–24. [Google Scholar]
- Wang, Y.G.; Wang, Z.F.; Yu, H.B.; Li, L.G.; Huang, J.L. Adaptive Equivalent Circuit Model with MIMO Fuzzy Control and SOC Estimation for Lithium-ion Batteries. Inf. Control 2015, 44, 263–269. [Google Scholar]
- He, W.; Ma, H.Y.; Zhang, Y.D.; Wang, S.; Dou, J.M. The State of Charge Estimation of Lithium-ion Batteries Using an Improved Extreme Learning Machine Approach. In Proceedings of the 34th Chinese Control and Decision Conference, Hefei, China, 15–17 August 2022; Volume 10, p. 5. [Google Scholar]
- Zhao, X.; Qian, X.; Xuan, D.; Jung, S. State of charge estimation of lithium-ionbattery based on multi-input extreme learning machine using online model parameter identification. J. Energy Storage 2022, 56, 105796. [Google Scholar] [CrossRef]
- Vedhanayaki, S.; Indragandhi, V. A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles. J. Energy Storage 2023, 72, 108777. [Google Scholar]
- Wang, C.; Yang, M.J.; Wang, X.; Xiong, Z.H.; Qian, F.; Deng, C.J.; Yu, C.; Zhang, Z.H.; Guo, X.F. A review of battery SOC estimation based on equivalent circuit models. J. Energy Storage 2025, 110, 115346. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, K.; Choudhury, U.; Yadav, A.K.; Ahmad, A.; Surender, K. Applications of artificial intelligence and cell balancing techniques for battery management system (BMS) in electric vehicles: A comprehensive review. Process Saf. Environ. Prot. 2024, 191, 2247–2265. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles—Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- NIO Technology (Anhui) Co., Ltd. A Battery System, SOC Estimation Method Therefor, and Computer Device and Medium. CN Patent CN112698223A, 8 January 2021. China National Intellectual Property Administration. [Google Scholar]
- Guangzhou XPeng Motors Technology Co., Ltd. Method, Device, Vehicle and Storage Medium for Calculating Battery State of Charge. CN Patent CN115616409A, 31 August 2022. China National Intellectual Property Administration. [Google Scholar]
- BYD Company Limited. SOC Estimation Method, System, Vehicle and Medium for Power Battery. CN Patent CN116413613A, 30 December 2021. China National Intellectual Property Administration. [Google Scholar]
- Contemporary Amperex Technology Co., Limited. SOC Estimation Method and Device for Lithium Iron Phosphate Batteries. CN Patent CN118818302A, 19 April 2023. China National Intellectual Property Administration. [Google Scholar]
- Chery Automobile Co., Ltd. Method, Device, Storage Medium and Equipment for Estimating Battery SOC Value. CN Patent CN118914888A, 18 July 2024. China National Intellectual Property Administration. [Google Scholar]
- Volkswagen, A.G. Method and Device for Determining the Remaining Capacity of a Battery. EP Patent EP3770621B1, 2 June 2020. European Patent Office. [Google Scholar]
- Toyota Motor Corporation. Battery System and Method for Estimating SOC of Secondary Battery. JP Application JP2019022416A, 12 February 2019. Japan Patent Office. [Google Scholar]
- Honda Motor Co., Ltd. State-of-Charge Estimation Method. U.S. Patent Application US2024142525A1, Application No. US18/495768, 27 October 2023. United States Patent Trademark Office. [Google Scholar]
- Audi, A.G. Method for Determining a State of Charge, Measuring Device, and Motor Vehicle. DE Patent Application DE102021115791A1, 18 June 2021. German Patent and Trade Mark Office (DPMA). [Google Scholar]
- Volvo Truck Corp. Device and Method for Enabling SOC Estimation in Electrical Energy Storage System of Hybrid Electric Vehicle. EP Application EP4005853A1, 24 November 2021. European Patent Office. [Google Scholar]




| Model | Equivalent Circuit | Advantages | Limitations |
|---|---|---|---|
| Voltage Source Model [48] (VSM) |  | 1. Simple structure 2. Fast calculation | 1. Oversimplifies 2. High estimation errors |
| Internal Resistance Model [49] (Rint Model) | 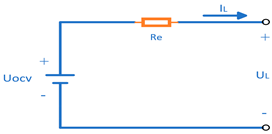 | 1. Simple structure 2. Easy parameter identification | 1. Fails to capture dynamic voltage behavior |
| Thevenin Equivalent Circuit Model [50,51] (TECM) | 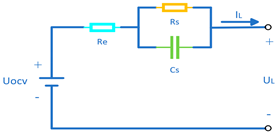 | 1. Accounts for polarization effects 2. Low computation | 1. Ignores distributed impedance characteristics |
| Partnership for a New Generation of Vehicles Model [52,53] (PNGV Model) | 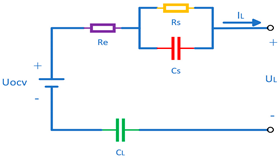 | 1. Accurate performance prediction across conditions | 1. Requires complex parameter optimization procedures |
| Dual Polarization Model [54,55] (DP Model) | 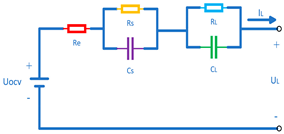 | 1. High simulation accuracy 2. Precise dynamic behavior modeling | 1. Assumes linear voltage–SOC relationship 2. Sensitive to variations in temperature and aging |
| n-th Order Resistor-Capacitor Network Model [56] (n-th RC Model) | 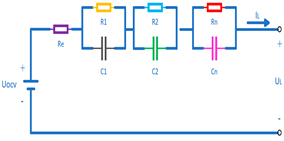 | 1. High fidelity 2. Multi-timescale dynamics | 1. Complex parameter identification 2. Significant computational load |
| Generalized Nonlinear Model [57,58] (GNL Model) | 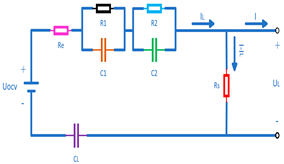 | 1. Incorporates multi-physics nonlinearities | 1. Challenges in parameter estimation and model resolution |
| Classification | Advantages | Disadvantages |
|---|---|---|
| BP [83] | 1. Simple structure, easy to comprehend 2. Relatively fast training (especially for small datasets) | 1. Cannot process time-series data 2. High computational cost for complex tasks |
| Hopfield [84] | 1. Solves optimization problems and associative memory 2. Energy function enables stability analysis | 1. Limited storage capacity 2. Prone to local minima in large-scale systems |
| CNN [85] | 1. Parameter sharing reduces complexity 2. Translation invariance ensures robustness | 1. Requires massive training data (typically >104 samples) 2. Black-box decision mechanism |
| RNN [86] | 1. Sequential data processing capability 2. Memory retention for temporal patterns | 1. Training instability (vanishing/exploding gradients) 2. Limited long-term dependency capture |
| LSTM [87] | 1. Gradient flow control prevents vanishing gradients 2. Long-term dependency learning (>1000 steps) | 1. Complex gating mechanisms (4× parameters vs. RNN) 2. High risk of overfitting |
| GRU [88] | 1. Simplified architecture (2 gates vs. LSTM’s 3) 2. Efficient short-term dependency modeling | 1. Compromised long-term memory (<500 steps) 2. Residual gradient issues in deep networks |
| Method Category | Accuracy | Real-Time Capability | Cost | Robustness | Typical Application Scenarios | Core Limitations |
|---|---|---|---|---|---|---|
| Experimental-based [106] | 4 | 2 | 3 | 4 | Laboratory parameter calibration, offline validation | Relies on offline testing, unable to track dynamically in real time |
| Model-based [107] | 3 | 5 | 4 | 3 | Real-time control in BMS, dynamic condition response | Ignores battery nonlinearities and aging dynamics |
| Data-driven [108,109] | 5 | 4 | 2 | 5 | Adaptation in complex environments, multi-factor coupling scenarios | Strong dependence on data quality, high training costs |
| Automaker | Algorithm | Key Technical Features | Advantages | Disadvantages | Vehicle Models |
|---|---|---|---|---|---|
| NIO [110] | Adaptive EKF | Real-time noise covariance updates | Superior Dynamic performance | Complex parameter tuning | ES8, ET7 |
| XPeng [111] | Particle Filter | Monte Carlo probability simulation | Extreme-condition accuracy | High computational load | G9, P7 |
| BYD [112] | Dual Kalman Filter | Stepwise SOC/SOH estimation | Robust in complex conditions | Needs high-end BMS chips | Han EV, Tang DM-i |
| CATL [113] | Coulomb + OCV | OCV error segmentation correction | Low cost | Low-temperature recalibration | NIO ES6 |
| Chery [114] | ECM + Online Parameter Identification | 1st-order RC model with temperature compensation | Low hardware cost | High-rate parameter lag | Tiggo e, Arrizo 5e |
| Volkswagen [115] | Fuzzy Logic + MPC | Fuzzy rules + multi-objective optimization | Effective for aged batteries | Extensive rule base calibration | ID.4, ID.6 |
| Toyota [116] | ECM + Sliding Window | 2nd-order RC error suppression | Long-term consistency | Slow response | Prius, bZ4X |
| Honda [117] | Regression- Based SOC Estimation | Pseudo-SOC value acquisition, correlation analysis | Improved accuracy post -depolarization | Complexity in correlation classification | Honda e |
| Audi [118] | Electrochemical + Observer | Physicochemical modeling with observer | Anti-aging precision | High ECU requirements | e-tron series |
| Volvo [119] | Voltage Level-Based SOC Estimation | Voltage level detection | Efficient SOC estimation in hybrid systems | Dependency on voltage levels | XC40 Recharge, C40 Recharge |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jia, H.; Xiao, P.; Jiang, H.; Chen, Y. Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles. Energies 2025, 18, 2144. https://doi.org/10.3390/en18092144
Li H, Jia H, Xiao P, Jiang H, Chen Y. Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles. Energies. 2025; 18(9):2144. https://doi.org/10.3390/en18092144
Chicago/Turabian StyleLi, Hongzhao, Hongsheng Jia, Ping Xiao, Haojie Jiang, and Yang Chen. 2025. "Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles" Energies 18, no. 9: 2144. https://doi.org/10.3390/en18092144
APA StyleLi, H., Jia, H., Xiao, P., Jiang, H., & Chen, Y. (2025). Research Progress on State of Charge Estimation Methods for Power Batteries in New Energy Intelligent Connected Vehicles. Energies, 18(9), 2144. https://doi.org/10.3390/en18092144





