Research on the Frequency Stability Analysis of Grid-Connected Double-Fed Induction Generator Systems
Abstract
1. Introduction
2. Mechanism Analysis of the Influence of Wind Power Grid Connection on Frequency Stability
2.1. Influence of Wind Power Grid Connection on the Level of System Inertia
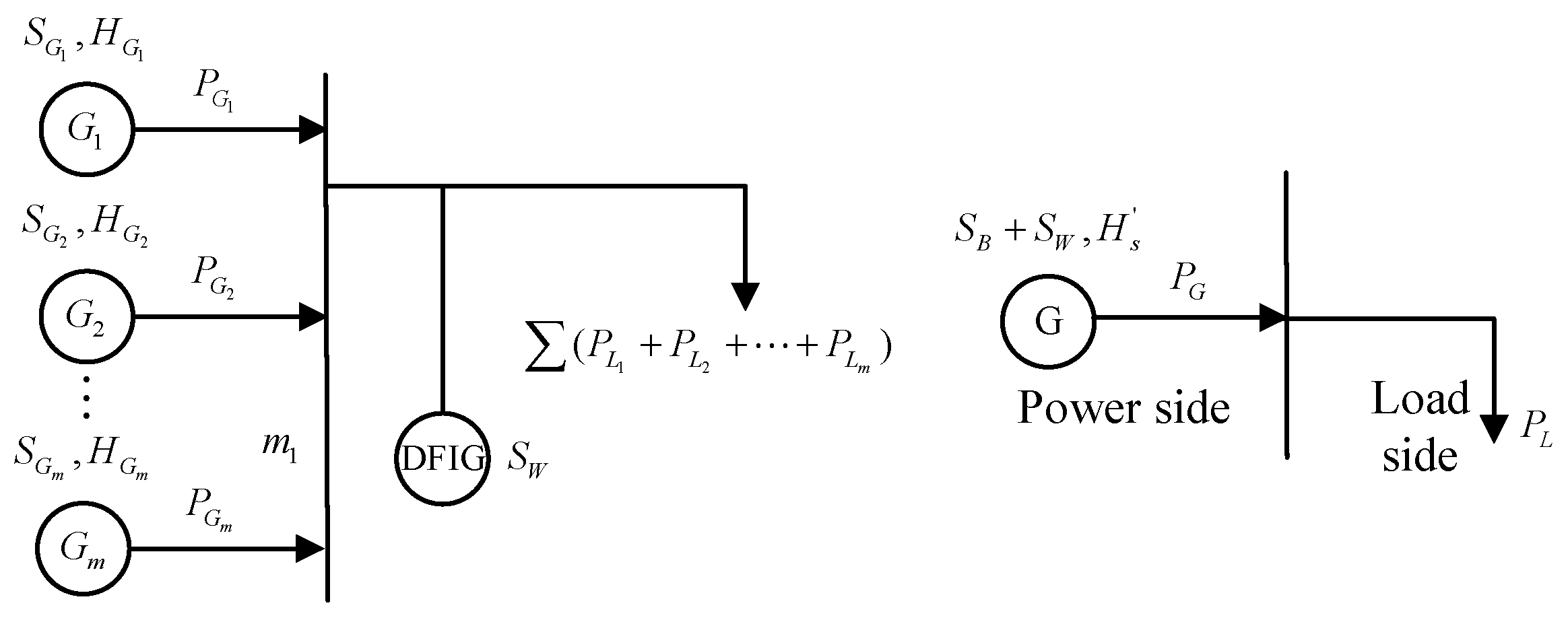
2.1.1. The Grid Connection of Wind Power Only Changes the Output of the Synchronous Machine
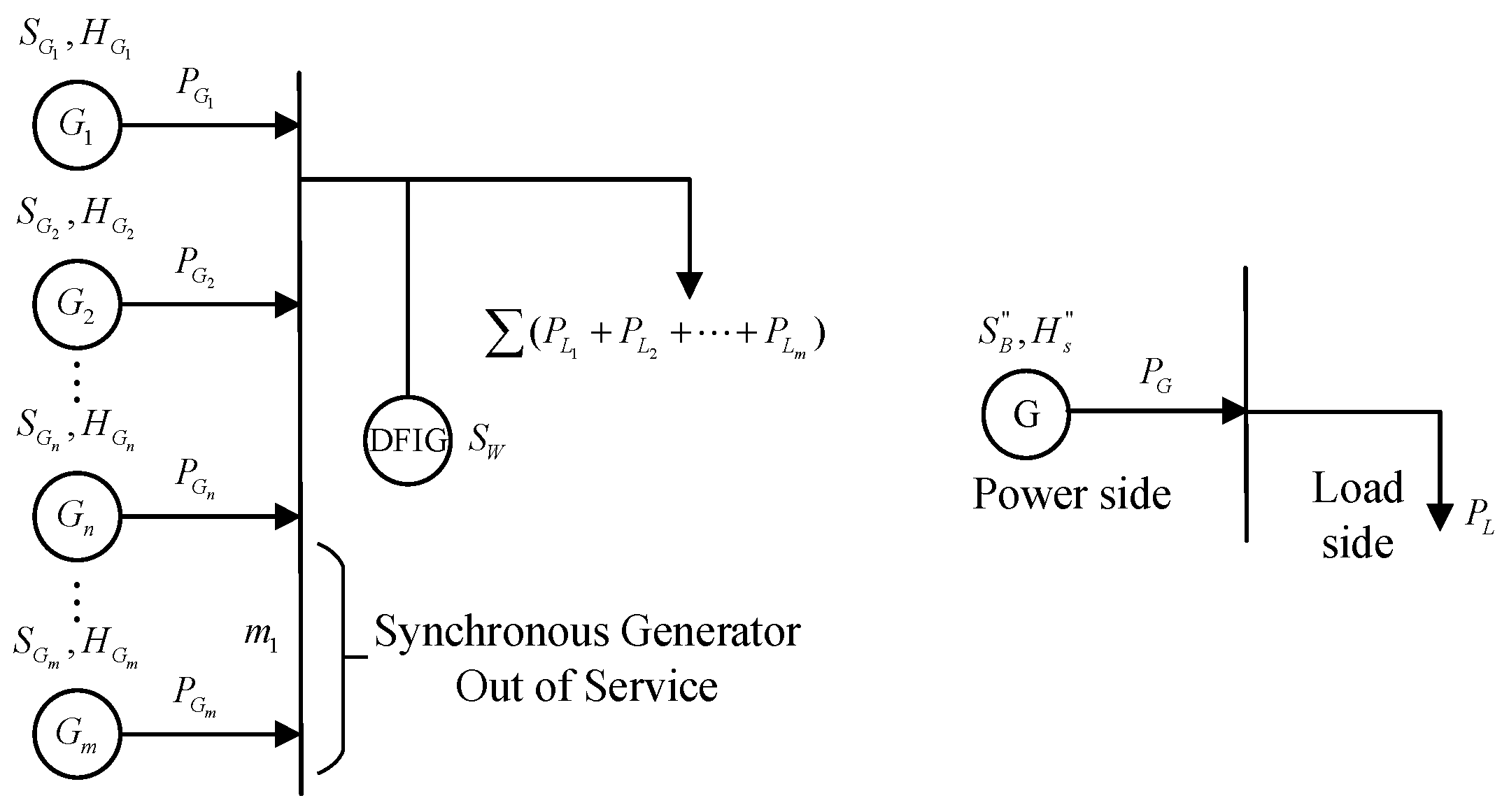
2.1.2. After the Wind Power Is Connected to the Grid, Some Synchronous Machines Are Out of Operation
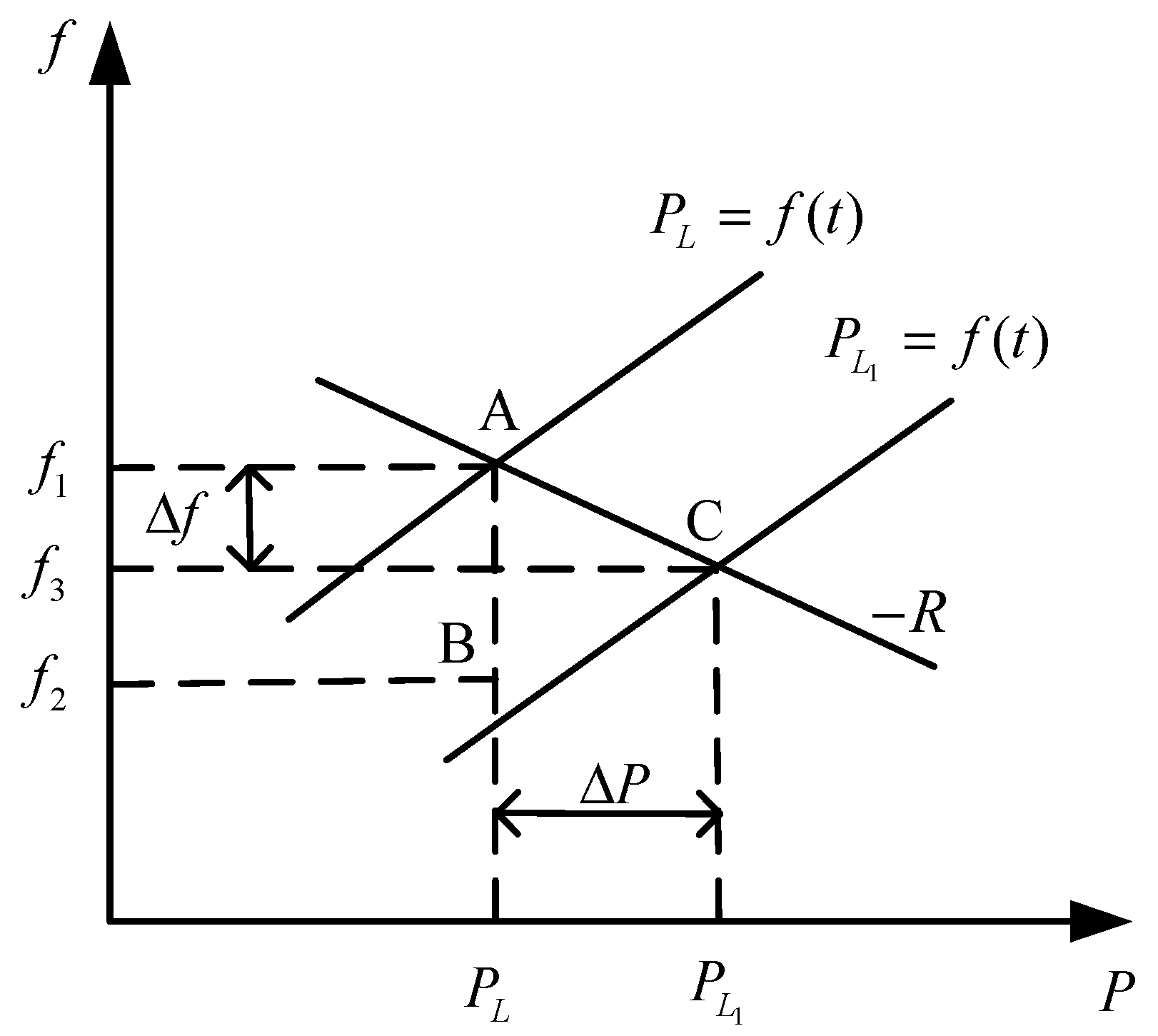
2.2. Influence of Wind Power Access on the Static Frequency Characteristics of the System
3. Quantitative Analysis of the Impact of Wind Power Grid Integration on Frequency Stability
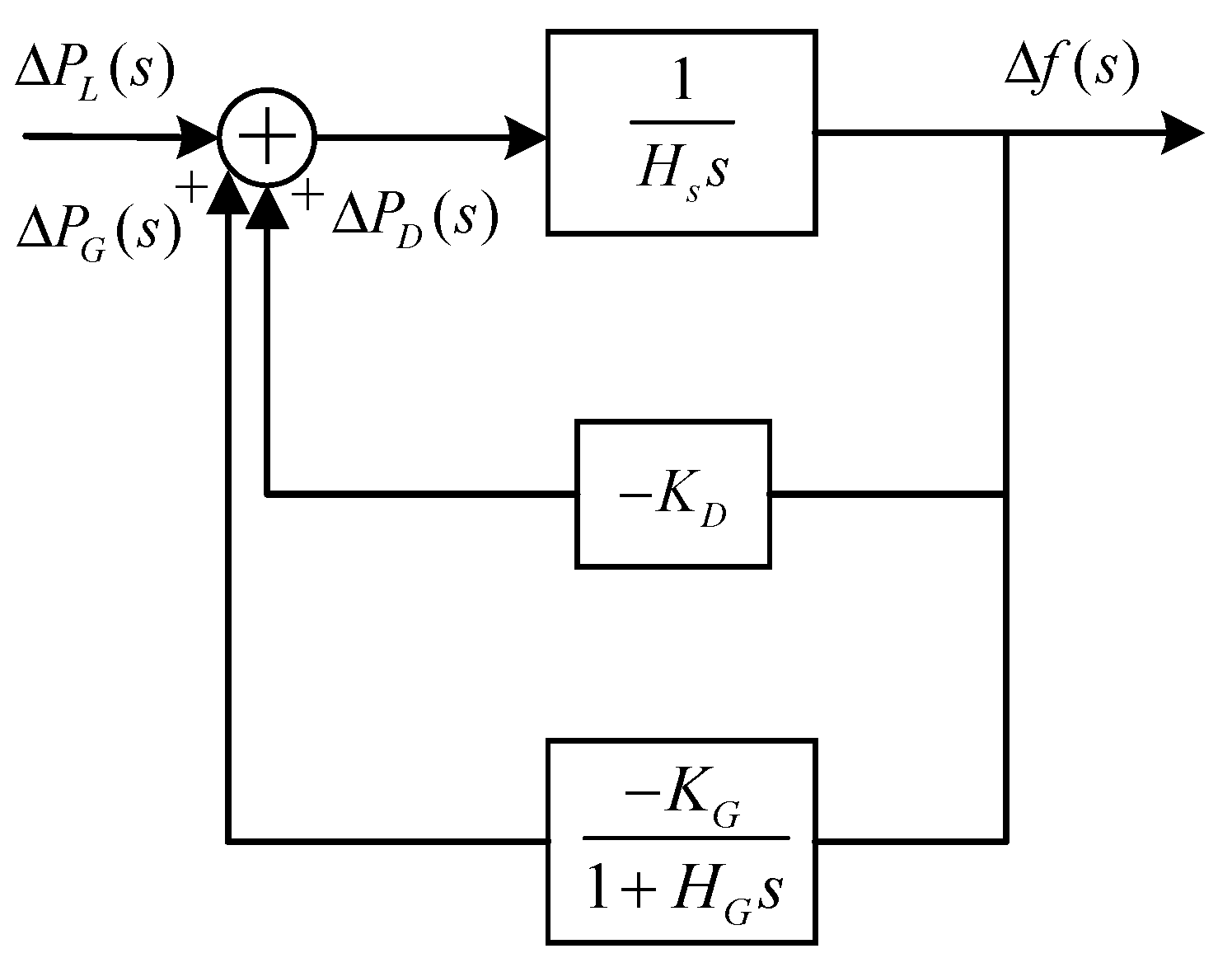
3.1. Frequency Characteristic Model of the Wind Power System
3.2. Derivation of the Quantitative Relationship Between Wind Power Penetration and System Frequency Stability Index
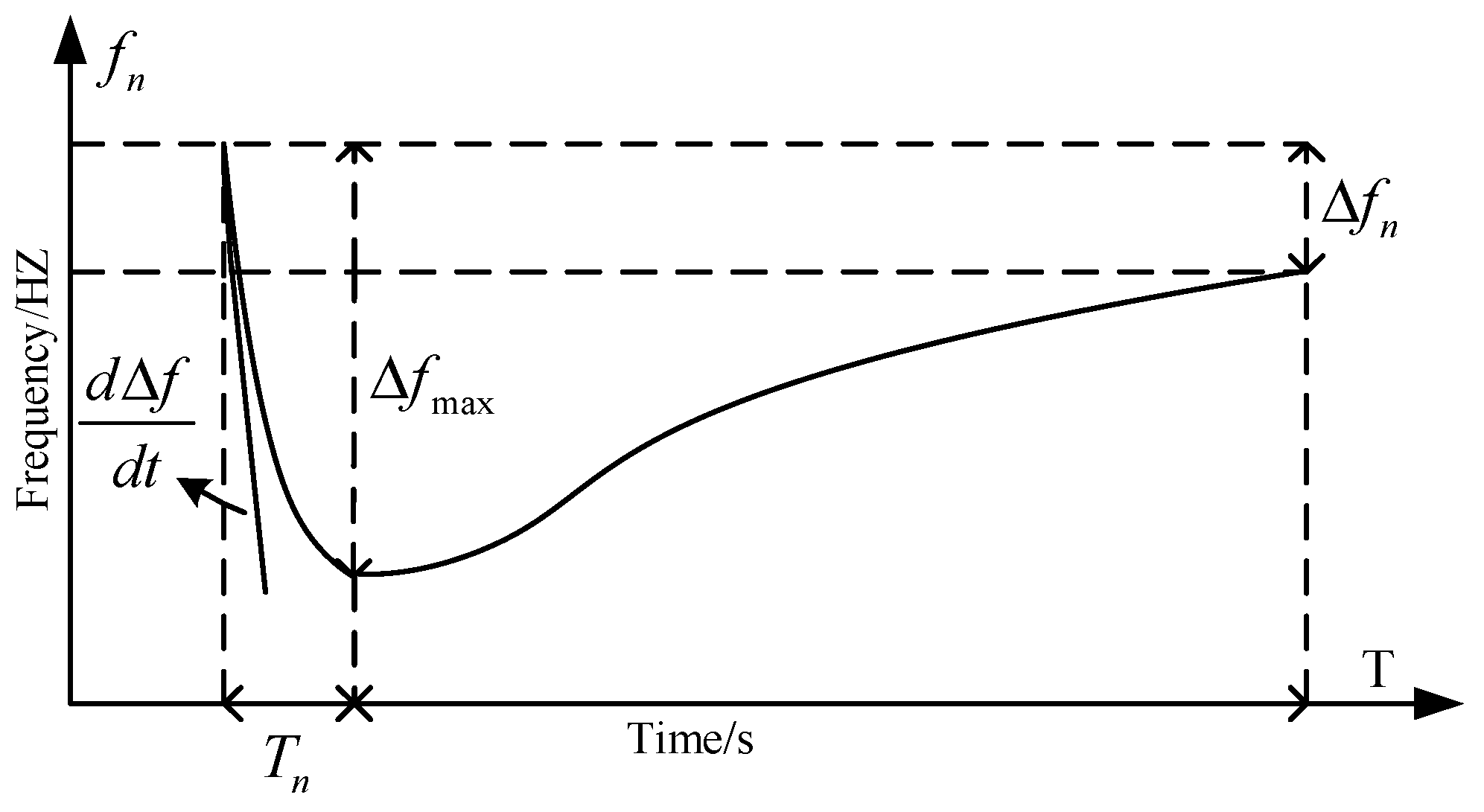
3.2.1. Steady-State Frequency Deviation Δfn
3.2.2. Rate of Change in Frequency dΔf/dt
3.2.3. Time Tn to Reach the Lowest Point of Frequency
3.2.4. Maximum Frequency Deviation Δfmax
4. Evaluation of Wind Power Grid-Connected Capabilities Considering Frequency Stability Constraints
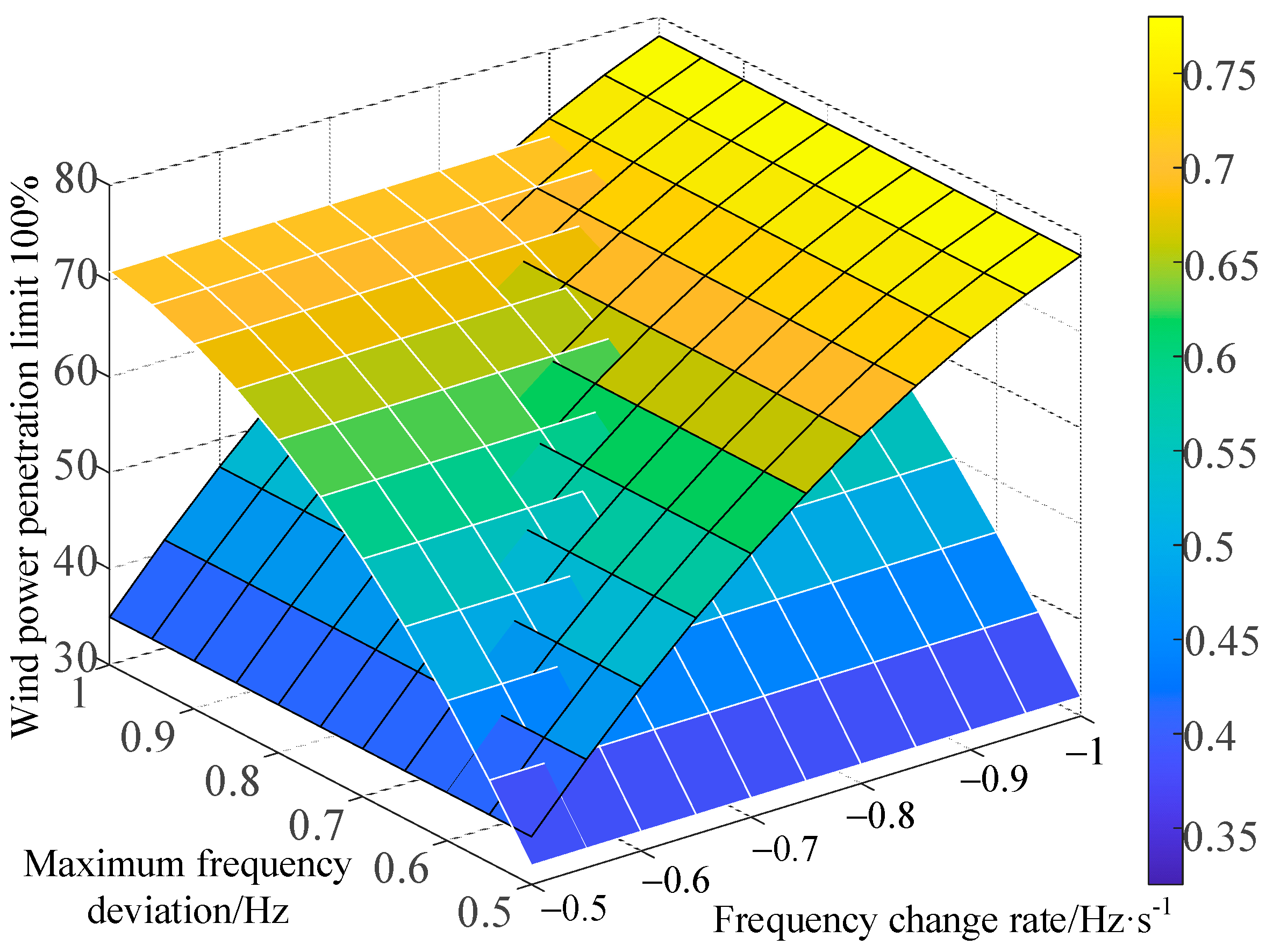
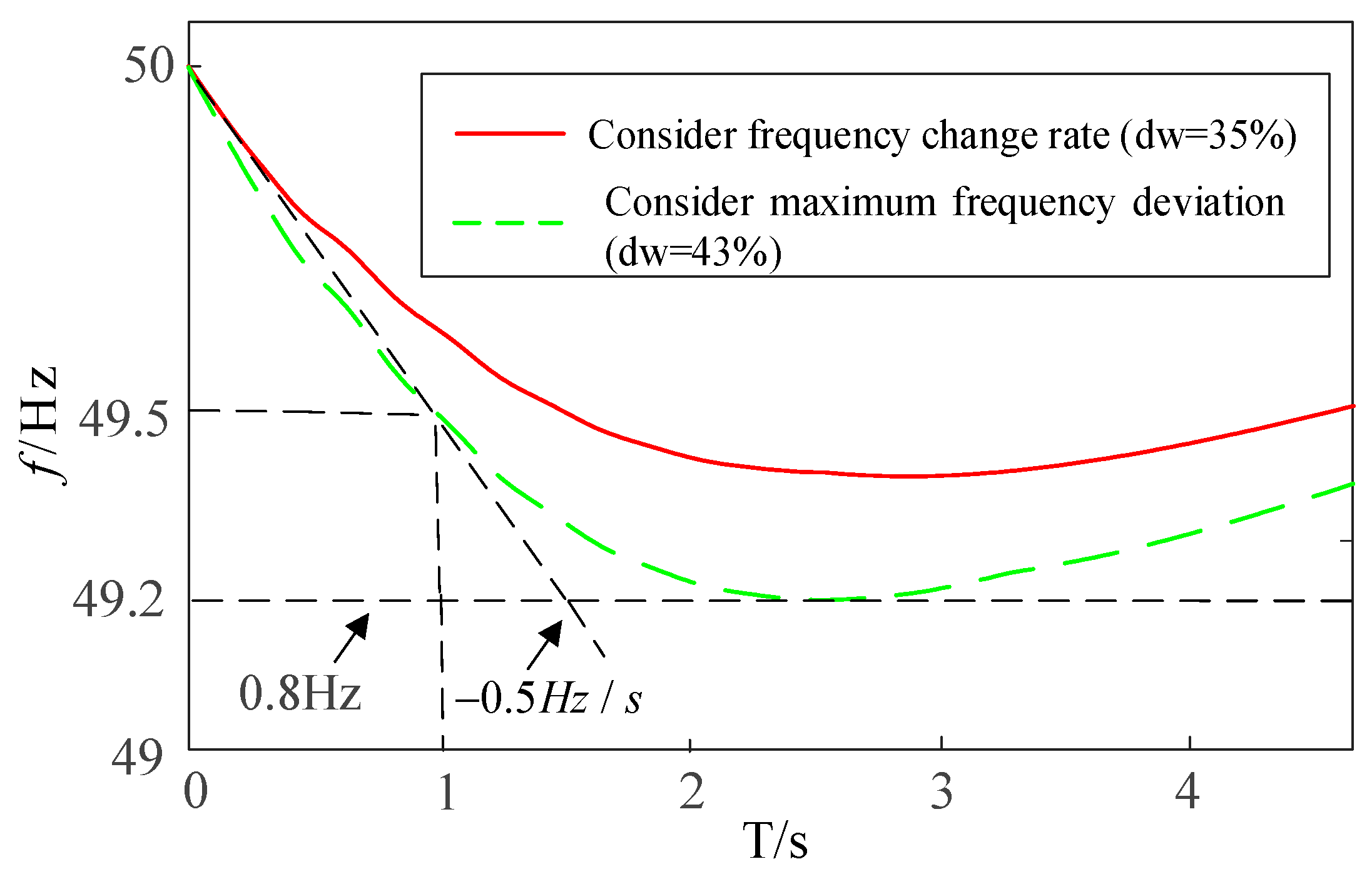
4.1. Calculation of Wind Power Penetration Limit Considering Maximum Frequency Deviation Constraint
4.2. Calculation of the Wind Power Penetration Limit Considering the Frequency Change Rate Constraint
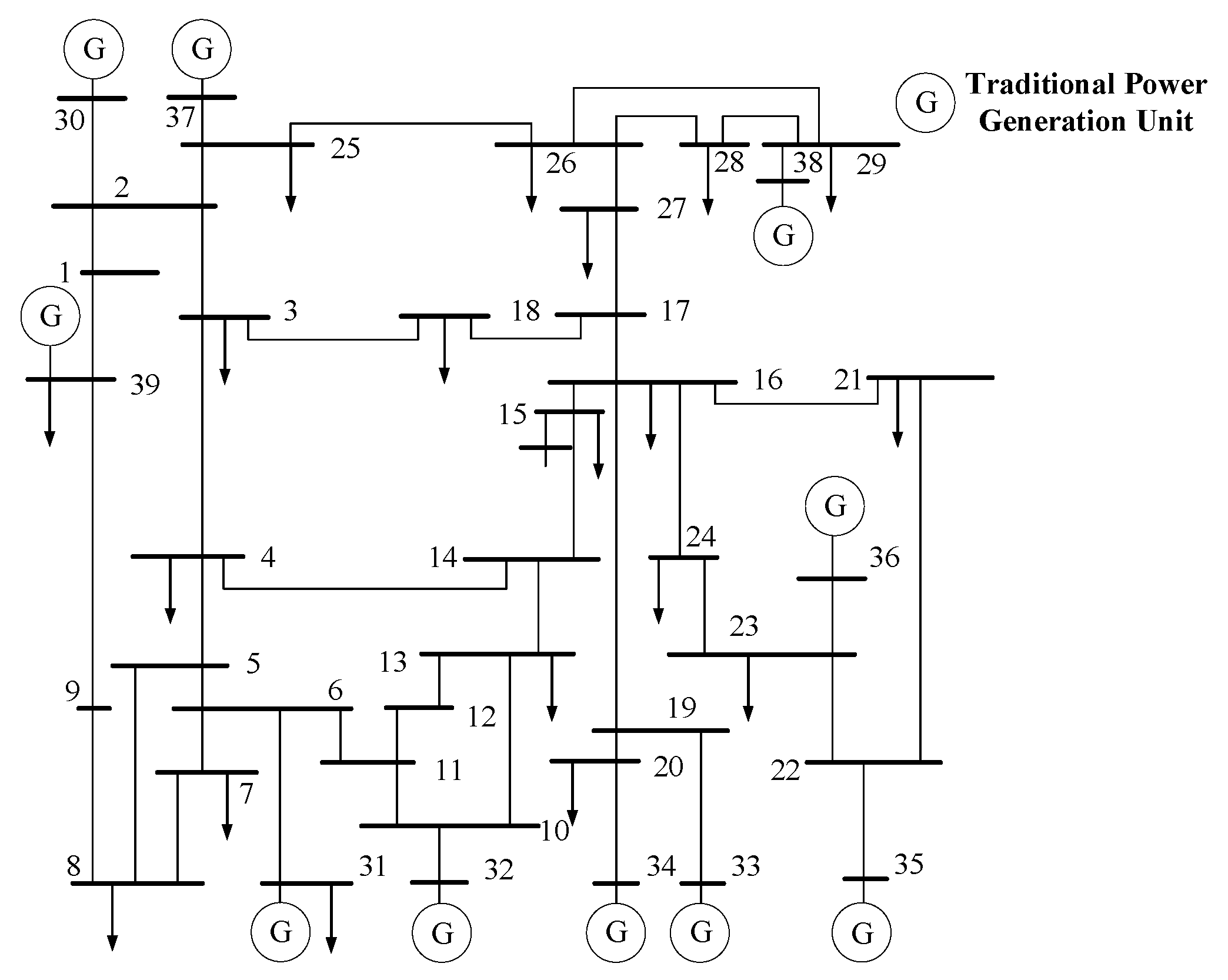
5. Case Analysis
5.1. Simulation Analysis of the Mechanism of the Influence of Wind Power Grid Connection on System Frequency Stability
- (1)
- Wind power grid connection only changes the output of synchronous machines
- (2)
- Replacement of synchronous machines with equal capacity for wind turbines
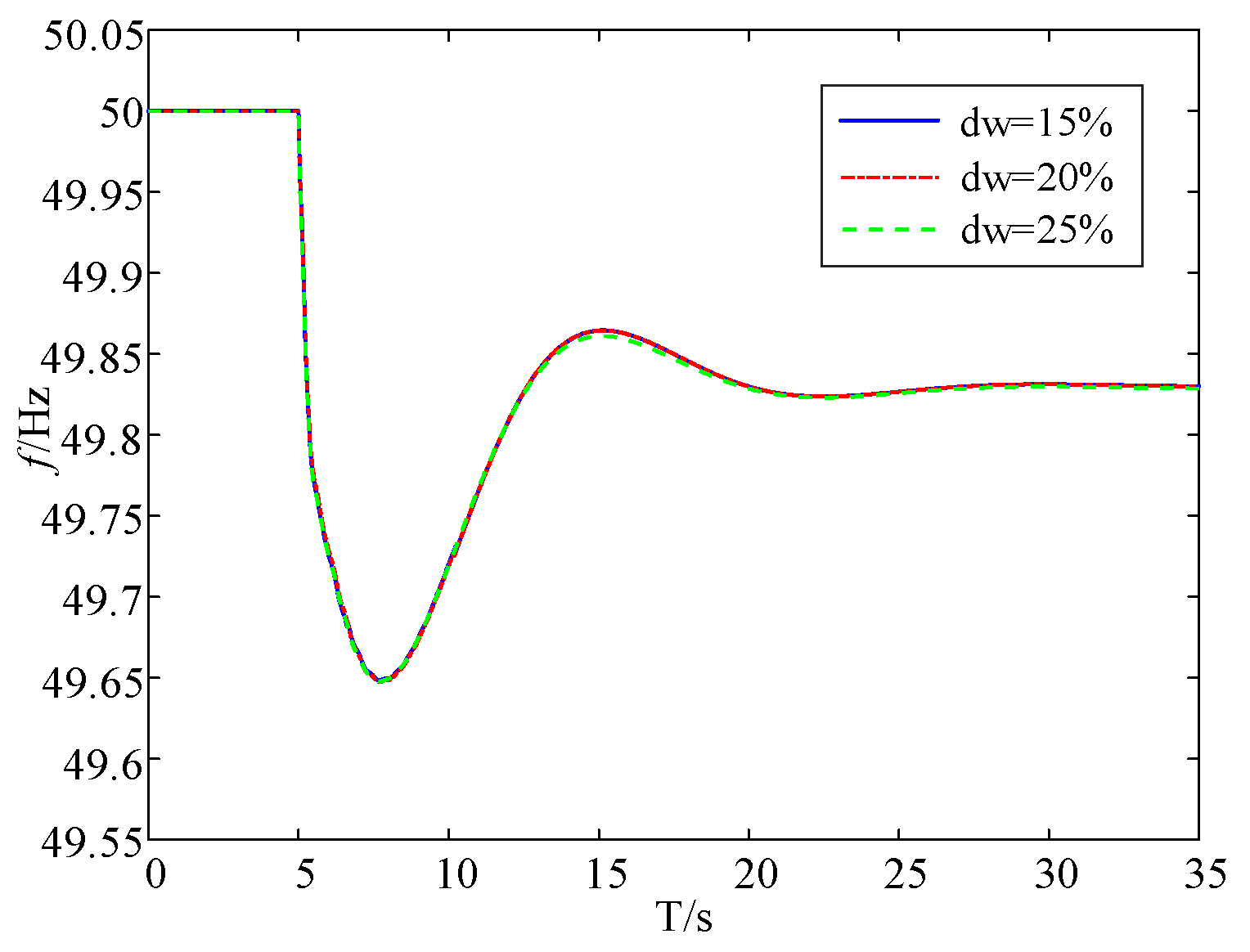
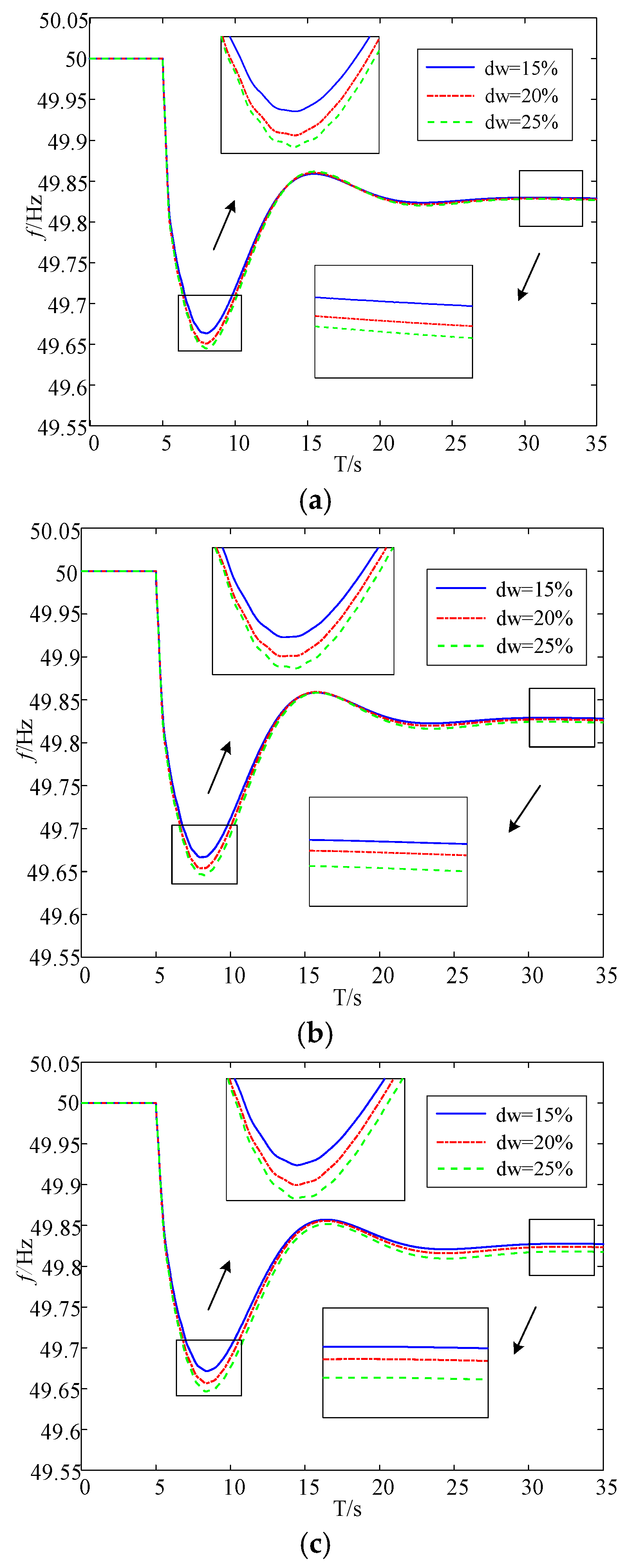
5.2. Validation of the Validity of the Quantitative Relationship Between Frequency Stability Indicators and Wind Power Penetration
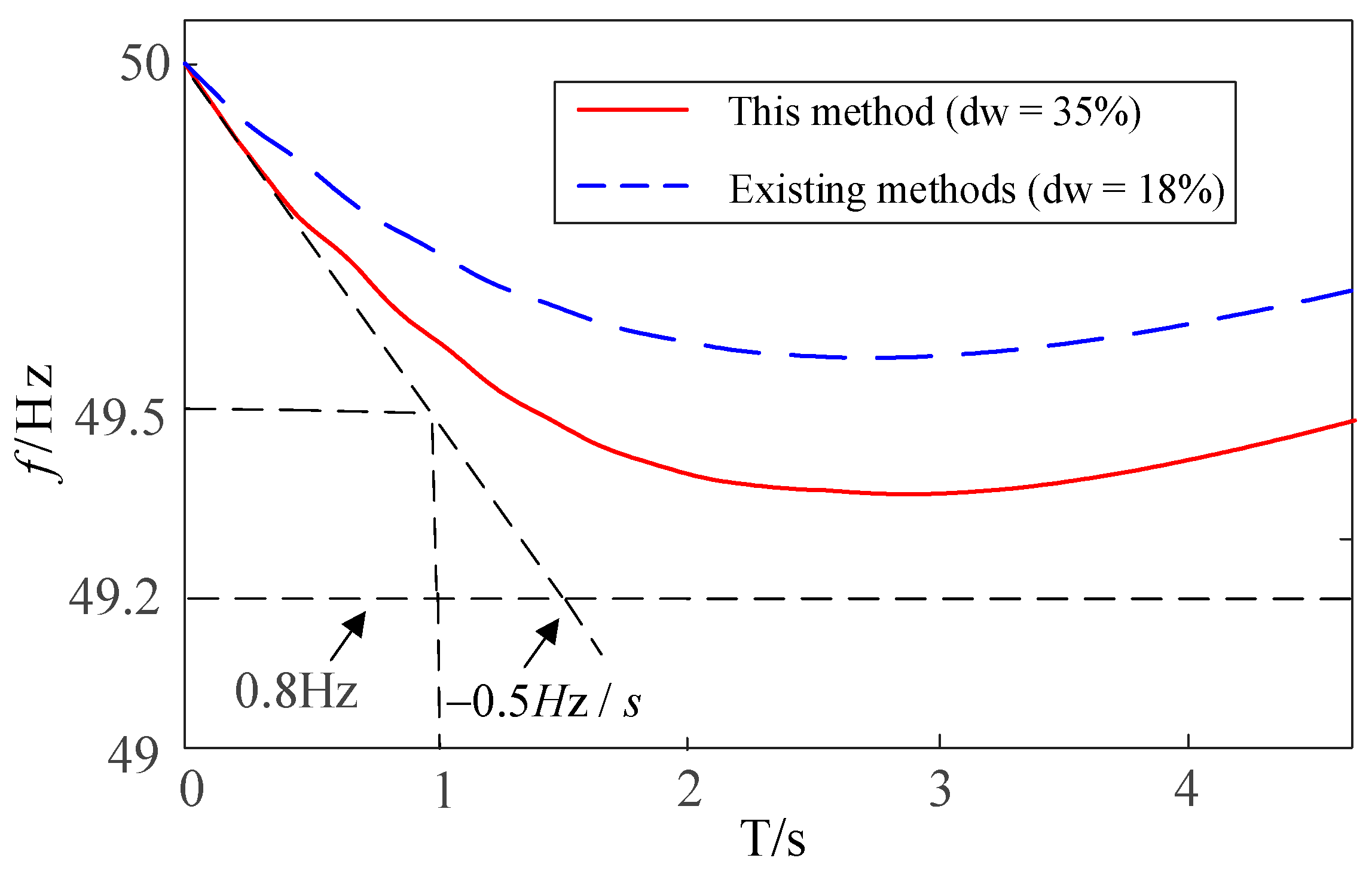
5.3. Calculation of Maximum Wind Power Penetration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Chen, M.; Zhong, H.; Ma, Z.; Liu, D.; He, G. A Review of Long-term Planning of New Power Systems with Large Share of Renewable Energy. Proc. CSEE 2023, 43, 555–580. [Google Scholar]
- Zhuo, Z.; Zhang, N.; Xie, X.; Li, H.; Kang, C. Key Technologies and Developing Challenges of Power System with High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2021, 45, 171–191. [Google Scholar]
- Ren, J.; Cheng, D.Z.; Song, Y.T. Influence of large-scale wind power integration on system frequency. Chin. J. Power Sources 2016, 40, 1491–1494. [Google Scholar]
- Ma, Y.D.; Liu, F.J.; Liu, P.L.; Yong, S.H.; Chen, J.; Liu, C.H.; Zhou, X.; Liu, Y.S. Analysis of the frequency characteristics of large-scale wind power grid-connected system considering under frequency load shedding response. Renew. Energy Resour. 2023, 41, 1352–1359. [Google Scholar]
- Cao, N.; Li, Z.P.; Yu, Q. Analysis on the Impact of LVRT of DFIG on Power Grid Frequency. Water Resour. Power 2021, 39, 161–164+145. [Google Scholar]
- Zhang, Q.W.; Wen, Y.F.; He, Y.; You, G.Z.; Li, H.X. Estimation of Medium-and Long-term Inertia Level Tendency for Power System and Its Application. Autom. Electr. Power Syst. 2024, 48, 54–65. [Google Scholar]
- Liu, Q.Y.; Yu, Z.H.; Zhang, L.L.; Lv, Y.; Wang, B.; Liu, T.; Xu, X. Online Frequency Support Capacity Assessment of Power Grid Based on Inertia Ratio. Power Syst. Technol. 2023, 47, 493–502. [Google Scholar]
- Guo, X.L.; Bi, T.S.; Liu, F.L.; Xu, G.Y.; Zhang, F.; Wang, H. Estimating maximum penetration level of renewable energy based on frequency stability constrains in networks with high-penetration wind and photovoltaic energy. Renew. Energy Resour. 2020, 38, 84–90. [Google Scholar]
- Hua, Y.Y. Assessment and Improvement of Wind Power Penetration Limits Considering Low Voltage Ride-Through Characteristics and Frequency Stability Constraints. Ph.D. Graduation Thesis, Zhejiang University, Hangzhou, China, 2023. [Google Scholar]
- Arani, M.; Mohamed, A. Analysis and mitigation of undesirable impacts of implementing frequency support controllers in wind power generation. IEEE Trans. Energy Convers. 2016, 31, 174–186. [Google Scholar] [CrossRef]
- Sun, H.D.; Wang, B.C.; Li, W.F.; Yang, C.; Wei, W.; Zhao, B. Research on Inertia System of Frequency Response for Power System with High Penetration Electronics. Proc. CSEE 2020, 40, 5179–5191. [Google Scholar]
- Saxena, A.; Shiva, C.K.; Shankar, R.; Vedik, B. Impacts of wind farms with multi-terminal HVDC system in frequency regulation using quasi-opposition pathfinder algorithm. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 1–13. [Google Scholar] [CrossRef]
- Liu, K.T.; Wang, X.R. A Wide-Area Measurement Data Based Method for Power System Dynamic Frequency Analysis. Power Syst. Technol. 2013, 37, 2201–2206. [Google Scholar]
- Li, S.C.; Tian, B.J.; Li, H.Z.; Luo, Y.; Huang, S.Y.; Xu, S.L. Method for limiting wind power output in time periods based on frequency safety constraints and a critical inertia calculation. Power Syst. Prot. Control 2022, 50, 60–71. [Google Scholar]
- Ju, P.; Zheng, Y.; Jin, Y.; Qin, C.; Jiang, Y.; Cao, L. Analytic assessment of the power system frequency security. IET Gener. Transm. Distrib. 2021, 15, 2215–2225. [Google Scholar] [CrossRef]
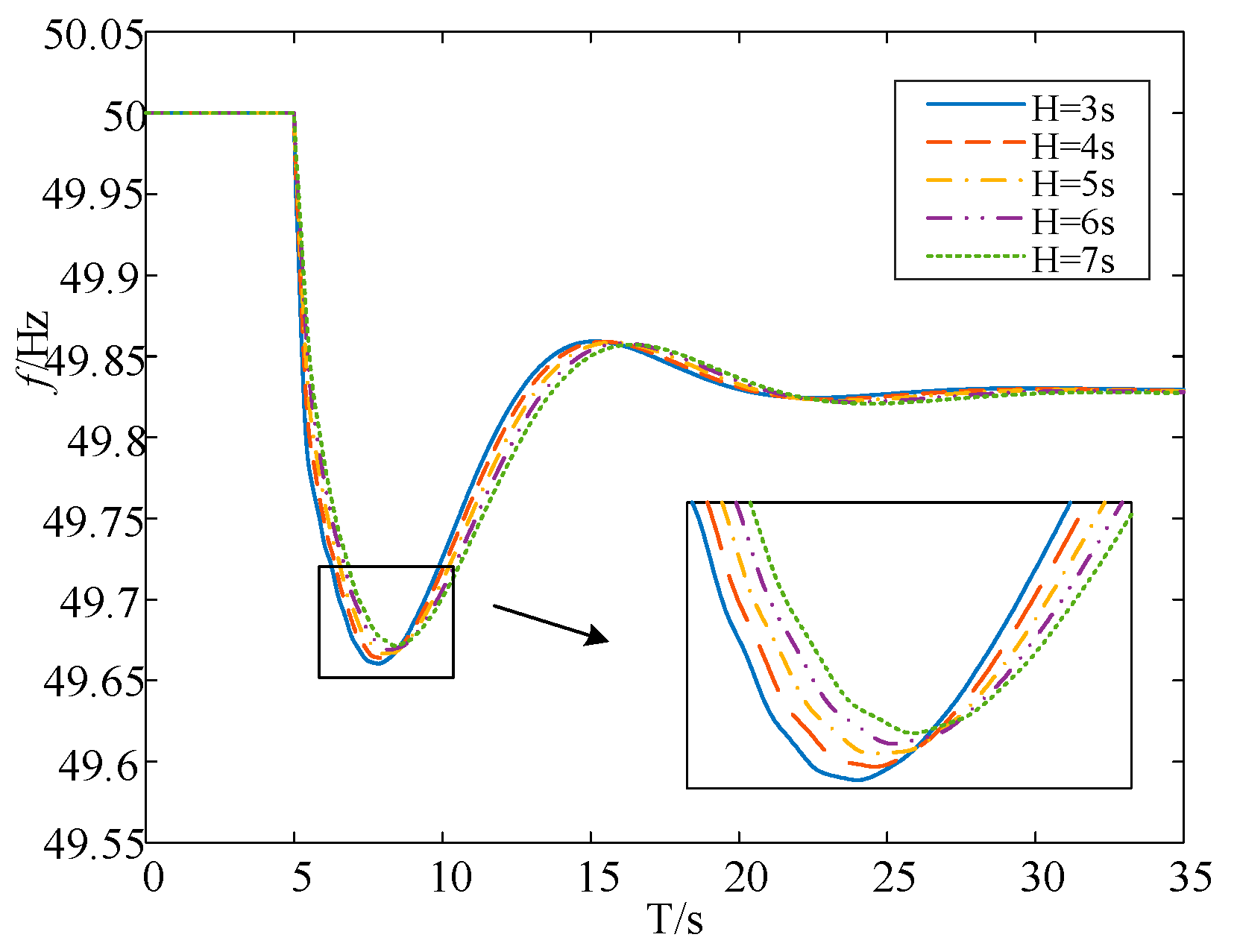
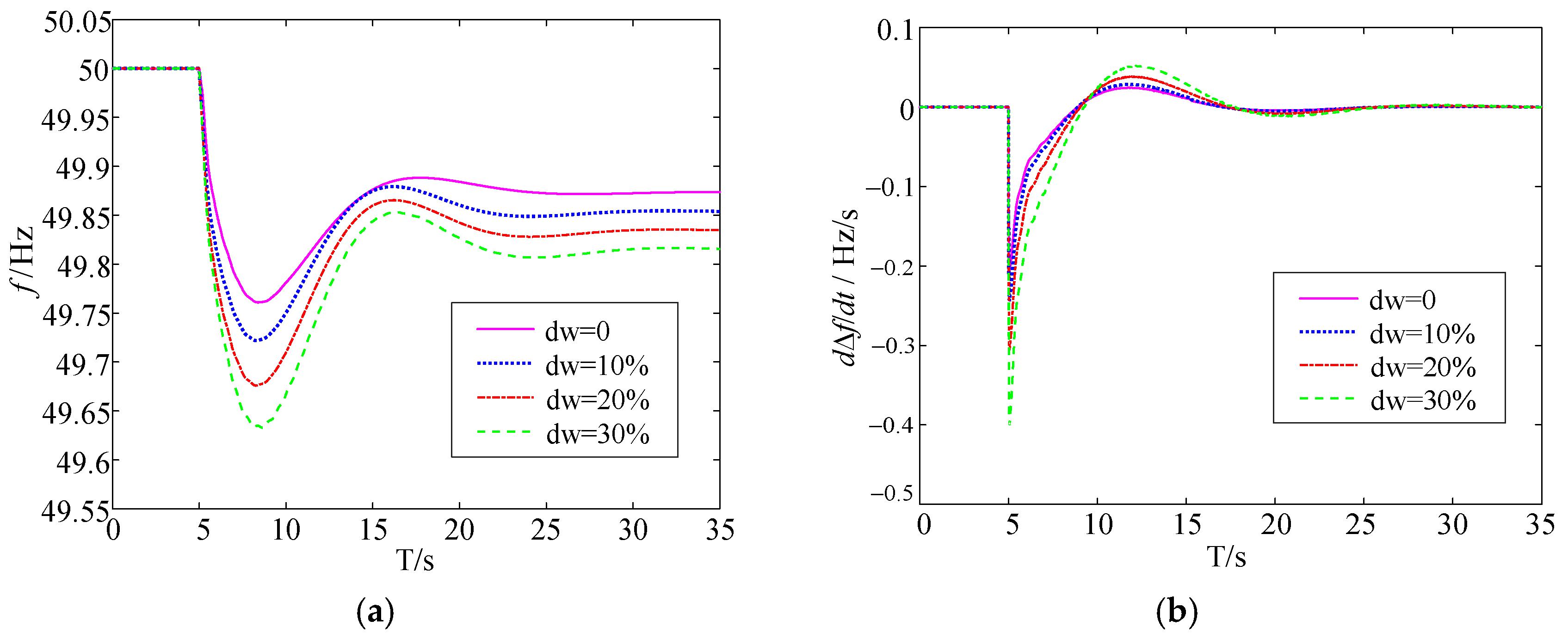
| Quantitative Indicators | No Wind and Electricity | 10% Penetration | 20% Penetration | 30% Penetration |
|---|---|---|---|---|
| dΔf/dt Influence degree | −0.206/−0.207 | −0.248/−0.244 | −0.309/−0.306 | −0.399/−0.394 |
| 0/0 | 20.4%/17.9% | 50.0%/47.9% | 93.7%/90.3% | |
| Tn Influence degree | 6.420/6.440 | 6.420/6.440 | 6.420/6.440 | 6.420/6.440 |
| 0/0 | 0/0 | 0/0 | 0/0 | |
| Δfmax Influence degree | 0.213/0.221 | 0.259/0.270 | 0.317/0.322 | 0.352/0.365 |
| 0/0 | 21.6%/22.2% | 48.8%/45.7% | 65.3%/65.1% | |
| Δfn Influence degree | 0.128/0.130 | 0.141/0.145 | 0.163/0.164 | 0.180/0.182 |
| 0/0 | 10.2%/11.5% | 27.3%/26.2% | 40.6%/40.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, P.; Sun, Y.; Yu, L.; Zhang, J.; Jiang, X.; Meng, G. Research on the Frequency Stability Analysis of Grid-Connected Double-Fed Induction Generator Systems. Energies 2025, 18, 2170. https://doi.org/10.3390/en18092170
Jia P, Sun Y, Yu L, Zhang J, Jiang X, Meng G. Research on the Frequency Stability Analysis of Grid-Connected Double-Fed Induction Generator Systems. Energies. 2025; 18(9):2170. https://doi.org/10.3390/en18092170
Chicago/Turabian StyleJia, Peng, Yun Sun, Linlin Yu, Jing Zhang, Xiaoliang Jiang, and Gaojun Meng. 2025. "Research on the Frequency Stability Analysis of Grid-Connected Double-Fed Induction Generator Systems" Energies 18, no. 9: 2170. https://doi.org/10.3390/en18092170
APA StyleJia, P., Sun, Y., Yu, L., Zhang, J., Jiang, X., & Meng, G. (2025). Research on the Frequency Stability Analysis of Grid-Connected Double-Fed Induction Generator Systems. Energies, 18(9), 2170. https://doi.org/10.3390/en18092170





