Internal Model Current Decoupling Control Strategy for Induction Motors
Abstract
1. Introduction
2. The Mathematical Model and Coupling Effect Analysis of the IM
2.1. Model of Induction Motor
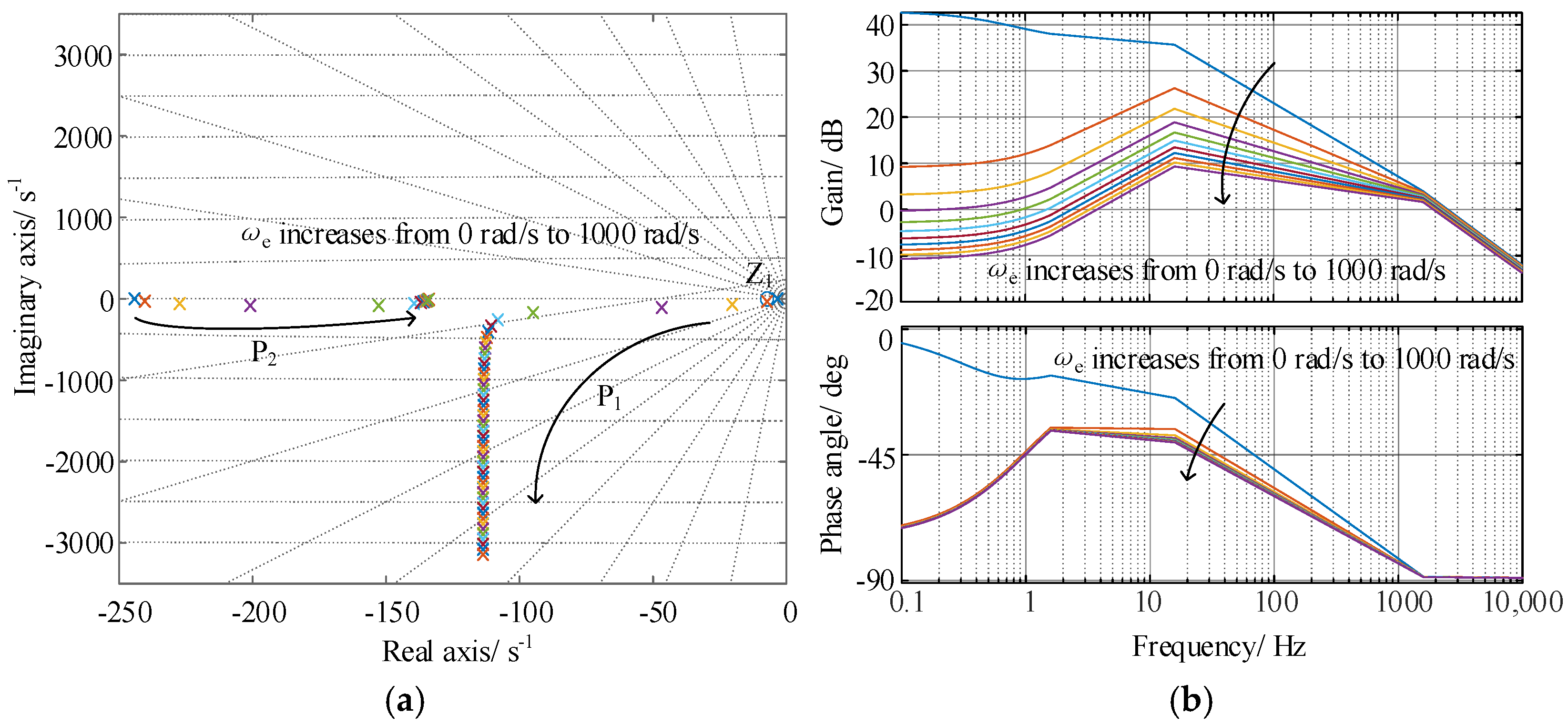
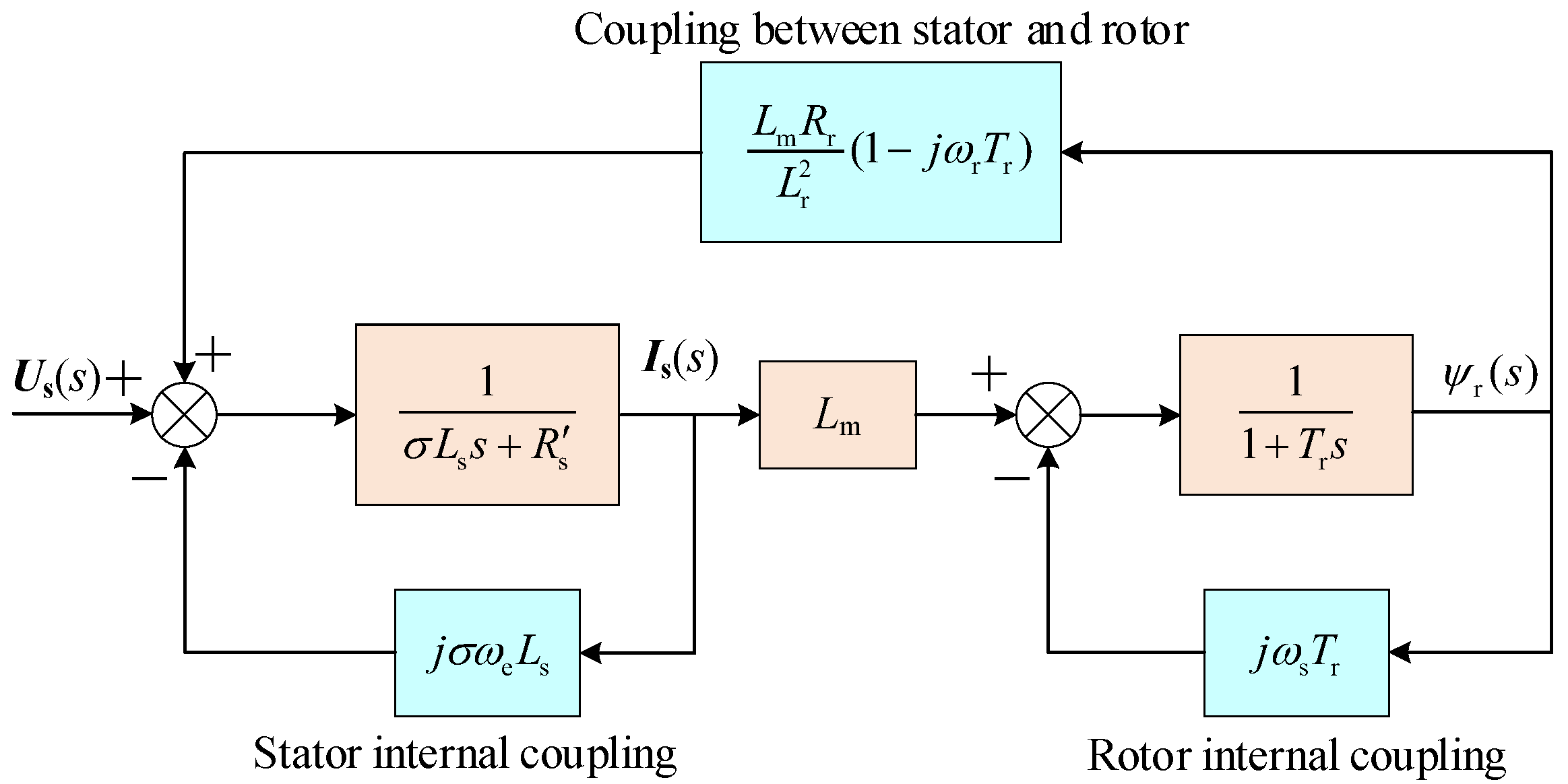
2.2. Coupling Effect Analysis
- (1)
- Stator internal coupling : This is generated by the rotating coordinate transformationl the coupling degree is directly proportional to the synchronous angular frequency ωe and the stator current Is(s). Under the condition of high speed and large current, this coupling term has a significant impact on system performance;
- (2)
- The coupling term between the stator and rotor : This term is directly proportional to the rotor angular frequency ωr, and the coupling between the stator and rotor increases as the speed increases. According to Equation (7), the rotor flux ψr(s) lags behind the stator current Is, and this part of the coupling component can be regarded as an external disturbance to the system, which is considered as electromotive force Es(s);
- (3)
- Rotor internal coupling : Its magnitude depends on the slip frequency ωs, and the rotor flux ψr(s), and is related to the rotor time constant Tr. ωs is usually small, so this term has little effect on the dynamic performance of the IM. When the motor operates with no load and zero speed, there is no internal coupling in the rotor.
3. Internal Model Current Decoupling Controller for IM
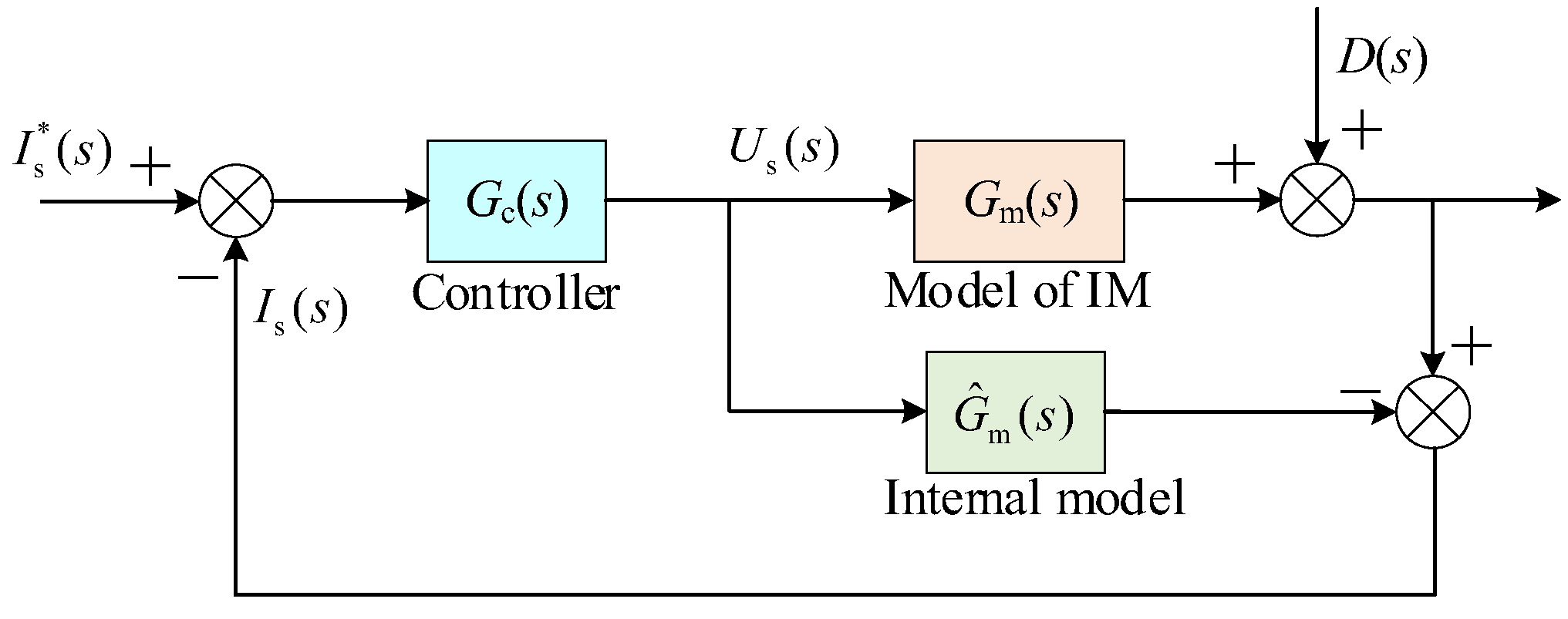
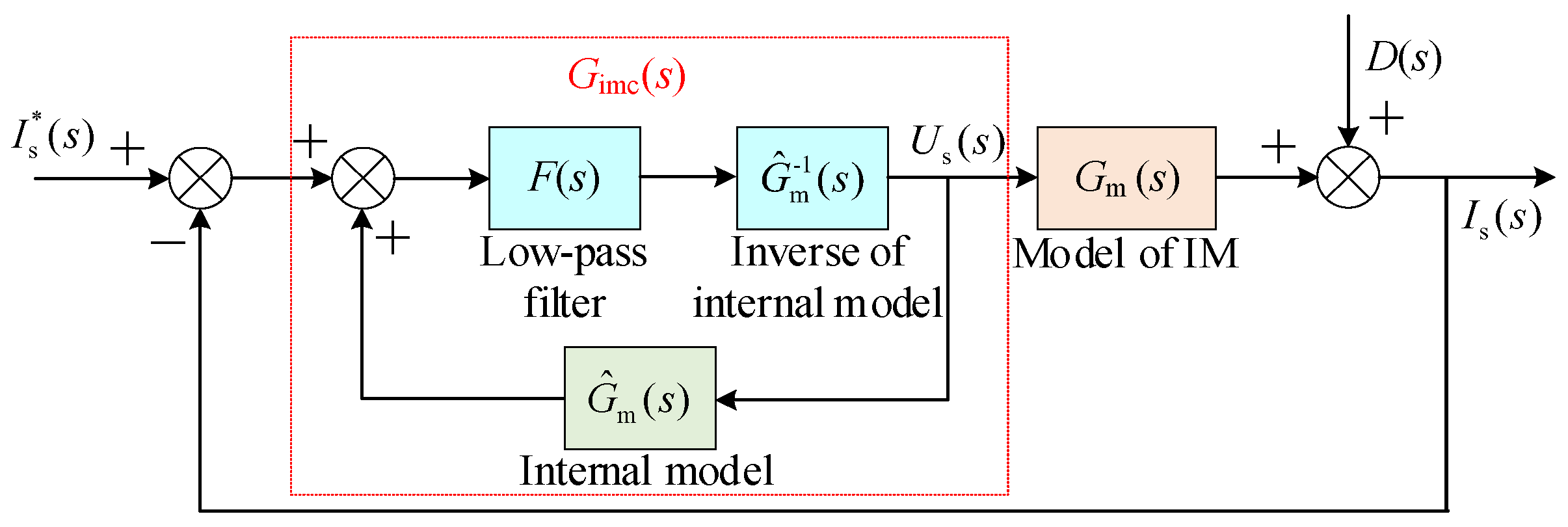
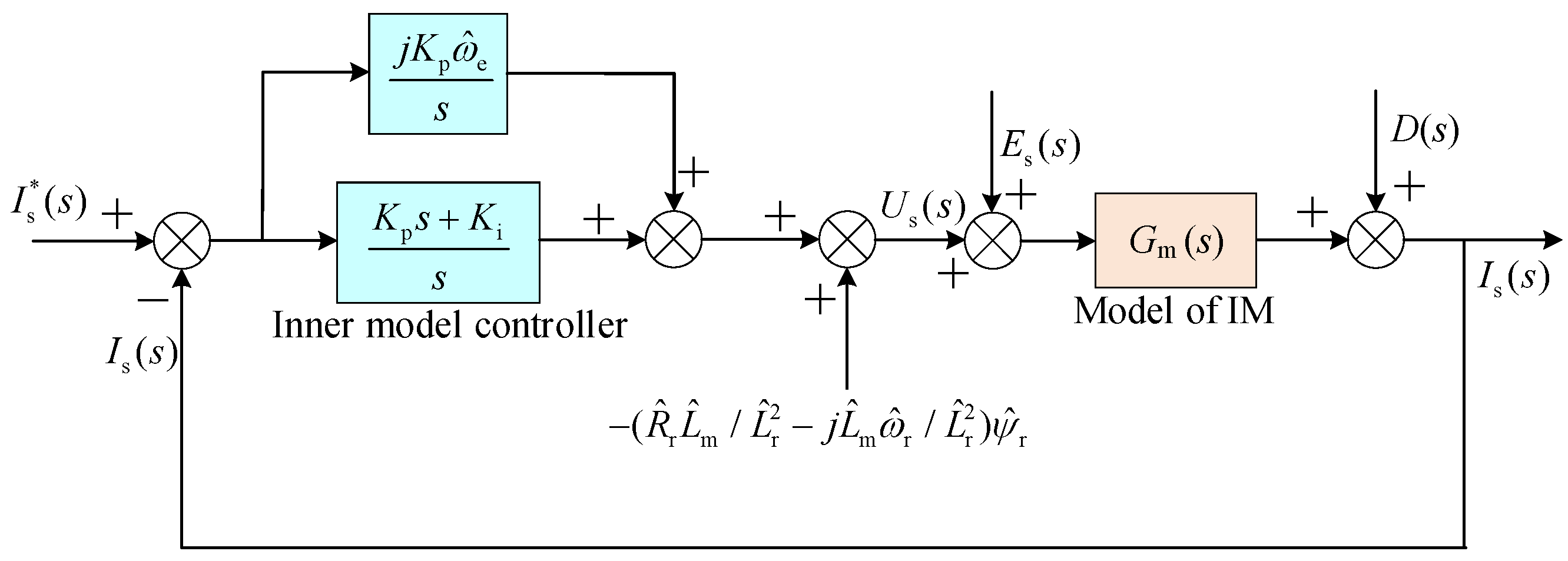
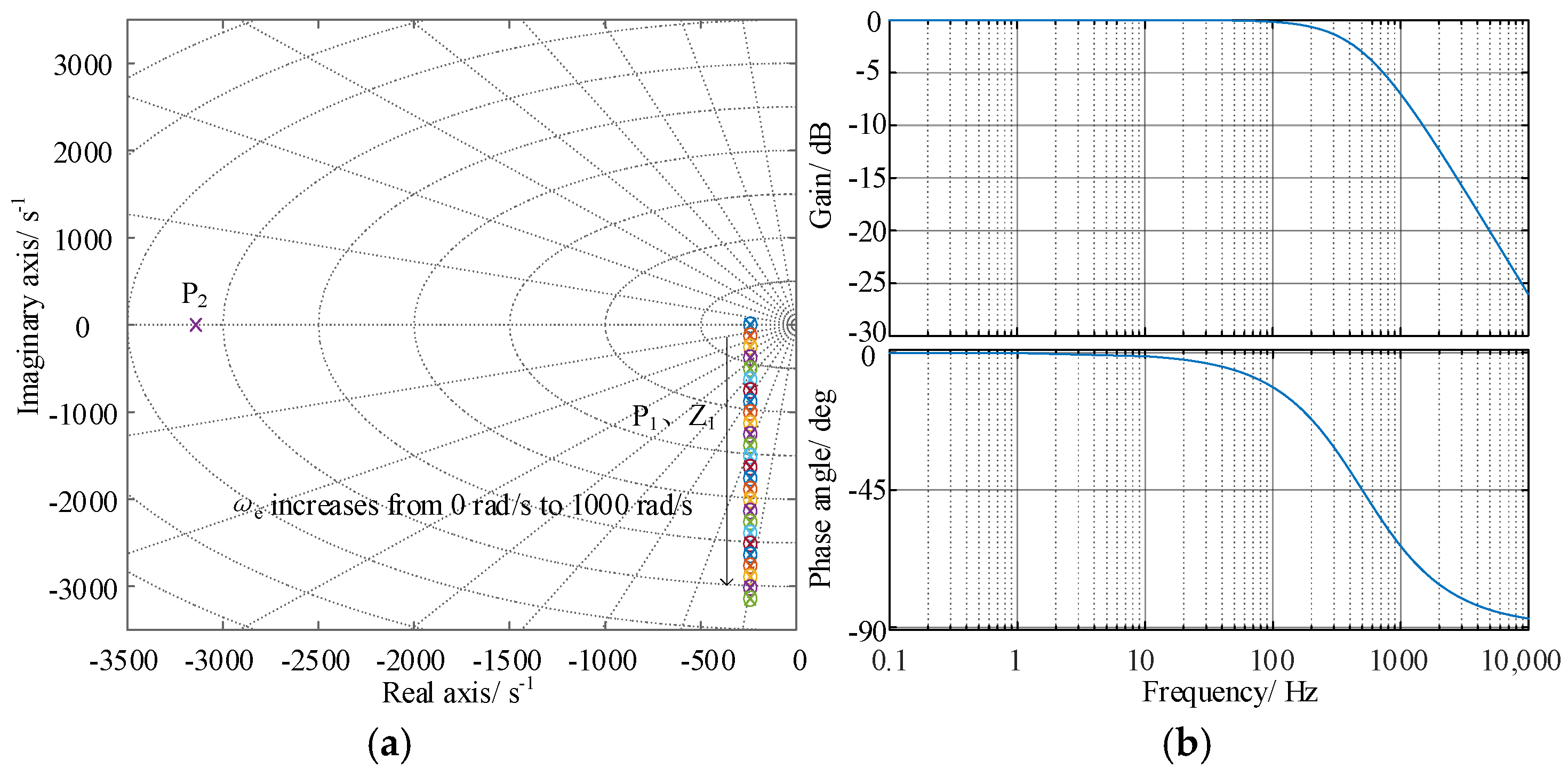
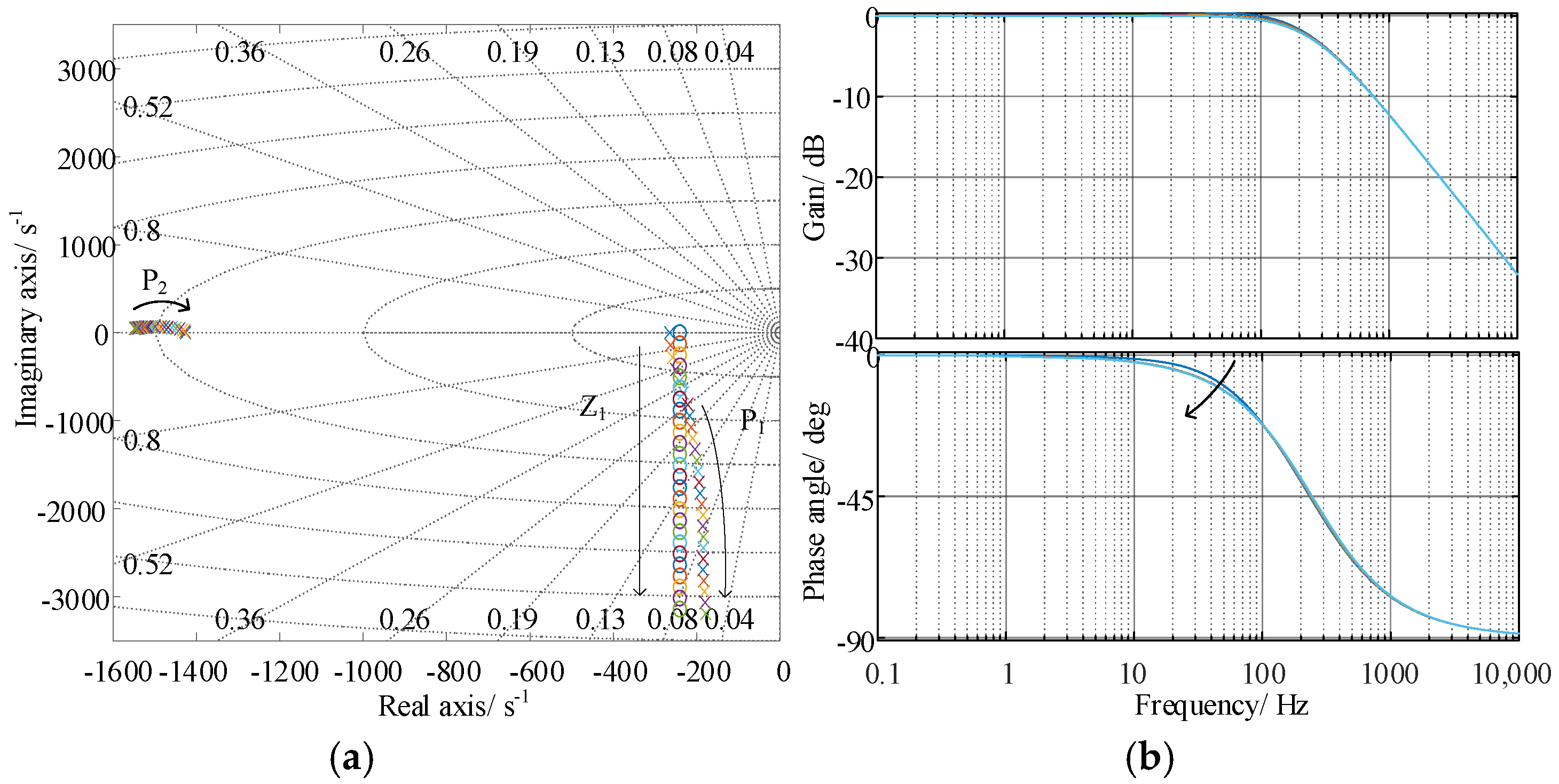
3.1. Design of Internal Model Current Decoupling Controller in Continuous Domain
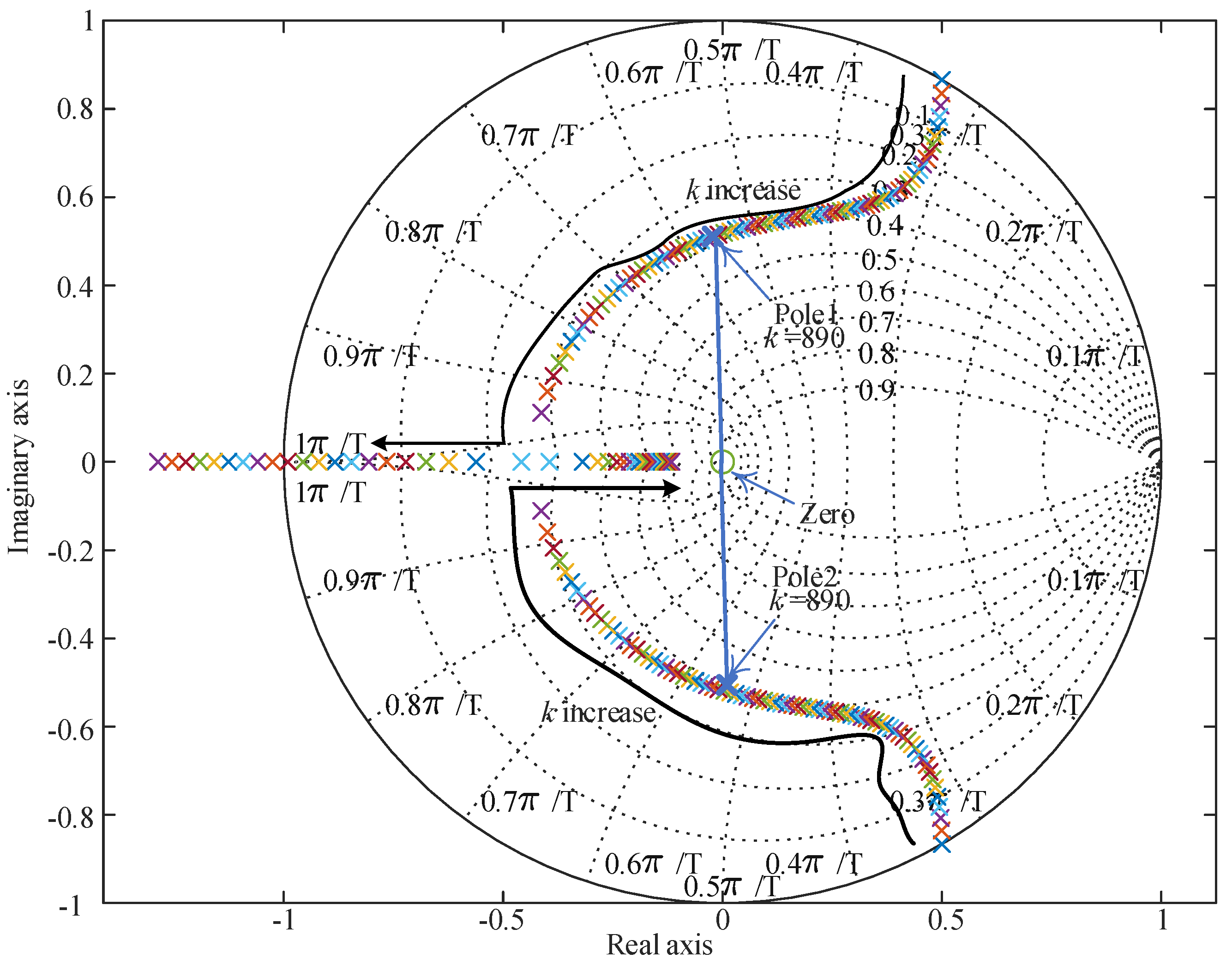
3.2. Design of Internal Model Current Decoupling Controller in Discrete Domain
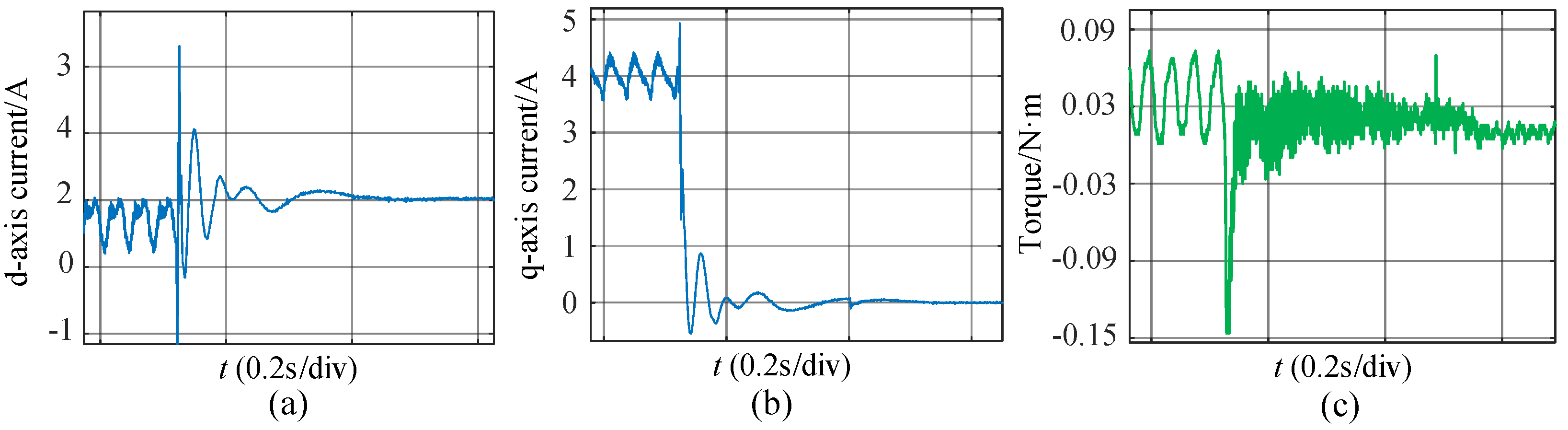
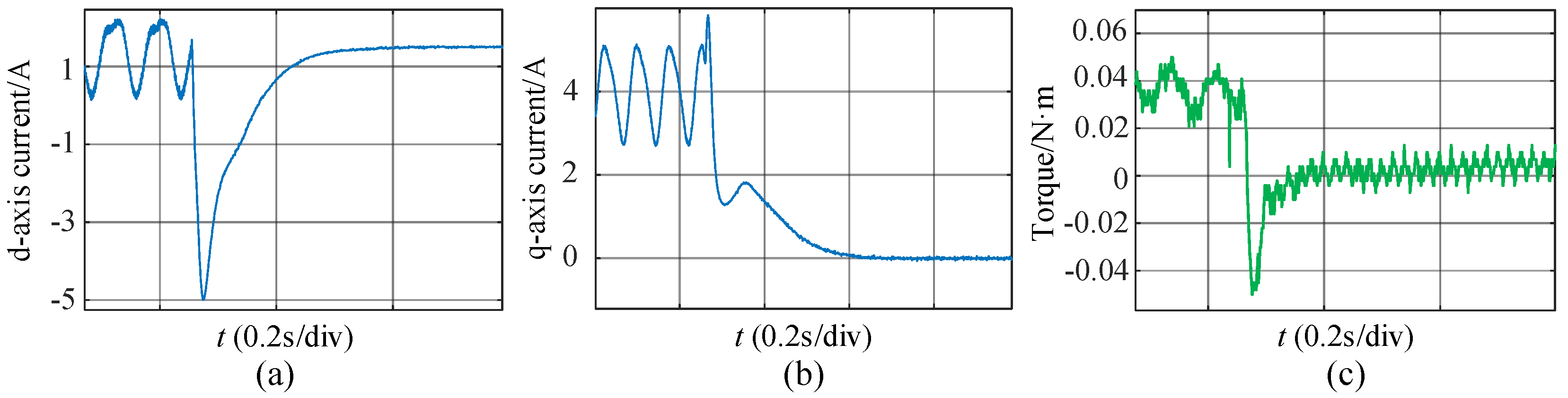
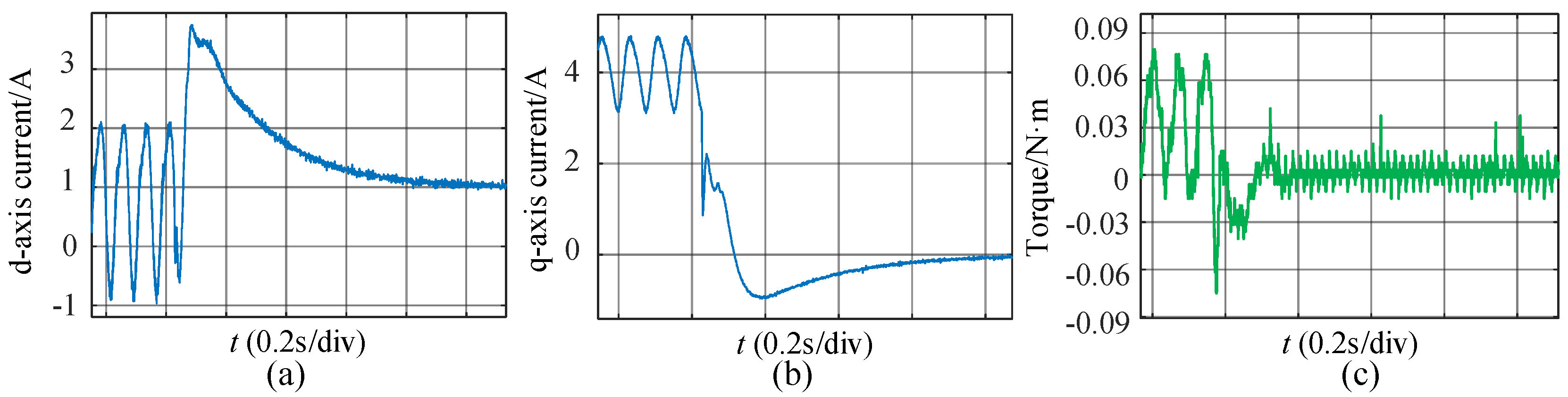
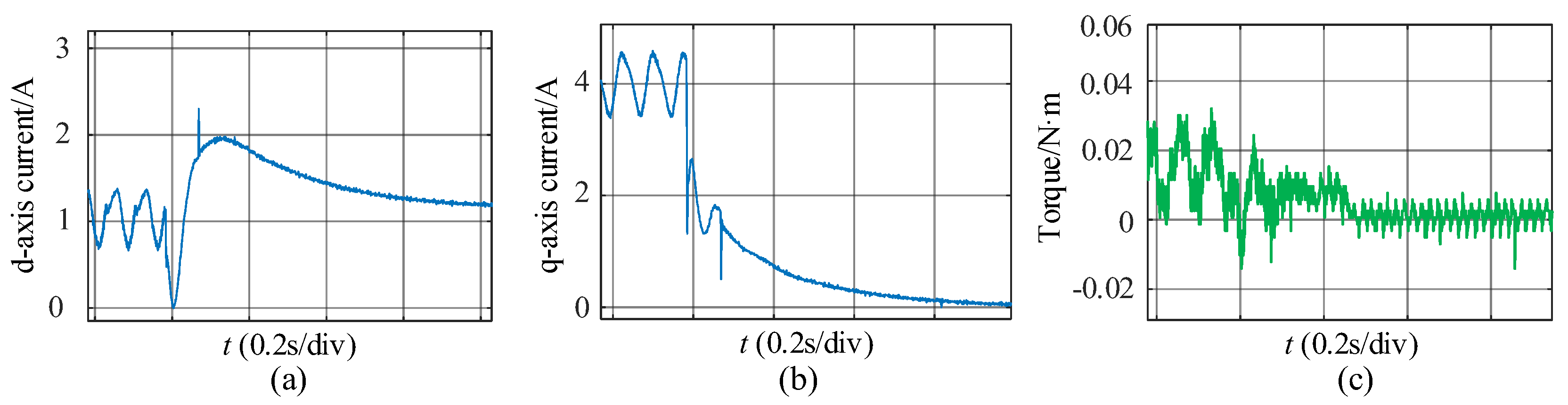
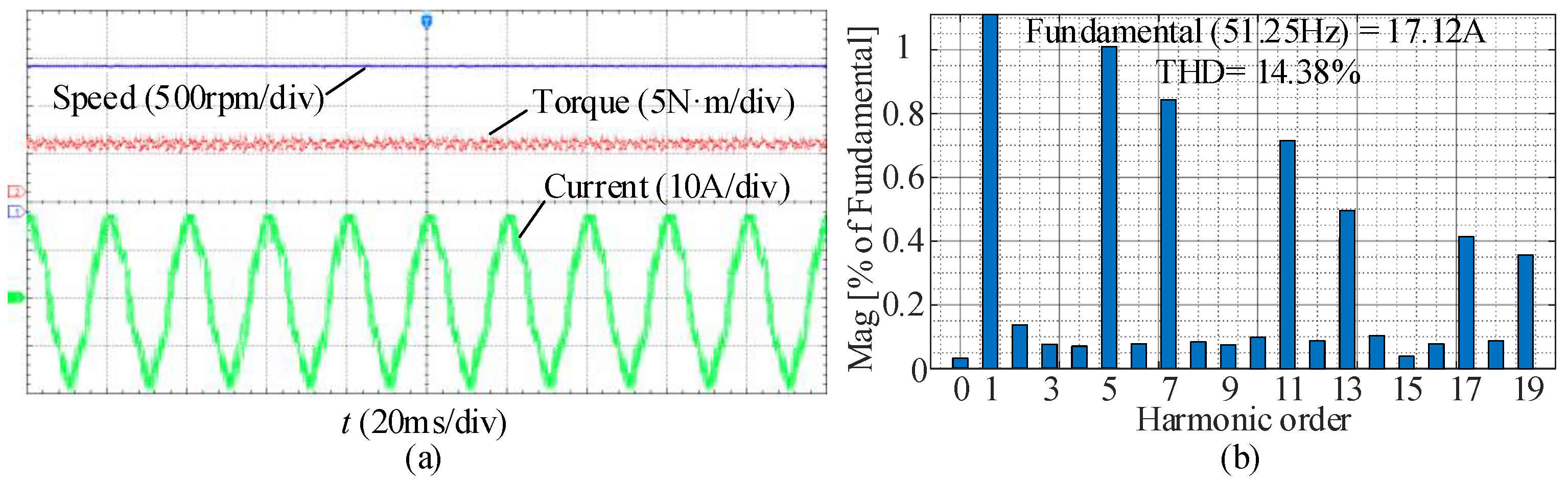
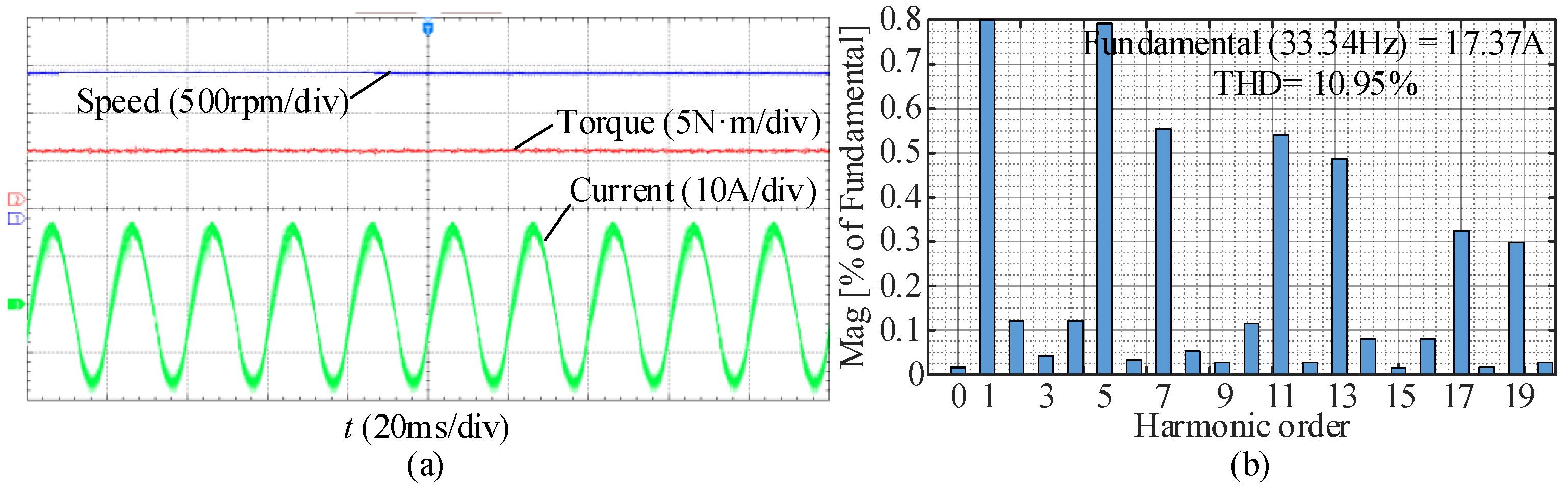
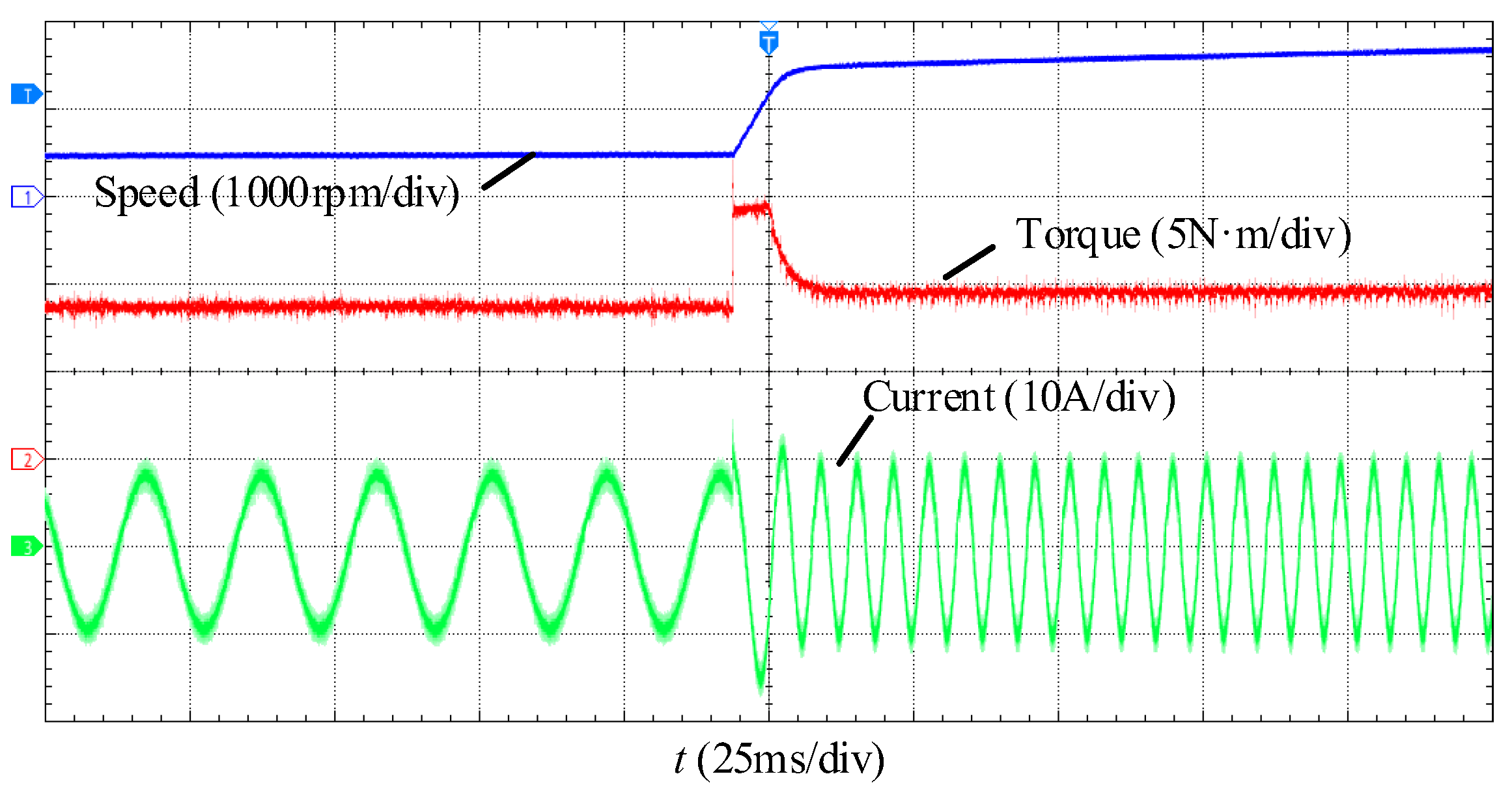
4. Experimental Results
5. Conclusions
- (1)
- There is a complex pole in the IM mathematical model: as the synchronous speed increases, the imaginary axis component of the complex pole increases, resulting in an increasing oscillation during the dynamic process;
- (2)
- The internal model controller generates a zero at the same position as the complex pole, eliminating the stator’s internal coupling. Meanwhile, it is insensitive to stator leakage inductance;
- (3)
- Considering sampling and control delay, an internal model controller is designed in a discrete domain, the parameter is determined according to the phase of the pole and the distance between the pole and the center of the unit circle. A good dynamic performance can be obtained under the switching frequency of 2 kHz.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, W.; Tong, Y.; Huang, S.; Liang, G.; Feng, C.; Wu, X.; Huang, S. A Carrier Self-Synchronization Method for Distributed Control Units in Multithree-Phase Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2024, 72, 4353–4363. [Google Scholar] [CrossRef]
- Onsal, M.; Demir, Y.; Aydin, M. Impact of Asymmetric and Symmetric Overhangs on Torque Quality and Axial Magnetic Force Computations in Surface Mounted PM Synchronous Motors. IEEE Trans. Magn. 2021, 58, 8201505. [Google Scholar] [CrossRef]
- Dong, Z.; Song, Z.; Wang, W.; Liu, C. Improved Zero-Sequence Current Hysteresis Control-Based Space Vector Modulation for Open-End Winding PMSM Drives With Common DC Bus. IEEE Trans. Ind. Electron. 2023, 70, 10755–10760. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Song, Y.; Qi, W.; Guo, Q.; Li, X.; Kong, L.; Chen, J. Real-Time Global Optimal Energy Management Strategy for Connected PHEVs Based on Traffic Flow Information. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20032–20042. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, R.; Liu, S.; Liu, C. Analysis of Winding-Connection Sequence in Multiphase Series-End Winding Motor Drives for Leg-Current Stress Reduction. IEEE Trans. Ind. Inform. 2025, 21, 1635–1644. [Google Scholar] [CrossRef]
- Arandhakar, S.; Jayaram, N.; Shankar, Y.R.; Gaurav; Kishore, P.S.V.; Halder, S. Emerging Intelligent Bidirectional Charging Strategy Based on Recurrent Neural Network Accosting EMI and Temperature Effects for Electric Vehicle. IEEE Access 2022, 10, 121741–121761. [Google Scholar] [CrossRef]
- Montoya-Acevedo, D.; Gil-González, W.; Montoya, O.D.; Restrepo, C.; González-Castaño, C. Adaptive Speed Control for a DC Motor Using DC/DC Converters: An Inverse Optimal Control Approach. IEEE Access 2024, 12, 154503–154513. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Miao, Y.; Zhang, X. A Double Vector Model Predictive Torque Control Method Based on Geometrical Solution for SPMSM Drive in Full Modulation Range. IEEE Trans. Ind. Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Zhang, B.; Liu, C. Half Open-End Winding Topology Based Nine-Leg VSI for Asymmetrical Six-Phase PMSM Drives. IEEE Trans. Power Electron. 2023, 38, 11399–11410. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, Y.; Mao, C. A Gain Design Method for a Linear Extended State Observers to Improve Robustness of Deadbeat Control. IEEE Trans. Energy Convers. 2020, 35, 2231–2239. [Google Scholar] [CrossRef]
- Dong, N.; Li, M.; Chang, X.; Zhang, W.; Yang, H.; Zhao, R. Robust Power Decoupling Based on Feedforward Decoupling and Extended State Observers for Virtual Synchronous Generator in Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 576–587. [Google Scholar] [CrossRef]
- Song, P.; Liu, Y.; Liu, T.; Wang, H.; Wang, L. A Novel Suppression Method for Low-Order Harmonics Causing Resonance of Induction Motor. Machines 2022, 10, 1206. [Google Scholar] [CrossRef]
- Liu, X.; Hou, M.; Wang, X. Complex Vector Analysis and 2DOF Internal Model Decoupling Control for Toroidal Motor. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Sun, X.; Wu, C.; Wang, J. Adaptive Compensation Flux Observer of Permanent Magnet Synchronous Motors at Low Carrier Ratio. IEEE Trans. Energy Convers. 2021, 36, 2747–2760. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z.-Q.; Freire, N.M.A. High Frequency Signal Injection Sensorless Control of Finite-Control-Set Model Predictive Control With Deadbeat Solution. IEEE Trans. Ind. Appl. 2022, 58, 3685–3695. [Google Scholar] [CrossRef]
- Wang, F.; He, L. FPGA-Based Predictive Speed Control for PMSM System Using Integral Sliding-Mode Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 972–981. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Tang, C.; Wang, L.; Zhu, Y.; Liu, H.; Wang, S. Sensorless Control Strategy for Permanent Magnet Synchronous Motor Based on Adaptive Non-Singular Fast Terminal Sliding Mode Observer. IEEE Trans. Appl. Supercond. 2024, 34, 5208905. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Miao, Y.; Wu, X.; Wang, Y.; Yi, L. An Improved Generalized Extended State Observer for Current Harmonic Compensation in Dual Three-Phase PMSMs. IEEE Trans. Power Electron. 2025, 40, 7136–7149. [Google Scholar] [CrossRef]
- Novak, M.; Xie, H.; Dragicevic, T.; Wang, F.; Rodriguez, J.; Blaabjerg, F. Optimal Cost Function Parameter Design in Predictive Torque Control (PTC) Using Artificial Neural Networks (ANN). IEEE Trans. Ind. Electron. 2021, 68, 7309–7319. [Google Scholar] [CrossRef]
- Kim, D.-J.; Hong, D.-K.; Choi, J.-H.; Chun, Y.-D.; Woo, B.-C.; Koo, D.-H. An Analytical Approach for a High Speed and High Efficiency Induction Motor Considering Magnetic and Mechanical Problems. IEEE Trans. Magn. 2013, 49, 2319–2322. [Google Scholar] [CrossRef]
- Miao, Y.; Liao, W.; Huang, S.; Liu, P.; Wu, X.; Song, P.; Li, G. DC-Link Current Minimization Scheme for IM Drive System Fed by Bidirectional DC Chopper-Based CSI. IEEE Trans. Transp. Electrif. 2023, 9, 2839–2850. [Google Scholar] [CrossRef]


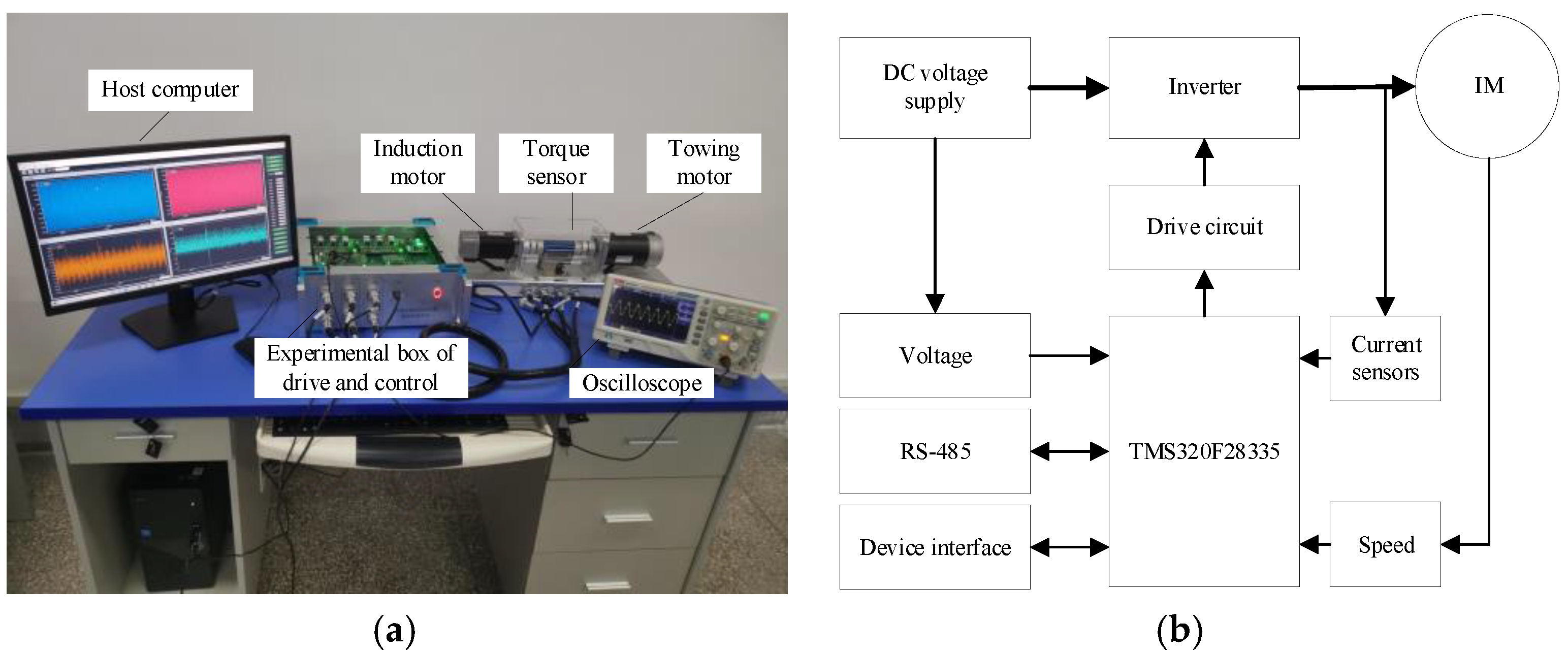
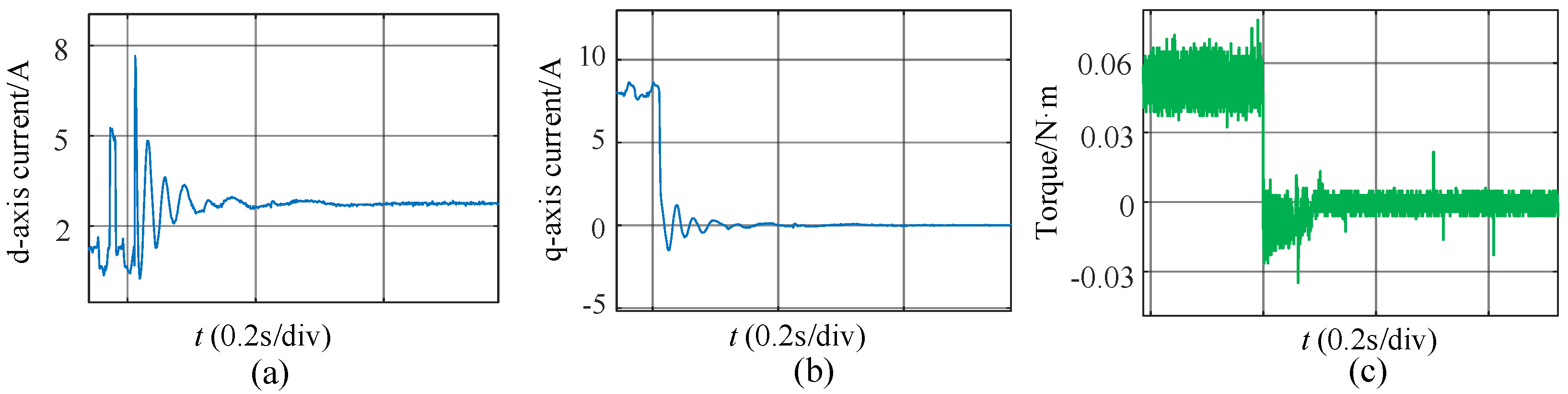

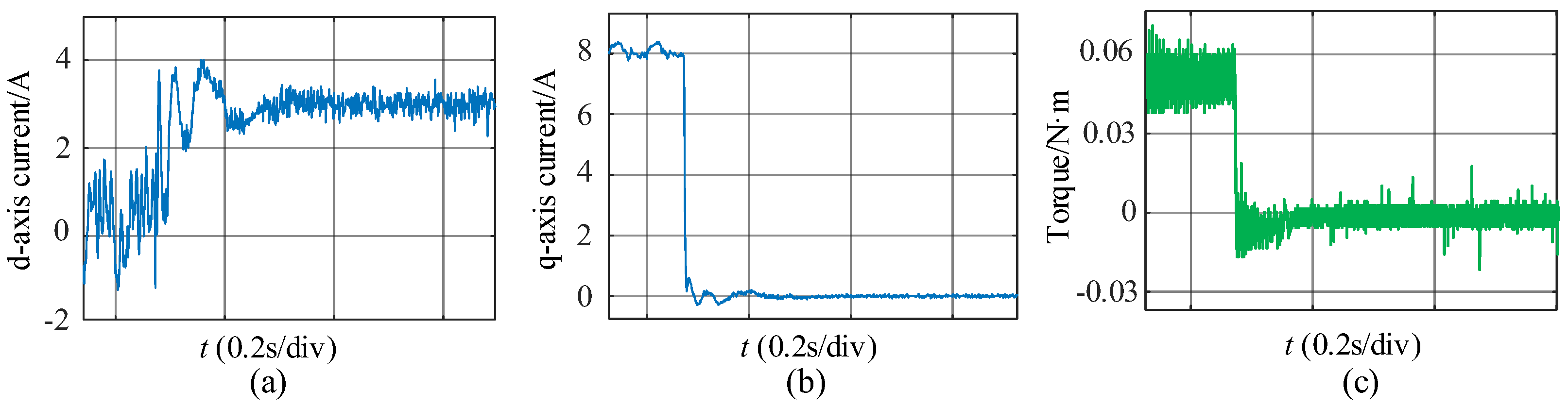
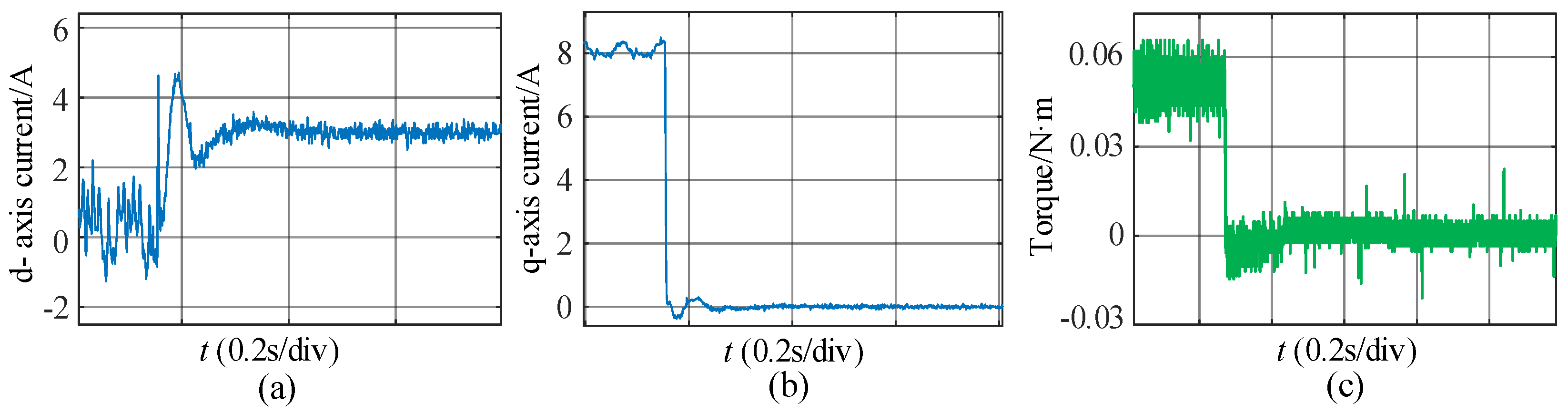
| Parameter | Value |
|---|---|
| Rated Power | 1 kW |
| Number of Pole Pairs | 2 |
| Rated Voltage | 48 V |
| Rated Speed | 3000 rpm |
| Stator Resistance | 0.25 Ω |
| Rotor Resistance | 0.25 Ω |
| Stator Inductance | 0.5 mH |
| Rotor Inductance | 0.5 mH |
| Excitation Inductance | 0.5 mH |
| Conduction Voltage Drop of Switching Tube | 0.7 V |
| Conduction Voltage Drop of Diode | 0.5 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Xu, Q.; Yang, T.; Tu, Y. Internal Model Current Decoupling Control Strategy for Induction Motors. Energies 2025, 18, 2171. https://doi.org/10.3390/en18092171
Xie Q, Xu Q, Yang T, Tu Y. Internal Model Current Decoupling Control Strategy for Induction Motors. Energies. 2025; 18(9):2171. https://doi.org/10.3390/en18092171
Chicago/Turabian StyleXie, Qiuyue, Qiwei Xu, Tao Yang, and Yuxiaoying Tu. 2025. "Internal Model Current Decoupling Control Strategy for Induction Motors" Energies 18, no. 9: 2171. https://doi.org/10.3390/en18092171
APA StyleXie, Q., Xu, Q., Yang, T., & Tu, Y. (2025). Internal Model Current Decoupling Control Strategy for Induction Motors. Energies, 18(9), 2171. https://doi.org/10.3390/en18092171






