Power Grid Clock Synchronization Optimization Based on Stackelberg Game Theory

Abstract

Clock synchronization, as the fundamental service in the power grid, provides a unified time standard for all kinds of power services, such as metering, controlling, and scheduling. Since massive new energy devices are connected to the power grid, they bring new demands for differentiated synchronization accuracy and dynamic access synchronization. Considering the limited communication resources of the power grid, we propose a master–slave clock synchronization method based on the two-layer Stackedberg game to satisfy the synchronization demand by diverse devices as much as possible. First, the master station dynamically prices users based on the required synchronization accuracy and the number of synchronous devices, creating a game process between users. Secondly, an iterative algorithm for solving game equilibrium is designed. Finally, the simulation results are given in MATLAB to prove that the proposed method can converge quickly and dynamically adjust allocation according to user demand. Furthermore, the network simulator Mininet and the open-source software-defined network framework Ryu are used to evaluate the performance of the proposed method. Compared with the bandwidth reservation scheme, our proposed method is more suitable for differentiated clock synchronization of resource-limited new energy power networks. This paper investigates the impact of network capacity changes on the clock synchronization accuracy of user equipment in power networks for the first time. Then, a two-layer Stackedberg game model has emerged to achieve optimal bandwidth allocation in the network and improve clock synchronization accuracy. Simulation results show that our method can not only meet the differentiated clock synchronization requirements but also achieve the optimal allocation in dynamic access scenarios.

1. Introduction

The integration of numerous new energy devices is transforming the traditional distribution networkrev [1]. The distribution networks not only need to realize reliable power delivery and distribution, but also meet the demand for the integration of “source-network-load-storage” [2] and flexible coupling with the upper-level grid [3]. The evolution of distribution networks is introducing a range of new power services, which raise the high precision requirements for clock synchronization [4]. However, traditional centralized time synchronization solutions are insufficient to meet the demand of the numerous dynamically connected new energy devices with differentiated clock synchronization. The limitation of centralized time synchronization is that it mainly relies on periodic data packet exchanges [5]. As the demand for higher precision synchronization increases and the number of devices grows, the communication capacity of the grid can no longer meet the transmission requirements for a large volume of data packets under a synchronization scheme [6].

The existing work on optimizing PTP (Precision Time Protocol) mainly focuses on reducing the asymmetry in transmission link delay estimation, link congestion, and accumulated clock errors [7]. Additionally, improving delay estimation accuracy contributes more to the performance improvement of PTP clock synchronization [8]. However, existing works have not thoroughly addressed robustness and adaptability under various network conditions and interference factors, which complicates direct application to current power communication networks [9]. In order to take the conditions into account, Puttnies et al. improved PTP synchronization accuracy using linear programming models [10]. Unfortunately, this approach relies on linear solvers that require considerable computational resources, complicating deployment in resource-limited power networks.

To analyze the impact of link congestion on synchronization, Hadžić et al. proposed a packet filtering technique using an earliest-arrival packet filter [11], which performs well in lightly loaded networks with low queuing delay probability but underperforms in high-load scenarios. Ha et al. implemented high-precision synchronization by prioritizing packets based on Differentiated Services architecture [12], but did not consider network scalability or the expansion of future power grids. Wang et al. used delay distribution estimation to reduce transmission time estimation errors under congestion conditions [13]. However, in practical power networks, the coexistence of multiple packets can interfere with estimation, affecting accuracy. Existing work typically relies on centralized timekeeping for link delay compensation [14] and packet congestion filtering [15]. In real power networks with massive device connections, diverse services coexist, information transmission volume is high, and topological relationships are complex [16].

Notice that clock synchronization schemes that are effective in other fields are difficult to use in smart grids with numerous new energy devices. With the extensive deployment of power equipment in electrical systems, satellite-based time synchronization proves economically prohibitive for most applications. Under the common situation with operational anomalies or insufficiently visible satellites, the synchronization accuracy deteriorates catastrophically (exceeding 100 ms) by signal reception failures [17]. Existing research ignores the dynamic and differentiated synchronization precision required by different devices and their resulting resource occupancy variations. Time-coded synchronization is commonly applied in wired networks, requiring the transmission of two signals: synchronized pulse information and serial port timing data [4]. As the precision requirements for synchronization increase, the encoded information volume expands, resulting in longer code sequences [18]. Consequently, synchronization accuracy becomes constrained by the bandwidth of power communication networks and their processing capabilities. To address the problem of detecting clock synchronization anomalies in substations, Meng et al. propose a synchronization anomaly detection method based on fuzzy neural networks [19], which achieves synchronization status judgment by comparing the difference between the reception time of the SCADA system. Liao et al. focus on multimodal communication scenarios in smart parks [20], and innovatively propose a dynamic clustering algorithm based on coalition game (CFG-DC), integrating power line carrier (PLC) and two-way industrial frequency communication (TWACS) technologies, establishing a comprehensive synchronization model that includes frequency offsets, timestamp jitter, and transmission delays. Simulation results show that the algorithm reduces the synchronization error by 60.7% compared with the traditional method, and still maintains high-precision synchronization within 15 μs under dynamic network topology. It advances the development of power system synchronization technology from communication architecture innovation and game-theory-based optimization, providing a new technical path to solve the time synchronization problem.

To address the contradiction between massive device synchronization precision demands and limited communication resources [21,22], we propose a master–slave clock synchronization scheme for power grids based on a Stackelberg bi-level game model. Based on a distribution network with dynamically connecting user devices, the Stackelberg bi-level game model is used to dynamically price communication resources. Combined with the user synchronization precision and device number requirements, our scheme can achieve efficient allocation. Moreover, the paper proves the existence of equilibrium in the Stackelberg game model and designs an iterative algorithm to find the equilibrium solution. The iterative algorithm guarantees precise computation with rapid convergence, establishing the pricing strategy for time-servers and the influence of users’ varying synchronization needs on game equilibrium. Our proposed master–slave synchronization optimization scheme can formulate effective communication resource allocation strategies based on users’ differentiated needs.

This paper is organized as follows. In Section 2, a game theory-based clock synchronization optimization strategy is proposed. In Section 3, our proposed algorithm is verificated and simulated in MATLAB. The results using virtual simulation platform are given in Section 4, and conclusions are drawn in Section 5.

2. Game-Theoretic Optimization Strategies for Clock Synchronization

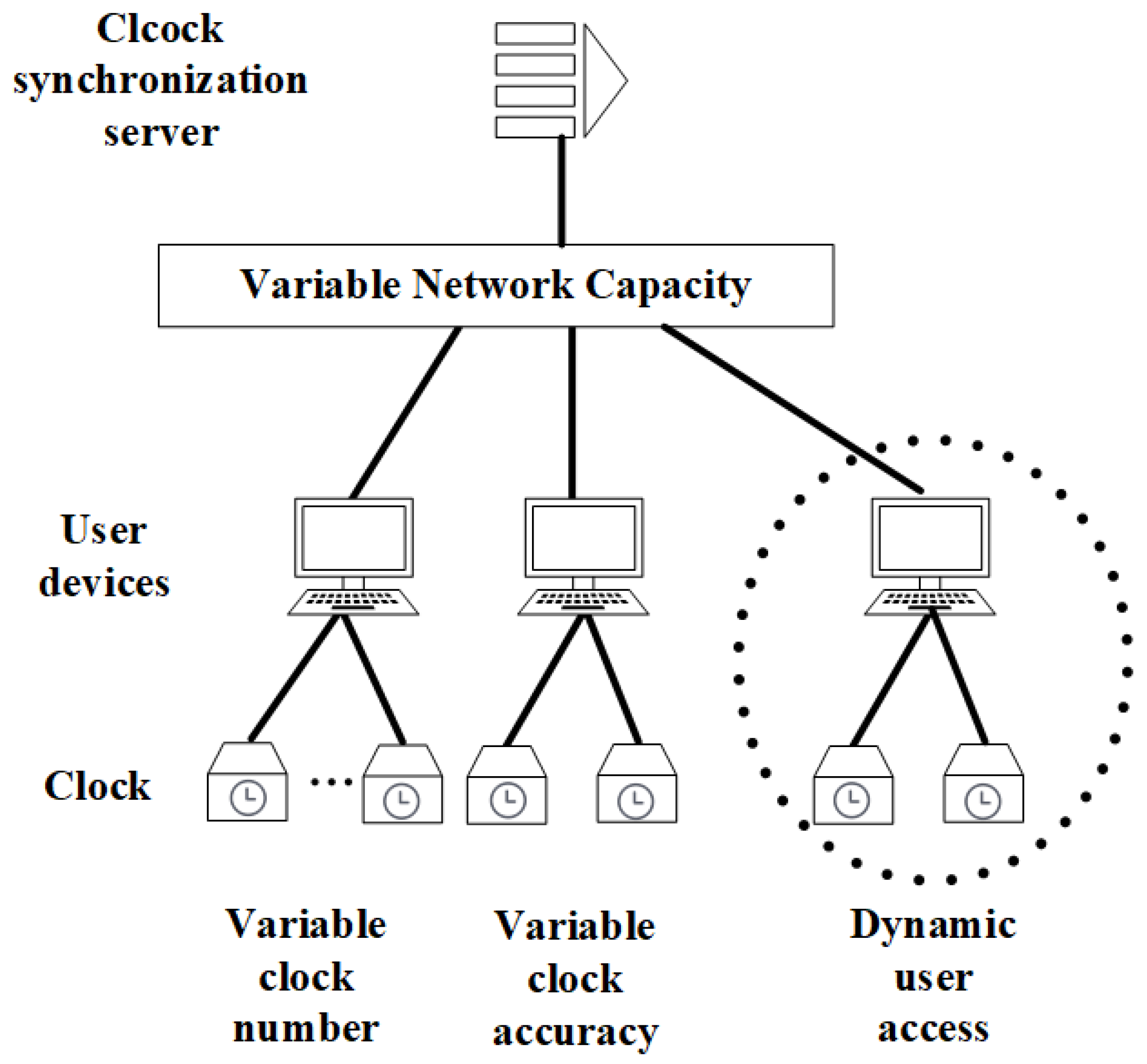
2.1. Stackelberg Game Model for Clock Synchronization

In the synchronization process, each device needs to receive data packets from the master station and send corresponding packets back to the master station, which occupies a certain amount of communication resources. This situation creates a competitive relationship among user devices. Therefore, a Stackelberg bi-level game model is used for dynamic resource allocation. In the master–slave synchronization architecture, the time synchronization server and the power consumption users act as players in the game. The time synchronization server acts as the leader, interacting with users who are the followers, and dynamically utilizes communication resources based on the leader’s pricing results.

Suppose the synchronization requirements of the time synchronization server and users $I=\left\{1,\dots ,n\right\}$ in the power grid. Then, the strategy space of the game, the revenue function of the time synchronization server, and the utility function of the users can be determined by the synchronization requirements. The strategy space consists of the synchronization bandwidth chosen by the users. The synchronization bandwidth occupied by user i is denoted as $b_i\in B_i$, where $B_i$ represents the set of network resources available to user i (i.e., the strategy space in the game). Assuming bandwidth is continuous and can be represented by real numbers, the communication capacity of the network where the time synchronization server is located as $Q>0$, and each user can occupy up to Q units of communication resources. If the user’s strategy is $b_i\in \left[0,Q\right]$, the strategy space of the user is $B_i\in \left[0,Q\right]$, which is a non-empty closed interval and a compact convex set on the real axis.

Stackelberg game is a bi-level game model chosen because the allocation of communication resources for synchronization in the network is determined not only by the server and users but also involves competition among users. As shown in Figure 1, the upper level of the Stackelberg game features the time synchronization server (master station) as the leader and users as followers. At this level, when users respond to the bandwidth requests, each network will predict the responses of the followers and adjust its pricing to maximize its total revenue. The leader is the master as the time server, followed by the power devices requesting synchronization, as the synchronization process must be performed periodically and consumes bandwidth. Pricing in this process is determined by the current network capacity and the amount of bandwidth determined based on synchronization accuracy. By playing with the cost of the accuracy required by the user and the pricing of the synchronization resources by the server, the optimum allocation of bandwidth is achieved and the synchronization accuracy of the whole system is improved.

The network revenue is given as follows:

$$max\sum p_i{b}_i,i=1,2,\dots ,n,$$

(1)

where $b_i$ represents the synchronization bandwidth used by user i, and $p_i$ is the pricing set by the time synchronization server for user i. When the revenue of the time synchronization server is maximized, the total utility of the users is also maximized. This indicates that the server’s dynamic pricing strategy has allocated resources in a way that maximizes the value for the users, thereby achieving the highest clock synchronization accuracy for the entire system.

According to Figure 1, the lower-level game is a non-cooperative game with n participants. The utility function of the users is a mapping from strategies to real numbers, which defines the user’s preference for strategies, i.e., the satisfaction level of users with the bandwidth allocation $b_i$ under the current pricing. The utility function can be defined as follows:

$$U_i=w_{i}log\left(1+Q{q}_i{w}_i{b}_i\right)-p_i{b}_i,\forall i=1,2,\dots ,n,$$

(2)

where $w_i$ represents the fuzzy relationship mapping of the clock synchronization accuracy required by user i. The higher the value, the higher the accuracy required. The $q_i$ denotes the number of synchronization devices required by user i, $b_i$ is the synchronization bandwidth used by user i, $p_i$ is the pricing set by the time synchronization server for user i, $U_i$ is the utility function for user i based on the current strategy, Q is the communication capacity of the network where the time synchronization server is located, and n is the number of users participating in the synchronization bandwidth resource allocation.

The change in user strategy must satisfy the network communication capacity constraint, which physically means that the total bandwidth usage by all users cannot exceed the current network communication capacity. And it can be given as follows:

$$\sum _{l=1}^n{b}_l⩽Q.$$

(3)

The utility function represents the degree of satisfaction of users with the current strategy. For users, a higher function value indicates greater satisfaction. To ensure fairness in the allocation of communication resources, a logarithmic function is used to model user utility, preventing the utility function value from approaching $-\infty$, when the allocated bandwidth or number of synchronization devices is 0. This avoids the phenomenon where the main server forces users to use resources to increase their satisfaction, which can lead to “forced selling”. Each user has an effective utility value, and the utility function must also satisfy additive. The sum of utilities for a class of users can represent the satisfaction level of that class of users.

The clock communication resource allocation process based on the Stackelberg two-layer game consists of the following four stages:

1.

User Request Stage: Users submit synchronization requests to the time synchronization server, including requirements for clock synchronization accuracy, the number of synchronization devices, and initial synchronization bandwidth needs.

2.

Centralized Pricing Stage: The time synchronization server applies differentiated pricing based on users’ synchronization accuracy requirements and communicates the pricing strategy to the users.

3.

Demand Feedback Stage: Users adjust their bandwidth strategies based on the server’s pricing strategy and their own synchronization needs, aiming to maximize their individual benefits. Users’ bandwidth strategies form a Nash equilibrium.

4.

Pricing Adjustment Stage: The time synchronization server adjusts pricing for users based on their current bandwidth usage to maximize its own revenue and communicates the updated pricing to the users.

Stages 1 through 4 are iteratively repeated, adjusting pricing and users’ synchronization bandwidth until both the server’s revenue and users’ benefits are maximized and the upper-layer game results in a Nash equilibrium.

2.2. Theoretical Analysis of Clock Synchronization Game Models

2.2.1. Proof of the Existence of Equilibria in Game Models

Theorem 1. 

The existence of a unique Nash Equilibrium in multi-user non-cooperative games under pricing conditions $p_i$.

Proof of Theorem 1 

The user utility can be represented as

$$U_i=w_{i}log\left(1+Q{q}_i{w}_i{b}_i\right)-p_i{b}_i.$$

(4)

Given the network capacity constraint specified in equation,

$$\sum _{l=1}^n{b}_l⩽Q.$$

(5)

Then, we can obtain the first and second derivatives of the user utility function as shown in the following:

$${\displaystyle \frac{\partial U_i}{\partial b_i}}={\displaystyle \frac{{w_i}^{2}Q{q}_i}{1+Q{q}_i{w}_i{b}_i}}-p_i,$$

(6)

$${\displaystyle \frac{{\partial }^2{U}_i}{\partial {b_i}^2}}=-{\displaystyle \frac{w_i{\left(w_{i}Q{q}_i\right)}^2}{{\left(1+Q{q}_i{w}_i{b}_i\right)}^2}}<0.$$

(7)

Since the user utility function is concave and the second derivative is negative, there exists an optimal point of utility that serves as the Nash equilibrium. According to the literature [23], the utility function meets the condition for the uniqueness of the Nash equilibrium point, thus completing the proof.

Further, it is necessary to solve for the equilibrium point of the Stackelberg game, at which neither the time synchronization server nor the user has any incentive to change their own strategy, causing the system to deviate from this state, as 

$$U_i\left(p_i^{*},B_i^{*}\right)\ge U_i\left(p_i^{*},B_i\right),R\left(p_i^{*},B_i^{*}\right)\ge R\left(p_i,B_i^{*}\right),\forall i,j.$$

(8)

The unique Nash equilibrium solution can be obtained using the Lagrangian method from optimization theory. The problem can be described as follows, where the objective function needs to be maximized subject to constraint conditions

$$\begin{array}{c}max{U}_i\left(b_i\right)\hfill \\ s.t.{\displaystyle \sum _{l=1}^n}{b}_l⩽Q.\end{array}$$

(9)

The Lagrangian function can be constructed as

$$L=w_{i}log\left(1+Q{q}_i{b}_i\right)-p_i{b}_i-\lambda \left[\sum _{l=1}^n{b}_l-Q\right],$$

(10)

where $\lambda ⩾0$ is referred to as the Lagrange multiplier. For any user i, solving for the optimal point using KKT (Karush–Kuhn–Tucker) conditions, the partial derivatives of the Lagrangian function need to be calculated as

$${\displaystyle \frac{\partial L}{\partial b_i}}=0\iff {\displaystyle \frac{{w_i}^{2}Q{q}_i}{1+Q{q}_i{w}_i{b}_i}}-p_i-\lambda =0.$$

(11)

$${\displaystyle \frac{\partial L}{\partial \lambda }}=0\iff \sum _{l=1}^n{b}_l=Q.$$

(12)

Let $\lambda =0$,

$$B_i\left(p_i\right)={\displaystyle \frac{{w_i}^{2}Q{q}_i}{p_i}}-{\displaystyle \frac{1}{Q{w}_i{q}_i}}.$$

(13)

Let $\lambda >0$,

$$\sum _{i=1}^n{B}_i\left(p_i\right)=\sum _{i=1}^n{\displaystyle \frac{{w_i}^{2}Q{q}_i}{p_i+\lambda }}-\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}=Q.$$

(14)

Transforming the equation gives

$$\sum _{k\ne i}^n{\displaystyle \frac{{w_k}^{2}Q{q}_k}{p_k+\lambda }}={\displaystyle \frac{{\displaystyle \sum _{k\ne i}^n}{w_k}^{2}Q{q}_k{\prod }_{l\ne k,i}^n{p}_l+\lambda }{{\prod }_{m\ne i}^n{p}_m+\lambda }}=Q+\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}-{\displaystyle \frac{{w_i}^{2}Q{q}_i}{p_i+\lambda }}.$$

(15)

Assuming that $\gamma =Q+{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{1}{Q{w}_i{q}_i}}-{\displaystyle \frac{{w_i}^{2}Q{q}_i}{p_i+\lambda }}$, the following equations can be obtained:

$$\gamma {\prod }_{m\ne i}^n\left(p_m+\lambda \right)-\sum _{k\ne i}^n{w_k}^{2}Q{q}_k{\prod }_{l\ne k,i}^n\left(p_l+\lambda \right)=0.$$

(16)

$$\gamma \left(p_t+\lambda \right){\prod }_{m\ne i,t}^n\left(p_m+\lambda \right)-\sum _{k\ne i}^n{w_k}^{2}Q{q}_k{\prod }_{l\ne k,i}^n\left(p_l+\lambda \right)=0.$$

(17)

Transforming the equation gives

$$-{\displaystyle \frac{n\left(n-1\right){w_t}^{2}Q{q}_t}{\left(p_t+\lambda \right)}}+nQ+n\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}=\sum _{i=1}^n{\displaystyle \frac{{w_i}^{2}Q{q}_i}{p_i+\lambda }}.$$

(18)

With Equation (13), the optimal bandwidth strategy is

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{1}{Q{w}_i{q}_i}}+Q=-{\displaystyle \frac{n\left(n-1\right){w_t}^{2}Q{q}_t}{\left(p_t+\lambda \right)}}+nQ+n{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{1}{Q{w}_i{q}_i}}\\ \iff {\displaystyle \frac{{w_t}^{2}Q{q}_t}{\left(p_t+\lambda \right)}}={\displaystyle \frac{Q}{n}}+{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\displaystyle \frac{1}{Q{w}_i{q}_i}}\end{array}.$$

(19)

Based on the above equation, the optimal bandwidth strategy and pricing can be calculated as follows:

$${B_i}^{*}={\displaystyle \frac{Q}{n}}+{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}-{\displaystyle \frac{1}{Q{w}_i{q}_i}},$$

(20)

$${p_i}^{*}={\displaystyle \frac{n{w_i}^{2}Q{q}_i}{Q+{\displaystyle \sum _{i=1}^n}\frac{1}{Q{w}_i{q}_i}}}.$$

(21)

According to the above formula, the system benefits can be derived as

$$R^{*}=\sum _{i=1}^n{p_i}^{*}{B_i}^{*}={\displaystyle \sum _{i=1}^n}{w}_i^{2}Q{q}_i-{\displaystyle \frac{n{\displaystyle \sum _{i=1}^n}{w}_i}{Q+{\displaystyle \sum _{i=1}^n}\frac{1}{Q{w}_i{q}_i}}}.$$

(22)

As $\partial R^{*}/\partial q_i>0$, the user’s demand for synchronization accuracy increases, and the system benefits increase. By the same token, as the number of devices that users need to synchronize increases, so does system revenue.

Based on the form of the optimal pricing and bandwidth allocation strategies at Nash equilibrium, the following conclusions can be drawn: (1) As a user’s demand for clock synchronization accuracy increases, their bandwidth usage at equilibrium also increases, leading to higher pricing by the time-server. (2) The main station charges higher fees to users with greater synchronization accuracy requirements and more synchronization devices. (3) Users with identical synchronization demands must pay higher prices in networks with smaller capacities.    □

2.2.2. The Lower Bounds on the Bandwidth Efficiency

In order to theoretically prove the effectiveness of the two-layer Stackelberg game model over the traditional static allocation method, the lower bounds on the bandwidth efficiency of our proposed method are derived and proved to outperform static allocation.

• From Equation (20), the equalized bandwidth allocation for user i can be obtained as follows:

  $${B_i}^{*}={\displaystyle \frac{Q}{n}}+{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}-{\displaystyle \frac{1}{Q{w}_i{q}_i}}.$$

  (23)
• The total bandwidth usage is

  $$\sum _{i=1}^n{B_i}^{*}=Q+\sum _{j=1}^n{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}-\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}}=Q.$$

  (24)
• Assuming $\sum w_i{q}_i\ge Q$, by using the Cauchy–Schwartz inequality, we can deduce that

  $$(\sum _{i=1}^n{w}_i{q}_i)(\sum _{i=1}^n{\displaystyle \frac{1}{Q{w}_i{q}_i}})\ge {\displaystyle \frac{n^2}{Q}}.$$

  (25)
• Substituting $\sum w_i{q}_i\ge Q$, we obtain

  $$\sum {\displaystyle \frac{1}{Q{w}_i{q}_i}}\ge {\displaystyle \frac{n^2}{Q·Q}}={\displaystyle \frac{n^2}{Q^2}}.$$

  (26)
• The lower bound of bandwidth efficiency is

  $$\eta ={\displaystyle \frac{{B_i}^{*}}{Q}}=1\ge {\displaystyle \frac{Q}{Q+\sum \frac{1}{Q{q}_i{w}_i}}}.$$

  (27)
  With the establishment of $\sum {\displaystyle \frac{1}{Q{q}_i{w}_i}}\ge 0$, the equation has always been established.
• The bandwidth efficiency of static allocation scheme is ${\eta }_{stastic}={\displaystyle \frac{1}{n}}$. When $n\ge 2$, our proposed method efficiency is

  $${\displaystyle \frac{Q}{Q+\sum \frac{1}{Q{q}_i{w}_i}}}\ge {\displaystyle \frac{Q}{Q+frac{n}^2{Q}^2}}>{\displaystyle \frac{1}{n}}.$$

  (28)

It is shown that the proposed algorithm still outperforms static allocation in overloaded scenarios.

2.3. Iterative Solution for Equilibria in Game Models

This section introduces an iteration-based algorithm designed to compute Nash equilibrium points and derive optimized strategies for clock synchronization. And the complexity of the iteration-based algorithm is also given to illustrate its applicability to large-scale networks.

2.3.1. Iterative Algorithm for Bandwidth Allocation

In the iterative process, participants cyclically update their respective strategies, while other agents dynamically optimize their decisions in response to evolving strategic profiles from counterparts, until the system converges to the Nash equilibrium. The specific algorithmic workflow is delineated as follows:

1.

Set an initial point $b^{\left(0\right)}=(b_1^{\left(0\right)},\dots ,b_N^{\left(0\right)})$, maximum number of iterations $T_{max}$, and covergence tolerance $ϵ>0$.

2.

While the iteration process continues, the server can obtain the current iteration state $b^{\left(k\right)}=(b_1^{\left(k\right)},\dots ,b_N^{\left(k\right)})$. For any user i, periodically adjust the bandwidth strategy:

$$b_i=\left\{\begin{array}{cc}{b}_i^{(k+1)},\hfill & \mathrm{if}j<i\hfill \\ b_i^{\left(k\right)},\hfill & \mathrm{if}j>i\hfill \end{array}\right..$$

(29)

3.

Check termination conditions: if $\forall i\in \mathcal{N},\parallel b_i^{(k+1)}-b_i^{\left(k\right)}\parallel \le ϵ$, then the Nash equilibrium is achieved. Otherwise:

-

If $k<T_{\max }$, return to Step 2;

-

If $k⩾T_{\max }$, it appears that no Nash equilibrium exists.

If the initial state $b^{\left(0\right)}$ already satisfies the Nash equilibrium, the algorithm terminates immediately at the optimal point $b^{(\ast )}$. Formally, $\forall i\in \mathcal{N}$, the termination condition holds globally. For more general case extension, let $b^{(\ast )}$ be a constrained local game equilibrium, with the existence of second-order derivatives $\forall i\in \mathcal{N}$. Corresponding extreme point exists $b_{-i}=b_{-i}^{\ast }$.

Given $\parallel b_i^{\left(1\right)}-b_i^{\left(0\right)}\parallel$, the iteration process yields the following:

$$\underset{k\to \infty }{lim}\underset{i\in \mathcal{N}}{max}\left|f_i\left({\mathbf{x}}^{\left(k\right)}\right)\right|=0.$$

(30)

This ensures the termination criterion is achievable within finite steps. For pricing phase operations in timing servers, each cycle requires periodic execution of the iterative process and bandwidth strategy adaptation via utility gradient:

$$B_i^{(k+1)}=B_i^{\left(k\right)}+\alpha {\displaystyle \frac{\nabla U_i\left(b_i\right)}{\nabla \left(b_i\right)}},$$

(31)

where $\alpha$ denotes the learning rate.

Following the achievement of Nash equilibrium in the lower-layer non-cooperative game, the timing server proceeds to adapt its pricing strategy according to users’ bandwidth demands. This price strategy adjustment can be formulated as an iterative optimization process:

$${p_i}^{t+1}={p_i}^t+\beta {\displaystyle \frac{\partial R}{\partial p_i}}.$$

(32)

During the simulation, since the initial pricing is set to 0, the user demand rises dramatically to exceed the network capacity. Then, there are two mitigation mechanisms required:

• With the increase in user demand, we set the user demand to be less than the network capacity. If the capacity is exceeded, the allocation is proportional to the demand;
• When ${\displaystyle \sum _{i=1}^n}{b}_i\left(\tau \right)\ge C$ exists, users readjust their bandwidth according to ${b_i}^{k+1}={b_i}^k-\alpha {\displaystyle \frac{\partial U_i\left(b_i\right)}{\partial b_i}}$.

In the upper layer of the game, pricing $P_t$ functions as the server-side production quantity. Through infinitesimal step size $\eta$, the system can be gradually approximated to the optimal point of system efficiency while the system is in the optimal synchronization equilibrium state. The pseudocode of the iterative algorithm for bandwidth allocation is given as Algorithm 1.

Algorithm 1 Iterative Algorithm for Bandwidth Allocation Modeling as Two-Layer Stackelberg Game.

Initialization: Users $i=\{1,2,\dots ,n\}$, pricing $p^{\left(0\right)}$, synchronization bandwidth allocation $b^{\left(0\right)}$.

1: Iteration Count $t\leftarrow 0$.   2: while  $∥b_{\mathrm{i}}^{(k+1)}-b_{\mathrm{i}}^{\left(k\right)}∥>\epsilon$  do   3:    The synchronization server adjusts pricing based on user synchronization needs and broadcasts it to all users.   4:    for $i=\{1,2,\dots ,n\}$ do   5:      ${\tau }_i\leftarrow 0$.   6:      while user i has not reached Nash equilibrium do   7:         ${b_{\mathrm{i}}}^{k+1}={b_{\mathrm{i}}}^k-\alpha {\displaystyle \frac{\partial U_{\mathrm{i}}\left(b_{\mathrm{i}}\right)}{\partial b_{\mathrm{i}}}}$ Inject all the residual voltages $\Delta V_{p,\tau }^s$ adjust its own strategy.   8:         ${\tau }_i={\tau }_i+1$.   9:      end while 10:      User uploads strategy to the server. 11:    end for 12:    $t=t+1$ 13: end while

Output: Clock synchronization policy after reallocation of bandwidth resources.

2.3.2. The Complexity Analysis of Iterative Algorithm

To further illustrate that the number of devices does not limit the iterative algorithm for bandwidth allocation, we theoretically derive the model complexity and illustrate its applicability to support scenarios with larger-scale devices. Let the number of users be n. The algorithm needs to accomplish the following operations in each round of iteration:

• User-level policy update: Each user computes the utility gradient and the complexity is $O\left(1\right)$. The total complexity in the period of user policy update is $O\left(n\right)$.
• Pricing update: As we have derived the equilibrium solution of pricing, we need to calculate the sum which complexity is $O\left(n\right)$. The total complexity in the period of pricing update is $O\left(n\right)$.

In summary, the single iteration time complexity is $O\left(n\right)$, which is linearly related to the number of users n. The convergence speed of the algorithm can be conducted as follows:

Define the convergence condition as $ma{x}_i\left|\right|b_i^{(k+1)}-b_i^{\left(k\right)}\left|\right|\le ϵ$

• The strong convexity of utility functions: Since the utility function is concave, its dual problem is convex optimization. According to the theory of convex optimization, the convergence rate of gradient descent is $O(1/k)$, i.e., it takes $O(1/ϵ)$ iterations to reach $ϵ$-approximate accuracy.
• Update steps setting: The fixed steps $\alpha$, $\beta$ need to satisfy $\alpha <{\displaystyle \frac{2}{L}}$, where L is the Lipschitz constant equal to the gradient.

  $$L=ma{x}_i{\displaystyle \frac{{\left(w_{i}Q{q}_i\right)}^2}{{(1+w_{i}Q{q}_i{b}_i)}^2}}\le ma{x}_i{\left(w_{i}Q{q}_i\right)}^2$$

  (33)
• Upper bound on the number of theoretical iterations: For $ϵ$-approximate equilibrium, the number of iterations satisfies $K=O\left({\displaystyle \frac{L}{\mu ϵ}}\right)$, where $\mu$ is the strongly convex coefficient of the utility function. In the simulation, the measured convergence number $K=600$ (with $ϵ=0.001$) is consistent with the theory.
• Total time complexity: The total time complexity of the algorithm is given as follows:

  $$T_{total}=K\times O\left(n\right)=O(n/ϵ).$$

  (34)

Under fixed precision $ϵ$, the complexity is linearly related to the number of users, which is suitable for large-scale grid scenarios.

3. Simulation Results Analysis

This section conducts numerical simulations using the MATLAB 2021b simulation platform. The network topology for the experiment is shown in Figure 2, we can adjust the number and the synchronization accuracy of clocks in the network and the network parameters to obtain the simulation results of the network.

3.1. Simulation Settings

The network topology in simulation is set as a centralized tree structure. The master clock node is a time server connected to two fixed devices and one variable device node. Each user device is additionally connected to 10 clocks, employing a linear clock model. The maximum number of iterations for the two-layer game process is set at 600, which denotes the maximum number of iterations required for users to adapt their bandwidth needs to reach a Nash equilibrium under a specified pricing strategy. Additionally, the number signifies the epoch of iterations required for the server to adjust pricing and optimize its benefits, considering current user demands. The specific parameters used in the simulation are detailed in

Table 1. Simulation parameter settings.

Parameter	Symbol	Initial Values
Pricing adjustment strategy step	$\alpha$	0.01
Bandwidth demand adjustment step	$\beta$	0.01
Initial pricing	$p^{\left(0\right)}$	(0.01, …, 0.01)
Initial bandwidth allocation	$b^{\left(0\right)}$	(0, …, 0)
Maximum number of iterations	K	600
Convergence tolerance	$\epsilon$	0.001

.

The simulation topology adopts the tree architecture, the master clock node connects to N user devices, and each user device hangs M synchronous sub-devices under it (default $M=10$). The parameter settings are as follows:

• Network capacity Q: set as 15 to 25 in the simulation to simulate different sizes of power grids.
• User requirement $w_i$ is the fuzzy relationship mapping of the clock synchronization accuracy, $q_i$ is the number of synchronization devices required by user.
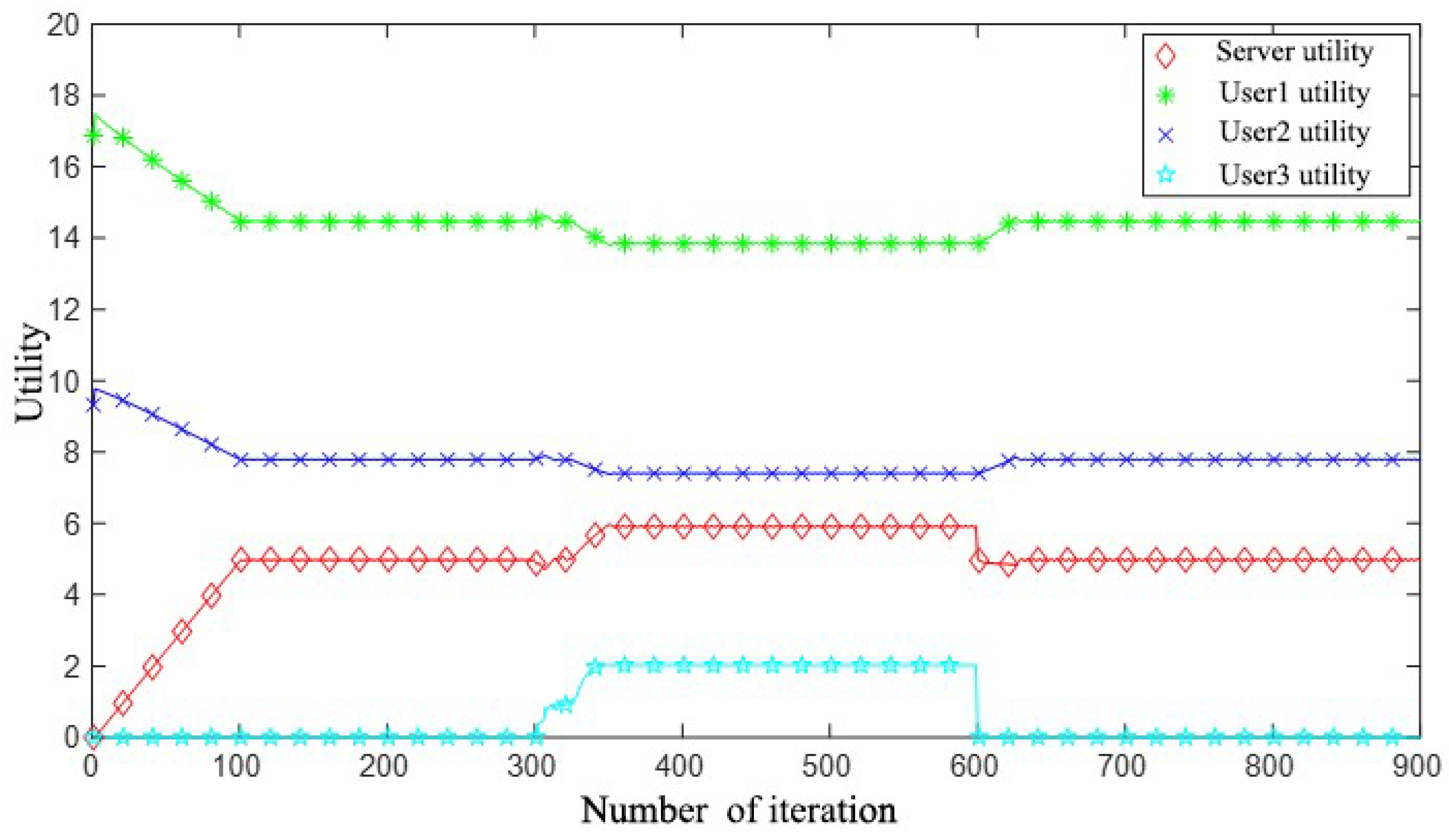
• Dynamic device access: randomly insert user requests in iterations (e.g., 300-th iteration to add new users, 600-th to exit).

The comparison method of reserving bandwidth is to distribute the bandwidth usage evenly for each device, and when the number of user devices is elevated, the synchronization accuracy will be reduced. In this paper, we analyze the synchronization process by analyzing the dynamic access, the number of access devices, and the change in the network capacity, and these conditions cover all the factors, which ensures the comprehensive evaluation of the algorithm research and proves that the game model is comprehensively superior to the baseline approach.

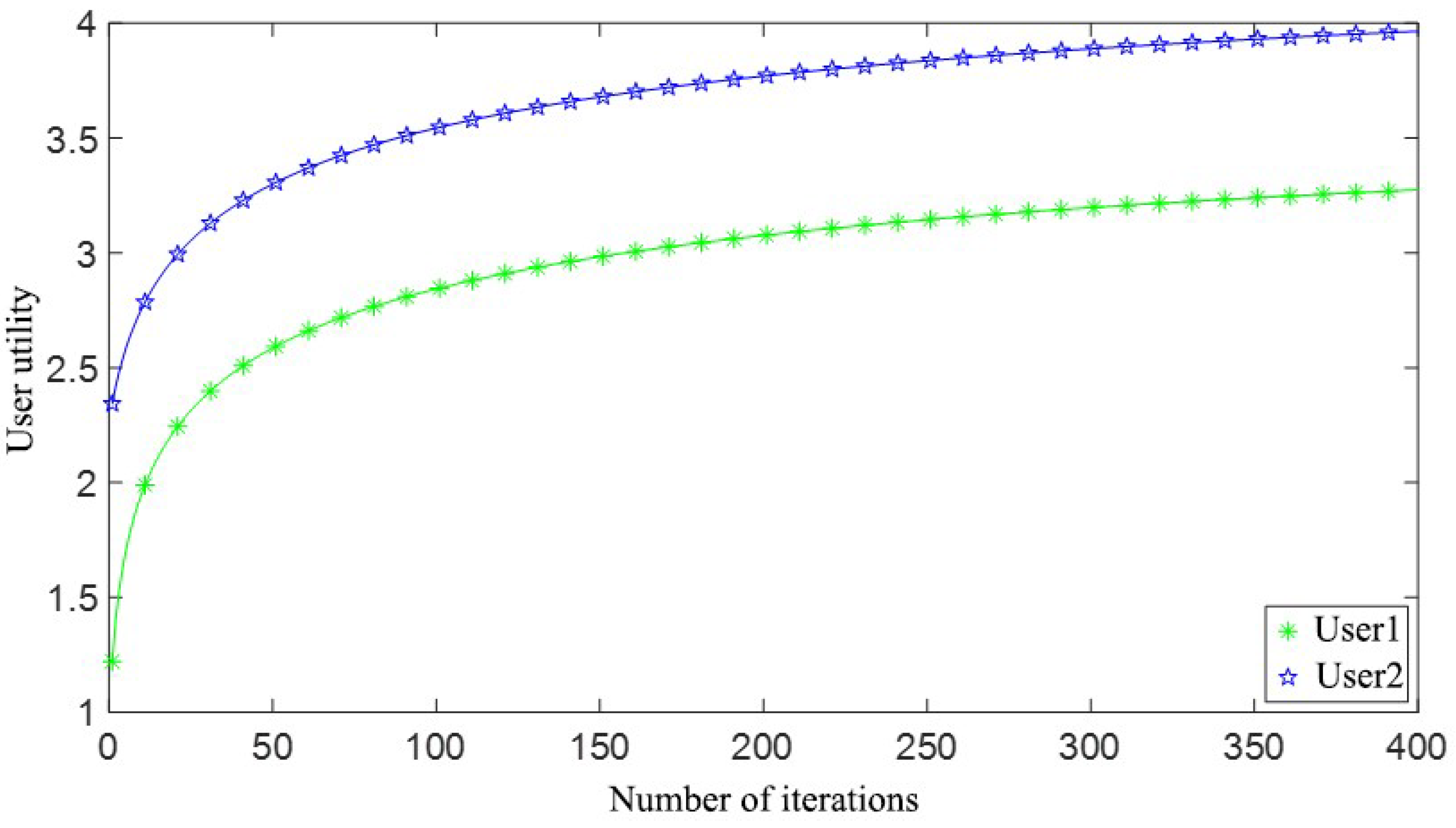
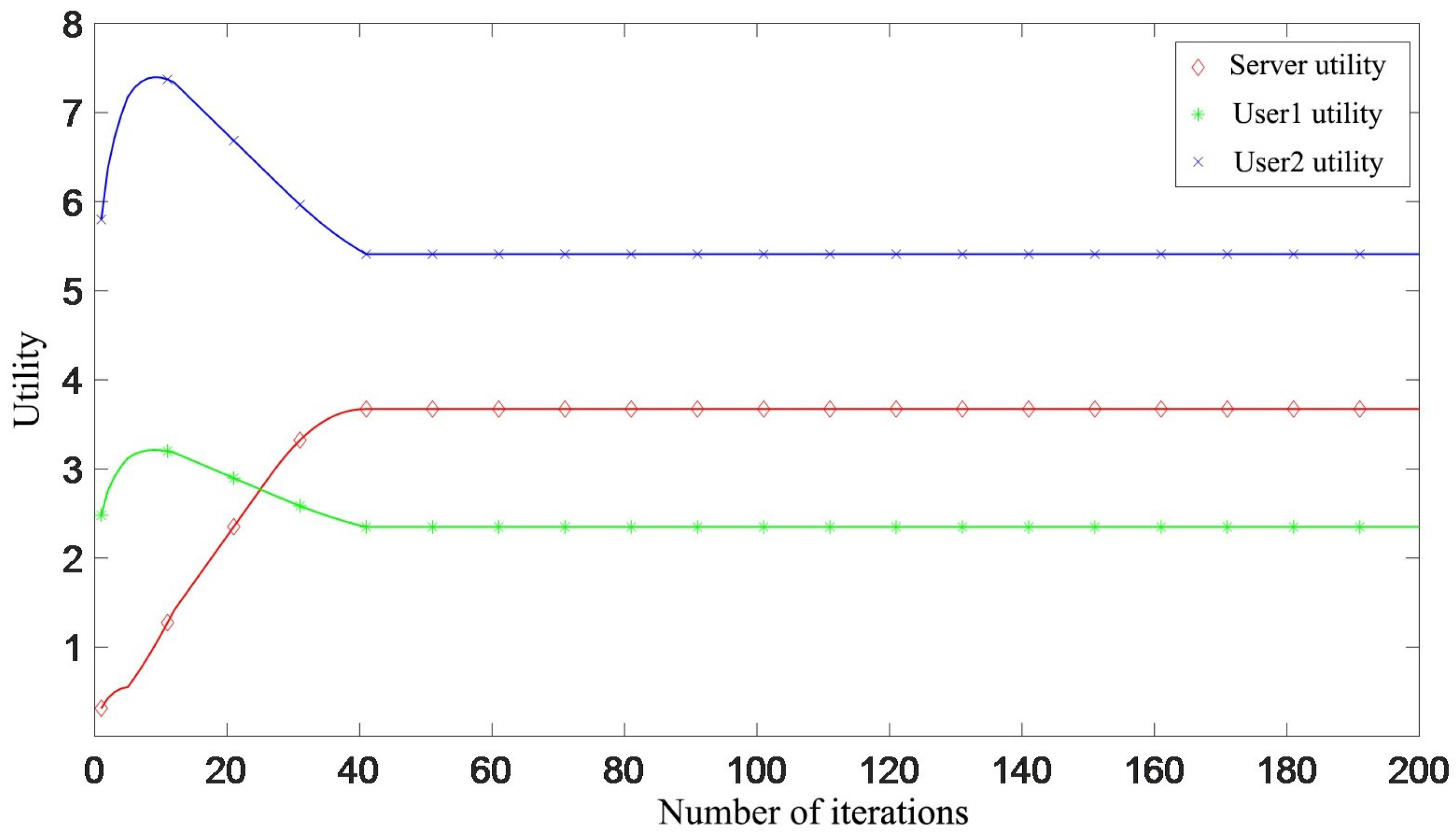
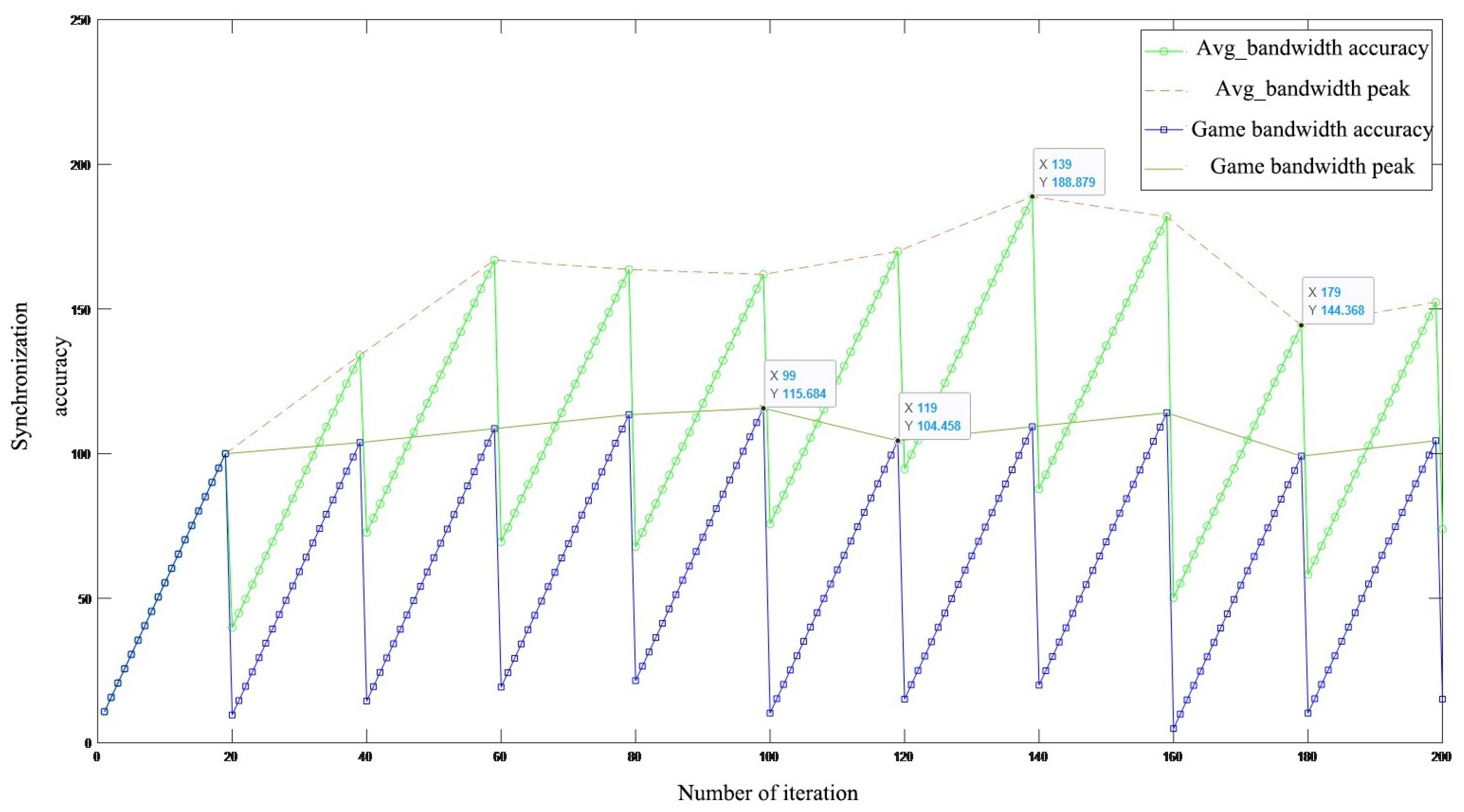
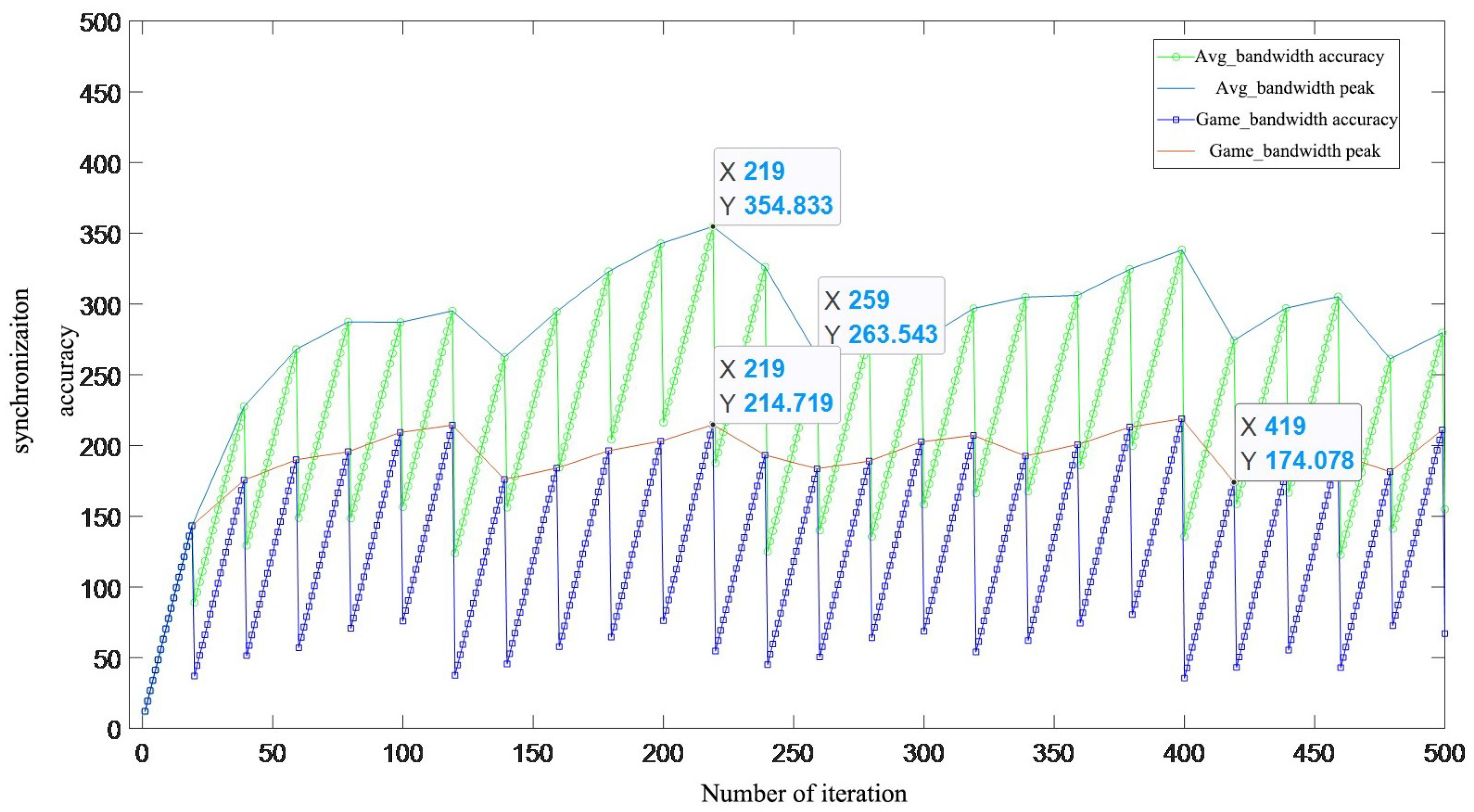
3.2. Convergence Analysis

In this section, the effectiveness of the proposed model in converging to the Nash equilibrium is validated, and the characteristics of the benefit function and user synchronization satisfaction curves during the convergence process are analyzed. The network capacity is set to 10, with users requiring synchronization for 1 and 2 devices, respectively. User 1 requires minute-level synchronization accuracy, with a synchronization accuracy value of 1, while User 2 requires second-level synchronization accuracy, with a value of 2. Other parameters follow the basic parameter settings from the previous section.

First, the non-cooperative game among users at the lower layer is analyzed under a given server pricing strategy. The main goal of the game is for the two users to adjust their bandwidth requirements based on the current pricing strategy. Each iteration of the upper-layer game includes one iteration of the lower-layer game. An iteration of the lower-layer game corresponds to one time slot within a signal cycle. The results of the utility function of the game are illustrated in Figure 3 and Figure 4.

In the early stages of the game, due to the network’s availability and lower user pricing, the usage of bandwidth for synchronization by users rapidly increases, leading to a swift rise in the utility function. As the game progresses, pricing gradually increases, leading to a slowdown in user demand and a gradual deceleration in the growth rate of user utility until Nash equilibrium is achieved. This confirms the convergence of the model.

In Figure 5, the overall trend of the utility function can be divided into three main phases based on the effects of demand and pricing:

1.

The server’s revenue rapidly increases. Due to the ample network resources and high synchronization demand from users, users quickly consume as much bandwidth as possible, leading to a substantial rise in the server’s revenue.

2.

The game has not yet reached equilibrium. With the current pricing, users continue to adjust their bandwidth strategies incrementally to optimize their own utility. Consequently, the server gradually adjusts its pricing, resulting in a slow decrease in the server’s revenue.

3.

Both user and server revenues stabilize, reaching an equilibrium state. Users with high synchronization accuracy requirements occupy more bandwidth. Once the system achieves equilibrium, and provided there are no new users or changes in user demand, the system will maintain this stable synchronization state.

Due to the dynamic nature of real-world power communication network typologies, the model needs to be validated for its applicability to dynamic access user devices in clock synchronization bandwidth allocation. We verify the game-theoretic effects of the proposed model under the scenario where two users are fixed, and one user joins dynamically. User 1 $\left(w=6,q=3\right)$ and User 2 $\left(w=3,q=2\right)$ are fixed users within the network. User 3 $\left(w=1,q=1\right)$ joins the network at the 300-th round and leaves the network at the 600-th round. The remaining parameters are kept constant throughout the experiment.

In Figure 6, for pricing strategy under the same server, under different network capacity, the user needs to pay the price in line with the previously mentioned smaller network capacity, which is higher pricing for the user; the larger the user demand, the higher the pricing characteristics needed to meet the model-differentiated pricing.

3.3. Synchronization Accuracy Simulation

To simulate clock synchronization results under limited bandwidth conditions where users allocate resources based on game theory, this study employs a linear clock model and compares its synchronization performance with the commonly used bandwidth allocation scheme, which reserves bandwidth based on the average number of user devices.

Firstly, the scenario with two users is examined, and the experimental results are presented in Figure 7. The simulation is conducted with the following parameters: both users require synchronization accuracy of 1 min, and the number of devices requiring synchronization is 3 for one user and 7 for the other. Each user device has 10 connected synchronization devices. To minimize system latency as much as possible, during each synchronization simulation, the clocks with the largest latency deviations are selected from the pre-allocated bandwidth to compensate for the delays. The deviation is minimized during each compensation process. Synchronization occurs every 20 iterations.

The comparison shows that the synchronization accuracy with game theory-based resource optimization is approximately 11.2 ms, while the average bandwidth allocation method yields an accuracy of about 44.5 ms. This demonstrates a clear improvement with the game theory approach.

To test scalability, a simulation with 1000 user devices was conducted, as shown in Figure 8. With a network capacity of 1000 and a synchronization accuracy requirement of 1 s for each device, and each user device having 500 connected synchronization devices, synchronization occurred every 10 iterations. Figure 8 indicates that the average accuracy with bandwidth allocation is about 91.3 ms, whereas the accuracy with game theory optimization is approximately 40.6 ms.

In this section, we compare the synchronization errors (in milliseconds) of the two methods, e.g., 11.2 ms for game-theoretic optimization and 44.5 ms for bandwidth reservation in the small-scale scenario (Figure 7), and 40.6 ms versus 91.3 ms in the large-scale scenario (Figure 8). These results directly reflect the difference in synchronization accuracy. The experimental results indicate that: (1) bandwidth allocation affects the accuracy and variability of clock synchronization; (2) proper bandwidth allocation improves synchronization performance.

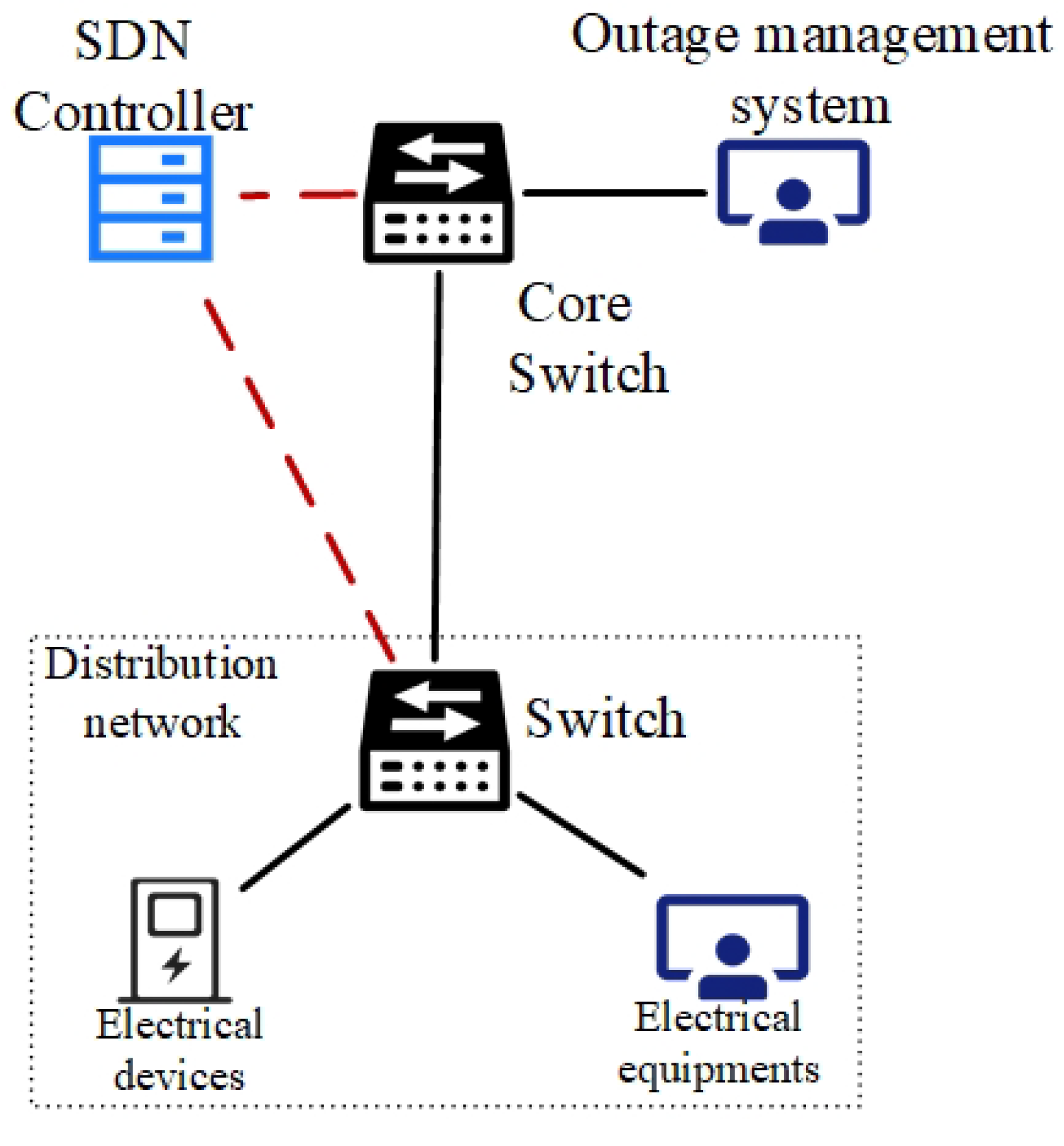
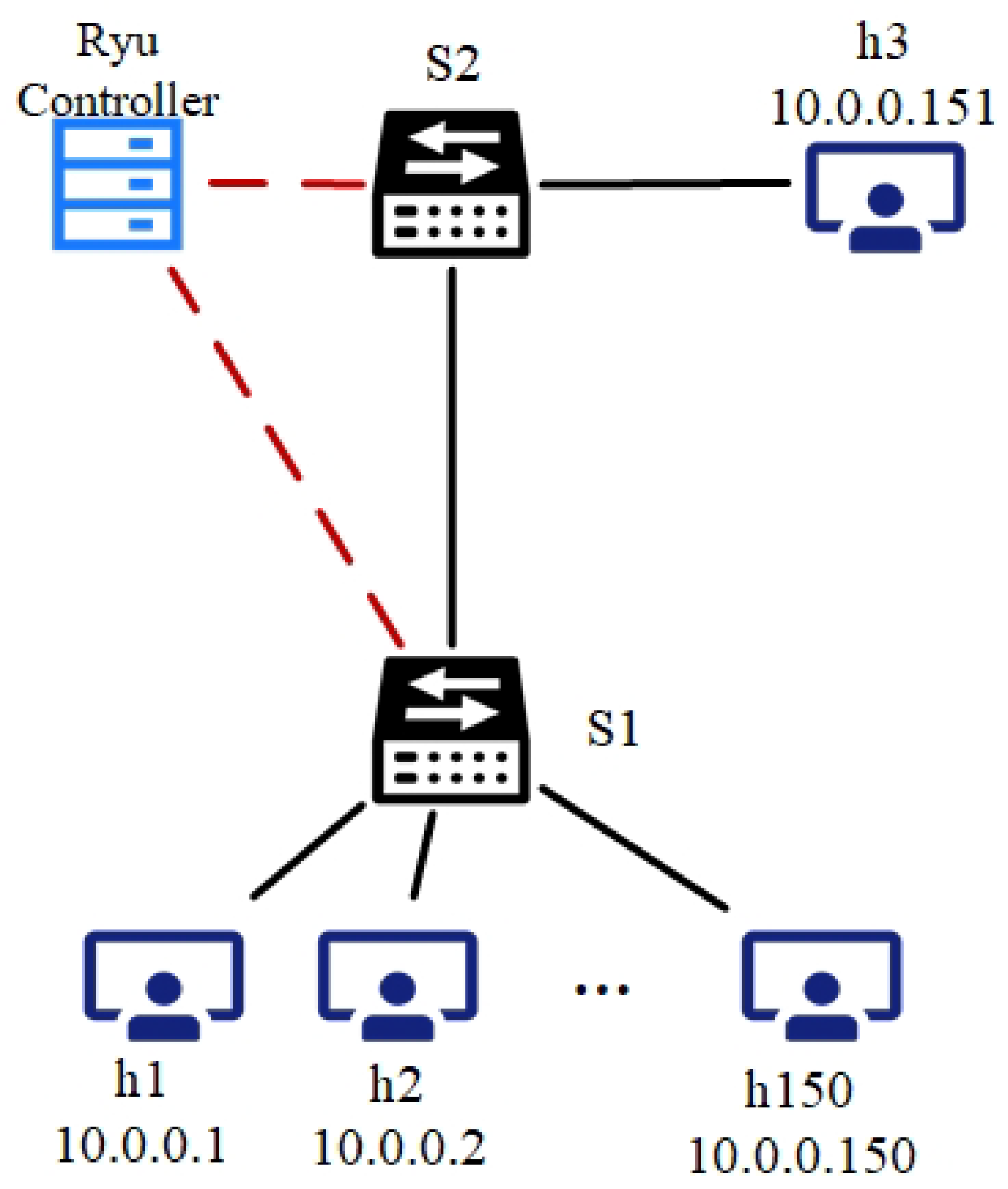
4. Virtual Simulation Platform

Clock synchronization for power system operations necessitates intelligent communication networks with guaranteed quality of service. To validate the effectiveness of the proposed game-theoretic model and ensure operational reliability with user synchronization performance, we implement the following experimental framework. Due to the demand for IP-based power networks, while the master station of the power grid can access larger-scale power user equipment, a further software-defined network (SDN) can be implemented in the power network to realize the dynamic configuration of network resources; therefore, the Mininet+Ryu architecture of the network simulator used in this paper can simulate the realization of the power network to a certain extent, show that the distribution game process can be dynamically adjusted according to user needs. In Figure 9, a Mininet-based software-defined networking (SDN) testbed is deployed to emulate synchronization packet transmission.

Specific simulation parameters are detailed in

Table 2. Testbed settings.

Parameter	Symbol
Operating system	Ubuntu 16.04 LTS
Compilation language	Python 2.7 & 3.5
SDN framework	Ryu 4.23
Dynamic network analysis library	NetworkX 2.1
Network simulation platform	Mininet2.3.0

. To validate the synchronization accuracy between average reserved bandwidth allocation and game-theoretic bandwidth allocation strategies under 150-user access conditions, the network topology is configured as shown in Figure 10, and the corresponding packet delay measurements are illustrated in Figure 11.

The network emulation platform setup consists of the following structure.

• Mininet simulates the grid communication network topology and generates dynamic traffic.
• Ryu controller implements SDN logic and dynamically adjusts queue priority via OpenFlow protocol to support synchronized packet low-latency transmission.
• MATLAB and Mininet interact via Socket API: MATLAB calculates the bandwidth allocation policy, Mininet enforces the policy and returns end-to-end delay data.
• Link bandwidth: 100 Mbps, propagation delay 1 ms (backbone link)/5 ms (edge link).

In this section, with the virtual simulation platform experiment, the end-to-end transmission delay of synchronization packets is measured by Mininet, which is 745 ms for the game-theoretic method and 2805 ms for the bandwidth reservation (Figure 11), which shows that the delay is significantly reduced. Due to the limited network bandwidth in the simulated environment, synchronization accuracy is constrained. The proposed game-theoretic allocation strategy achieves a synchronization accuracy of 745 ms, significantly outperforming the 2805 ms latency observed under the average reserved bandwidth approach. This demonstrates a 3.76-fold improvement in synchronization precision through optimized resource allocation.

Compared to the average allocation strategy, the bandwidth allocation strategy based on the game-theoretic model significantly reduces the transmission delay of synchronous data packets and decreases the delay jitter during propagation. This simulation verifies that optimizing communication resource allocation through game-theoretic approaches tailored to user demands can effectively enhance synchronization accuracy.

5. Conclusions

It is known that excessive load on a network leads to performance degradation and network congestion. The introduction of new energy devices into the power communication network causes noise interference, which reduces communication capacity and impairs the synchronization process of centralized timing due to packet congestion.

This paper proposes a clock communication resource allocation model based on a Stackelberg two-level game, mathematically formalizing the abstract problem by considering the game-theoretic relationships between network synchronization servers and user devices, as well as between user devices themselves. The existence of Nash equilibrium in the game model is verified, and an iterative algorithm is designed to solve for this equilibrium. The conclusions drawn from the simulation of delays are as follows: (1) The algorithm converges and the Nash equilibrium exists, as demonstrated by numerical simulations. (2) In networks with dynamically joining users, the algorithm quickly converges and adjusts resource allocation dynamically based on user demand. (3) The proposed Stackelberg game-based clock communication resource allocation model is effective for both static and dynamic power communication networks, improving the network’s clock synchronization performance. Inspired by the Stackelberg game, this paper discusses the challenge faced when a significant number of power devices connect to the network. The existing power communication network cannot meet the synchronization accuracy requirements of all these devices. Therefore, it is essential to dynamically allocate network resources using game theory to enhance the synchronization accuracy of the power network.

However, many challenges remain in dynamic adaptability, security, and industrial deployment within the future smart grid. Our future work will prioritize AI-driven optimization, lightweight computation, and cross-domain standardization to advance clock synchronization in next-generation power systems.