Parametric Sensitivity of a PEM Electrolyzer Mathematical Model: Experimental Validation on a Single-Cell Test Bench
Abstract
:1. Introduction
2. Materials and Methods
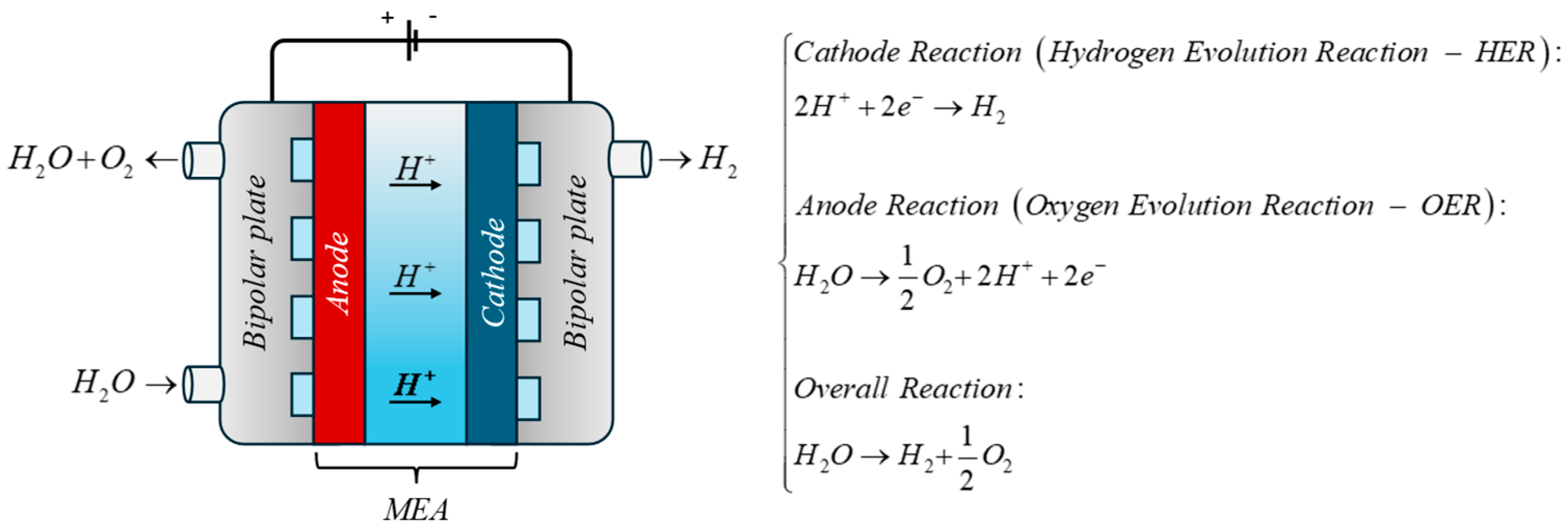
2.1. Test Bench
2.2. Testing Protocols
3. Mathematical Model
3.1. Model Description
3.1.1. Open-Circuit Voltage
3.1.2. Activation Overvoltage
3.1.3. Ohmic Overvoltage
3.1.4. Diffusion Overvoltage
3.2. Model Identification
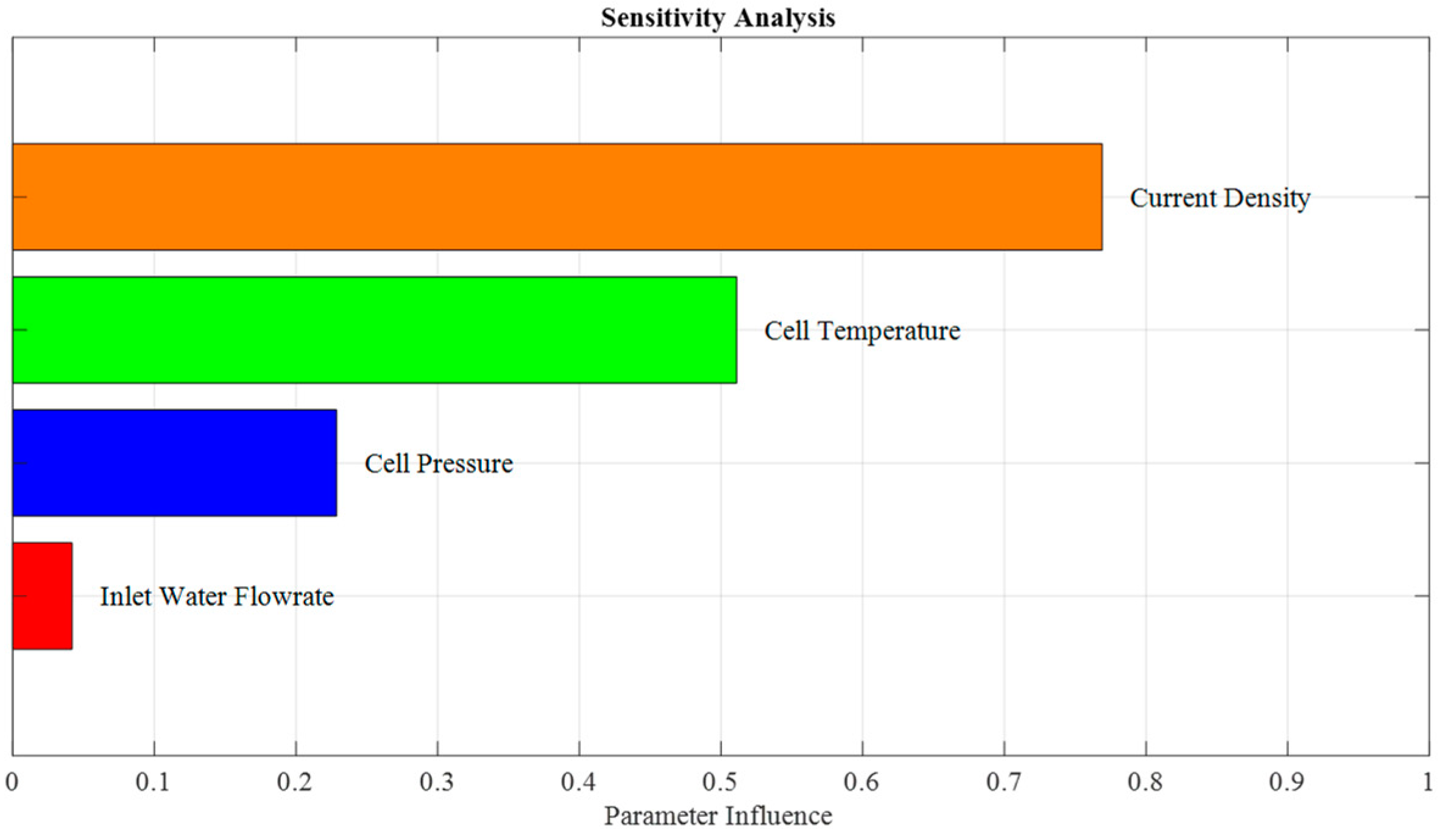
3.2.1. Sensitivity Analysis of Model Output
- (1)
- At fixed values of parameters contained in Table 2, SAMO was run by considering the cell voltage as the output of the model and operating variables as the input vector. Input values were generated using a Gaussian distribution with a 5% standard deviation around their nominal values. The input variables were then sorted based on their influence on the cell voltage.
- (2)
- No correlations were considered among these four variables.
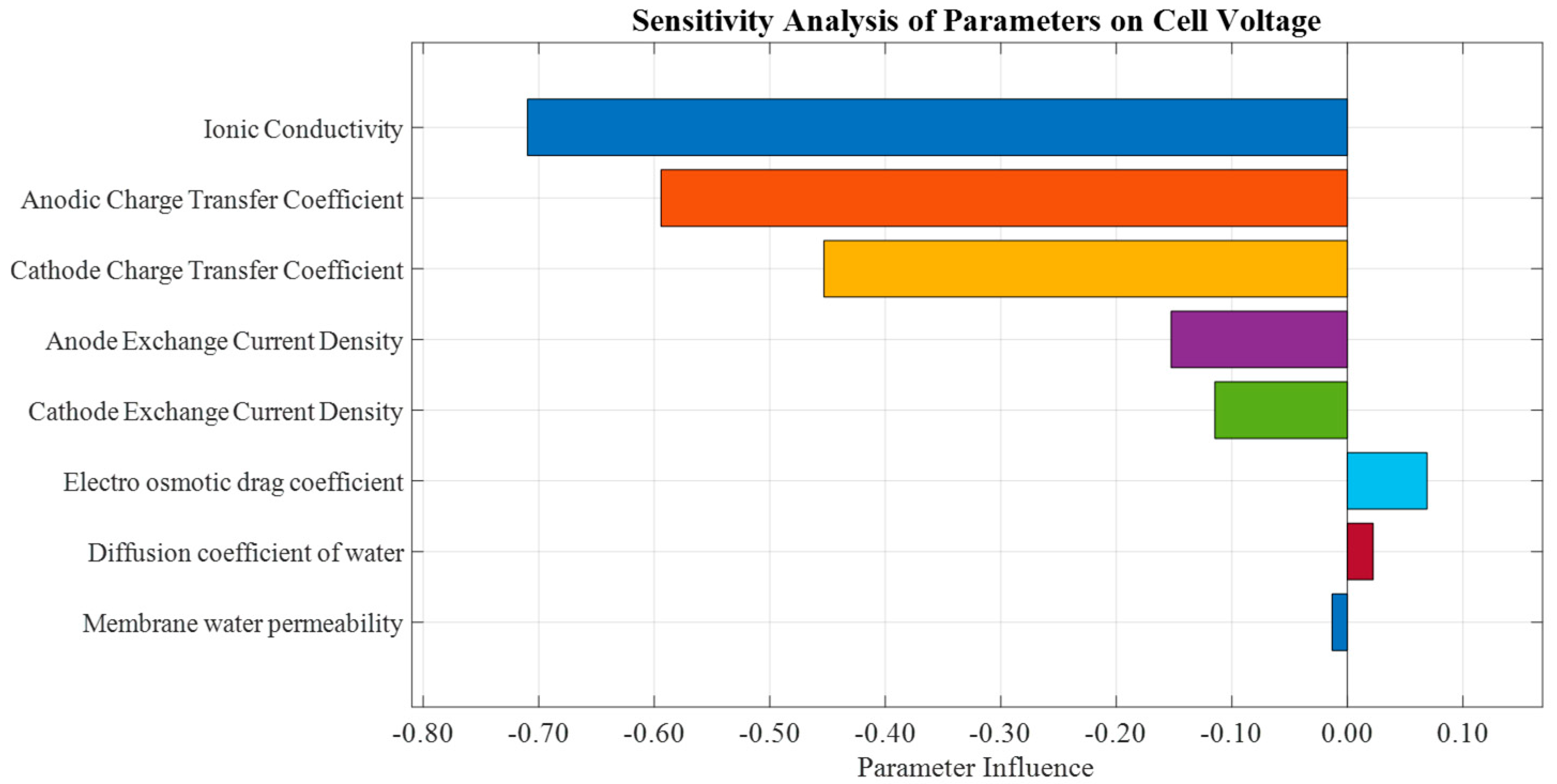
3.2.2. Parametric Sensitivity
4. Results
4.1. Sensitivity Analysis of the Model
4.2. Parametric Sensitivity of the Model
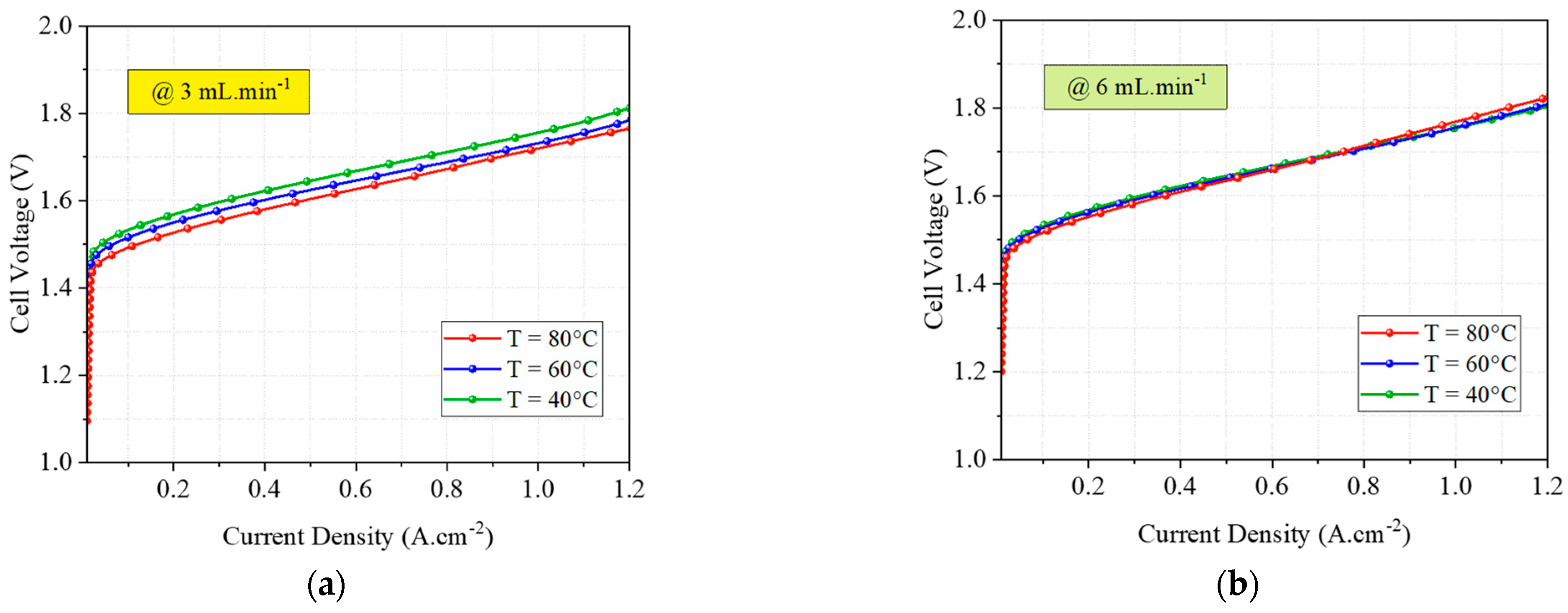
4.3. Experimental Tests
4.4. Parameter Estimation
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kopp, M.; Coleman, D.; Stiller, C.; Scheffer, K.; Aichinger, J.; Scheppat, B. Energiepark Mainz: Technical and Economic Analysis of the Worldwide Largest Power-to-Gas Plant with PEM Electrolysis. Int. J. Hydrogen Energy 2017, 42, 13311–13320. [Google Scholar] [CrossRef]
- Boudellal, M. Power-to-Gas: Renewable Hydrogen Economy for the Energy Transition; De Gruyter: Berlin, Germany, 2018; ISBN 978-3-11-055981-1. [Google Scholar]
- Hermesmann, M.; Müller, T.E. Green, Turquoise, Blue, or Grey? Environmentally Friendly Hydrogen Production in Transforming Energy Systems. Prog. Energy Combust. Sci. 2022, 90, 100996. [Google Scholar] [CrossRef]
- Liu, W.; Zuo, H.; Wang, J.; Xue, Q.; Ren, B.; Yang, F. The Production and Application of Hydrogen in Steel Industry. Int. J. Hydrogen Energy 2021, 46, 10548–10569. [Google Scholar] [CrossRef]
- Feng, Q.; Yuan, X.-Z.; Liu, G.; Wei, B.; Zhang, Z.; Li, H.; Wang, H. A Review of Proton Exchange Membrane Water Electrolysis on Degradation Mechanisms and Mitigation Strategies. J. Power Sources 2017, 366, 33–55. [Google Scholar] [CrossRef]
- El-Shafie, M. Hydrogen Production by Water Electrolysis Technologies: A Review. Results Eng. 2023, 20, 101426. [Google Scholar] [CrossRef]
- Qazi, U.Y. Future of Hydrogen as an Alternative Fuel for Next-Generation Industrial Applications; Challenges and Expected Opportunities. Energies 2022, 15, 4741. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, S.; Chi, B.; Tu, Z. Technological Limitations and Recent Developments in a Solid Oxide Electrolyzer Cell: A Review. Int. J. Hydrogen Energy 2024, 50, 548–591. [Google Scholar] [CrossRef]
- Lahrichi, A.; El Issmaeli, Y.; Kalanur, S.S.; Pollet, B.G. Advancements, Strategies, and Prospects of Solid Oxide Electrolysis Cells (SOECs): Towards Enhanced Performance and Large-Scale Sustainable Hydrogen Production. J. Energy Chem. 2024, 94, 688–715. [Google Scholar] [CrossRef]
- Marini, S.; Salvi, P.; Nelli, P.; Pesenti, R.; Villa, M.; Berrettoni, M.; Zangari, G.; Kiros, Y. Advanced Alkaline Water Electrolysis. Electrochim. Acta 2012, 82, 384–391. [Google Scholar] [CrossRef]
- Zeng, K.; Zhang, D. Recent Progress in Alkaline Water Electrolysis for Hydrogen Production and Applications. Prog. Energy Combust. Sci. 2010, 36, 307–326. [Google Scholar] [CrossRef]
- Vincent, I.; Bessarabov, D. Low Cost Hydrogen Production by Anion Exchange Membrane Electrolysis: A Review. Renew. Sustain. Energy Rev. 2018, 81, 1690–1704. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, L.; Zhang, J.; Wang, J.; Hu, Y.; Jiang, H.; Li, C. Anion Exchange Membrane Water Electrolyzer: Electrode Design, Lab-Scaled Testing System and Performance Evaluation. EnergyChem 2022, 4, 100087. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A Comprehensive Review on PEM Water Electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Wallnöfer-Ogris, E.; Grimmer, I.; Ranz, M.; Höglinger, M.; Kartusch, S.; Rauh, J.; Macherhammer, M.-G.; Grabner, B.; Trattner, A. A Review on Understanding and Identifying Degradation Mechanisms in PEM Water Electrolysis Cells: Insights for Stack Application, Development, and Research. Int. J. Hydrogen Energy 2024, 65, 381–397. [Google Scholar] [CrossRef]
- Niyati, A.; Moranda, A.; Beigzadeh Arough, P.; Navarra, F.M.; Paladino, O. Electrochemical Performance of a Hybrid NiCo2O4@NiFelt Electrode at Different Operating Temperatures and Electrolyte pH. Energies 2024, 17, 3703. [Google Scholar] [CrossRef]
- Abdin, Z.; Webb, C.J.; Gray, E.M. Modelling and Simulation of a Proton Exchange Membrane (PEM) Electrolyser Cell. Int. J. Hydrogen Energy 2015, 40, 13243–13257. [Google Scholar] [CrossRef]
- Folgado, F.J.; González, I.; Calderón, A.J. Simulation Platform for the Assessment of PEM Electrolyzer Models Oriented to Implement Digital Replicas. Energy Convers. Manag. 2022, 267, 115917. [Google Scholar] [CrossRef]
- Awasthi, A.; Scott, K.; Basu, S. Dynamic Modeling and Simulation of a Proton Exchange Membrane Electrolyzer for Hydrogen Production. Int. J. Hydrogen Energy 2011, 36, 14779–14786. [Google Scholar] [CrossRef]
- Marefatjouikilevaee, H.; Auger, F.; Olivier, J.-C. Static and Dynamic Electrical Models of Proton Exchange Membrane Electrolysers: A Comprehensive Review. Energies 2023, 16, 6503. [Google Scholar] [CrossRef]
- Han, B.; Mo, J.; Kang, Z.; Yang, G.; Barnhill, W.; Zhang, F.-Y. Modeling of Two-Phase Transport in Proton Exchange Membrane Electrolyzer Cells for Hydrogen Energy. Int. J. Hydrogen Energy 2017, 42, 4478–4489. [Google Scholar] [CrossRef]
- Marangio, F.; Santarelli, M.; Cali, M. Theoretical Model and Experimental Analysis of a High Pressure PEM Water Electrolyser for Hydrogen Production. Int. J. Hydrogen Energy 2009, 34, 1143–1158. [Google Scholar] [CrossRef]
- Hwang, J.J.; Lai, L.K.; Wu, W.; Chang, W.R. Dynamic Modeling of a Photovoltaic Hydrogen Fuel Cell Hybrid System. Int. J. Hydrogen Energy 2009, 34, 9531–9542. [Google Scholar] [CrossRef]
- Choi, P. A Simple Model for Solid Polymer Electrolyte (SPE) Water Electrolysis. Solid State Ion. 2004, 175, 535–539. [Google Scholar] [CrossRef]
- Ma, Z.; Witteman, L.; Wrubel, J.A.; Bender, G. A Comprehensive Modeling Method for Proton Exchange Membrane Electrolyzer Development. Int. J. Hydrogen Energy 2021, 46, 17627–17643. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Shomope, I.; Al-Othman, A.; Alshraideh, H. Prediction of Hydrogen Production in Proton Exchange Membrane Water Electrolysis via Neural Networks. Int. J. Thermofluids 2024, 24, 100849. [Google Scholar] [CrossRef]
- Brezak, D.; Kovač, A.; Firak, M. MATLAB/Simulink Simulation of Low-Pressure PEM Electrolyzer Stack. Int. J. Hydrogen Energy 2023, 48, 6158–6173. [Google Scholar] [CrossRef]
- Harrison, K.W.; Hernández-Pacheco, E.; Mann, M.; Salehfar, H. Semiempirical Model for Determining PEM Electrolyzer Stack Characteristics. J. Fuel Cell Sci. Technol. 2005, 3, 220–223. [Google Scholar] [CrossRef]
- Gomez Vidales, A.; Millan, N.C.; Bock, C. Modeling of Anion Exchange Membrane Water Electrolyzers: The Influence of Operating Parameters. Chem. Eng. Res. Des. 2023, 194, 636–648. [Google Scholar] [CrossRef]
- Milewski, J.; Guandalini, G.; Campanari, S. Modeling an Alkaline Electrolysis Cell through Reduced-Order and Loss-Estimate Approaches. J. Power Sources 2014, 269, 203–211. [Google Scholar] [CrossRef]
- Biaku, C.Y.; Dale, N.V.; Mann, M.D.; Salehfar, H.; Peters, A.J.; Han, T. A Semiempirical Study of the Temperature Dependence of the Anode Charge Transfer Coefficient of a 6 kW PEM Electrolyzer. Int. J. Hydrogen Energy 2008, 33, 4247–4254. [Google Scholar] [CrossRef]
- Sezer, N.; Bayhan, S.; Fesli, U.; Sanfilippo, A. A Comprehensive Review of the State-of-the-Art of Proton Exchange Membrane Water Electrolysis. Mater. Sci. Energy Technol. 2025, 8, 44–65. [Google Scholar] [CrossRef]
- García-Valverde, R.; Espinosa, N.; Urbina, A. Simple PEM Water Electrolyser Model and Experimental Validation. Int. J. Hydrogen Energy 2012, 37, 1927–1938. [Google Scholar] [CrossRef]

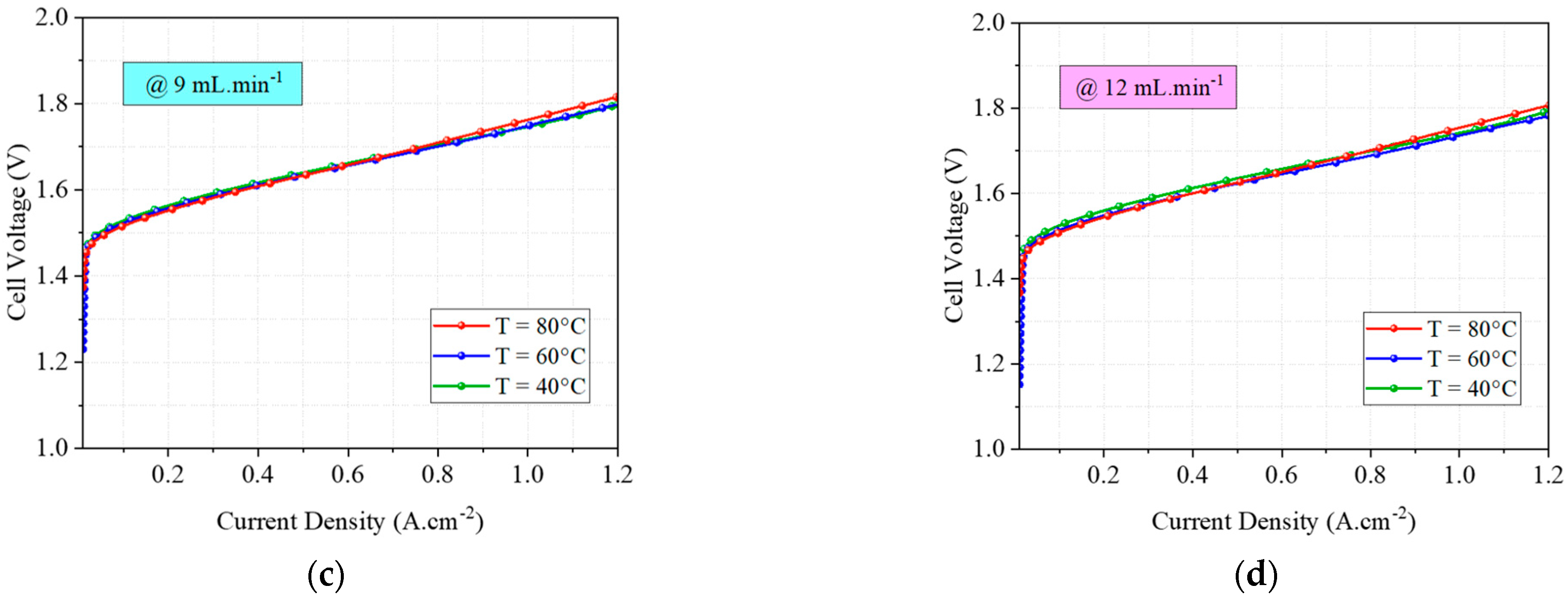
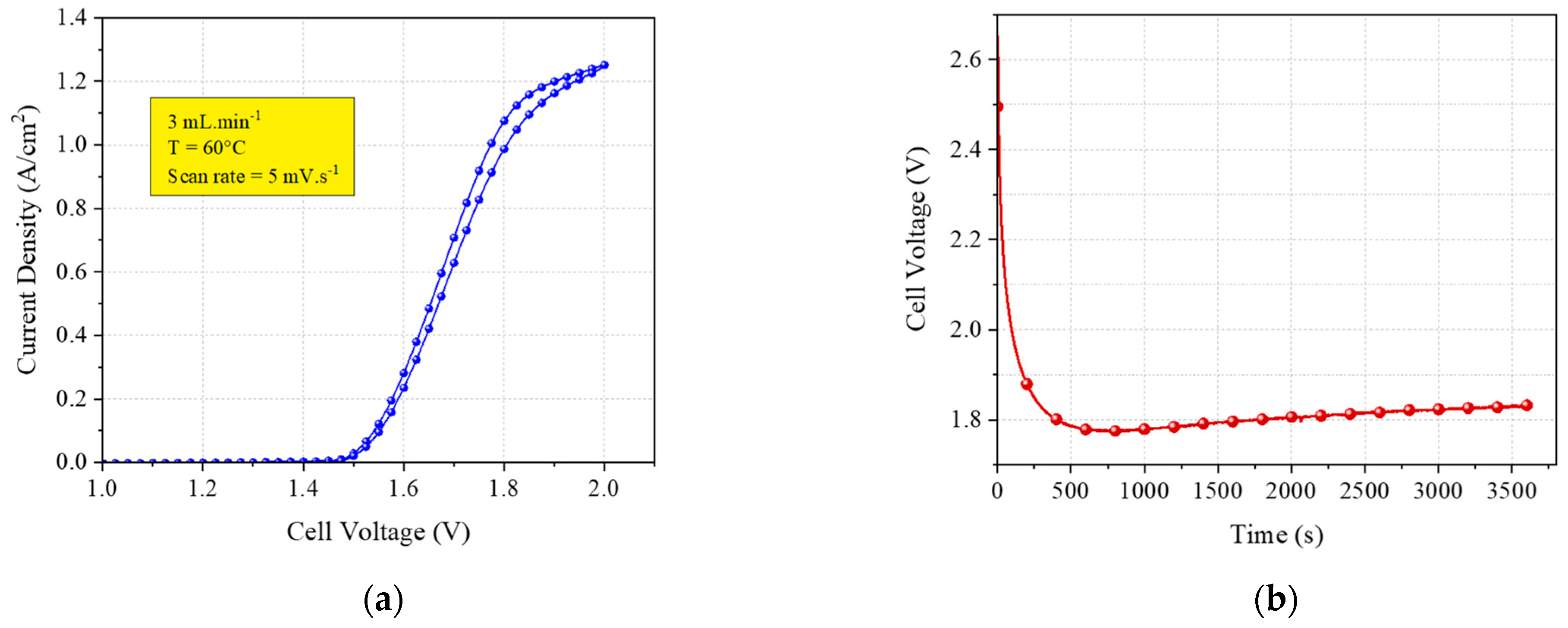

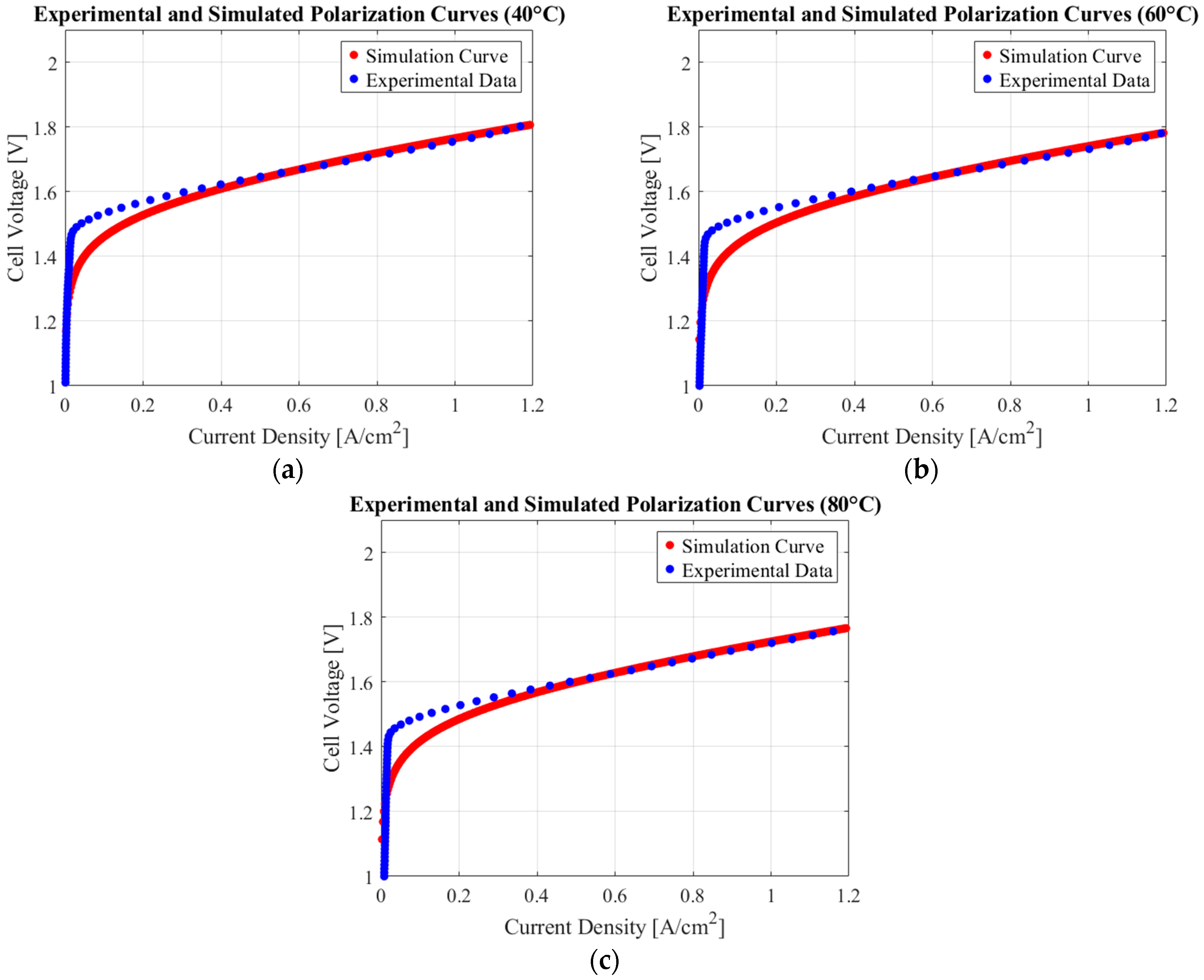
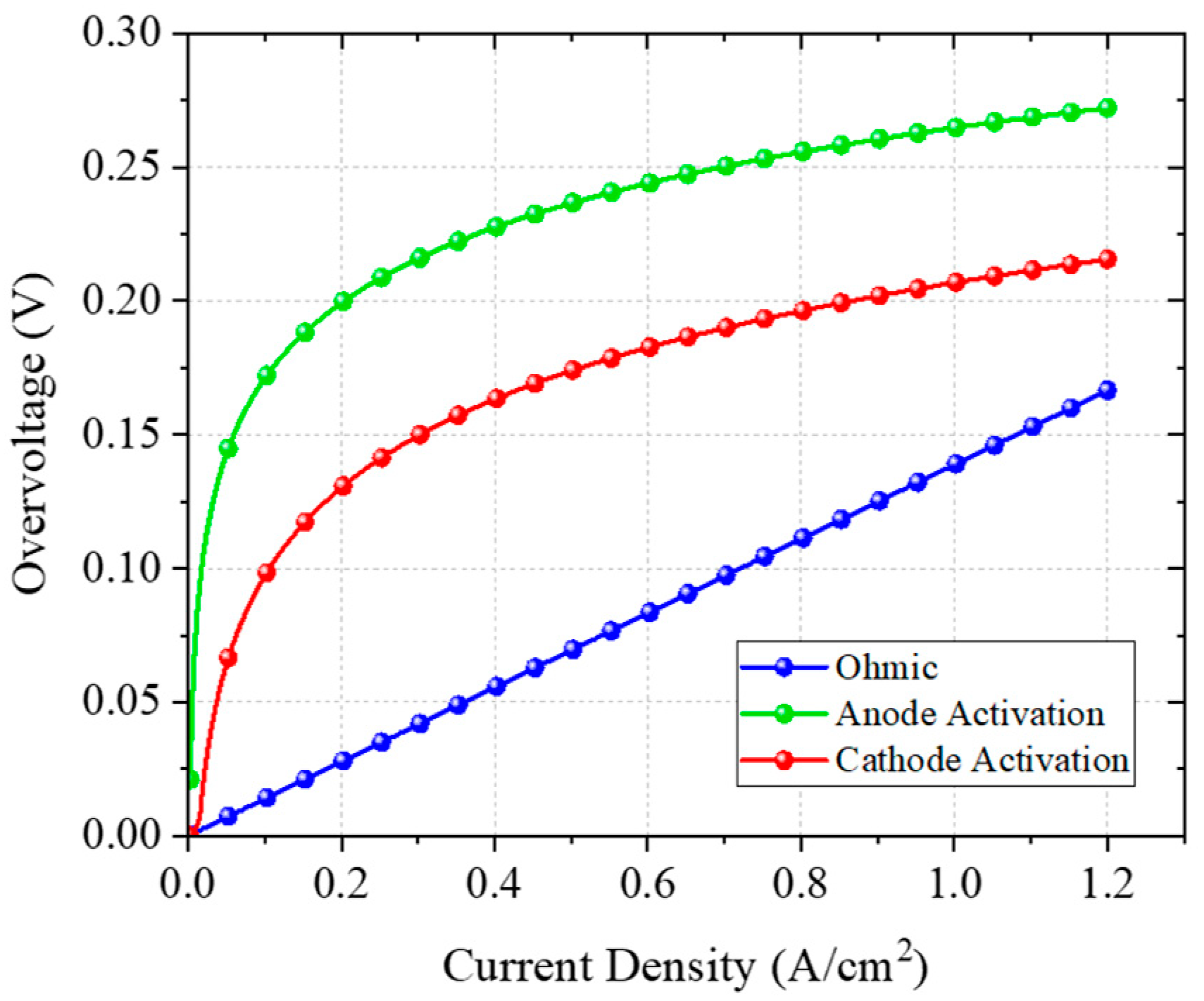


| Variable | Value | Unit | Type |
|---|---|---|---|
| Cell temperature T | 313.15–353.15 | K | Input |
| Cell pressure P | 1.013 × 105 | Pa | Input |
| Inlet water flow rate | 3–12 | mL min−1 | Input |
| Outlet water flow rate | 0–12 | mL min−1 | Input |
| Inlet water temperature Tw | 313.15–363.15 | K | Input (considered = T) |
| Cell Current | 0–6 | A | Input |
| Cell Voltage | 0–1.82 | V | Output |
| Cell power | 0–11 | W | Output (correlated) |
| Cathode current density jC | 0–1.2 | A cm−2 | State |
| Anode current density jA | 0–1.2 | A cm−2 | State |
| Anode pressure pA | 1.013 × 105 | Pa | State |
| Cathode pressure pC | 1.013 × 105 | Pa | State |
| Parameter | Value | Unit | |
|---|---|---|---|
| Universal gas constant R | 8.314 | J mol−1 K−1 | - |
| Faraday’s constant F | 96,485.3 | A s mol−1 | - |
| Water density H2O ρH2O | 1000 | kg m−3 | fixed value (correlations with T) |
| Cathode thickness δel,cat | 0.045–0.05 | cm | fixed value, measured |
| Anode thickness δel,an | 0.045–0.05 | cm | fixed value, measured |
| Water molar mass Mm,H2O | 18 | g mol−1 | - |
| Oxygen molar mass Mm,O2 | 32 | g mol−1 | - |
| Water viscosity μH2O | 1.1 × 10−2 | g cm−1 s | fixed value (correlations with T) |
| Membrane water permeability Kdarcy | 1.58 × 10−14 ± 10% | cm2 | to be estimated |
| Membrane thickness δm | 1.27 × 10−2 | Cm | fixed value, measured |
| Cathode exchange current density j0,c | 1 × 10⁻3–3.03 × 10−1 | A cm−2 [32] | to be estimated |
| Anode exchange current density j0,a | 1 × 10−10–5.93 × 10−3 | A cm−2 [32] | to be estimated |
| Ionic conductivity σ | 0.075–0.097 | S cm−1 [27] | to be estimated |
| Critical pressure of H2 | 1.28 × 106 | Pa | fixed value |
| Critical temperature of H2 | 33.3 | K | fixed value |
| Critical pressure of O2 | 4.97 × 106 | Pa | fixed value |
| Critical temperature of O2 | 154.4 | K | fixed value |
| Critical pressure of H2O | 21.83 × 106 | Pa | fixed value |
| Critical temperature of H2O | 647.3 | K | fixed value |
| Empirical coefficient a | 3.640 × 10−4 | [27] | fixed value, previously estimated |
| Empirical coefficient b | 2.334 | [27] | fixed value, previously estimated |
| Empirical coefficient c | 0.785 | [27] | fixed value, previously estimated |
| Cathode charge transfer coefficient αC | 0.25–0.5 | [32] | to be estimated |
| Anode charge transfer coefficient αA | 0.2–2 | [32] | to be estimated |
| Diffusion coefficient of water through the membrane Dw | 1.28 × 10−10 ± 10% | m2 s−1 | fixed value, previously estimated |
| Electro osmotic drag coefficient nd | 3 ± 10% | molH2O molH+−1 | to be estimated |
| Hydrogen gas partial pressure pH2 | (0.5–1)⋅pc | Pa | |
| Oxygen gas partial pressure pO2 | (0.2–1)⋅pA | Pa | |
| Water vapor partial pressure pH2O | (0–1) pA | Pa | |
| Anode and cathode cross-sectional surface area SA and SC | 6.25 | cm2 | fixed value, measured |
| Active cell surface and total area of the membrane Am | 5 | cm2 | fixed value, measured |
| Porosity of the electrode ε | 0.3 | fixed value, measured | |
| Percolation threshold of the electrode εp | 0.11 | fixed value, estimated | |
| Distance between the anode or cathode and the membrane dam, dcm | 0.00001 | m | fixed value, measured |
| Parameter | Initial Guess | Lower Bound | Upper Bound |
|---|---|---|---|
| Cathode exchange current density (j0,C) | 10−3 (A·cm−2) | 1 × 10⁻3 (A·cm−2) | 3.03 × 10⁻1 (A·cm−2) |
| Anode exchange current density (j0,A) | 10−7 (A·cm−2) | 1 × 10⁻10 (A·cm−2) | 5.93 × 10⁻3 (A·cm−2) |
| Cathode charge transfer coefficient (αC) | 0.5 | 0.25 | 0.5 |
| Anode charge transfer coefficient (αA) | 0.5 | 0.2 | 2 |
| Ionic conductivity | 0.08 (S·cm−1) | 0.07 (S·cm−1) | 0.097 (S·cm−1) |
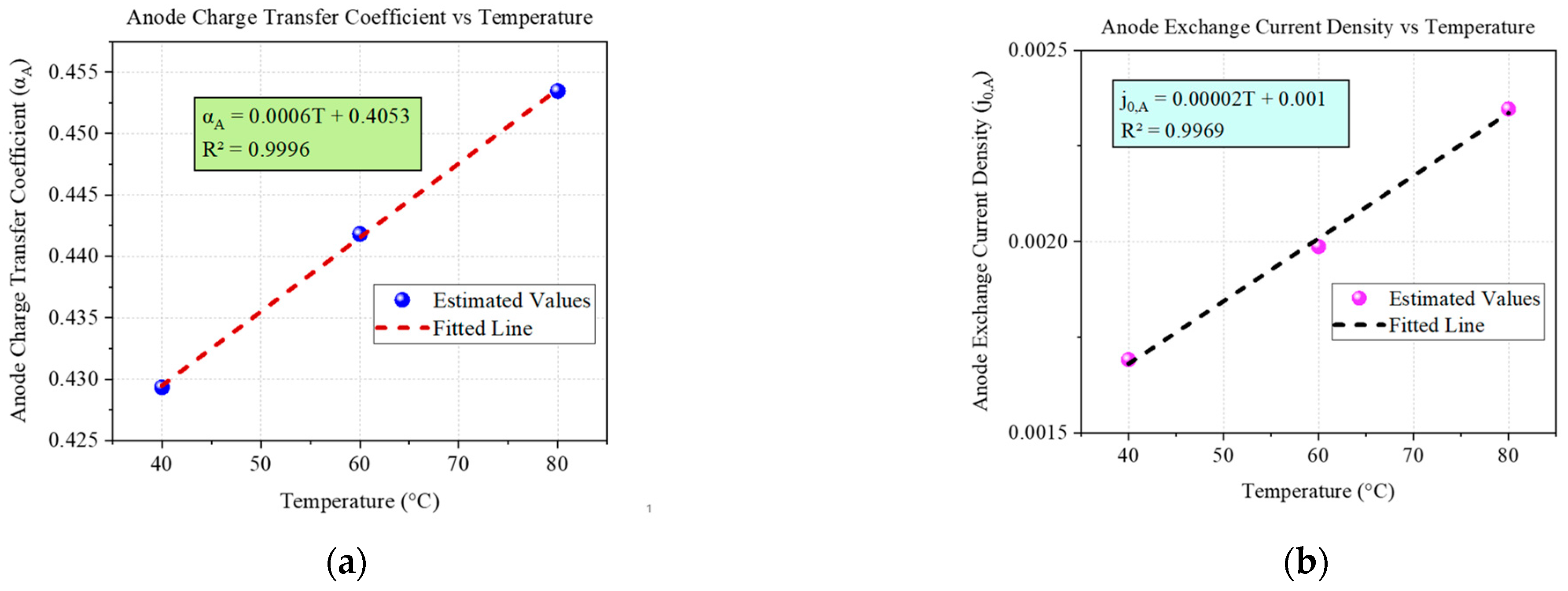
| Temperature | Anode Charge Transfer Coefficient (αA) | Cathode Charge Transfer Coefficient (αC) | Anode Exchange Current Density (j0,A) | Cathode Exchange Current Density (j0,C) | Ionic Conductivity |
|---|---|---|---|---|---|
| 40 °C | 0.42933 | 0.30782 | 0.0016912 | 0.0099411 | 0.087375 |
| 60 °C | 0.44182 | 0.32602 | 0.0019873 | 0.01117 | 0.088853 |
| 80 °C | 0.45347 | 0.3429 | 0.0023465 | 0.012528 | 0.089585 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beigzadeh Arough, P.; Moranda, A.; Niyati, A.; Paladino, O. Parametric Sensitivity of a PEM Electrolyzer Mathematical Model: Experimental Validation on a Single-Cell Test Bench. Energies 2025, 18, 2217. https://doi.org/10.3390/en18092217
Beigzadeh Arough P, Moranda A, Niyati A, Paladino O. Parametric Sensitivity of a PEM Electrolyzer Mathematical Model: Experimental Validation on a Single-Cell Test Bench. Energies. 2025; 18(9):2217. https://doi.org/10.3390/en18092217
Chicago/Turabian StyleBeigzadeh Arough, Pouya, Arianna Moranda, Ataollah Niyati, and Ombretta Paladino. 2025. "Parametric Sensitivity of a PEM Electrolyzer Mathematical Model: Experimental Validation on a Single-Cell Test Bench" Energies 18, no. 9: 2217. https://doi.org/10.3390/en18092217
APA StyleBeigzadeh Arough, P., Moranda, A., Niyati, A., & Paladino, O. (2025). Parametric Sensitivity of a PEM Electrolyzer Mathematical Model: Experimental Validation on a Single-Cell Test Bench. Energies, 18(9), 2217. https://doi.org/10.3390/en18092217









