Abstract
Nuclear steam supply systems (NSSSs) are critical to achieving safe, efficient, and flexible nuclear power generation. While deep reinforcement learning (DRL) has shown potential in optimizing NSSS control, existing single-agent approaches apply the same optimization strategies to all subsystems. This simplification ignores subsystem-specific control requirements and limits both optimization efficacy and adaptability. To resolve this gap, we propose a multi-agent reinforcement learning (MARL) framework that independently optimizes each subsystem while ensuring global coordination. Our approach extends the current NSSS optimization framework from a single-agent model to a multi-agent one and introduces a novel MARL method to foster effective exploration and stability during optimization. Experimental findings demonstrate that our method significantly outperforms DRL-based approaches in optimizing thermal power and outlet steam temperature control. This research pioneers the application of MARL to NSSS optimization, paving the way for advanced nuclear power control systems.
1. Introduction
Nuclear energy plays a crucial role in global decarbonization, with the nuclear steam supply system (NSSS) converting reactor thermal energy into steam for power generation [1]. Conventional proportional–integral–derivative (PID) controllers are widely used in NSSSs for their simplicity and stability but struggle with the system’s inherent nonlinearity and multi-variable coupling [2]. This challenge is especially pronounced in advanced reactors such as modular high-temperature gas-cooled reactors (MHTGRs), where stringent requirements for load-following and steam temperature stability call for more advanced control strategies [3,4]. As a result, advanced control optimization techniques are needed to enhance system response and performance in NSSS operations.
Model predictive control (MPC) methodologies have significantly enhanced the control capabilities of NSSS by utilizing system models to predict future behaviors and adjust control actions accordingly [5,6,7,8]. For example, dynamic matrix control (DMC), a variant of MPC, has demonstrated effectiveness in NSSSs for MHTGRs by solving finite-horizon quadratic programming problems [9]. However, a notable limitation hinders the broader application of MPC. First, the efficacy of MPC is contingent upon accurate system models, which may not be available due to the nonlinearities and complexities intrinsic to NSSSs.
The rise of deep reinforcement learning (DRL) presents a model-free alternative. DRL empowers agents to engage with their environment and discern optimal control strategies through trial and error [10,11,12]. This adaptability makes DRL particularly well suited for complex, nonlinear systems like NSSSs. For example, ET-SAC, an enhanced version of Soft Actor–Critic (SAC) [13,14] equipped with an Event-Triggered (ET) mechanism, has effectively modified the setpoint of the coordinated control system in MHTGR-based NSSSs [15]. This optimized setpoint is utilized by the subsystems (reactor, steam generator, and fluid network) within the NSSS, resulting in significant improvements in transient performance concerning thermal power and outlet steam temperature during load-following scenarios. Although DRL shows potential in optimizing multiple control objectives, further enhancements are needed to strengthen coordination among different control subsystems in NSSSs. The current DRL-based optimization approach for NSSSs treats the reactor, steam generator, and fluid network as a unified system, applying the same optimized setpoint across all components. This simplification overlooks the distinct dynamics of each subsystem, potentially limiting the effectiveness of optimization. For instance, the control strategies necessary for optimizing thermal power in the reactor can vary considerably from those required for regulating steam temperature in the steam generator or fluid network. These differences underscore the challenges faced by single-agent DRL methods in addressing the intricate interactions among NSSS subsystems.
Multi-agent reinforcement learning (MARL) presents a promising strategy to overcome these issues. By allowing each subsystem optimizer to function as an individual agent with its own tailored parameters, MARL facilitates more accurate and coordinated management throughout the system [16,17,18]. This method acknowledges the distinct dynamics of each subsystem, thereby improving overall system efficiency, responsiveness, and stability. However, MARL also brings forth additional challenges compared to single-agent DRL, such as heightened complexity in multi-agent coordination and the need for effective sampling strategies. Ensuring that multiple agents can learn independently while still collaborating to meet overarching optimization objectives necessitates a careful balance between exploration and exploitation. These challenges render MARL a more complex approach to implement, particularly in real-time control systems like NSSSs. Significantly, the use of MARL for NSSS control remains largely uncharted territory, marking a considerable research gap in the field. Addressing this gap is vital for propelling NSSS control systems toward greater autonomy, adaptability, and performance, ultimately ensuring safer and more efficient nuclear power generation.
To this motivation, this article evolves the NSSS optimization framework from a single-agent model to a multi-agent framework. This significant change facilitates the independent optimization of setpoints across the reactor, steam generator, and fluid network subsystems. Additionally, a novel MARL method is introduced to optimize NSSS control objectives within the expanded framework. The method combines the multi-agent deep deterministic policy gradient (MADDPG) framework with dynamic experience buffers (DEBs), termed MADDPG-DEB. Specifically, MADDPG-DEB features three separate buffers to address different experiences. The PID buffer preserves essential baseline PID control trajectories to ensure safety during initial training, the good buffer retains high-performance optimization trajectories to support the learning process, and the running buffer gathers real-time interaction data to adapt to environmental changes. A dynamic sampling strategy adjusts the weight of these buffers based on agent performance, allowing the system to prioritize safety, stability, and high-performance exploration in real time. Experiments demonstrate that the proposed framework and MARL method significantly enhance the transient performance optimization of thermal power and outlet steam temperature compared to the DRL-based control optimization.
The remainder of this article is outlined as follows. Section 2 details the expanded NSSS control optimization framework, and our proposed MADDPG-DEB method is elaborated in Section 3. In Section 4, the experimental results are discussed, demonstrating the effectiveness of the proposed approach, and Section 5 concludes the article and indicates future work.
2. Problem Formulation
In this section, we first introduce the NSSS multi-agent control optimization framework. Next, we formulate the NSSS multi-agent control optimization problem as a fully cooperative multi-agent task, employing decentralized partially observable Markov decision processes (DEC-POMDPs) as the standard.
2.1. NSSS Multi-Agent Control Optimization Framework
The MHTGR-based nuclear steam supply system (NSSS) comprises three tightly coupled subsystems: the reactor, the once-through steam generator (OTSG), and the fluid network (FN). The reactor generates thermal power through sustained fission reactions, while the OTSG transfers this heat to produce steam. The FN manages the circulation of feedwater and steam. These subsystems are highly interdependent and require precise coordination. This is especially important during load-following operations, which involve dynamic adjustments to thermal power and outlet steam temperature. Traditionally, NSSS coordination control employs a centralized architecture. In this setup, the thermal power setpoint is determined by external load requirements and translated into operational targets, such as neutron flux, coolant temperatures, and flow rates. This process relies on static mapping tables based on thermal–hydraulic models and reactor physics. A coordinated set of controllers then modulates key actuators to reach these targets. A detailed discussion of the coordinated control scheme and its implementation can be found in [19].
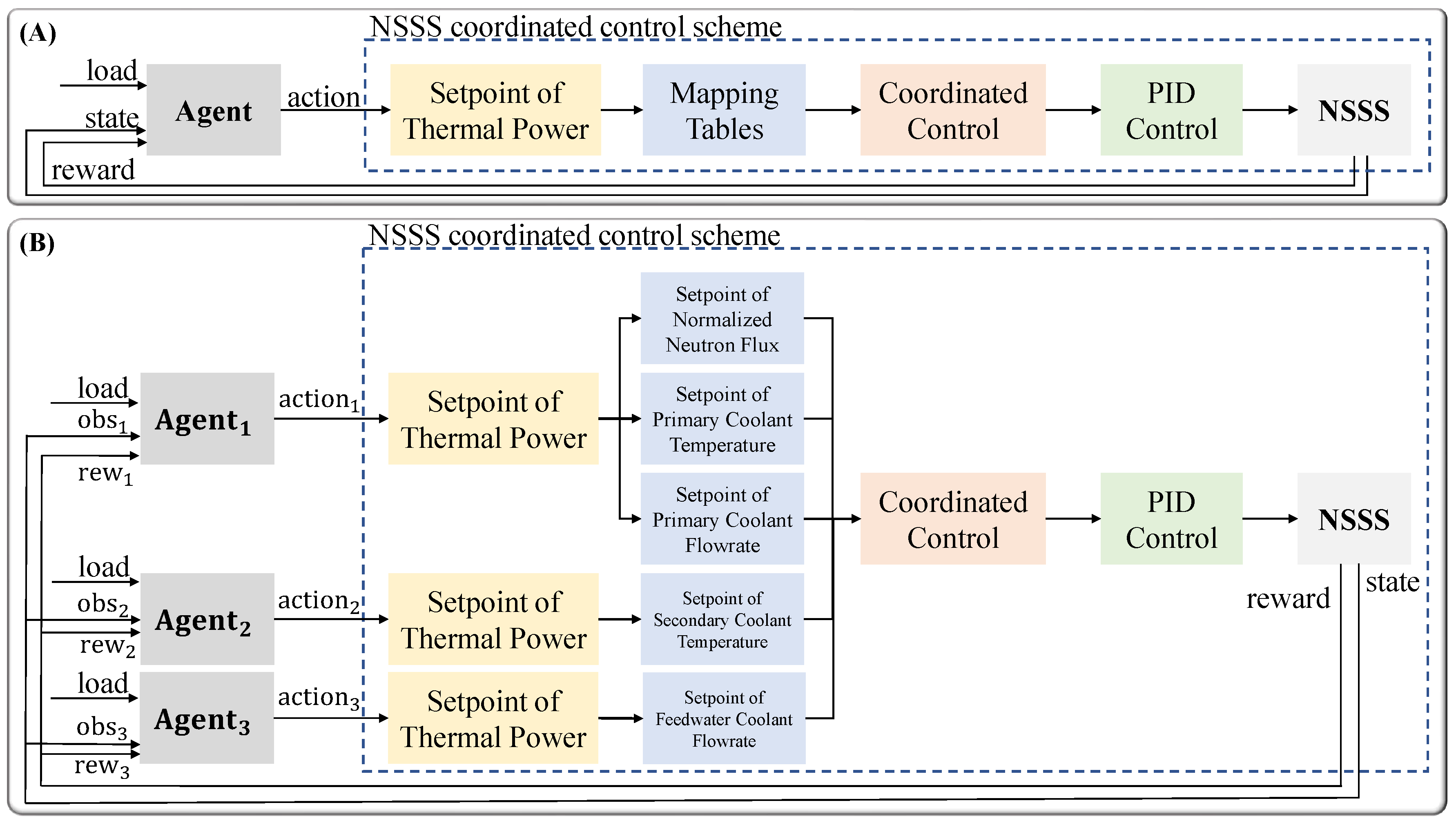
Traditional coordination control strategies ensure closed-loop stability during operation. However, they often fail to deliver satisfactory transient performance in load-following scenarios. To address these limitations, we previously developed a single-agent control optimization framework [15]. As shown in Figure 1A, a DRL agent computes an optimized thermal power setpoint based on critical NSSS operational parameters. Compared to traditional PID-only control, this optimization framework greatly enhances the transient responses of thermal power and outlet steam temperature. Despite these improvements, the single-agent framework has limitations. It struggles to capture the complex dynamics of the NSSS. By treating the reactor, OTSG, and FN as a single unit, a single optimized thermal power setpoint is applied across all subsystems. This ignores their unique operational characteristics. To address these issues, this study proposes a multi-agent control optimization framework based on MARL. Unlike the single-agent approach, the multi-agent framework treats the reactor, OTSG, and FN as separate agents. Each agent independently optimizes its own setpoints. As shown in Figure 1B, the reactor agent adjusts the setpoints of normalized neutron flux, primary coolant temperature, and primary coolant flow rate. The OTSG agent adjusts the setpoint of the secondary coolant temperature. The FN agent adjusts the setpoint of the feedwater coolant flow rate. These agents collaborate to enhance transient performance in thermal power and outlet steam temperature. This decentralized approach leverages the distinct dynamics of each subsystem, promising better transient performance and system resilience.
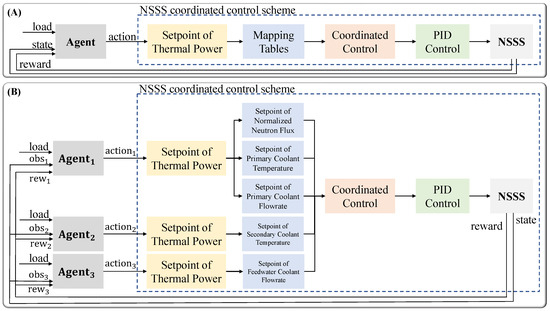
Figure 1.
NSSS control optimization frameworks: (A) single-agent approach; (B) multi-agent approach.
2.2. Control Optimization Problem Formulation
In our previous work [15], we modeled the NSSS control optimization problem as a Markov Decision Process (MDP) to support the single-agent control optimization framework. The MDP was defined by the tuple . The state space included key operational parameters of NSSS. The action space contained adjustments to a unified thermal power setpoint used across all subsystems. The function gave the likelihood of transitioning to state given the current state s and action a. The reward function reflected the objectives of control optimization, while constituted the discount factor that reconciled immediate and future rewards. Within this MDP framework, a single agent learned a policy to maximize the expected cumulative reward. Although this MDP formulation proved effective in enhancing transient performance compared to conventional PID control, it assumed uniform control over the NSSS, which overlooked the distinct dynamics of individual subsystems.
To address the constraints of the single-agent MDP formulation, in this paper, we employ a Decentralized Partially Observable MDP (DEC-POMDP) to model the multi-agent control optimization problem. The DEC-POMDP is formalized by the tuple , where denotes the set of agents. The global state space includes all key operational parameters of NSSS. The action space for each agent i encompasses setpoint adjustments like secondary coolant temperature for the OTSG agent. is the state transition function with joint action . is the shared reward function optimizing control objectives. The observation space for each agent captures local measurements like neutron flux. specifies the observation probability, and is the discount factor. Within this framework, each agent derives a decentralized policy from its local observations, collaboratively maximizing the shared reward. This DEC-POMDP approach suits the NSSS’s multi-agent control optimization framework, where subsystems with partial observability must coordinate for global stability.
3. Method
This section presents a multi-agent reinforcement learning approach to address the NSSS coordinated control problem, modeled as a DEC-POMDP within the proposed multi-agent framework. First, we introduce an enhanced multi-agent deep deterministic policy gradient (MADDPG) algorithm, termed MADDPG-DEB. This algorithm incorporates a dynamic experience buffer (DEB) to promote stable and effective exploration during training. Next, to illustrate this MARL approach, we provide a case study focused on optimizing thermal power and outlet steam temperature, showing how the coordinated control problem is modeled within this framework.
3.1. MADDPG-DEB Algorithm
The MADDPG algorithm [20] extends the deep deterministic policy gradient (DDPG) [21] to multi-agent environments, enabling collaborative decision-making among distributed entities. Built on an actor–critic architecture, MADDPG assigns each agent i an actor network parameterized by , which maps its local observation to a continuous action . Additionally, each agent is equipped with a critic network parameterized by , which evaluates the action-value function based on joint observations and joint actions . MADDPG follows the centralized training with a decentralized execution (CTDE) paradigm. During training, each critic network leverages joint observations and actions to learn interdependencies among agents. During execution, each actor operates independently using only its local observation , eliminating the need for real-time inter-agent communication. To enhance sample efficiency and training stability, MADDPG employs experience replay. Transitions of the form are stored in a replay buffer , where denotes individual rewards and represents the next joint observations. Mini-batches sampled from are used to update both the actor and critic networks. The critic is updated by minimizing the temporal difference (TD) error, defined as:
where the target value is computed using the target critic with parameters :
with the discount factor and representing the target actor network for each agent, parameterized by . The actor update follows the deterministic policy gradient:
where denotes the collection of actions produced by all agents’ actor networks. This gradient ascent aligns the actor’s policy with the critic’s evaluation of the joint action-value function. To ensure training stability, soft updates are applied to the target networks:
where is a small interpolation factor, and exploration during training is facilitated by adding noise to the actor’s output, typically sampled from a stochastic process. This ensures sufficient coverage of the action space during training.
While the standard MADDPG algorithm effectively addresses multi-agent coordination problems in complex environments, its application to NSSSs has significant limitations. Its uniform sampling from a replay buffer that includes both successful and unsafe experiences can reinforce unstable policies, slowing convergence and risking safety violations. To overcome this, we introduce MADDPG-DEB, which replaces the traditional buffer with a dynamic experience buffer (DEB) comprising three sub-buffers. A safe buffer is pre-filled with transitions from validated PID controllers. These safe experiences, which have been tested in nuclear operations, help to reduce the risk of unsafe deviations during the optimization policy learning process. Moreover, a good buffer stores high-performing experiences collected during training, where agents achieve superior rewards or maintain system stability. It accelerates convergence to optimal control policies by prioritizing quality data for learning. Moreover, a running buffer captures real-time agents–environment interactions. It facilitates continuous exploration, enabling agents to adapt to evolving system dynamics. A key innovation of MADDPG-DEB lies in its dynamic sampling strategy. During training, the probability of sampling from each sub-buffer is adjusted based on all agents’ performance and the training phase. In the early stages, when policies are unstable, a higher proportion of samples is drawn from the safe sub-buffer . This prioritizes learning from stable, safety-compliant transitions, reducing the risk of reinforcing hazardous actions. As performance improves, sampling shifts toward the running buffer and the good buffer , refining exploration with quality data. Additionally, transitions leading to unsafe states are filtered or down-weighted from sampling, further enhancing stability. The pseudocode for MADDPG-DEB is presented in Algorithm 1.
| Algorithm 1 MADDPG-DEB for NSSS Control Optimization |
|
3.2. Observations, Actions, and Rewards
To effectively apply the MARL-based agent to NSSS coordination control optimization, the design of observations, actions, and rewards for each agent is as crucial as the MARL algorithm itself. To this end, we present a detailed design scheme using the optimization of thermal power and outlet steam temperature under load-following conditions in the NSSS as a case study.
The observation space in the NSSS environment captured the dynamic behavior of the system, enabling RL-based agents to make informed decisions. For future applications in NPPs, observations should be derived directly from measurable plant data or inferred from them, including information relevant to control objectives. Specifically, each agent’s observation space included both target and reference values, such as the initial thermal power, target thermal power, and the current thermal power setpoint. These parameters reflected the system’s operating conditions and intended control targets. Additionally, deviations from these targets were included to quantify performance tracking, encompassing nuclear power deviation, thermal power deviation, and steam temperature deviation. Optimized setpoints from the MHTGR, the OTSG, and fluid network modules were also incorporated, reflecting real-time adjustments made by the RL-based agents. Furthermore, the observation space included critical variables of the NSSS. The inlet and outlet parameters for primary flow, including flow rate, temperature, and pressure, provide real-time feedback on the thermal and hydraulic conditions within the reactor core. The control rod speed, reactivity, and nuclear power collectively reflect the dynamic state of the reactor core. The feedwater mass flow rate, temperature, and pressure are essential for regulating steam production and ensuring efficient heat transfer. Complementing these are additional variables such as thermal power, steam pressure, and outlet steam temperature.
The action space was designed to enable RL agents to dynamically adjust the thermal power setpoint, thereby modulating the NSSS response under load-following conditions. Each action represented a correction to the rate of change in the thermal power setpoint for the respective MHTGR, OTSG, or fluid network module. Specifically, the action space consisted of continuous values constrained within a range of of full power per minute, corresponding to a maximum adjustment rate of of full power per minute. This constraint reflected the realistic operational limits of the NSSS, ensuring that adjustments remained within safe bounds to prevent excessive overshoot or instability. Physically, these actions modified the transition rate of the thermal power setpoint from its initial value to the target value, allowing agents to optimize the system’s response to varying load demands. By carefully bounding the action space, the design mitigated risks associated with abrupt or unsafe control actions, aligning with the stringent safety requirements of nuclear operations.
The reward function was carefully designed to steer RL agents in achieving precise control over thermal power and outlet steam temperature. At the same time, it aimed to minimize undesirable behaviors such as overshooting and oscillations. This function balanced accuracy, stability, and safety. The reward function consisted of several components, each targeting specific control objectives. First, the thermal-power-following reward incentivized the agent to minimize the deviation between the actual thermal power and its target value,
This term encouraged the agent to reduce tracking errors promptly by penalizing the absolute deviation. Moreover, a penalty was included to reduce the overshoot during power transitions,
This penalty discouraged overshooting beyond the target power, adapting to whether the system was ramping down or up, thus enhancing transition stability. Additionally, the steam-temperature-following reward was designed to maintain a stable outlet steam temperature for NSSS operation,
This component promoted accurate tracking of the target steam temperature, ensuring thermal stability in steam production. The total reward was computed as the sum of these components,
where the weights , , and are empirically tuned to prioritize precision and stability under varying load-following scenarios. To further elucidate, these weights can be adjusted based on operational priorities (e.g., emphasizing temperature stability over power tracking), offering design flexibility.
4. Simulation Results
In this section, we first describe the training process, which allows MARL agents to learn control optimization policies through iterative interactions with the NSSS environment. Then, we further demonstrate the superior performance of our proposed multi-agent optimization approach by comparing it to both the original PID controllers and the single-agent optimization approach.
4.1. Training Process
The training process was conducted within a simulation environment where the MHTGR-based NSSS was implemented using MATLAB/Simulink R2020a. This simulation environment was developed by the foundational work in [22] and was validated with real-world data. Its efficacy was supported by prior studies, including works in [9,15,19]. The MARL-based agents were constructed in a Python 3.7 environment using the PyTorch 1.10.2 framework [23].
At the beginning of each training episode, the thermal power setpoint was initialized to of the reactor full power (RFP). The MHTGR-based NSSS module then operated for 8000 s to reach a stable state at this RFP condition. Following this, the training phase began. At the 8000 s mark, the thermal power setpoint was gradually reduced from to RFP at a constant rate of RFP per minute. During that dynamic adjustment, the NSSS state was sampled every 20 s and sent to the MARL-based agents for processing. Each agent then executed actions according to its policy , receiving a reward r calculated via Equation (8). The parameters , , and were set to , , and , respectively. This iterative process continued within each episode until either the total simulation time reached 10,000 s or the control performance exceeded predefined error thresholds: a thermal power deviation greater than or a steam temperature deviation exceeding 3 °C. After completing 400 training episodes, the actor-network parameters for all agents were extracted, denoted as , which enhanced the agents’ ability to optimize NSSS control performance.
In this work, the actor and critic networks were designed as fully connected deep neural networks, each comprising three hidden layers with 64 neurons and employing Rectified Linear Unit (ReLU) activation functions. The actor network’s output layer, consisting of a single neuron, was scaled using a hyperbolic tangent (tanh) function to ensure actions were appropriately bounded. The critic network output a single Q-value. Each buffer capacity was transitions, with a minibatch size of 256. At the start of training, of the batch was sampled from the safe buffer and from the running buffer . As the running reward exceeded the average performance of trajectories in , the batch composition shifted to from , from , and from the good buffer . When the running reward significantly exceeded that of , of the batch was sampled from and from . This annealing process gradually shifted the focus from safety to exploration, improving performance as the agents progressed. The discount factor was set to , and the target network update rate was . The Adam optimizer, with a learning rate of , was used to update both the actor and critic networks. Additionally, multi-GPU acceleration was achieved through Distributed Data Parallel (DDP) techniques, enhancing computational efficiency.
4.2. Training Results
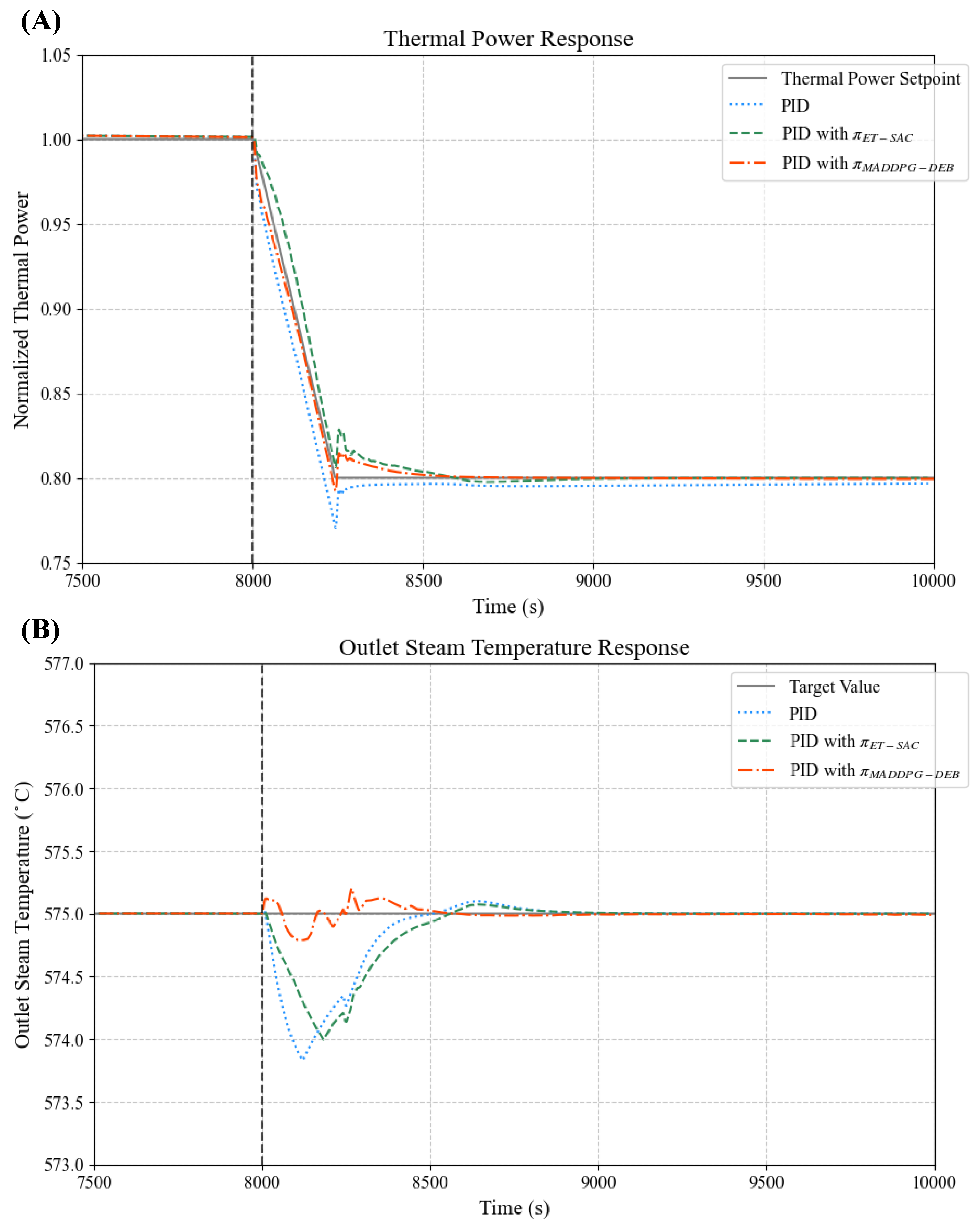
To evaluate the performance of our proposed multi-agent approach, the MADDPG-DEB algorithm was evaluated through a comparative study against two baselines: traditional PID controllers without an optimizer and PID controllers enhanced with a single-agent DRL-based optimizer, as introduced in our previous work [15]. The single-agent optimizer, trained under the same conditions as MADDPG-DEB, was denoted as . We plotted the trajectories of thermal power and outlet steam temperature under the power ramp-down condition from RFP to RFP with the rate of RFP/min. Figure 2A displays the thermal power trajectories. The gray solid line represents the thermal power setpoint trajectory. The optimized thermal power responses are shown as a red dashed line () and a green dashed line (), while the blue dotted line represents the unoptimized PID controller, included to emphasize the advantages of RL-based optimization. Meanwhile, Figure 2B presents the target outlet steam temperature as a black solid line, with red and green dashed lines for and , respectively. The blue dotted line is for the unoptimized PID.
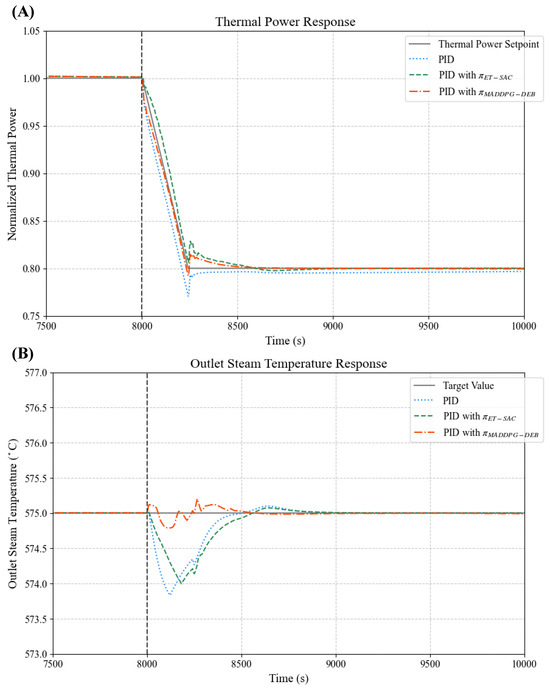
Figure 2.
Responses of normalized thermal power and outlet steam temperature of NSSS module under load-following ramp-down condition: (A) thermal power response; (B) outlet steam temperature response.
The experimental results clearly demonstrate the superior performance of our proposed multi-agent approach over the baseline methods. In Figure 2A, the thermal power trajectory under (red dashed line) closely follows the setpoint (gray solid line) during the power ramp-down from RFP to RFP. It exhibits minimal deviation and rapid convergence to the target. By contrast, the unoptimized PID controller (blue dotted line) displayed significant overshoot and a prolonged settling time, while (green dashed line) offered improvement over the PID but fell short of the precision achieved by MADDPG-DEB. Similarly, Figure 2B shows that the outlet steam temperature under (red dashed line) remained closely aligned with the target (black solid line), maintaining stability with minimal fluctuations. The baselines, however, exhibited larger deviations and slower stabilization, with the unoptimized PID controller again showing the weakest performance. Notably, MADDPG-DEB achieved faster response times, reaching steady-state conditions more rapidly for both thermal power and outlet steam temperature.
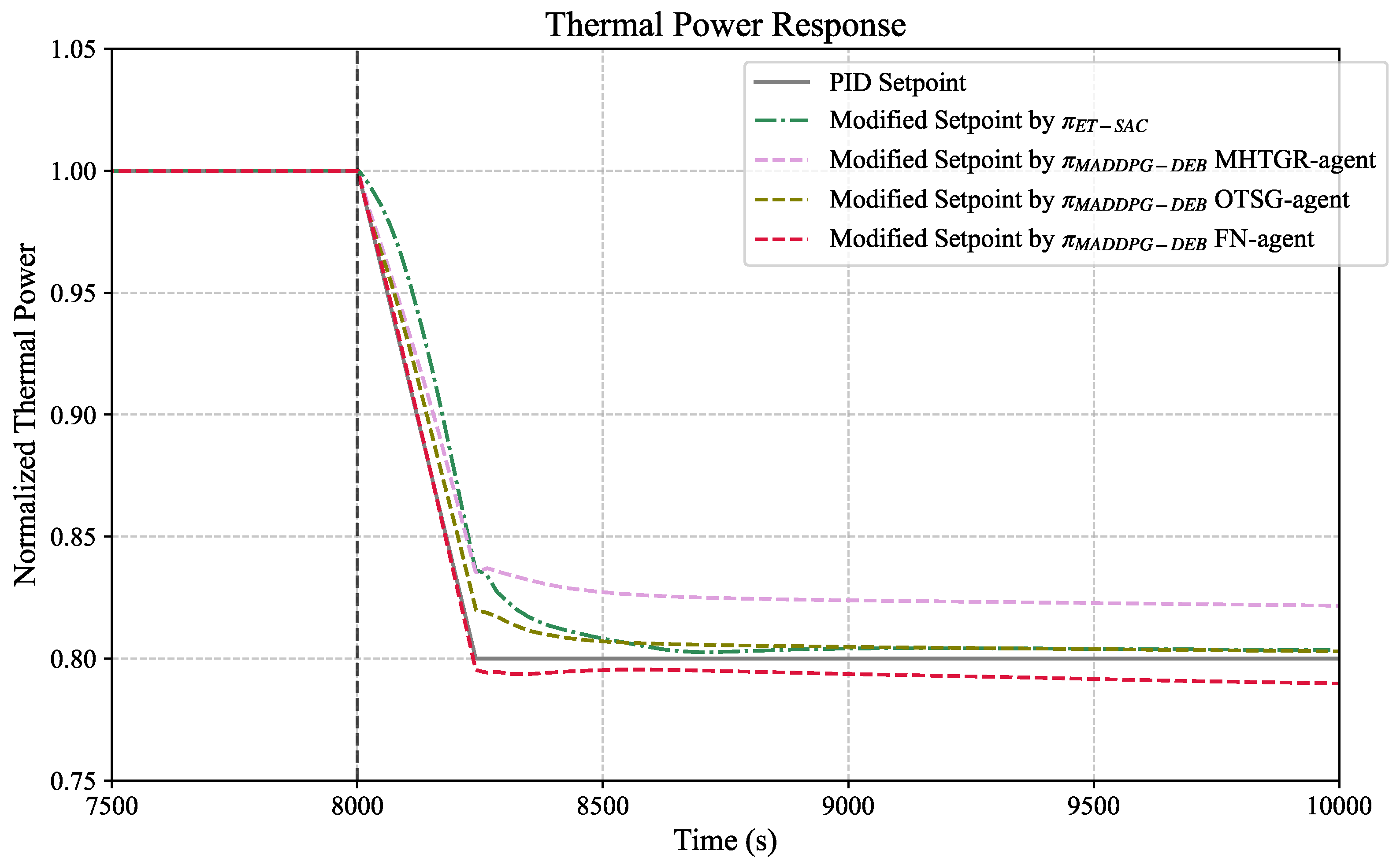
To understand the reasons for its superiority, we analyzed insights drawn from the setpoint trajectories, as illustrated in Figure 3. The gray solid line represents the original thermal power setpoint used by traditional PID controllers. MADDPG-DEB generated distinct thermal power setpoint trajectories for each subsystem, while applied a single, uniform trajectory across all modules. The MHTGR agent’s setpoint trajectory showed the most aggressive adjustments among the three, initially decreasing more rapidly than the PID setpoint. This behavior reflected the MHTGR’s role as the primary heat source, requiring swift power adjustments to meet the load demand. The OTSG agent’s trajectory, while also decreasing, followed a more gradual descent compared to the MHTGR. Its setpoint remained slightly above the PID setpoint during the transition, ensuring a smoother thermal response. The FN agent’s trajectory exhibited the smallest deviation from the PID setpoint. Notably, the FN setpoint consistently lay below the PID setpoint, reflecting a conservative approach to prevent overcompensation in flow dynamics. These optimized trajectories collectively demonstrated a coordinated control optimization strategy. Compared to the linear PID setpoint, which lacked adaptability, the MADDPG-DEB trajectories enabled more responsive and stable system-wide performance, as evidenced by the reduced overshoot and faster stabilization in thermal power and steam temperature responses. This subsystem-specific optimization, coupled with implicit coordination among agents, allowed MADDPG-DEB to reduce overshoot and accelerate stabilization compared to the uniform strategy of and the unoptimized PID controllers.
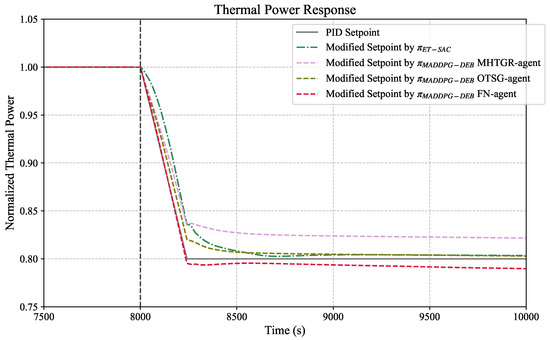
Figure 3.
Optimized thermal power setpoint trajectories under load-following conditions.
The multi-agent framework offers significant advantages, including tailored optimization for individual subsystems and enhanced decision-making through agent collaboration. However, it also presents challenges, such as an expanded action space and increased training complexity, which are inherent to multi-agent systems. These issues can undermine performance if not addressed effectively. For example, conventional multi-agent approaches, like the standard MADDPG method, often struggle in such environments. In our experiments, the baseline MADDPG failed to converge, underscoring these difficulties. To overcome these challenges, we introduced the DEB mechanism. DEB accelerates learning and reduces the risk of unstable policies by prioritizing safe and high-performing experiences during training. This approach enhances coordination among agents and ensures synchronization across subsystems. While DEB serves as an effective sampling strategy, our future work will focus on developing safe multi-agent reinforcement learning methods specifically tailored to the NSSS to meet the unique requirements of each subsystem, potentially broadening their applicability and effectiveness in complex multi-agent environments.
5. Conclusions
This article introduced a novel multi-agent framework to improve the coordination control performance of the nuclear steam supply system. To address the challenges of multi-agent optimization problems, such as an expanded action space and increased training complexity, we introduced the dynamic experience buffer mechanism integrated with the multi-agent deep deterministic policy gradient algorithm, forming MADDPG-DEB. By prioritizing safe and high-performing experiences during training, DEB accelerated learning and reduced the risk of unstable policies. Case studies on thermal power and outlet steam temperature regulation under load-following conditions demonstrated the framework’s effectiveness. Unlike the current single-agent optimization framework, the proposed multi-agent framework enabled subsystem-specific optimization policies for individual NSSS modules, improving operational flexibility and precision. We believe this work provides a new way for the complex control optimization tasks of NSSSs. Future research will focus on refining the DEB mechanism and developing safe multi-agent reinforcement learning methods tailored to NSSSs to further improve control performance under more complex conditions.
Author Contributions
Conceptualization, T.Z., Z.D. and X.H.; methodology, T.Z.; software, Z.D., Z.C. and T.Z.; validation, T.Z.; formal analysis, T.Z.; investigation, T.Z.; resources, Z.D. and X.H.; data curation, T.Z. and Z.C.; writing—original draft preparation, T.Z.; writing—review and editing, Z.D.; visualization, T.Z.; supervision, Z.D. and X.H.; project administration, T.Z.; funding acquisition, T.Z. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China (Grant No. 62406168, No. 62120106003).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to patent protection.
Acknowledgments
This work was additionally supported by the LingChuang Research Project of China National Nuclear Corporation.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DDP | Distributed Data Parallel |
| DDPG | Deep deterministic policy gradient |
| DEB | Dynamic experience buffer |
| DEC-POMDP | Decentralized partially observable Markov decision process |
| DRL | Deep reinforcement learning |
| DMC | Dynamic matrix control |
| ET-SAC | Soft Actor–Critic with Event-Triggered Mechanism |
| FN | Fluid network |
| MADDPG | Multi-agent deep deterministic policy gradient |
| MARL | Multi-agent reinforcement learning |
| MHTGR | Modular high-temperature gas-cooled reactor |
| MPC | Model predictive control |
| NPP | Nuclear Power Plant |
| NSSS | Nuclear steam supply system |
| OTSG | Once-through steam generator |
| PID | Proportional–integral–derivative |
| ReLU | Rectified Linear Unit |
| RFP | Reactor full power |
| TD | Temporal difference |
References
- Poudel, B.; Gokaraju, R. Small modular reactor (SMR) based hybrid energy system for electricity & district heating. IEEE Trans. Energy Convers. 2021, 36, 2794–2802. [Google Scholar]
- Salehi, A.; Safarzadeh, O.; Kazemi, M.H. Fractional order PID control of steam generator water level for nuclear steam supply systems. Nucl. Eng. Des. 2019, 342, 45–59. [Google Scholar] [CrossRef]
- Al Rashdan, A.; Roberson, D. A frequency domain control perspective on Xenon resistance for load following of thermal nuclear reactors. IEEE Trans. Nucl. Sci. 2019, 66, 2034–2041. [Google Scholar] [CrossRef]
- Panciak, I.; Diab, A. Dynamic Multiphysics Simulation of the Load-Following Behavior in a Typical Pressurized Water Reactor Power Plant. Energies 2019, 17, 6373. [Google Scholar] [CrossRef]
- Gyun, N.M.; Ho, S.S.; Cheol, K.W. A model predictive controller for nuclear reactor power. Nucl. Eng. Technol. 2003, 35, 399–411. [Google Scholar]
- Holkar, K.; Waghmare, L.M. An overview of model predictive control. Int. J. Control Autom. 2010, 3, 47–63. [Google Scholar]
- Vajpayee, V.; Mukhopadhyay, S.; Tiwari, A.P. Data-driven subspace predictive control of a nuclear reactor. IEEE Trans. Nucl. Sci. 2017, 65, 666–679. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Das, D.K. Explicit model predictive controller for power control of molten salt breeder reactor core. Nucl. Eng. Des. 2021, 384, 111492. [Google Scholar] [CrossRef]
- Jiang, D.; Dong, Z. Dynamic matrix control for thermal power of multi-modular high temperature gas-cooled reactor plants. Energy 2020, 198, 117386. [Google Scholar] [CrossRef]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An introduction to deep reinforcement learning. Found. Trends® Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Zhang, T.; Dong, Z.; Huang, X. Multi-objective optimization of thermal power and outlet steam temperature for a nuclear steam supply system with deep reinforcement learning. Energy 2024, 286, 129526. [Google Scholar] [CrossRef]
- Buşoniu, L.; Babuška, R.; De Schutter, B. Multi-agent reinforcement learning: An overview. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 183–221. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Canese, L.; Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-agent reinforcement learning: A review of challenges and applications. Appl. Sci. 2021, 11, 4948. [Google Scholar] [CrossRef]
- Dong, Z.; Pan, Y.; Zhang, Z.; Dong, Y.; Huang, X. Model-free adaptive control law for nuclear superheated-steam supply systems. Energy 2017, 135, 53–67. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Dong, Z.; Pan, Y.; Zhang, Z.; Dong, Y.; Huang, X. Dynamical modeling and simulation of the six-modular high temperature gas-cooled reactor plant HTR-PM600. Energy 2018, 155, 971–991. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).