Dispatch for the Industrial Micro-Grid with an Integrated Photovoltaic-Gas-Manufacturing Facility System Considering Carbon Emissions and Operation Costs
Abstract
:1. Introduction
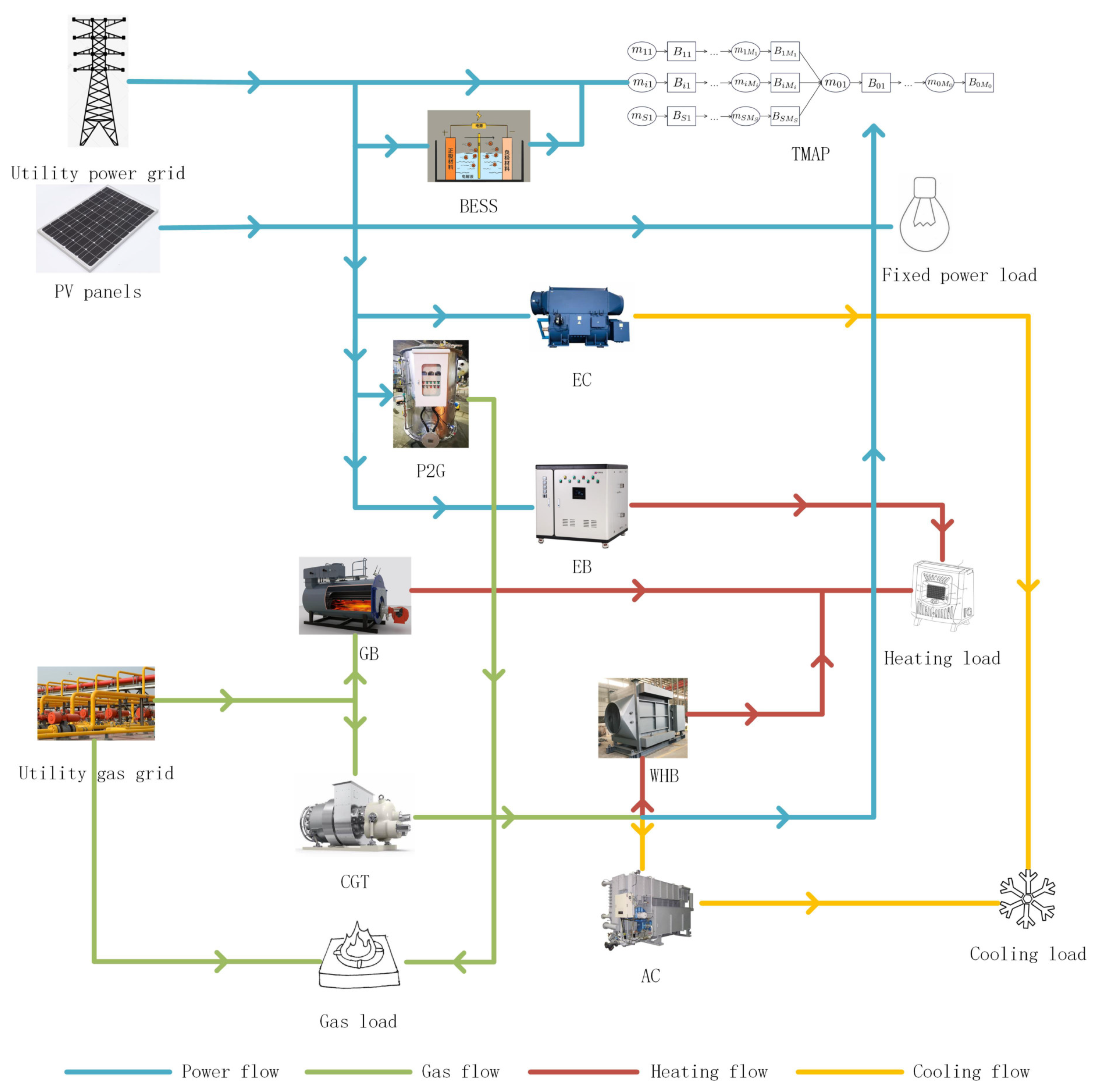
2. Problem Formulation
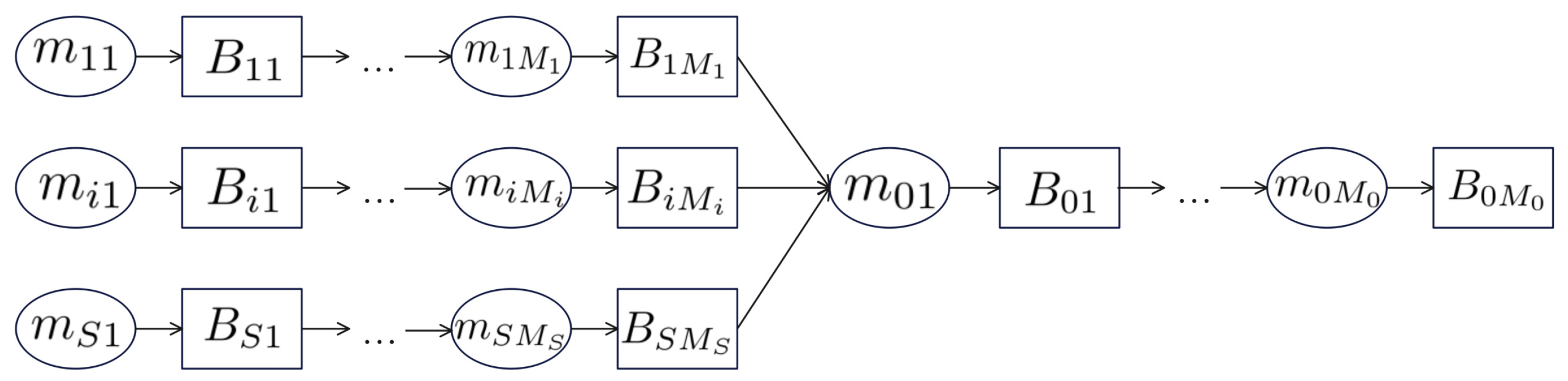
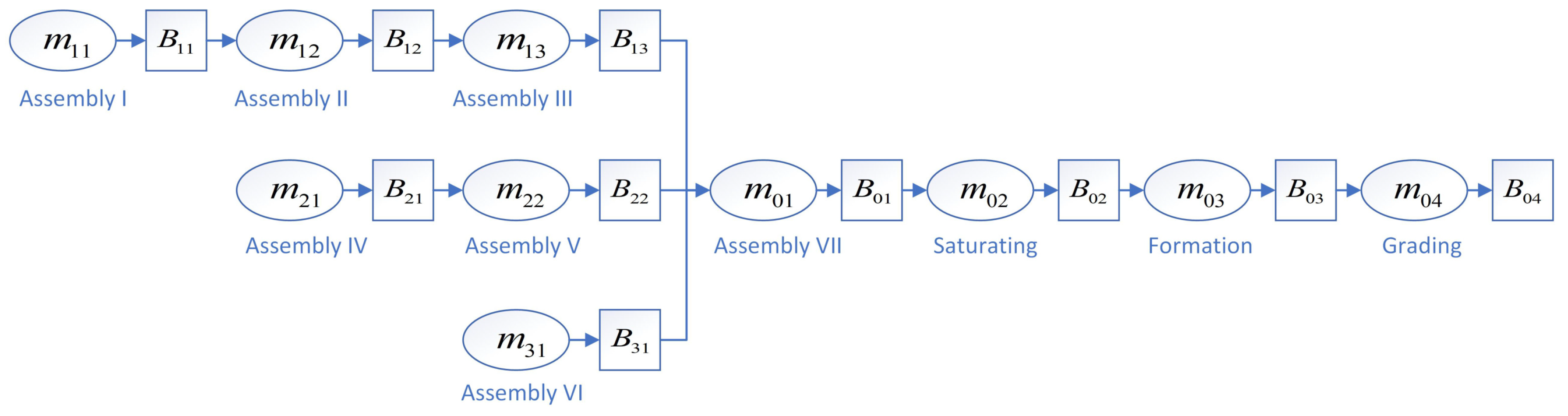
2.1. Typical Manufacturing Assembly Process
2.2. Battery Energy Storage System
2.3. Photovoltaic Power Generation
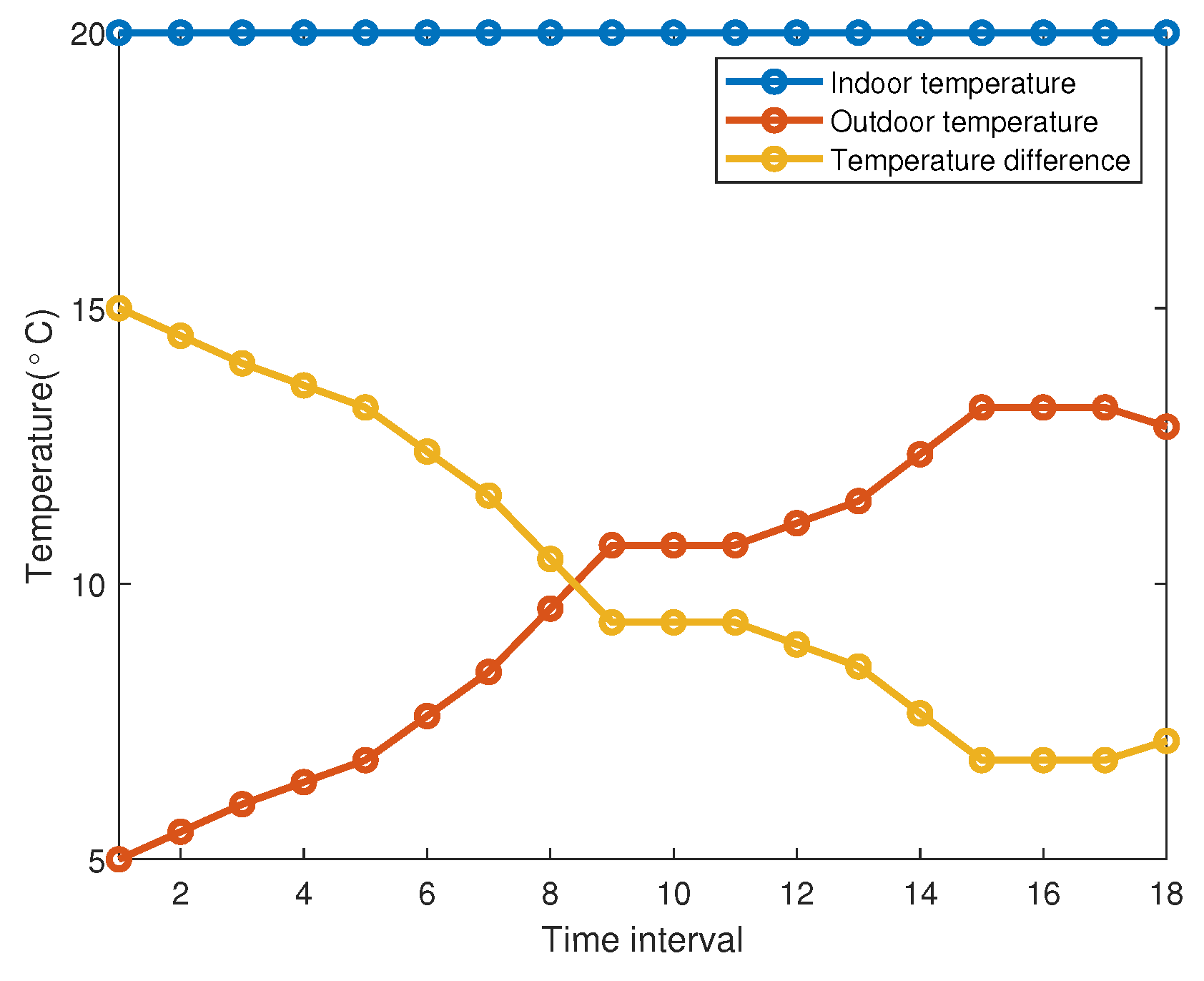
2.4. Heating Load and Cooling Load
2.5. Conventional Gas Turbine
2.6. Power to Gas
2.7. Electrical Boiler
2.8. Electrical Cooler
2.9. Gas Boiler
2.10. Energy Balance
3. Problem Solving
4. Simulation
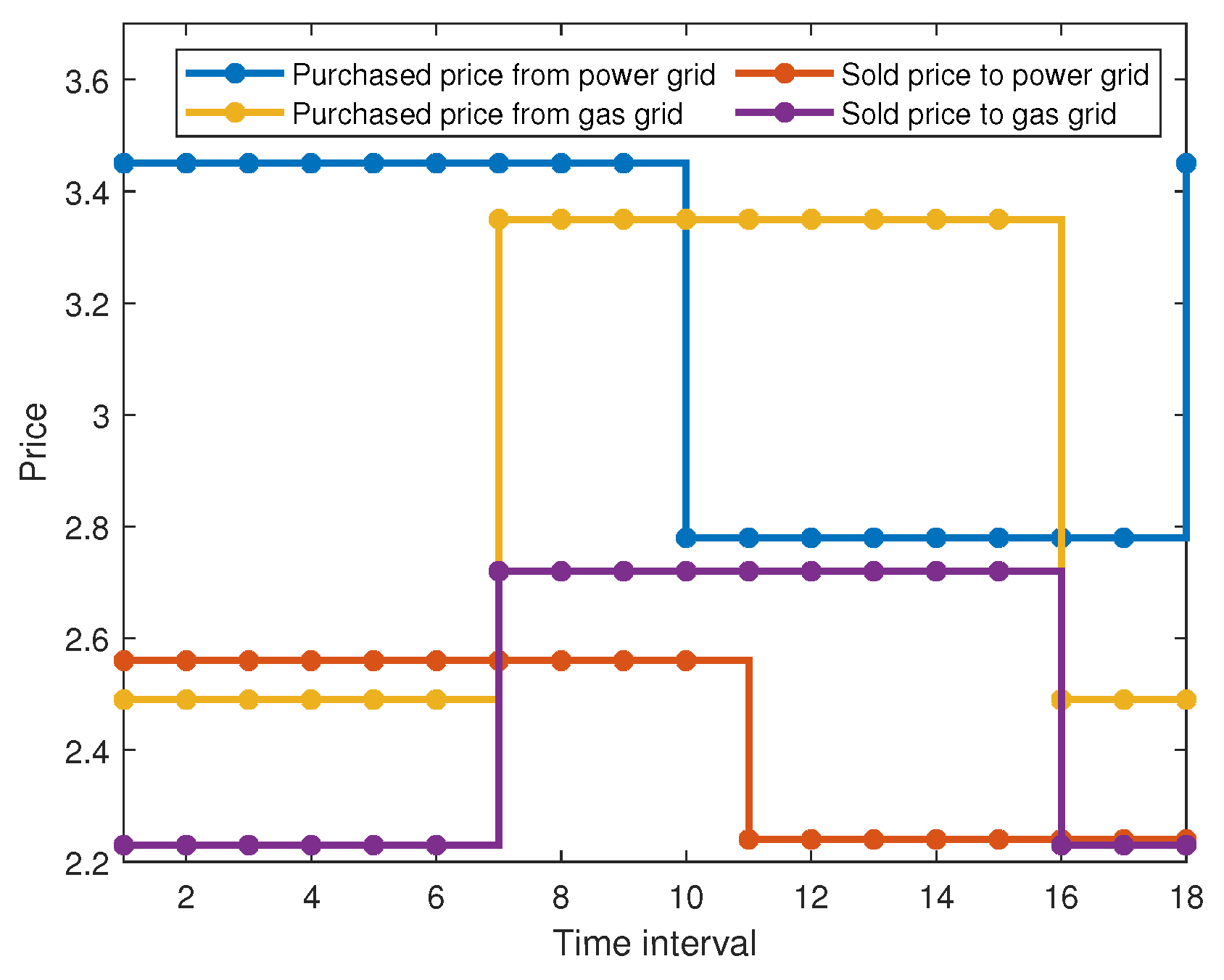
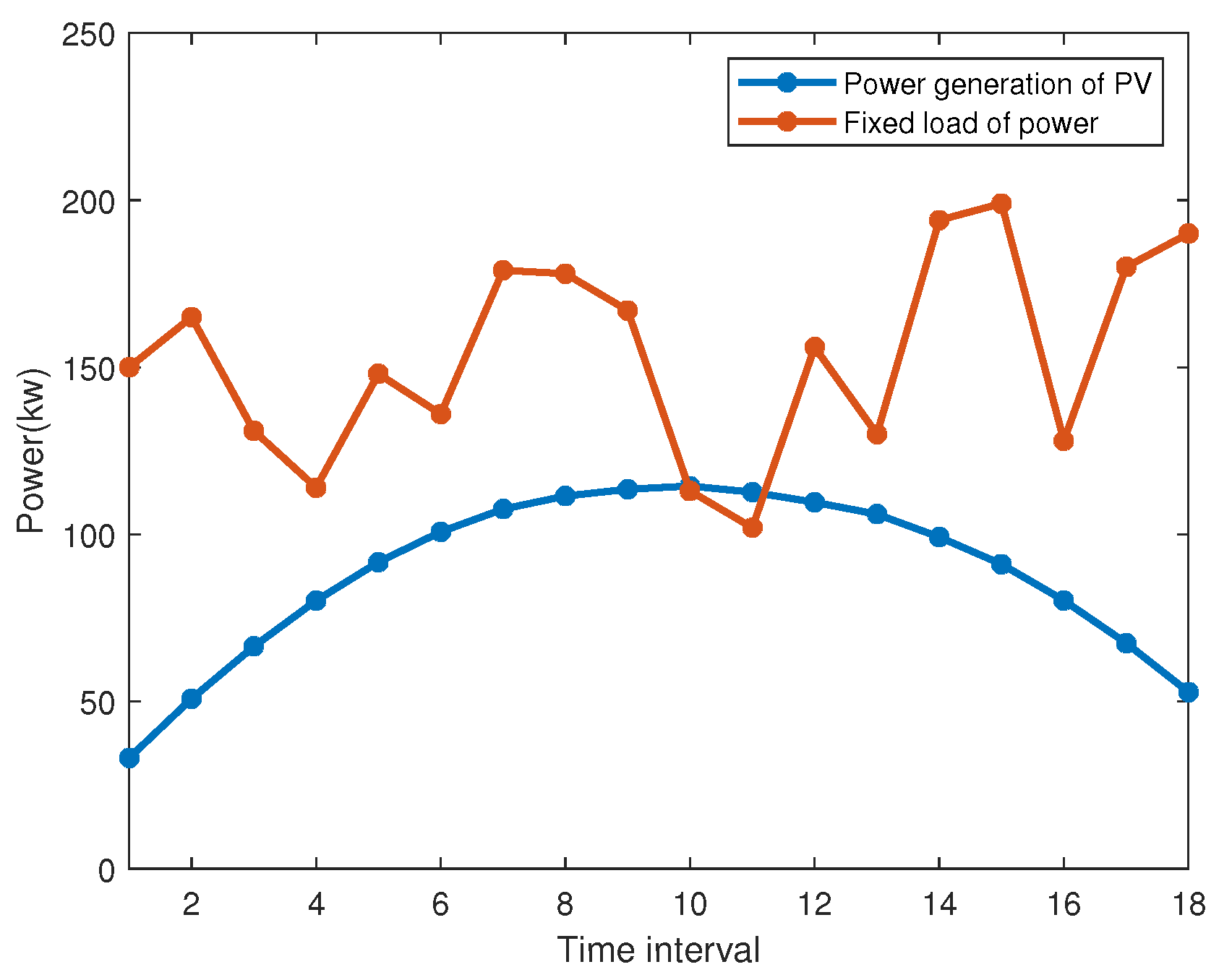
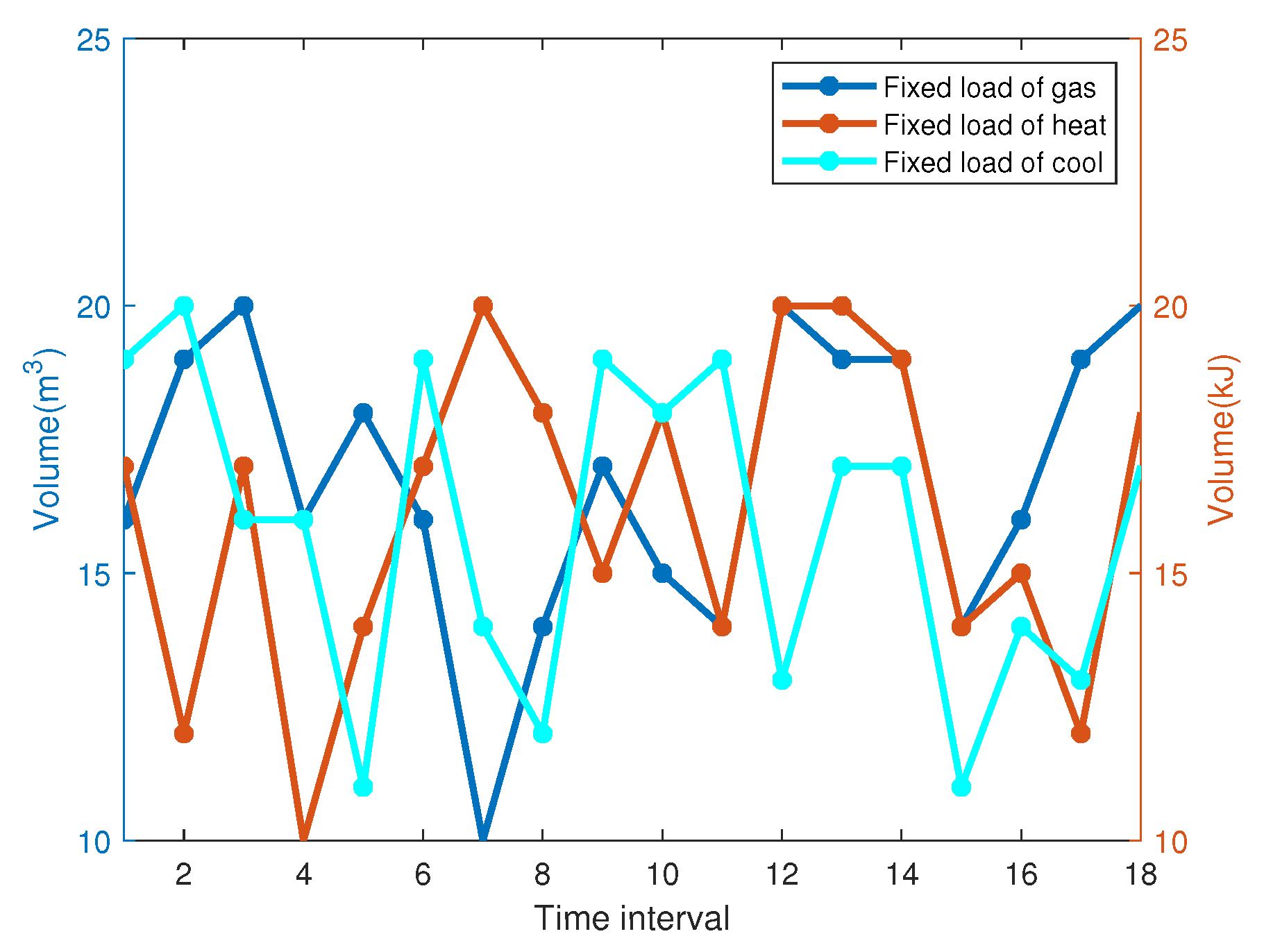
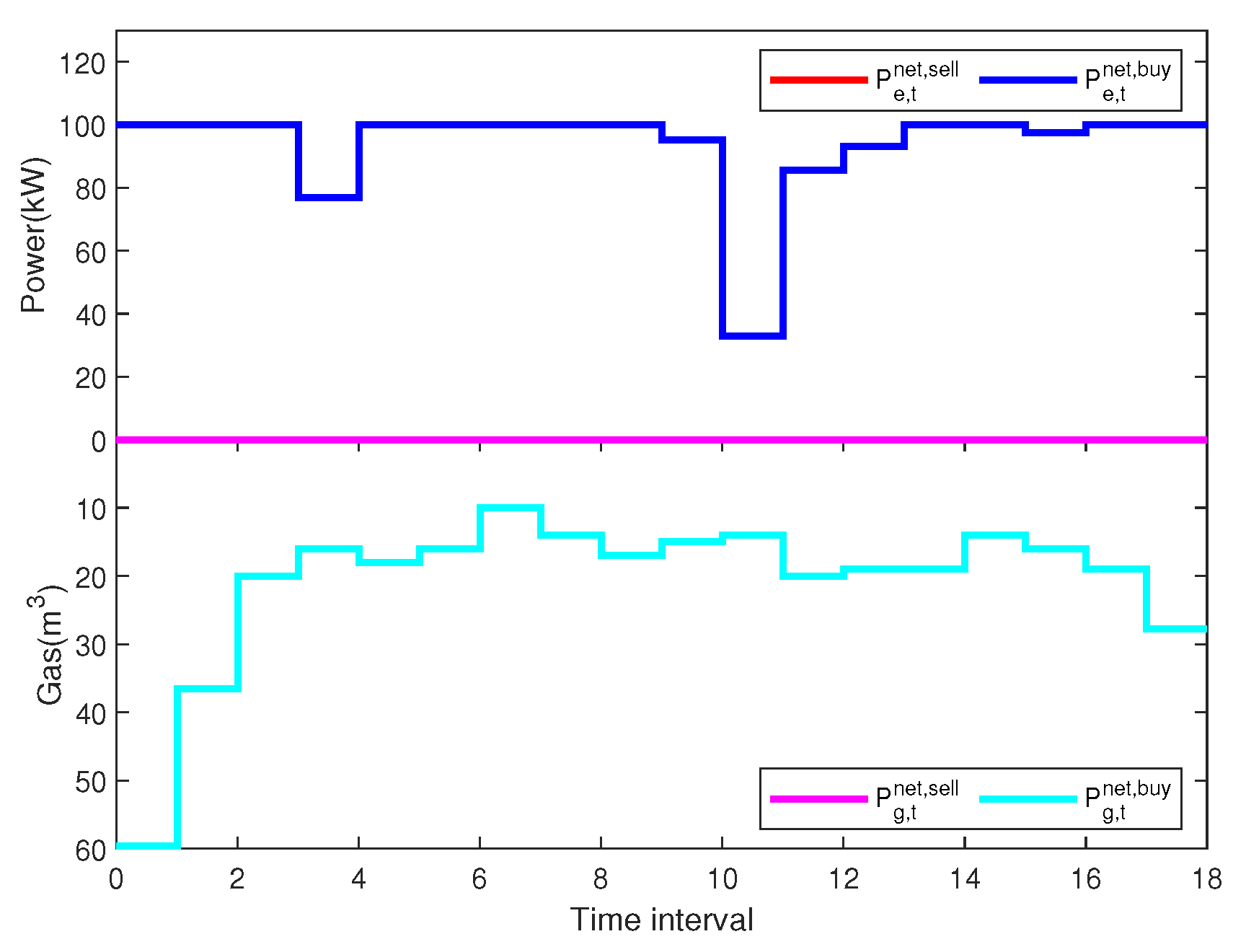
4.1. Simulation Setup
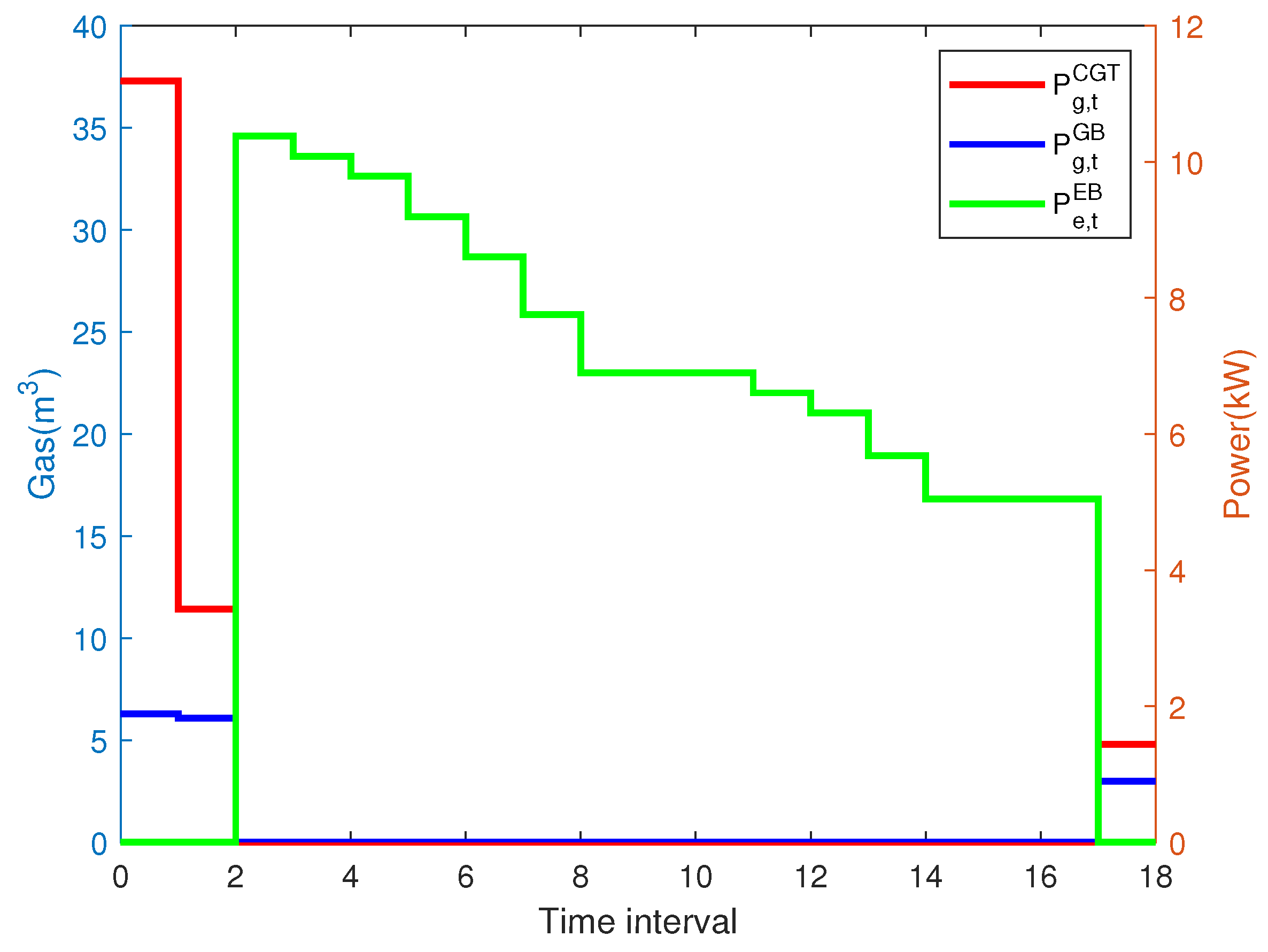
4.2. Simulation Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ufa, R.A.; Malkova, Y.Y.; Gusev, A.L.; Ruban, N.Y.; Vasilev, A.S. Algorithm for optimal pairing of res and hydrogen energy storage systems. Int. J. Hydrogen Energy 2021, 46, 33659–33669. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Xia, L.C.; Jiang, L.Y.; Ge, Q.B.; Yu, F. Distributed bandit online optimisation for energy management in smart grids. Int. J. Syst. Sci. 2023, 54, 2957–2974. [Google Scholar] [CrossRef]
- Liu, L.N.; Yang, G.H. Distributed energy resource coordination for a microgrid over unreliable communication network with dos attacks. Int. J. Syst. Sci. 2024, 55, 237–252. [Google Scholar] [CrossRef]
- Lian, J.J.; Zhang, Y.S.; Ma, C.; Yang, Y.; Chaima, E. A review on recent sizing methodologies of hybrid renewable energy systems. Energy Convers. Manag. 2019, 199, 112027. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Niaz, I.A. An optimized home energy management system with integrated renewable energy and storage resources. Energies 2017, 10, 549. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.L.; Li, G.Q.; Wang, J.L.; Zhao, D.B.; Chen, C. Improving operational flexibility of integrated energy system with uncertain renewable generations considering thermal inertia of buildings. Energy Convers. Manag. 2020, 207, 112526. [Google Scholar] [CrossRef]
- Gao, J.; Shao, Z.G.; Chen, F.X.; Lak, M. Energy trading strategies for integrated energy systems considering uncertainty. Energies 2025, 18, 935. [Google Scholar] [CrossRef]
- Wang, M.; Yu, H.; Jing, R.; Liu, H.; Chen, P.D.; Li, C.E. Combined multi-objective optimization and robustness analysis framework for building integrated energy system under uncertainty. Energy Convers. Manag. 2020, 208, 112589. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, G.S.; Ma, K. Hierarchical dispatch using two-stage optimisation for electricity markets in smart grid. Int. J. Syst. Sci. 2016, 47, 3529–3536. [Google Scholar] [CrossRef]
- Liang, P.R.; Zhang, H.H.; Liang, R. Cooperative game enabled low-carbon energy dispatching of multi-regional integrated energy systems considering carbon market. Energies 2025, 18, 759. [Google Scholar] [CrossRef]
- Jiang, P.; Dong, J.; Huang, H. Optimal integrated demand response scheduling in regional integrated energy system with concentrating solar power. Appl. Therm. Eng. 2020, 166, 114754. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.Y.; Yang, L.X. A two-stage multi-objective optimal scheduling in the integrated energy system with We-Energy modeling. Energy 2021, 215, 119121. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G.Q. Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Huang, H.X.; Liang, R.; Lv, C.X.; Lu, M.T.; Gong, D.W.; Yin, S.L. Two-stage robust stochastic scheduling for energy recovery in coal mine integrated energy system. Appl. Energy 2021, 290, 116759. [Google Scholar] [CrossRef]
- Li, B.; Li, X.; Su, Q.Y. A system and game strategy for the isolated island electric-gas deeply coupled energy network. Appl. Energy 2022, 306, 118013. [Google Scholar] [CrossRef]
- Zhu, G.; Gao, Y.; Sun, H. Optimization scheduling of a wind-photovoltaic-gas-electric vehicles community-integrated energy system considering uncertainty and carbon emissions reduction. Sustain. Energy Grids Netw. 2023, 33, 100973. [Google Scholar] [CrossRef]
- Naderi, E.; Azizivahed, A.; Asrari, A. A step toward cleaner energy production: A water saving-based optimization approach for economic dispatch in modern power systems. Electr. Power Syst. Res. 2022, 204, 107689. [Google Scholar] [CrossRef]
- Naderi, E.; Mirzaei, L.; Trimble, J.P.; Cantrell, D.A. Multi-objective optimal power flow incorporating flexible alternating current transmission systems: Application of a wavelet-oriented evolutionary algorithm. Electr. Power Compon. Syst. 2024, 52, 766–795. [Google Scholar] [CrossRef]
- Duan, P.F.; Feng, M.D.; Zhao, B.X.; Xue, Q.W.; Li, K.; Chen, J.L. Operational optimization of regional integrated energy systems with heat pumps and hydrogen renewable energy under integrated demand response. Sustainability 2024, 16, 1217. [Google Scholar] [CrossRef]
- Yang, J.; Li, C.H.; Ma, K.; Liu, H.R.; Guo, S.L. Multi-energy pricing strategy for port integrated energy systems based on contract mechanism. Energy 2024, 290, 130114. [Google Scholar] [CrossRef]
- Liu, L.Z.; Su, X.L.; Chen, L.J.; Wang, S.; Li, J.W.; Liu, S.W. Elite genetic algorithm based self-sufficient energy management system for integrated energy station. IEEE Trans. Ind. Appl. 2024, 60, 1023–1033. [Google Scholar] [CrossRef]
- Sun, Q.R.; Wu, Z.; Gu, W.; Zhang, X.P.; Lu, Y.A.; Liu, P.; Lu, S.; Qiu, H.F. Resilience assessment for integrated energy system considering gas-thermal inertia and system interdependency. IEEE Trans. Smart Grid 2024, 15, 1509–1524. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Siano, P.; Aghaei, J.; Masoum, M.A.S.; Li, F.X.; Catalao, J.P.S. Comprehensive review of the recent advances in industrial and commercial DR. IEEE Trans. Ind. Inform. 2019, 15, 3757–3771. [Google Scholar] [CrossRef]
- Li, Y.C.; Hong, S.H. Real-time demand bidding for energy management in discrete manufacturing facilities. IEEE Trans. Ind. Electron. 2017, 64, 739–749. [Google Scholar] [CrossRef]
- Lu, R.Z.; Li, Y.C.; Li, Y.T.; Jiang, J.H.; Ding, Y.M. Multi-agent deep reinforcement learning based demand response for discrete manufacturing systems energy management. Appl. Energy 2020, 276, 115473. [Google Scholar] [CrossRef]
- Ding, Y.M.; Hong, S.H.; Li, X.H. A demand response energy management scheme for industrial facilities in smart grid. IEEE Trans. Ind. Inform. 2014, 10, 2257–2269. [Google Scholar] [CrossRef]
- Yu, M.M.; Lu, R.Z.; Hong, S.H. A real-time decision model for industrial load management in a smart grid. Appl. Energy 2016, 183, 1488–1497. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H.C.; Song, Y.H.; Wang, L.; Ahmad, T.; Luo, X. Demand response for industrial micro-grid considering photovoltaic power uncertainty and battery operational cost. IEEE Trans. Smart Grid 2021, 12, 3043–3055. [Google Scholar] [CrossRef]
- Wu, Q.; Song, Q.K. Isolated industrial micro-grid demand response with assembly process based on distributionally robust chance constraint. Int. J. Syst. Sci. 2024, 55, 2211–2223. [Google Scholar] [CrossRef]
- Wu, Q.; Song, Q.K.; He, X.; Chen, G.; Huang, T.W. Distributed peer-to-peer energy trading framework with manufacturing assembly process and uncertain renewable energy plants in multi-industrial micro-grids. Energy 2024, 302, 131876. [Google Scholar] [CrossRef]

| Time Step t | Consumed Power |
|---|---|
| ⋯ | ⋯ |
| ⋯ | ⋯ |
| ⋯ | ⋯ |
| Time Step t | Consumed Power |
|---|---|
| ⋯ | ⋯ |
| ⋯ | ⋯ |
| ⋯ | ⋯ |
| Task | Machine | Production Rate | Power Consumption Rate |
|---|---|---|---|
| Assembly I | 35 Unit/h | 22.8 kW/h | |
| Assembly II | 32 Unit/h | 20.8 kW/h | |
| Assembly III | 40 Unit/h | 25.6 kW/h | |
| Assembly IV | 30 Unit/h | 26.2 kW/h | |
| Assembly V | 26 Unit/h | 24.6 kW/h | |
| Assembly VI | 30 Unit/h | 26.2 kW/h | |
| Assembly VII | 25 Unit/h | 12.4 kW/h | |
| Saturating | 24 Unit/h | 10.2 kW/h | |
| Formation | 30 Unit/h | 13.6 kW/h | |
| Grading | 28 Unit/h | 9.5 kW/h |
| Proposed Model | Single-Objective Model I | Single-Objective Model II | |
|---|---|---|---|
| 165.2898 | 155.9281 | 598.0418 | |
| 6399.8 | 6602.1 | 6328.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Song, Q. Dispatch for the Industrial Micro-Grid with an Integrated Photovoltaic-Gas-Manufacturing Facility System Considering Carbon Emissions and Operation Costs. Energies 2025, 18, 2224. https://doi.org/10.3390/en18092224
Wu Q, Song Q. Dispatch for the Industrial Micro-Grid with an Integrated Photovoltaic-Gas-Manufacturing Facility System Considering Carbon Emissions and Operation Costs. Energies. 2025; 18(9):2224. https://doi.org/10.3390/en18092224
Chicago/Turabian StyleWu, Qian, and Qiankun Song. 2025. "Dispatch for the Industrial Micro-Grid with an Integrated Photovoltaic-Gas-Manufacturing Facility System Considering Carbon Emissions and Operation Costs" Energies 18, no. 9: 2224. https://doi.org/10.3390/en18092224
APA StyleWu, Q., & Song, Q. (2025). Dispatch for the Industrial Micro-Grid with an Integrated Photovoltaic-Gas-Manufacturing Facility System Considering Carbon Emissions and Operation Costs. Energies, 18(9), 2224. https://doi.org/10.3390/en18092224






