Abstract
This study presents a comparative analysis of PLANS (v. /2019/12/10) and EA-PSM (v. 19.11.15.0) software for power system simulations, focusing on their applications in enhancing energy security and grid reliability. Utilizing the Newton–Raphson algorithm for power flow calculations, both tools offer robust solutions for network balance, addressing various issues, such as voltage distortions and reactive power injection. The research highlights the critical role of these simulations in integrating renewable energy sources and ensuring efficient, sustainable, and resilient power systems. Additionally, the study underscores the multidimensional aspect of energy security as a cornerstone of national stability and economic prosperity.
1. Introduction
Photovoltaic (PV) micro-installations are becoming increasingly popular as small-scale energy sources directly connected to low-voltage grids at consumer locations, often supported by governmental initiatives. In several regions and countries, this distributed generation model has started to play a noticeable role in electricity production. This distributed generation model contributes significantly to overall electricity production [1]. However, such installations can affect the power grid, causing issues, such as reactive power injection, voltage distortions, and other concerns about power quality [2]. The level of disturbances varies depending on the type of inverters used. Addressing these challenges, particularly in terms of power quality and stability, often requires advanced devices, such as flexible AC transmission systems (FACTS), although their high cost can be a limiting factor for smaller energy producers [2]. The use of simulation tools enables early assessment of the impacts of these installations, allowing for optimized connection conditions. As modern grids evolve, simulation tools are becoming increasingly vital in managing complexity, supporting renewable integration, and ensuring overall system resilience.
This study focusses on analyzing voltage quality parameters in low-voltage networks with distributed generation, using EA-PSM software for grid modeling and simulation. The paper provides an in-depth analysis of the calculation procedures used in the PLANS and EA-PSM software, which are essential for understanding and simulating complex grid dynamics. These advanced simulation tools play a crucial role in predicting power grid behavior under various operational scenarios, including the integration of renewable energy sources [3,4]. By delving into the theoretical aspects of simulations, this research highlights how PLANS and EA-PSM contribute to effective grid management, allowing the prediction and control of power grid behavior under different conditions. Ensuring energy security requires not only physical infrastructure but also reliable tools to analyze, simulate, and prepare for diverse operational conditions. In this context, simulation software, such as PLANS and EA-PSM, support proactive grid management, enabling early detection of instability risks, assessment of renewable integration impacts, and evaluation of resilience under stress scenarios. The ability to model grid behavior across multiple scales directly contributes to maintaining secure, stable, and uninterrupted energy supply. This approach is vital to maintaining energy security [2], ensuring that power systems are not only efficient and sustainable, but also resilient against potential disruptions.
The increasing PV systems integration into low-voltage grids has been widely studied [5], with research highlighting the impact of inverter types on power quality. Studies indicate that voltage dips, swells, and harmonic distortions are common problems, with total harmonic distortion (THD) contributing to excessive heat generation in components, leading to failures and inefficiencies. Advanced inverter technologies and control strategies [6], such as cascaded feedforward neural networks and hybrid switched-inductor converters, help mitigate these issues by maintaining acceptable THD levels [7]. Furthermore, fault ride through (FRT) capability is critical for grid stability during voltage dips, ensuring that PV systems remain connected and provide reactive power support [8].
Topological analysis of electrical power transmission networks using methods, like graph convolutional networks [9,10], has emerged as a crucial approach to understanding and improving grid resilience and efficiency. These studies provide insights into network vulnerability, controllability, and fault tolerance, helping to identify critical nodes and optimize the network to prevent cascading failures and enhance fault detection [8]. Simulation tools, such as PLANS and EA-PSM, play an instrumental role in modeling and analyzing PV system impacts on low-voltage grids, allowing researchers to predict grid behavior [11] under different scenarios, optimize connection conditions, and mitigate power quality issues before implementation [9]. This study addresses a gap in the literature by providing practical insight into the use of real-world simulation tools—PLANS and EA-PSM—which are widely used for national energy system planning but rarely documented in open scientific sources.
The paper is structured as follows: Section 2 presents a review of power system simulation tools; Section 3 discusses renewable energy integration and its impact on grid stability; Section 4 explores topological analysis methods and failure detection strategies; Section 5 delves into computational advances in power flow analysis; finally, Section 6 concludes with key findings and future research directions.
2. Power System Simulation Tools in Literature
The reliability and security of power systems have been extensively studied, with simulation tools playing a critical role in analyzing network behavior under various operational conditions. The increasing penetration of renewable energy sources (RESs) requires robust methodologies for power system stability, making simulation-based approaches essential to predict grid performance, mitigate risks, and optimize energy distribution. Power system modeling and simulation have evolved significantly over the years, with numerous tools having been developed to assess grid stability, power flow, and fault detection. Newton–Raphson-based approaches have been widely adopted in power system simulations due to their quadratic convergence and robustness in solving nonlinear power flow equations [10]. Traditional tools, such as PLANS and EA-PSM [12,13], have been used extensively in industry and academia for power grid modeling, integrating complex network behaviors and providing information on power stability and quality.
The Newton–Raphson method remains a standard technique for solving power flow problems [9]. Its effectiveness has been demonstrated in various studies, particularly in the context of renewable energy integration. Moreover, modern enhancements to the Newton–Raphson method, such as hybrid implementations with artificial intelligence, have improved computational efficiency, making them viable for real-time grid operation [14].
In addition to classical power flow solvers, other tools, such as PSS®E, PowerWorld, DIgSILENT PowerFactory, and OpenDSS, have gained popularity for their comprehensive simulation capabilities [1,2]. These platforms support a wide range of functionalities, including transient stability analysis, harmonic studies, and probabilistic load flow, making them indispensable in both operational planning and academic research. Open-source alternatives, such as MATPOWER and GridLAB-D, have also gained traction for their flexibility, transparency, and integration with scripting environments, like MATLAB and Python [3,4].
2.1. Renewable Energy Integration and Grid Stability
The increasing share of RESs, particularly photovoltaic (PV) and wind energy, has raised concerns about grid stability. The replacement of synchronous generators with inverter-based RES leads to a decrease in system inertia [6], affecting frequency stability and voltage regulation. Studies have highlighted how FACTS devices and advanced inverter control strategies help mitigate these problems [11]. However, the cost and complexity of these solutions pose challenges, especially for smaller energy producers.
To address this, simulation tools are being updated to incorporate dynamic modeling of inverter-based resources, facilitating the evaluation of low-inertia systems under fault conditions and renewable intermittency [5,14]. Co-simulation frameworks, which couple electromagnetic transient (EMT) and phasor domain simulations, are increasingly used to analyze these complex interactions [7].
Research by Li and Vittal has highlighted the effectiveness of co-simulation platforms in capturing interactions between transmission systems and renewable energy sources, demonstrating enhanced accuracy and reliability in dynamic stability studies. Such frameworks help system operators and planners manage increased variability and uncertainties from renewable generation [15].
2.2. Topological Analysis and Failure Detection
With the increasing complexity of modern power grids, topological analysis has become a crucial tool to assess network vulnerability and resilience. Research on the non-local impact of link failures has provided insight into network reaction mechanisms and flow redistribution after disturbances [16]. Such studies have proven instrumental in identifying critical nodes within the network, helping to optimize protective strategies and improving overall system robustness.
Graph-based approaches have also been applied to failure modeling, using such methods as graph convolutional networks to enhance predictive capabilities [6]. The combination of simulation tools with topological analytics improves reliability assessments of the grid, facilitating preemptive measures against cascading failures. Studies have shown that integrating graph theory with dynamic simulation can uncover hidden fragilities in interdependent infrastructure systems, including water, communication, and gas networks [8]. The non-local effects of line outages are increasingly analyzed using coupled simulation-topology models, revealing counterintuitive phenomena where failures in peripheral branches can impact core transmission corridors [17]. Advanced approaches using graph neural networks have demonstrated superior performance in learning optimal power flow and fault localization tasks, improving grid resilience and providing valuable tools for real-time network management [18,19].
2.3. Advancements in Computational Power Flow Analysis
Recent advances in parallel computing have led to significant improvements in power flow analysis methodologies. High-performance computing (HPC) environments have enabled the acceleration of Newton–Raphson-based simulations, with GPU-based implementations achieving speedups of more than 100 times compared to traditional CPU-based methods [20].
Moreover, hybrid approaches integrating Newton–Raphson with machine learning have shown promising results in refining power system operation rules and improving real-time simulation capabilities [21]. These innovations indicate a shift toward intelligent, adaptive grid management systems that can dynamically respond to fluctuating energy demands and system perturbations.
As power systems grow in complexity, simulation speed becomes critical for real-time grid operation and decision making. High-performance computing (HPC) has enabled parallelized simulation algorithms capable of handling massive datasets and fine temporal resolutions. GPU-based implementations of Newton–Raphson solvers have demonstrated performance improvements of over 100× compared to CPU-only versions [22].
New frameworks now incorporate digital twin technology, where real-time sensor data feeds into continuously updated simulation models that provide predictive insights and decision support [23]. These systems are particularly valuable in managing smart grids and distributed energy resources (DERs), where rapid response and adaptability are essential.
Machine learning algorithms are being trained on massive simulation datasets to predict system behavior under a wide variety of conditions, offering predictive capabilities that were previously unfeasible [24]. Reinforcement learning and surrogate modeling have also found applications in optimal power flow (OPF), load forecasting, and voltage control [25,26].
The convergence of physics-based and data-driven modeling is further pushing the boundaries of power system simulation. Models trained via ML can approximate power flow or transient responses without needing to solve full equations, offering near-instantaneous results for operational scenarios and contingency planning [27]. Tools, such as Simscape Electrical and Modelica-based environments, are enabling multi-domain modeling, supporting the simulation of hybrid electric systems that incorporate mechanical, thermal, and control subsystems [28]. These capabilities are essential as the future grid becomes increasingly integrated with distributed energy resources (DERs), electric vehicles, and storage systems.
3. Power Simulation Software
3.1. EAPSM: Electric Power System Model
EAPSM (Electric Power System Model) [13] is a specialized software used for simulating power systems, offering tools to accurately model electric power network dynamics [MATSUDA]. Studies, like [4], highlight its efficacy in transient stability analysis, emphasizing the need for precise modeling. Siozinys et al. [16] compared EA-PSM with other software, noting its accuracy and computational efficiency. EA-PSM’s broader capabilities include detailed asset performance analysis and risk assessment in power systems [24], particularly for asset reliability and performance metrics under various conditions. EA-PSM has been employed in various studies to model the integration of RES, showcasing its capability to simulate voltage distortions and reactive power fluctuations in low-voltage networks.
In power grids, EA-PSM helps integrate renewable sources, like wind and solar energy, addressing challenges, such as intermittent power generation and quality issues. The software is instrumental in electrical grid modeling and renewable energy integration, including aspects, such as reactive power regulation and harmonic impact.
The recent literature on EA-PSM underscores its role in energy security research, which is vital in transmission, distribution, and industrial network calculations. It helps in reactive power analysis, prevents disconnections, and integrates renewable energy. The arc flash analysis and relay protection coordination software are key for safety and reliability in power systems. Furthermore, it models the impacts of EV charging infrastructure on grid reliability and harmonic generation, crucial in contemporary energy systems [7]. The EA-PSM’s features make it essential for managing modern power systems’ complexities and ensuring their efficiency and reliability amidst technological advancements and evolving challenges [8].
3.2. PLANS
PLANS is a Polish-developed software [12] that has been a staple in the engineering community for more than two decades, and is specifically used to simulate loads and flows in power grids. It has gained widespread adoption among Polish distribution system operators (DSOs), such as PGE, ENEA, TAURON, and ENERGA, evidenced by the long-standing organization of workshops aimed at enhancing proficiency in its application. Its primary functionality lies in the calculation of power grid flows, and its compatibility with the native network data storage format has contributed significantly to its widespread use in Poland.
Software is engineered to conduct graph theory-based topological analysis, striving to mirror the actual behavior of power grids as closely as possible, with a focus on real electrical parameters, such as voltage, current, and flow. PLANS supports various data formats, including the widely recognised Polish KDM format, extensively utilized in the Polish energy sector, as well as the EPC format and binary (BIN) files. The EPC format, a simple text file format devised by General Electric for use in its PSLF software, primarily contains power flow data. On the contrary, the BIN format, which is not human-readable, encapsulates similar data to KDM or EPC but in a more condensed form.
In PLANS, the nodes are grouped into several categories, with the basic types being PQ (load nodes where active and reactive power are known and voltage is calculated), PV (generation nodes where active power and voltage module are given, and reactive power and voltage angle are computed), and PV with limited reactive power production. Additionally, there is the balancing node, essential for maintaining the network’s cohesion and usually representing the power-loss compensating entity, often a power plant. The incorrect assignment of node types can lead to network segmentation issues.
PLANS enables the display of power grid data in tabular formats and through program-specific windows for various elements, such as branches, lines, transformers, nodes, generators, loads, and areas. The software’s power flow calculations are pivotal for determining nodal voltages based on predefined grid loads and configurations. Users can iterate these voltages after data loading or editing, including alterations in connection layouts, element deactivation, load adjustments, or voltage modifications at power plant nodes.
One of PLANS’ notable features is its macro language, JMP, a programming language that facilitates the automation of repetitive computational tasks commonly executed in the software [12]. This language enables users to script custom actions, such as modifying grid parameters, executing flow calculations, identifying and recording branch and node overruns, and conducting line exclusions. The naming of many program functions in Polish reflects the software’s origins and primary user base.
3.3. PLANS vs. EA-PSM
PLANS and EA-PSM are both simulation tools used for power system analysis, yet they differ significantly in scope, modeling philosophy, and practical applications. PLANS is a specialized software suite developed and widely used in Poland by distribution system operators (DSOs) for the operational analysis of medium- and low-voltage networks. It emphasizes detailed modeling of electrical parameters—including load imbalance, transformer vector groups, and asymmetrical faults—and is based on robust implementations of power flow methods, such as Newton–Raphson, Gauss–Seidel, and others [COSTA, DAS]. The tool includes automated procedures for constructing admittance matrices from real network topologies and supports iterative analysis for both balanced and unbalanced states. Its strength lies in its precision and alignment with the specific structure of Polish distribution systems, making it an industry standard tool for national grid planning and diagnostics.
On the contrary, EA-PSM (Energy Analysis—Power System Model) is an open research-orientated platform with broad modeling capabilities, including transmission-level studies, renewable integration, and long-term planning scenarios [26]. It supports extensive customization, dynamic simulations, and graphical user interfaces, making it more suitable for exploratory studies, academic use, and complex techno-economic assessments [24]. In this study, the capabilities of PLANS and EA-PSM are described with respect to their use of the Newton–Raphson algorithm for power flow calculations. PLANS is recognized for its precise modeling suitable for detailed distribution grid analysis, whereas EA-PSM offers more generalized and scalable modeling applicable to diverse planning scenarios. Discussing both tools highlights the complementary balance between precision in modeling specific network details and broader, research-oriented flexibility.
Although commercial tools, such as PowerWorld, DIgSILENT, or MATLAB, offer robustness and ease of use through predefined models, these frameworks may impose structural limitations when applied to custom or region-specific networks [26]. In particular, adapting such tools to detailed DSO-level grid topologies or non-standard configurations may prove challenging. PLANS and EA-PSM were chosen in this study precisely due to their adaptability, transparency, and alignment with real-world Polish distribution system formats. Their flexible modeling environments allow researchers to explore network behaviors beyond predefined templates, which is crucial when evaluating practical grid conditions and simulating atypical or evolving infrastructure scenarios.
4. NEWTON Algorithm
Both the PLANS and EA-PSM software packages are integral tools in the domain of power system modeling and analysis. A crucial feature they share is the utilization of the Newton–Raphson algorithm for solving the power flow equations, which is essential for calculating the network balance in transmission systems. Because it combines numerical stability with efficient convergence, the Newton–Raphson technique remains a preferred choice for solving nonlinear equations in power system studies [11]. This algorithm solves nonlinear algebraic equations, which are fundamental in determining the steady-state operating condition of electrical power systems [9]. The power flow problem involves finding the voltage magnitude and phase angle at each bus in the network such that the power generation meets the power demand, considering the physical constraints of the transmission network [29].
PLANS (Power Line Analysis Software) employs the Newton–Raphson algorithm to ensure precise and reliable power flow calculations. The software is designed to handle complex transmission networks, facilitating detailed analysis of various scenarios including load flow studies, fault analysis, and network optimization. Using the Newton–Raphson method, PLANS can efficiently solve power flow equations, providing critical information on voltage stability, reactive power management, and overall system performance. Similarly, EA-PSM (Electrical Analysis–Power System Modeling) uses the Newton–Raphson algorithm to perform comprehensive power flow analyses. EA-PSM supports a range of functionalities, including short-circuit analysis, harmonic analysis, and dynamic simulations [24]. The use of the Newton–Raphson method allows EA-PSM to accurately model and analyze the power grid, ensuring that the network remains balanced under different operating conditions. This is particularly important for integrating renewable energy sources, where variability in power generation can pose significant challenges to grid stability.
The Newton–Raphson algorithm’s application in both PLANS and EA-PSM offers several advantages, as follows:
- Quadratic convergence: The method converges quickly, typically in a few iterations, making it highly efficient for large-scale power systems [10].
- Robustness: It provides reliable solutions even for highly nonlinear systems, ensuring accurate power flow results [19].
- Flexibility: The algorithm can be adapted to include various constraints and scenarios of the system, enhancing the software’s analytical capabilities [29].
The integration of the Newton–Raphson algorithm into PLANS and EA-PSM underscores its significance in modern power system analysis tools. Using this robust and efficient method, both software packages ensure accurate and reliable calculations of network balance in transmission systems, contributing to the overall stability and efficiency of power grids.
Below are the principles of calculating power flow using the Newton–Raphson algorithm, as applied in PLANS and EA-PSM, also shown simplified on Figure 1.
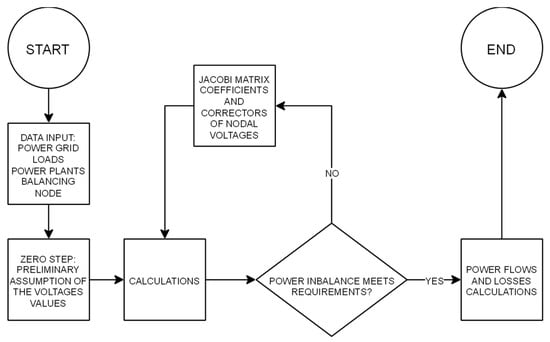
Figure 1.
Newton method algorithm.
- Formulation of power flow equations: Power flow equations are formulated on the basis of the balance of active and reactive power at each bus in the network. The equations are expressed in terms of voltage magnitudes and phase angles. In this context, represents the bus admittance matrix, the complex voltage vector, and the specified complex power, where is active and is reactive power.
- Initialization: Initial guesses are made for the bus voltages and angles. Typically, voltage magnitudes are set to per unit and angles to radians for all buses except the slack bus.
- Jacobian matrix construction: The Jacobian matrix, which represents the partial derivatives of the power flow equations with respect to the voltage magnitudes and angles, is constructed.
- Iterative solution: The Newton–Raphson iterative process involves solving the linearized power flow equations. In each iteration, the mismatch between the calculated and specified power values is computed. The Jacobian matrix is used to update the voltage magnitudes and angles.
- Convergence check: The iterations continue until the mismatches are within a predefined tolerance level, indicating that the solution has converged.
- Final solution: Once convergence is achieved, the final voltage magnitudes and angles are used to calculate other parameters of interest, such as line flows, losses, and bus power injections.
These steps ensure that both PLANS and EA-PSM can provide accurate and reliable solutions for power flow analysis, which are essential for effective power system operation and planning [3].
If we denote the number of load nodes as and the number of power plant nodes as , the total number of nodes in the model can be expressed as follows:
Consequently, the state vector X consists of coordinates, corresponding to the voltages at the nodes, excluding the balancing node. These voltages can be expressed in both trigonometric and algebraic forms, as follows:
where represents the voltage phase, with . The state vector’s coordinates can be expressed as voltage magnitudes U and phase angles δ. Alternatively, the vector can also be formulated in terms of the components and . Other electrical parameters, including power values, power losses, and branch currents, are derived from voltage differences between nodes. The state vector takes the following form: or .
The relationship between power nodes (representing power flow into the node) and node voltages can be expressed as follows:
The voltages are considered as interphase values, ensuring that the computed power is three-phase. For system balance, the total nodal power must be equal to the total load power, as follows:
where represents the vector of computed nodal powers, while denotes the specified power. This leads to the equation . When expressing the state vector with coordinates defined by voltage magnitudes and phase angles, the equations can be formulated as follows:
As a result of applying the Newton method, a total of equations are obtained. Meanwhile, the voltages at the power plant nodes (denoted by G) are predetermined. This ensures that the number of equations corresponds to the number of specified voltages, maintaining consistency in the system, as follows:
In certain cases, Equation (7) may still be valid under specific conditions for the remaining nodes that have not experienced failure. However, the overall simulation results may not converge because the disconnected part of the system is not receiving the necessary electrical power—either due to complete isolation from the power plant nodes or because the power plant nodes themselves lack the required electrical power for normal operation. Within Equations (5) and (6), the following quantities can be identified:
that is, the nodal power of the i-th node, and the following Equation (9):
which represents the grid admittance matrix elements.
The equations presented describe the mathematical model of the power grid in a steady-state condition. Within this framework, the following element models can be identified:
- Power grid—Y matrix;
- Load—P and Q capacities;
- Power plants—P power and U voltage;
- Balancing node—U voltage and its δ phase.
The system of equations formulated in this manner is solved using iterative methods. One commonly used approach is the Newton–Raphson method, which relies on linear approximations of function increments by expanding them into a Taylor series, as follows:
where is the Jacobi matrix. The correction sought is as follows:
The iterative dependence is given as follows:
Recent advances in artificial intelligence (AI) and cybersecurity have begun to influence how power systems are simulated and protected. AI algorithms are increasingly integrated into simulation environments to detect anomalies, optimize control strategies, and predict failures before they occur [30]. At the same time, growing concerns about cyber threats—especially attacks targeting SCADA systems and distributed energy resources (DERs)—highlight the need for security-aware simulation platforms [31]. Enhancing tools, like PLANS and EA-PSM, with AI-driven diagnostics and resilience testing features is becoming an important research direction in the context of modern grid protection.
To illustrate the Newton–Raphson method for power flow calculations, we provide a practical example in Python (v. 3.11.7 used) (see Appendix A). This implementation demonstrates how to solve the power flow equations for a simple power system using an iterative approach similar to the methods used in the PLANS and EA-PSM software.
5. Test Cases
To illustrate the Newton–Raphson method for power flow calculations, we provide a practical example in Python. This implementation demonstrates how to solve the power flow equations for a simple power system using an iterative approach similar to the methods used in the PLANS and EA-PSM software.
5.1. Description and Input Parameters
The test cases analyzed in this study are based on simplified two-bus systems designed to illustrate the behavior of power flow under varying load and network conditions. This significant simplification is an issue of serious limitations related to the publication of real case scenario results—the power grid is an important element of the energy national critical infrastructure and it is not easy to propose artificial scenarios that will reflect real environmental conditions. Each case uses a defined admittance matrix () representing a symmetric low-voltage connection, with elements reflecting typical line impedance values in short radial segments. The specified power injections ( and ) at the bus were selected to represent realistic household or small commercial loads, including both inductive and capacitive components. The initial voltage values () were set at pu with a zero angle, representing nominal voltage conditions at all buses. These parameters were chosen to maintain simplicity while reflecting the relevant grid behaviors in distribution-level scenarios. Calculations were performed for a simple power system consisting of two buses, where one acts as a slack bus and the other as a PQ bus. The input parameters were as follows:
- Admittance matrix (): Defines the electrical connections between buses and their impedance properties. Elements of the matrix are expressed as complex numbers, as follows: (the real part is conductance , and the imaginary part is susceptance ).
- Specified power for buses (). Active and reactive power at a given bus in the following complex form: .
- Initial voltage values (): Initial voltage values for Newton–Raphson iterations. Usually assumed to be 1 pu (per unit) initially.
- Maximum number of iterations and convergence tolerance: Iterations stop when the difference between successive power values is less than the tolerance , or when the iteration limit (10) is reached.
5.2. Base Case
- Admittance matrix :
- Load ():Bus 1:Bus 2:
- Initial voltages ():Bus 1:Bus 2:
- Results:
Final voltages: []
Iterations to converge: 4
The base case represents a standard power system configuration with moderate network admittance and load conditions. The admittance matrix is balanced, allowing for stable power exchange between nodes. The Newton–Raphson method successfully converged in four iterations, with only minor voltage deviations observed. This scenario serves as a benchmark, demonstrating the method’s effectiveness under normal operating conditions and highlighting the system’s inherent stability.
5.2.1. Case 2: Higher Admittance, Higher Load
Increased admittance and higher load.
- Admittance matrix :
- Load ():Bus 1: S = 0 + 0jBus 2: S = 1.0 − 0.5j
- Initial voltages ():Bus 1:Bus 2:
- Results:
Final voltages: []
Iterations to converge: 5
In this case, an increase in network admittance improves power transfer capabilities by reducing impedance and enhancing electrical connectivity between nodes. However, the introduction of a higher load results in greater voltage variations, requiring five iterations to achieve convergence. The findings suggest that while higher admittance contributes to improved stability and power flow efficiency, it also increases the system’s sensitivity to load fluctuations, necessitating a more extensive iterative process to reach equilibrium.
5.2.2. Case 3: Lower Admittance, Lower Load
- Admittance matrix ::
- Load (Sspce):Bus 1: S = 0 + 0jBus 2: S = 0.8 − 0.3j
- Initial voltages ():Bus 1:Bus 2:
- Results:
Final voltages: []
Iterations to converge: 3
A reduction in both admittance and load leads to a power system with lower power transfer intensity and minimal voltage fluctuations. This results in a faster convergence of the Newton–Raphson method, which is completed in three iterations. The lower admittance decreases the influence of individual node interactions, reducing the impact of disturbances and leading to a more stable numerical solution. However, such a configuration may limit the flexibility of the system in handling increased loads, potentially affecting operational reliability in high-demand scenarios.
5.3. General Conclusions
The results obtained from the Newton–Raphson power flow calculations for the three test cases (see details in Table 1) reveal key insights into the impact of network admittance and load variations on voltage stability and computational efficiency.

Table 1.
Summary of all test cases.
Base case: This scenario, with standard admittance values and moderate load, serves as a benchmark for comparison. The system converged in four iterations, with only minor deviations in voltage magnitude and phase angle from the initial conditions. This confirms the robustness of the Newton–Raphson method under normal operating conditions.
Higher admittance, higher load: In this case, increasing the admittance of the system resulted in a stronger electrical coupling between nodes, reducing impedance and facilitating greater power exchange. However, the higher load also introduced larger voltage deviations, leading to a higher number of iterations (five) before achieving convergence. The results indicate that higher admittance can enhance system stability but may require more computational effort due to increased power flow sensitivity.
Lower admittance, lower load: A reduction in network admittance and load led to a system with a lower power flow intensity and correspondingly smaller voltage deviations. This facilitated faster convergence (three iterations) as the system exhibited minimal perturbations. However, reduced admittance may limit power transfer capacity, which can be a constraint in high-demand scenarios.
- Higher admittance improves power transfer efficiency but can lead to increased voltage deviations and a slightly higher computational burden.
- Larger loads introduce more significant voltage fluctuations, requiring more iterations to achieve a stable solution.
- Lower admittance results in faster numerical convergence but may restrict power system flexibility in managing load fluctuations.
These findings emphasize the trade-offs between system admittance, load conditions, and numerical efficiency in power flow analysis, highlighting the need for customized network parameter tuning to balance computational performance with grid stability.
5.4. Qualitative Comparison of PLANS and EA-PSM
A direct numerical comparison between PLANS and EA-PSM is not feasible due to differences in architecture, data formats, and licensing constraints. However, a qualitative assessment reveals distinct advantages. PLANS is tailored to the operational needs of Polish distribution system operators, offering detailed modeling of LV and MV networks with strong compatibility with utility data. EA-PSM, on the other hand, provides greater flexibility for academic and research applications, supporting scenario-based analyses, renewable integration studies, and planning-oriented simulations. These tools serve complementary purposes—PLANS ensures practical alignment with field operations, while EA-PSM supports broader analytical exploration.
6. Conclusions
This research provides a comparative analysis of the PLANS and EA-PSM software, highlighting their role in power system simulation for enhancing energy security and grid reliability. The Newton–Raphson algorithm, implemented in both PLANS and EA-PSM, served as a computational backbone for solving power flow equations. Its robustness and convergence properties ensured reliable results in the evaluation of grid behavior under various operating conditions. The study highlights the importance of these simulations in predicting grid behavior under various scenarios, particularly with the integration of renewable energy sources, and addresses certain challenges, such as voltage distortions and reactive power injection. The principles of the Newton–Raphson method are detailed, showing its application in both PLANS and EA-PSM, which includes formulating power flow equations, initializing guesses for bus voltages, constructing the Jacobian matrix, iterating solutions, checking convergence, and finalizing the results. This approach is crucial to maintaining energy security, ensuring that power systems are efficient, sustainable, and resilient against disruptions.
Energy security is a multidimensional aspect of national security, as it underpins the stability and functioning of modern societies. Secure and reliable energy systems are vital not only for economic prosperity but also for national defense, public health, and overall societal well-being. The robustness of energy infrastructure against disruptions—whether from natural disasters, cyberattacks, or geopolitical tensions—directly affects a nation’s ability to maintain essential services and support economic activities. In recent years, cyber threats targeting power grids have increased, posing a significant risk to energy infrastructure. Cyberattacks on supervisory control and data acquisition (SCADA) systems and distributed energy resources (DERs) can lead to large-scale blackouts, financial losses, and geopolitical instability. Strengthening cybersecurity measures within power system simulations is essential to ensure grid resilience and prevent malicious intrusions that could compromise national security.
Moreover, advances in artificial intelligence (AI) and machine learning (ML) have enabled the development of more sophisticated simulation models that can detect and respond to cyber threats in real-time. The integration of AI-driven security measures into PLANS and EA-PSM could enhance the detection of anomalies, unauthorized access, and potential cyber threats before they escalate to become critical failures. Additionally, digital twin technology, which replicates power grid operations in a virtual environment, is becoming an essential tool to test the resilience of the power system against cyber threats, physical attacks, and climate-related disruptions.
As nations increasingly rely on renewable energy sources, ensuring grid stability amid unpredictable power fluctuations remains a major challenge. Continuous improvement of power system simulations will be essential to adapt to these evolving risks. Future research should focus on integrating cybersecurity protocols into power system simulation tools and developing cross-border strategies for collaboration on energy security. By leveraging advanced technologies and predictive modeling, power system simulations will continue to play a key role in protecting critical energy infrastructure against emerging threats, ultimately supporting global energy resilience and national security.
This simplified Newton–Raphson implementation highlights the fundamental principles used in commercial software, like PLANS and EA-PSM, for power system simulations. This method ensures efficient convergence while solving large-scale power system equations, ultimately helping to analyze network stability and energy security.
Scalability of the Newton–Raphson Implementation
The Python implementation presented in this study serves primarily as a conceptual and educational example. However, the underlying Newton–Raphson approach is scalable, and with the use of sparse matrix techniques and efficient solvers available in libraries, such as SciPy or pandapower, it can be adapted to simulate larger and more complex power grids.
Author Contributions
Conceptualization, P.H. and D.S.; methodology, P.H.; software, P.H.; validation, P.H. and D.S.; formal analysis, P.H.; investigation, P.H. and D.S.; resources, P.H.; data curation, P.H.; writing—original draft preparation, P.H. and D.S.; writing—review and editing, D.S.; visualization, P.H.; supervision, D.S.; project administration, D.S.; funding acquisition, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The power flow problem involves solving nonlinear algebraic equations that describe the balance of active and reactive power at each bus in the power system. Let us consider a simple two-bus system with a slack bus and a bus.
The Python implementation serves primarily as a conceptual and educational example. However, the underlying Newton–Raphson approach is scalable, and with the use of sparse matrix techniques and efficient solvers available in various libraries, such as SciPy or pandapower, it can be adapted to simulate larger and more complex power grids.
Python Code
| import numpy as np def newton_raphson_power_flow(Ybus, S_spec, V_init, max_iter=10, tol=1e-6): V = V_init.copy() n = len(V) for iteration in range(max_iter): # Calculate power injections based on current voltages S_calc = V * np.conj(Ybus @ V) # Compute mismatches mismatch = S_spec - S_calc P_mismatch = mismatch.real Q_mismatch = mismatch.imag if np.linalg.norm(mismatch) < tol: print(f"Converged in {iteration+1} iterations.") return V # Compute Jacobian matrix numerically J = np.zeros((2*n, 2*n)) delta = 1e-4 # Small perturbation for i in range(n): V_perturb = V.copy() V_perturb[i] += delta S_perturb = V_perturb * np.conj(Ybus @ V_perturb) J[:, i] = (S_perturb.real - S_calc.real) / delta # dP/dV J[:, i + n] = (S_perturb.imag - S_calc.imag) / delta # dQ/dV # Solve for voltage updates delta_V = np.linalg.solve(J, np.concatenate((P_mismatch, Q_mismatch))) V += delta_V[:n] + 1j * delta_V[n:] print("Did not converge within maximum iterations.") return V # Example Data: Simple 2-bus system Ybus = np.array([[10-5j, -10+5j], [-10+5j, 10-5j]]) # Example admittance matrix S_spec = np.array([0 + 0j, 1.0 - 0.5j]) # Specified power injection V_init = np.array([1+0j, 1+0j]) # Initial voltage guess # Run power flow calculation V_final = newton_raphson_power_flow(Ybus, S_spec, V_init) print("Final voltages:", V_final) |
References
- Bórawski, P.; Holden, L.; Bełdycka-Bórawska, A. Perspectives of Photovoltaic Energy Market Development in the European Union. Energy 2023, 270, 126804. [Google Scholar] [CrossRef]
- Popescu, C.; Panait, M.; Palazzo, M.; Siano, A. Energy Transition in European Union—Challenges and Opportunities. In Energy Transition. Industrial Ecology; Khan, S.A.R., Panait, M., Puime Guillen, F., Raimi, L., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Beňa, L.; Nowak, M.; Kusiński, M. Analysis of the Impact of Micro Photovoltaic Installations on the Voltage in the Low Voltage Distribution Network. Int. J. Power Syst. Eng. 2021, 12, 89–101. [Google Scholar]
- Gwatidzo, N.; Akindeji, K.T.; Kabeya, M. Industrial Level 100 MW RE Grid Connection Preliminary Technical Feasibility Study. J. Renew. Energy Stud. 2023, 18, 67–82. [Google Scholar]
- Lagace, P.J.; Vuong, M.H.; Kamwa, I. Improving Newton–Raphson Convergence for Fuzzy Power Flow with Levenberg–Marquardt Method. Int. J. Electr. Power Energy Syst. 2008, 146, 108855. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Y. A Novel Newton Current Equation Method on Power Flow Analysis in Microgrid. IEEE Trans. Sustain. Energy 2010, 1, 34–45. [Google Scholar]
- Fuentes, S.; Villafafila-Robles, R.; Lerner, E. Composed Index for the Evaluation of the Energy Security of Power Systems: Application to the Case of Argentina. Energies 2020, 13, 3998. [Google Scholar] [CrossRef]
- Motakatla, V.R.; Liu, W.; Hao, J.; Padullaparti, H.V.; Kumar, U.; Choi, S.L.; Mendoza, I. Integrated Transmission and Distribution Co-Simulation Platform for Demonstration of Bulk Grid Services Using Distributed Energy Resources. Energies 2024, 17, 3215. [Google Scholar] [CrossRef]
- Nguyen, H. Newton-Raphson Method in Complex Form for Power System Load Flow Analysis. IEEE Trans. Power Syst. 2000, 15, 123–131. [Google Scholar] [CrossRef]
- Da Costa, V.M.; Martins, N.N.; Pereira, J.L.R. Developments in the Newton Raphson Power Flow Formulation Based on Current Injections. IEEE Trans. Power Syst. 1999, 14, 497–502. [Google Scholar] [CrossRef]
- Chanhome, S.; Chaitusaney, S. Enhanced Newton–Raphson Power Flow Algorithm for Unbalanced LV Networks. IET Gener. Transm. Distrib. 2021, 15, 469–477. [Google Scholar] [CrossRef]
- PLANS Software Website. Available online: http://www.plans.com.pl/ (accessed on 24 February 2025).
- EA-PSM Software Website. Available online: https://eapsm.net/ (accessed on 24 February 2025).
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- Li, H.; Vittal, V. Co-Simulation for Power System Dynamic Analysis. In Proceedings of the IEEE PES General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Siozinys, V.; Siozinys, M.; Rimkus, A.; Dapkute, A. Virtual Power Plant as a Tool for Cost-Reflective Network Charging and Energy Management. Elektron. Elektrotechnika 2023, 29, 35–42. [Google Scholar]
- Motter, A.E.; Lai, Y.C. Cascade-Based Attacks on Complex Networks. Phys. Rev. E 2002, 66, 065102(R). [Google Scholar] [CrossRef] [PubMed]
- Owerko, D.; Gama, F.; Ribeiro, A. Optimal Power Flow Using Graph Neural Networks. IEEE Trans. Power Syst. 2020, 36, 2563–2573. [Google Scholar]
- Strake, J.; Kaiser, F.; Basiri, F. Non-Local Impact of Link Failures in Linear Flow Networks. arXiv 2018, arXiv:1803.04572. [Google Scholar] [CrossRef]
- Wang, Z.; Wende-von Berg, S.; Braun, M. Fast Parallel Newton-Raphson Power Flow Solver for Large Number of System Calculations with CPU and GPU. arXiv 2021, arXiv:2101.02270. [Google Scholar] [CrossRef]
- Barati, M. Enhancing ACPF Analysis: Integrating Newton-Raphson Method with Gradient Descent and Computational Graphs. arXiv 2024, arXiv:2406.10390. [Google Scholar]
- Huang, H.; Wang, J. Accelerated Power Flow Calculations Using GPU-Based Parallel Computing Techniques. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference, Gothenburg, Sweden, 11–13 October 2010; pp. 1–5. [Google Scholar]
- Zhou, K.; Yang, S. Digital Twin Framework and Its Application to Power Grid. CSEE J. Power Energy Syst. 2019, 5, 156–163. [Google Scholar]
- United States Department of Energy, Pacific Northwest National Laboratory (PNNL). DSO+T Project: Integrated Distribution System Operations with Transactive Coordination; PNNL Report. 2020. Available online: https://www.pnnl.gov/main/publications/external/technical_reports/PNNL-32170-3.pdf (accessed on 28 March 2025).
- Sioshansi, F.P. Smart Grid: Integrating Renewable, Distributed and Efficient Energy; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Glover, J.D.; Overbye, T.; Sarma, M.S. Power System Analysis and Design, 6th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wen, B.; Wang, J.; Guo, Y. Big Data Analytics for Smart Grid: A Review. Renew. Sustain. Energy Rev. 2018, 91, 720–733. [Google Scholar]
- Khan, T.S.; Nazaripouya, H. Analyzing the Implementation of the Newton Raphson Based Power Flow Formulation in CPU+GPU Computing Environment. In Proceedings of the 2023 North American Power Symposium (NAPS), Asheville, NC, USA, 15–17 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Das, D.; Kashinath, H. Improved Modified Newton–Raphson Method for Islanded Microgrid Power Flow Analysis. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 25–33. [Google Scholar] [CrossRef]
- Budka, K.C.; Deshpande, J.G.; Thottan, M. Communication Networks for Smart Grids; Springer: London, UK, 2014. [Google Scholar]
- Farhangi, H. A Road Map to Integration: Perspectives on Smart Grid Development. IEEE Power Energy Mag. 2014, 12, 52–66. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).