Combustion Characteristics of Liquid Ammonia Direct Injection Under High-Pressure Conditions Using DNS
Abstract
:1. Introduction
2. Configuration Details and Numerical Methods
2.1. Configuration Details
2.2. Numerical Methods
2.2.1. Numerical Methods of the Gas Phase
2.2.2. Numerical Methods of the Liquid Phase
3. Results and Discussion
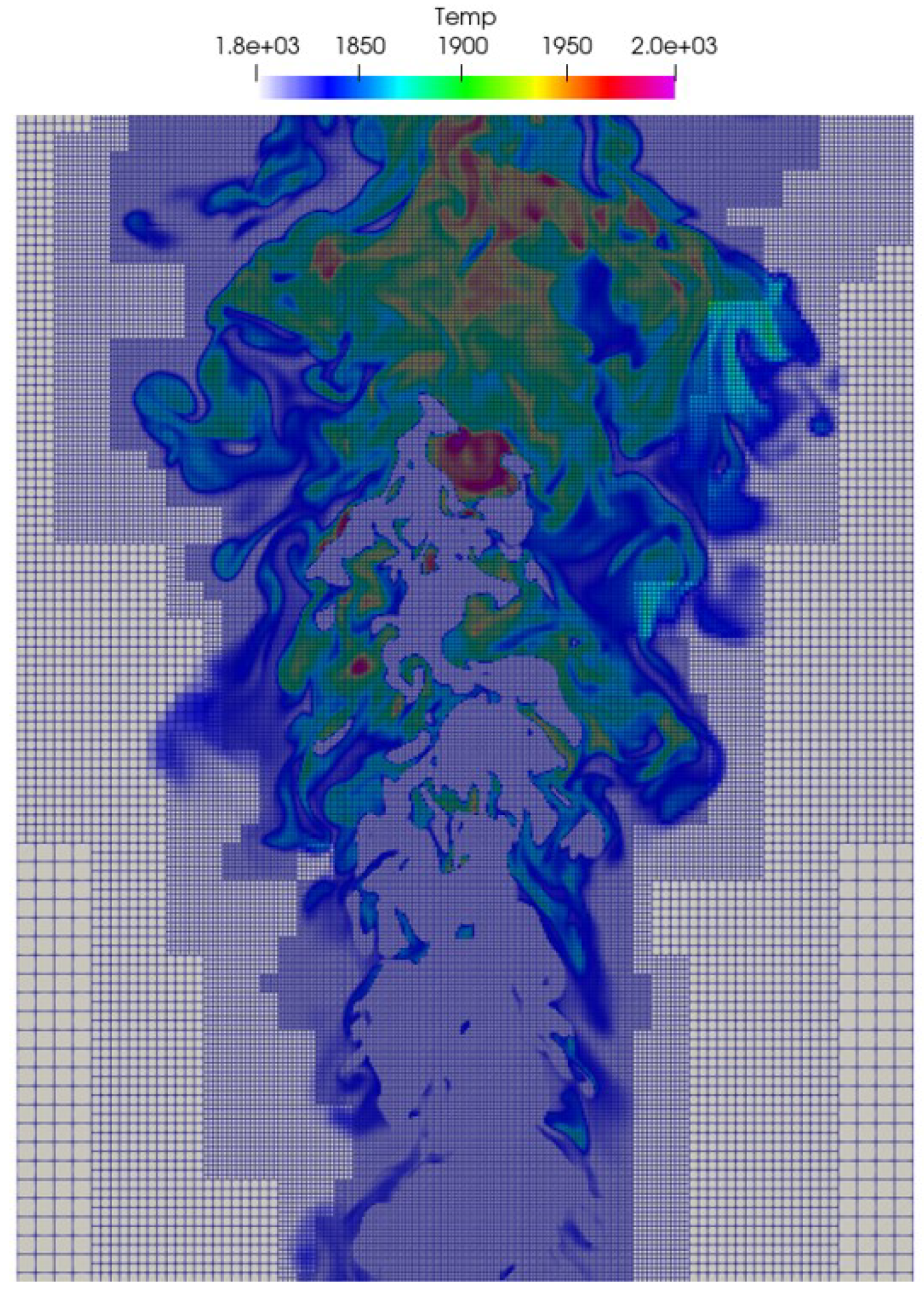
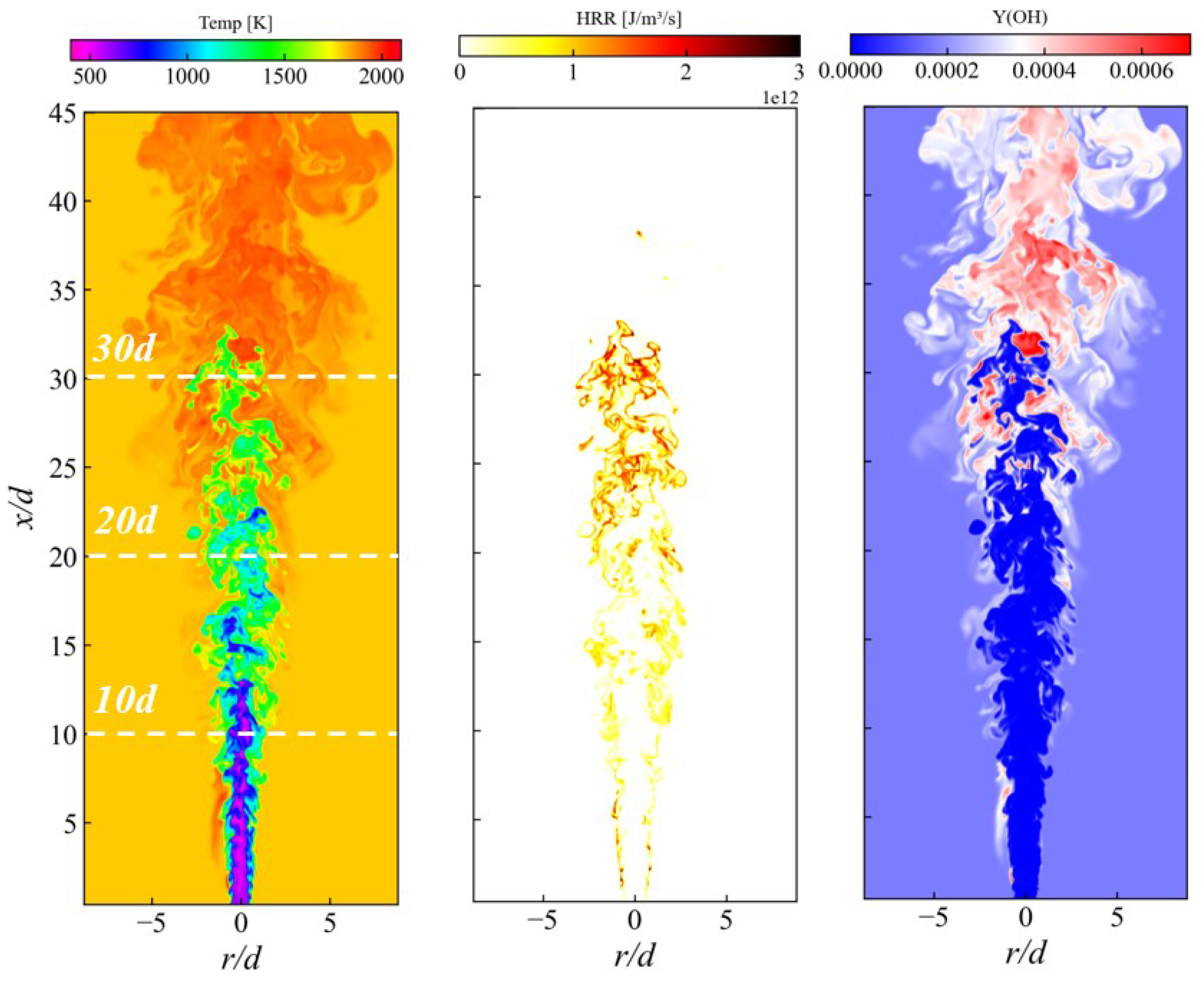
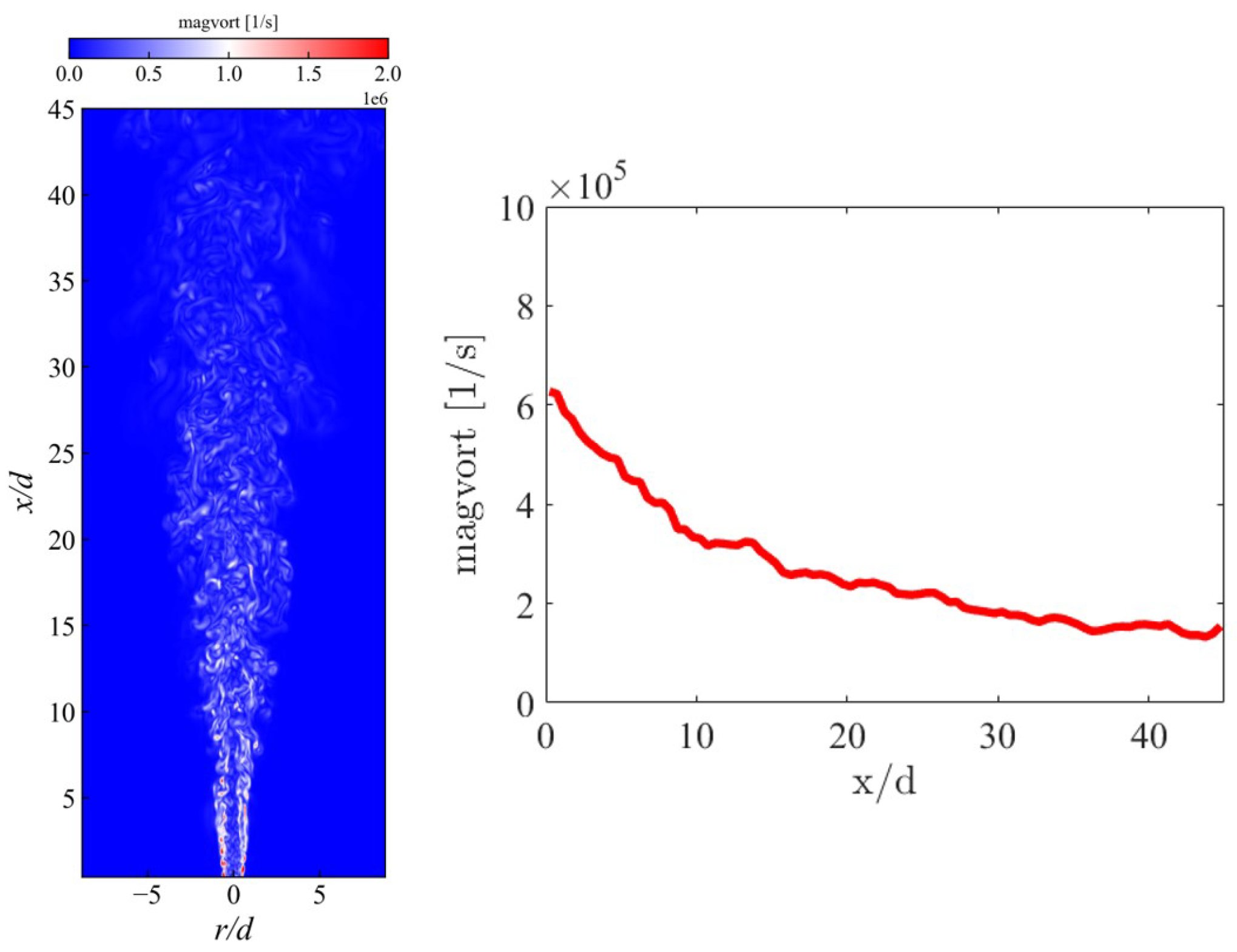
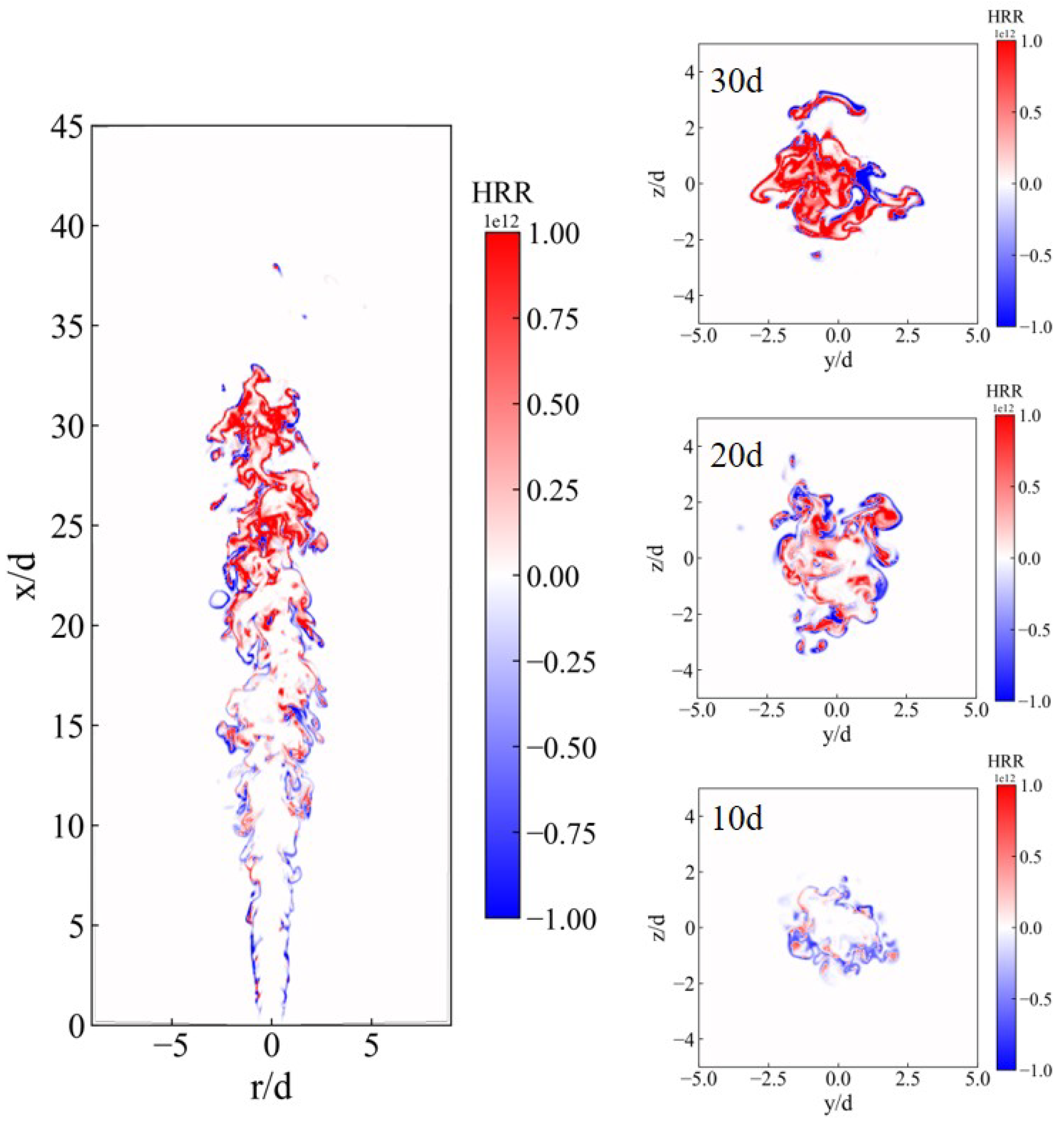
3.1. Instantaneous Characteristics of Ammonia Spray Flames
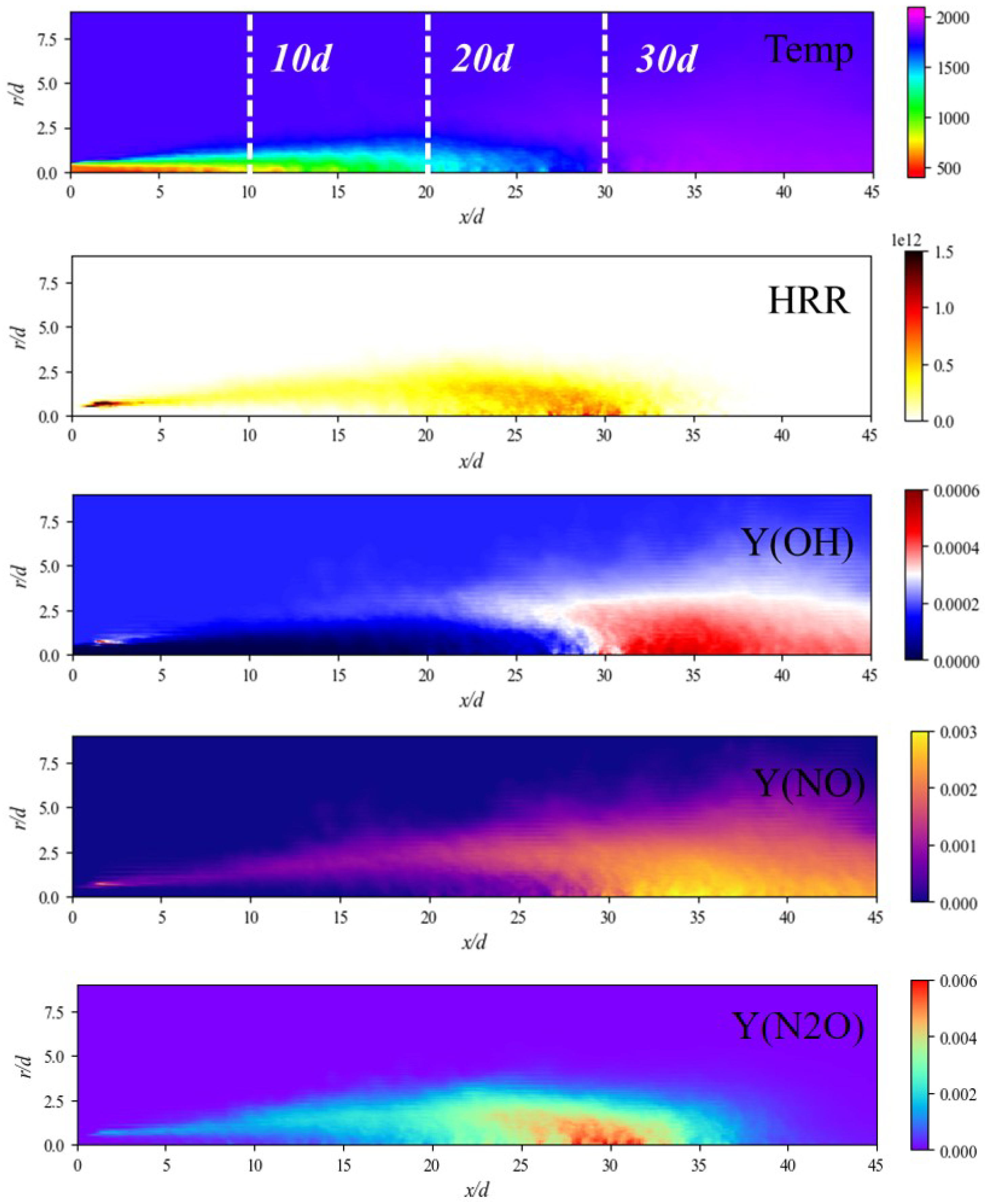
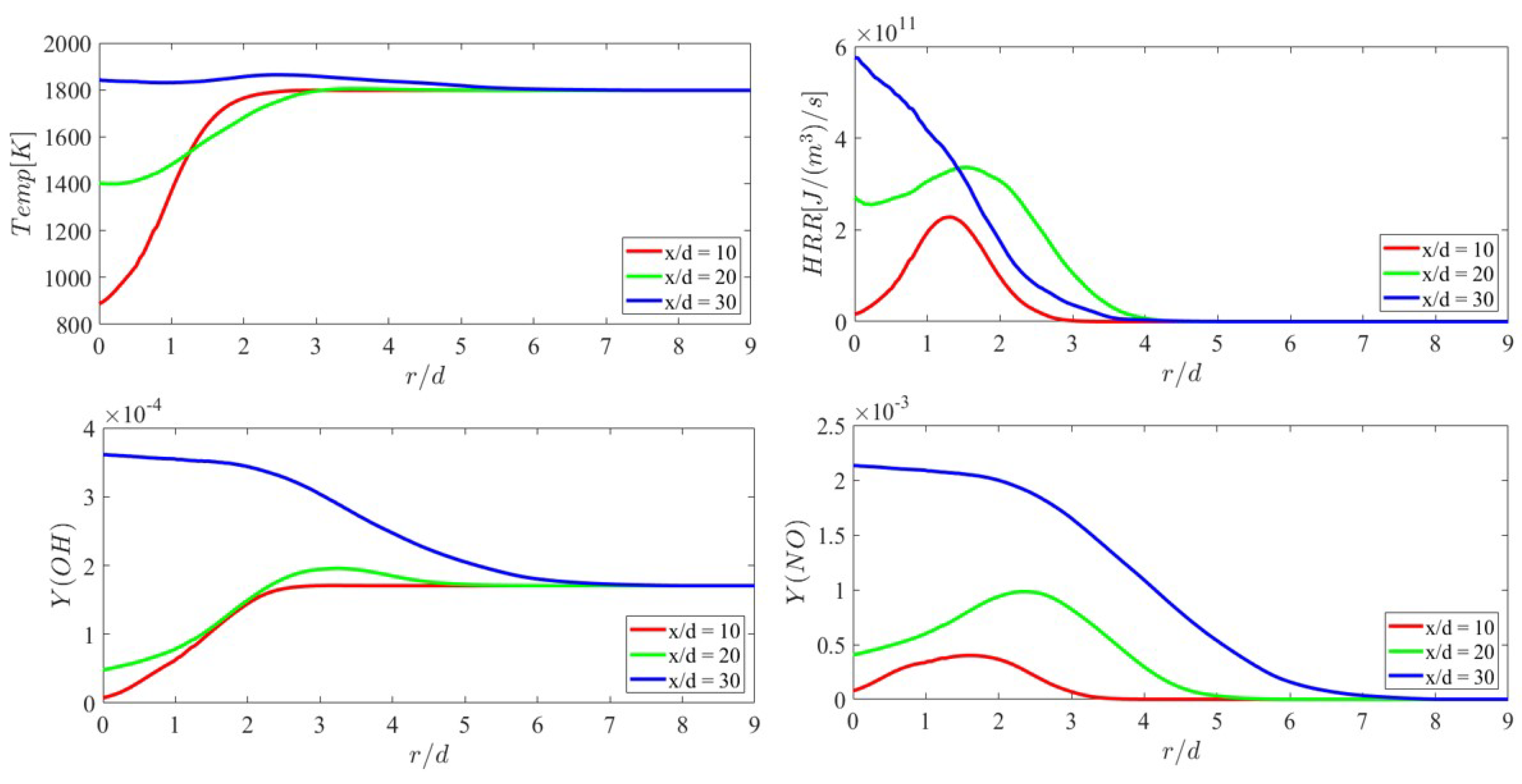
3.2. Mean Flame Structure
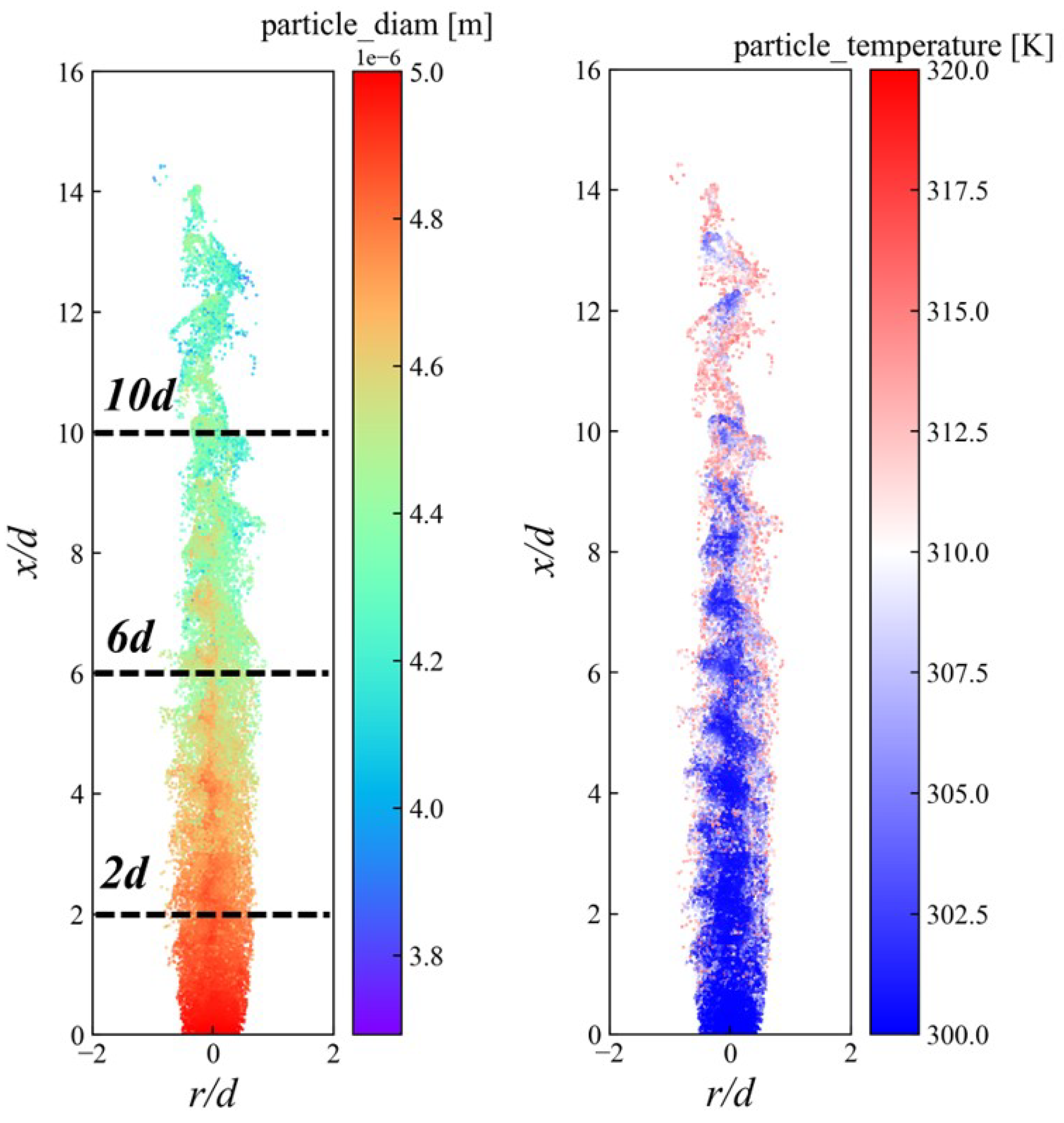
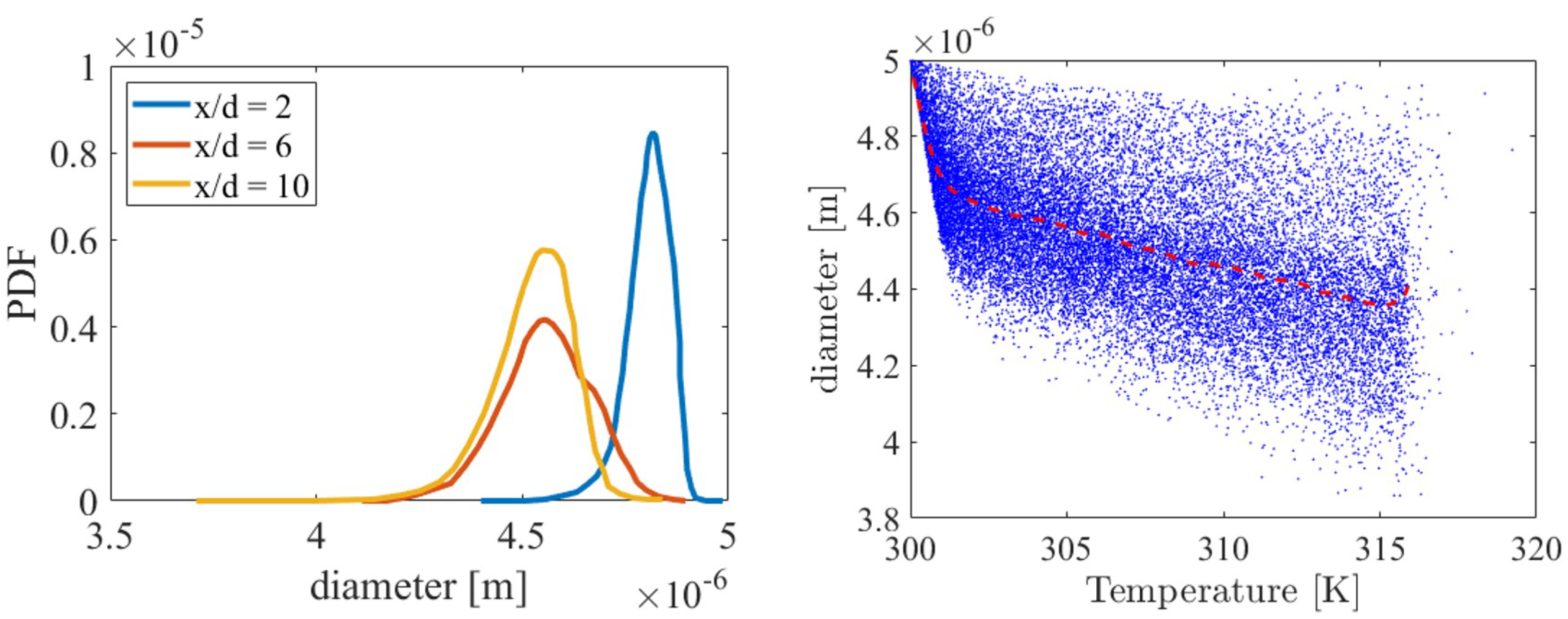
3.3. Distribution of Ammonia Particles
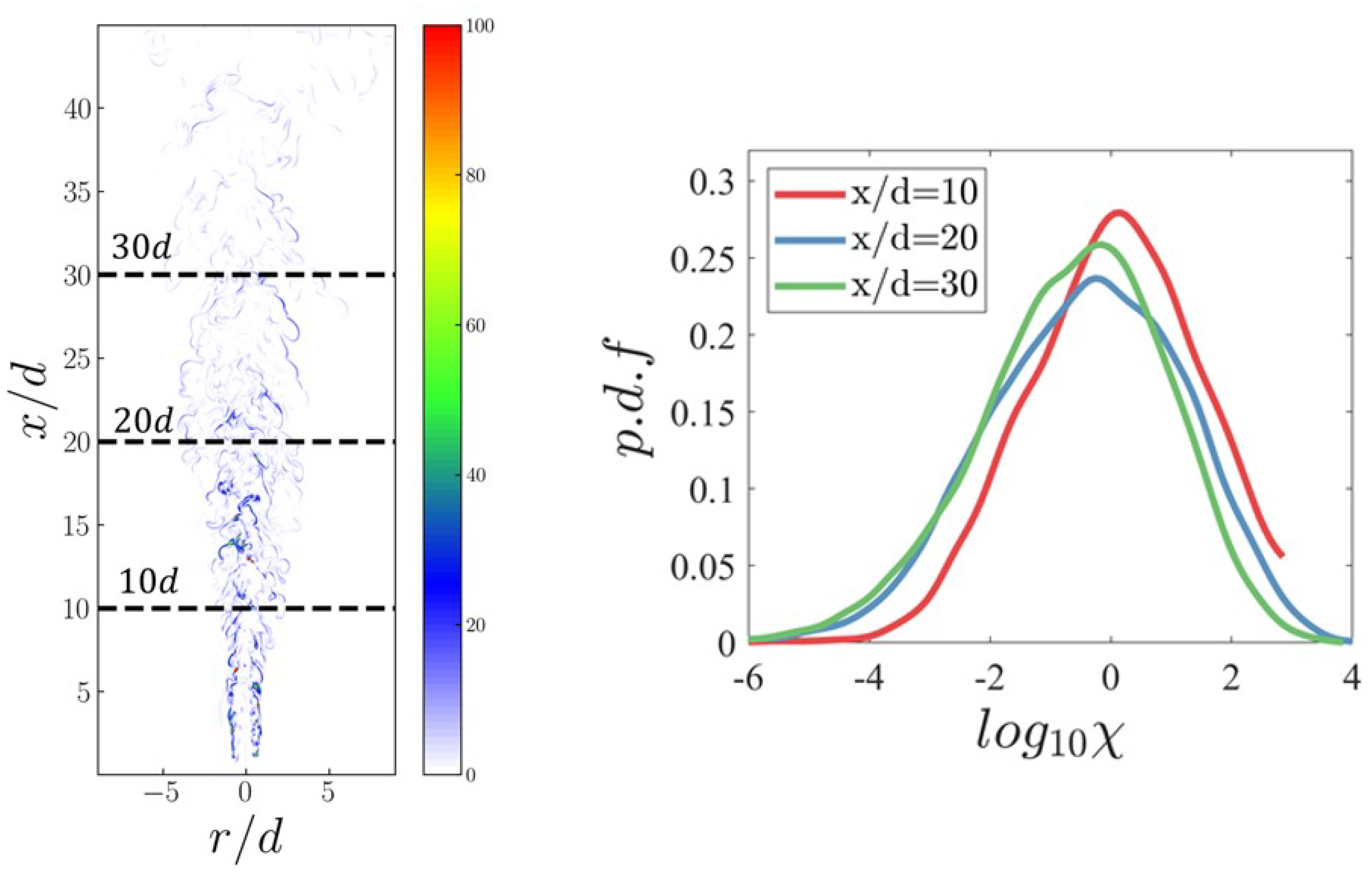
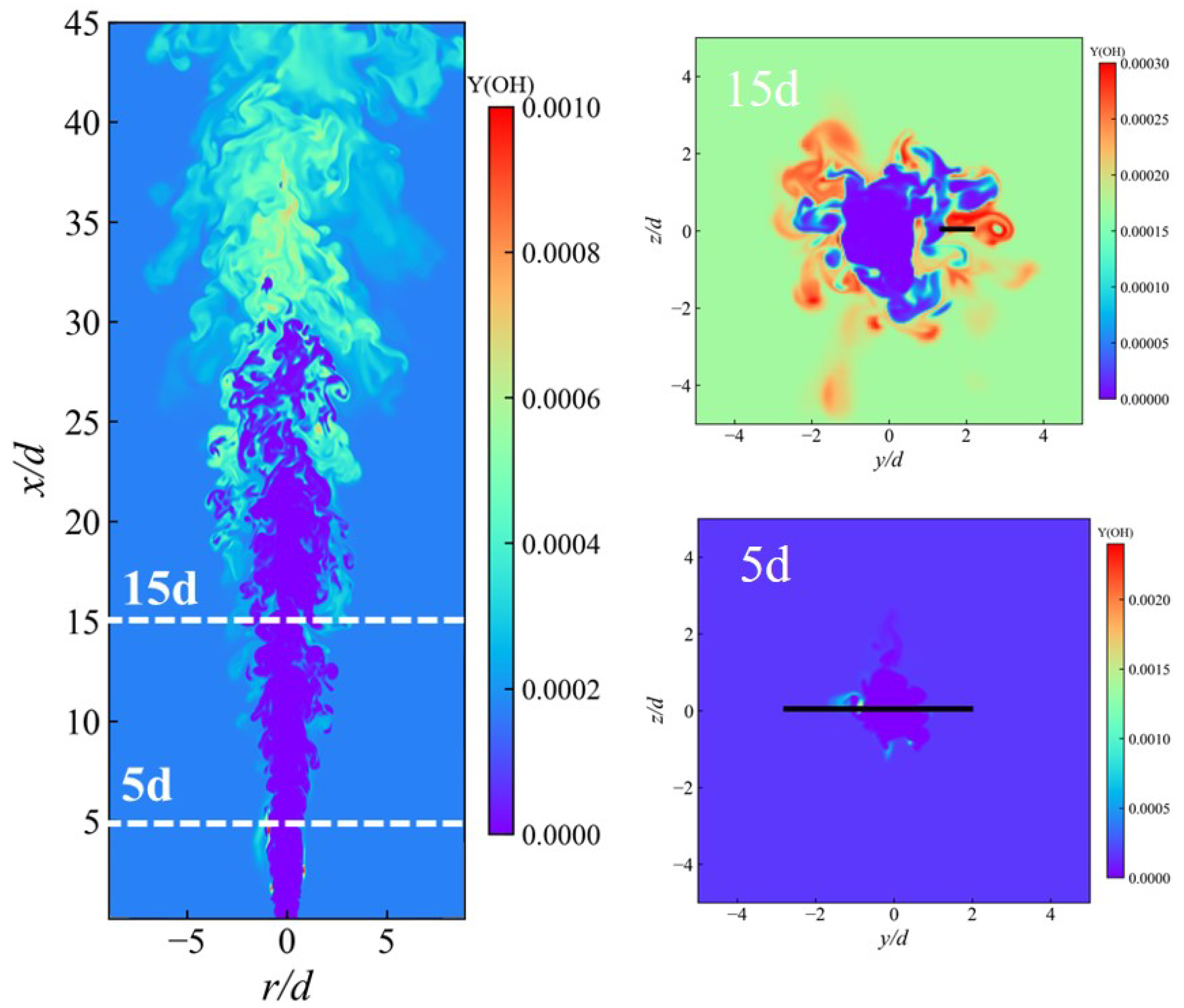
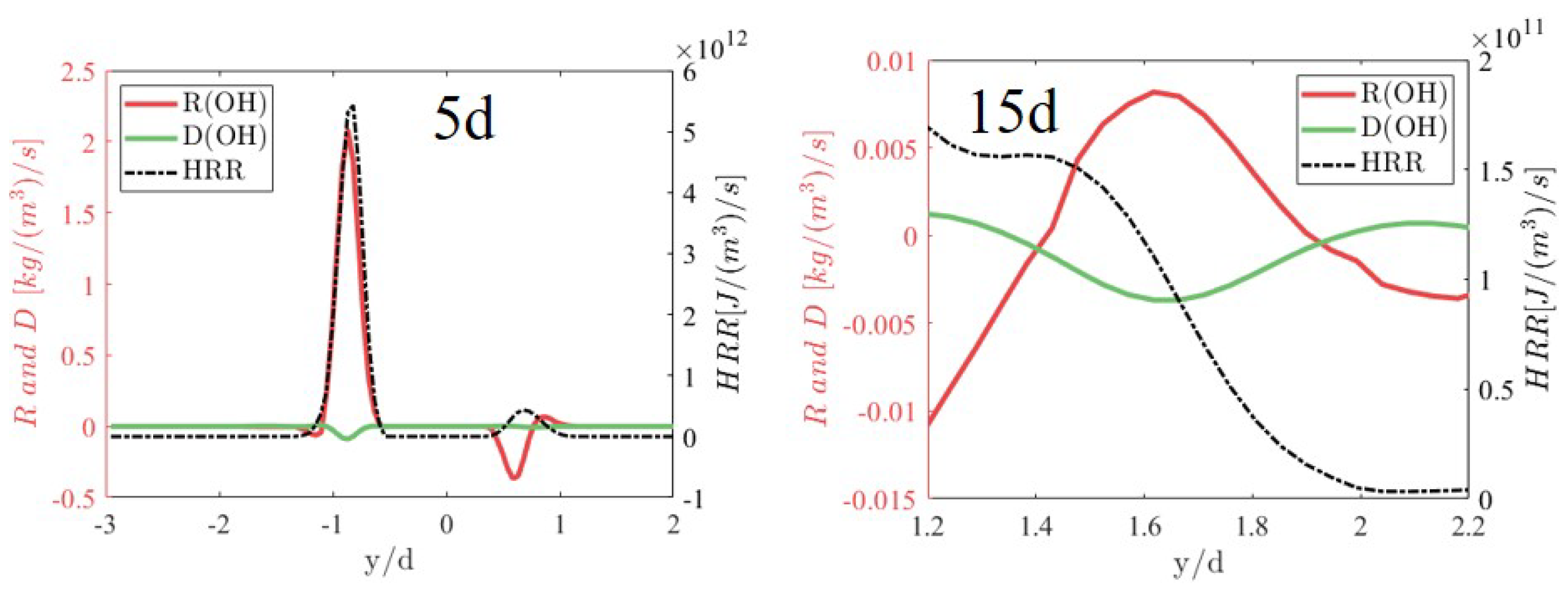
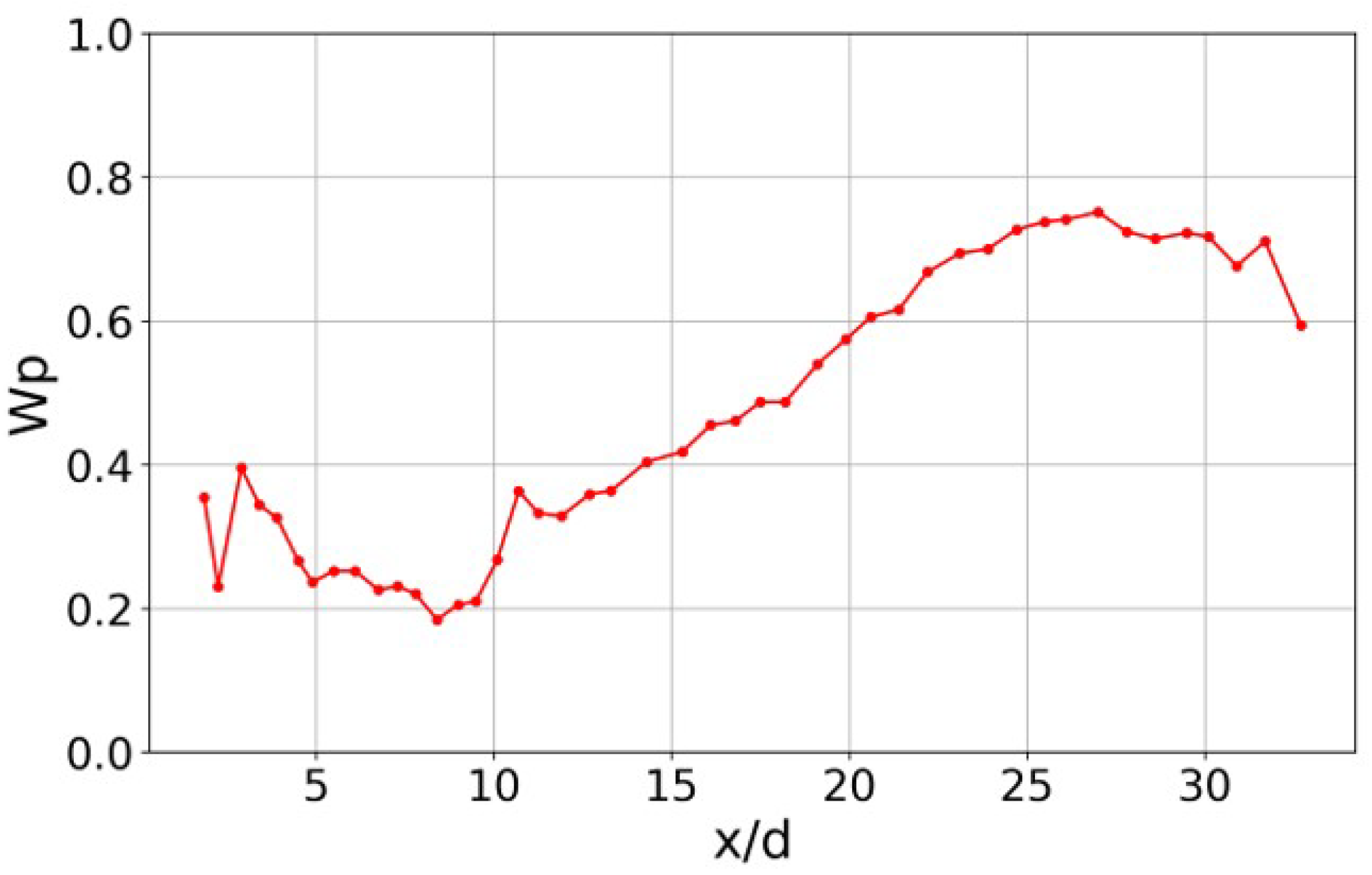
3.4. Flame Stabilization Mechanism
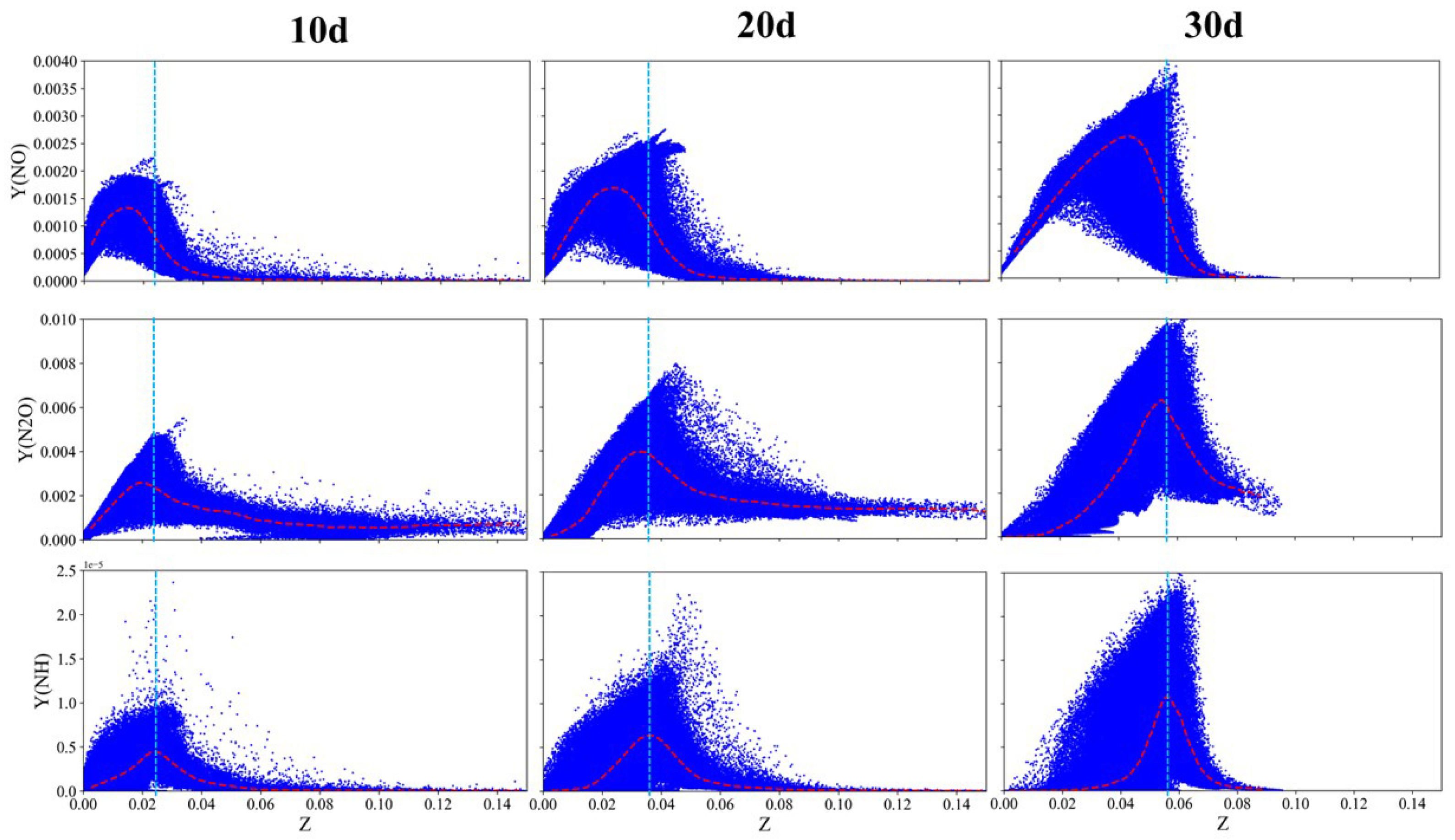
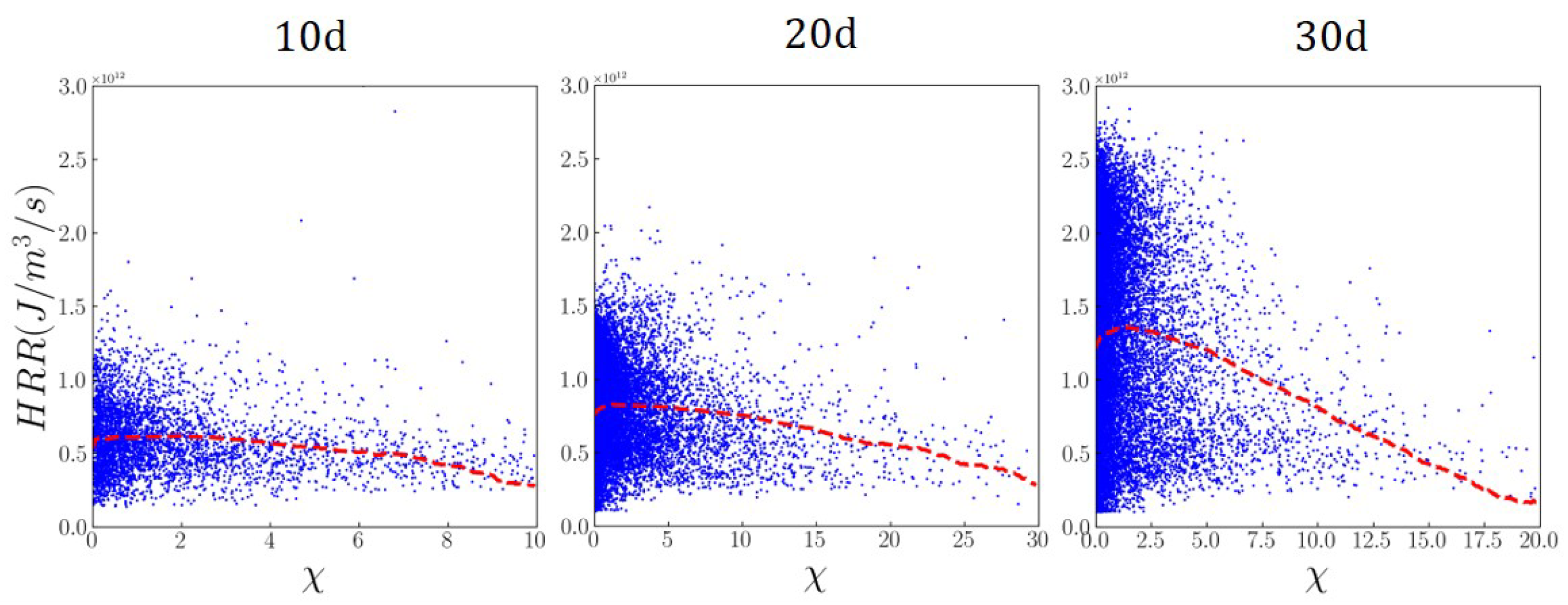
3.5. Combustion Modes of Ammonia Spray Flames
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Valera-Medina, A.; Xiao, H.; Owen-Jones, M.; David, W.; Bowen, P. Ammonia for power. Prog. Energy Combust. Sci. 2018, 69, 63–102. [Google Scholar] [CrossRef]
- Cai, T.; Zhao, D. Overview of Autoignition and Flame Propagation Properties for Ammonia Combustion. AIAA J. 2023, 61, 1–25. [Google Scholar] [CrossRef]
- Fan, Q.; Liu, X.; Cai, X.; Brackmann, C.; Aldén, M.; Bai, X.S.; Li, Z. Structure and scalar correlation of ammonia/air turbulent premixed flames in the distributed reaction zone regime. Combust. Flame 2022, 241, 112090. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, X.; Wang, J.; Huang, Z.; Tan, H. The blow-off and transient characteristics of co-firing ammonia/methane fuels in a swirl combustor. Proc. Combust. Inst. 2021, 38, 5181–5190. [Google Scholar] [CrossRef]
- Rieth, M.; Gruber, A.; Chen, J. A direct numerical simulation study on NO and N2O formation in turbulent premixed ammonia/hydrogen/nitrogen-air flames. Proc. Combust. Inst. 2023, 39, 2279–2288. [Google Scholar] [CrossRef]
- Tian, T.; Wang, H.; Chen, J.H.; Li, Z.; Aldén, M.; Luo, K.; Fan, J. Direct numerical simulations of laboratory-scale NH3/air jet flames: Analysis of flame structure, flame stabilization and NO emission characteristics. Combust. Flame 2025, 274, 114007. [Google Scholar] [CrossRef]
- Okafor, E.C.; Yamashita, H.; Hayakawa, A.; Somarathne, K.K.A.; Kudo, T.; Tsujimura, T.; Uchida, M.; Ito, S.; Kobayashi, H. Flame stability and emissions characteristics of liquid ammonia spray co-fired with methane in a single stage swirl combustor. Fuel 2021, 287, 119433. [Google Scholar] [CrossRef]
- Uchida, M.; Ito, S.; Suda, T. Development of Liquid Ammonia Direct Spray Combustion Gas Turbine. IHI Eng. Rev. 2022, 55. [Google Scholar]
- Wang, R.; Zhang, M.; An, Z.; Cai, X.; Liu, J.; Wang, J.; Huang, Z. Topology characteristics of liquid ammonia swirl spray flame. Proc. Combust. Inst. 2024, 40, 105740. [Google Scholar] [CrossRef]
- Scharl, V.; Sattelmayer, T. Ignition and combustion characteristics of diesel piloted ammonia injections. Fuel Commun. 2022, 11, 100068. [Google Scholar] [CrossRef]
- Scharl, V.; Lackovic, T.; Sattelmayer, T. Characterization of ammonia spray combustion and mixture formation under high-pressure, direct injection conditions. Fuel 2023, 333, 126454. [Google Scholar] [CrossRef]
- Zhang, Z.; Long, W.; Cui, Z.; Dong, P.; Tian, J.; Tian, H.; Meng, X. Visualization study on the ignition and diffusion combustion process of liquid phase ammonia spray ignited by diesel jet in a constant volume vessel. Energy Convers. Manag. 2023, 299, 117889. [Google Scholar] [CrossRef]
- Wang, N.; Li, T.; Zhou, X.; Li, S.; Chen, R. Characteristics of high-pressure ammonia spray combustion under diesel-like conditions. Appl. Therm. Eng. 2024, 257, 124335. [Google Scholar] [CrossRef]
- Krisman, A.; Hawkes, E.R.; Talei, M.; Bhagatwala, A.; Chen, J.H. Characterisation of two-stage ignition in diesel engine-relevant thermochemical conditions using direct numerical simulation. Combust. Flame 2016, 172, 326–341. [Google Scholar] [CrossRef]
- Demosthenous, E.; Borghesi, G.; Mastorakos, E.; Cant, R.S. Direct numerical simulations of premixed methane flame initiation by pilot n-heptane spray autoignition. Combust. Flame 2016, 163, 122–137. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Squires, K. Point-particle methods for disperse flows. In Computational Methods for Multiphase Flow; Cambridge University Press: Cambridge, UK, 2007; pp. 282–319. [Google Scholar]
- Tian, T.; Song, C.; Wang, H.; Xu, C.; Luo, K.; Fan, J. The effects of turbulence on the flame structure and NO formation of ammonia turbulent premixed combustion at various equivalence ratios. Fuel 2023, 332, 126127. [Google Scholar] [CrossRef]
- Chai, W.S.; Bao, Y.; Jin, P.; Tang, G.; Zhou, L. A review on ammonia, ammonia-hydrogen and ammonia-methane fuels. Renew. Sustain. Energy Rev. 2021, 147, 111254. [Google Scholar] [CrossRef]
- Henry de Frahan, M.T.; Rood, J.S.; Day, M.S.; Sitaraman, H.; Yellapantula, S.; Perry, B.A.; Grout, R.W.; Almgren, A.; Zhang, W.; Bell, J.B.; et al. PeleC: An adaptive mesh refinement solver for compressible reacting flows. Int. J. High Perform. Comput. Appl. 2022, 37, 115–131. [Google Scholar] [CrossRef]
- Henry de Frahan, M.T.; Esclapez, L.; Rood, J.; Wimer, N.T.; Mullowney, P.; Perry, B.A.; Owen, L.; Sitaraman, H.; Yellapantula, S.; Hassanaly, M.; et al. The Pele Simulation Suite for Reacting Flows at Exascale. In Proceedings of the 2024 SIAM Conference on Parallel Processing for Scientific Computing (PP), Baltimore, MD, USA, 5–8 March 2024; pp. 13–25. [Google Scholar]
- Sitaraman, H.; Yellapantula, S.; Henry de Frahan, M.T.; Perry, B.; Rood, J.; Grout, R.; Day, M. Adaptive mesh based combustion simulations of direct fuel injection effects in a supersonic cavity flame-holder. Combust. Flame 2021, 232, 111531. [Google Scholar] [CrossRef]
- Owen, L.D.; Ge, W.; Rieth, M.; Arienti, M.; Esclapez, L.; S Soriano, B.; Mueller, M.E.; Day, M.; Sankaran, R.; Chen, J.H. PeleMP: The Multiphysics Solver for the Combustion Pele Adaptive Mesh Refinement Code Suite. J. Fluids Eng. 2023, 146, 041103. [Google Scholar] [CrossRef]
- Howarth, T.; Picciani, M.; Richardson, E.; Day, M.; Aspden, A. Direct numerical simulation of a high-pressure hydrogen micromix combustor: Flame structure and stabilisation mechanism. Combust. Flame 2024, 265, 113504. [Google Scholar] [CrossRef]
- Ramachandran, S.; Srinivasan, N.; Taneja, T.S.; Zhang, H.; Yang, S. Numerical study of turbulent non-premixed cool flames at high and supercritical pressures: Real gas effects and dual peak structure. Combust. Flame 2023, 249, 112626. [Google Scholar] [CrossRef]
- Faeth, G. Current status of droplet and liquid combustion. Prog. Energy Combust. Sci. 1977, 3, 191–224. [Google Scholar] [CrossRef]
- Schiller, L. A drag coefficient correlation. Zeit. Ver. Deutsch. Ing. 1933, 77, 318–320. [Google Scholar]
- Abramzon, B.; Sirignano, W. Droplet vaporization model for spray combustion calculations. Int. J. Heat Mass Transfer 1989, 32, 1605–1618. [Google Scholar] [CrossRef]
- Wang, H.; Luo, K.; Fan, J. Effects of turbulent intensity and droplet diameter on spray combustion using direct numerical simulation. Fuel 2014, 121, 311–318. [Google Scholar] [CrossRef]
- Tang, J.C.K.; Wang, H.; Bolla, M.; Wehrfritz, A.; Hawkes, R.E. A DNS evaluation of mixing and evaporation models for TPDF modelling of nonpremixed spray flames. Proc. Combust. Inst. 2019, 37, 3363–3372. [Google Scholar] [CrossRef]
- Ge, W.; Sankaran, R.; Chen, J.H. Development of a CPU/GPU portable software library for Lagrangian–Eulerian simulations of liquid sprays. Int. J. Multiphase Flow 2020, 128, 103293. [Google Scholar] [CrossRef]
- Bilger, R. The structure of turbulent nonpremixed flames. In Proceedings of the Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1989; Volume 22, pp. 475–488. [Google Scholar]
- Wang, H.; Luo, K.; Hawkes, E.R.; Chen, J.H.; Fan, J. Turbulence, evaporation and combustion interactions in n-heptane droplets under high pressure conditions using DNS. Combust. Flame 2021, 225, 417–427. [Google Scholar] [CrossRef]
- Jung, K.S.; Kim, S.O.; Lu, T.; Chung, S.H.; Lee, B.J.; Yoo, C.S. Differential diffusion effect on the stabilization characteristics of autoignited laminar lifted methane/hydrogen jet flames in heated coflow air. Combust. Flame 2018, 198, 305–319. [Google Scholar] [CrossRef]
- Pei, Y.; Hawkes, E.R.; Bolla, M.; Kook, S.; Goldin, G.M.; Yang, Y.; Pope, S.B.; Som, S. An analysis of the structure of an n-dodecane spray flame using TPDF modelling. Combust. Flame 2016, 168, 420–435. [Google Scholar] [CrossRef]
- Luo, K.; Pitsch, H.; Pai, M.; Desjardins, O. Direct numerical simulations and analysis of three-dimensional n-heptane spray flames in a model swirl combustor. Proc. Combust. Inst. 2011, 33, 2143–2152. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Li, X.; Li, J.; Huang, H.; Kobayashi, N. Large eddy simulation of ammonia-diesel dual fuel spray combustion: Effects of ambient condition on ignition characteristics. Chem. Eng. J. 2024, 501, 157698. [Google Scholar] [CrossRef]
- Yamashita, H.; Shimada, M.; Takeno, T. A numerical study on flame stability at the transition point of jet diffusion flames. In Proceedings of the Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1996; Volume 26, pp. 27–34. [Google Scholar]
- Meng, Q.; Wang, H.; Chang, Z.; Cheng, M.; Huang, Z.; Luo, K.; Fan, J. Direct numerical simulation studies of spray jet flames in hot vitiated crossflow. Fuel 2025, 389, 134543. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Luo, K.; Fan, J. A DNS study of pulverized coal combustion in a hot turbulent environment: Effects of particle size, mass loading and preferential concentration. Combust. Flame 2023, 254, 112839. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Wang, H.; Meng, Q.; Luo, K.; Fan, J. Combustion Characteristics of Liquid Ammonia Direct Injection Under High-Pressure Conditions Using DNS. Energies 2025, 18, 2228. https://doi.org/10.3390/en18092228
Huang Z, Wang H, Meng Q, Luo K, Fan J. Combustion Characteristics of Liquid Ammonia Direct Injection Under High-Pressure Conditions Using DNS. Energies. 2025; 18(9):2228. https://doi.org/10.3390/en18092228
Chicago/Turabian StyleHuang, Ziwei, Haiou Wang, Qian Meng, Kun Luo, and Jianren Fan. 2025. "Combustion Characteristics of Liquid Ammonia Direct Injection Under High-Pressure Conditions Using DNS" Energies 18, no. 9: 2228. https://doi.org/10.3390/en18092228
APA StyleHuang, Z., Wang, H., Meng, Q., Luo, K., & Fan, J. (2025). Combustion Characteristics of Liquid Ammonia Direct Injection Under High-Pressure Conditions Using DNS. Energies, 18(9), 2228. https://doi.org/10.3390/en18092228





