Design of a Four-Branch LCL-Type Grid-Connecting Interface for a Three-Phase, Four-Leg Active Power Filter
Abstract
:1. Introduction

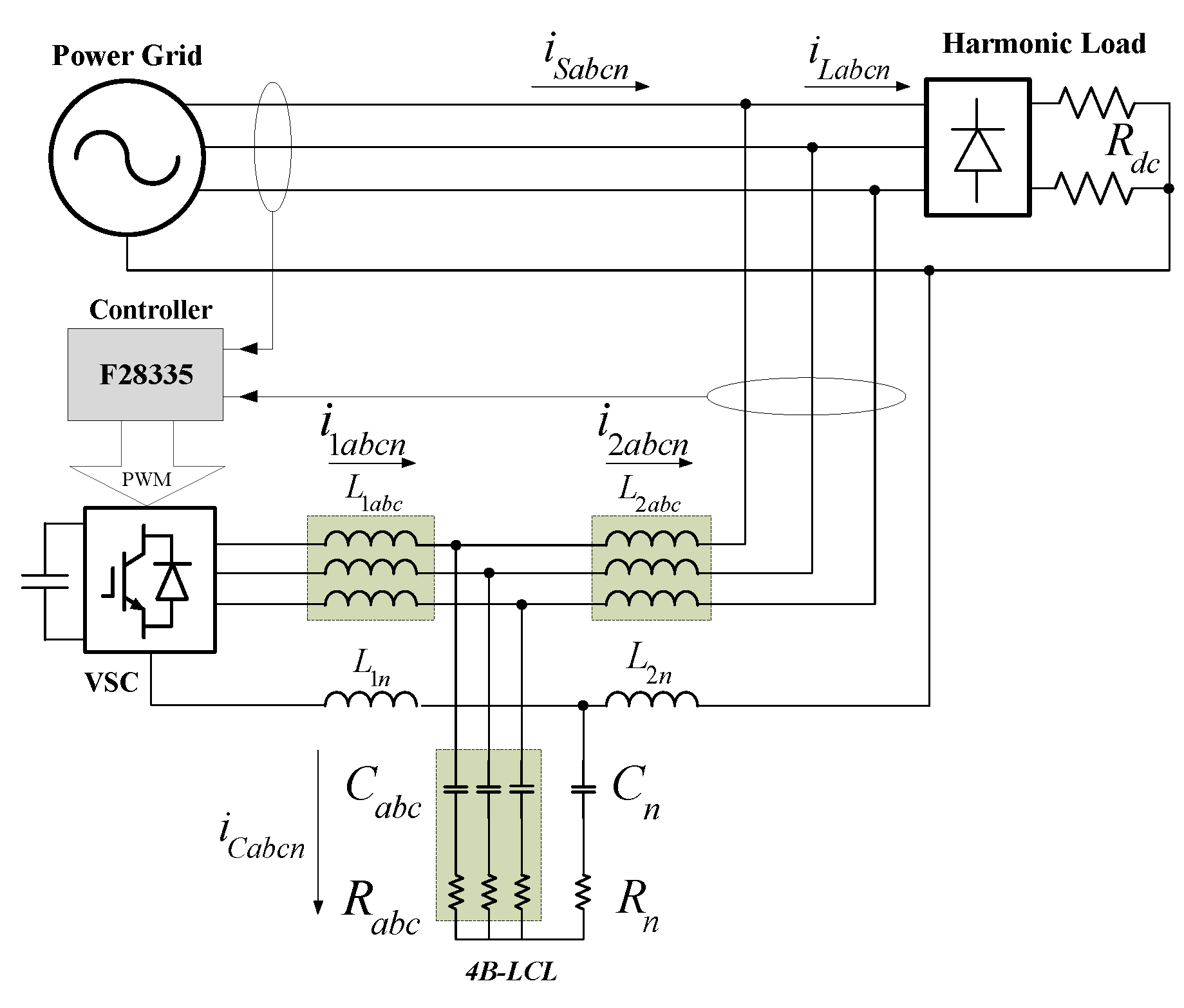
2. System Description and Modeling
2.1. Topology Description
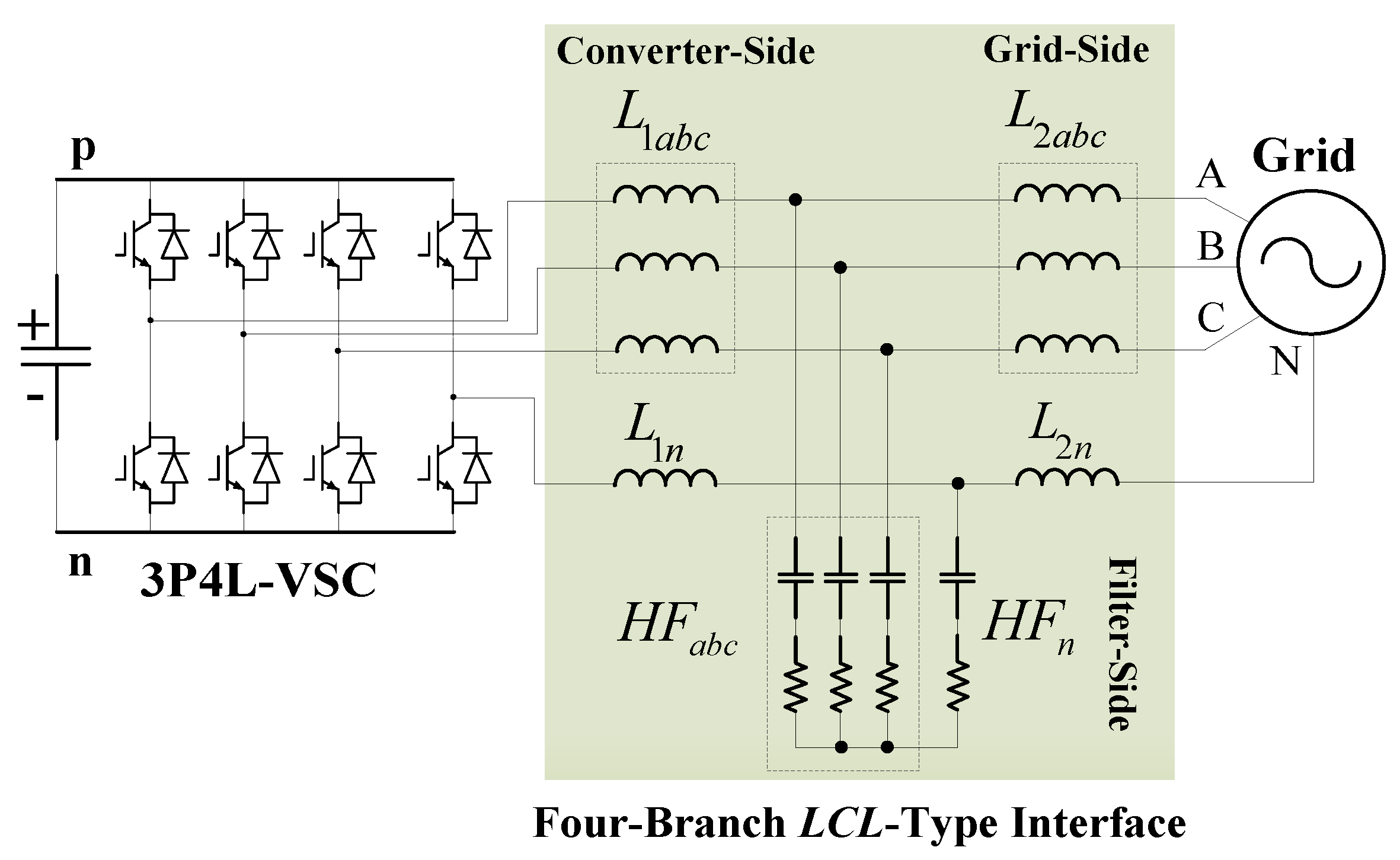
2.2. Topology Analysis
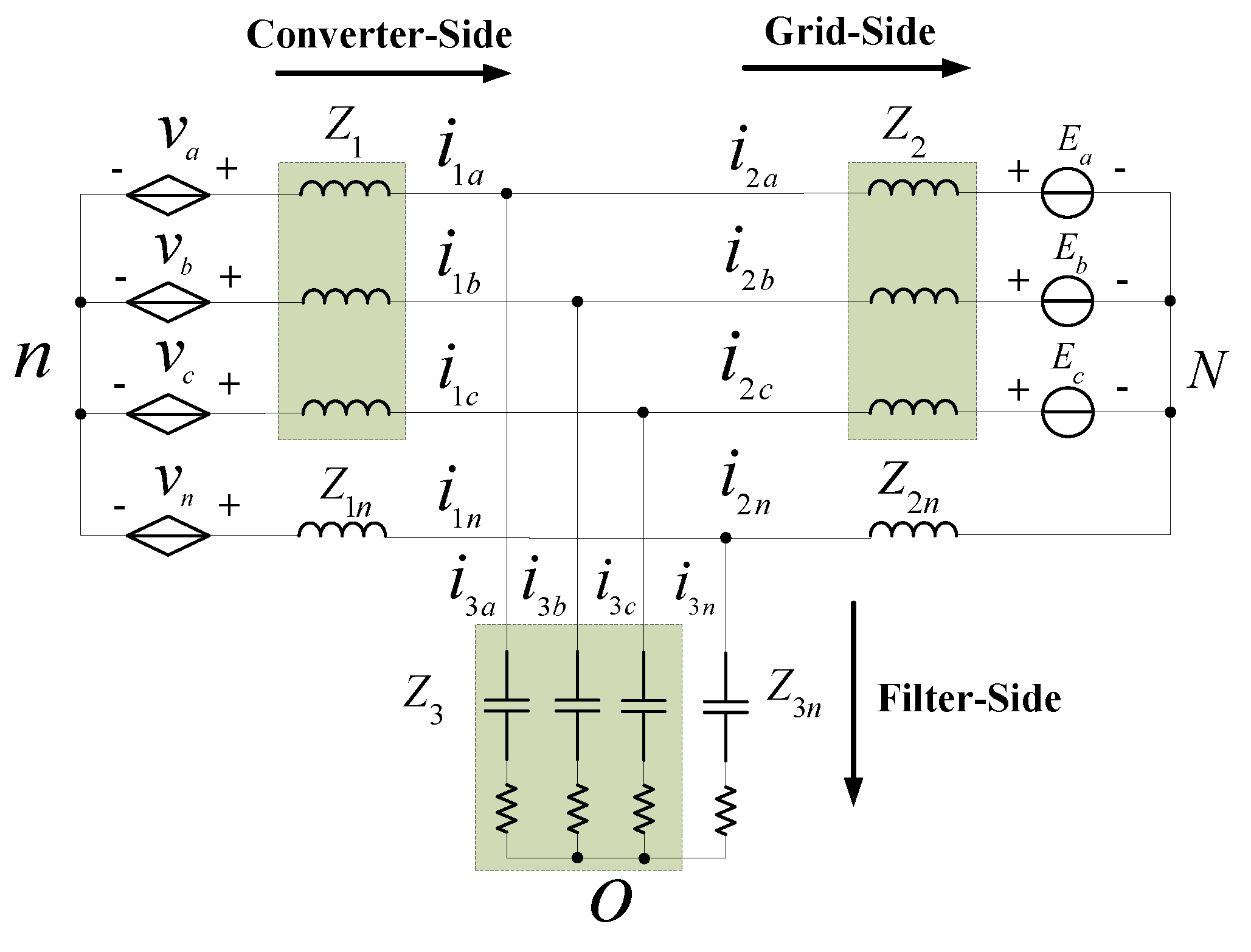
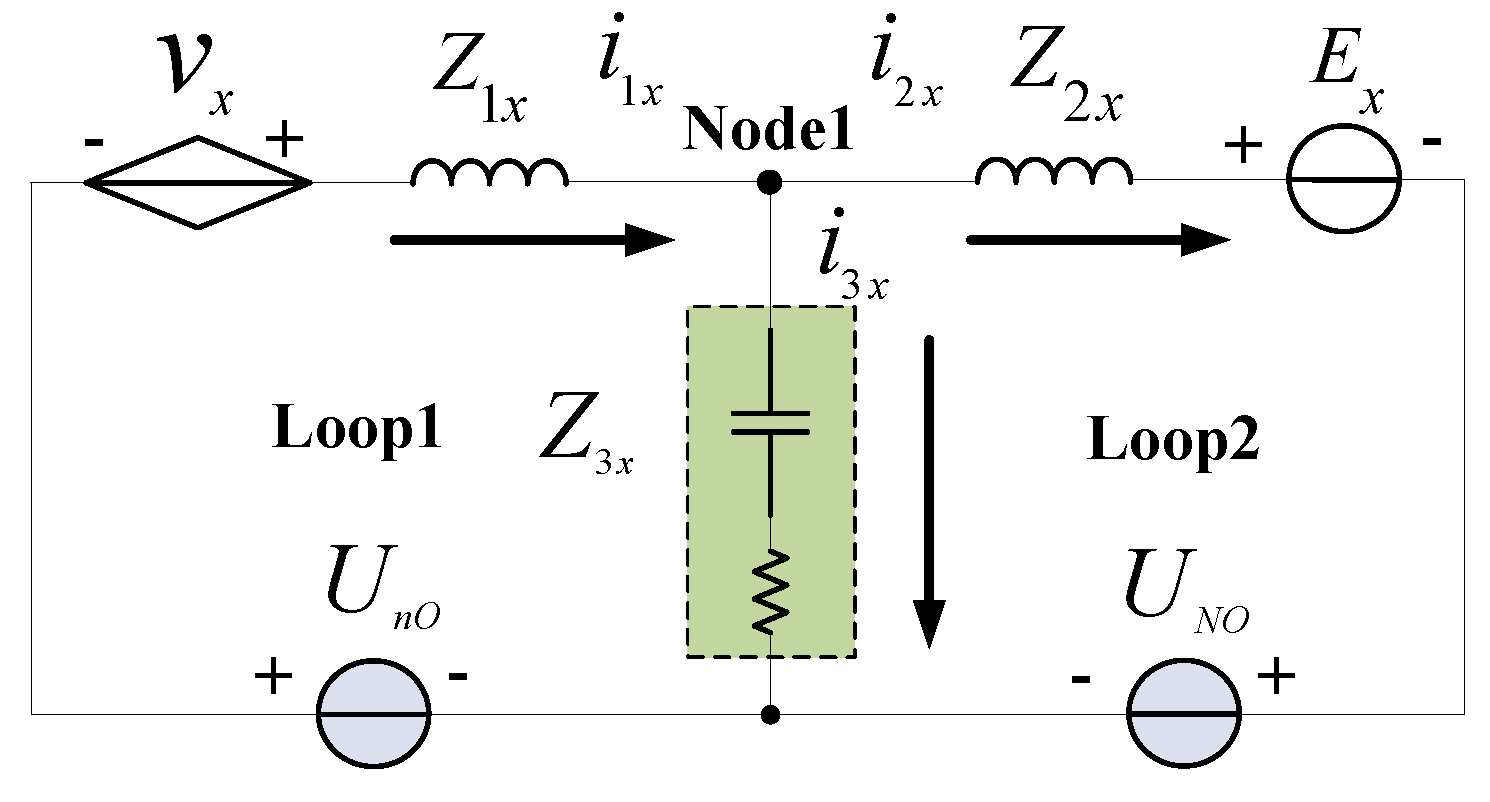
2.2.1. Analysis in the Per-Phase Perspectives
2.2.2. Analysis in the Non-Zero-Sequence and Zero-Sequence Perspectives
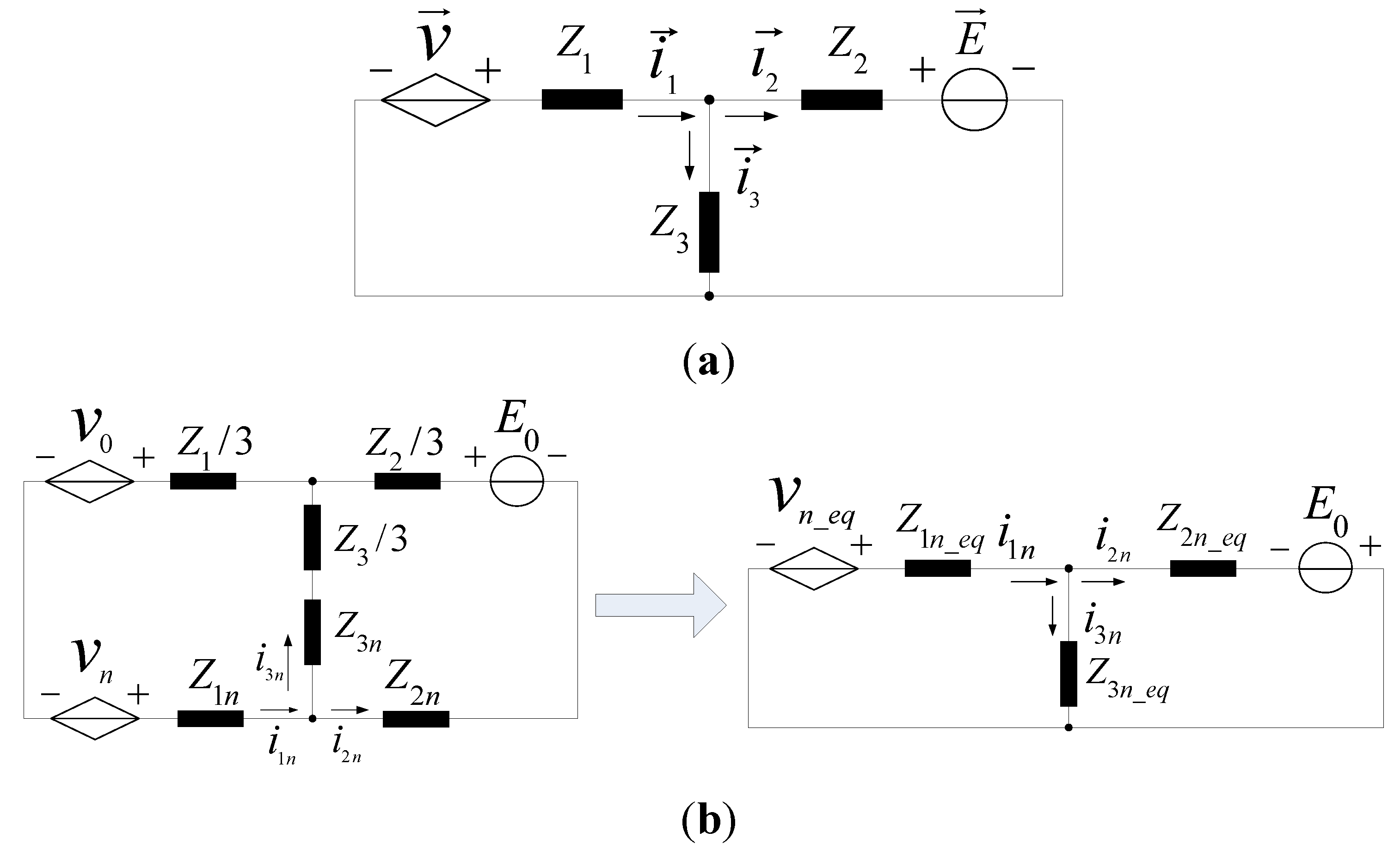
2.3. Model for Parameter Design

3. Parameter Design
3.1. Circuit Characteristic


3.2. Design Procedure

3.2.1. Determination of the Performance Requirements
3.2.2. Meeting the Performance Requirements
3.2.3. Verification of the Performance Index
4. Simulation
| Symbol | Quantity | Value |
|---|---|---|
| Erms | Phase grid voltage | 200–240 V |
| fgh | Highest background voltage harmonics frequency | 550 Hz |
| h | Highest frequency order of the output current harmonics | 20 |
| m | DC Voltage Utilization Ratio | 1// |
| Vdc | DC Link Voltage | 800 V |
| fs | Switching Frequency | 10 KHz |
| Irms | Rated Output Current in phases A, B, C, and N | 100 A |
| Ir1 | Converter-side current ripple rms in phases A, B, C, and N | ≤12 A |
| Ir2 | Grid-side current ripple rms in phases A, B, C, and N | ≤1 A |
| Symbol | Quantity | Value |
|---|---|---|
| P1 | Dual-side impedance amplitude in the fundamental frequency | ≤0.87 Ω |
| P2 | Dual-side impedance amplitude in the switching frequency | ≥295.2 Ω |
| P3 | Converter-side impedance amplitude in the switching frequency | ≥10.0 Ω |
| P4 | Filter-side impedance amplitude in the fundamental frequency | ≥40.0 Ω |
| P5 | Dual-side impedance amplitude in the series resonant frequency | approximately 1.0 Ω |
| fres | Dual-side series resonant frequency | [2.0 KHz, 5.0 KHz) |
| f01 | Grid-side parallel resonant frequency | [1.1 KHz, fres) |
| Symbol | Quantity | Value: the selected (the calculated) |
|---|---|---|
| L1 | Converter-side inductance | 0.23 mH (0.273 mH) |
| L2 | Grid-side inductance | 0.10 mH (0.086 mH) |
| C | Filter-side capacitance | 60 µF (56.92 µF) |
| R | Filter-side resistance | 0.2 Ω (0.196 Ω) |
| P1 | Performance Index Output in phases A, B, and C | 0.1 Ω |
| P2 | 301.0 Ω | |
| P3 | 14.2 Ω | |
| P4 | 53.1 Ω | |
| P5 | 0.93 Ω | |
| fres | 2.46 KHz | |
| f01 | 2.05 KHz |
| Symbol | Quantity | Value: the selected (the calculated) |
|---|---|---|
| L1n | Converter-side inductance | 0.32 mH (0.312 mH) |
| L2n | Grid-side inductance | 0.14 mH (0.138 mH) |
| Cn | Filter-side capacitance | 42 µF (41.74 µF) |
| Rn | Filter-side resistance | 0.15Ω (0.145 Ω) |
| L1n_eq | Equivalent Value in phase N | 0.40 mH |
| L2n_eq | 0.16 mH | |
| Cn_eq | 33.53 µF | |
| Rn_eq | 0.21 Ω | |
| P1n | Performance Index Output in phase N | 0.028 Ω |
| P2n | 559.4 Ω | |
| P3n | 19.2 Ω | |
| P4n | 94.88 Ω | |
| P5n | 1.23 Ω | |
| fres_n | 2.53 KHz | |
| f01_n | 2.21 KHz |
4.1. Current Ripple Filtering in Different PWM Voltage Modulation Indexes
| PWM Voltage | Switching frequency current rms/A | Damping resister power loss (w) | ||
|---|---|---|---|---|
| Modulation index | Switching frequency voltage | Converter-side (A,N) | Grid-side (A,N) | |
| 0.0 | 357.93, 600.93 | 90.04, 120.33 | 4.09, 6.04 | 1632 W |
| 0.2 | 300.12, 463.46 | 60.02, 98.12 | 3.09, 5.83 | 800 W |
| 0.4 | 260.34, 300.62 | 50.17, 70.58 | 2.09, 3.92 | 300 W |
| 0.6 | 190.83, 263.91 | 30.18, 50.11 | 1.09, 1.93 | 93 W |
| 1.0 | 90.34, 220.46 | 12.13, 20.65 | 0.21, 1.19 | 21 W |

4.2. Current Ripple Filtering by the LCL Branch in Phase N

5. Experimental Results
5.1. Experimental Platform


5.2. Experimental Results
5.2.1. Current Ripple Filtering


5.2.2. Harmonic Compensation


6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grino, R.; Cardoner, R.; Costa-Castello, R.; Fossas, E. Digital repetitive control of a three-phase four-wire shunt active filter. IEEE Trans. Ind. Electron. 2007, 54, 1495–1503. [Google Scholar] [CrossRef]
- Montero, M.; Cadaval, E.; Gonzalez, F. Comparison of control strategies for shunt active power filters in three-phase four-wires systems. IEEE Trans. Power Electron. 2007, 22, 229–236. [Google Scholar] [CrossRef]
- Le, J.; Jiang, Q.R.; Han, Y.D. The analysis of hysteresis current control strategy of three-phase four-wire APF based on the unified mathematic model. In Proceedings of the CSEE, Harbin, China, 23–25 May 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 85–91. [Google Scholar]
- Kanaan, H.Y.; Georges, S.; Mendalek, N.; Hayek, A.; Al-Haddad, K. A linear decoupling control for a PWM three-phase four-wire shunt active power filter. In Proceedings of the Electro Technical Conference, Ajaccio, France, 5–7 May 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Petterson, S.; Salo, M.; Tuusa, H. Applying an LCL-filter to a four-wire active power filter. In Proceedings of the Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar]
- Khadkikar, V.; Chandra, A.; Singh, B. Digital signal processor implementation and performance evaluation of split capacitor, four-leg and three H-bridge-based three-phase four-wire shunt active filters. IET Power Electron. 2011, 4, 463–470. [Google Scholar] [CrossRef]
- Lin, J.Y.; Wang, Z.S.; Chen, H.M.; Li, C. High performance controller design for three-phase four-leg inverters. CSEE 2007, 27, 101–105. [Google Scholar]
- Hirve, S.; Chatterjee, K.; Fernandes, B.G.; Imayavaramban, M.; Dwari, S. PLL-less active power filter based on one-cycle control for compensating unbalanced loads in three-phase four-wire system. IEEE Trans. Power Del. 2007, 22, 2457–2465. [Google Scholar] [CrossRef]
- Le, J.; Liu, K.P.; Tan, T.Y. A novel compound switching control strategy of the 4-leg shunt active power filter. CSEE 2011, 36, 62–70. [Google Scholar]
- Guo, W.F.; Xu, D.G.; Wu, J.; Wang, L.G. Novel control method for LCL active power filter. CSEE 2010, 30, 42–48. [Google Scholar]
- Liu, F.; Zha, X.M.; Duan, S.X. Design and research on parameter of LCL filter in three-phase grid-connected inverter. Trans. China Electr. Tech. Soc. 2010, 25, 110–116. [Google Scholar]
- Liu, Q.; Peng, L.; Kang, Y.; Tang, S.Y.; Wu, D.L.; Qi, Y. A novel design and optimization method of an LCL filter for a shunt active power filter. IEEE Trans. Ind. Electron. 2014, 61, 4000–4010. [Google Scholar] [CrossRef]
- Chen, Y.; Jin, X.M.; Tong, Y.B. Grid-side LCL-filter of three-phase voltage source PWM rectifier. Trans. China Electr. Tech. Soc. 2007, 22, 124–129. [Google Scholar]
- Wang, Y.Q.; Wu, F.J.; Sun, L.; Sun, Q. Optimized design of LCL filter for minimal damping power loss. CSEE 2010, 30, 90–95. [Google Scholar]
- Ahmed, K.H.; Finney, S.J.; Williams, B.W. Passive filter design for three-phase inverter interfacing in distributed generation. In Proceedings of Compatibility in Power Electronics, Gdansk, Poland, 29 May–1 June 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Wu, J.; Ma, X.; Hou, R.; Xu, D.G. Optimization of APF LCL output filter based on genetic algorithm. Trans. China Electr. Tech. Soc. 2011, 26, 159–164. [Google Scholar]
- Shri, A.; Popovic, J.; Ferreira, J.A.; Gerber, M.B. Design and control of a three-phase four-leg inverter for solid-state transformer applications. In Proceedings of Power Electronics and Applications, Lille, France, 2–6 September 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Gabe, I.J.; Montagner, V.F.; Pinheiro, H. Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter. IEEE Trans. Power Electron. 2009, 24, 1444–1452. [Google Scholar] [CrossRef]
- Reznik, A.; Simões, M.G.; Al-Durra, A.; Muyeen, S.M. LCL filter design and performance analysis for grid-inter connected systems. IEEE Trans. Ind. Appl. 2014, 50, 1225–1232. [Google Scholar] [CrossRef]
- Wang, H.; Dou, Z.L.; Zhang, J.W.; Cai, X. Study on voltage sensor-less control for wind grid connection inverter with LCL filter. Trans. China Electr. Tech. Soc. 2013, 28, 188–194. [Google Scholar]
- Xu, J.M.; Xie, S.J.; Xiao, H.F. Research on control mechanism of active damping for LCL filters. CSEE 2012, 32, 27–33. [Google Scholar]
- Qiu, Z.L.; Yang, E.X.; Kong, J.; Chen, G.Z. Current loop control approach for LCL-based shunt active power filter. CSEE 2009, 29, 15–20. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. In Proceedings of Industry Applications Conference, Chicago, IL, USA, 30 September–4 October 2001; IEEE: Piscataway, NJ, USA, 2005; pp. 1281–1291. [Google Scholar]
- Pena, A.R.; Liserre, M.; Blaabjerg, F.; Sebastian, R.; Dannehl, J.; Fuchs, F.W. Analysis of the passive damping losses in LCL-filter-based grid converters. IEEE Trans. Power Electron. 2013, 28, 2642–2646. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized design of high performance shunt active power filter with output LCL filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Liu, K.; Ji, Y.; Wang, Y.; Zhao, J. Design of a Four-Branch LCL-Type Grid-Connecting Interface for a Three-Phase, Four-Leg Active Power Filter. Energies 2015, 8, 1606-1627. https://doi.org/10.3390/en8031606
Cao W, Liu K, Ji Y, Wang Y, Zhao J. Design of a Four-Branch LCL-Type Grid-Connecting Interface for a Three-Phase, Four-Leg Active Power Filter. Energies. 2015; 8(3):1606-1627. https://doi.org/10.3390/en8031606
Chicago/Turabian StyleCao, Wu, Kangli Liu, Yongchao Ji, Yigang Wang, and Jianfeng Zhao. 2015. "Design of a Four-Branch LCL-Type Grid-Connecting Interface for a Three-Phase, Four-Leg Active Power Filter" Energies 8, no. 3: 1606-1627. https://doi.org/10.3390/en8031606
APA StyleCao, W., Liu, K., Ji, Y., Wang, Y., & Zhao, J. (2015). Design of a Four-Branch LCL-Type Grid-Connecting Interface for a Three-Phase, Four-Leg Active Power Filter. Energies, 8(3), 1606-1627. https://doi.org/10.3390/en8031606





