Research on Heat Recovery Technology for Reducing the Energy Consumption of Dedicated Ventilation Systems: An Application to the Operating Model of a Laboratory
Abstract
:1. Introduction
2. Dedicated Ventilation System Based on Heat Recovery Technology


3. Simulations and Calculations
| Parameters | Laboratory | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Indoor temperature (°C) | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
| Indoor relative humidity (RH) (%) | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Lighting load (W/m2) | 2 | 3 | 4 | 5 | 5 | 10 | 5 | 5 | 10 | 10 |
| Small power load (W/m2) | 20 | 13.8 | 15 | 20 | 17 | 16 | 17 | 17 | 20 | 20 |
| Occupancy (m2/person) | 8 | 8 | 7 | 7 | 7.5 | 7.5 | 5 | 4 | 4 | 4 |
| Ventilation rate (L/s/person) | 13.5 | 8 | 12.4 | 20 | 19 | 15 | 15 | 15 | 15 | 15 |
| Conditions | Parameters | Range |
|---|---|---|
| Indoor conditions (design conditions) | TR | 22 °C |
| RHR | 50% | |
| Outdoor conditions | To | 25 to 35 °C at 2.5 °C intervals |
| RHo | 50% to 80% at 10% intervals | |
| Airflow rate | VFA | 0.1 to 0.3 m3/s at 0.05 °C intervals |
- (a)
- They have the same state point (0 to 6) in the two systems.
- (b)
- The DX, in the conventional system, carries out its normal cooling and dehumidifying functions (from 0 to 2), but with improved latent capacity because of the pre-cooling function of the HPHX.
- (c)
- Air transport occurs adiabatically between the DX and HPHX.
- (d)
- The energy transfer rates are equal and opposite {namely (h3-h2) = (h0-h1) because the air mass flow rates are equal} in the two parts of the HPHX.
- (e)
- The chamber has considerable latent loads which are essential to the reheating part of the traditional system.
- (f)
- Air properties including the specific heat and density are constant throughout.
| Type | HLSV—500—60 | |||||
|---|---|---|---|---|---|---|
| Basic dimensions (mm) | W | 1000 | W1 | 500 | W2 | 500 |
| H | 481 | |||||
| L | 300 | |||||
| Material of frame | Q235 | Material of pipe | Cu | Material of fin | Al | - |
| Arrange of heat pipe | 11 | Row | 6 | Column | - | - |
| Weight (kg) | 43 | |||||
| Refrigerant | R134a | |||||

3.1. The Energy Saving Calculations for the Fresh Air (FA) System
- = air density, kg/m3;
- Cpa = air specific heat, kJ/kg·K;
- VFA = FA supply flow rate, m3/s;
- h0 = outdoor air enthalpy hourly, kJ/kg;
- h2 = leaving cooling air enthalpy in DX, kJ/kg;
- t2 = leaving cooling air temperature in DX, °C;
- t3 = leaving heat pipe condenser section air temperature, °C;
- τ= time, s.
- t0 = outdoor air temperature, °C;
- t1 = leaving heat pipe evaporator section air temperature, °C;
- ηHP = effectiveness of the heat pipe (HP);
- ωs = air moisture contents at the various states denoted by the subscript, kg/kg (s = 0, 1, 2, 3).
- COP = coefficient of performance of the FA system;
- ε1 = energy saving potential of the FA system, %;
- m = total running hours, h.
3.2. The Energy Saving Calculation for the Whole System
- = air density, kg/m3;
- VRA = return air supply flow rate, m3/s;
- VFA = FA supply flow rate, m3/s;
- VS = supply air supply flow rate, m3/s (VS = VRA + VFA);
- h0 = outdoor air enthalpy hourly, kJ/kg;
- h2 = leaving cooling air enthalpy in DX, kJ/kg;
- h5 = supply air enthalpy hourly, kJ/kg;
- h6 = space design air enthalpy hourly, kJ/kg.
4. Results and Analysis
4.1. The Energy Simulation Results of Dedicated Ventilation System with Heat Pipe Heat Exchanger (HPHX)
- (1)
- The number of hours when the space is used in one year based on the use of the HPHX for FA treatment.
- (2)
- The number of hours when the HPHX is applicable.
- (3)
- The indoor air conditions (state 6 in Figure 1b) which were determined by the space peak cooling load in the evaluations must be kept constant.
| Laboratory | Location | Indoor Conditions | Applicable Hours | High RH Hours | % of High RH Hours | ||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | RH (%) | h0.45 | h0.6 | h0.45 | h0.6 | h0.45 | h0.6 | ||
| 1 | Guang Zhou | 22 | 50% | 2248 | 2280 | 38 | 37 | 1.69% | 1.62% |
| 2 | Hong Kong | 22 | 50% | 2267 | 2267 | 29 | 27 | 1.28% | 1.19% |
| 3 | Hong Kong | 22 | 50% | 2282 | 2288 | 20 | 20 | 0.88% | 0.87% |
| 4 | Shen Zhen | 22 | 50% | 2209 | 2210 | 14 | 14 | 0.63% | 0.63% |
| 5 | Dong Guan | 22 | 50% | 2155 | 2155 | 26 | 21 | 1.01% | 0.97% |
| 6 | Shen Zhen | 22 | 50% | 2164 | 2267 | 34 | 34 | 0.86% | 1.50% |
| 7 | Hong Kong | 22 | 50% | 2271 | 2271 | 9 | 9 | 0.42% | 0.40% |
| 8 | Macau | 22 | 50% | 2228 | 2232 | 9 | 7 | 0.40% | 0.31% |
| 9 | Zhu Hai | 22 | 50% | 2161 | 2161 | 25 | 23 | 0.56% | 1.06% |
| 10 | Hui Zhou | 22 | 50% | 2255 | 2257 | 12 | 11 | 0.53% | 0.49% |
| Max | - | 22 | 50% | 2282 | 2288 | 38 | 37 | 1.69% | 1.62% |
| Min | - | 22 | 50% | 2155 | 2155 | 9 | 7 | 0.40% | 0.31% |
| Mean | - | 22 | 50% | 2224 | 2238.8 | 21.6 | 20.3 | 0.83% | 0.91% |
4.2. Energy Saving Potential



4.3. Comparison of the Dedicated System with Laboratory, Cinema and Office Building Systems


5. Experimental

- QAHU(τ) = cooling load from AHU at time (τ), kW;
- QFA(τ) = cooling load from FA at time (τ), kW;
- QH(τ) = heating load from the heat and moisture generators at time (τ), kW; the heat generator is from 0 kW to 12 kW and the moisture generator is from 0 kW to 4.8 kW.
| Parameter | Abbreviation | Instrument | Varied Range | Accuracy |
|---|---|---|---|---|
| Temperature | tw and t | Type K thermocouples | −50 to 100 °C | ±(0.05% rdg + 0.5 °C) |
| Air flow rate | Ma | Thermal anemometer | 0–5 m/s | ± 1.5% |
| Power | W | Power meter | 0 to 1 × 106 A (a.c.) | ± (0.25% rdg + 0.05% F.S.) |
6. Results, Comparison and Discussion
6.1. Heat Pipe (HP) Effectiveness

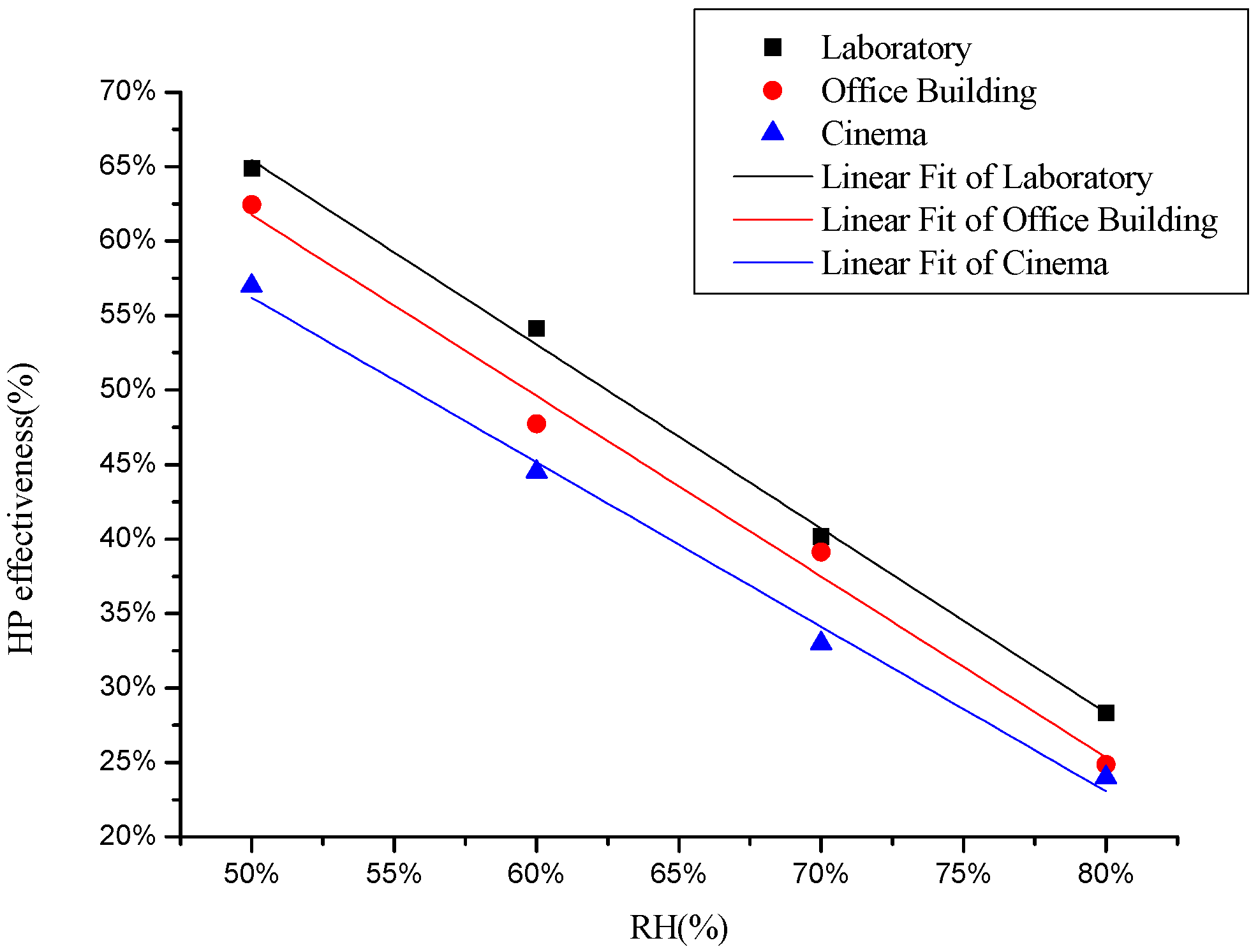

6.2. Energy Saving Calculation



7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| HPHX | Heat pipe heat exchanger |
| COP | Coefficient of performance |
| HP | Heat pipe |
| NHRS | The time the decoupling objective cannot be achieved |
| FA | Fresh air |
| DX | Direct-expansionDirect-expansion |
| h0,1,2,3 | 0–3 point air enthalpy (kJ/kg) |
| ω0,1,2,3 | 0–3 point air moisture contents (kg/kg) |
| Cpa | Air specific heat( kJ/kg·K) |
| t0,1 | 0 and 1 air temperature (°C) |
| HTB2 | A model for the thermal environment of building in operation |
| t0 | Outdoor air temperature (°C) |
| HVAC | Heating ventilation and air conditioning |
| QDXN,O | The net total cooling load for fresh air treatment (kW) |
| HDX,O | The net total reheating load for fresh air treatment (kW) |
| ρ | Air density (kg/m3) |
| VFA | Fresh air supply flow rate (m3/s) |
| t2 | Leaving cooling air temperature in DX (°C) |
| t3 | Leaving heat pipe condenser section air temperature (°C) |
| τ | Time (s) |
| t1 | Leaving heat pipe evaporator section air temperature (°C) |
| ηHP | Effectiveness of the heat pipe (%) |
| ωs | Air moisture contents at the various states denoted by the subscript (kg/kg; s = 0, 1, 2, 3) |
| ε1 | Energy saving potential of the fresh air system (%) |
| m | Total running hour (h) |
| HDXN,O | The net total reheating load for fresh air treatment (kW) |
| QFCN,O | The net total returning air load for fresh air treatment (kW) |
| VRA | Return air supply flow rate (m3/s) |
| VS | Supply air supply flow rate (m3/s; vs = vra + vfa) |
| h5 | Supply air enthalpy hourly (kJ/kg) |
| h6 | Space design air enthalpy hourly (kJ/kg) |
| ε2 | Energy saving potential of the whole system (%) |
| η0.45 | Heat pipe of effectiveness 0.45 |
| η0.6 | Heat pipe of effectiveness 0.6 |
| SHR | Sensible heat ratio |
| AHU | Air handling unit |
| QAHU(τ) | Cooling load from air handling unit at time (τ) (kW) |
| QFA(τ) | Cooling load from fresh air at time (τ) (kW) |
| QH(τ) | Heating load from the heat and moisture generators at time (τ) (kW) |
| PID | Proportion integration differentiation |
| t | Dry-bulb temperatures (°C) |
| tw | Wet-bulb temperatures (°C) |
| Ma | Air flow rate (m/s) |
| W | Power (kW) |
| DBT | Dry-bulb temperature |
| RH | Relative humidity |
| R2 | Coefficient of determination |
| hset | Space air enthalpy (22 °C, 50%) per s (kJ/kg) |
| QFA(τ)′ | Cooling load from fresh air at time (τ) for the conventional system (kW) |
| εAC | The energy saving potential (%) |
| QH(τ)′ | Heating load from the heat and moisture generators at time (τ) for the conventional system (kW) |
References
- Sekhar, S.C. Higher space temperatures and better thermal comfort—A tropical analysis. Energy Build. 1995, 23, 63–70. [Google Scholar] [CrossRef]
- Electrical and Mechanical Services Department. Hong Kong Energy End—Use Data (1990–2000); The Hong Kong SAR Government: Hong Kong, China, 2002.
- Amos-Abanyie, S.; Akuffo, F.O.; Kutin-Sanwu, V. Effects of Thermal Mass, Window Size, and Night-Time Ventilation on Peak Indoor Air Temperature in the Warm-Humid Climate of Ghana. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.A.M. Investigation of Performance of Heat Pipe as Heat Exchanger Using Alternative Refrigerants. J. Energy Eng. 2013, 139, 18–24. [Google Scholar] [CrossRef]
- Liu, G. The application of heat pipe heat exchanger in exhaust gas heat recovery system and its thermodynamic analysis. In Proceedings of the 8th International Heat Pipe Conference, Beijing, China, 14–18 September 1992; pp. 582–585.
- Sun, J.Y.; Shyu, R.J. Waste Heat Recovery Using Heat Pipe Heat Exchanger for Industrial Practices. In Proceedings of the 5th International Heat Pipe Symposium, Melbourne, Australia, 17–20 November 1996.
- Ma, G.; Zhou, F.; Liu, T.; Wang, L.; Zhang, X.; Liu, Z. Study on Optimal Operating Mode of a Thermosyphon Heat Exchanger Unit in a Shopping Center. J. Energy Eng. 2013, 139, 275–280. [Google Scholar] [CrossRef]
- O’Connor, D.; Calautit, J.K.; Hughes, B.R. A study of passive ventilation integrated with heat recovery. Energy Build. 2014, 82, 799–811. [Google Scholar] [CrossRef]
- Riffat, S.B.; Gan, G. Determination of effectiveness of heat-pipe heat recovery for naturally-ventilated buildings. Appl. Therm. Eng. 1998, 18, 121–130. [Google Scholar] [CrossRef]
- Hughes, B.R.; Chaudhry, H.N.; Calautit, J.K. Passive energy recovery from natural ventilation air streams. Appl. Energy 2014, 113, 127–140. [Google Scholar] [CrossRef]
- Calautit, J.K.; O'Connor, D.; Hughes, B.R. A natural ventilation wind tower with heat pipe heat recovery for cold climates. Renew. Energy 2015. [Google Scholar] [CrossRef]
- Yau, Y.H. Application of a heat pipe heat exchanger to dehumidification enhancement in a HVAC system for tropical climates-a baseline performance characteristics study. Int. J. Therm. Sci. 2007, 46, 164–171. [Google Scholar] [CrossRef]
- Yau, Y.H. The use of a double heat pipe heat exchanger system for reducing energy consumption of treating ventilation air in an operating theatre—A full year energy consumption model simulation. Energy Build. 2008, 40, 917–925. [Google Scholar] [CrossRef]
- Yau, Y.H.; Ahmadzadehtalatapeh, M. A review on the application of horizontal heat pipe heat exchangers in air conditioning systems in the tropics. Appl. Therm. Eng. 2010, 30, 77–84. [Google Scholar] [CrossRef]
- Ahmadzadehtalatapeh, M.; Yau, Y.H. The application of heat pipe heat exchangers to improve the air quality and reduce the energy consumption of the air conditioning system in a hospital ward—A full year model simulation. Energy Build. 2011, 43, 2344–2355. [Google Scholar] [CrossRef]
- Ge, G.; Xiao, F.; Xu, X. Model-based optimal control of a dedicated outdoor air-chilled ceiling system using liquid desiccant and membrane-based total heat recovery. Appl. Energy 2011, 88, 4180–4190. [Google Scholar] [CrossRef]
- Gendebien, S.; Bertagnolio, S.; Lemort, V. Investigation on a ventilation heat recovery exchanger: Modeling and experimental validation in dry and partially wet conditions. Energy Build. 2013, 62, 176–189. [Google Scholar] [CrossRef]
- Zhang, L.; Lee, W.L. Evaluating the use heat pipe for dedicated ventilation of office buildings in Hong Kong. Energy Convers. Manag. 2011, 52, 1983–1989. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.-F. Research on Energy Saving Potential for Dedicated Ventilation Systems Based on Heat Recovery Technology. Energies 2014, 7, 4261–4280. [Google Scholar] [CrossRef]
- Lewis, P.T.; Alexander, D.K. Htb2: A flexible model for dynamic building simulation. Build. Environ. 1990, 25, 7–16. [Google Scholar] [CrossRef]
- Alexander, D.K. HTB2 User Manual Version; Welsh School of Architecture R&D, University of Wales College of Cardiff: Cardiff, UK, 1997. [Google Scholar]
- Product Manual of Heat Pipe. Beijing Zhong Ke Long Zi Heat Pipe Technology Company Limited, 2015. Available online: http://www.zklz.com (accessed on 14 May 2015).
- Product Manual of Heat Pipe. Dezhou Ya Tai Heat Pipe Technology COMPANY Limited. Available online: http://www.yatai.cc (accessed on 21 June 2015).
- Lee, W.L.; Yik, F.W.H.; Burnett, J. Simplifying Energy Performance Assessment Method in the Hong Kong building Environmental Method. Build. Serv. Eng. Res. Technol. 2005, 22, 113–132. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, Y.F. Research on Heat Recovery Technology for Reducing the Energy Consumption of Dedicated Ventilation Systems: An Application to the Operating Model of a Laboratory. Energies 2016, 9, 24. https://doi.org/10.3390/en9010024
Zhang L, Zhang YF. Research on Heat Recovery Technology for Reducing the Energy Consumption of Dedicated Ventilation Systems: An Application to the Operating Model of a Laboratory. Energies. 2016; 9(1):24. https://doi.org/10.3390/en9010024
Chicago/Turabian StyleZhang, Lian, and Yu Feng Zhang. 2016. "Research on Heat Recovery Technology for Reducing the Energy Consumption of Dedicated Ventilation Systems: An Application to the Operating Model of a Laboratory" Energies 9, no. 1: 24. https://doi.org/10.3390/en9010024
APA StyleZhang, L., & Zhang, Y. F. (2016). Research on Heat Recovery Technology for Reducing the Energy Consumption of Dedicated Ventilation Systems: An Application to the Operating Model of a Laboratory. Energies, 9(1), 24. https://doi.org/10.3390/en9010024





