An Adaptive Energy Management System for Electric Vehicles Based on Driving Cycle Identification and Wavelet Transform
Abstract
:1. Introduction
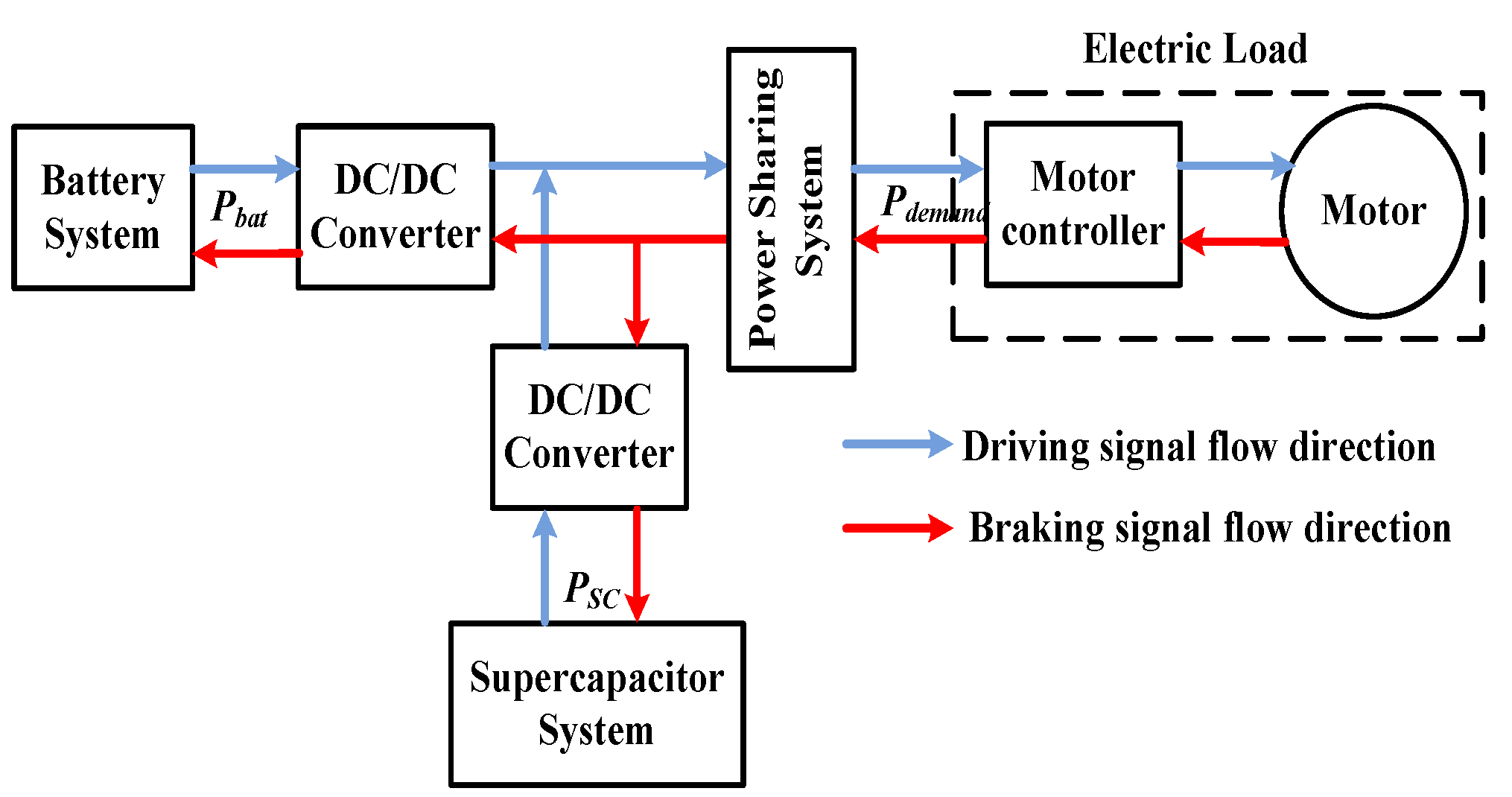
2. Model Development of the HESS
2.1. Dynamic Model of the Battery
2.2. Dynamic Model of the Supercapacitor
2.3. DC/DC Converter and Motor Models
3. Energy Management System Based on DCI and Haar-WT
3.1. DCI Method
3.1.1. Characteristic Parameters Analysis
3.1.2. Slide Time Window Design
3.1.3. Optimal Slide Time Window Length
3.2. Harr-WT Algorithm
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DCI | Driving cycle identification |
| LVQ | Learning vector quantization |
| HESS | Hybrid energy storage system |
| WT | Wavelet transform |
| ESS | Energy storage system |
| DC | Direct current |
| ADVISOR | Advanced vehicle simulator |
| EMS | Energy management system |
| MPC | Model predictive control |
| FC | Fuel cell |
| NiMH | Nickel metal hyoride |
| PNGVs | Partnership for a New Generation Vehicles |
| RC | Resistance and capacitor |
| INDIA_HWY_SAMPLE | Indian Highway Sample |
| HWFET | Highway Fuel Economy Test |
| UDDS | Urban Dynamometer Driving Schedule |
| WVUSUB | West Virginia Suburban Driving Schedule |
| INDIA_URBAN_SAMPLE | Indian Urban Sample |
| UKBUS6 | London Bus Route |
| SoC | State of charge |
| SoV | State of voltage |
| DoD | Depth of discharge |
References
- Lukic, S.M.; Cao, J.; Bansal, R.C.; Rodriguez, F.; Emadi, A. Energy Storage Systems for Automotive Applications. IEEE Trans. Ind. Electron. 2008, 55, 2258–2267. [Google Scholar] [CrossRef]
- He, H.-W.; Xiong, R.; Chang, Y.-H. Dynamic Modeling and Simulation on a Hybrid Power System for Electric Vehicle Applications. Energies 2010, 3, 1821–1830. [Google Scholar] [CrossRef]
- Nelson, R.F. Power requirements for batteries in hybrid electric vehicles. J. Power Sources 2000, 9, 12–26. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C. Emerging energy-efficient technologies for hybrid electric vehicles. Proc. IEEE 2007, 95, 821–835. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery management system—An overview of its application in the smart grid and electric vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Khaligh, A.; Li, Z.; Emadi, A. Battery, ultracapacitor, fuel cell and hybrid energy storage systems for electric, hybrid electric, fuel cell, and plug-in hybrid electric vehicles: State-of-the-art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Ren, G.Z.; Ma, G.Q.; Cong, N. Review of electrical energy storage system for vehicular applications. Renew. Sustain. Energy Rev. 2015, 41, 225–236. [Google Scholar] [CrossRef]
- Pay, S.; Baghzouz, Y. Effectiveness of Battery-Supercapacitor Combination in Electric Vehicles. In Proceedings of 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; pp. 728–733.
- Schupbach, R.M.; Balda, J.C. The role of ultracapacitors in an energy storage unit for vehicle power management. In Proceedings of 2003 IEEE 58th Vehiclar Technology Conference (VTC2003-Fall), Orlando, FL, USA, 6–9 October 2003; pp. 3236–3240.
- Ortuzar, M.; Moreno, J.; Dixon, J. Ultracapacitor-Based Auxiliary Energy System for an Electric Vehicle: Implementation and Evaluation. IEEE Trans. Ind. Electron. 2007, 54, 2147–2156. [Google Scholar] [CrossRef]
- Guidi, G.; Undeland, T.; Hori, Y. Effectiveness of Supercapacitor as Power-Assist in Pure EV Using a Sodium-Nickel Chloride Battery as Main Energy Storage. In Proceedings of International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Stavanger, Norway, 13–16 May 2009; pp. 13–16.
- Gao, L.; Dougal, R.A.; Liu, S. Power enhancement of an actively controlled battery/ultracapacitor hybrid. IEEE Trans. Power Electron. 2005, 20, 236–243. [Google Scholar] [CrossRef]
- Carter, R.; Cruden, A.; Hall, P.J. Optimizing for Efficiency or Battery Life in a Battery/Supercapacitor Electric Vehicle. IEEE Trans. Veh. Technol. 2012, 61, 1526–1533. [Google Scholar] [CrossRef]
- Ruetschi, P. Aging mechanisms and service life of lead-acid batteries. J. Power Sources 2004, 127, 33–44. [Google Scholar] [CrossRef]
- Lailler, P.; Zaninotto, F.; Nivet, S.; Torcheux, L.; Sarrau, J.-F.; Vaurijoux, J.-P.; Devilliers, D. Study of the softening of the positive active-mass in valve-regulated lead-acid batteries for electric-vehicle applications. Journal of Power Sources 1999, 78, 204–213. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Hegazy, O.; van den Bossche, P.; Coosemans, T.; van Mierlo, J. Electrical Double-Layer Capacitors in Hybrid Topologies—Assessment and Evaluation of Their Performance. Energies 2012, 5, 4533–4568. [Google Scholar] [CrossRef]
- Ju, F.; Zhang, Q.; Deng, W.W.; Li, J.S. Review of structures and control of battery-supercapacitor hybrid energy storage system for electric vehicles. In Proceedings of the 2014 IEEE International Conference on Automation Science and Engineering (CASE), Taipei, Taiwan, 18–22 August 2014; pp. 18–22.
- Kuperman, A.; Aharon, I. Battery/ultracapacitor hybrids for pulsed current loads: A re-view. Renew. Sustain. Energy Rev. 2011, 15, 981–992. [Google Scholar] [CrossRef]
- Ortuzar, M.; Moreno, J.; Dixon, J. Ultracapacitor based auxiliary energy system for an electric vehicle: Implementation and evaluation. IEEE Trans. Ind. Electron. 2007, 54, 2147–2156. [Google Scholar] [CrossRef]
- Onar, O.C.; Khaligh, A. A Novel Integrated Magnetic Structure Based DC/DC Converter for Hybrid Battery/Ultracapacitor Energy Storage Systems. IEEE Trans. Smart Grid 2012, 3, 296–307. [Google Scholar] [CrossRef]
- Baisden, A.C.; Emadi, A. ADVISOR-Based Model of a Battery and Ultra-Capacitor Energy Source for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2004, 53, 199–205. [Google Scholar] [CrossRef]
- Trovão, J.P.; Pereirinha, P.G.; Jorge, H.M.; Henggeler Antunes, C. A multi-level energy management system for multi-source electric vehicles–An integrated rule-based meta-heuristic approach. Appl. Energy 2013, 105, 304–318. [Google Scholar] [CrossRef]
- Zhang, C.H.; Shi, Q.S.; Cui, N.X.; Li, W.H. Particle Swarm Optimization for energy management fuzzycontroller design in dual-source electric vehicle. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1405–1410.
- Ates, Y.; Erdinc, O.; Uzunoglu, M.; Vural, B. Energy management of an FC/UC hybrid vehicular power system using a combined neural network-wavelet transform based strategy. Int. J. Hydrog. Energy 2010, 35, 774–783. [Google Scholar] [CrossRef]
- Dusmez, S.; Khaligh, A. A supervisory power-splitting approach for a new ultracapacitor-battery vehicle deploying two propulsion machines. IEEE Trans. Ind. Inf. 2014, 10, 1960–1971. [Google Scholar] [CrossRef]
- Martínez, J.S.; Hissel, D.; Pera, M.C.; Amiet, M. Practical control structure and energy management of a test bed hybrid electric vehicle. IEEE Trans. Veh. Technol. 2011, 60, 4139–4152. [Google Scholar] [CrossRef]
- Hannan, M.A.; Azidin, F.A.; Mohamed, A. Multi-sources model and control algorithm of an energy management system for light electric vehicles. Energy Convers. Manag. 2012, 62, 123–130. [Google Scholar] [CrossRef]
- Moreno, J.; Ortuzar, M.E.; Dixon, J.W. Energy-Management System for a Hybrid Electric Vehicle, Using Ultracapacitors and Neural Networks. IEEE Trans. Ind. Electron. 2006, 53, 614–623. [Google Scholar] [CrossRef]
- Choi, M.-E.; Kim, S.-W.; Seo, S.-W. Energy Management Optimization in a Battery/Supercapacitor Hybrid Energy Storage System. IEEE Trans. Smart Grid 2012, 3, 463–472. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Jang, M. A model predictive control system for a hybrid battery-ultracapacitor power source. IEEE Trans. Power Electron. 2014, 29, 1469–1479. [Google Scholar] [CrossRef]
- Santucci, A.; Sorniotti, A.; Lekakou, C. Power split strategies for hybrid energy storage systems for vehicular applications. J. Power Sources 2014, 258, 395–407. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Demetriades, G. Application of explicit mode predictive control to a hybrid battery-ultracapacitor power source. J. Power Sources 2015, 277, 84–94. [Google Scholar] [CrossRef]
- Zhang, X.; Chris, C.T.M.; Masrur, A.; Daniszewski, D. Wavelet-transform-based power management of hybrid vehicles with multiple on-board energy sources including fuel cell, battery and ultracapacitor. J. Power Sources 2008, 185, 1533–1543. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, T.; Filipi, Z. Frequency domain power distribution strategy for series hybrid electric vehicles. SAE Int. J. Altern. Powertrains 2012, 1, 208–218. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Yan, B.J.; Yang, C.; Marina Martínez, C.; Cao, D. Multimode energy management for plug-In hybrid electric buses based on driving cycles prediction. IEEE Trans. Transp. Syst. 2016, PP, 1–11. [Google Scholar] [CrossRef]
- Hu, X.S.; Jiang, J.C.; Egardt, B.; Cao, D.P. Advanced power-source integration in hybrid electric vehicles: Multicriteria optimization approach. IEEE Trans. Ind. Electron. 2015, 6, 7847–7858. [Google Scholar] [CrossRef]
- Lin, C.; Chou, B.; Chen, Q. Performance Comparison of battery power input equivalent circuit model for EVs. J. Chin. Automot. Eng. 2006, 28230–28234. [Google Scholar]
- Spyker, R.L.; Nelms, R.M. Analysis of double-layer capacitors supplying constant power loads. IEEE Trans. Aerospace Electron. Syst. 2000, 36, 1439–1443. [Google Scholar]
- Lin, C.C.; Jeon, S.; Peng, H.; Lee, J.M. Driving pattern recognition for control of hybrid electric trucks. Veh. Syst. Dyn. 2004, 42, 41–58. [Google Scholar] [CrossRef]
- Langari, R.; Won, J.S. Intelligent energy management agent for a parallel hybrid vehicle-part I: System architecture and design of the driving situation identification process. IEEE Trans. Veh. Technol. 2005, 54, 925–934. [Google Scholar] [CrossRef]
- He, H.; Sun, C.; Zhang, X. A method for identification of driving patterns in hybrid electric vehicles based on a LVQ neural network. Energies 2012, 5, 3363–3380. [Google Scholar] [CrossRef]
- Mao, P.L.; Aggarwal, R.K. A Novel Approach to the Classification of the Transient Phenomena in Power Transformers Using Combined Wavelet Transform and Neural Network. IEEE Trans. Power Deliv. 2001, 16, 654–660. [Google Scholar] [CrossRef]
- Capilla, C. Application of the Haar wavelet transform to detect micro-seismic signal arrivals. J. Appl. Geophys. 2006, 59, 36–46. [Google Scholar] [CrossRef]
- Joseph, L.; Minh-Nghi, T. A wavelet-based approach for the identification of damping in nonlinear oscillators. Int. J. Mech. Sci. 2005, 47, 1262–1281. [Google Scholar] [CrossRef]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A wavelet-fuzzy logic based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid vehicular power system. J. Power Sources 2009, 194, 369–380. [Google Scholar] [CrossRef]






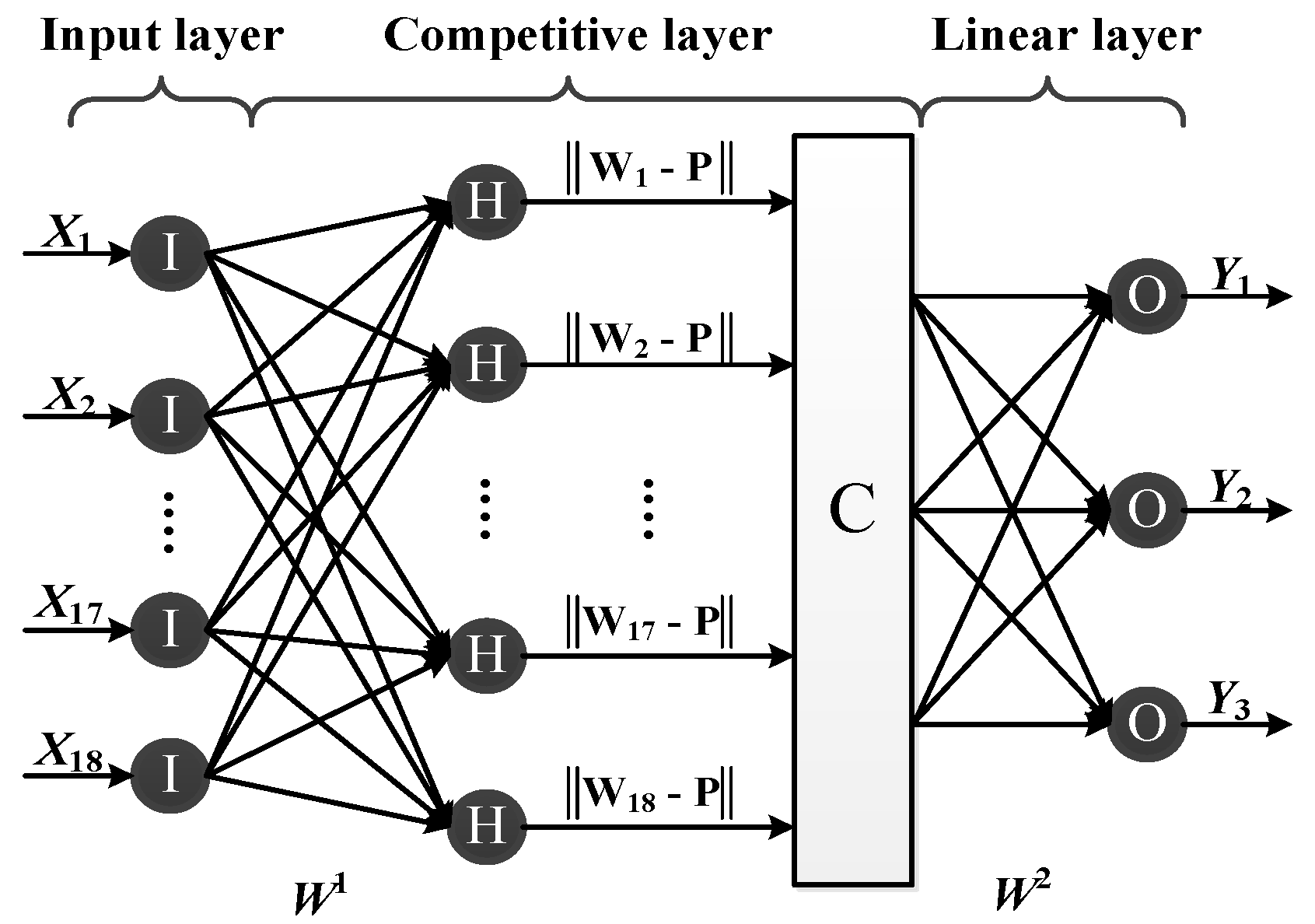
























| Names and math description |
|---|
| Max velocity max(v(t)) |
| Average velocity mean(v(t)) |
| Velocity standard deviation std(v(t)) |
| Max positive acceleration max(abs(a(t))) |
| Average positive acceleration mean(abs(a(t))) |
| Positive acceleration standard deviation std(abs(a(t))) |
| Max negative acceleration max(−abs(a(t))) |
| Average negative acceleration mean(−abs(a(t))) |
| Negative acceleration standard deviation std(−abs(a(t))) |
| Idle percent sum(v(t) = 0)/n |
| Constant velocity percent sum(a(t) = 0)/n |
| Velocity range percent 1 sum(v1 < v(t) < v2)/n |
| Velocity range percent 2 sum(v2 < v(t) < v3)/n |
| Velocity range percent 3 sum(v3 < v(t) < v4)/n |
| Positive acceleration range percent 1 sum(a1 < abs(a(t)) < a2)/n |
| Positive acceleration range percent 2 sum(a2 < abs(a(t)) < a3)/n |
| Positive acceleration range percent 3 sum(a3 < abs(a(t)) < a4)/n |
| Negative acceleration range percent 1 sum(a1 < −abs(a(t)) < a2)/n |
| Negative acceleration range percent 2 sum(a2 < −abs(a(t)) < a3)/n |
| Negative acceleration range percent 3 sum(a3 < −abs(a(t)) < a4)/n |
| Parameters Amount Unit |
|---|
| Mass 1550 kg |
| Frontal area 2.13 m2 |
| Tire radius 0.3 m |
| Drag coefficient 0.36 |
| Rolling resistance coefficient 0.02 |
| Parameters Amount Unit |
|---|
| Battery Type Lithium-ion battery |
| Nominal voltage 280 V |
| Nominal capacity 20 Ah |
| Number of cells 72 |
| Parameters Amount Unit |
|---|
| Supercapacitor Type Maxwell BMO3000 |
| Nominal voltage 140 V |
| Nominal capacity 55 F |
| Number of cells 55 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Deng, W. An Adaptive Energy Management System for Electric Vehicles Based on Driving Cycle Identification and Wavelet Transform. Energies 2016, 9, 341. https://doi.org/10.3390/en9050341
Zhang Q, Deng W. An Adaptive Energy Management System for Electric Vehicles Based on Driving Cycle Identification and Wavelet Transform. Energies. 2016; 9(5):341. https://doi.org/10.3390/en9050341
Chicago/Turabian StyleZhang, Qiao, and Weiwen Deng. 2016. "An Adaptive Energy Management System for Electric Vehicles Based on Driving Cycle Identification and Wavelet Transform" Energies 9, no. 5: 341. https://doi.org/10.3390/en9050341
APA StyleZhang, Q., & Deng, W. (2016). An Adaptive Energy Management System for Electric Vehicles Based on Driving Cycle Identification and Wavelet Transform. Energies, 9(5), 341. https://doi.org/10.3390/en9050341





