Shear Behavior of Hybrid Fiber Reinforced Concrete Deep Beams
Abstract
:1. Introduction
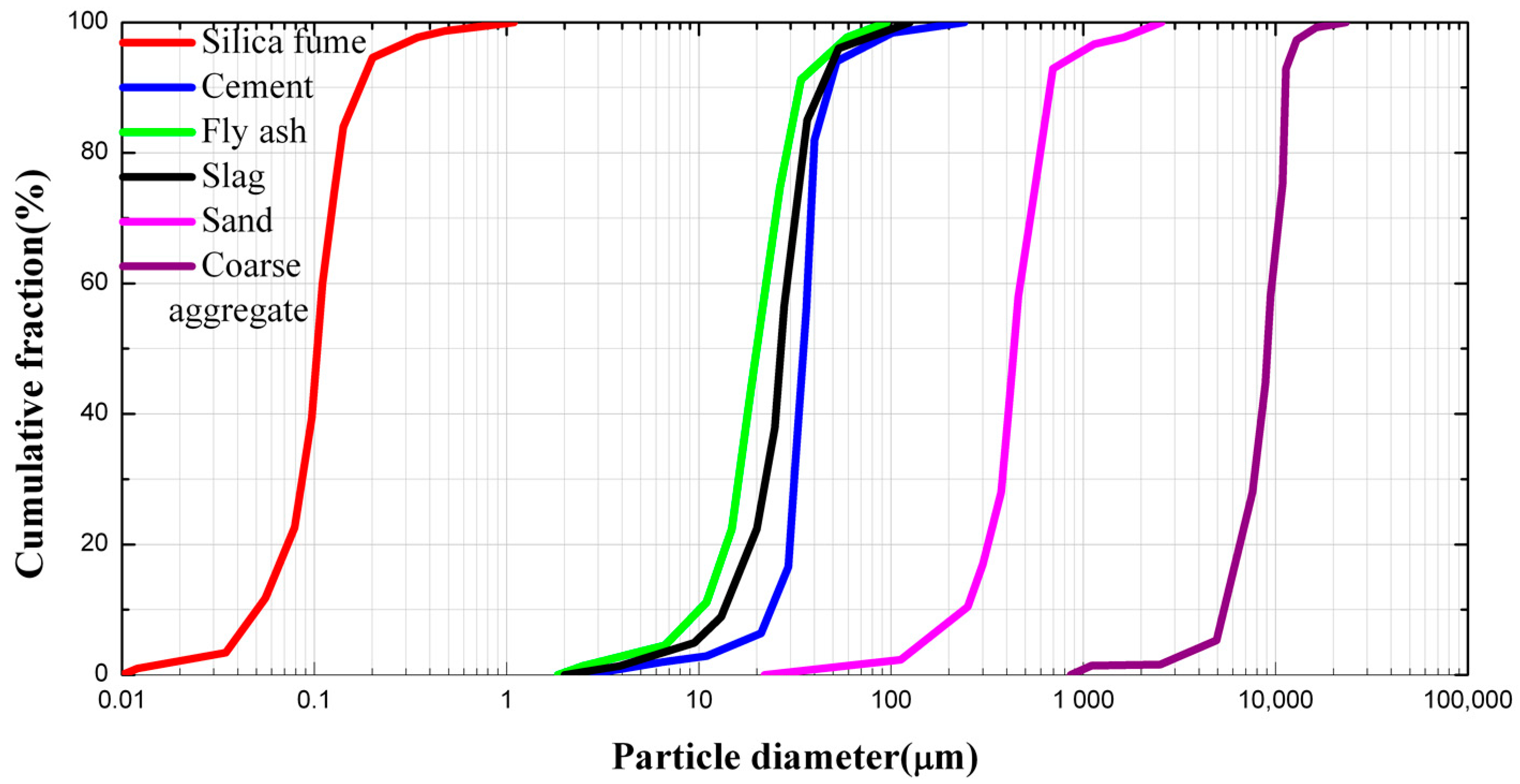
2. Material Investigated
2.1. Material Proportions
2.2. Material Fabrication
2.3. Flowability Test
2.4. Compressive Test
2.5. Tensile Test
2.6. Flexural Test
3. Experimental Investigation of HFRC Deep Beams
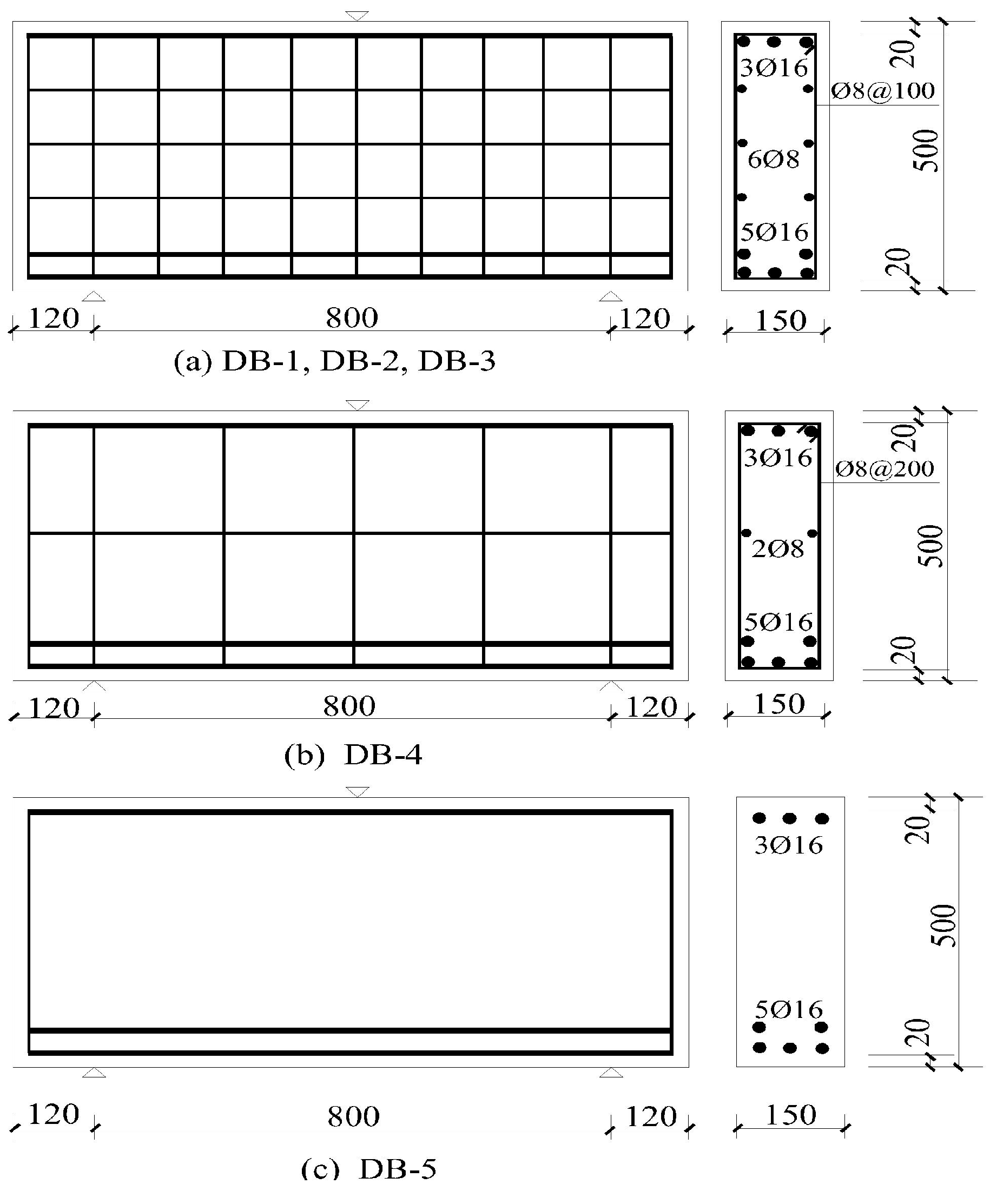
3.1. Detail of Deep Beams
3.2. Material Properties
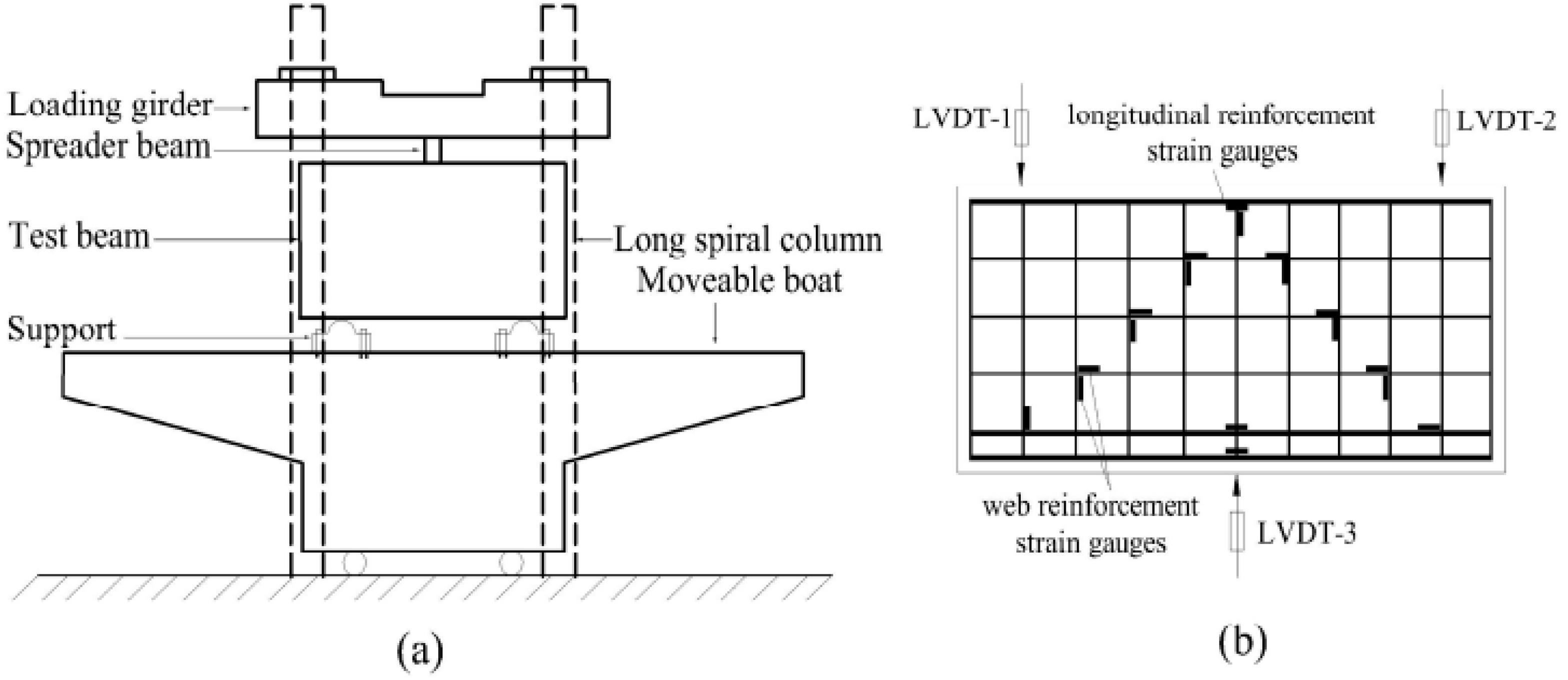
3.3. Test Content and Layout
4. Results and Discussion
4.1. Crack Patterns
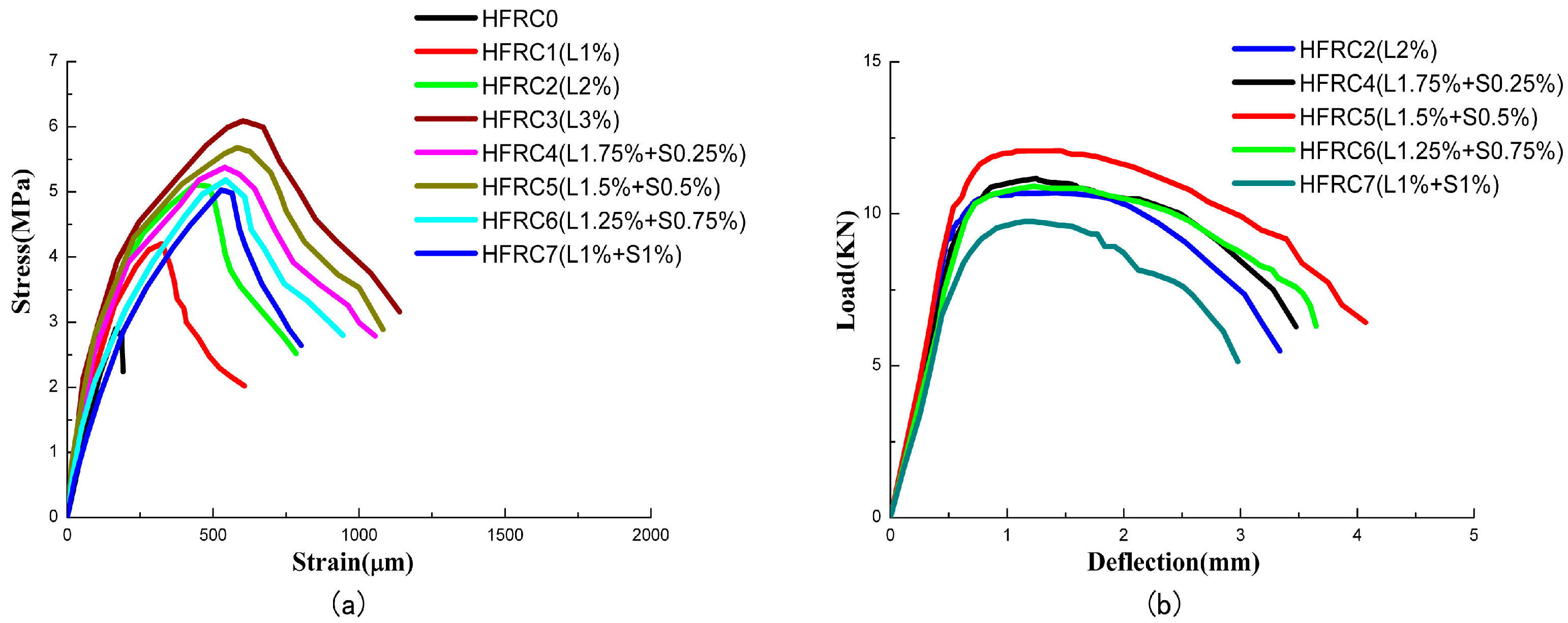
4.2. Load-Deflection Behavior
4.3. Ultimate Load and Deflection
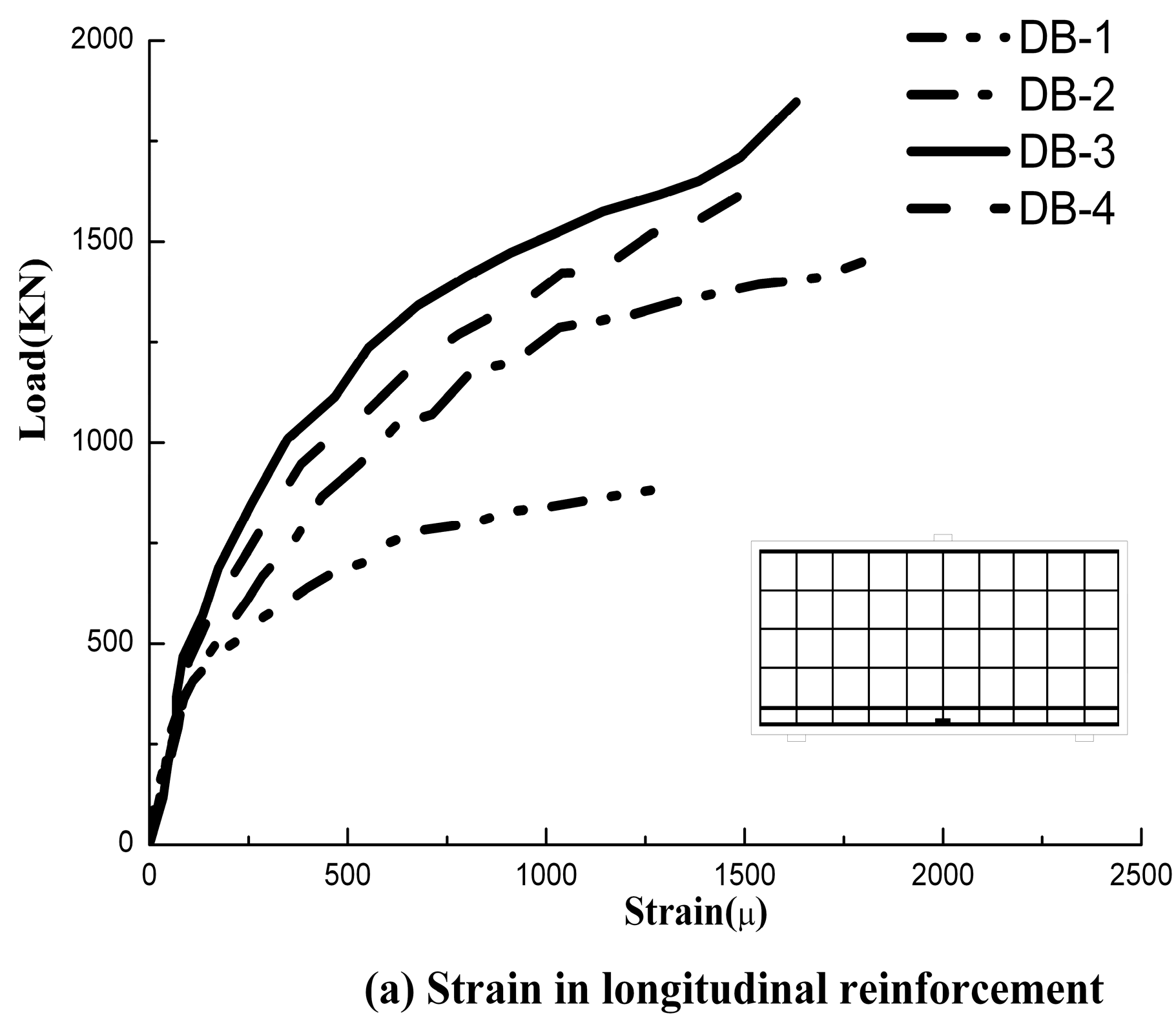
4.4. Strains in Reinforcement and Concrete
4.5. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falkner, H.; Huang, Z.; Teutsch, M. Comparative study of plain and steel fiber reinforced concrete ground slab. Concr. Int. 1995, 17, 45–51. [Google Scholar]
- Buratti, N.; Ferracuti, B.; Savoia, M. Concrete crack reduction in tunnel linings by steel fiber-reinforced concretes. Constr. Build. Mater. 2003, 44, 249–259. [Google Scholar] [CrossRef]
- Sorelli, L.; Meda, A.; Plizzari, G.A. Steel fibre concrete slabs on grade: a structural matter. ACI Struct. J. 2006, 103, 551–558. [Google Scholar]
- Brant, A.M. Fibre reinforced cement-based composites after over 40 years of development in building and civil engineering. Compos. Struct. 2008, 86, 3–9. [Google Scholar] [CrossRef]
- Ashour, S.A.; Hasanain, G.S.; Wafa, F.F. Shear behavior of high-strength fiber reinforced concrete beams. ACI Struct. J. 1992, 89, 176–184. [Google Scholar]
- Shin, S.W.; Oh, J.G.; Ghosh, S.K. Shear behavior of laboratory-sized high-strength concrete beams reinforced with bars and steel fibers. In Fiber Reinforced Concrete: Developments and Innovations; Daniel, J.I., Shah, S.P., Eds.; American Concrete Institute: Farmington Hills, MI, USA, 1994; pp. 181–200. [Google Scholar]
- Khuntia, M.; Stojadinovic, B.; Goel, S. Shear strength of normal and high-strength fiber reinforced concrete beams without stirrups. ACI Struct. J. 1999, 96, 282–290. [Google Scholar]
- Cucchiara, C.; Mendola, L.L.; Papia, M. Effectiveness of stirrups and steel fibers as shear reinforcement. Cem. Concr. Compos. 2004, 26, 777–786. [Google Scholar] [CrossRef]
- Dinh, H.H.; Parra-Montesinos, G.J.; Wight, J.K. Shear behavior of steel fiber reinforced concrete beams without stirrup reinforcement. ACI Struct. J. 2010, 107, 597–606. [Google Scholar]
- Meda, A.; Menelli, F.; Plizzari, G.A. Flexural behaviour of RC beams in fibre reinforced concrete. Compos. Part B 2012, 43, 2930–2937. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Sharma, A. Effect of fibre content on behavior of concrete beams with and without stirrups. ACI Struct. J. 2014, 111, 1157–1166. [Google Scholar]
- Qian, C.X.; Stroeven, P. Development of hybrid polypropylene-steel fibre-reinforced concrete. Cem. Concr. Res. 2000, 30, 63–69. [Google Scholar] [CrossRef]
- Koichi, M.; Tetsuya, I.; Toshiharu, K. Multi-scale modeling of concrete performance. J. Adv. Concr. Technol. 2003, 1, 91–126. [Google Scholar]
- Rossie, P. High performance multimodal fiber reinforced cement composites (HPMFRCC): The LCPC experience. ACI Mat. J. 1997, 94, 478–483. [Google Scholar]
- Banthia, N.; Gupta, R. Hybrid fiber reinforced concrete (HyFRC): Fiber synergy in high strength matrices. Mater. Struct. 2004, 37, 707–716. [Google Scholar] [CrossRef]
- Lawler, J.S.; Zampini, D.; Shah, S.P. Microfiber and macro-fiber hybrid fiber-reinforced concrete. J. Mater. Civ. Eng. 2005, 17, 595–604. [Google Scholar] [CrossRef]
- Aydin, A.C. Self-compactability of high volume hybrid fiber reinforced concrete. Constr. Build. Mater. 2007, 21, 1149–1154. [Google Scholar] [CrossRef]
- Kim, D.J.; Naaman, A.E.; El-Tawil, S. Comparative flexural behavior of four fiber reinforced cementitious composites. Cem. Concr. Compos. 2008, 30, 917–928. [Google Scholar] [CrossRef]
- Akcay, B.; Tasdemir, M.A. Mechanical behaviour and fibre dispersion of hybrid steel fibre reinforced self-compacting concrete. Constr. Build. Mater. 2012, 28, 287–293. [Google Scholar] [CrossRef]
- Vandewalle, L. Hybrid Fiber Reinforced Concrete. In Measuring, Monitoring and Modeling Concrete Properties; Konsta-Gdoutos, M.S., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 77–82. [Google Scholar]
- Sivakumar, A.; Santhanam, M. A quantitative study on the plastic shrinkage cracking in high strength hybrid fibre reinforced concrete. Cem. Concr. Compos. 2007, 29, 575–581. [Google Scholar] [CrossRef]
- Trono, W.; Jen, G.; Moreno, D. Confinement and tension stiffening effects in high performance self-consolidated hybrid fiber reinforced concrete composites. In High Performance Fiber Reinforced Cement Composites 6; Parra-Montesinos, G.J., Reinhardt, H.W., Naaman, A.E., Eds.; Springer: Berlin, Germany, 2012; pp. 255–262. [Google Scholar]
- Aguilar, G.M.; Parra-Montesions, G.J.; Ramires, J.A. Experimental evaluation of design procedures of deep reinforced concrete beams. ACI Struct. J. 2002, 99, 539–548. [Google Scholar]
- Mohammad, H.M.; Jumaat, M.Z.; Jameel, M. Experimental investigation to compare the modulus of rupture in high strength self-compacting concrete deep beams and high strength concrete normal beams. Constr. Build. Mater. 2012, 30, 265–273. [Google Scholar]
- Choi, Y.W.; Lee, H.K.; Chu, S.B.; Cheong, S.H.; Jung, W.Y. Shear Behavior and Performance of Deep Beams Made with Self-Compacting Concrete. Int. J. Concr. Struct. Mater. 2012, 6, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, R.; Darish, I.Y.S. Fiber concrete deep beams in shear. ACI Struct. J. 1988, 85, 141–148. [Google Scholar]
- Mansur, M.A.; Ong, K.C.G. Behavior of reinforced fiber concrete deep beams in shear. ACI Struct. J. 1991, 88, 98–105. [Google Scholar]
- Fang, I.K.; Wu, J.Y. Shear behavior of fiber-reinforced HPC deep beam. ACI Spec. Publ. 1994, 149, 523–544. [Google Scholar]
- Robin, G.T.; Alejandra, Q. Replacement of deformed side-face steel reinforcement in deep beams with steel fibers. Structures 2015, 3, 130–136. [Google Scholar]
- Campione, G. Flexural Behavior of steel fibrous Reinforced Concrete Deep Beams. J. Struct. Eng. (ASCE) 2012, 138, 235–246. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Flores, C.A.; Chao, S.H. Behavior of steel fiber-reinforced concrete deep beams with large opening. ACI Struct. J. 2012, 109, 193–204. [Google Scholar]
- Moradi, M.; Esfahani, M.R. Application of strut-and-tie method for steel fiber reinforced concrete deep beams. Constr. Build. Mater. 2017, 131, 423–437. [Google Scholar] [CrossRef]
- ASTM C143. Standard Test Method for Slump of Hydraulic-Cement Concrete; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ASTM C1611. Standard Test Method for Slump Flow of Self-Consolidating Concrete; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- ASTM C1609-12. Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading); ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]






| Groups | Cement (kg/m3) | Silica (kg/m3) | Fly Ash (kg/m3) | Slag (kg/m3) | Fine Sand (kg/m3) | Coarse Aggregate (kg/m3) | Water (kg/m3) | Super Plasticizer (kg/m3) | Fibers Volumes (L, S) (%) |
|---|---|---|---|---|---|---|---|---|---|
| HFRC0 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 1.6 | 0, 0 |
| HFRC1 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 1.6 | 1, 0 |
| HFRC2 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 2.4 | 2, 0 |
| HFRC3 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 2.4 | 3, 0 |
| HFRC4 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 2.4 | 1.75, 0.25 |
| HFRC5 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 2.4 | 1.5, 0.5 |
| HFRC6 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 2.4 | 1.25, 0.75 |
| HFRC7 | 325 | 32.5 | 195 | 97.5 | 722 | 868 | 160 | 1.0 | 1, 1 |
| Types | lf (mm) | df (mm) | Ef (GP) | Tensile Strength (MPa) | Shape |
|---|---|---|---|---|---|
| Long steel fiber | 30 | 0.55 | 210 | 1345 | Hook |
| Short steel fiber | 13 | 0.20 | 210 | 2000 | Straight |
| Groups | Slump (mm) | Slump Flow (mm) | Compressive Strength (MPa) | Tensile Strength (MPa) | Flexural Strength (MPa) |
|---|---|---|---|---|---|
| HFRC0 | 270 | 720 | 80.3 | 2.92 | 3.95 |
| HFRC1 | 259 | 690 | 84.4 | 3.93 | 7.57 |
| HFRC2 | 235 | 590 | 92.6 | 5.11 | 10.71 |
| HFRC3 | 173 | 435 | 99.5 | 6.12 | 13.99 |
| HFRC4 | 222 | 562 | 93.0 | 5.45 | 11.16 |
| HFRC5 | 210 | 533 | 99.8 | 5.78 | 12.08 |
| HFRC6 | 199 | 497 | 101.4 | 5.23 | 10.83 |
| HFRC7 | 181 | 458 | 103.8 | 5.02 | 9.75 |
| Specimens | Fibers Volumes (L, S) (%) | |||||
|---|---|---|---|---|---|---|
| DB-1 | 0, 0 | 66.2 | 56.2 | 3.05 | 3.05 | 3.56 × 104 |
| DB-2 | 0.75, 0.25 | 68.2 | 57.3 | 3.85 | 6.92 | 3.63 × 104 |
| DB-3 | 1.5, 0.5 | 71.7 | 60.8 | 5.22 | 10.23 | 3.82 × 104 |
| DB-4 | 1.5, 0.5 | 72.1 | 61.1 | 5.29 | 10.42 | 3.89 × 104 |
| DB-5 | 1.5, 0.5 | 71.5 | 60.5 | 5.34 | 10.35 | 3.81 × 104 |
| Specimens | |||
|---|---|---|---|
| DB-1 | 301.3 | 857.2 | 3.8 |
| DB-2 | 657.2 | 1430.2 | 6.0 |
| DB-3 | 844.3 | 1815.0 | 6.7 |
| DB-4 | 761.2 | 1634.9 | 6.1 |
| DB-5 | 685.4 | 1458.4 | 5.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, K.; Qi, T.; Liu, H.; Wang, H. Shear Behavior of Hybrid Fiber Reinforced Concrete Deep Beams. Materials 2018, 11, 2023. https://doi.org/10.3390/ma11102023
Ma K, Qi T, Liu H, Wang H. Shear Behavior of Hybrid Fiber Reinforced Concrete Deep Beams. Materials. 2018; 11(10):2023. https://doi.org/10.3390/ma11102023
Chicago/Turabian StyleMa, Kaize, Ting Qi, Huijie Liu, and Hongbing Wang. 2018. "Shear Behavior of Hybrid Fiber Reinforced Concrete Deep Beams" Materials 11, no. 10: 2023. https://doi.org/10.3390/ma11102023
APA StyleMa, K., Qi, T., Liu, H., & Wang, H. (2018). Shear Behavior of Hybrid Fiber Reinforced Concrete Deep Beams. Materials, 11(10), 2023. https://doi.org/10.3390/ma11102023





