Fundamentals of Force-Controlled Friction Riveting: Part I—Joint Formation and Heat Development
Abstract
:1. Introduction
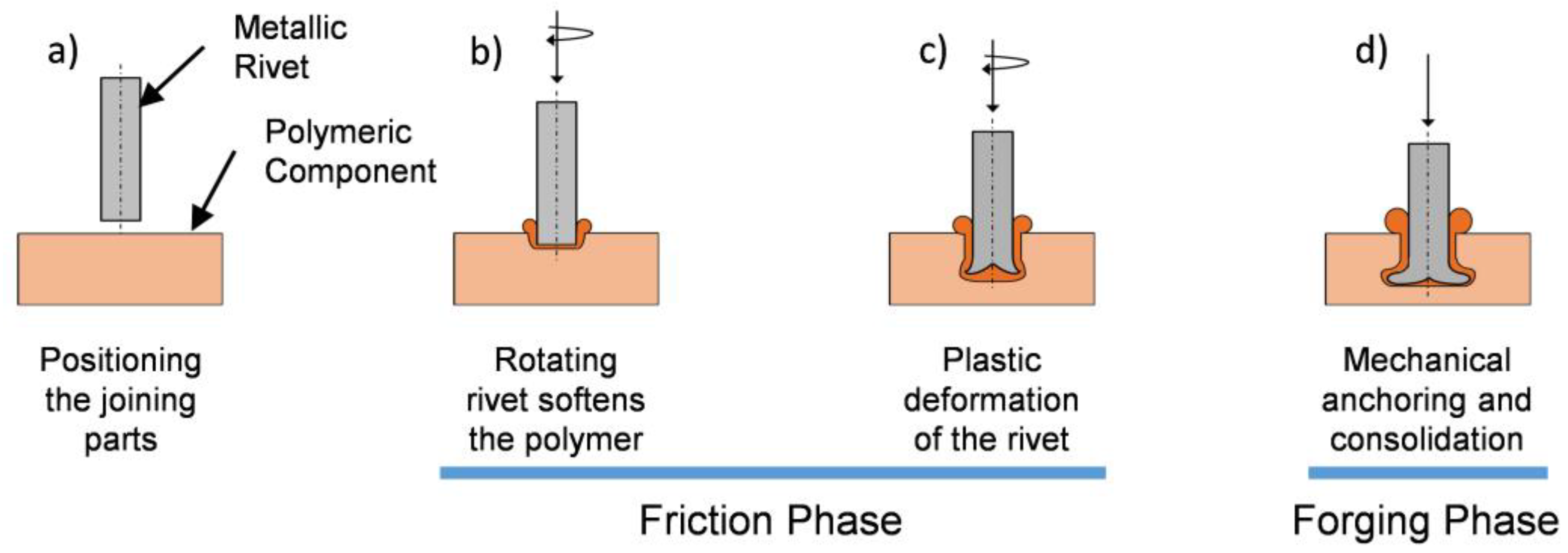
2. Force-Controlled Friction Riveting
3. Materials and Methods
3.1. Base Materials
3.2. Joining Procedure
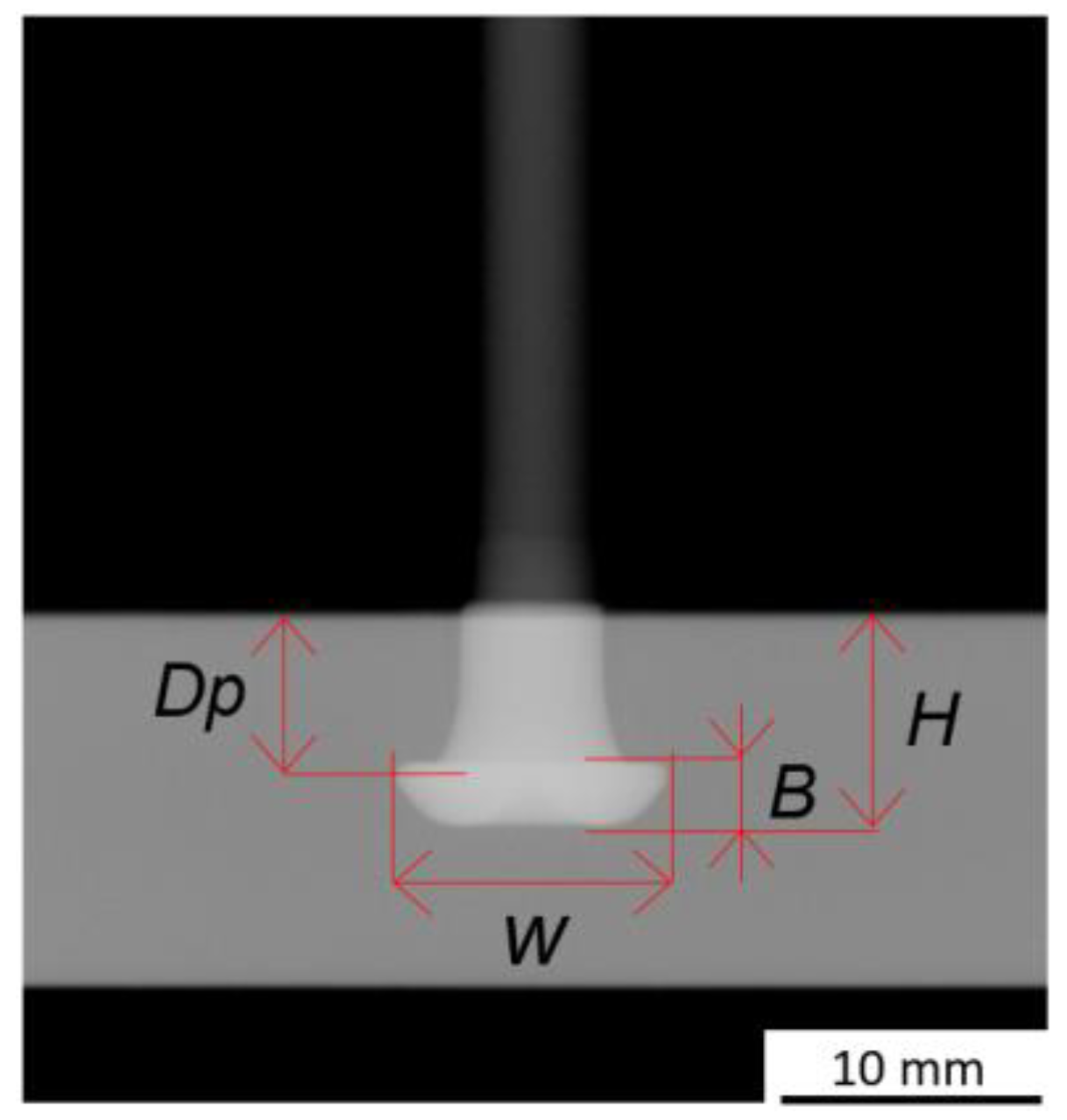
3.3. Non-Destructive Joint Analysis
3.4. Energy Input
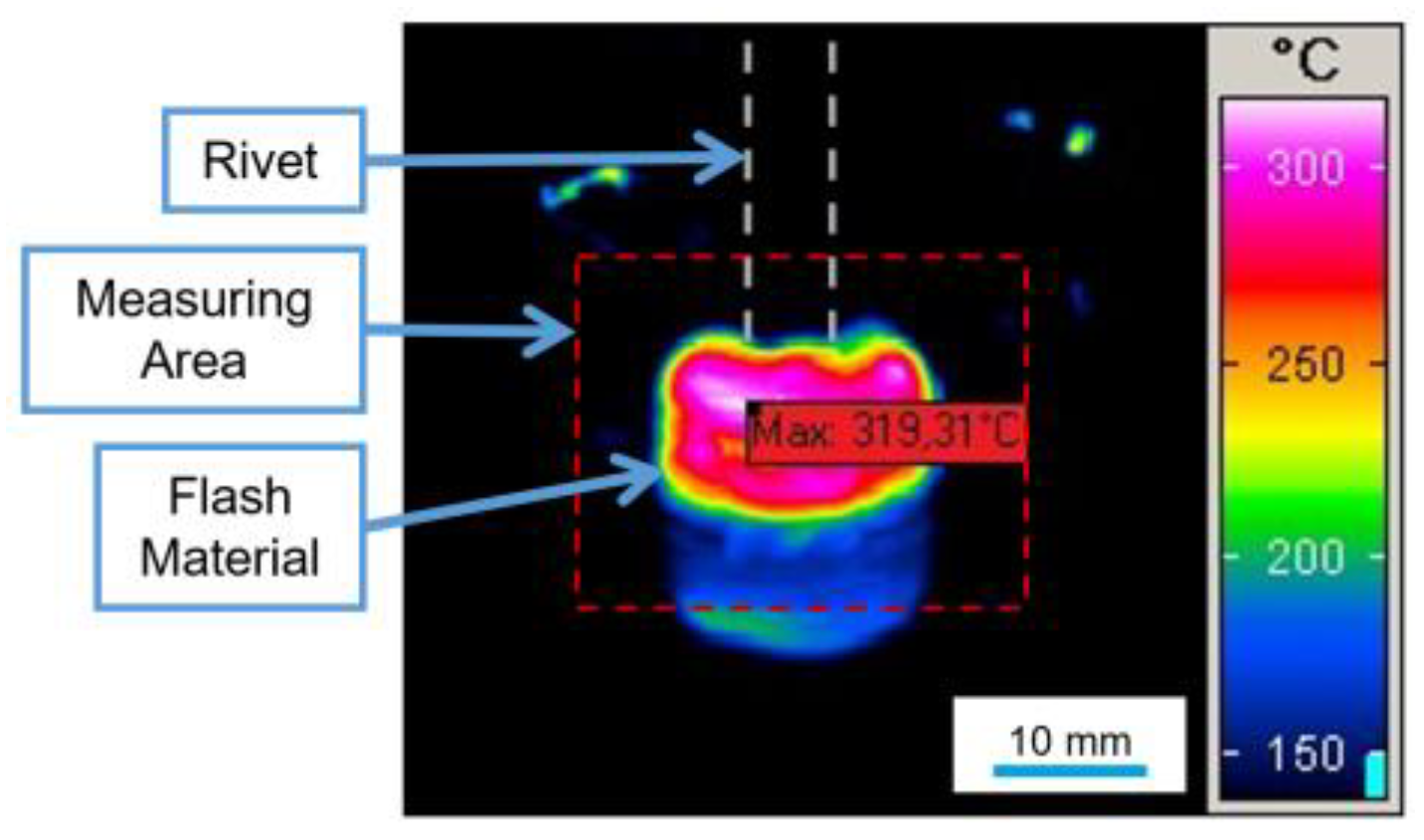
3.5. Temperature Measurement
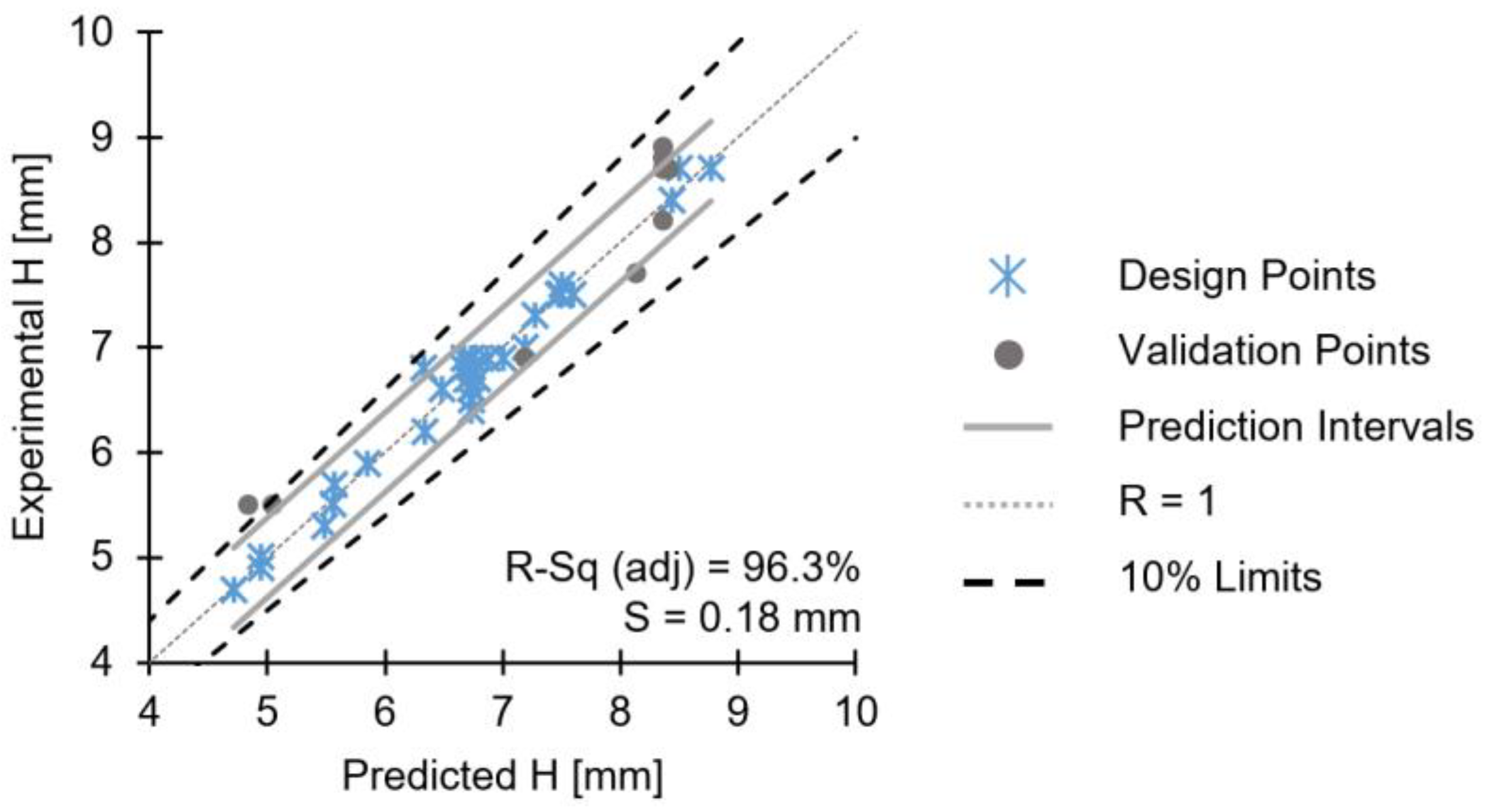
3.6. Design of Experiments and Statistical Analysis
4. Results and Discussion
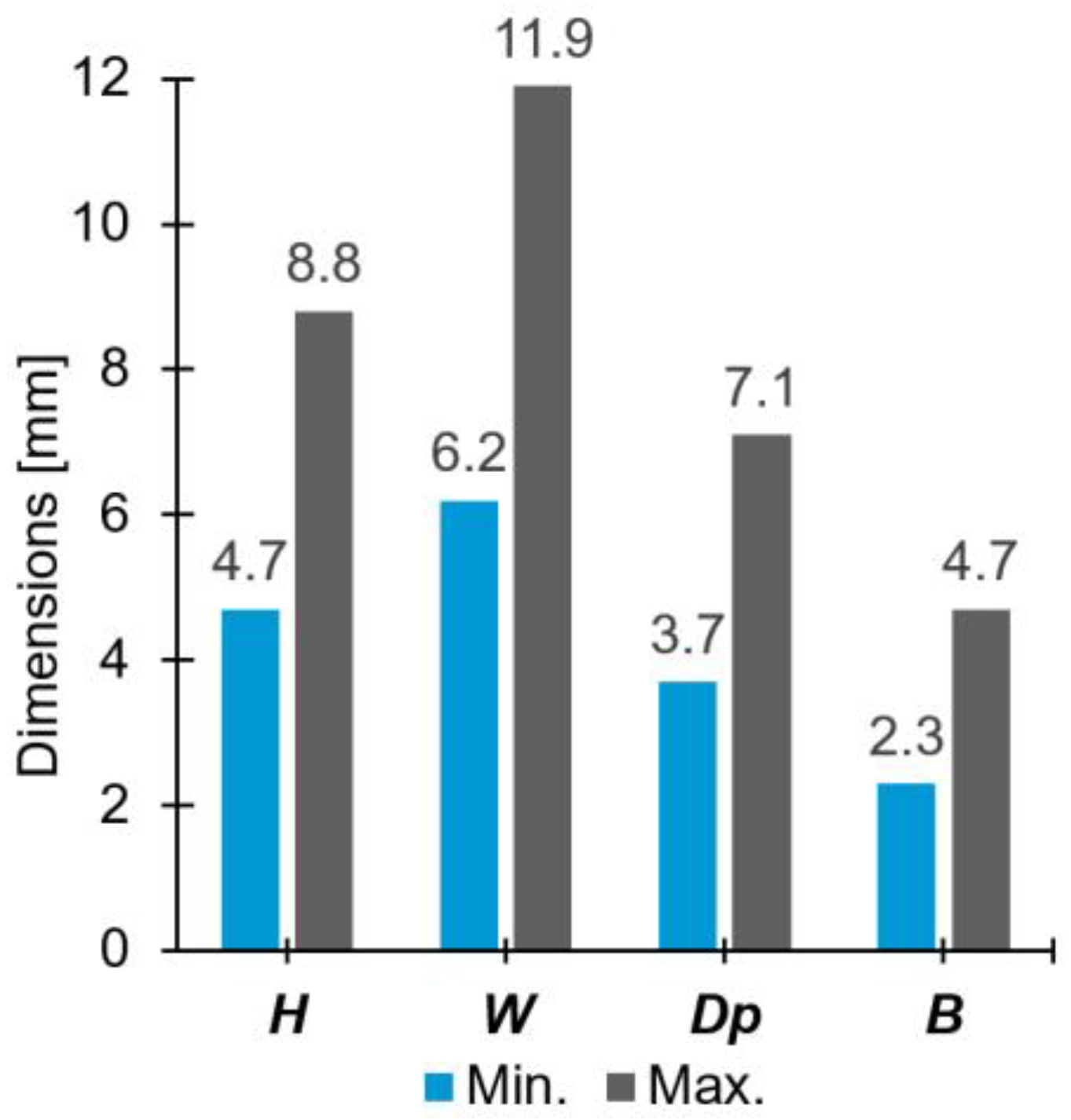
4.1. Joint Formation
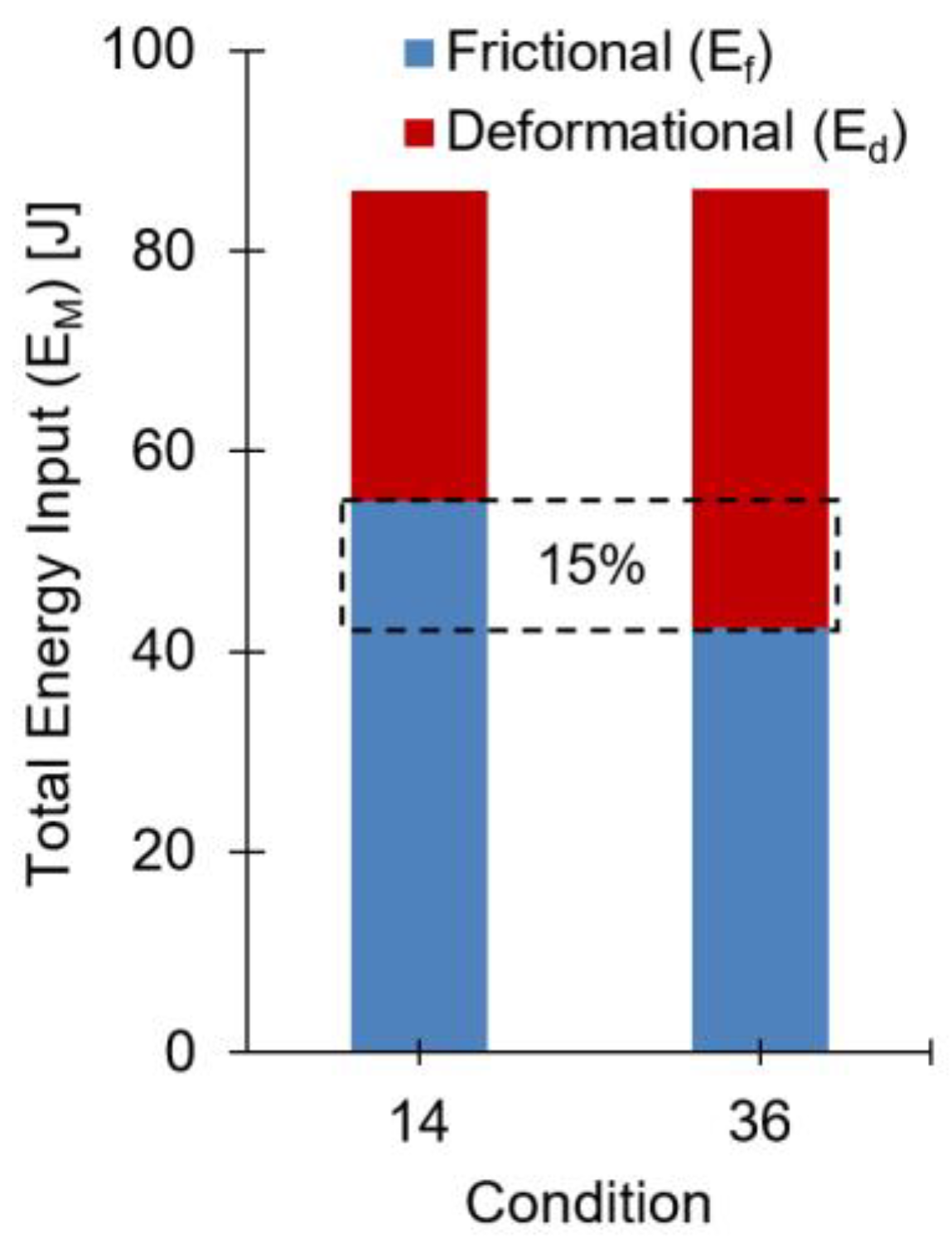
4.2. Mechanical Energy Input
4.3. Influence of the Process Parameters on Joint Formation
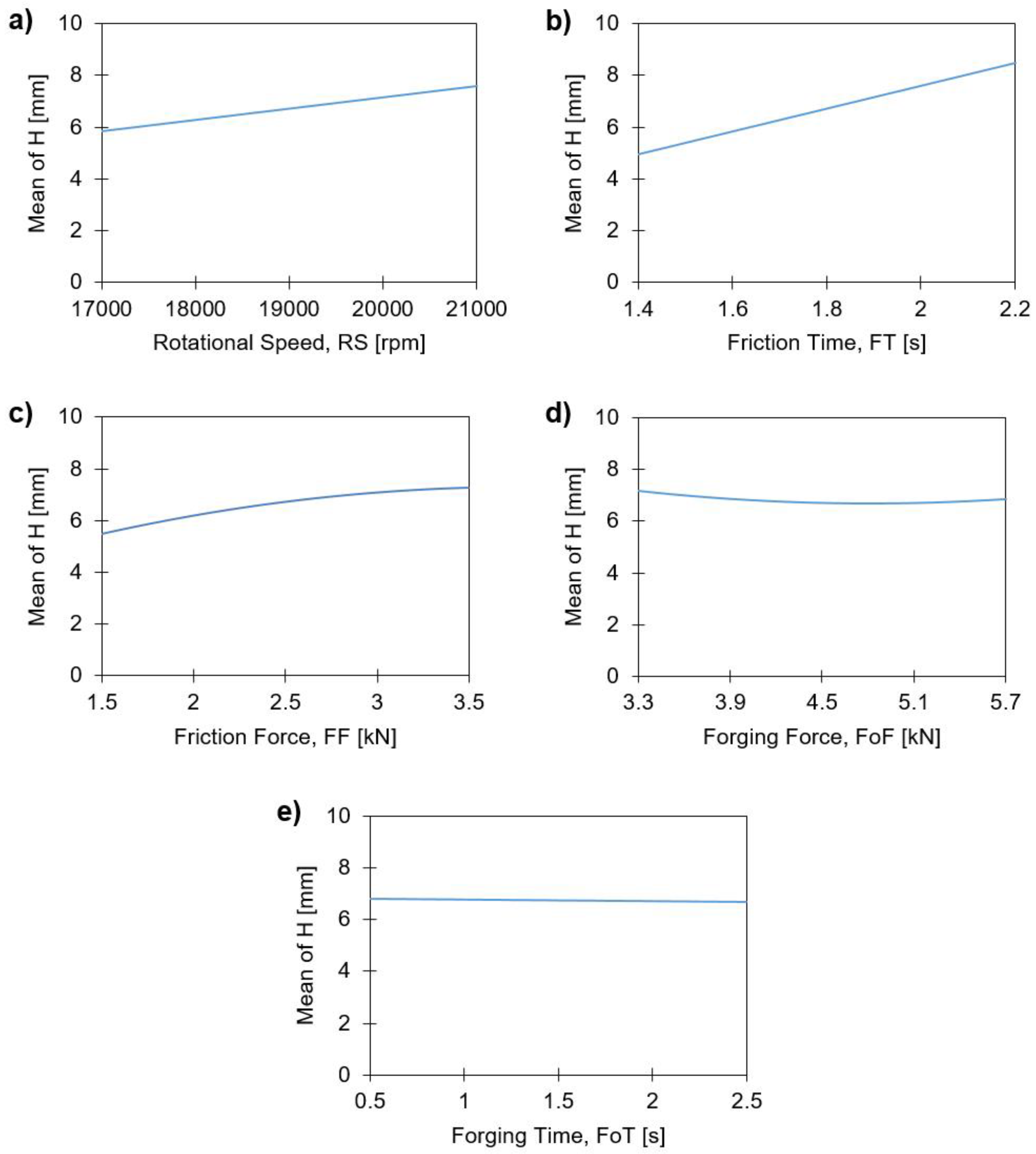
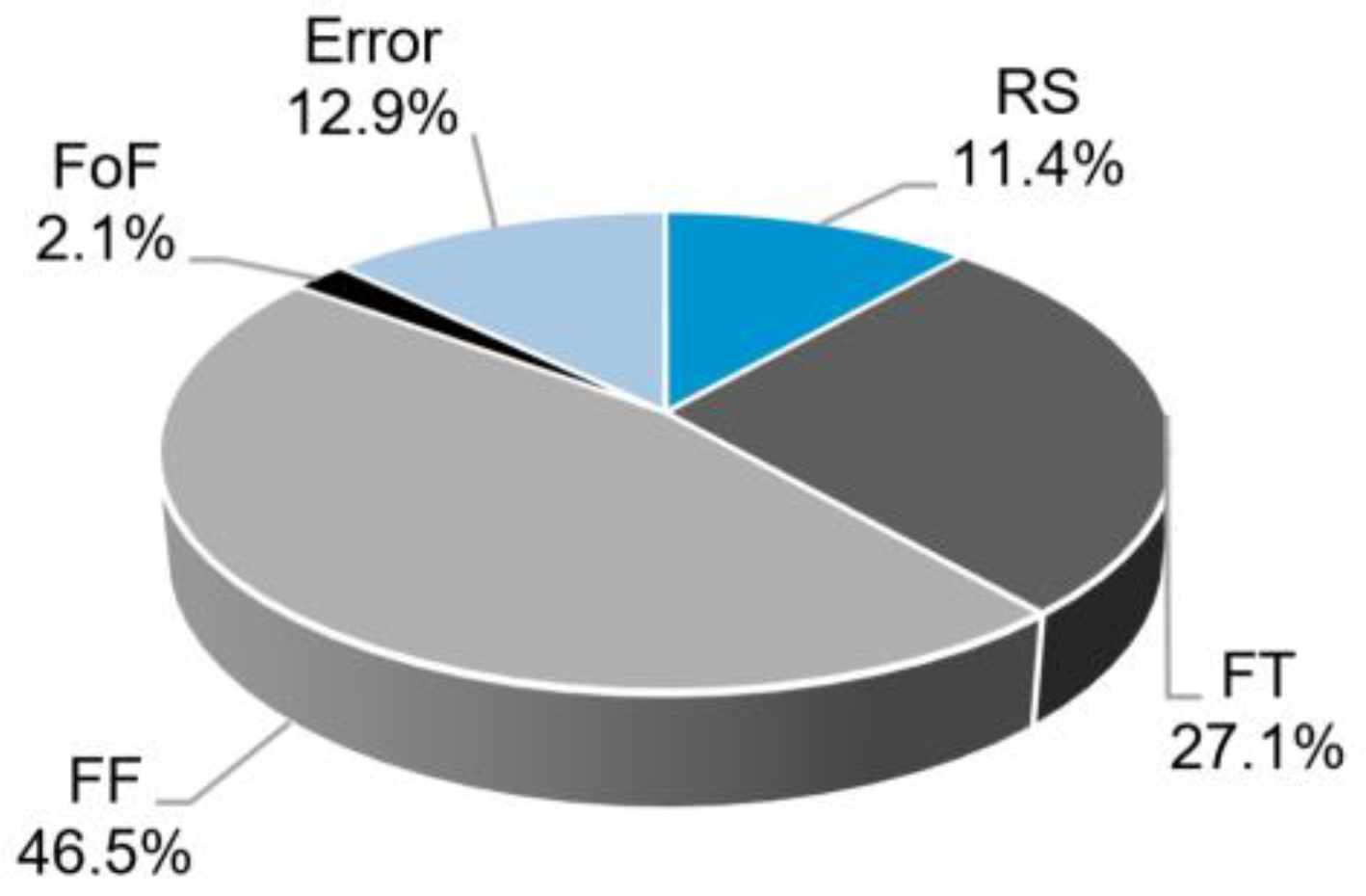
4.3.1. Influence on the Rivet Penetration Depth, H
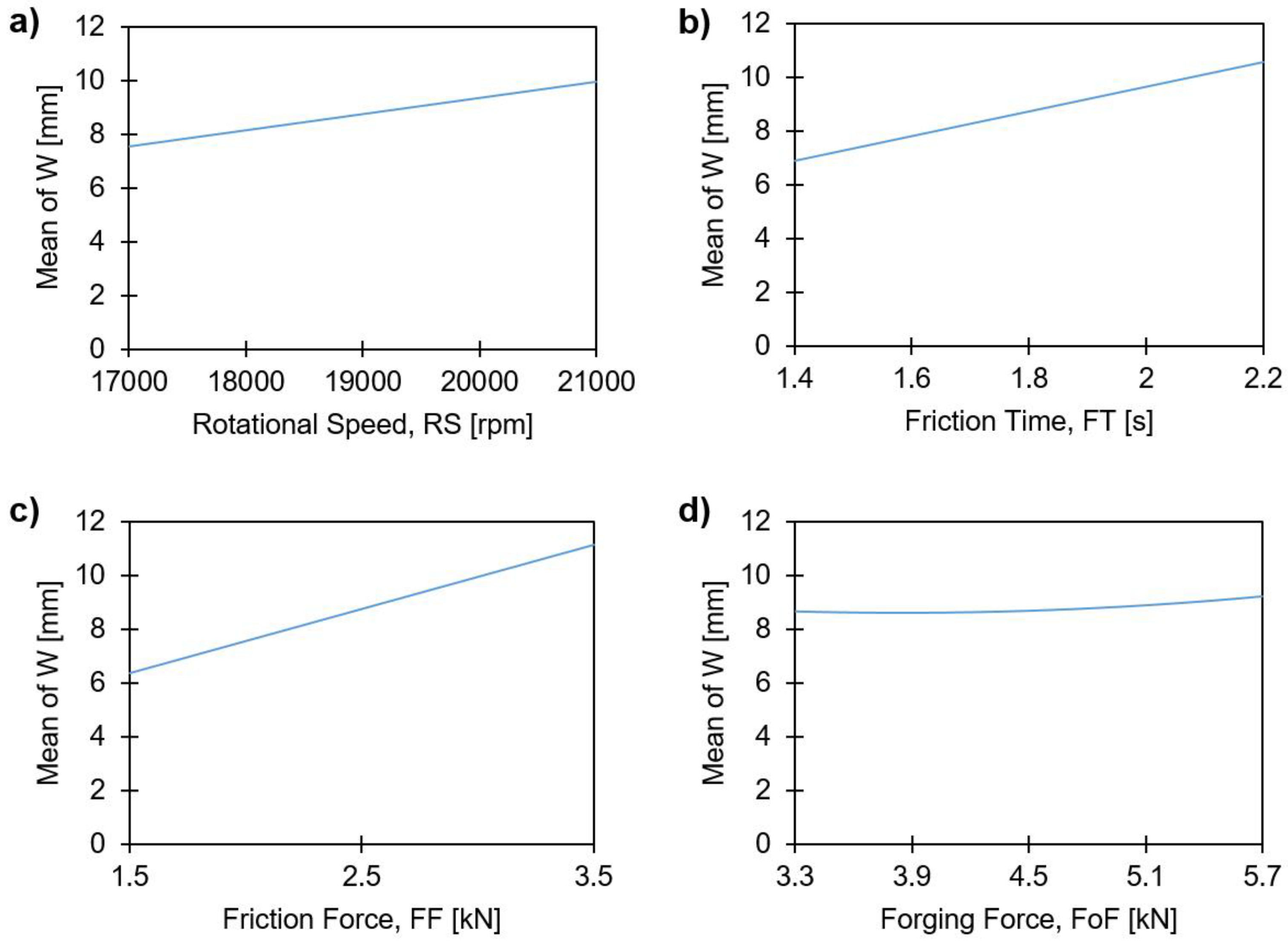
4.3.2. Influence on the Maximum Width of the Deformed Rivet Tip, W
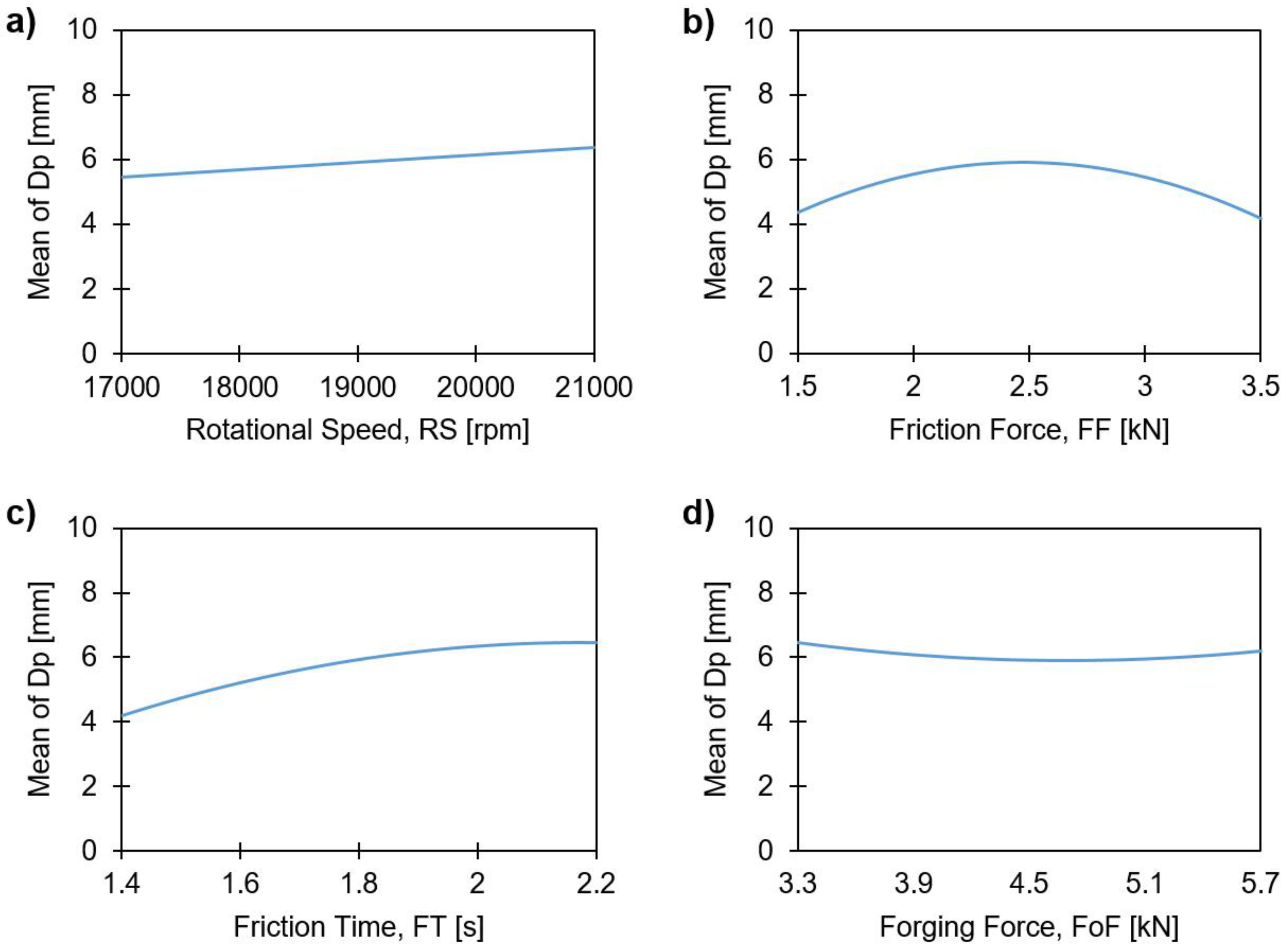
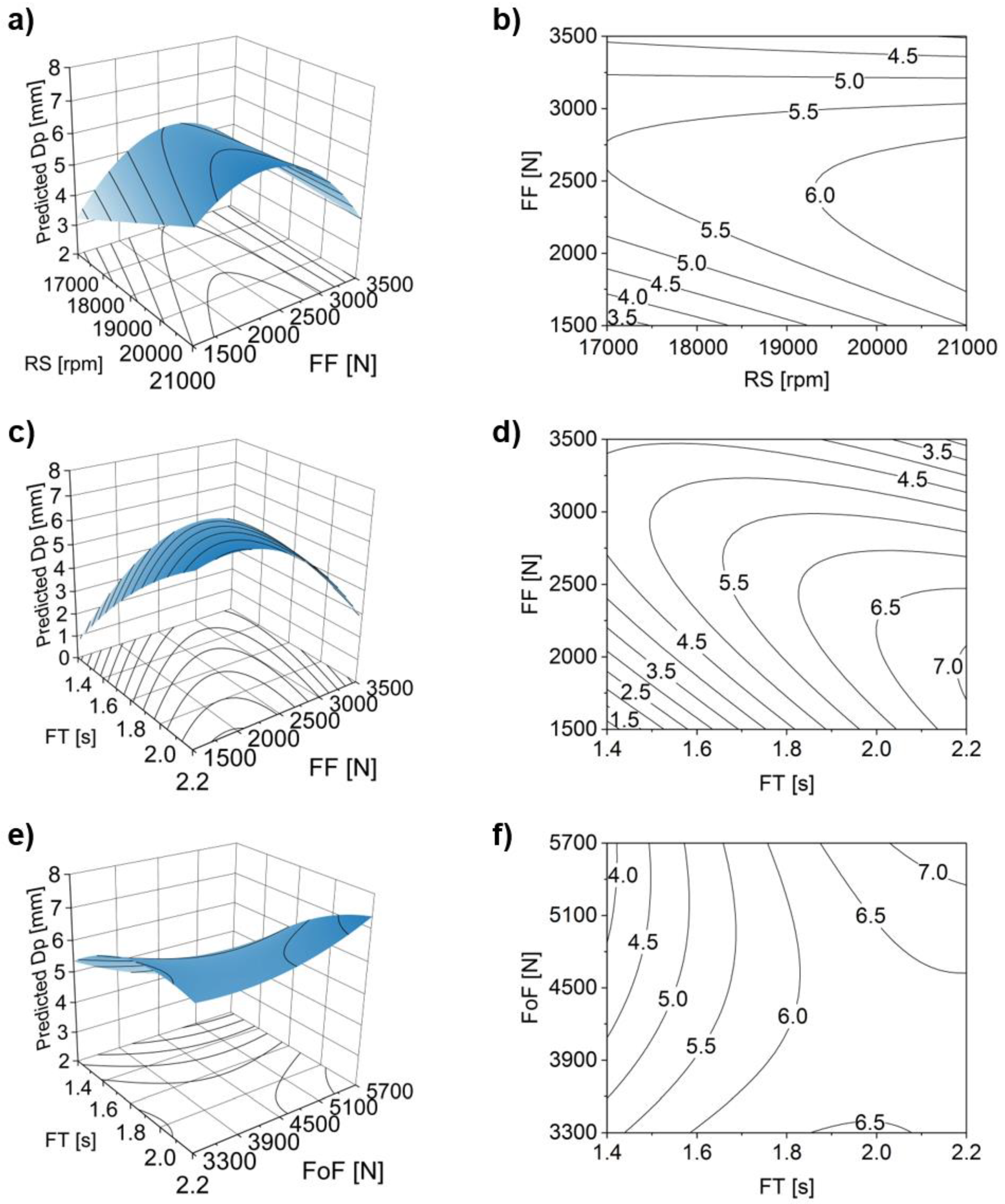
4.3.3. Influence on the Anchoring Depth, Dp
4.3.4. Summary of the Findings
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Timmis, A.J.; Hodzic, A.; Koh, L.; Bonner, M.; Soutis, C.; Schäfer, A.W.; Dray, L. Environmental impact assessment of aviation emission reduction through the implementation of composite materials. Int. J. Life Cycle Assess. 2015, 20, 233–243. [Google Scholar] [CrossRef] [Green Version]
- Amancio-Filho, S.T.; Dos Santos, J.F. Joining of polymers and polymer-metal hybrid structures: Recent developments and trends. Polym. Eng. Sci. 2009, 49, 1461–1476. [Google Scholar] [CrossRef]
- Baldan, A. Adhesively-bonded joints and repairs in metallic alloys, polymers and composite materials: Adhesives, adhesion theories and surface pretreatment. J. Mater. Sci. 2004, 39, 1–49. [Google Scholar] [CrossRef]
- Budynas, R.; Nisbett, K. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-007-352-928-8. [Google Scholar]
- Ghassemieh, E. Materials in automotive application, state of the art and prospects. New Trends Dev. Automot. Ind. 2011, 20, 365–394. [Google Scholar] [CrossRef]
- Mallick, P. Materials, Design and Manufacturing for Lightweight Vehicles; Woodhead Publishing: Cambridge, UK, 2010; ISBN 978-184-569-463-0. [Google Scholar]
- Amancio-Filho, S.T.; Beyer, M.; dos Santos, J.F. Method of Connecting a Metallic Bolt to a Plastic Workpiece. U.S. Patent 7,575,149, 18 August 2009. [Google Scholar]
- Amancio-Filho, S.T.; Dos Santos, J.F. Influence of processing parameters on microstructure and properties of a polyetherimide joined by fricriveting: Investigation of rotational speed. In Proceedings of the Annual Technical Conference—ANTEC, Chicago, IL, USA, 22–24 June 2009. [Google Scholar]
- Altmeyer, J.; dos Santos, J.F.; Amancio-Filho, S.T. Effect of the friction riveting process parameters on the joint formation and performance of Ti alloy/short-fibre reinforced polyether ether ketone joints. Mater. Des. 2014, 60, 164–176. [Google Scholar] [CrossRef]
- Rodrigues, C.F.; Blaga, L.A.; dos Santos, J.F.; Canto, L.B.; Hage, E.; Amancio-Filho, S.T. FricRiveting of aluminum 2024-T351 and polycarbonate: Temperature evolution, microstructure and mechanical performance. J. Mater. Process. Technol. 2014, 214, 2029–2039. [Google Scholar] [CrossRef] [Green Version]
- Blaga, L.; Bancilă, R.; dos Santos, J.F.; Amancio-Filho, S.T. Friction Riveting of glass–fibre-reinforced polyetherimide composite and titanium grade 2 hybrid joints. Mater. Des. 2013, 50, 825–829. [Google Scholar] [CrossRef] [Green Version]
- Borba, N.; Afonso, C.; Blaga, L.; dos Santos, J.; Canto, L.; Amancio-Filho, S. On the Process-Related Rivet Microstructural Evolution, Material Flow and Mechanical Properties of Ti-6Al-4V/GFRP Friction-Riveted Joints. Materials 2017, 10, 184. [Google Scholar] [CrossRef] [PubMed]
- Proenca, B.C.; Blaga, L.A.; Dos Santos, J.F.; Canto, L.B.; Amancio-Filho, S.T. Force controlled friction riveting of glass fiber reinforced polyamide 6 and aluminum alloy 6056 hybrid joints. In Proceedings of the Annual Technical Conference—ANTEC, Orlando, FL, USA, 23–25 March 2015. [Google Scholar]
- Amancio-Filho, S.T. Friction Riveting: Development and Analysis of a New Joining Technique for Polymer-Metal Multi-Materials Structures. Ph.D. Thesis, Technische Universität Hamburg-Harburg, Hamburg, Germany, 1 July 2007. [Google Scholar]
- Amancio-Filho, S.T.; dos Santos, J.F. Henry Granjon Prize Competition 2009 Winner Category A: “Joining and Fabrication Technology” Friction Riveting: Development and Analysis of a New Joining Technique for Polymer-Metal Multi-Material Structures. Weld. World 2011, 55, 13–24. [Google Scholar] [CrossRef]
- Wirth, J.G. Discovery and Development of Polyetherimides. In High Performance Polymers: Their Origin and Development; Springer: Dordrecht, The Netherlands, 1986; pp. 195–205. [Google Scholar]
- Johnson, R.O.; Burlhis, H.S. Polyetherimide: A new high-performance thermoplastic resin. J. Polym. Sci. Polym. Symp. 2007, 70, 129–143. [Google Scholar] [CrossRef]
- Fukuhara, M. Temperature dependency of elastic moduli and internal dilational and shear frictions of polyetherimide. J. Appl. Polym. Sci. 2003, 90, 759–764. [Google Scholar] [CrossRef]
- Thomas, S.; Visakh, P.M. Handbook of Engineering and Specialty Thermoplastics; Scrivener Publishing LLC: Salem, MA, USA, 2012; Volume 4, ISBN 978-111-822-906-4. [Google Scholar]
- Davis, J.R. ASM Specialty Handbook: Aluminum and Aluminum Alloys; ASM International: Almere, The Netherlands, 1993; ISBN 978-087-170-496-2. [Google Scholar]
- Ma, T.J.; Li, W.; Yang, S.Y. Impact toughness and fracture analysis of linear friction welded Ti-6Al-4V alloy joints. Mater. Des. 2009, 30, 2128–2132. [Google Scholar] [CrossRef]
- Crawford, R.J.; Tam, Y. Friction welding of plastics. J. Mater. Sci. 1981, 16, 3275–3282. [Google Scholar] [CrossRef]
- Stokes, V.K. Analysis of the friction (spin)-welding process for thermoplastics. J. Mater. Sci. 1988, 23, 2772–2785. [Google Scholar] [CrossRef]
- Abibe, A.B.; Dos Santos, J.F.; Amancio-Filho, S.T. Friction Staking: A novel staking joining method for hybrid structures. In Proceedings of the Annual Technical Conference—ANTEC, Las Vegas, NV, USA, 28–30 April 2014. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley and Sons: New York, NY, USA, 2001. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef] [Green Version]
- Amancio-Filho, S.T.; Dos Santos, J.F. Preliminary analytical modeling of heat input in friction riveting. In Proceedings of the Annual Technical Conference—ANTEC, Indianapolis, IN, USA, 23–25 May 2016. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2003; ISBN 978-047-120-454-1. [Google Scholar]
- Dealy, J.M.; Wissbrun, K.F. Melt Rheology and Its Role in Plastics Processing: Theory and Applications; Chapman & Hall: London, UK, 1990; ISBN 978-041-273-910-1. [Google Scholar]
- Hamielec, A.E.; Hodgins, J.W.; Tebbens, K. Polymer reactors and molecular weight distribution: Part II. Free radical polymerization in a batch reactor. AIChE J. 1967, 13, 1087–1091. [Google Scholar] [CrossRef]
- Sacks, M.E.; Lee, S.-I.; Biesenberger, J.A. Effect of temperature variations on molecular weight distributions: Batch, chain addition polymerizations. Chem. Eng. Sci. 1973, 28, 241–257. [Google Scholar] [CrossRef]
- Johnson, R.O.; Teutsch, E.O. Thermoplastic aromatic polyimide composites. Polym. Compos. 1983, 4, 162–166. [Google Scholar] [CrossRef]











| Element | Al | Cr | Cu | Fe | Mg | Mn | Si | Ti | Zn |
|---|---|---|---|---|---|---|---|---|---|
| Weight (wt%) | 90.7–94.7 | ≤0.10 | 3.8–4.9 | ≤0.50 | 1.2–1.8 | 0.3–0.9 | ≤0.50 | ≤0.15 | ≤0.25 |
| Condition | Process Parameters | Condition | Process Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RS (rpm) | FT (s) | FoT (s) | FF (N) | FoF (N) | RS (rpm) | FT (s) | FoT (s) | FF (N) | FoF (N) | ||
| 1 | 18,000 | 1.6 | 1 | 2000 | 5100 | 19 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 2 | 20,000 | 1.6 | 1 | 2000 | 3900 | 20 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 3 | 18,000 | 2 | 1 | 2000 | 3900 | 21 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 4 | 20,000 | 2 | 1 | 2000 | 5100 | 22 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 5 | 18,000 | 1.6 | 2 | 2000 | 3900 | 23 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 6 | 20,000 | 1.6 | 2 | 2000 | 5100 | 24 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 7 | 18,000 | 2 | 2 | 2000 | 5100 | 25 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 8 | 20,000 | 2 | 2 | 2000 | 3900 | 26 | 19,000 | 1.8 | 1.5 | 2500 | 4500 |
| 9 | 18,000 | 1.6 | 1 | 3000 | 3900 | 27 | 17,000 | 1.8 | 1.5 | 2500 | 4500 |
| 10 | 20,000 | 1.6 | 1 | 3000 | 5100 | 28 | 21,000 | 1.8 | 1.5 | 2500 | 4500 |
| 11 | 18,000 | 2 | 1 | 3000 | 5100 | 29 | 19,000 | 1.4 | 1.5 | 2500 | 4500 |
| 12 | 20,000 | 2 | 1 | 3000 | 3900 | 30 | 19,000 | 2.2 | 1.5 | 2500 | 4500 |
| 13 | 18,000 | 1.6 | 2 | 3000 | 5100 | 31 | 19,000 | 1.8 | 0.5 | 2500 | 4500 |
| 14 | 20,000 | 1.6 | 2 | 3000 | 3900 | 32 | 19,000 | 1.8 | 2.5 | 2500 | 4500 |
| 15 | 18,000 | 2 | 2 | 3000 | 3900 | 33 | 19,000 | 1.8 | 1.5 | 1500 | 4500 |
| 16 | 20,000 | 2 | 2 | 3000 | 5100 | 34 | 19,000 | 1.8 | 1.5 | 3500 | 4500 |
| 17 | 19,000 | 1.8 | 1.5 | 2500 | 4500 | 35 | 19,000 | 1.8 | 1.5 | 2500 | 3300 |
| 18 | 19,000 | 1.8 | 1.5 | 2500 | 4500 | 36 | 19,000 | 1.8 | 1.5 | 2500 | 5700 |
| Condition | Joint Formation Measurements | Condition | Joint Formation Measurements | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H (mm) | Dp (mm) | B (mm) | W (mm) | H (mm) | Dp (mm) | B (mm) | W (mm) | ||
| 1 | 4.7 | 3.7 | 2.8 | 6.2 | 19 | 6.8 | 6.1 | 2.6 | 9.3 |
| 2 | 6.8 | 5.0 | 3.8 | 7.3 | 20 | 6.9 | 6.1 | 3.2 | 9.2 |
| 3 | 6.8 | 6.4 | 2.8 | 7.4 | 21 | 6.5 | 6.0 | 3.0 | 7.8 |
| 4 | 7.5 | 7.0 | 4.7 | 9.3 | 22 | 6.6 | 6.0 | 3.5 | 8.6 |
| 5 | 4.9 | 4.4 | 2.3 | 6.2 | 23 | 6.6 | 6.0 | 2.7 | 7.3 |
| 6 | 5.5 | 5.0 | 3.2 | 7.0 | 24 | 6.8 | 6.0 | 3.2 | 9.1 |
| 7 | 6.9 | 6.4 | 4.4 | 7.8 | 25 | 6.6 | 5.8 | 3.8 | 9.2 |
| 8 | 7.5 | 7.1 | 3.2 | 8.4 | 26 | 6.9 | 6.3 | 3.3 | 9.0 |
| 9 | 6.2 | 5.7 | 2.5 | 8.2 | 27 | 5.9 | 5.1 | 3.0 | 7.7 |
| 10 | 6.6 | 5.3 | 3.7 | 10.0 | 28 | 7.5 | 6.0 | 3.6 | 9.9 |
| 11 | 7.6 | 5.7 | 3.8 | 10.0 | 29 | 4.9 | 4.2 | 2.4 | 6.7 |
| 12 | 8.4 | 5.4 | 4.2 | 11.3 | 30 | 8.7 | 6.0 | 3.3 | 11.5 |
| 13 | 5.7 | 5.0 | 3.0 | 9.2 | 31 | 6.7 | 5.8 | 3.0 | 8.4 |
| 14 | 6.7 | 5.5 | 2.9 | 9.6 | 32 | 6.9 | 6.0 | 3.4 | 9.3 |
| 15 | 7.5 | 5.4 | 3.1 | 9.9 | 33 | 5.3 | 4.1 | 3.0 | 6.5 |
| 16 | 8.7 | 6.1 | 4.7 | 11.9 | 34 | 7.3 | 4.0 | 5.4 | 10.6 |
| 17 | 6.4 | 5.6 | 3.1 | 7.5 | 35 | 7.0 | 6.3 | 2.6 | 8.3 |
| 18 | 6.6 | 5.7 | 3.4 | 9.5 | 36 | 6.9 | 5.9 | 4.2 | 9.8 |
| Condition | Energy Input | Condition | Energy Input | Condition | Energy Input | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ef (J) | Ed (J) | EM (J) | Ef (J) | Ed (J) | EM (J) | Ef (J) | Ed (J) | EM (J) | |||
| 1 | 10 | 14 | 24 | 13 | 45 | 33 | 78 | 25 | 36 | 32 | 68 |
| 2 | 26 | 20 | 46 | 14 | 55 | 31 | 86 | 26 | 40 | 31 | 71 |
| 3 | 33 | 20 | 53 | 15 | 82 | 39 | 120 | 27 | 28 | 23 | 51 |
| 4 | 39 | 38 | 77 | 16 | 122 | 86 | 208 | 28 | 46 | 37 | 83 |
| 5 | 14 | 14 | 29 | 17 | 39 | 25 | 63 | 29 | 17 | 19 | 36 |
| 6 | 16 | 20 | 36 | 18 | 42 | 34 | 76 | 30 | 84 | 52 | 136 |
| 7 | 35 | 30 | 65 | 19 | 42 | 32 | 74 | 31 | 36 | 28 | 64 |
| 8 | 41 | 16 | 57 | 20 | 42 | 31 | 73 | 32 | 40 | 32 | 73 |
| 9 | 36 | 24 | 60 | 21 | 29 | 27 | 56 | 33 | 21 | 17 | 38 |
| 10 | 40 | 43 | 83 | 22 | 30 | 28 | 59 | 34 | 88 | 72 | 159 |
| 11 | 63 | 43 | 106 | 23 | 24 | 23 | 47 | 35 | 34 | 24 | 59 |
| 12 | 90 | 66 | 155 | 24 | 37 | 30 | 67 | 36 | 42 | 44 | 86 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pina Cipriano, G.; Blaga, L.A.; F. dos Santos, J.; Vilaça, P.; Amancio-Filho, S.T. Fundamentals of Force-Controlled Friction Riveting: Part I—Joint Formation and Heat Development. Materials 2018, 11, 2294. https://doi.org/10.3390/ma11112294
Pina Cipriano G, Blaga LA, F. dos Santos J, Vilaça P, Amancio-Filho ST. Fundamentals of Force-Controlled Friction Riveting: Part I—Joint Formation and Heat Development. Materials. 2018; 11(11):2294. https://doi.org/10.3390/ma11112294
Chicago/Turabian StylePina Cipriano, Gonçalo, Lucian A. Blaga, Jorge F. dos Santos, Pedro Vilaça, and Sergio T. Amancio-Filho. 2018. "Fundamentals of Force-Controlled Friction Riveting: Part I—Joint Formation and Heat Development" Materials 11, no. 11: 2294. https://doi.org/10.3390/ma11112294
APA StylePina Cipriano, G., Blaga, L. A., F. dos Santos, J., Vilaça, P., & Amancio-Filho, S. T. (2018). Fundamentals of Force-Controlled Friction Riveting: Part I—Joint Formation and Heat Development. Materials, 11(11), 2294. https://doi.org/10.3390/ma11112294








