Study on Damage Accumulation and Life Prediction with Loads below Fatigue Limit Based on a Modified Nonlinear Model
Abstract
1. Introduction
2. Damage Model
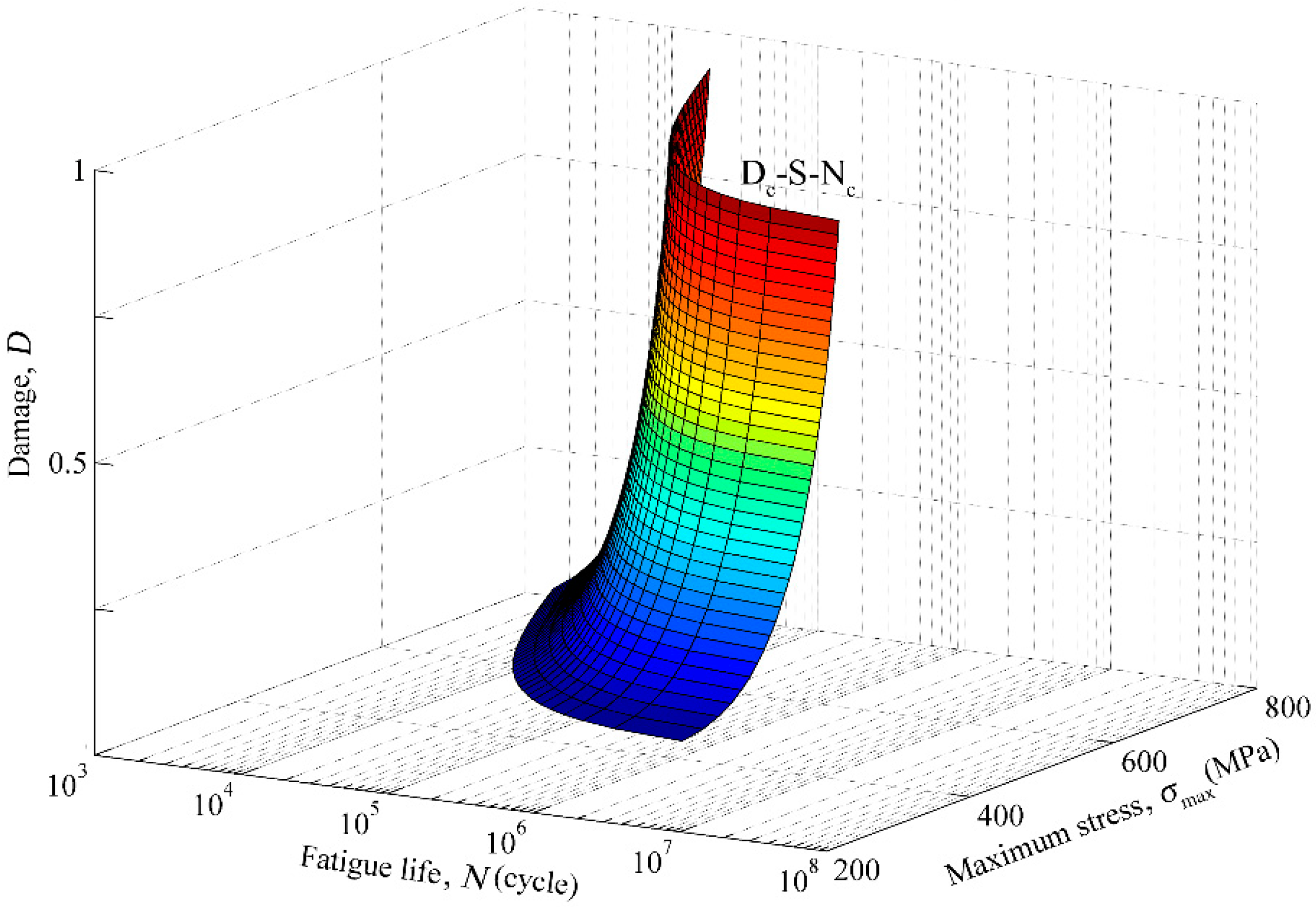
2.1. Nonlinear Damage Accumulation
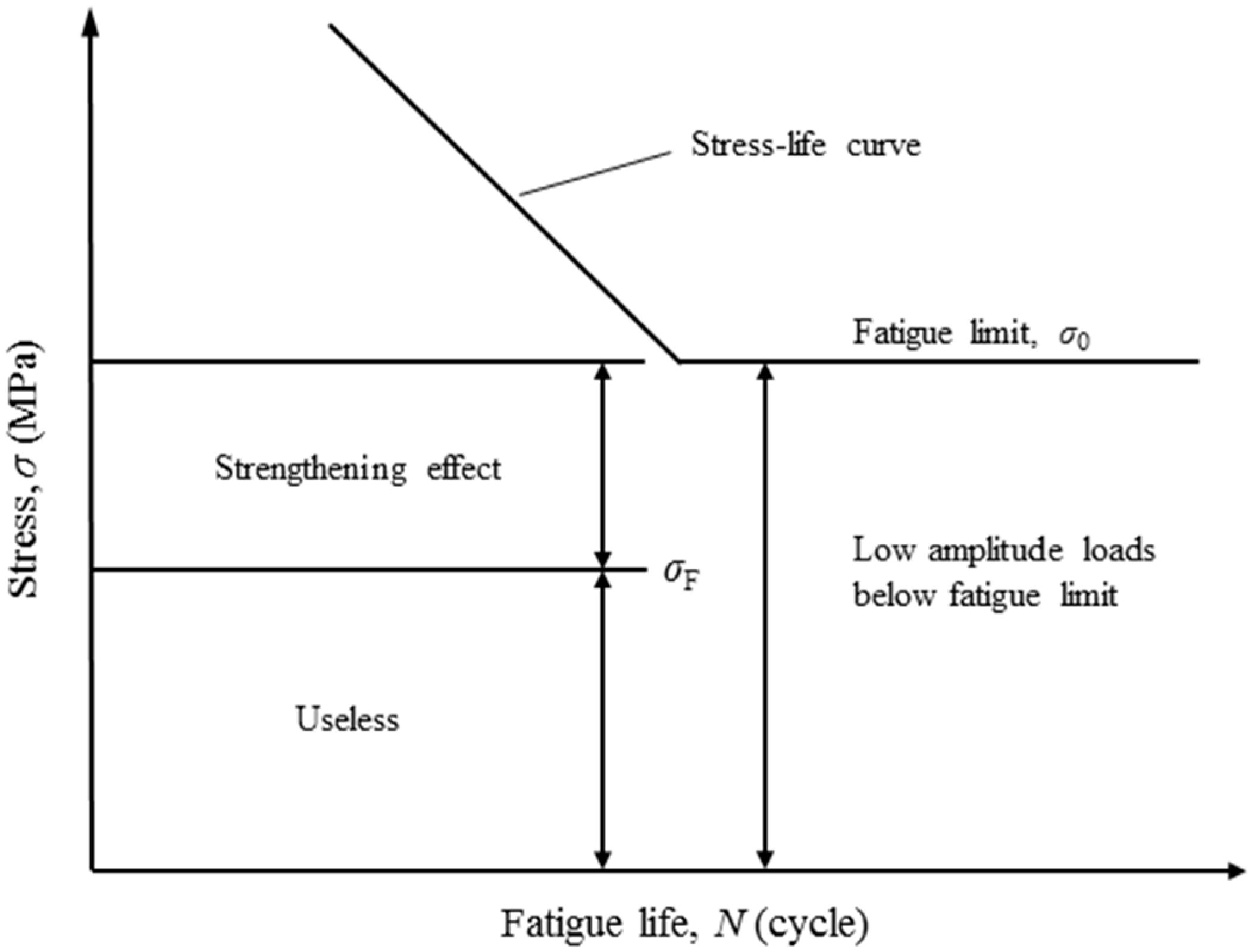
2.2. Effect of Load Below Fatigue Limit
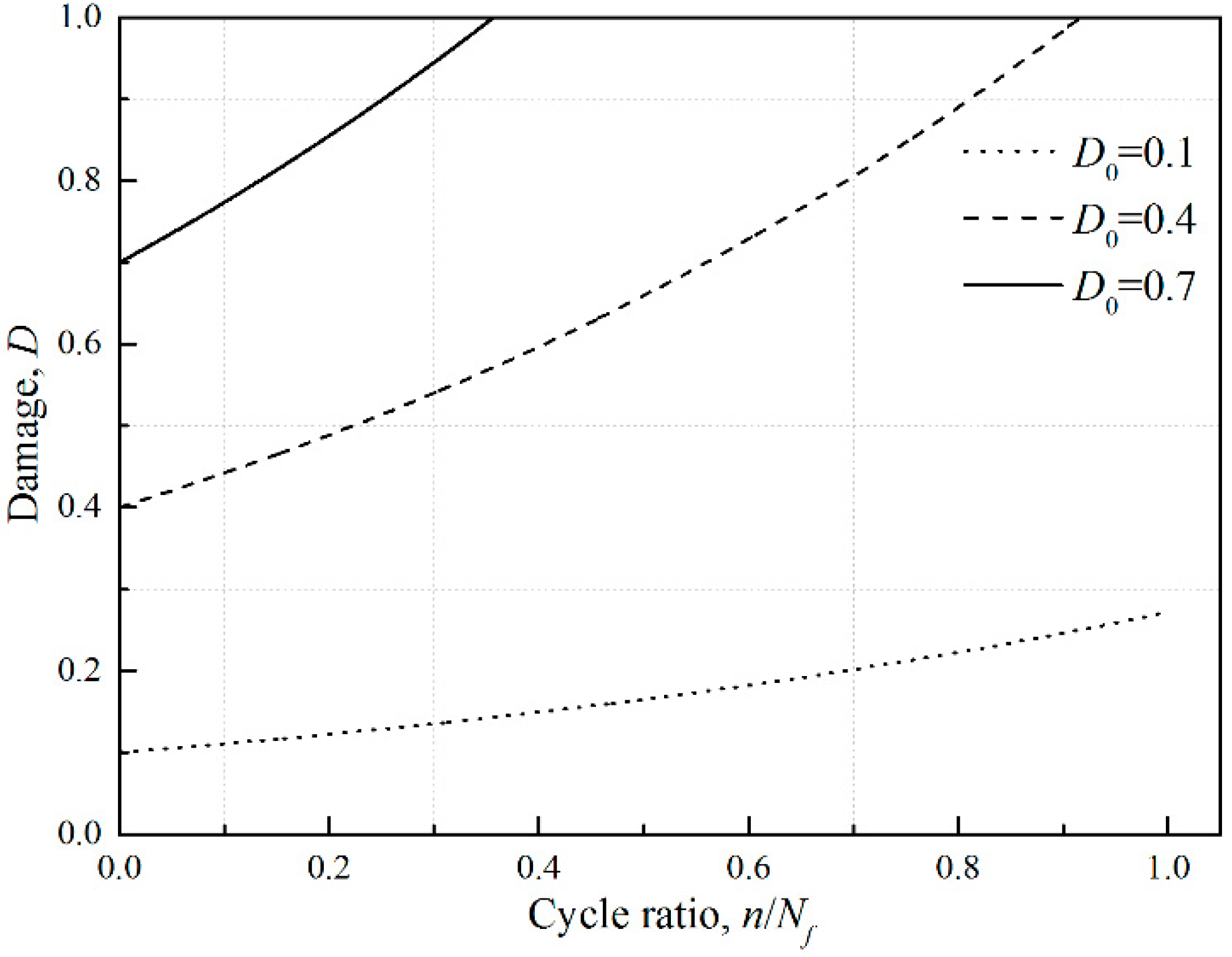
2.3. Proposed Model
3. Model Verification and Discussion
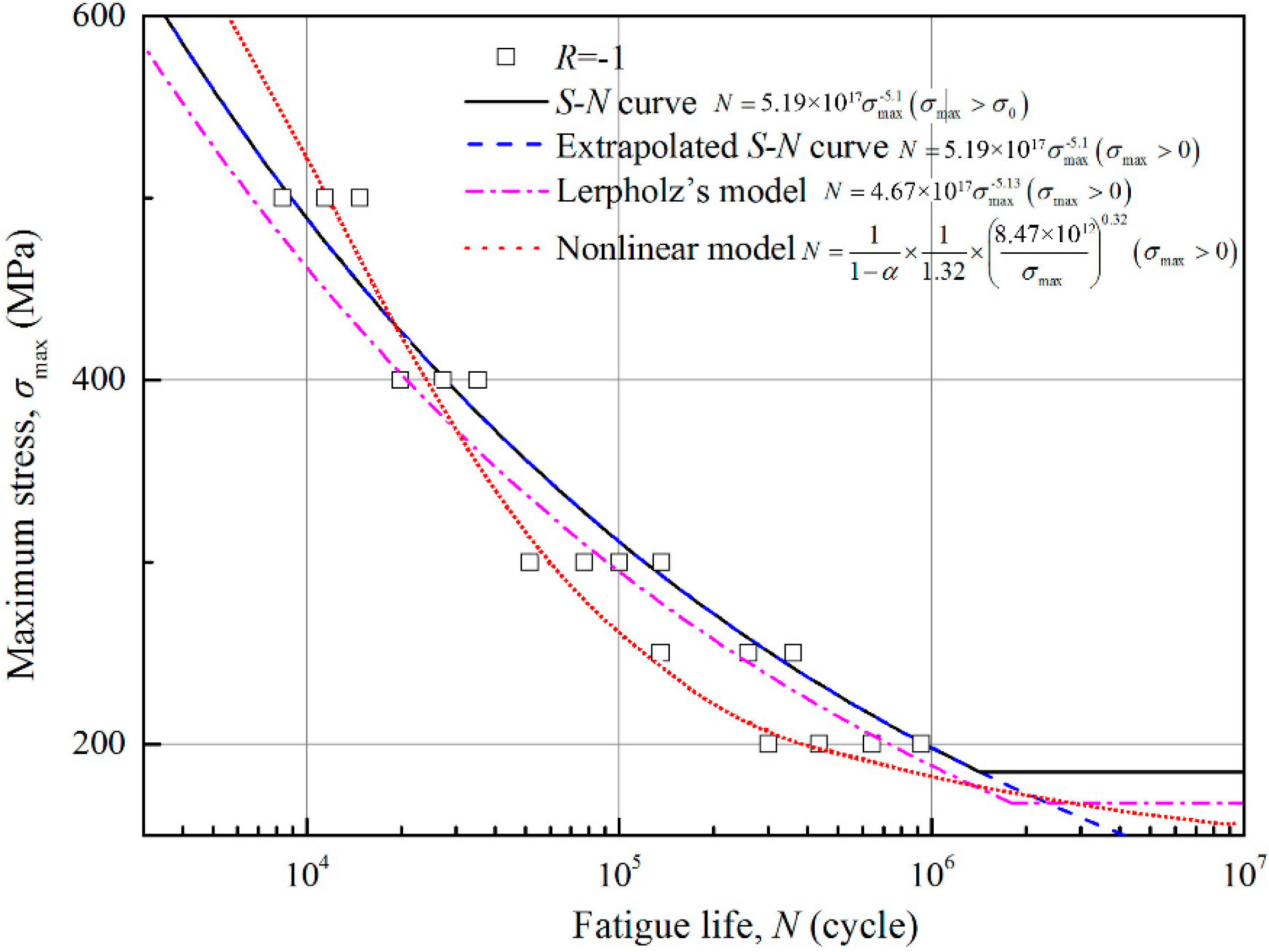
3.1. Model Verification
3.2. Discussion
4. Life Prediction of a Compressor Blade
4.1. Blade Model
4.2. Numerical Simulation
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| D | fatigue damage |
| Di | cumulative damage at the ith loading cycle |
| D0 | initial damage |
| Dc | critical damage |
| m′ | strengthening coefficient |
| N | loading cycles |
| ni | loading cycles of the ith-level load |
| Nf | fatigue life |
| Ni* | equivalent fatigue life subjected to the ith-level load |
| Yi | cyclic ratio |
| membership function | |
| Σ | stress |
| σi | stress of the ith-level load |
| σa | stress amplitude |
| σF | lower limit of strengthening stress |
| σm | mean stress |
| σmax | maximum stress |
| σmin | minimum stress |
| σ0 | fatigue limit |
| b0, M0, α, β | material parameters |
| k, α′, β′, σc | membership function parameters |
References
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art. Homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative fatigue damage. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar]
- Marco, S.M.; Starkey, W.L. A concept of fatigue damage. Trans. ASME 1954, 76, 627–632. [Google Scholar]
- Corten, H.T.; Dolan, T.J. Cumulative fatigue damage. In Proceedings of the International Conference on Fatigue of Metals, London, UK, 10–14 September 1956; Institution of Mechanical Engineering and American Society of Mechanical Engineers: London, UK, 1956; p. 235. [Google Scholar]
- Manson, S.S. Interfaces between fatigue, creep, and fracture. Int. J. Fract. Mech. 1966, 2, 327. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical implementation of the double linear damage rule and damage curve approach for treating cumulative fatigue damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Benkabouche, S.; Guechichi, H.; Amrouche, A.; Benkhettab, M. A modified nonlinear fatigue damage accumulation model under multiaxial variable amplitude loading. Int. J. Mech. Sci. 2015, 100, 180–194. [Google Scholar] [CrossRef]
- Peng, Z.; Huang, H.Z.; Zhou, J.; Li, Y.F. A New Cumulative fatigue damage rule based on dynamic residual S–N curve and material memory concept. Metals 2018, 8, 456. [Google Scholar] [CrossRef]
- Franke, L.; Dierkes, G. A non-linear fatigue damage rule with an exponent based on a crack growth boundary condition. Int. J. Fatigue 1999, 21, 761–767. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An Irreversible Thermodynamic Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–224. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. A model of mechanothermodynamic entropy in tribology. Entropy 2017, 19, 115. [Google Scholar] [CrossRef]
- Diel, S.; Huber, O. A continuum damage mechanics model for the static and cyclic fatigue of cellular composites. Materials 2017, 10, 951. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Plumtree, A. A fatigue damage accumulation model based on continuum damage mechanics and ductility exhaustion. Int. J. Fatigue 1998, 20, 495–501. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Nobile, R. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model. Int. J. Fatigue 2006, 28, 89–95. [Google Scholar] [CrossRef]
- Hosoi, A.; Kawada, H.; Yoshino, H. Fatigue characteristics of quasi-isotropic CFRP laminates subjected to variable amplitude cyclic two-stage loading. Int. J. Fatigue 2006, 28, 1284–1289. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, S.; Lin, J. A nonlinear continuous damage model based on short-crack concept under variable amplitude loading. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 79–94. [Google Scholar] [CrossRef]
- Albedah, A.; Khan, S.M.A.; Benyahia, F.; Bouiadjra, B.B. Effect of load amplitude change on the fatigue life of cracked Al plate repaired with composite patch. Int. J. Fatigue 2016, 88, 1–9. [Google Scholar] [CrossRef]
- Peng, Z.; Huang, H.Z.; Zhu, S.P.; Gao, H. A fatigue driving energy approach to high-cycle fatigue life estimation under variable amplitude loading. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 180–193. [Google Scholar] [CrossRef]
- Sinclair, G.M. An investigation of the coaxing effect in fatigue of metals. In Proceedings of the American Society for Testing & Materials, New York, NY, USA, 26 June 1952; pp. 743–758. [Google Scholar]
- Nakagawa, T.; Ikai, Y. Strain ageing and the fatigue limit in carbon steel. Fatigue Fract. Eng. Mater. Struct. 1979, 2, 13–21. [Google Scholar] [CrossRef]
- Miller, K.J.; Mohamed, H.J.; De Los Rios, E.R. Fatigue damage accumulation above and below the fatigue limit. In The Behavior of Short Fatigue Cracks; Mechanical Engineering Publications: London, UK, 1986; pp. 491–511. [Google Scholar]
- Lu, X.; Zheng, S. Changes in mechanical properties of vehicle components after strengthening under low-amplitude loads below the fatigue limit. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 847–855. [Google Scholar]
- Lu, X.; Zheng, S. Strengthening and damaging under low-amplitude loads below the fatigue limit. Int. J. Fatigue 2009, 31, 341–345. [Google Scholar]
- Zhao, L.H.; Feng, J.Z.; Zheng, S.L. Effect of cyclic stresses below the endurance limit on the fatigue life of 40Cr steel. Strength Mater. 2018, 50, 1–9. [Google Scholar] [CrossRef]
- Saki, T. Review and prospects for current studies on very high cycle fatigue of metallic materials for machine structure use. In Proceedings of the 4th International Conference on Very High Cycle Fatigue (VHCF-4), Ann Arbor, MI, USA, 19–22 August 2007; TMS (The Minerals, Metals and Materials Society): Pittsburgh, PA, USA, 2007; pp. 3–12. [Google Scholar]
- Zhu, S.P.; Huang, H.Z.; Wang, Z.L. Fatigue life estimation considering damaging and strengthening of low-amplitude loads under different load sequences using fuzzy sets approach. Int. J. Damage Mech. 2011, 20, 876–899. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Lesne, P.M. A non-linear continuous fatigue damage model. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 1–17. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Kędziora, P.; Romanowicz, P.; Muc, A. Fuzzy sets—Fatigue tests. Compos. Theor. Pract. 2016, 16, 90–95. [Google Scholar]
- Muc, A. A fuzzy set approach to interlaminar cracks simulation problem. Int. J. Fatigue 2002, 24, 419–427. [Google Scholar] [CrossRef]
- Monsalve, A.; Paez, M.; Toledano, M.; Artigas, A.; Sepúlveda, Y.; Valencia, Y.N. S–N–P curves in 7075 T7351 and 2024 T3 aluminium alloys subjected to surface treatments. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 748–758. [Google Scholar] [CrossRef]
- Nakajima, M.; Jung, J.W.; Uematsu, Y. Coaxing effect in stainless steels and high-strength steels. Key Eng. Mat. 2007, 345, 235–238. [Google Scholar] [CrossRef]
- Dombi, J. Membership function as an evaluation. Fuzzy Set. Syst. 1990, 35, 1–21. [Google Scholar] [CrossRef]
- Huang, H.Z. Calculation of fuzzy reliability in the case of random stress and fuzzy fatigue strength. Chin. J. Mech. Eng. 2000, 13, 197–200. [Google Scholar] [CrossRef]
- Liu, K.G.; Yan, C.L.; Zhang, S.M. Fatigue life estimation for using fuzzy mathematics. Acta Aeronaut Astronaut Sin. 2006, 27, 227–231. [Google Scholar]
- Pieczyński, A.; Obuchowicz, A. Application of the general Gaussian membership function for the fuzzy model parameters tunning. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 7–11 June 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 350–355. [Google Scholar]
- Ghosh, M.; Das, D.; Chakraborty, C.; Ray, A.K. Automated leukocyte recognition using fuzzy divergence. Micron 2010, 41, 840–846. [Google Scholar] [CrossRef] [PubMed]
- Schijve, J. Fatigue of Structures and Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Leipholz, H.H.E. Lifetime prediction for metallic specimens subjected to loading with varying intensity. Comput. Struct. 1985, 20, 239–246. [Google Scholar] [CrossRef]
- Leipholz, H.H.E. On the modified S–N curve for metal fatigue prediction and its experimental verification. Eng. Fract. Mech. 1986, 23, 495–505. [Google Scholar] [CrossRef]
- Leipholz, H.H.E.; Topper, T.; El Menoufy, M. Lifetime prediction for metallic components subjected to stochastic loading. Comput. Struct. 1983, 16, 499507. [Google Scholar] [CrossRef]
- Zhao, L.H.; Zheng, S.L.; Feng, J.Z.; Zhou, H.F.; Xing, Y.F. Fatigue assessment of rear axle under service loading histories considering the strengthening and damaging effects of loads below fatigue limit. Int. J. Automot. Technol. 2014, 15, 843–852. [Google Scholar] [CrossRef]
- Zhao, L.H.; Zheng, S.; Feng, J. Fatigue life prediction under service load considering strengthening effect of loads below fatigue limit. Chin. J. Mech. Eng. 2014, 27, 1178–1185. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, J.; Lin, J. Study on the fatigue life and damage accumulation of a compressor blade based on a modified nonlinear damage model. Fatigue Fract. Eng. Mater. Struct. 2017, 41, 1077–1088. [Google Scholar] [CrossRef]
- Kou, H.J.; Lin, J.; Zhang, J.; Fu, X. Dynamic and fatigue compressor blade characteristics during fluid-structure interaction: Part I-Blade modelling and vibration analysis. Eng. Fail. Anal. 2017, 76, 80–98. [Google Scholar] [CrossRef]


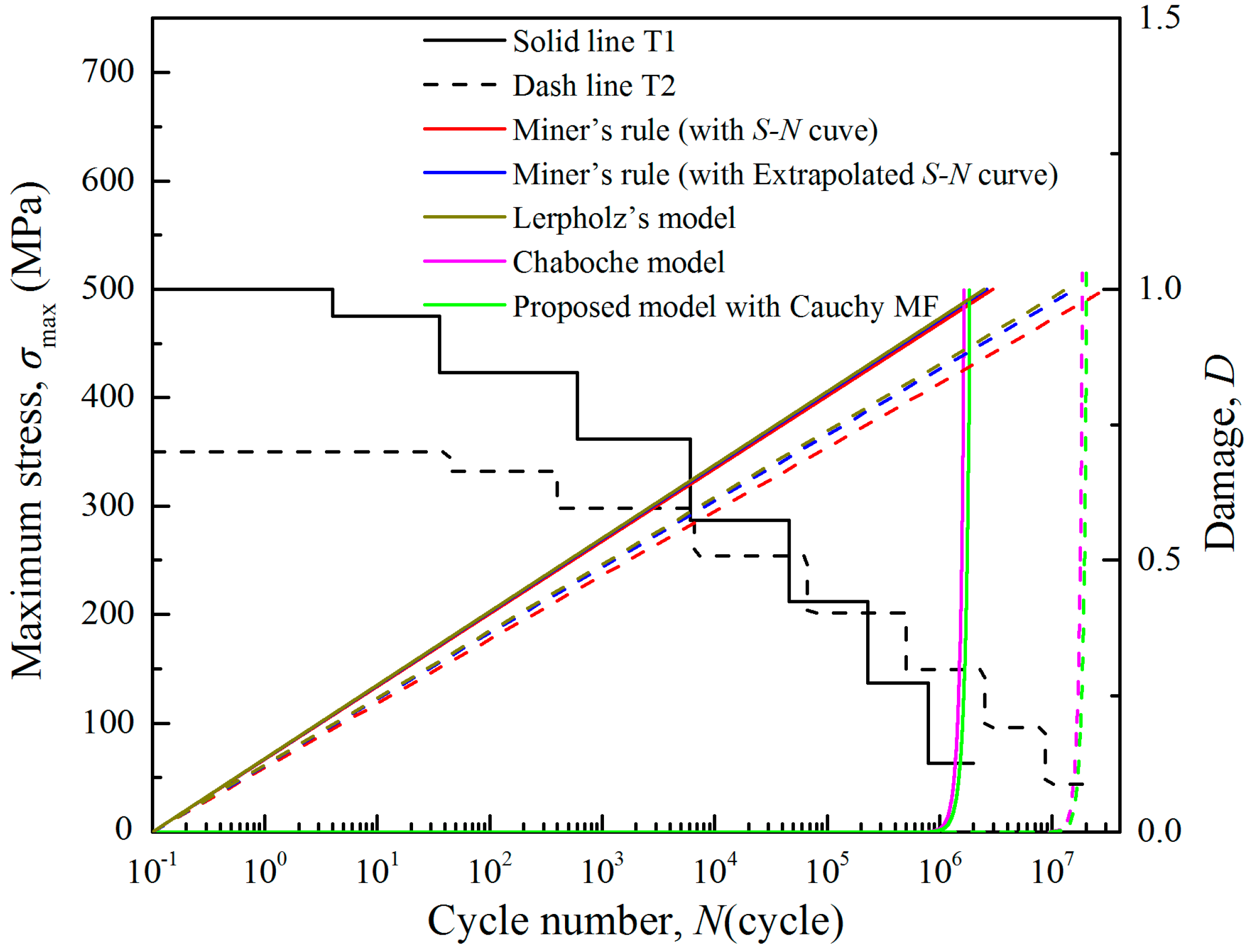
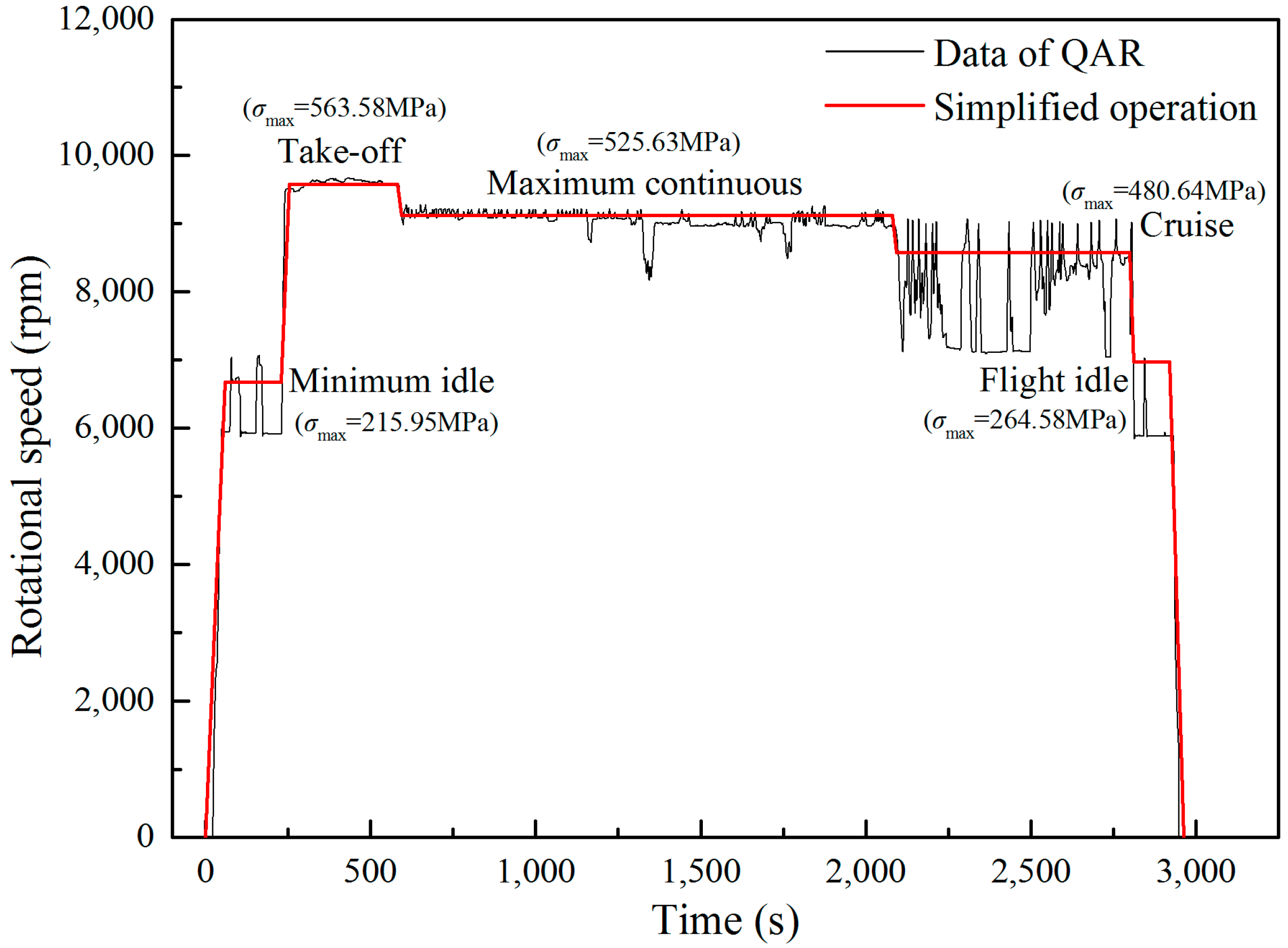
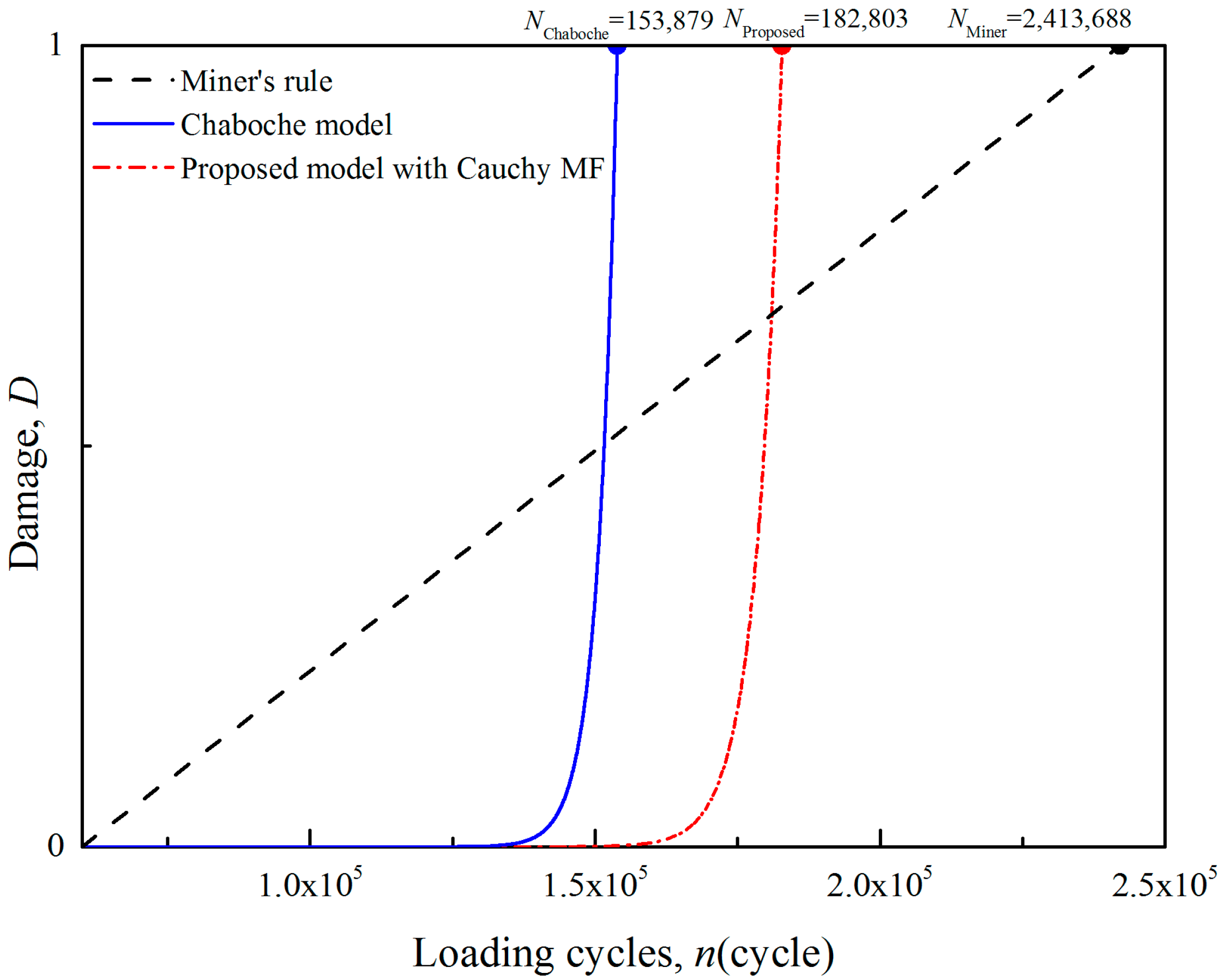
| T1 | T2 | ||||
|---|---|---|---|---|---|
| Loading Level | σi (MPa) | ni (Cycle) | Loading Level | σi (MPa) | ni (cycle) |
| 1 | 500 | 4 | 1 | 350 | 44 |
| 2 | 475 | 32 | 2 | 332 | 352 |
| 3 | 423 | 560 | 3 | 298 | 6160 |
| 4 | 362 | 5440 | 4 | 254 | 59,840 |
| 5 | 287 | 40,000 | 5 | 201 | 440,000 |
| 6 | 212 | 184,000 | 6 | 149 | 2,024,000 |
| 7 | 137 | 560,000 | 7 | 96 | 6,160,000 |
| 8 | 63 | 1,210,000 | 8 | 44 | 13,310,000 |
| Method | T1 | T2 | ||
|---|---|---|---|---|
| Fatigue Life (Cycle) | Relative Error (%) | Fatigue Life (Cycle) | Relative Error (%) | |
| Test | 2,000,036 | - | 22,000,396 | - |
| Wöhler model (S–N curve) | 2,980,258 | 49.01 | 29,739,204 | 35.18 |
| Wöhler model (extrapolated S–N curve) | 2,632,432 | 31.62 | 16,045,967 | 27.07 |
| Leipholz’s model | 2,575,804 | 28.79 | 14,309,047 | 34.96 |
| Chaboche model | 1,639,758 | 18.02 | 18,460,752 | 16.09 |
| Modified model (Trapezoidal MF) | 2,247,234 | 12.35 | 24,601,638 | 11.82 |
| Modified model (Quadratic parabola MF) | 2,320,038 | 15.99 | 25,115,005 | 14.16 |
| Modified model (Cubic parabola MF) | 2,387,111 | 19.35 | 26,078,819 | 18.54 |
| Modified model (Square root MF) | 2,208,623 | 10.43 | 24,161,781 | 9.83 |
| Modified model (Normal MF) | 1,819,343 | 9.03 | 20,027,736 | 8.97 |
| Modified model (Γ MF) | 2,185,874 | 9.29 | 24,115,718 | 9.61 |
| Modified model (Cauchy MF) | 1,842,027 | 7.96 | 20,156,752 | 8.38 |
| Method | 40Cr Half Shaft | TL1114 Rear Axle | ||
|---|---|---|---|---|
| Fatigue Life (Load Blocks) | Relative Error (%) | Fatigue Life (Load Blocks) | Relative Error (%) | |
| Test | 1158 | - | 490 | - |
| Chaboche model | 909 | 21.5 | 417 | 14.9 |
| Modified model (Cauchy MF) | 1129 | 2.5 | 510 | 4.08 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Fu, X.; Lin, J.; Liu, Z.; Liu, N.; Wu, B. Study on Damage Accumulation and Life Prediction with Loads below Fatigue Limit Based on a Modified Nonlinear Model. Materials 2018, 11, 2298. https://doi.org/10.3390/ma11112298
Zhang J, Fu X, Lin J, Liu Z, Liu N, Wu B. Study on Damage Accumulation and Life Prediction with Loads below Fatigue Limit Based on a Modified Nonlinear Model. Materials. 2018; 11(11):2298. https://doi.org/10.3390/ma11112298
Chicago/Turabian StyleZhang, Junhong, Xi Fu, Jiewei Lin, Zhiyuan Liu, Nuohao Liu, and Bin Wu. 2018. "Study on Damage Accumulation and Life Prediction with Loads below Fatigue Limit Based on a Modified Nonlinear Model" Materials 11, no. 11: 2298. https://doi.org/10.3390/ma11112298
APA StyleZhang, J., Fu, X., Lin, J., Liu, Z., Liu, N., & Wu, B. (2018). Study on Damage Accumulation and Life Prediction with Loads below Fatigue Limit Based on a Modified Nonlinear Model. Materials, 11(11), 2298. https://doi.org/10.3390/ma11112298






