Model Establishment of a Co-Based Metal Matrix with Additives of WC and Ni by Discrete Element Method
Abstract
:1. Introduction
2. Metal Matrix Discrete Element Method (DEM) Model Establishment and Calibration
2.1. Metal Matrix
2.2. Bonds in the Metal Matrix Model
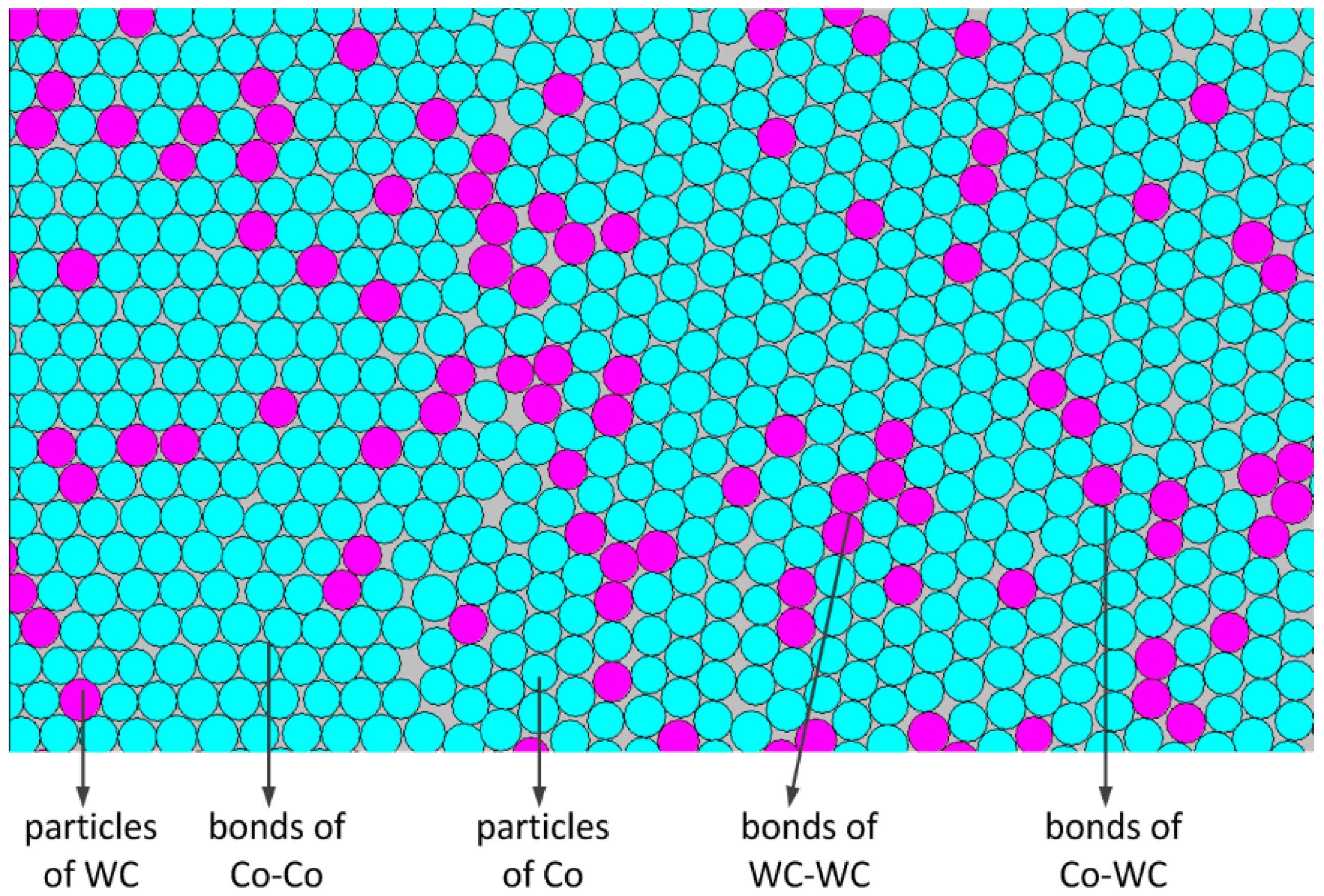
- In the DEM model of the CoX matrix, which is without any additives, the bonded pair is only the Co–Co pair. The bond boundary of Co‒Co includes Co–Co bond1 and Co–Co bond2, which are a parallel bond and contact bond, respectively, as shown in Figure 4.
- In the DEM model of CoX–WC, the addition of WC particles introduces two new bonded pairs: WC–WC and Co–WC.
- In the DEM model of CoX–Ni, the addition of Ni particles introduces two new bonded pairs: Ni–Ni and Co–Ni.
- In the DEM model of CoX–WC–Ni, the simultaneous addition of WC and Ni introduces a new bonded pair: Ni–WC.
2.3. Microcosmic Parameters
2.3.1. Inversion Method for Microcosmic Parameters
2.3.2. Calibration of Microcosmic Parameters for CoX–WC–Ni
3. Experimental Setup
3.1. Metal Matrix Composition
3.2. Fabrication of Metal Matrix
3.3. Three-Point Bending Test and Compression Test
4. Calibration Results
5. Validation and Discussion
6. Concluding Remarks
- When building the DEM model of the diamond metal matrix, skeletal substances in the matrix are treated as particles in the model and bonding substances can be represented as parallel bonds between particles.
- Besides the parallel bond, the contact bond should be considered during the construction of the DEM model of the diamond segment matrix because of its elasticity.
- The step-by-step calibration of microcosmic parameters is effective for the DEM model of metal matrix with multiple additives.
- The constructed CoX–WC–Ni DEM model exhibited a satisfactory ability to predict TRS, and the error rate is less than 10%. It will be useful for the design of a metal matrix.
Author Contributions
Funding
Conflicts of Interest
References
- Oliveira, L.J.; Bobrovnitchii, G.S.; Filgueira, M. Processing and characterization of impregnated diamond cutting tools using a ferrous metal matrix. Int. J. Refract. Met. Hard Mater. 2007, 25, 328–335. [Google Scholar] [CrossRef]
- Dhokey, N.B.; Utpat, K.; Gosavi, A.; Dhoka, P. Hot–press sintering temperature response of diamond cutting tools and its correlation with wear mechanism. Int. J. Refract. Met. Hard Mater. 2013, 36, 289–293. [Google Scholar] [CrossRef]
- Naidich, Y.V.; Umankii, V.P.; Lavrinenko, I.A. Metal and alloy bond strengths to diamond. Ind. Diam. Rev. 1984, 6, 84–89. [Google Scholar]
- Steven, W.W. Diamond retention in sintered cobalt bonds for stone cutting and drilling. Diam. Relat. Mater. 1999, 8, 2043–2052. [Google Scholar]
- Wang, Q. Diamond Tools by Sintering; Standard Press of China: Beijing, China, 2000. [Google Scholar]
- Xu, X.P.; Tie, X.R.; Wu, H.R. The effects of a Ti coating on the performance of metal–bonded diamond composites containing rare earth. Int. J. Refract. Met. Hard Mater. 2007, 25, 289–293. [Google Scholar] [CrossRef]
- Duan, N.; Yu, Y.; Wang, W.; Xu, X. SPH and FE coupled 3D simulation of monocrystal SiC scratching by single diamond grit. Int. J. Refract. Met. Hard Mater. 2017, 64, 279–393. [Google Scholar] [CrossRef]
- Borowiecka, J.J.; Lachowski, J. Modelling of retention of a diamond particle in matrices based on Fe and Cu. Proc. Eng. 2017, 177, 289–296. [Google Scholar] [CrossRef]
- Xu, J.Y.; Sheikh, A.H.; Xu, C.S. 3D Finite element modelling of diamond pull–out failure in impregnated diamond bits. Diam. Relat. Mater. 2017, 71, 1–12. [Google Scholar] [CrossRef]
- Li, Y. Mechanisms and Techniques for Deep Sawing of Granite; Working Paper; Machinery Manufacturing and Automation Institution, Huaqiao University: Quanzhou, China, 2004. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. Discrete numerical model for granular assemblies of solids. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Li, X.; Chu, X.; Feng, Y.T. A discrete particle model and numerical modeling of the failure modes of granular materials. Eng. Comput. 2005, 22, 894–920. [Google Scholar] [CrossRef]
- Zhao, D.; Nezami, E.G.; Hashash, Y.M.A.; Ghaboussi, J. Three-dimensional discrete element simulation for granular materials. Eng. Comput. 2006, 23, 749–770. [Google Scholar] [CrossRef]
- Rajeev, S. Discrete Element Modeling of Silicon Nitride Ceramics; Working Paper; Department of Industrial Engineering, The University of Texas: Austin, TX, USA, 2009. [Google Scholar]
- Liu, Y. Discrete-Element Methods for Asphalt Concrete Development and Application of User–Defined Microstructural Models and a Viscoelastic Micromechanical Model. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2011. [Google Scholar]
- Ostanin, I.; Ballarini, R.; Potyond, D.; Dumitrica, T. A distinct element method for large scale simulations of carbon nanotube assemblies. J. Mech. Phys. Solids 2013, 61, 762–782. [Google Scholar] [CrossRef]
- Ostanin, I.; Ballarini, R.; Dumitrica, T. Distinct element method modeling of carbon nanotube bundles with intertube sliding and dissipation. J. Appl. Mech. 2014, 81, 1–10. [Google Scholar] [CrossRef]
- Ostanin, I.; Ballarini, R.; Dumitrica, T. Distinct element method for multiscale modeling of cross-linked carbonnanotube bundles: From soft to strong nanomaterials. J. Mater. Res. 2015, 30, 19–25. [Google Scholar] [CrossRef]
- Chen, X.Y.; Huang, G.Q.; Tan, Y.Q.; Yu, Y.Q.; Guo, H.; Xu, X.P. Percent Reduction in Transverse Rupture Strength of Metal Matrix Diamond Segments Analysed via Discrete-Element Simulations. Materials 2018, 11, 1048. [Google Scholar] [CrossRef] [PubMed]
- Benvenuti, L.; Kloss, C.; Pirker, S. Identification of DEM simulation parameters by Artificial Neural Networks and bulk experiments. Powder Technol. 2016, 291, 456–465. [Google Scholar] [CrossRef]
- Chen, X.Y.; Yu, Y.Q.; Xu, X.P. A preliminary Study on DEM simulation of the Bending Strength of diamond Segments. Solid State Phenom. 2011, 175, 201–205. [Google Scholar] [CrossRef]
- Tillmann, W.; Gathen, M.; Vogli, E.; Kronholz, C. New materials and methods beckon for diamond tools. Met. Powder Rep. 2007, 62, 43–46. [Google Scholar] [CrossRef]
- Ismail, M.A.; Joer, H.A.; Randolph, M.F.; Meritt, A. Cementation of porous materials using calcite. Geotechnique 2002, 52, 313–324. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. Particle Flow Code in 2 Dimensions; Version 3.1; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 1998. [Google Scholar]
- Shi, C.; Xu, W.Y. Techniques and Practice for Numerical Simulation of Particle Flow; Beijing Construction Industry Press: Beijing, China, 2015. [Google Scholar]
- Grima, A.P.; Wypych, P.W. Discrete element simulations of granular pile formation: Method for calibrating discrete element models. Eng. Comput. 2011, 28, 314–339. [Google Scholar] [CrossRef]








| Percentage of WC | Number of WC Particles | WC–WC Bonds | WC–Co Bonds | ||
|---|---|---|---|---|---|
| Number | Proportion | Number | Proportion | ||
| 10% | 12,550 | 4959 | 1.9% | 60,956 | 24.6% |
| 5% | 6275 | 1241 | 0.5% | 32,929 | 13.3% |
| 3% | 3765 | 464 | 0.2% | 20,317 | 8.2% |
| Metal Matrix | Particles in the Model | Bonded Pairs between Particles |
|---|---|---|
| CoX | Co | Co–Co |
| CoX–WC | Co, WC | Co–Co, Co–WC, WC–WC |
| CoX–Ni | Co, Ni | Co–Co, Co–Ni, Ni–Ni |
| CoX–WC–Ni | Co, Ni, WC | Co–Co, Co–WC, WC–WC, Co–Ni, Ni–Ni, Ni–WC |
| Ingredient | Average Granularity (µm) | Purity (%) |
|---|---|---|
| Cobalt (Co) | 48 | 99.7 |
| Copper (Cu) | 48 | 99.5 |
| Tin (Sn) | 74 | 98.0 |
| Nickel (Ni) | 48 | 99.6 |
| Tungsten carbide (WC) | 48 | 99.9 |
| No. | Matrix | CoX (wt %) | WC (wt %) | Ni (wt %) |
|---|---|---|---|---|
| 1 | CoX100 | 100 | 0 | 0 |
| 2 | CoX97–WC3 | 97 | 3 | 0 |
| 3 | CoX95–WC5 | 95 | 5 | 0 |
| 4 | CoX90–WC10 | 90 | 10 | 0 |
| 5 | CoX97–Ni3 | 97 | 0 | 3 |
| 6 | CoX94–WC3–Ni3 | 94 | 3 | 3 |
| 7 | CoX90–WC5–Ni5 | 90 | 5 | 5 |
| 8 | CoX80–WC10–Ni10 | 80 | 10 | 10 |
| Particles | Particles | ||
|---|---|---|---|
| Co | WC | Ni | |
| ρ, Density of particles, g/cm3 | 8.90 | 15.63 | 8.88 |
| Ec, Elasticity modulus of particles, (Pa) | 1.3 × 1010 | 8 × 1011 | 9 × 109 |
| μ, Friction coefficient | 0.80 | 0.05 | 0.80 |
| Rmax/Rmin * | 1.13 | 1.13 | 1.13 |
| Bonds | Microcosmic Parameters | Type of Particle Bonds | |||||
|---|---|---|---|---|---|---|---|
| Co–Co | WC–WC | Co–WC | Ni–Ni | Co–Ni | Ni–WC | ||
| Contact bond | Normal strength (Pa) | 6 × 107 | 12 × 107 | 10 × 107 | 7 × 107 | 7.5 × 107 | 9.5 × 107 |
| Shear strength (Pa) | 6 × 107 | 12 × 107 | 10 × 107 | 7 × 107 | 7.5 × 107 | 9.5 × 107 | |
| Parallel bond | Elasticity modulus (Pa) | 1.3 × 109 | |||||
| Normal strength (Pa) | 3 × 108 | ||||||
| Shear strength (Pa) | 3 × 108 | ||||||
| Radius multiplier | 1 | ||||||
| The Content of WC | TRS | Ec | UCS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment (MPa) | Simulation (MPa) | Error (%) | Experiment (GPa) | Simulation (GPa) | Error (%) | Experiment (MPa) | Simulation (MPa) | Error (%) | |
| 3% | 1054 ± 85 | 1180 | 11.9 | 13.9 ± 0.9 | 15.3 | 10.1 | 1713 ± 82 | 1819 | 6.2 |
| 5% | 1015 ± 79 | 1144 | 12.7 | 13.7 ± 0.7 | 14.2 | 3.7 | 1751 ± 77 | 1893 | 8.2 |
| 10% | 967 ± 82 | 1038 | 7.3 | 13.4 ± 0.8 | 13.7 | 2.2 | 1825 ± 83 | 1965 | 7.7 |
| TRS | CoX90–(WC5–Ni5) | CoX80–(WC10–Ni10) |
|---|---|---|
| Simulation | 1110 MPa | 981 MPa |
| Experimental | 1035 MPa | 923 MPa |
| Error rate | 7.7% | 5.9% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Huang, G.; Tan, Y.; Huang, H.; Guo, H.; Xu, X. Model Establishment of a Co-Based Metal Matrix with Additives of WC and Ni by Discrete Element Method. Materials 2018, 11, 2319. https://doi.org/10.3390/ma11112319
Chen X, Huang G, Tan Y, Huang H, Guo H, Xu X. Model Establishment of a Co-Based Metal Matrix with Additives of WC and Ni by Discrete Element Method. Materials. 2018; 11(11):2319. https://doi.org/10.3390/ma11112319
Chicago/Turabian StyleChen, Xiuyu, Guoqin Huang, Yuanqiang Tan, Hui Huang, Hua Guo, and Xipeng Xu. 2018. "Model Establishment of a Co-Based Metal Matrix with Additives of WC and Ni by Discrete Element Method" Materials 11, no. 11: 2319. https://doi.org/10.3390/ma11112319
APA StyleChen, X., Huang, G., Tan, Y., Huang, H., Guo, H., & Xu, X. (2018). Model Establishment of a Co-Based Metal Matrix with Additives of WC and Ni by Discrete Element Method. Materials, 11(11), 2319. https://doi.org/10.3390/ma11112319






