Theoretical and Experimental Investigation of Surface Topography Generation in Slow Tool Servo Ultra-Precision Machining of Freeform Surfaces
Abstract
:1. Introduction
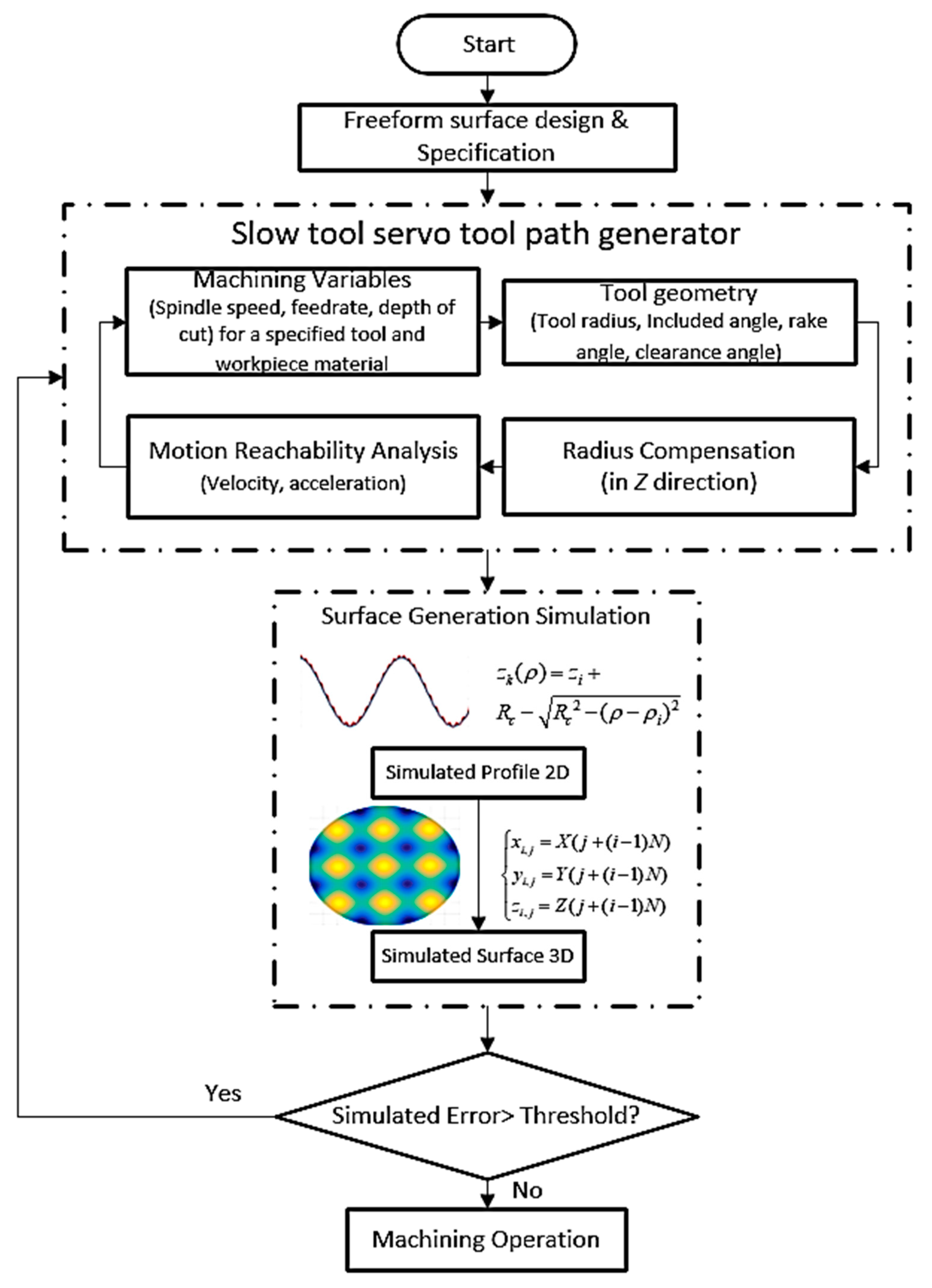
2. Tool Path Generation
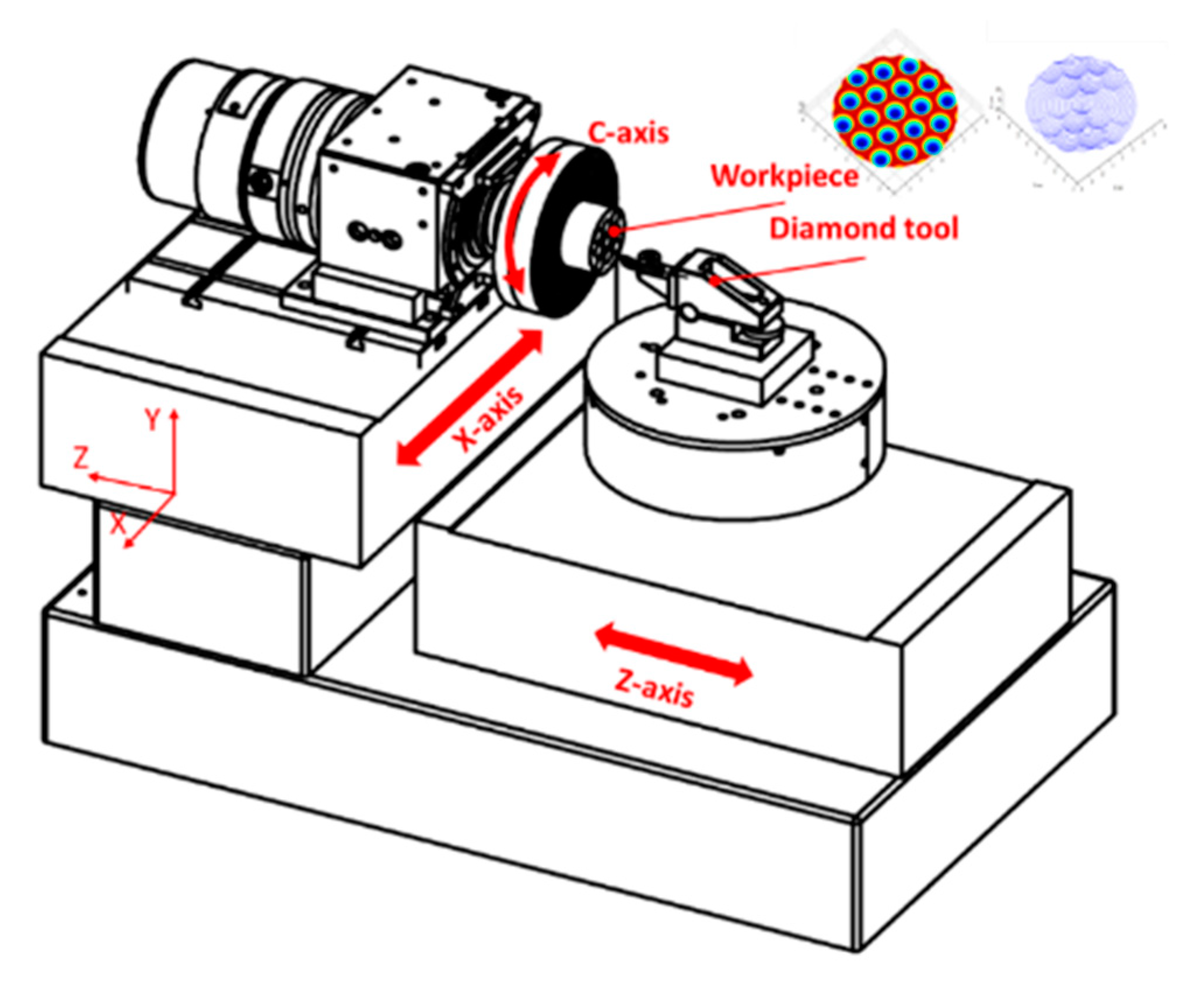
2.1. STS Machining Principle
2.2. Tool Geometry Selection
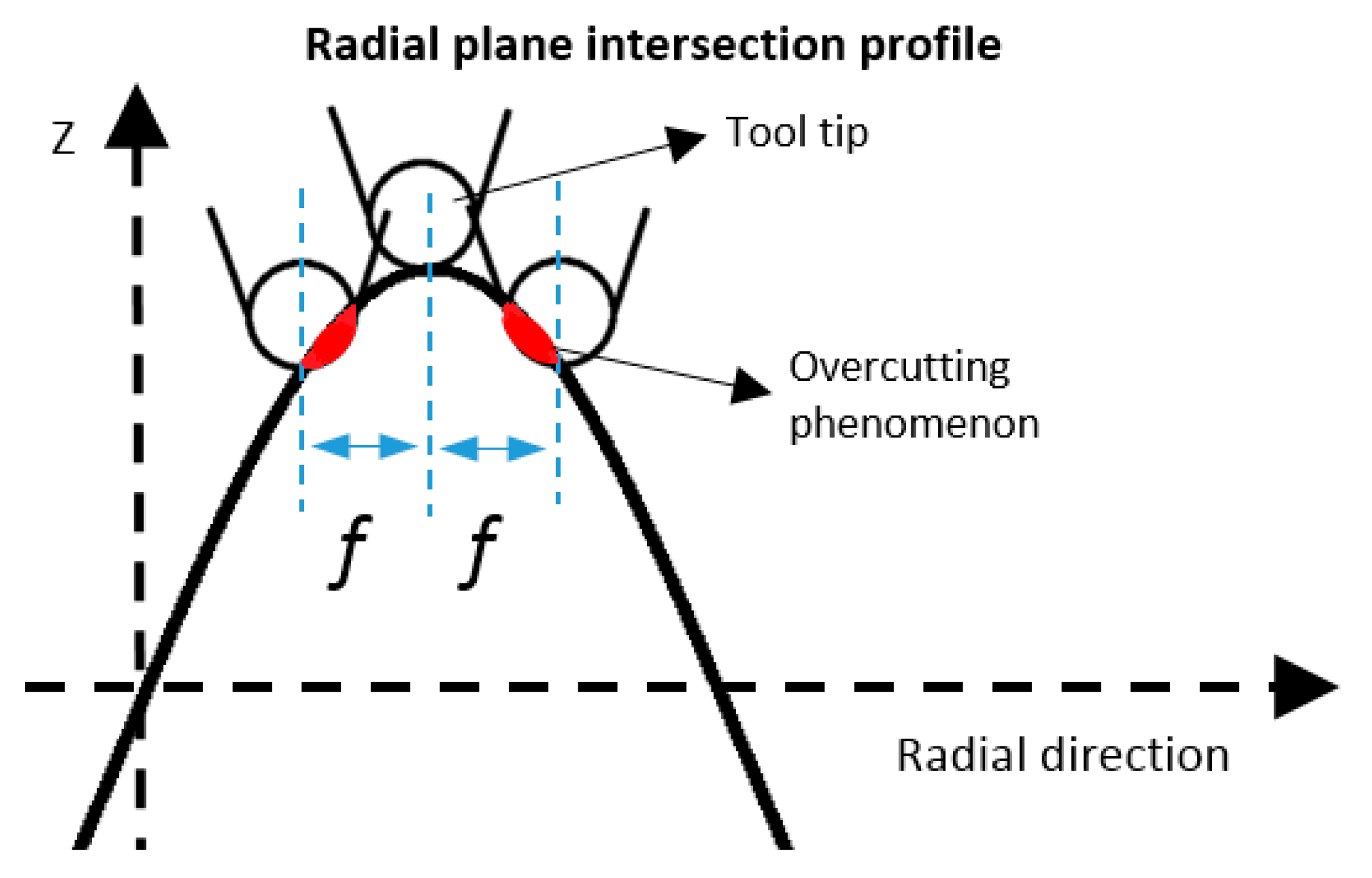
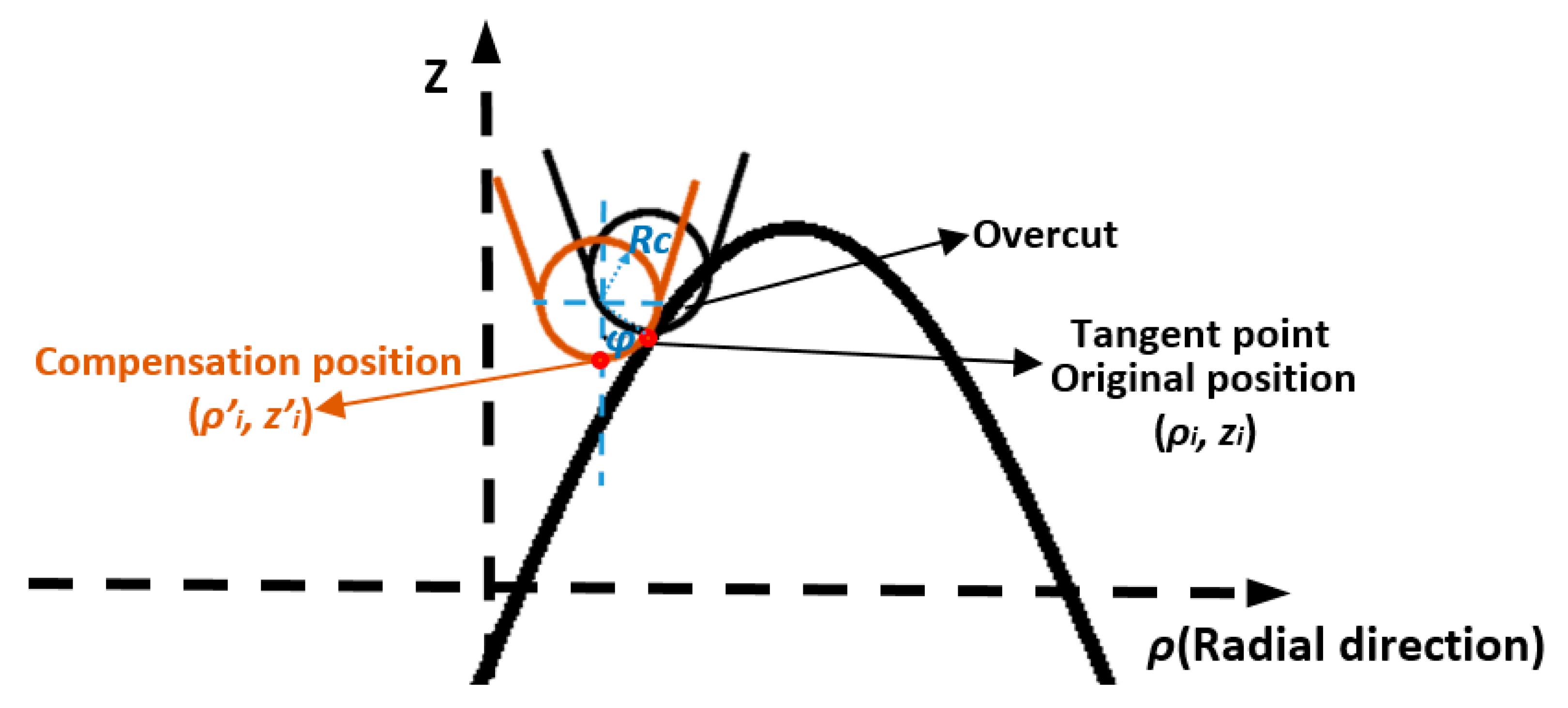
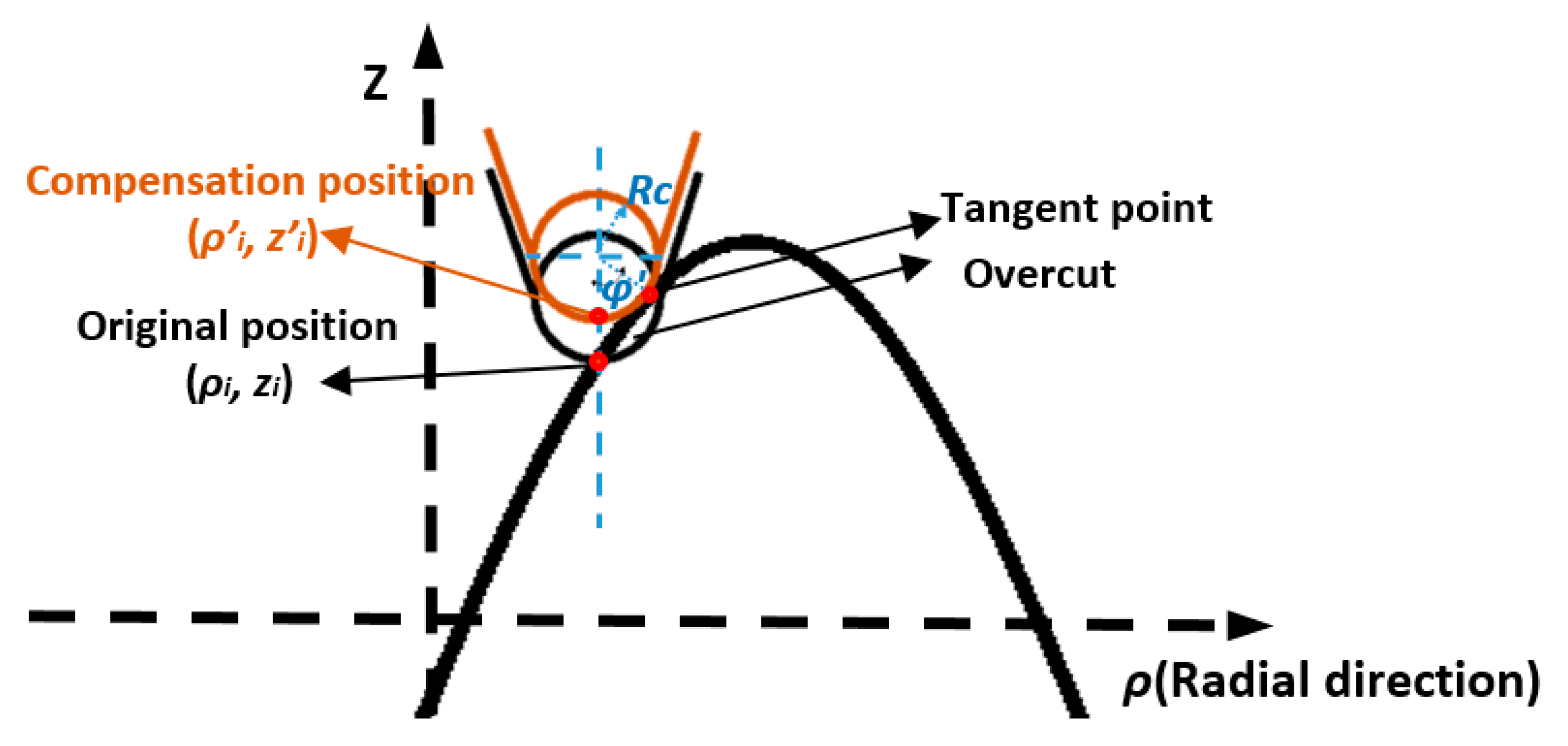
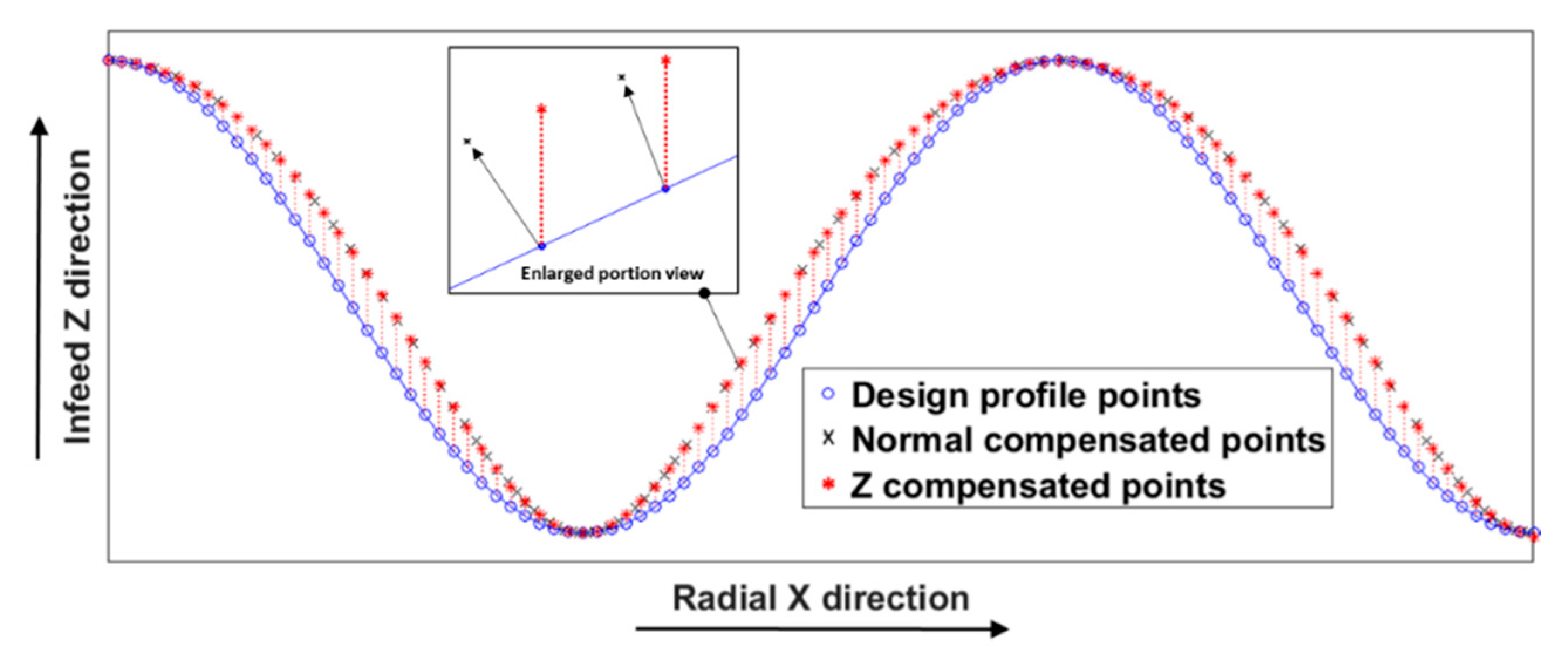
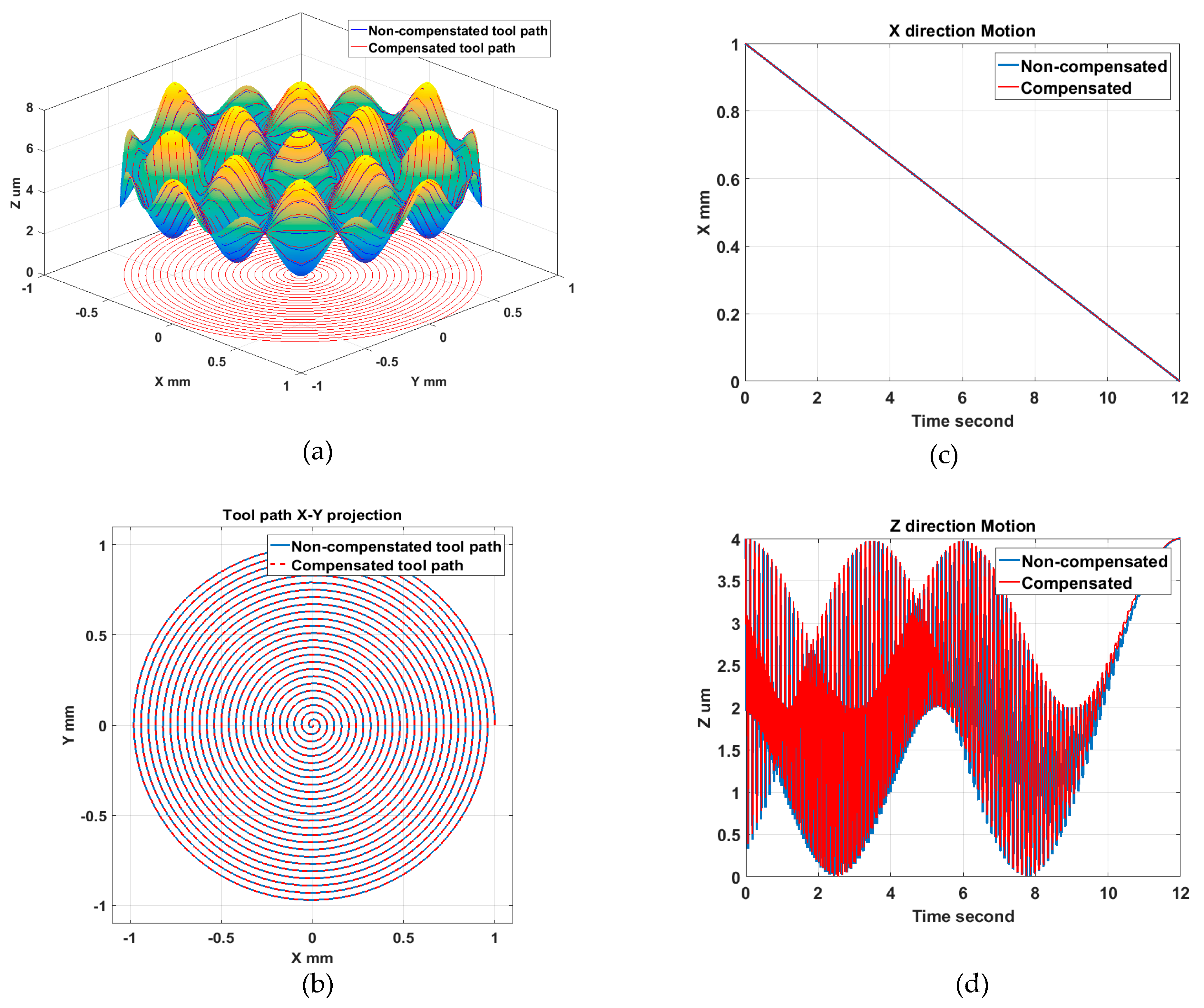
2.3. Tool Radius Compensation
3. Surface Generation Simulation and Analysis
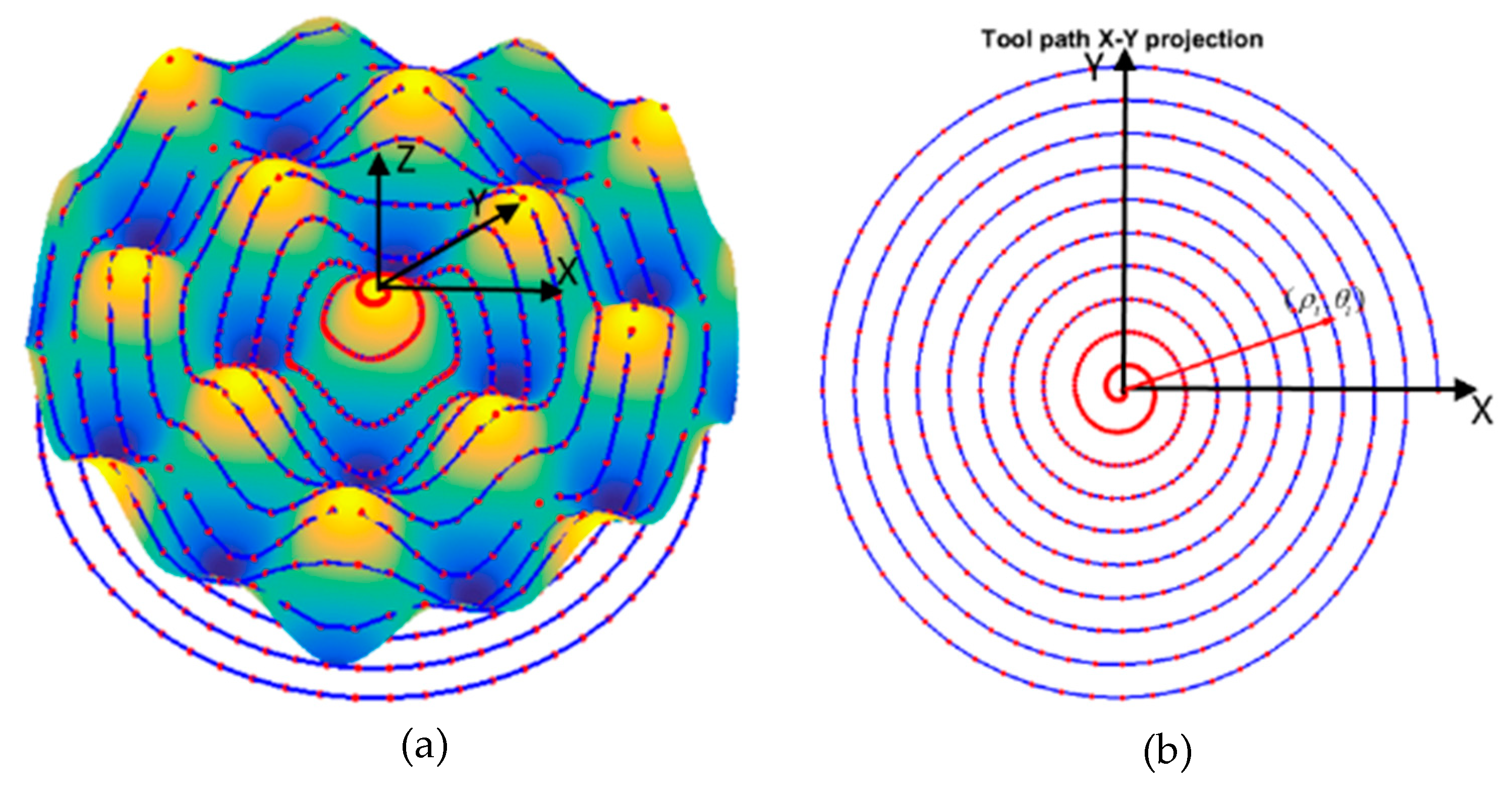
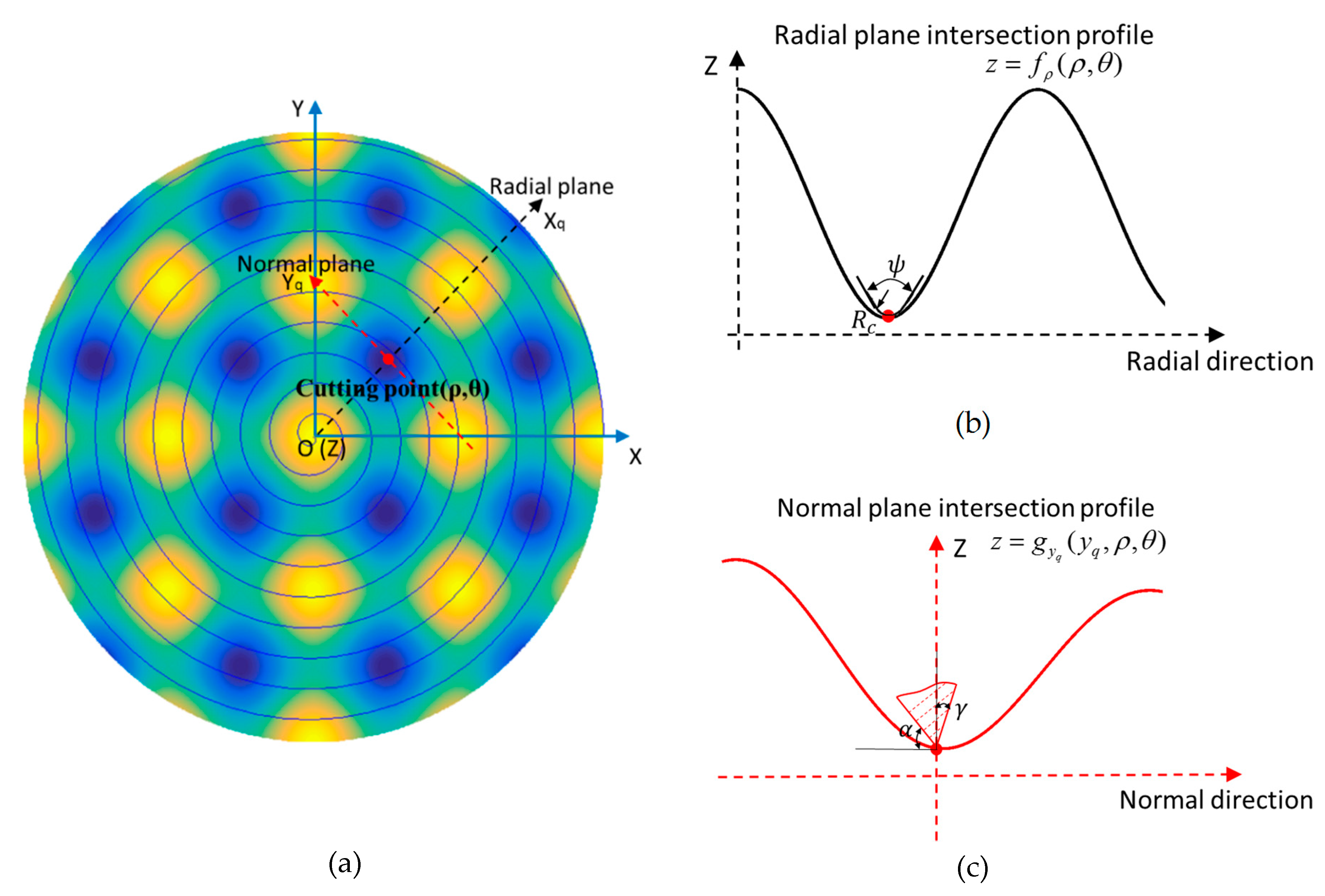
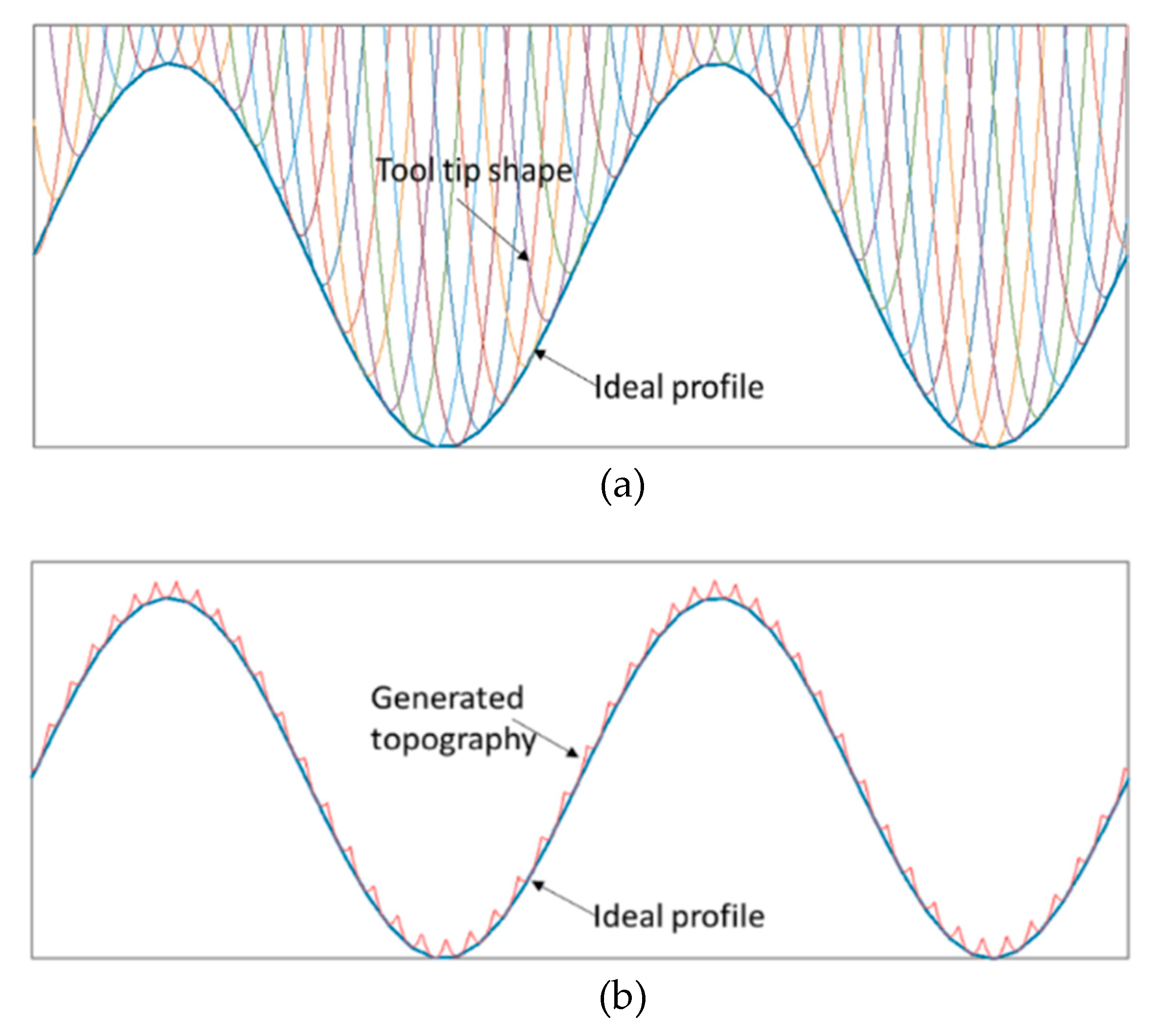
3.1. Principles
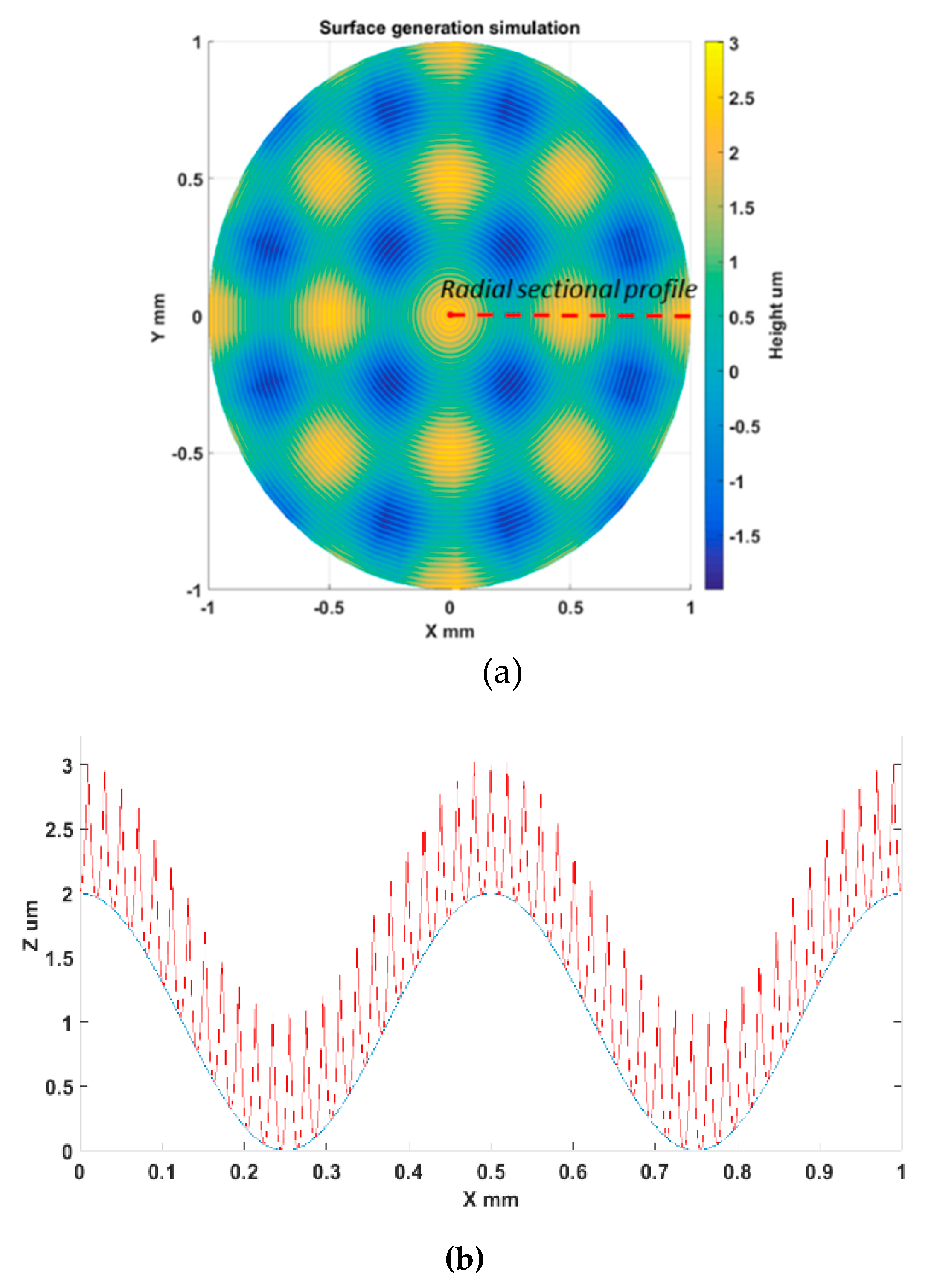
3.2. Simulation Analysis
4. Experiments and Discussion
4.1. Experimental Setup
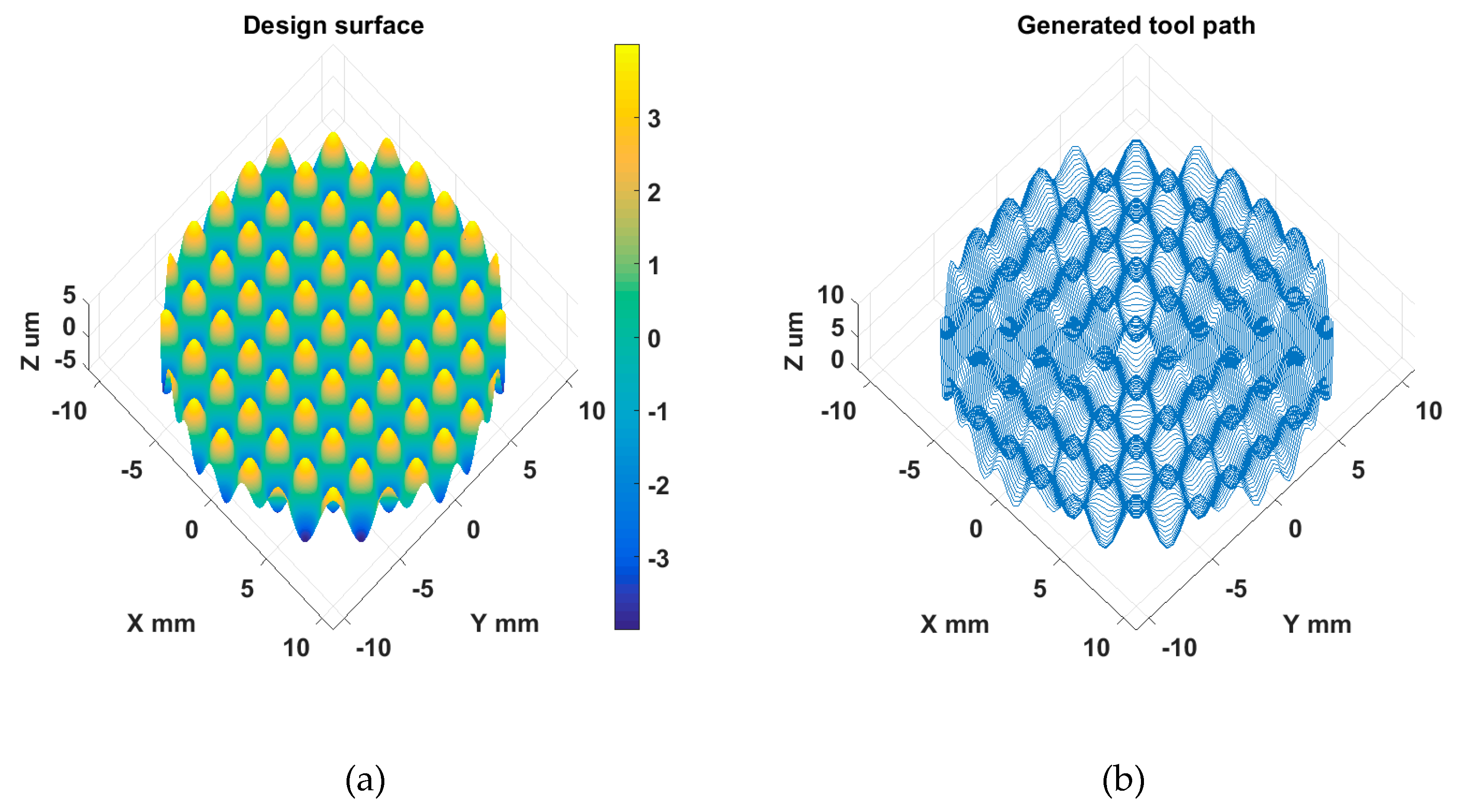
4.2. Sinusoidal Grid Surface Machining
4.3. MLA Surface Machining
5. Conclusions
- (1)
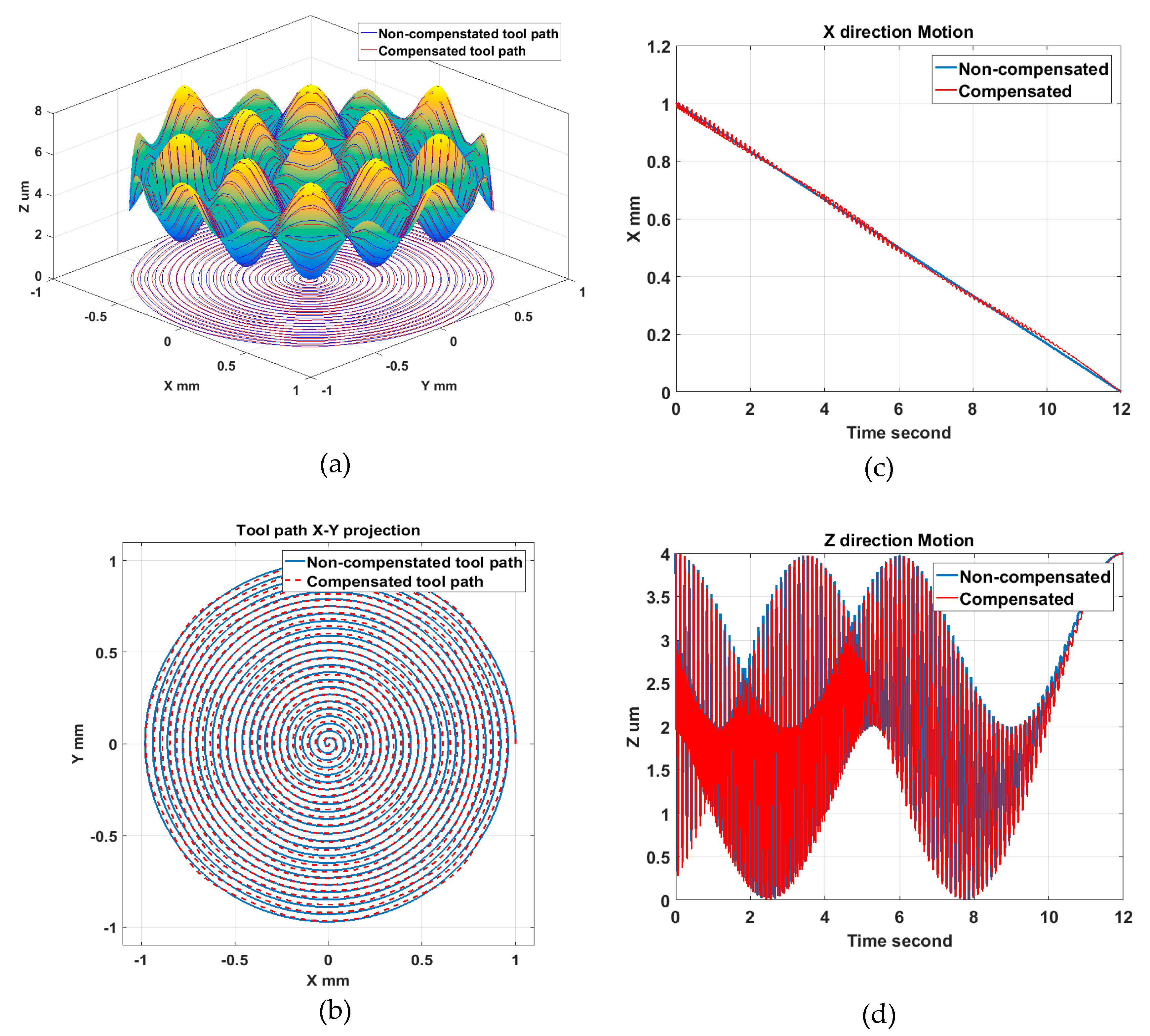
- To avoid the overcut of a rounded tool tip, tool radius compensation in the Z direction was performed to ensure no high frequency motion is imposed on the dynamic-limited X axis. Tool path motion analysis validated the Z direction compensation method and it was shown to be advantageous over conventional normal direction compensation methods.
- (2)
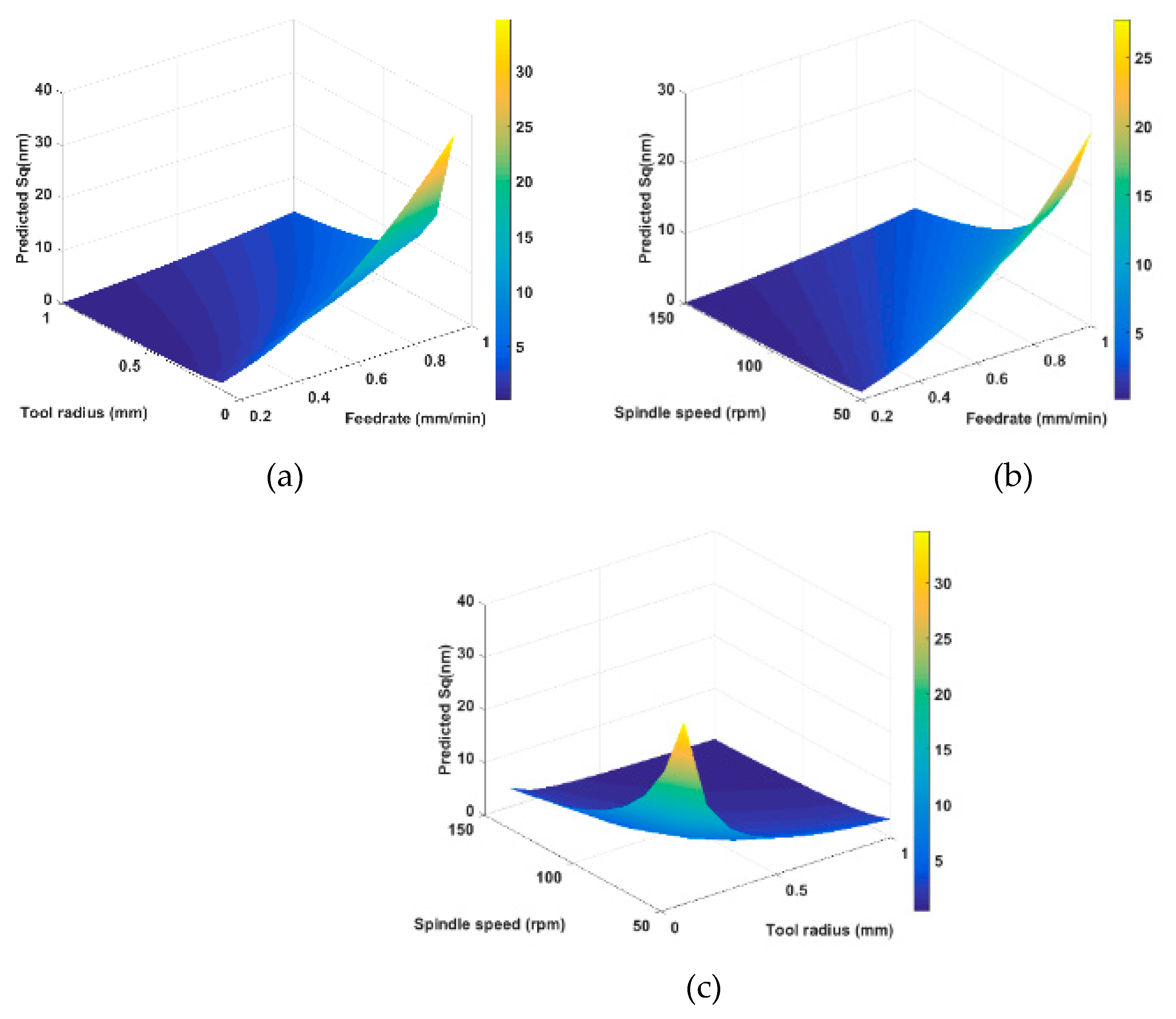
- The development of surface generation simulation allows prediction of the surface topography under various tool and machining variables. From the simulation results, it can be concluded that a better surface finish (lower Sq value) can be obtained under a higher spindle speed, a smaller feedrate and a larger tool radius. The simulation analysis also reveals the surface generation mechanism (such as the overcutting phenomenon) without the need for costly trial and error tests. With the proposed tool radius compensation method, waviness error components resulting from the overcut can be totally eliminated.
- (3)
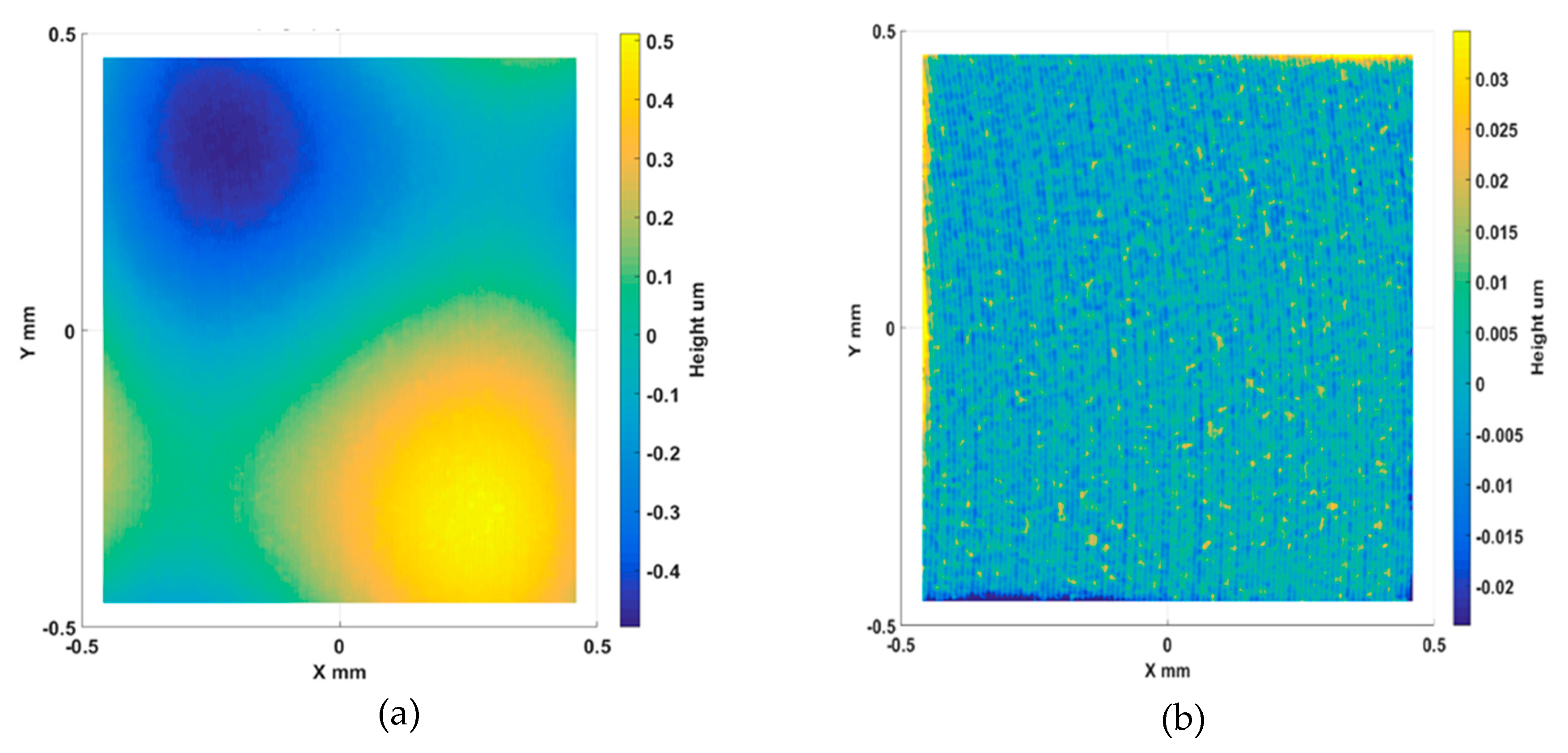
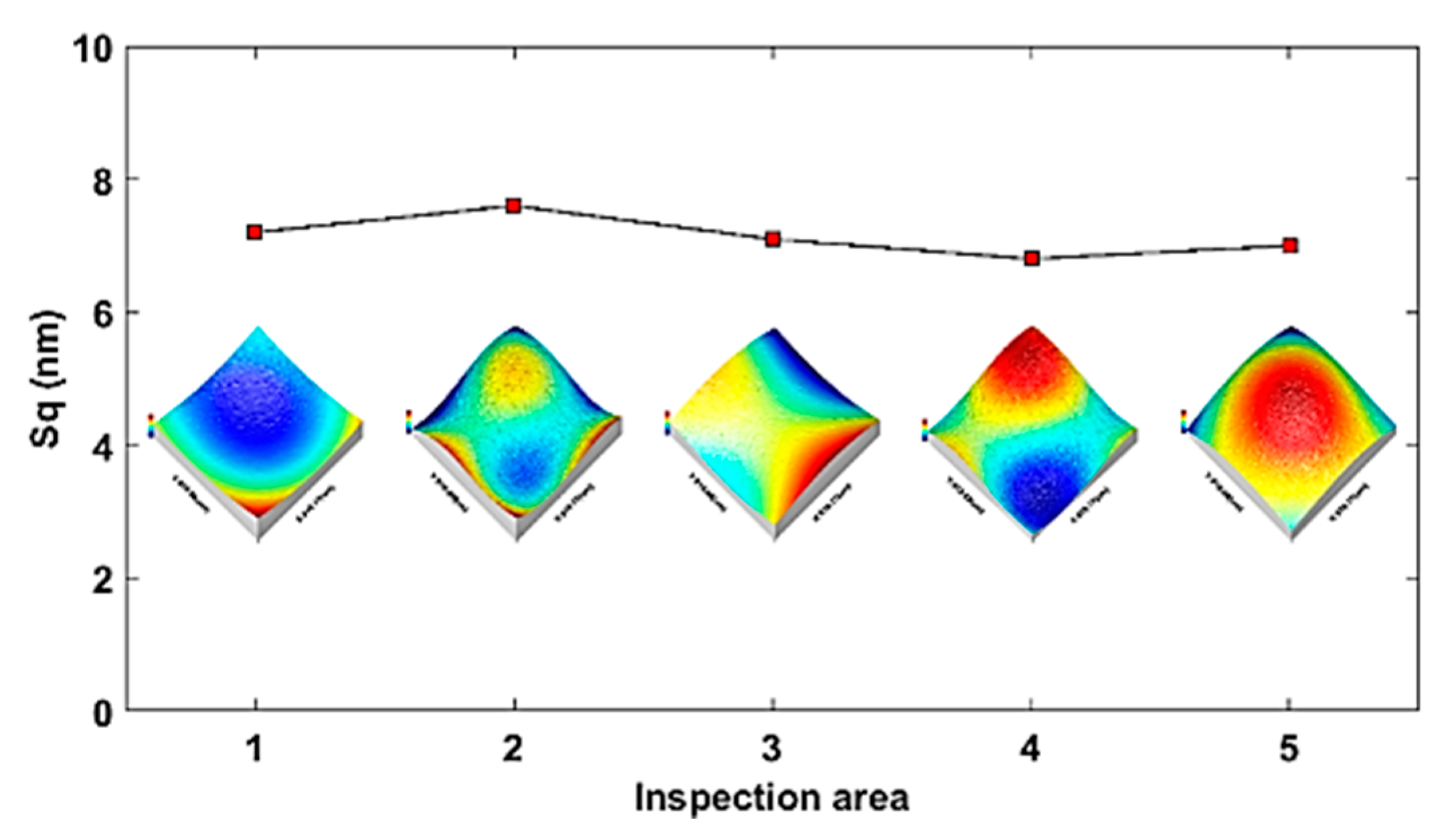
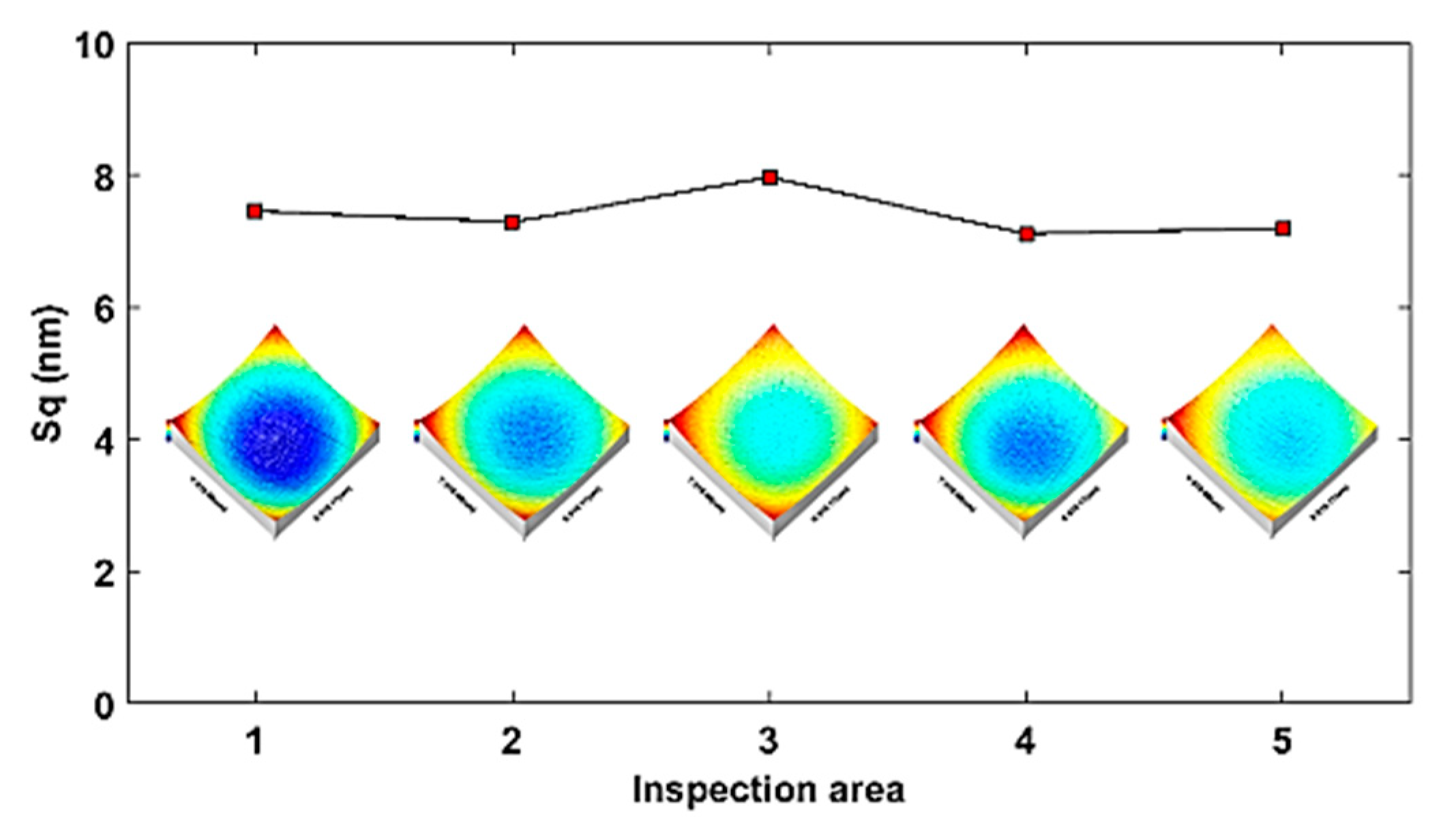
- Machining experiments of a sinusoidal grid and MLA sample demonstrated the effectiveness of the proposed STS machining to fabricate optical freeform surfaces with a nanometric surface topography (less than 10 nm). The measurement results show uniform topography distribution over the entire surface and agree well with the simulation results.
Author Contributions
Acknowledgments
Funding
Conflicts of Interest
References
- Fuse, K.; Okada, T.; Ebata, K. Diffractive/refractive hybrid F-theta lens for laser drilling of multilayer printed circuit boards. In SPIE Conference Proceedings; International Society for Optics and Photonics: Washington, DC, USA, 2003; pp. 95–100. [Google Scholar]
- Cheng, D.; Wang, Y.; Hua, H.; Talha, M. Design of an optical see-through head-mounted display with a low f-number and large field of view using a freeform prism. Appl. Opt. 2009, 48, 2655–2668. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Santosa, F. A numerical method for progressive lens design. Math. Models Methods Appl. Sci. 2004, 14, 619–640. [Google Scholar] [CrossRef]
- Dross, O.; Mohedano, R.; Hernandez, M.; Cvetkovic, A.; Benitez, P.; Miñano, J.C. Illumination optics: Köhler integration optics improve illumination homogeneity. Laser Focus World 2009, 45, 135–150. [Google Scholar]
- Jiang, X.J.; Whitehouse, D.J. Technological shifts in surface metrology. CIRP Ann.-Manuf. Technol. 2012, 61, 815–836. [Google Scholar] [CrossRef]
- Fang, F.Z.; Zhang, X.D.; Weckenmann, A.; Zhang, G.X.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann.-Manuf. Technol. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Yi, A.; Li, L. Design and fabrication of a microlens array by use of a slow tool servo. Opt. Lett. 2005, 30, 1707–1709. [Google Scholar] [CrossRef] [PubMed]
- Brinksmeier, E.; Mutlugünes, Y.; Klocke, F.; Aurich, J.; Shore, P.; Ohmori, H. Ultra-precision grinding. CIRP Ann.-Manuf. Technol. 2010, 59, 652–671. [Google Scholar] [CrossRef]
- Klocke, F.; Brecher, C.; Brinksmeier, E.; Behrens, B.; Dambon, O.; Riemer, O.; Schulte, H.; Tuecks, R.; Waechter, D.; Wenzel, C. Deterministic Polishing of Smooth and Structured Molds. In Fabrication of Complex Optical Components; Springer: Berlin/Heidelberg, Germany, 2013; pp. 99–117. [Google Scholar]
- Yin, Z.; Dai, Y.; Li, S.; Guan, C.; Tie, G. Fabrication of off-axis aspheric surfaces using a slow tool servo. Int. J. Mach. Tools Manuf. 2011, 51, 404–410. [Google Scholar] [CrossRef]
- Mukaida, M.; Yan, J. Ductile machining of single-crystal silicon for microlens arrays by ultraprecision diamond turning using a slow tool servo. Int. J. Mach. Tools Manuf. 2016, 115, 2–14. [Google Scholar] [CrossRef]
- Chen, C.-C.; Cheng, Y.-C.; Hsu, W.-Y.; Chou, H.-Y.; Wang, P.-J.; Tsai, D.P. Slow Tool Servo Diamond Turning of Optical Freeform Surface for Astigmatic Contact Lens; Optical Manufacturing and Testing IX, 2011; International Society for Optics and Photonics: Washington, DC, USA, 2011; p. 812617. [Google Scholar]
- Krolczyk, G.M.; Maruda, R.W.; Krolczyk, J.B.; Nieslony, P.; Wojciechowski, S.; Legutko, S. Parametric and nonparametric description of the surface topography in the dry and MQCL cutting conditions. Measurement 2018, 121, 225–239. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Maruda, R.W.; Nieslony, P.; Wieczorowski, M. Surface morphology analysis of Duplex Stainless Steel (DSS) in Clean Production using the Power Spectral Density. Measurement 2016, 94, 464–470. [Google Scholar] [CrossRef]
- Jiang, X.; Scott, P.J.; Whitehouse, D.J.; Blunt, L. Paradigm shifts in surface metrology. Part II. The current shift. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 2071–2099. [Google Scholar] [CrossRef] [Green Version]
- Beaucamp, A.; Freeman, R.; Morton, R.; Ponudurai, K.; Walker, D. Removal of Diamond-Turning Signatures on x-ray Mandrels and Metal Optics by Fluid-Jet Polishing; Advanced Optical and Mechanical Technologies in Telescopes and Instrumentation, 2008; International Society for Optics and Photonics: Washington, DC, USA, 2008; p. 701835. [Google Scholar]
- Agarwal, S.; Rao, P.V. A probabilistic approach to predict surface roughness in ceramic grinding. Int. J. Mach. Tools Manuf. 2005, 45, 609–616. [Google Scholar] [CrossRef]
- Kong, L.; Cheung, C.; Kwok, T. Theoretical and experimental analysis of the effect of error motions on surface generation in fast tool servo machining. Precis. Eng. 2014, 38, 428–438. [Google Scholar] [CrossRef]
- Zhou, J.; Li, L.; Naples, N.; Sun, T.; Allen, Y.Y. Fabrication of continuous diffractive optical elements using a fast tool servo diamond turning process. J. Micromech. Microeng. 2013, 23, 075010. [Google Scholar] [CrossRef]
- Venkataraman, P. Applied Optimization with MATLAB Programming; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Gao, W.; Dejima, S.; Shimizu, Y.; Kiyono, S.; Yoshikawa, H. Precision measurement of two-axis positions and tilt motions using a surface encoder. CIRP Ann.-Manuf. Technol. 2003, 52, 435–438. [Google Scholar] [CrossRef]
- Chang, S.-I.; Yoon, J.-B.; Kim, H.; Kim, J.-J.; Lee, B.-K.; Shin, D.H. Microlens array diffuser for a light-emitting diode backlight system. Opt. Lett. 2006, 31, 3016–3018. [Google Scholar] [CrossRef] [PubMed]






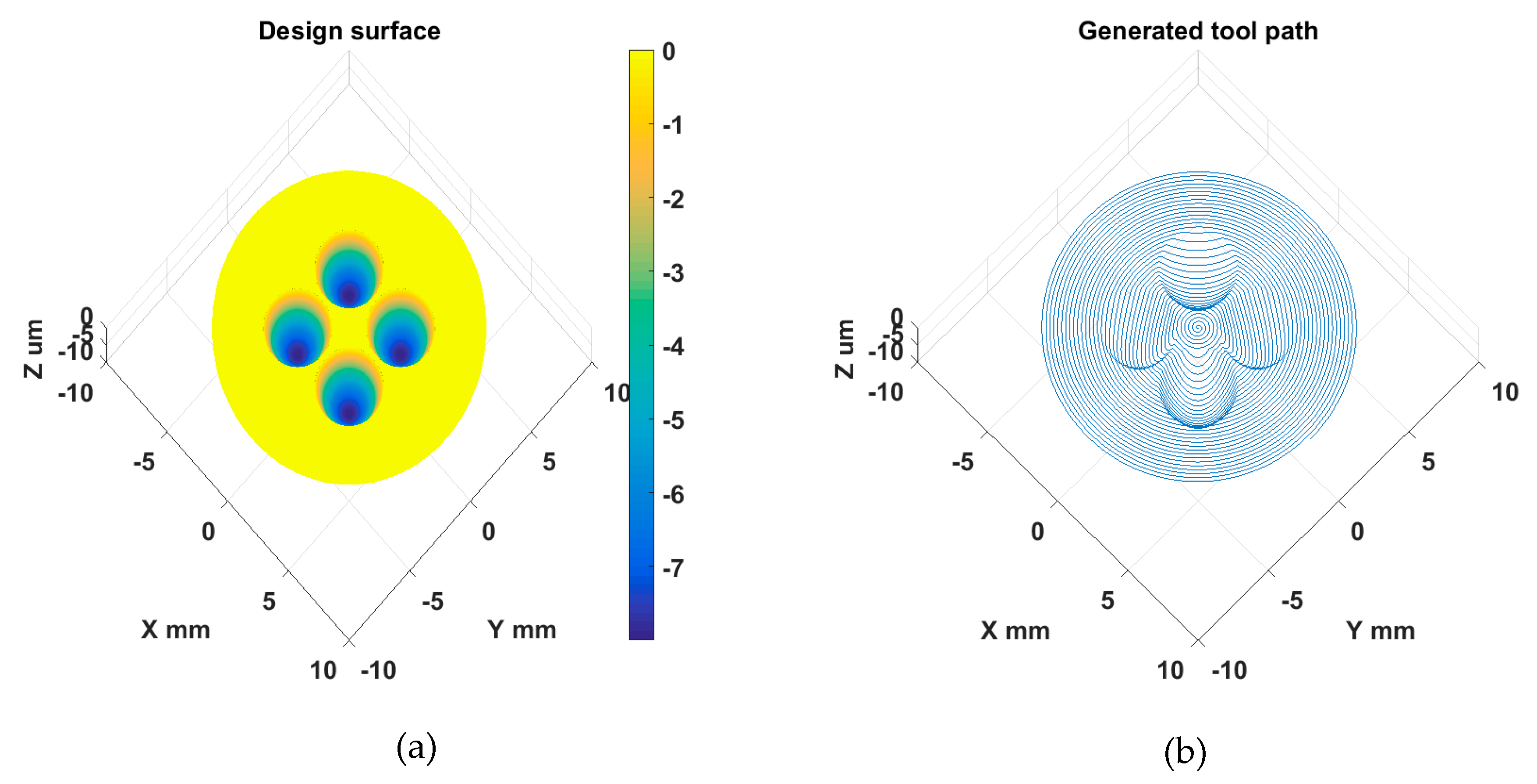
| Parameters | Value |
|---|---|
| Density (g/cm3) | 2.70 |
| Modulus of elasticity (GPa) | 70 |
| Tensile strength (MPa) | 260 |
| Shear strength (MPa) | 170 |
| Thermal conductivity (W/m.K) | 180 |
| Parameters | Value |
|---|---|
| Machining mode | STS |
| Spindle speed (rpm) | 50 |
| Feedrate (mm/min) | 0.5 |
| Cutting depth (μm) | 3 |
| Parameters | Value |
|---|---|
| Manufacturer | Contour fine tooling |
| Tool material | Single crystal |
| Tool tip radius (mm) | 0.514 |
| Rake angle (deg) | 0 |
| Clearance angle (deg) | 10 |
| Included angle (deg) | 60 |
| Parameters | Value |
|---|---|
| Nominal feature shape | Sphere |
| Pattern | 2 × 2 |
| Center Spacing (mm) | 4.243 |
| Aperture radius (mm) | 2 |
| Chord height (μm) | 8 |
| Radius of curvature (mm) | 250.004 |
| Sample | Measured Average Sq (nm) | Standard Deviation Sq (nm) | Simulated Sq (nm) |
|---|---|---|---|
| Sinusoidal grid | 7.1 | 0.30 | 6.7 |
| MLA | 7.4 | 0.34 | 6.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Qiao, Z.; Walton, K.; Liu, Y.; Xue, J.; Wang, B.; Jiang, X. Theoretical and Experimental Investigation of Surface Topography Generation in Slow Tool Servo Ultra-Precision Machining of Freeform Surfaces. Materials 2018, 11, 2566. https://doi.org/10.3390/ma11122566
Li D, Qiao Z, Walton K, Liu Y, Xue J, Wang B, Jiang X. Theoretical and Experimental Investigation of Surface Topography Generation in Slow Tool Servo Ultra-Precision Machining of Freeform Surfaces. Materials. 2018; 11(12):2566. https://doi.org/10.3390/ma11122566
Chicago/Turabian StyleLi, Duo, Zheng Qiao, Karl Walton, Yutao Liu, Jiadai Xue, Bo Wang, and Xiangqian Jiang. 2018. "Theoretical and Experimental Investigation of Surface Topography Generation in Slow Tool Servo Ultra-Precision Machining of Freeform Surfaces" Materials 11, no. 12: 2566. https://doi.org/10.3390/ma11122566
APA StyleLi, D., Qiao, Z., Walton, K., Liu, Y., Xue, J., Wang, B., & Jiang, X. (2018). Theoretical and Experimental Investigation of Surface Topography Generation in Slow Tool Servo Ultra-Precision Machining of Freeform Surfaces. Materials, 11(12), 2566. https://doi.org/10.3390/ma11122566







