A Semi-Analytical Extraction Method for Interface and Bulk Density of States in Metal Oxide Thin-Film Transistors
Abstract
:1. Introduction
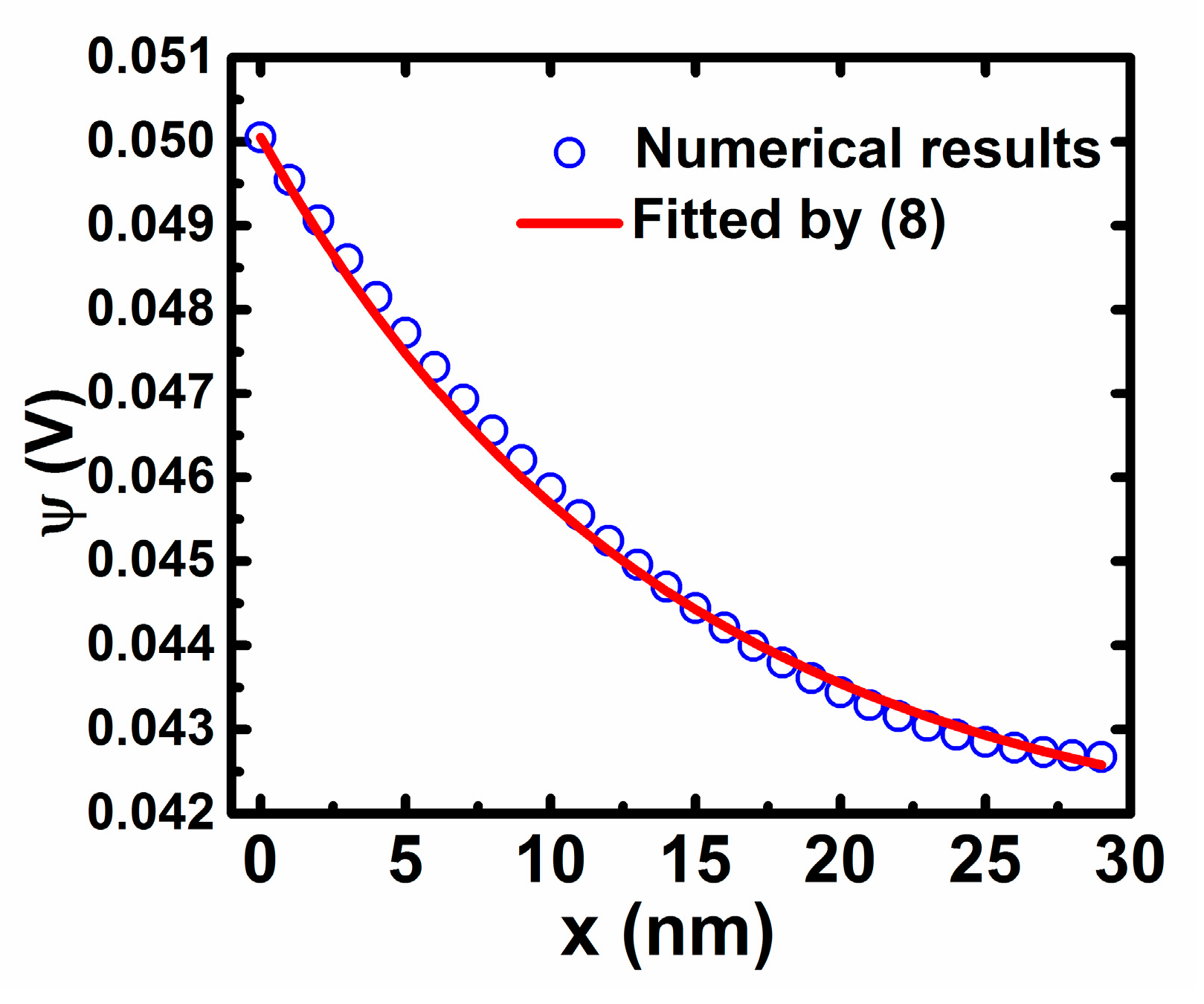
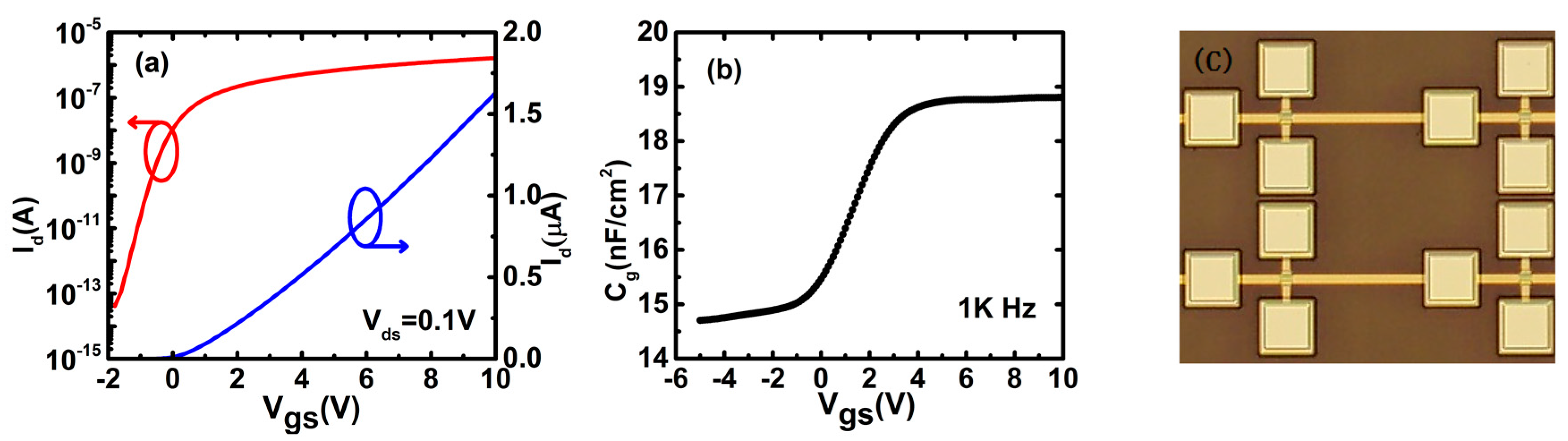
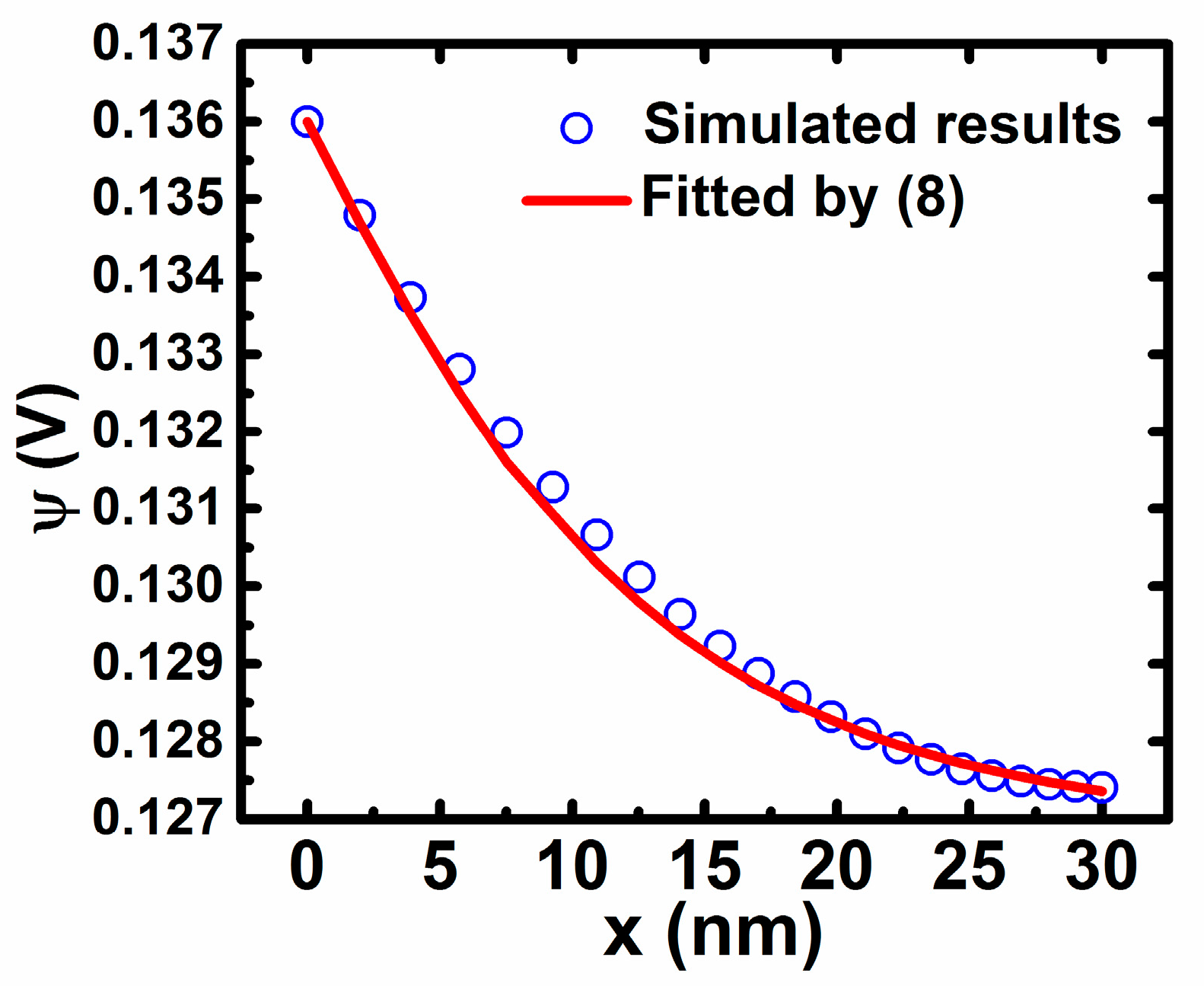
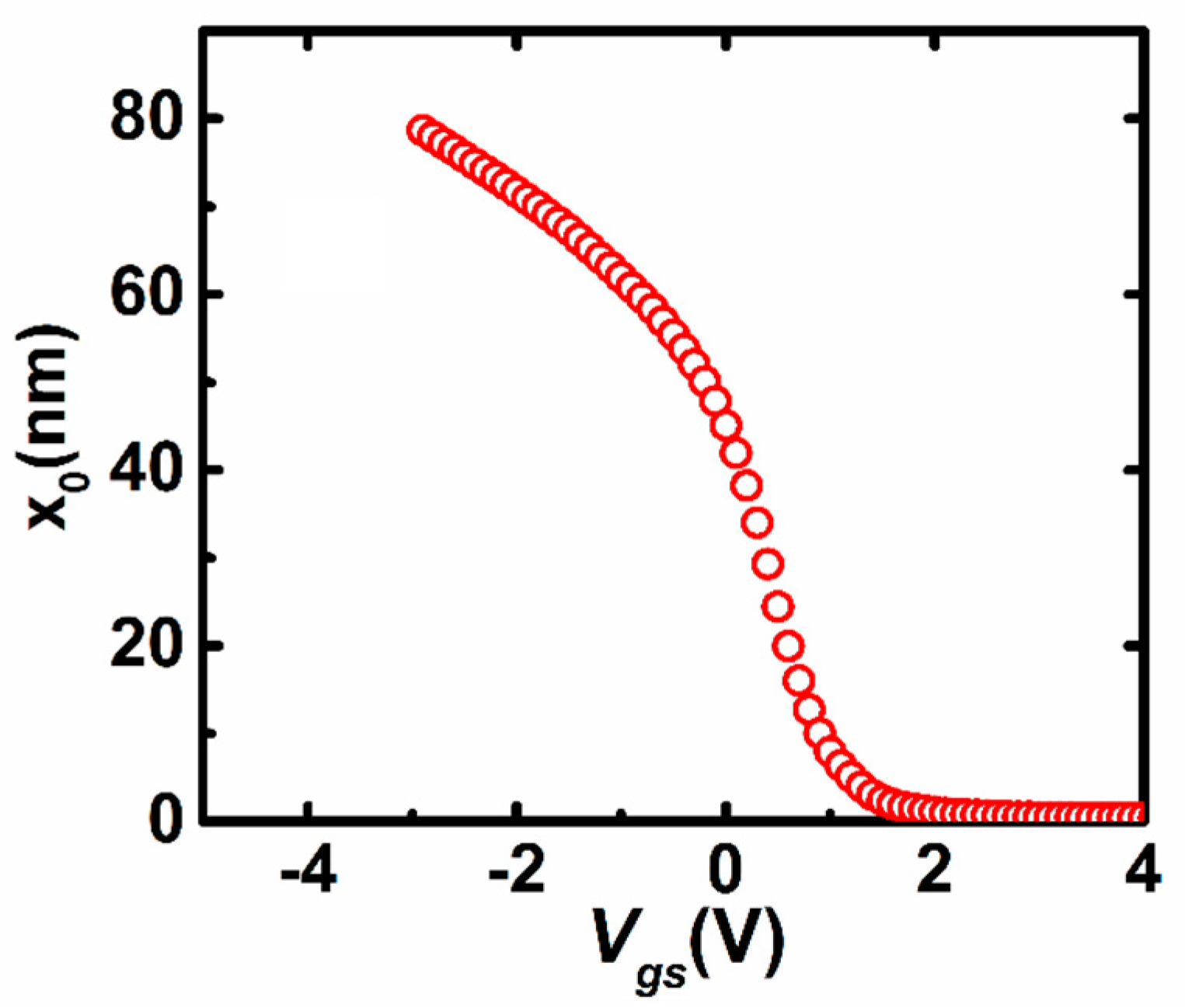
2. Extraction Method
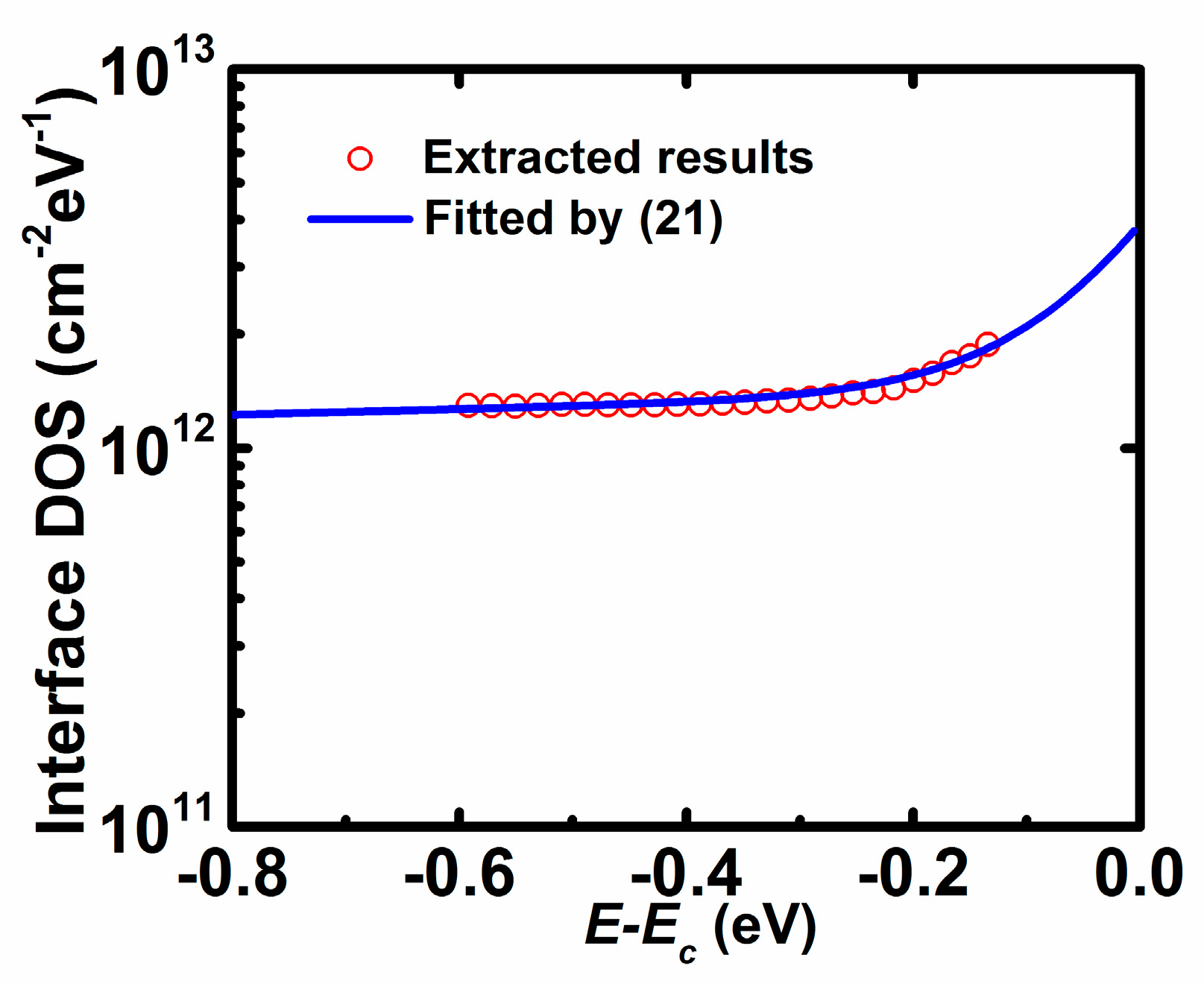
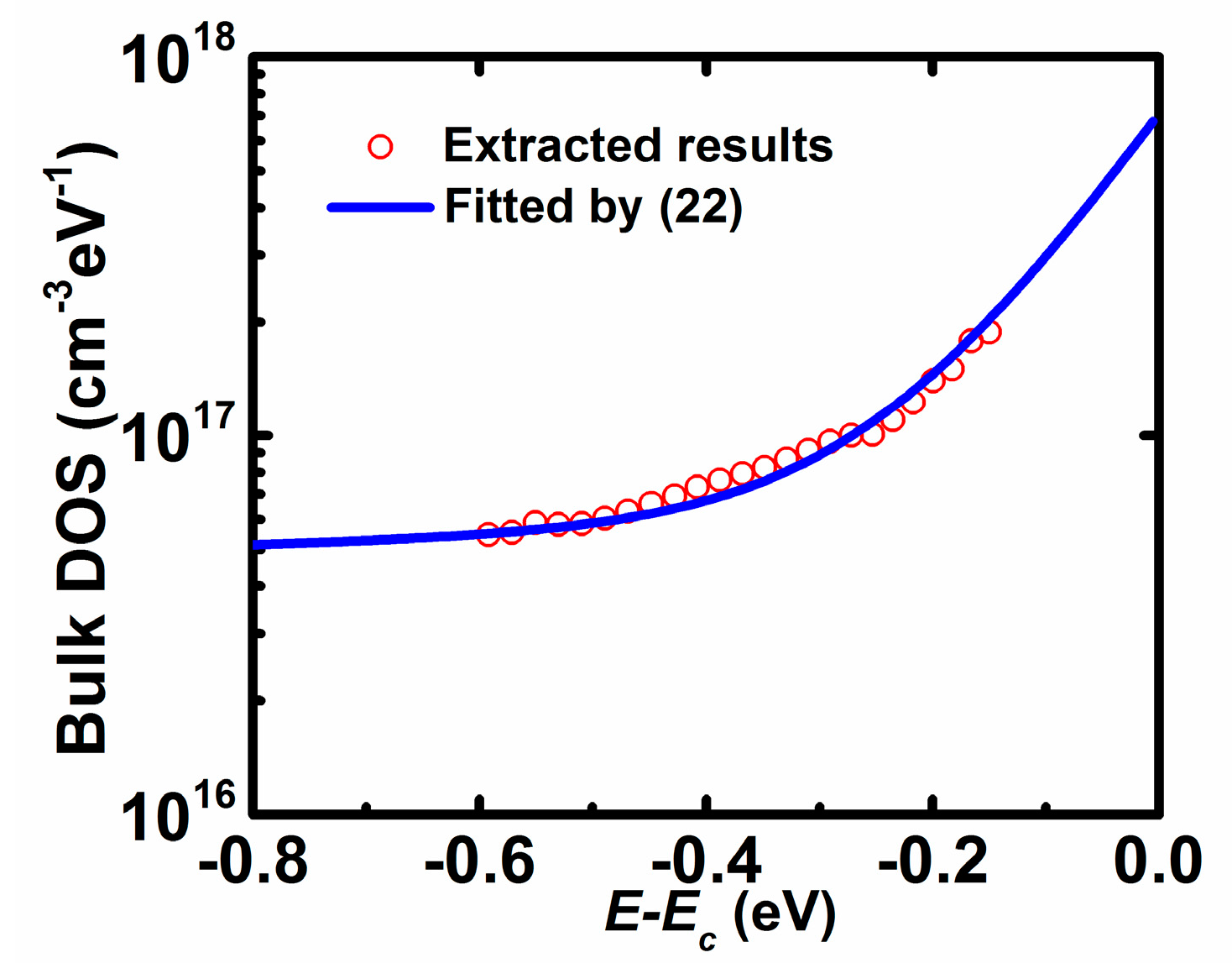
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Yue, K. Thin film transistor technology—Past, present, and future. Electrochem. Soc. Interface 2013, 22, 55–61. [Google Scholar]
- Nomura, K.; Ohta, H.; Takagi, A.; Kamiya, T.; Hirano, M.; Hosono, H. Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors. Nature 2004, 432, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Park, J.S.; Maeng, W.-J.; Kim, H.-S.; Park, J.-S. Review of recent developments in amorphous oxide semiconductor thin-film transistor devices. Thin Solid Films 2012, 520, 1679–1693. [Google Scholar] [CrossRef]
- Lin, Z.; Lan, L.; Xiao, P.; Sun, S.; Li, Y.; Song, W.; Gao, P.; Wang, L.; Ning, H.; Peng, J. High-mobility thin film transistors with neodymium—Substituted indium oxide active layer. Appl. Phys. Lett. 2015, 107, 112108. [Google Scholar] [CrossRef]
- Sheng, J.; Lee, H.-J.; Oh, S.; Park, J.-S. Flexible and high-performance amorphous indium zinc oxide thin-film transistor using low-temperature atomic layer deposition. ACS Appl. Mater. Interfaces 2016, 8, 33821–33828. [Google Scholar] [CrossRef] [PubMed]
- Yu, E.K.-H.; Jun, S.; Kim, D.H.; Kanicki, J. Density of states of amorphous In-Ga-Zn-O from electrical and optical characterization. J. Appl. Phys. 2014, 116, 154505. [Google Scholar] [CrossRef]
- Nicollian, E.H.; Brews, J.R. MOS (Metal Oxide Semiconductor) Physics and Technology; Wiley–Interscience: New York, NY, USA, 1982. [Google Scholar]
- Kimura, M.; Nakanishi, T.; Nomura, K.; Kamiya, T.; Hosono, H. Trap densities in amorphous-InGaZnO4 thin-film transistors. Appl. Phys. Lett. 2008, 92, 133512. [Google Scholar] [CrossRef]
- Bae, H.; Choi, H.; Jun, S.; Jo, C.; Kim, Y.H.; Hwang, J.S.; Ahn, J.; Oh, S.; Bae, J.-U.; Choi, S.-J.; et al. Single-scan monochromatic photonic capacitance-voltage technique for extraction of subgap DOS over the bandgap in amorphous semiconductor TFTs. IEEE Electron Dev. Lett. 2013, 34, 1524–1526. [Google Scholar] [CrossRef]
- Chen, C.; Abe, K.; Kumomi, H.; Kanicki, J. Density of states of a-InGaZnO from temperature-dependent field-effect studies. IEEE Trans. Electron Dev. 2009, 56, 1177–1183. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.; Kim, S.; Jeon, Y.; Jeon, K.; Park, J.-H.; Park, J.; Song, I.; Kim, C.J.; Park, Y.; et al. Extraction of subgap density of states in amorphous InGaZnO thin-film transistors by using multifrequency capacitance-voltage characteristics. IEEE Electron Dev. Lett. 2010, 31, 231–233. [Google Scholar]
- Lui, O.K.B.; Tam, S.W.B.; Migliorato, P.; Shimoda, T. Method for the determination of bulk and interface density of states in thin-film transistors. J. Appl. Phys. 2001, 89, 6453–6458. [Google Scholar] [CrossRef]
- Kimura, M. Extraction technique of trap densities in thin films and at insulator interfaces of thin-film transistors. IEEE Electron Dev. Lett. 2010, 31, 570–572. [Google Scholar] [CrossRef]
- Hastas, N.A.; Tassis, D.H.; Dimitriadis, C.A.; Kamarinos, G. Determination of interface and bulk traps in the subthreshold region of polycrystalline silicon thin-film transistors. IEEE Trans. Electron Dev. 2003, 50, 1991–1994. [Google Scholar] [CrossRef]
- Tsuji, H.; Kamakura, Y.; Taniguchi, K. Simple extraction method of interface trap density in thin-film transistors. J. Electrochem. Soc. 2009, 156, H430–H433. [Google Scholar] [CrossRef]
- Dehuff, N.L.; Kettenring, E.S.; Hong, D.; Chiang, H.Q.; Wager, J.F.; Hoffman, R.L.; Park, C.H.; Keszler, D.A. Transparent thin-film transistors with zinc indium oxide channel layer. J. Appl. Phys. 2005, 97, 064505. [Google Scholar] [CrossRef]
- Wu, W.-J.; Chen, C.-L.; Hu, X.; Xia, X.-H.; Zhou, L.; Xu, M.; Wang, L.; Peng, J.-B. Analytical extraction method for density of states in metal oxide thin-film transistors by using low-frequency capacitance-voltage characteristics. J. Disp. Technol. 2016, 12, 888–891. [Google Scholar] [CrossRef]
- Fung, T.-C.; Chuang, C.-S.; Chen, C.; Abe, K.; Cottle, R.; Townsend, M.; Kumomi, H.; Kanicki, J. Two-dimensional numerical simulation of radio frequency sputter amorphous In-Ga-Zn-O thin-film transistors. J. Appl. Phys. 2009, 106, 084511. [Google Scholar] [CrossRef]
- Migliorato, P.; Seok, M.; Jang, J. Determination of flat band voltage in thin film transistors: The case of amorphous-indium gallium zinc oxide. Appl. Phys. Lett. 2012, 100, 073506. [Google Scholar] [CrossRef]
- Park, J.S.; Kim, H.; Kim, I.D. Overview of electroceramic materials for oxide semiconductor thin film transistors. J. Electroceram. 2014, 32, 117–140. [Google Scholar] [CrossRef]
- Conley, J.F. Instabilities in oxide semiconductor transparent thin film transistors. In Proceedings of the 2009 IEEE International Integrated Reliability Workshop Final Report, South Lake Tahoe, CA, USA, 18–22 October 2009; pp. 50–55. [Google Scholar]
- Hsieh, H.-H.; Kamiya, T.; Nomura, K.; Hosono, H.; Wu, C.-C. Modeling of amorphous ingazno(4) thin film transistors and their subgap density of states. Appl. Phys. Lett. 2008, 92, 133503. [Google Scholar] [CrossRef]
- Kimura, M.; Takizawa, T.; Inoue, S.; Shimoda, T. Analytical current-voltage model for polycrystalline-silicon thin-film transistors. Appl. Phys. Lett. 2002, 80, 2326–2328. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wu, W.; Zhou, L.; Xu, M.; Wang, L.; Ning, H.; Peng, J. A Semi-Analytical Extraction Method for Interface and Bulk Density of States in Metal Oxide Thin-Film Transistors. Materials 2018, 11, 416. https://doi.org/10.3390/ma11030416
Chen W, Wu W, Zhou L, Xu M, Wang L, Ning H, Peng J. A Semi-Analytical Extraction Method for Interface and Bulk Density of States in Metal Oxide Thin-Film Transistors. Materials. 2018; 11(3):416. https://doi.org/10.3390/ma11030416
Chicago/Turabian StyleChen, Weifeng, Weijing Wu, Lei Zhou, Miao Xu, Lei Wang, Honglong Ning, and Junbiao Peng. 2018. "A Semi-Analytical Extraction Method for Interface and Bulk Density of States in Metal Oxide Thin-Film Transistors" Materials 11, no. 3: 416. https://doi.org/10.3390/ma11030416
APA StyleChen, W., Wu, W., Zhou, L., Xu, M., Wang, L., Ning, H., & Peng, J. (2018). A Semi-Analytical Extraction Method for Interface and Bulk Density of States in Metal Oxide Thin-Film Transistors. Materials, 11(3), 416. https://doi.org/10.3390/ma11030416






