Next Article in Journal
Unusually Small Thermal Expansion of Ordered Perovskite Oxide CaCu3Ru4O12 with High Conductivity
Next Article in Special Issue
Silicon Nitride-Based Composites with the Addition of CNTs—A Review of Recent Progress, Challenges, and Future Prospects
Previous Article in Journal
Micro-Tensile Behavior of Mg-Al-Zn Alloy Processed by Equal Channel Angular Pressing (ECAP)
Previous Article in Special Issue
Determining the Nitrogen Content in (Oxy)Nitride Materials
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 11
Issue 9
10.3390/ma11091646
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

29Si NMR Chemical Shifts in Crystalline and Amorphous Silicon Nitrides

by
Ilia Ponomarev
and
Peter Kroll
*
Department of Chemistry and Biochemistry, The University of Texas at Arlington, 700 Planetarium Place, Arlington, TX 76019, USA
*
Author to whom correspondence should be addressed.
Materials 2018, 11(9), 1646; https://doi.org/10.3390/ma11091646
Submission received: 30 July 2018 / Revised: 4 September 2018 / Accepted: 5 September 2018 / Published: 7 September 2018
(This article belongs to the Special Issue Nitride Ceramics: Synthesis, Properties and Applications)
Browse Figures
Versions Notes

Abstract

:
We investigate 29Si nuclear magnetic resonance (NMR) chemical shifts, δiso, of silicon nitride. Our goal is to relate the local structure to the NMR signal and, thus, provide the means to extract more information from the experimental 29Si NMR spectra in this family of compounds. We apply structural modeling and the gauge-included projector augmented wave (GIPAW) method within density functional theory (DFT) calculations. Our models comprise known and hypothetical crystalline Si3N4, as well as amorphous Si3N4 structures. We find good agreement with available experimental 29Si NMR data for tetrahedral Si[4] and octahedral Si[6] in crystalline Si3N4, predict the chemical shift of a trigonal-bipyramidal Si[5] to be about −120 ppm, and quantify the impact of Si-N bond lengths on 29Si δiso. We show through computations that experimental 29Si NMR data indicates that silicon dicarbodiimide, Si(NCN)2 exhibits bent Si-N-C units with angles of about 143° in its structure. A detailed investigation of amorphous silicon nitride shows that an observed peak asymmetry relates to the proximity of a fifth N neighbor in non-bonding distance between 2.5 and 2.8 Å to Si. We reveal the impact of both Si-N(H)-Si bond angle and Si-N bond length on 29Si δiso in hydrogenated silicon nitride structure, silicon diimide Si(NH)2.
Keywords:
silicon nitride; NMR; DFT; GIPAW

Graphical Abstract

1. Introduction

Silicon nitride is a hard (bulk modulus of γ-Si3N4—290 GPa [1]) and oxidation-resistant material that finds a broad variety of applications: from engine parts, ball bearings, cutting tools, thermal shock resistant ceramics [2], to dielectric materials in electronics [3], heterogeneous catalyst support [4], ceramic fibers [5], or nanowires [6]. Better knowledge of the local structure is essential for broadening the range of applications of this kind of materials.
Over the last decade several studies addressed NMR calculations of crystalline and amorphous silica and silicates [7,8,9,10]. Those studies show the power of state-of-the-art quantum-chemical calculations to support experimental characterization and analytics [11,12]. Computationally-enhanced 29Si NMR spectroscopy enables extracting information on Si-O-Si angle distribution [8] as well as Q-unit speciation [9] and the degree of condensation of the silica network in sol-gel-derived SiO2-RxOy glasses [10]. Combining experimental and computational NMR studies allowed to resolve the debate of the abundance of boroxol rings in vitreous B2O3 [13].
Here we provide—for the first time—GIPAW [14] calculations for silicon nitride in crystalline and amorphous form. Our goal is to relate the local structure of Si in nitrides to 29Si NMR δiso. We explore known and hypothetical crystalline structures of Si3N4 to reveal the effect of coordination number on 29Si NMR and provide predictions for the chemical shift of 5-coordinated Si in nitrides, which have not been experimentally found yet. We take a closer look on the effects of local structure on 29Si δiso for Si[6] and Si[4] species. We explore a variety of local geometry features in amorphous Si3N4 models and reveal the effect of certain local structure parameters on 29Si NMR signal. We also consider two different types of compounds comprising SiN4 tetrahedra, but differently-connected N atoms: silicon carbodiimide Si(NCN)2 and silicon diimide Si(NH)2.

2. Computational Methods

We perform density functional theory [15] calculations using the Vienna Ab Initio Simulation (VASP) package (version 5.3.5) [16,17]. We use the projector augmented wave (PAW) method [18,19] and approximate electron exchange and correlation by the Perdew-Burke-Ernzerhoff (PBE) generalized gradient approximation (GGA). For optimizations of both amorphous and crystalline models we rely on standard pseudopotentials provided with the VASP package and use an energy cutoff of 500 eV for the expansion of the wave function into the plane-wave basis set. We sample the Brillouin zone at the Γ-point only for amorphous models, while we choose appropriate k-point meshes for crystalline models. NMR calculations are carried out using the GIPAW algorithm [14] as implemented in the VASP code. For those we choose an energy cutoff of 600 eV and find 29Si NMR chemical shifts converged to better than 0.2 ppm.
For calibration of chemical shifts we compute silicon nitride polymorphs as well as ternary M-Si-N structures with structural data taken from the Inorganic Crystal Structure Database [20]: α-Si3N4 [21], β-Si3N4 [22], γ-Si3N4 [23,24], BaSi6N8 [25], Li2SiN2 [26], and SrSi6N8 [27]. Keeping the reported experimental lattice parameters constant we first optimize atomic positions (forces lower than 5 meV/Å) and, thereafter, compute absolute 29Si NMR chemical shifts. Results of NMR calculations are given in Table 1 together with experimental data. The relation between computed absolute chemical shifts and experimental isotropic chemical shifts is shown in Figure 1. A best fit is obtained by a linear relation with the slope of unity:
  δ iso = σ iso + 338.6  
Similar relations have been used previously for polymorphs of SiO2 as well as for a variety of silicates [7,10]. Using this calibration, computed chemical shifts agree with experimental data with a maximum deviation of 2 ppm.
The spinel-type γ-Si3N4 is the only silicon nitride exhibiting a six-fold octahedrally-coordinated Si[6] site, with a chemical shift of −225 ppm [29]. To investigate more highly coordinated Si sites (CN = 5, 6, 7) and their 29Si chemical shifts, we computed a series of hypothetical crystalline structures with composition Si3N4. Model structures are generated from binary A3X4- and ternary A2BX4-structure types by replacing all cations with Si and all anions with N. Crystallographic data of these structures is provided in the Supporting Information.
Amorphous silicon nitride models are generated by two different approaches. A set of network models was generated using a modified Wooten, Winer and Waire (WWW) algorithm [30,31,32] with subsequent DFT optimizations. Another set of models was produced by molecular dynamics simulations (MD) using the empirical potential of Garofalini et al. [33] integrated into the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code [34]. In a recent study we showed that this potential produces structures with low defect concentrations and close to a DFT local minimum [35]. We followed a standard melt-quench procedure by first heating the system to 8000 K and then quenching it in 280 ps (Δt = 1 fs) down to room temperature. Finally, we optimized all models within DFT as described above.

3. Results and Discussion

3.1. Effects of Coordination Number—Known and Hypothetical Crystalline Si3N4 Structures

In Figure 2 we collect computed 29Si NMR chemical shifts of Si sites in a variety of known and hypothetical silicon nitride, Si3N4, structures as a function of their nitrogen coordination number. Structural data as well as computed 29Si NMR chemical shifts of each model are provided in the Supporting Information (Table S1).
In general, higher coordination number lowers the shielding of Si nucleus causing decrease in chemical shift. This is consistent with observations of chemical shifts in polymorphs of SiO2 and silicates, where NMR chemical shifts of Si[6] have significantly more negative values (−191.1 ppm for stishovite [36], in the range from −210 to −220 ppm for silicophosphates [37]) than Si[4]. In particular, 29Si NMR chemical shifts of tetrahedrally coordinated Si[4] sites fall into the range from −37 to −57 ppm. Notably, examples of relatively high δiso values of −26.5 ppm and −30.2 ppm are two models, in which Si[4] sites are engaged into two 2-rings.
Among the five-fold coordinated Si[5]-sites, a trigonal-bipyramidal coordination (4 sites) yields δiso of −115 to −121 ppm. A square pyramidal Si[5] (two sites) is shifted to less negative δiso values, we found −76.4 ppm and −98.7 ppm, respectively. Two Si[5] sites appearing with shifts lower than −140 ppm are better described as 5 + 1 coordination, with a distance of only 2.5 Å to the 6th nitrogen neighbor. We discuss the impact of such “extended” bonds on 29Si NMR chemical shifts more thoroughly for amorphous systems further below.
We compute the 29Si NMR chemical shift of octahedrally coordinated Si[6] in spinel-type γ-Si3N4 to −228.4 ppm, which is consistent with the experimental value of −225 ppm [29]. Hence, our calibration is justified and applies even for significantly larger chemical shifts. The (almost perfect) octahedral coordination of Si in γ-Si3N4 falls onto the lowest values of chemical shifts, however. Values of δiso for other six-fold coordinated Si[6] sites fall into the range from −150 ppm to −230 ppm. We note that one “outlier” appears at −125 ppm. It displays strong differences of Si-N bond lengths to its neighbors, which is analyzed below.
We computed only one site for each three-fold (trigonal) coordinated Si[3] and seven-fold (pentagonal bipyramidal) coordinated Si[7]. They align with the overall trend: δiso of Si[3] is significantly higher than for Si[4], and δiso of Si[7] (which is better described as 5 + 2 coordination) is comparable to the lowest values of Si[6].

3.2. Impact of Local Structure—Distortions of Crystalline Si3N4 Models

The key factor impacting 29Si NMR chemical shifts of four-fold tetrahedrally-coordinated Si[4] sites in silicates, where Si is coordinated by four (bridging) O atoms, is the Si-O-Si bond angle on neighboring oxygen atoms [7,8,9,10,36,38,39,40]. Hence, experimental 29Si NMR data can be used for structural investigations, for instance in silicate glasses [7,8,9], and experimental “resolution” can be enhanced by thorough computational studies. The importance of the bond angle at O—rather than bond distances to and angles at the Si site—stems from the fact that silicates display almost perfect tetrahedral Si sites. Furthermore, the dependence of δiso on the Si-O bond distance is rather weak.
In silicon nitrides Si sites are coordinated by N atoms. With N typically being three-fold coordinated by Si (for instance in α-Si3N4 and β-Si3N4), the parameter corresponding to the bond angle at O in oxide systems then is the degree of pyramidalization of N. Similar to the bond angle at O, the pyramidalization at N characterizes the localization of electrons at the anion site which, in turn, impacts the shielding at the Si nucleus and, consequently, the 29Si NMR chemical shifts. We express the pyramidalization of N as the ratio of height h of N above the plane formed by its three coordinating Si atoms and average Si-N bond length d (see Figure 3a). The parameter h/d, thus, is a measure of how much the N atom is out of the plane formed by its three Si neighbors.
The model structure best suited to study this potential correlation between pyramidalization and 29Si NMR chemical shifts is that of (hypothetical) wII-Si3N4, which the willemite-II structure [41,42,43]. With a single Si site and only two independent structural parameters, lattice parameter and one positional parameter of N, it allows a facile change of pyramidalization while maintaining constant Si-N bond distances. Thus, we compute the 29Si NMR chemical shift for a series of different pyramidalization at N and results are shown in Figure 3b. Essentially, δiso changes less than 1 ppm over a wide range until the N is so far above the plane that Si-N-Si angles are smaller than those in a regular tetrahedron (109.47°). Only for extreme distortions does a decrease of 29Si δiso occur. This, however, is in this special case augmented by an increase of Si coordination from 4 to 8.
To highlight the impact of Si-N bond lengths on 29Si NMR chemical shifts we scale the structure of β-Si3N4 by changing cell parameters while keeping fractional coordinates constant, and further compute NMR of those “scaled” structures. The results are shown in Figure 4 and are compared with similar data obtained for α–cristobalite SiO2. Interestingly, the bond distance dependence of δiso for tetrahedral Si[4] is very similar for SiO2 and Si3N4. However, for the range of typical bond distances occurring in oxides and nitrides of silicon, a change in bond distance has significantly different impact on δiso. As mentioned earlier, typical Si[4]-O bond lengths fall into a range of 1.6–1.7 Å, and small (up to 0.05 Å) bond length variations yield only small (<1 ppm) changes of 29Si NMR chemical shifts. On the other side, typical Si[4]-N bond lengths are about 1.7–1.8 Å. In this range the slope of the curve is about significantly steeper, and a change of 1 pm (0.01 Å) in bond length yields about a 1 ppm change in chemical shift.
The bond length dependence of 29Si NMR chemical shifts appears significantly more pronounced for six-fold coordinated Si[6]. In Figure 5a we plot δiso for Si[6] in (hypothetical) crystalline models as a function of the average Si-N bond length around that site. The graph includes data for the octahedral Si[6] site in spinel-type γ-Si3N4 obtained by scaling the structure. Due to its location at a high-symmetry position, the Si[6] site in spinel-type γ-Si3N4 exhibits six equal Si-N bonds.
If we regard the data for the Si[6] site in spinel-type γ-Si3N4 as a benchmark curve characterizing the bond length dependency for Si[6] sites, we notice some significant discrepancies among the computed chemical shifts. Strong deviations from the curve only occur towards higher δiso values, and are related to distorted coordination environments around the Si[6] sites. Most important is an asymmetry among the Si-N bond lengths of that site. To illustrate this, we plot the deviation of the computed 29Si NMR δiso for the distorted Si[6] site as a function of the difference between the shortest and the longest Si-N bond for that site (Figure 5b). The data shows clearly the strong influence that an irregular environment can have on the chemical shift of Si[6].

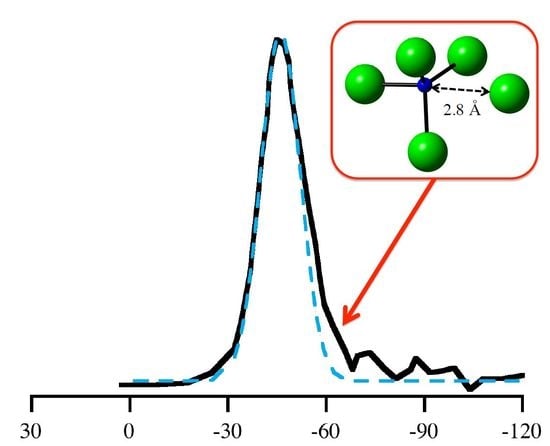
3.3. Special Case of the Silicon Dicarbodiimide—A Bond Angle Dependence for a SiN4 Environment

Computation of 29Si NMR chemical shifts and their comparison with experimental data also provide further insights into the riddle of silicon carbodiimide, Si(NCN)2. The structure of Si(NCN)2 is isostructural to β-cristobalite SiO2 [44], with the complex carbodiimide anion [NCN]2− replacing the oxide O2−. With its relation to the cristobalite SiO2-system, Si(NCN)2 comprises SiN4-tetrahedra, and since the N atoms are bonding to Si and C, there is a bond angle appearing at N. The experimental structure of Si(NCN)2 (sp.gr. Pm–3m, (221)) exhibits linear Si-N-C angles with very short Si-N and N-C distances, and is considered an “average” structure only. Computational studies indicate that the lowest energy configuration of Si(NCN)2 exhibits bent Si-N-C angles and relates best to the structure of α-cristobalite SiO2 [45]. However, density functional theory calculations using a variety of exchange-correlation functionals yield much larger lattice parameters than observed [45]. Only recently, negative thermal expansion (NTE) of Si(NCN)2 was proposed as the mechanism for a contraction of Si(NCN)2 at higher temperatures, and a strong NTE effect was indeed measured [46,47].
The experimental 29Si NMR chemical shift determined for the Si[4] site in Si(NCN)2 is δiso = −103 ppm [44]. Computations approach this value only within scaling studies of the proposed lowest energy model (sp.gr. P–4n2, (118)), shown in Figure 6a. Agreement between computed and experimental chemical shift is present, if the cell volume of the computed tetragonal model adopts a value of V = 219 Å3. A cubic cell with the same volume will have a lattice parameter of a = 6.025 Å, which is only slightly smaller (by 2.5%) than the experimental cell parameter of 6.189 Å.
Another way to support the likelihood of bent Si-N-C angles is to develop a correlation function between 29Si NMR chemical shift value and Si-N-C bond angle at the N–following similar work for polymorphs of SiO2 and other silicates [7,10]. Starting with a (asymmetrical) distortion of the cubic structure of Si(NCN)2, we optimize the model for a variety of volumes. As a result we obtain a set of structures with almost constant bond lengths, but quite different Si-N-C angles. We compute 29Si NMR chemical shifts for both Si[4] sites in those structures and plot δiso as a function of the average Si-N-C angle around each site. The resulting linear correlation function is shown in Figure 6 (bottom). A chemical shift of −103 ppm as in the experiment is related to an average Si-N-C bond angle of 143°—and a linear angle can be excluded, similar to the case of β-cristobalite SiO2.

3.4. Amorphous Si3N4

In recent years, DFT calculations have become an indispensable tool enhancing the analytical strength of experimental NMR studies of glasses and amorphous materials [8,9,10,13,40,48]. Several experimental 29Si NMR studies of amorphous silicon nitride, Si3N4, have been reported [5,49,50]. They show a typical broad “peak” located at δiso ≈ −46 to −49 ppm. The width of the peak, typically, is a full width at half maximum (FWHM) of 20–30 ppm, depending strongly on the quality of the material and its residual hydrogen content. A characteristic feature of many spectra is an asymmetry towards more negative values, as shown in Figure 7 [49].
To analyze the correlations between structure and chemical shifts in amorphous Si3N4, we generated a variety of amorphous models comprising 112 or 224 atoms. On one side we used a network approach and on the other classical MD with an empirical potential [33]. After DFT optimization the models exhibit predominantly Si[4] (on average about 2% Si[3], 4% Si[5]) and N[3] species (4% N[2], 6% N[4]). About a quarter of all N atoms are involved in 2-ring structures. While we compute the chemical shifts for all Si sites, we only consider Si[4] bonded to N[3] not involved in 2-rings in our further analysis. Essentially, network and classical MD models provide the same quality of NMR data.
We first study the impact of pyramidalization of N and of the Si-N bond length on 29Si NMR chemical shifts, which is shown in Figure 8. For the wide range of distortions our models exhibit, we find that most of the computed δiso data fits well between −40 ppm and −60 ppm. None of the models shows extreme pyramidalization, and Si-N bond lengths fall well between 172 and 180 pm. We note, however, that the data of δiso for Si-N bond lengths does not align well with the correlation obtained by scaling β-Si3N4. Moreover, it shows a higher scatter for longer bond lengths. Both of these issues will be addressed later. Overall, none of these plots reveals a systematic trend that may help to explain asymmetry of the experimental 29Si NMR data of amorphous Si3N4.
We then explored further correlations between 29Si NMR chemical shifts and structural parameters. Among many hypotheses we studied, the proximity of the fifth closest N atom—the next-nearest beyond the four bonding N atoms—to the Si[4] site stood out. This correlation between 29Si NMR chemical shift and distance of the fifth closest N to Si is shown in Figure 9. In contrast to crystalline models of α-Si3N4 and β-Si3N4, where the first coordination shell of Si[4] is well-defined and the next-nearest neighbor is another Si atom, an amorphous structure may comprise N atoms as next-nearest neighbor in proximity to Si[4]. Interestingly, our process of distorting N positions in wII-Si3N4 to achieve higher pyramidalization (Figure 3b) also brings additional neighbors (four at a time) into the coordination sphere of the Si site, which is why we include that data in Figure 9.
Figure 9 shows that within a “critical” distance of 2.8 Å a fifth neighboring N atom has significant impact on the 29Si NMR chemical shift. Thus, a possible explanation for the observed asymmetry of the (see Figure 7) is the proximity of a fifth N in non-bonding distance between 2.5 and 2.8 Å. Previously, Carduner et al. proposed some influence of N albeit in a much further distance of 3.8 Å [28]. We find that the intrusion of additional N atoms into the coordination sphere of Si is also the principal reason for changes in δiso when distorting wII-Si3N4 models earlier. The pyramidalization of N was a geometrical effect going along the much stronger impact of increasing the coordination of Si. Figure 9 indicates that the changes in 29Si NMR chemical shifts upon distorting wII-Si3N4 are consistent with the proximity effects observed in amorphous models.
Having revealed the obvious influence of a fifth N atom in the coordination sphere of Si on its 29Si chemical shift, we can identify those impacted sites and eliminate them from the correlation between 29Si δiso and average Si-N bond length. Hence, we obtain a new correlation diagram shown in Figure 10. If we plot the deviation of δiso of amorphous Si3N4 from the correlation line β-Si3N4 for a given average bond length, we obtain the residual, which is given in Figure 10b. This residual is centered almost at 0 and, as we tested, is independent from bond length. While the far majority of data falls within +/−10 ppm of the projection obtained from scaling β-Si3N4, we see that a few Si[4] are still deviating by up to 30 ppm in chemical shift.
For the experimental data of Carduner et al. shown in Figure 7 we can now also estimate the number of Si atoms impacted by proximity of 5th N. Decomposing the total asymmetric curve using two symmetric Gaussian contributions, we find one centered at −46 ppm (σ = 6 ppm) and the other at −60 ppm (σ = 5 ppm). The ratio of areas under the two curves is 7:1, and can be interpreted that in the amorphous structure about 12% of Si encounter a 5th neighboring N in close proximity.
In further systematic analysis we looked for correlations between 29Si δiso—or any residual—and various geometrical parameters and properties. Among these were tetrahedral angles at Si[4], distance to the next Si, computed charge on N, local density around Si[4], and involvement of Si[4] in small-membered rings, especially 3-membered rings. None of these tests revealed further pronounced effects on 29Si NMR chemical shifts in Si3N4.
Overall, our results agree well with experimentally measured 29Si NMR spectra of amorphous Si3N4 or Si3N4 nanopowders, which feature a broad peak centered at −46 to −49 ppm with FWHM of around 25 ppm and distorted towards lower δiso values [5,49,50]. We find that the asymmetry can be related to Si[4] sites with a fifth N atom in proximity closer than 2.8 Å. We note, however, that contamination with oxygen and the presence of oxynitride species (Si-N3O, with 29Si δiso values of −60 to −63 ppm [49]) may also held responsible for an asymmetry.

3.5. Amorphous Hydrogenated Silicon Nitride

Amorphous silicon nitride synthesized by chemical vapor deposition (CVD) or by sol-gel methods typically contains significant amounts of hydrogen [3,4,51]. While hydrogen is incorporated mainly as NHx species, it impacts the 29Si NMR chemical shifts of a hydrogenated silicon nitride, SiNx:H. To analyze the effect, we study amorphous silicon diimide, Si(NH)2, as a model system.
Si(NH)2 is topologically equivalent to SiO2, which is why we can easily generate amorphous Si(NH)2 models from models of amorphous silica. We start with SiO2 models free of 3-rings [40], replace O by N to form the Si-N-Si link, and add the H atom with a N-H distance of 1.1 Å into the Si-N-Si plane pointing outwards. We then optimize models using our standard procedure and compute NMR signals. 29Si NMR chemical shifts range from −25 to −50 ppm, overlapping the range for 29Si δiso that we computed for amorphous silicon nitride (−20 to −70 ppm, see above). In analogy to work on vitreous silica and amorphous silicates [7,8,9,10,39,40], we can quickly establish a linear correlation between the 29Si δiso and the average Si-N-Si angle Θ on N atoms surrounding the Si[4] site (see Figure 11a).
For the angular correlation we find δiso = (28.2–0.486 Θ) ppm. Hence, the slope of the angular correlation for the nitride is just half of that for the oxide [40]. We observe a residual with a FWHM of 6.4 ppm, which is significantly higher than FWHM for SiO2 (1.0) [40], but comparable to results obtained for soda-silica and hafnia-soda-silica glasses [10]. Further analysis shows that the residual correlates with the Si-N bond lengths at the Si[4] site, see Figure 11b. According to Figure 4, this impact of Si-N bonds lengths on δiso is expected. The effect of both bond length and bond angle is summarized in the double fit equation: δ i s o = ( 28.2 − 0.486 ⋅ Θ ¯ ) + ( 141 ⋅ d ¯ S i N − 244.8 ) , with the average bond angle Θ ¯ given in degrees and the average bond length d ¯ S i N given in Å. Accordingly, the resulting FWHM of the residual for the double fit is reduced to 5.7 ppm (see Figure 11c).

4. Summary and Conclusions

We study the 29Si NMR chemical shift, δiso, in crystalline and amorphous silicon nitrides using density functional theory calculations and the GIPAW algorithm. The computational approach reproduces available experimental data of Si[4] and Si[6] sites in crystalline α-, β-, and γ-Si3N4, and predicts the δiso of a trigonal-bipyramidal Si[5] to −120 ppm. We show the significant effect of Si-N bond lengths on 29Si δiso, about 1 ppm change for 1 pm of changed bond length. For silicon dicarbodiimide, Si(NCN)2, a comparison between experimental and computed chemical shifts shows that the Si-N-C angle at N is indeed bent, and not linear as the XRD patterns indicates. We propose that the peak asymmetry of Si[4] observed in experimental spectra of amorphous silicon nitride is related to the proximity of a fifth N neighbor in non-bonding distance between 2.5 and 2.8 Å. The chemical shift of Si[4] in hydrogenated silicon nitride correlates with the Si-NH-Si angle, albeit the additional dependence on Si-N bond distance increases the complexity of an analysis. Overall, we demonstrate through several examples the power of quantum-chemical calculations for improved characterization of crystalline and amorphous silicon nitride.

Supplementary Materials

The following are available online at https://www.mdpi.com/1996-1944/11/9/1646/s1, Table S1. Results of NMR calculations of hypothetical Si3N4 structures, as well as crystallographic information files of the hypothetical structures.

Author Contributions

Conceptualization, I.P. and P.K.; Methodology, I.P. and P.K.; Validation, I.P. and P.K.; Formal Analysis, I.P. and P.K.; Writing-Original Draft Preparation, I.P. and P.K.; Writing-Review & Editing, I.P. and P.K.; Visualization, I.P. and P.K.; Project Administration, P.K.; Funding Acquisition, P.K.

Funding

This work was supported by the NSF (DMR-1463974, CMMI-1634448, OISE 1743701).

Acknowledgments

Computational work was made possible through generous grants by the Texas Advanced Computing Center (TACC) at The University of Texas at Austin.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zerr, A.; Kempf, M.; Schwarz, M.; Kroke, E.; Goken, M.; Riedel, R. Elastic moduli and hardness of cubic silicon nitride. J. Am. Ceram. Soc. 2002, 85, 86–90. [Google Scholar] [CrossRef]
  2. Riley, F.L. Silicon nitride and related materials. J. Am. Ceram. Soc. 2000, 83, 245–265. [Google Scholar] [CrossRef]
  3. Hector, A.L. Synthesis and processing of silicon nitride and related materials using preceramic polymer and non-oxide sol-gel approaches. Coord. Chem. Rev. 2016, 323, 120–137. [Google Scholar] [CrossRef] [Green Version]
  4. Sardar, K.; Bounds, R.; Carravetta, M.; Cutts, G.; Hargreaves, J.S.J.; Hector, A.L.; Hriljac, J.A.; Levason, W.; Wilson, F. Sol-gel preparation of low oxygen content, high surface area silicon nitride and imidonitride materials. Dalton Trans. 2016, 45, 5765–5774. [Google Scholar] [CrossRef] [PubMed]
  5. Sun, X.; Liu, H.T.; Cheng, H.F. Oxidation behavior of silicon nitride fibers obtained from polycarbosilane fibers via electron beam irradiation curing. RSC Adv. 2017, 7, 47833–47839. [Google Scholar] [CrossRef] [Green Version]
  6. Chung, Y.K.; Koo, J.H.; Kim, S.A.; Chi, E.O.; Cho, J.Y.; Sohn, W.B.; Kim, M.Y.; Park, C. Growth mechanism of Si3N4 nanowires from amorphous Si3N4 powders synthesized by low-temperature vapor-phase reaction. Crystengcomm 2016, 18, 3247–3255. [Google Scholar] [CrossRef]
  7. Charpentier, T.; Ispas, S.; Profeta, M.; Mauri, F.; Pickard, C.J. First-principles calculation of O-17, Si-29, and Na-23 NMR spectra of sodium silicate crystals and glasses. J. Phys. Chem. B 2004, 108, 4147–4161. [Google Scholar] [CrossRef]
  8. Charpentier, T.; Kroll, P.; Mauri, F. First-principles nuclear magnetic resonance structural analysis of vitreous silica. J. Phys. Chem. C 2009, 113, 7917–7929. [Google Scholar] [CrossRef]
  9. Ispas, S.; Charpentier, T.; Mauri, F.; Neuville, D.R. Structural properties of lithium and sodium tetrasilicate glasses: Molecular dynamics simulations versus NMR experimental and first-principles data. Solid State Sci. 2010, 12, 183–192. [Google Scholar] [CrossRef]
  10. Ponomarev, I.; Kroll, P. Impact of transition metal cations on the Si-29 NMR signal in metal oxide glasses: A dft case study of hafnia silica glass. J. Phys. Chem. C 2017, 121, 24152–24158. [Google Scholar] [CrossRef]
  11. Charpentier, T. The paw/gipaw approach for computing NMR parameters: A new dimension added to nmr study of solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. [Google Scholar] [CrossRef] [PubMed]
  12. Bonhomme, C.; Gervais, C.; Babonneau, F.; Coelho, C.; Pourpoint, F.; Azais, T.; Ashbrook, S.E.; Griffin, J.M.; Yates, J.R.; Mauri, F.; et al. First-principles calculation of NMR parameters using the gauge including projector augmented wave method: A chemist’s point of view. Chem. Rev. 2012, 112, 5733–5779. [Google Scholar] [CrossRef] [PubMed]
  13. Ferlat, G.; Charpentier, T.; Seitsonen, A.P.; Takada, A.; Lazzeri, M.; Cormier, L.; Calas, G.; Mauri, F. Boroxol rings in liquid and vitreous B2O3 from first principles. Phys. Rev. Lett. 2008, 101, 065504. [Google Scholar] [CrossRef] [PubMed]
  14. Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef]
  15. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864. [Google Scholar] [CrossRef]
  16. Kresse, G.; Hafner, J. Ab-initio molecular-dynamics simulation of the liquid-metal amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  17. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  18. Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
  19. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  20. Belsky, A.; Hellenbrandt, M.; Karen, V.L.; Luksch, P. New developments in the inorganic crystal structure database (icsd): Accessibility in support of materials research and design. Acta Crystallogr. B-Struct. Sci. 2002, 58, 364–369. [Google Scholar] [CrossRef]
  21. Toraya, H. Crystal structure refinement of alpha-Si3N4 using synchrotron radiation powder diffraction data: Unbiased refinement strategy. J. Appl. Crystallogr. 2000, 33, 95–102. [Google Scholar] [CrossRef]
  22. du Boulay, D.; Ishizawa, N.; Atake, T.; Streltsov, V.; Furuya, K.; Munakata, F. Synchrotron x-ray and ab initio studies of beta-Si3N4. Acta Crystallogr. B 2004, 60, 388–405. [Google Scholar] [CrossRef] [PubMed]
  23. Zerr, A.; Miehe, G.; Serghiou, G.; Schwarz, M.; Kroke, E.; Riedel, R.; Fuess, H.; Kroll, P.; Boehler, R. Synthesis of cubic silicon nitride. Nature 1999, 400, 340–342. [Google Scholar] [CrossRef]
  24. Schwarz, M.; Miehe, G.; Zerr, A.; Kroke, E.; Poe, B.T.; Fuess, H.; Riedel, R. Spinel-Si3N4: Multi-anvil press synthesis and structural refinement. Adv. Mater. 2000, 12, 883–887. [Google Scholar] [CrossRef]
  25. Stadler, F.; Schnick, W. The reduced nitridosilicate baSi6N8. Z. Anorg. Allg. Chem. 2007, 633, 589–592. [Google Scholar] [CrossRef]
  26. Pagano, S.; Zeuner, M.; Hug, S.; Schnick, W. Single-crystal structure determination and solid-state NMR investigations of lithium nitridosilicate Li2SiN2 synthesized by a precursor approach employing amorphous “Si(CN2)2”. Eur. J. Inorg. Chem. 2009, 1579–1584. [Google Scholar] [CrossRef]
  27. Stadler, F.; Oeckler, O.; Senker, J.; Hoppe, H.A.; Kroll, P.; Schnick, W. Sr Si6N8—A reduced nitridosilicate with a Si-Si bond. Angew. Chem. Int. Ed. 2005, 44, 567–570. [Google Scholar] [CrossRef] [PubMed]
  28. Carduner, K.R.; Blackwell, C.S.; Hammond, W.B.; Reidinger, F.; Hatfield, G.R. 29Si NMR characterization of alpha-silicon and beta-silicon nitride. J. Am. Chem. Soc. 1990, 112, 4676–4679. [Google Scholar] [CrossRef]
  29. Sekine, T.; Tansho, M.; Kanzaki, M. Si-29 magic-angle-spinning nuclear-magnetic-resonance study of spinel-type Si3N4. Appl. Phys. Lett. 2001, 78, 3050–3051. [Google Scholar] [CrossRef]
  30. Kroll, P. Modelling polymer-derived ceramics. J. Eur. Ceram. Soc. 2005, 25, 163–174. [Google Scholar] [CrossRef]
  31. Kroll, P. Structure and reactivity of amorphous silicon nitride investigated with density-functional methods. J. Non-Cryst. Solids 2001, 293, 238–243. [Google Scholar] [CrossRef]
  32. Kroll, P. A dft study of amorphous silicon oxynitride. J. Non-Cryst. Solids 2005, 351, 1127–1132. [Google Scholar] [CrossRef]
  33. Garofalini, S.H.; Luo, W.W. Molecular dynamics simulations of calcium silicate intergranular films between silicon nitride crystals. J. Am. Ceram. Soc. 2003, 86, 1741–1752. [Google Scholar] [CrossRef]
  34. Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
  35. Dasmahapatra, A.; Kroll, P. Modeling amorphous silicon nitride: A comparative study of empirical potentials. Comput. Mater. Sci. 2018, 148, 165–175. [Google Scholar] [CrossRef]
  36. Smith, J.V.; Blackwell, C.S. Nuclear magnetic-resonance of silica polymorphs. Nature 1983, 303, 223–225. [Google Scholar] [CrossRef]
  37. Bonhomme, C.; Gervais, C.; Coelho, C.; Pourpoint, F.; Azais, T.; Bonhomme-Coury, L.; Babonneau, F.; Jacob, G.; Ferrari, M.; Canet, D.; et al. New perspectives in the paw/gipaw approach: Jp-o-si coupling constants, antisymmetric parts of shift tensors and nqr predictions. Magn. Reson. Chem. 2010, 48, S86–S102. [Google Scholar] [CrossRef] [PubMed]
  38. Oestrike, R.; Yang, W.H.; Kirkpatrick, R.J.; Hervig, R.L.; Navrotsky, A.; Montez, B. High-resolution Na-23, Al-27, and Si-29 NMR-spectroscopy of framework aluminosilicate glasses. Geochim. Cosmochim. Acta 1987, 51, 2199–2209. [Google Scholar] [CrossRef]
  39. Mauri, F.; Pasquarello, A.; Pfrommer, B.G.; Yoon, Y.G.; Louie, S.G. Si-O-Si bond-angle distribution in vitreous silica from first-principles 29Si NMR analysis. Phys. Rev. B 2000, 62, R4786–R4789. [Google Scholar] [CrossRef]
  40. Nimmo, J.P.; Kroll, P. First-principles calculations and analysis of Si-29 nuclear magnetic resonance chemical shifts in silicon oxycarbide ceramics. J. Phys. Chem. C 2014, 118, 29952–29961. [Google Scholar] [CrossRef]
  41. Marumo, F.; Syono, Y. Crystal structure of Zn2SiO4-ii, a high-pressure phase of willemite. Acta Crystallogr. B-Struct. Sci. 1971, 27, 1868–1870. [Google Scholar] [CrossRef]
  42. Kroll, P. Pathways to metastable nitride structures. J. Solid State Chem. 2003, 176, 530–537. [Google Scholar] [CrossRef]
  43. Teter, D.M.; Hemley, R.J. Low-compressibility carbon nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
  44. Riedel, R.; Greiner, A.; Miehe, G.; Dressier, W.; Fuess, H.; Bill, J.; Aldinger, F. The first crystalline solids in the ternary Si-C-N system. Angew. Chem. Int. Ed. 1997, 36, 603–606. [Google Scholar] [CrossRef]
  45. Kroll, P.; Riedel, R.; Hoffmann, R. Silylated carbodiimides in molecular and extended structures. Phys. Rev. B 1999, 60, 3126–3139. [Google Scholar] [CrossRef]
  46. Kroll, P.; Andrade, M.; Yan, X.H.; Ionescu, E.; Miehe, G.; Riedel, R. Isotropic negative thermal expansion in beta-Si(NCN)2 and its origin. J. Phys. Chem. C 2012, 116, 526–531. [Google Scholar] [CrossRef]
  47. Riedel, R.; Horvath-Bordon, E.; Kroll, P.; Miehe, G.; Dzivenko, D.; Kleebe, H.J.; van Aken, P.A.; Lauterbach, S. Novel binary and ternary phases in the Si-C-N system. J. Ceram. Soc. J. 2008, 116, 674–680. [Google Scholar] [CrossRef] [Green Version]
  48. Pedone, A.; Charpentier, T.; Malavasi, G.; Menziani, M.C. New insights into the atomic structure of 45S5 bioglass by means of solid-state NMR spectroscopy and accurate first-principles simulations. Chem. Mater. 2010, 22, 5644–5652. [Google Scholar] [CrossRef]
  49. Carduner, K.R.; Carter, R.O.; Milberg, M.E.; Crosbie, G.M. Determination of phase-composition of silicon-nitride powders by Si-29 magic angle spinning nuclear-magnetic-resonance spectroscopy. Anal. Chem. 1987, 59, 2794–2797. [Google Scholar] [CrossRef]
  50. Yue, Y.; Li, D.H.; Ye, C.H. Characterization of laser synthesized silicon nitride powders with nanoscale by solid-state NMR. J. Mater. Sci. Lett. 1996, 15, 1079–1080. [Google Scholar] [CrossRef]
  51. Yamamoto, Y.; Yokota, H.; Kojima, N.; Hayashi, S.; Kobayashi, T.; Sekine, T.; Sugahara, Y. Effects of structural differences in starting materials on the formation behavior of cubic silicon nitride by shock compression. J. Ceram. Soc. J. 2013, 121, 741–744. [Google Scholar] [CrossRef] [Green Version]
Materials 11 01646 g001 550
Figure 1. Relation between experimental data and computed absolute 29Si NMR chemical shifts of Si sites in a variety of crystalline silicon nitrides. The calibration curve is a linear fit (unit slope) to the data.
Figure 1. Relation between experimental data and computed absolute 29Si NMR chemical shifts of Si sites in a variety of crystalline silicon nitrides. The calibration curve is a linear fit (unit slope) to the data.
Materials 11 01646 g001
Materials 11 01646 g002 550
Figure 2. Relation between experimental data and computed absolute 29Si NMR chemical shifts of Si sites in a variety of crystalline silicon nitrides. The calibration curve is a linear fit (unit slope) to the data.
Figure 2. Relation between experimental data and computed absolute 29Si NMR chemical shifts of Si sites in a variety of crystalline silicon nitrides. The calibration curve is a linear fit (unit slope) to the data.
Materials 11 01646 g002
Materials 11 01646 g003 550
Figure 3. (a) Representation of the pyramidalized N atom. (b) changes in 29Si NMR chemical shift with increase of the degree of pyramidalization of N atom expressed as the relation of height of nitrogen over the plane of its neighboring Si atoms (h) to the Si-N bond length (dSi-N). The correlation was obtained for the wII-Si3N4 model by changing the N position while adjusting cell parameters to maintain a Si-N bond length of 1.733 Å.
Figure 3. (a) Representation of the pyramidalized N atom. (b) changes in 29Si NMR chemical shift with increase of the degree of pyramidalization of N atom expressed as the relation of height of nitrogen over the plane of its neighboring Si atoms (h) to the Si-N bond length (dSi-N). The correlation was obtained for the wII-Si3N4 model by changing the N position while adjusting cell parameters to maintain a Si-N bond length of 1.733 Å.
Materials 11 01646 g003
Materials 11 01646 g004 550
Figure 4. Correlation between average Si-O or Si-N bond lengths and 29Si NMR chemical shifts. The y-axis has been adjusted to allow better comparison between the curves. The correlations are obtained by the scaling of SiO2 α-cristobalite and β-Si3N4 models, respectively.
Figure 4. Correlation between average Si-O or Si-N bond lengths and 29Si NMR chemical shifts. The y-axis has been adjusted to allow better comparison between the curves. The correlations are obtained by the scaling of SiO2 α-cristobalite and β-Si3N4 models, respectively.
Materials 11 01646 g004
Materials 11 01646 g005a 550Materials 11 01646 g005b 550
Figure 5. (a) 29Si δiso of Si[6] sites in hypothetical crystalline Si3N4 plotted versus average Si-N bond length. The inserted line represents data for the Si[6] site in spinel-type γ-Si3N4, computed after scaling the structure. (b) Deviation of the computed 29Si NMR δiso for the distorted Si[6] sites plotted versus the difference between shortest and longest Si-N bond for that site. The dashed line represents a linear fit to the data.
Figure 5. (a) 29Si δiso of Si[6] sites in hypothetical crystalline Si3N4 plotted versus average Si-N bond length. The inserted line represents data for the Si[6] site in spinel-type γ-Si3N4, computed after scaling the structure. (b) Deviation of the computed 29Si NMR δiso for the distorted Si[6] sites plotted versus the difference between shortest and longest Si-N bond for that site. The dashed line represents a linear fit to the data.
Materials 11 01646 g005aMaterials 11 01646 g005b
Materials 11 01646 g006 550
Figure 6. (a) Computed 29Si NMR δiso of the proposed P4n2-Si(NCN)2 obtained by contracting the volume of the structure. The chemical shift is plotted versus the corresponding “cubic” lattice parameter, a = V1/3. (b) The relation between the computed 29Si NMR δiso and the average Si-N-C angle around Si site. Experimental data of δiso in Si(NCN)2 is −103 ppm [44].
Figure 6. (a) Computed 29Si NMR δiso of the proposed P4n2-Si(NCN)2 obtained by contracting the volume of the structure. The chemical shift is plotted versus the corresponding “cubic” lattice parameter, a = V1/3. (b) The relation between the computed 29Si NMR δiso and the average Si-N-C angle around Si site. Experimental data of δiso in Si(NCN)2 is −103 ppm [44].
Materials 11 01646 g006
Materials 11 01646 g007 550
Figure 7. Replotting the data of 29Si NMR of amorphous Si3N4 according to the results of Carduner et al. in [49]. (1) the full line refers to the experimental 29Si NMR data. (2) and (3) are two Gaussian distributions (centered at −46 ppm and at −60 ppm) used for decomposing the asymmetric experimental curve. (4) is the sum of (2) and (3). The ratio of areas under Gaussians 2 and 3 is approximately 7:1.
Figure 7. Replotting the data of 29Si NMR of amorphous Si3N4 according to the results of Carduner et al. in [49]. (1) the full line refers to the experimental 29Si NMR data. (2) and (3) are two Gaussian distributions (centered at −46 ppm and at −60 ppm) used for decomposing the asymmetric experimental curve. (4) is the sum of (2) and (3). The ratio of areas under Gaussians 2 and 3 is approximately 7:1.
Materials 11 01646 g007
Materials 11 01646 g008 550
Figure 8. 29Si NMR δiso in amorphous Si3N4, plotted versus average degree of pyramidalization of neighboring N atoms (a) and average Si-N bond length (b). Red dots and lines depict the correlations obtained for distortions of crystalline models, wII-Si3N4 (left) and β-Si3N4 (right), respectively.
Figure 8. 29Si NMR δiso in amorphous Si3N4, plotted versus average degree of pyramidalization of neighboring N atoms (a) and average Si-N bond length (b). Red dots and lines depict the correlations obtained for distortions of crystalline models, wII-Si3N4 (left) and β-Si3N4 (right), respectively.
Materials 11 01646 g008
Materials 11 01646 g009 550
Figure 9. 29Si NMR δiso plotted versus the distance to the 5th nearest N atom. Black-and-white dots represent computed results for the amorphous models. Red dots and line are results for distorted wII-Si3N4 models (see Figure 3b).
Figure 9. 29Si NMR δiso plotted versus the distance to the 5th nearest N atom. Black-and-white dots represent computed results for the amorphous models. Red dots and line are results for distorted wII-Si3N4 models (see Figure 3b).
Materials 11 01646 g009
Materials 11 01646 g010a 550Materials 11 01646 g010b 550
Figure 10. (a) Correlation between 29Si δiso and average Si-N bond length for Si [4] without a fifth N within 2.8 Å. Red dots and line depict the correlation obtained for scaling crystalline β-Si3N4. (b) Histogram of deviations of data points of amorphous Si3N4 from the correlation line β-Si3N4 (“Residual”).
Figure 10. (a) Correlation between 29Si δiso and average Si-N bond length for Si [4] without a fifth N within 2.8 Å. Red dots and line depict the correlation obtained for scaling crystalline β-Si3N4. (b) Histogram of deviations of data points of amorphous Si3N4 from the correlation line β-Si3N4 (“Residual”).
Materials 11 01646 g010aMaterials 11 01646 g010b
Materials 11 01646 g011 550
Figure 11. (a) Angular correlation between average Si-N-Si angle surrounding a Si[4] site in amorphous Si(NH)2 and its 29Si chemical shift. (b) Residual (deviations of data points from linear fit) plotted vs. the average Si-N bond length. (c) Residual of the two-variable fit (bond angle and bond length; equation see text) along with the mean deviation from fit (μ) and standard deviation (σ).
Figure 11. (a) Angular correlation between average Si-N-Si angle surrounding a Si[4] site in amorphous Si(NH)2 and its 29Si chemical shift. (b) Residual (deviations of data points from linear fit) plotted vs. the average Si-N bond length. (c) Residual of the two-variable fit (bond angle and bond length; equation see text) along with the mean deviation from fit (μ) and standard deviation (σ).
Materials 11 01646 g011
Table
Table 1. Experimental 29Si NMR chemical shifts, δiso, computed absolute shifts, σiso, and predicted δiso of Si sites in a variety of crystalline silicon nitrides. The predicted value δisocalc is based on a fit to the data; see Figure 1 and Equation (1).
Table 1. Experimental 29Si NMR chemical shifts, δiso, computed absolute shifts, σiso, and predicted δiso of Si sites in a variety of crystalline silicon nitrides. The predicted value δisocalc is based on a fit to the data; see Figure 1 and Equation (1).
StructureSiteδisoexp (ppm)σisocomp (ppm)δisocomp (ppm)
BaSi6N8 [25]1−54.3−394.4−56.2
2−28.0−366.2−28.0
Li2SiN2 [26]1−34.7−374.5−36.3
SrSi6N8 [27]1−52.0−391.1−52.9
2−28.0−365.8−27.6
α-Si3N4 [21,28]1−48.9−385.4−47.2
2−46.8−384.7−46.5
β-Si3N4 [22,28]1−48.7−386.7−48.5
γ-Si3N4 [23,24,29]1 (Si[4])−50.0−390.2−52.0

Share and Cite

MDPI and ACS Style

Ponomarev, I.; Kroll, P. 29Si NMR Chemical Shifts in Crystalline and Amorphous Silicon Nitrides. Materials 2018, 11, 1646. https://doi.org/10.3390/ma11091646

AMA Style

Ponomarev I, Kroll P. 29Si NMR Chemical Shifts in Crystalline and Amorphous Silicon Nitrides. Materials. 2018; 11(9):1646. https://doi.org/10.3390/ma11091646

Chicago/Turabian Style

Ponomarev, Ilia, and Peter Kroll. 2018. "29Si NMR Chemical Shifts in Crystalline and Amorphous Silicon Nitrides" Materials 11, no. 9: 1646. https://doi.org/10.3390/ma11091646

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop