Simulation of the Impact of Ionized Impurity Scattering on the Total Mobility in Si Nanowire Transistors
Abstract
:1. Introduction
2. Simulation Method and Physics
2.1. Simulation Framework
2.2. Subband Details and Electrostatics
2.3. 1D Scattering Rates
2.3.1. Acoustic Phonon Scattering
2.3.2. Optical Phonon Scattering
2.3.3. Surface Roughness Scattering
2.3.4. Ionized Impurity Scattering
2.4. Mobility Calculation
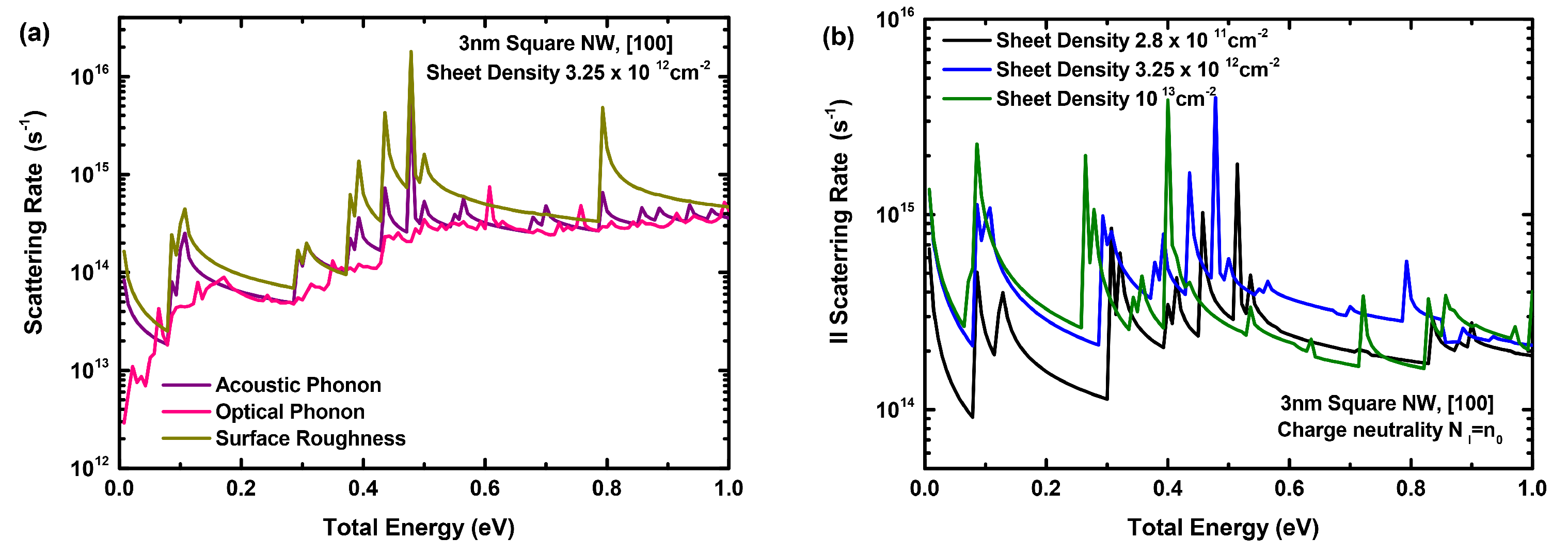
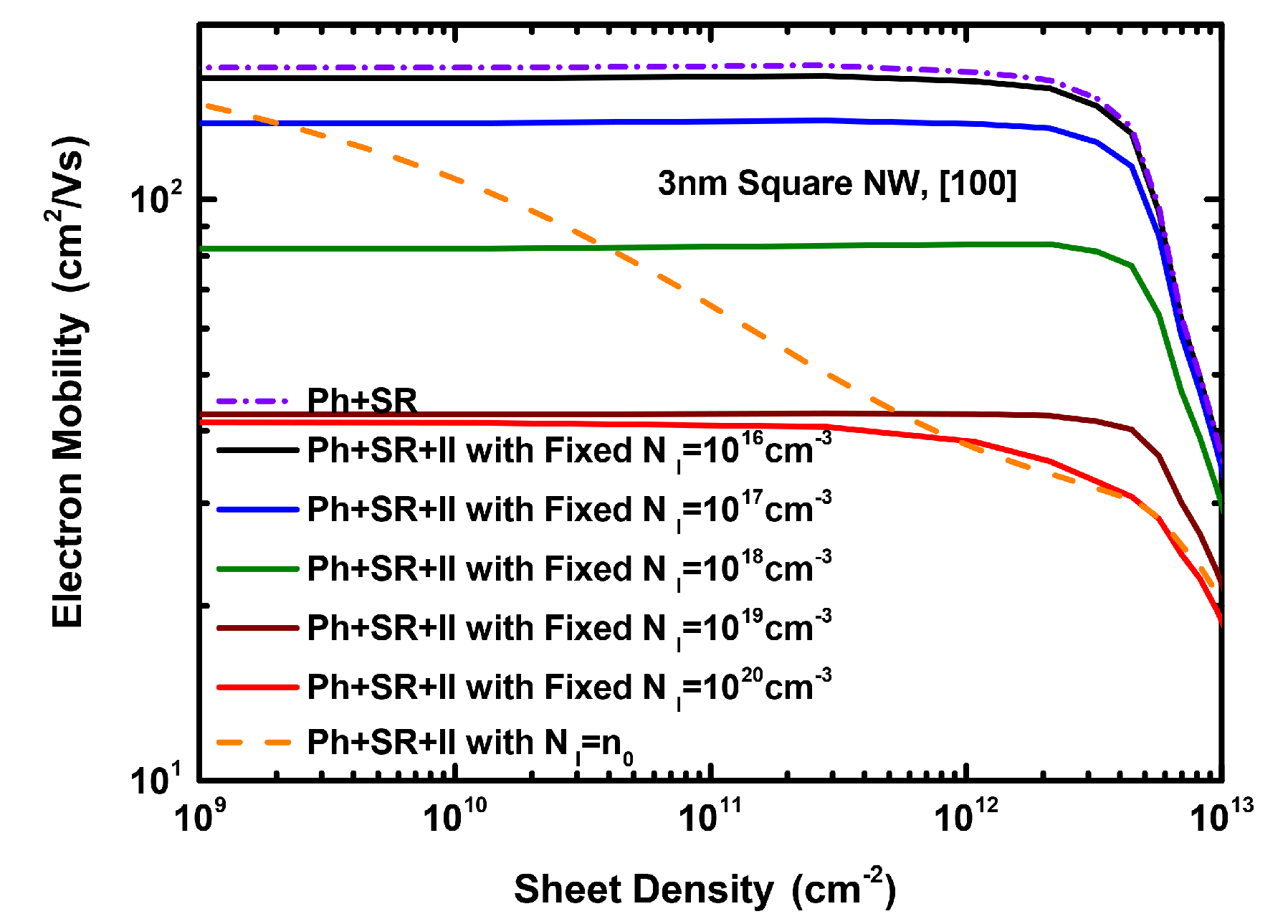
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ionescu, A.M.; Riel, H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature 2011, 479, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Björk, M.T.; Knoch, J.; Schmid, H.; Riel, H.; Riess, W. Silicon nanowire tunneling field-effect transistors. Appl. Phys. Lett. 2008, 92, 193504. [Google Scholar] [CrossRef]
- Imenabadi, R.M.; Saremi, M.; Vandenberghe, W.G. A Novel PNPN-Like Z-Shaped Tunnel Field- Effect Transistor With Improved Ambipolar Behavior and RF Performance. IEEE Trans. Electron Devices 2017, 64, 4752–4758. [Google Scholar] [CrossRef]
- Saremi, M.; Afzali-Kusha, A.; Mohammadi, S. Ground plane fin-shaped field effect transistor (GP-FinFET): A FinFET for low leakage power circuits. Microelectron. Eng. 2012, 95, 74–82. [Google Scholar] [CrossRef]
- Khandelwal, S.; Duarte, J.P.; Khan, A.I.; Salahuddin, S.; Hu, C. Impact of parasitic capacitance and ferroelectric parameters on negative capacitance FinFET characteristics. IEEE Electron Device Lett. 2017, 38, 142–144. [Google Scholar] [CrossRef]
- Ferry, D.K.; Gilbert, M.J.; Akis, R. Some considerations on nanowires in nanoelectronics. IEEE Trans. Electron Devices 2008, 55, 2820–2826. [Google Scholar] [CrossRef]
- Appenzeller, J.; Knoch, J.; Bjork, M.T.; Riel, H.; Schmid, H.; Riess, W. Toward nanowire electronics. IEEE Trans. Electron Device 2008, 55, 2827–2845. [Google Scholar] [CrossRef]
- Yu, B.; Wang, L.; Yuan, Y.; Asbeck, P.M.; Taur, Y. Scaling of nanowire transistors. IEEE Trans. Electron Device 2008, 55, 2846–2858. [Google Scholar] [CrossRef]
- Lu, W.; Xie, P.; Lieber, C.M. Nanowire transistor performance limits and applications. IEEE Trans. Electron Device 2008, 55, 2859–2876. [Google Scholar] [CrossRef]
- Tienda-Luna, I.M.; Ruiz, F.G.; Godoy, A.; Biel, B.; Gamiz, F. Surface roughness scattering model for arbitrarily oriented silicon nanowires. J. Appl. Phys. 2011, 110, 084514. [Google Scholar] [CrossRef]
- Jin, S.; Fischetti, M.V.; Tang, T.-W. Modeling of electron mobility in gated silicon nanowires at room temperature: Surface roughness scattering, dielectric screening, and band nonparabolicity. J. Appl. Phys. 2007, 102, 083715. [Google Scholar] [CrossRef]
- Sadi, T.; Towie, E.; Nedjalkov, M.; Riddet, C.; Alexander, C.; Wang, L.; Georgiev, V.; Brown, A.; Millar, C.; Asenov, A. One-dimensional multi-subband Monte Carlo simulation of charge transport in Si nanowire transistors. In Proceedings of the Simulation of Semiconductor Processes and Devices 2016, Nuremberg, Germany, 5 October 2016; pp. 23–26. [Google Scholar] [CrossRef]
- Zhang, W.; Delerue, C.; Niquet, Y.-M.; Allan, G.; Wang, E. Atomistic modeling of electron-phonon coupling and transport properties in n-type [110] silicon nanowires. Phys. Rev. B 2010, 82, 115319. [Google Scholar] [CrossRef]
- Niquet, Y.-M.; Delerue, C.; Rideau, D.; Videau, B. Fully atomistic simulations of phonon-limited mobility of electrons and holes in 〈001〉-, 〈110〉-, and 〈111〉-oriented Si nanowires. IEEE Trans. Electron Device 2012, 59, 1480–1487. [Google Scholar] [CrossRef]
- Niquet, Y.-M.; Delerue, C.; Krzeminski, C. Effects of strain on the carrier mobility in silicon nanowires. Nano Lett. 2012, 12, 3545–3550. [Google Scholar] [CrossRef] [PubMed]
- Ramayya, E.B.; Vasileska, D.; Goodnick, S.M.; Knezevic, I. Electron transport in silicon nanowires: The role of acoustic phonon confinement and surface roughness scattering. J. Appl. Phys. 2008, 104, 063711. [Google Scholar] [CrossRef] [Green Version]
- GARAND User Guide. Synopsys, Inc. 2017. Available online: https://solvnet.synopsys.com (accessed on 31 December 2018).
- Neophytou, N.; Kosina, H. Atomistic simulations of low-field mobility in Si nanowires: Influence of confinement and orientation. Phys. Rev. B 2011, 84, 085313–085328. [Google Scholar] [CrossRef]
- Medina-Bailon, C.; Sadi, T.; Nedjalkov, M.; Lee, J.; Berrada, S.; Carrillo-Nunez, H.; Georgiev, V.; Selberherr, S.; Asenov, A. Study of the 1D scattering mechanisms’ impact on the mobility in Si nanowire transistors. In Proceedings of the 2018 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS), Granada, Spain, 19–21 March 2018. [Google Scholar] [CrossRef]
- Nedjalkov, M.; Ellinghaus, P.; Weinbub, J.; Sadi, T.; Asenov, A.; Dimov, I.; Selberherr, S. Stochastic analysis of surface roughness models in quantum wires. Comput. Phys. Commun. 2018, 228, 30–37. [Google Scholar] [CrossRef]
- Boykin, T.B.; Klimeck, G.; Oyafuso, F. Valence band effective-mass expressions in the sp3d5s* empirical tight-binding model applied to a Si and Ge parametrization. Phys. Rev. B 2004, 69, 115201. [Google Scholar] [CrossRef]
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645–705. [Google Scholar] [CrossRef]
- Asenov, A. Random dopant induced threshold voltage lowering and fluctuations in sub-0.1 μm MOSFETs: A 3-D atomistic simulation study. IEEE Trans. Electron Device 1998, 45, 2505–2513. [Google Scholar] [CrossRef]
- Akhavan, N.D.; Jolley, G.; Umana-Membreno, G.A.; Antoszewski, J.; Faraone, L. Discrete Dopant Impurity Scattering in p-Channel Silicon Nanowire Transistors: A k.p Approach. IEEE Trans. Electron Device 2014, 61, 386–393. [Google Scholar] [CrossRef]
- Vallett, A.L.; Minassian, S.; Kaszuba, P.; Datta, S.; Redwing, J.M.; Mayer, T.S. Fabrication and Characterization of Axially Doped Silicon Nanowire Tunnel Field-Effect Transistors. Nano Lett. 2010, 10, 4813–4818. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.D.D.; Lee, C.S.; Au, F.C.K.; Tong, S.Y.; Lee, S.T. Small-Diameter Silicon Nanowire Surfaces. Science 2003, 299, 1874–1877. [Google Scholar] [CrossRef] [PubMed]
- Markussen, T.; Rurali, R.; Jauho, A.-P.; Brandbyge, M. Scaling Theory Put into Practice: First-Principles Modeling of Transport in Doped Silicon Nanowires. Phys. Rev. Lett. 2007, 99, 076803. [Google Scholar] [CrossRef] [PubMed]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadi, T.; Medina-Bailon, C.; Nedjalkov, M.; Lee, J.; Badami, O.; Berrada, S.; Carrillo-Nunez, H.; Georgiev, V.; Selberherr, S.; Asenov, A. Simulation of the Impact of Ionized Impurity Scattering on the Total Mobility in Si Nanowire Transistors. Materials 2019, 12, 124. https://doi.org/10.3390/ma12010124
Sadi T, Medina-Bailon C, Nedjalkov M, Lee J, Badami O, Berrada S, Carrillo-Nunez H, Georgiev V, Selberherr S, Asenov A. Simulation of the Impact of Ionized Impurity Scattering on the Total Mobility in Si Nanowire Transistors. Materials. 2019; 12(1):124. https://doi.org/10.3390/ma12010124
Chicago/Turabian StyleSadi, Toufik, Cristina Medina-Bailon, Mihail Nedjalkov, Jaehyun Lee, Oves Badami, Salim Berrada, Hamilton Carrillo-Nunez, Vihar Georgiev, Siegfried Selberherr, and Asen Asenov. 2019. "Simulation of the Impact of Ionized Impurity Scattering on the Total Mobility in Si Nanowire Transistors" Materials 12, no. 1: 124. https://doi.org/10.3390/ma12010124
APA StyleSadi, T., Medina-Bailon, C., Nedjalkov, M., Lee, J., Badami, O., Berrada, S., Carrillo-Nunez, H., Georgiev, V., Selberherr, S., & Asenov, A. (2019). Simulation of the Impact of Ionized Impurity Scattering on the Total Mobility in Si Nanowire Transistors. Materials, 12(1), 124. https://doi.org/10.3390/ma12010124






