Mechanical Behaviour of Stamped Aluminium Alloy Components by Means of Response Surfaces
Abstract
1. Introduction
2. Materials
3. Methodology
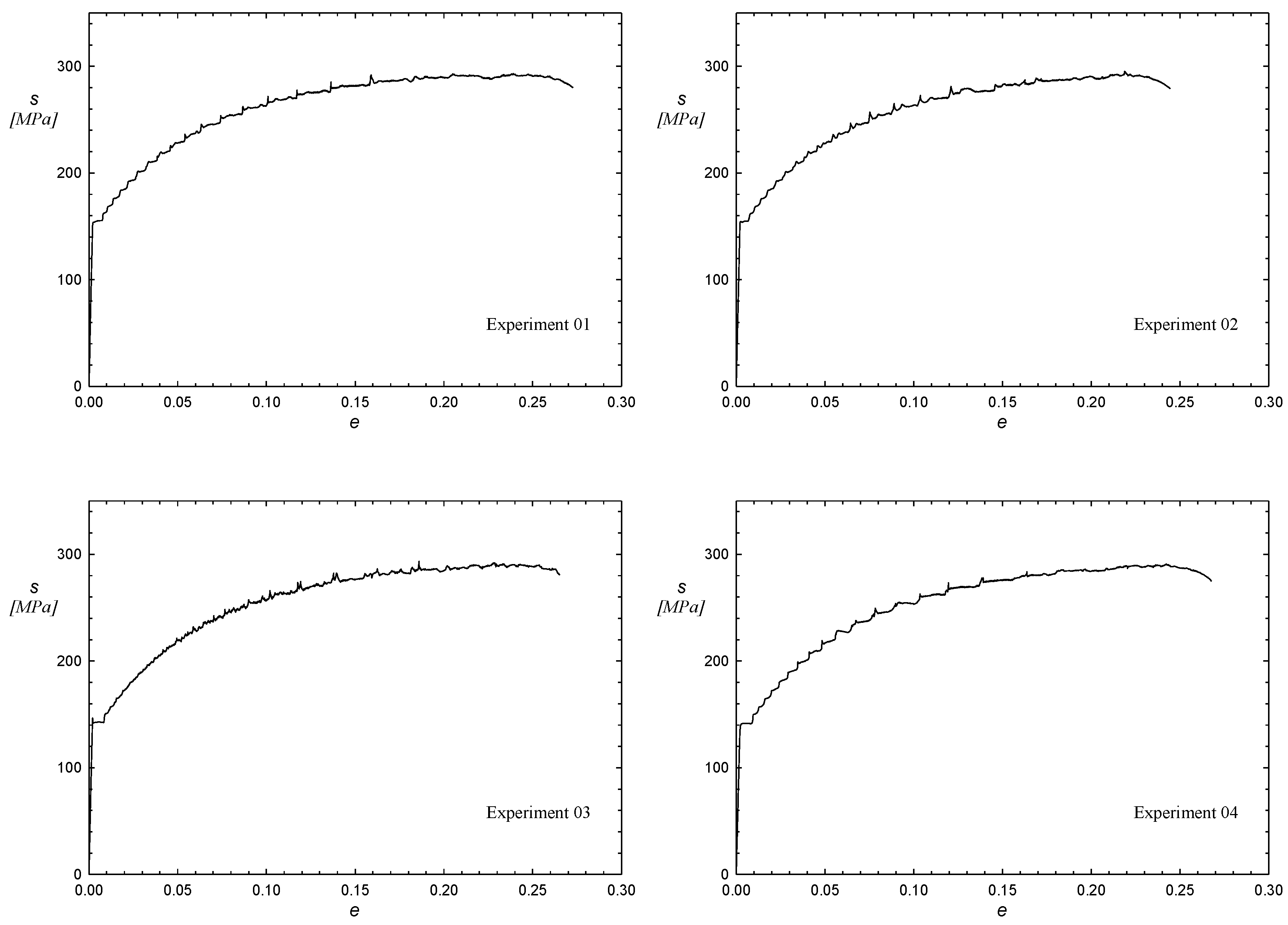
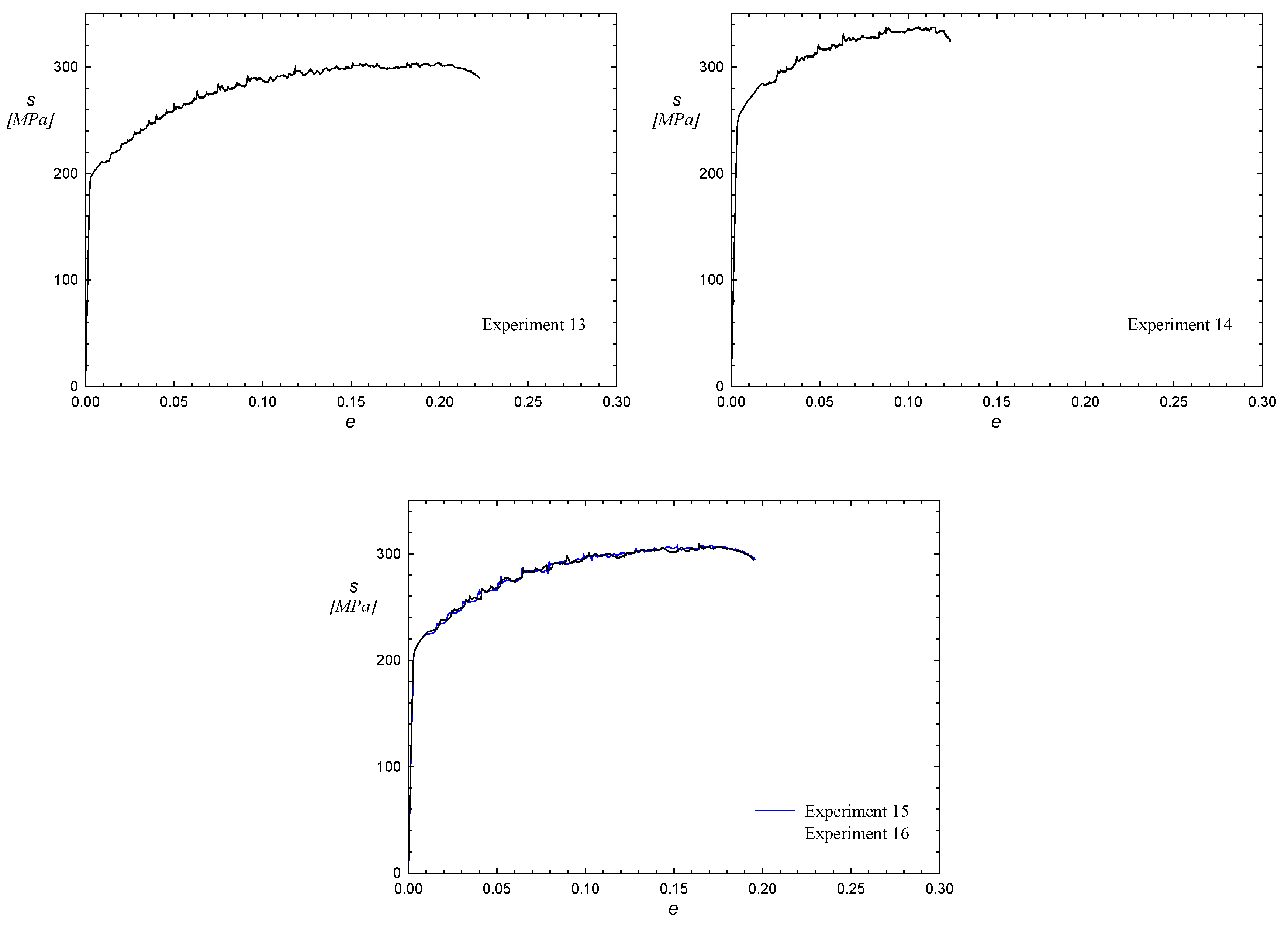
3.1. Experimental Tests
3.2. Response Surface
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santos, A.D.; Reis, A.; Duarte, J.F.; Teixeira, P.; Rocha, A.B.; Oliveira, M.C.; Alves, J.L.; Menezes, L. A benchmark for validation of numerical results in sheet metal forming. J. Mater. Process. Tech. 2004, 155, 1980–1985. [Google Scholar] [CrossRef][Green Version]
- Aydemir, A.; De Vree, J.H.P.; Brekelmans, W.A.M.; Geers, M.G.D.; Sillekens, W.H.; Werkhoven, R.J. An adaptive simulation approach designed for tube hydroforming processes. J. Mater. Process. Tech. 2005, 159, 303–310. [Google Scholar] [CrossRef]
- Ting, D.; Yuqi, L.; Zhibing, Z.; Zhigang, L. Fast FE analysis system for sheet metal stamping—FASTAMP. J. Mater. Process. Tech. 2007, 187, 402–406. [Google Scholar] [CrossRef]
- Cuesta, I.I.; Alegre, J.M. Hardening evaluation of stamped aluminium alloy components using the small punch test. Eng. Fail. Anal. 2012, 26, 240–246. [Google Scholar] [CrossRef]
- Khuri, A.I.; Cornell, J.A. Statistics: Textbooks and monographs, 81. In Response Surfaces: Design and Analyses; Marcel Dekker: New York, NY, USA, 1987. [Google Scholar]
- Kuehl, R.O. Diseño de Experimentos: Principios Estadísticos Para el Diseño y Análisis de Investigaciones; Thomson Learning: Toronto, ON, Canada, 2001. [Google Scholar]
- Montgomery, D.C. Diseño y análisis de experimentos; Grupo Editorial Iberoamérica: Madrid, Spain, 1991. [Google Scholar]
- Cuesta, I.I.; Alegre, J.M. Determination of plastic collapse load of pre-cracked Small Punch Test specimens by means of response surfaces. Eng. Fail. Anal. 2012, 23, 1–9. [Google Scholar] [CrossRef]
- Palanivel, R.; Koshy Mathews, P.; Murugan, N. Development of mathematical model to predict the mechanical properties of friction stir welded AA6351 aluminium alloy. J. Eng. Sci. Technol. Rev. 2011, 4, 25–31. [Google Scholar] [CrossRef]
- Kumar, P.M.; Kumar, B.C. Modeling of machining parameters for MRR in EDM using response surface methodology. Proc. NCMSTA 2008, 8, 534–542. [Google Scholar]
- Mondal, D.P.; Das, S.; Prasad, B.K. Study of erosive-corrosive wear characteristic of an aluminium alloy composite through factorial design of experiments. Wear 1998, 217, 1–6. [Google Scholar] [CrossRef]
- Shetty, R.; Pai, R.B.; Rao, S.S.; Kamath, V. Machinability study on discontinuously reinforced aluminium composites (DRACs) using response surface methodology and Taguchi’s design of experiments under dry cutting condition. Maejo Int. J. Sci. Technol. 2008, 2, 227–239. [Google Scholar]
- Rana, R.S.; Purohit, R.; Mishra, P.M.; Sahu, P.; Dwivedi, S. Optimization of mechanical properties of AA 5083 nano SiC composites using design of experiment technique. In Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2017; pp. 3882–3890. [Google Scholar]
- Lin, S.; Nie, Z.; Huang, H.; Li, B. Annealing behavior of a modified 5083 aluminum alloy. In Materials and Design; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1607–1612. [Google Scholar]
- Sato, S.; Okoshi, N. Mechanical properties of 5083 and 7N01 aluminum alloy pre-deformed by simple tension. J. Jpn. Ins. Light Met. 1977, 27, 480–487. [Google Scholar] [CrossRef]
- Hecht, R.L.; Kannan, K. Superplasticity and Superplastic Forming; Ghosh, A.K., Bieler, T.R., Eds.; Minerals, Metals and Materials Society: Warrendale, PA, USA, 1995; p. 259. [Google Scholar]
- Kaibyshev, R.; Musin, F.; Lesuer, D.R.; Nieh, T.G. Superplastic behavior of an Al–Mg alloy at elevated temperatures. Mater. Sci. Eng. A 2003, 342, 169–177. [Google Scholar] [CrossRef]
- ASTM E 8M. Standard test methods of tension testing of metallic materials In Annual Book or ASTM Standards; American Society for Testing and Materials: West Conshohocken, PA, USA, 2001. [Google Scholar]
- Mathieu, D.; Beal, A.; Phan-Tan-Luu, R. NEMRODW, LPRAI, Marsella. Available online: http://www.nemrodw.com (accessed on 5 June 2019).





| Mn (%) | Si (%) | Cr (%) | Cu (%) | Pb (%) | Fe (%) | Ti (%) | Mg (%) |
|---|---|---|---|---|---|---|---|
| 0.436 | 0.186 | 0.083 | 0.063 | 0.016 | 0.393 | 0.012 | 4.449 |
| Variable Parameters | |
|---|---|
| (min.) | [20,60] |
| (°C) | [90,180] |
| (%) | [0,15] |
| Experiment Matrix | Experimentation Plan | Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment NUM. | (min) | (°C) | (%) | (MPa) | (MPa) | (%) | |||
| 1 | –1 | –1 | –1 | 20 | 90 | 0 | 155.3 | 293.1 | 27.27 |
| 2 | 1 | –1 | –1 | 60 | 90 | 0 | 155.1 | 295.3 | 24.46 |
| 3 | –1 | 1 | –1 | 20 | 180 | 0 | 143.1 | 293.3 | 26.53 |
| 4 | 1 | 1 | –1 | 60 | 180 | 0 | 142.2 | 290.7 | 26.77 |
| 5 | –1 | –1 | 1 | 20 | 90 | 15 | 295.4 | 342.5 | 13.45 |
| 6 | 1 | –1 | 1 | 60 | 90 | 15 | 281.7 | 335.9 | 12.05 |
| 7 | –1 | 1 | 1 | 20 | 180 | 15 | 215.5 | 318.3 | 20.55 |
| 8 | 1 | 1 | 1 | 60 | 180 | 15 | 211.2 | 315.8 | 17.26 |
| 9 | −1.682 | 0 | 0 | 6.4 | 135 | 7.5 | 223.7 | 308.9 | 21.30 |
| 10 | 1.682 | 0 | 0 | 73.6 | 135 | 7.5 | 208.6 | 309.8 | 18.82 |
| 11 | 0 | −1.682 | 0 | 40 | 59.3 | 7.5 | 264.7 | 317.8 | 14.43 |
| 12 | 0 | 1.682 | 0 | 40 | 210.7 | 7.5 | 176.3 | 303.6 | 27.14 |
| 13 | 0 | 0 | −1.682 | 40 | 135 | −5.1# | 202.1 | 304.2 | 22.25 |
| 14 | 0 | 0 | 1.682 | 40 | 135 | 20.1 | 265.6 | 342.7 | 10.87 |
| 15 | 0 | 0 | 0 | 40 | 135 | 7.5 | 214.9 | 308.3 | 19.66 |
| 16 | 0 | 0 | 0 | 40 | 135 | 7.5 | 214.6 | 309.5 | 19.51 |
(Experiment 9 and 13 Deactivated) | ||||||
|---|---|---|---|---|---|---|
| Coefficient | Value | Significance (%) | Value | Significance (%) | Value | Significance (%) |
| b0 | 214.41 | 0.0445 *** | 309.42 | <0.01 *** | 19.38 | 0.246 ** |
| b1 | −1.58 | 2.89 * | −0.49 | 78.2 | −0.87 | 2.10 * |
| b2 | −23.19 | 0.157 ** | −5.09 | 2.39 * | 2.52 | 0.723 ** |
| b3 | 51.50 | 0.0890 *** | 14.58 | 0.0129 *** | −4.37 | 0.413 ** |
| b11 | −1.76 | 3.18 * | −0.59 | 78.8 | 0.57 | 3.93 * |
| b22 | 1.27 | 3.59 * | −0.35 | 86.9 | 0.88 | 2.53 * |
| b33 | −13.26 | 0.381 ** | 3.57 | 11.3 | −0.50 | 4.12 * |
| b12 | 0.56 | 8.6 | −0.47 | 84.0 | 0.24 | 10.0 |
| b13 | −1.63 | 2.96 * | −0.85 | 71.7 | −0.36 | 6.8 |
| b23 | −15.71 | 0.307 ** | −4.95 | 6.9 | 1.37 | 1.76 * |
| Experimentation Plan | Responses | |||||
|---|---|---|---|---|---|---|
| Experiment NUM. | ||||||
| 17 | 40 | 135 | 17.87 | 259.1 | 338.2 | 12.38 |
| 18 | 15 | 180 | 0 | 143.4 | 301.2 | 25.0 |
| 19 | 15 | 180 | 0 | 142.3 | 301.7 | 23.7 |
| Experiment NUM. | Exp. | Calc. | Diff. | Exp. | Calc. | Diff. | Exp. | Calc. | Diff. |
|---|---|---|---|---|---|---|---|---|---|
| 17 | 259.1 | 260.2 | −1.1 | 338.2 | 336.3 | 1.9 | 12.38 | 12.4 | −0.02 |
| 18 | 143.4 | 139.9 | 3.5 | 301.2 | 297.1 | 4.1 | 25.0 | 26.5 | −1.5 |
| 19 | 142.3 | 139.9 | 2.4 | 301.7 | 297.1 | 4.6 | 23.7 | 26.5 | −2.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuesta, I.I.; Almaguer-Zaldivar, P.M.; Alegre, J.M. Mechanical Behaviour of Stamped Aluminium Alloy Components by Means of Response Surfaces. Materials 2019, 12, 1838. https://doi.org/10.3390/ma12111838
Cuesta II, Almaguer-Zaldivar PM, Alegre JM. Mechanical Behaviour of Stamped Aluminium Alloy Components by Means of Response Surfaces. Materials. 2019; 12(11):1838. https://doi.org/10.3390/ma12111838
Chicago/Turabian StyleCuesta, Isidoro Iván, Pavel Michel Almaguer-Zaldivar, and Jesús Manuel Alegre. 2019. "Mechanical Behaviour of Stamped Aluminium Alloy Components by Means of Response Surfaces" Materials 12, no. 11: 1838. https://doi.org/10.3390/ma12111838
APA StyleCuesta, I. I., Almaguer-Zaldivar, P. M., & Alegre, J. M. (2019). Mechanical Behaviour of Stamped Aluminium Alloy Components by Means of Response Surfaces. Materials, 12(11), 1838. https://doi.org/10.3390/ma12111838





