In Silico Optimization of Femoral Fixator Position and Configuration by Parametric CAD Model
Abstract
:1. Introduction
2. Materials and Methods
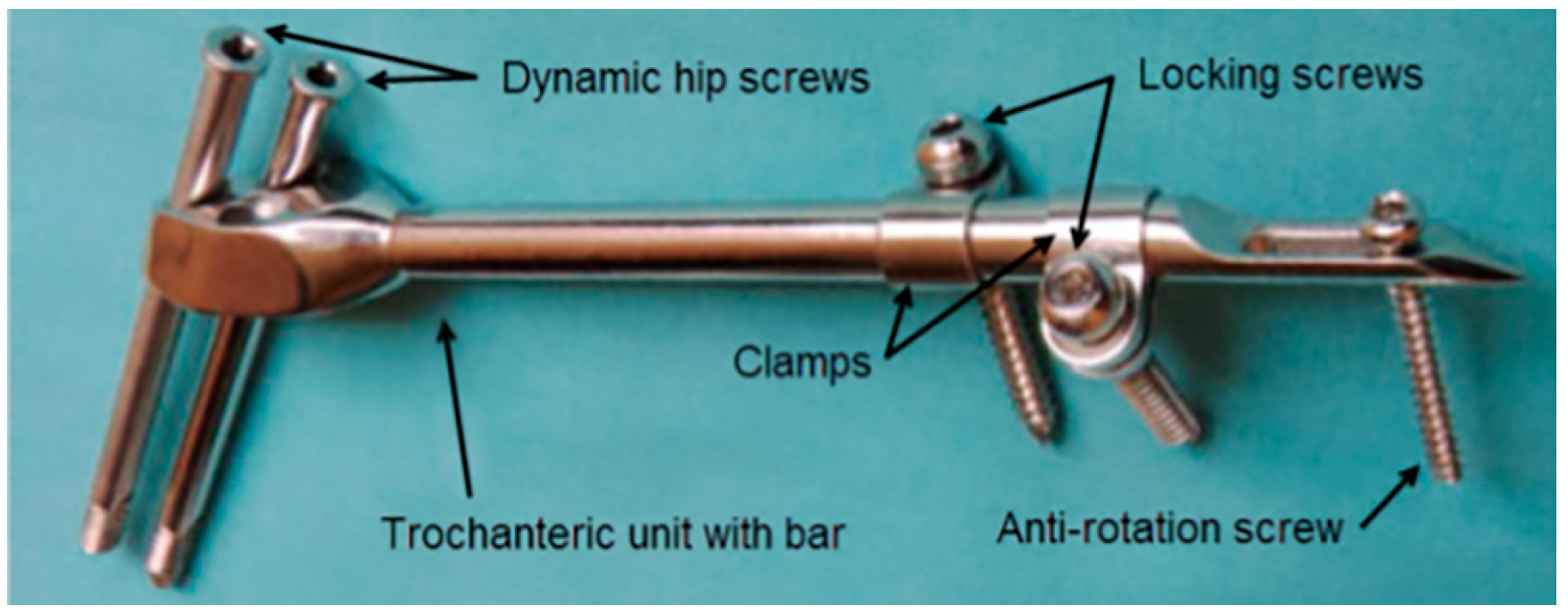
2.1. Fixation Device
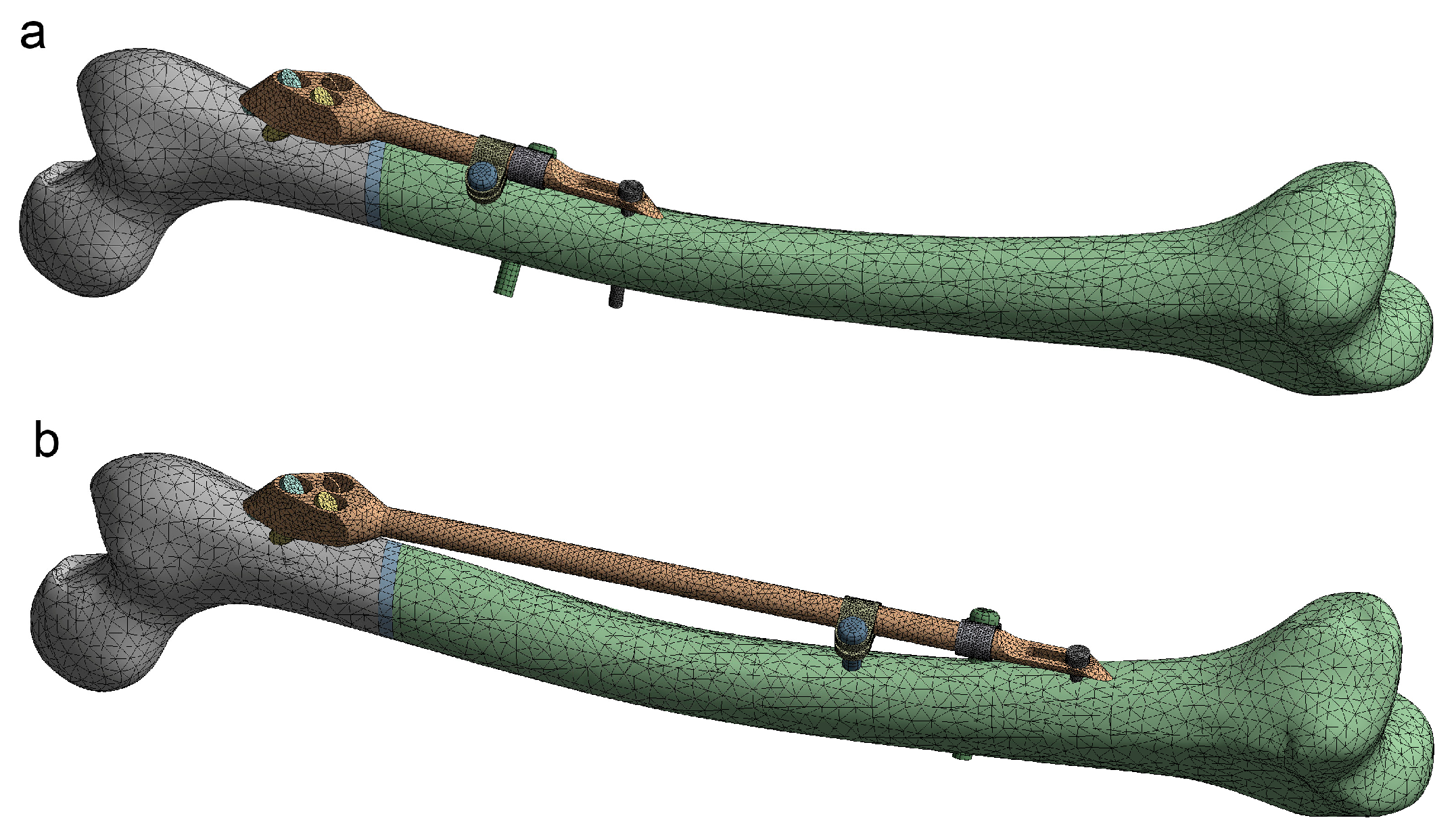
2.2. Approach to CAD Modeling of the Femur–SIF Assembly
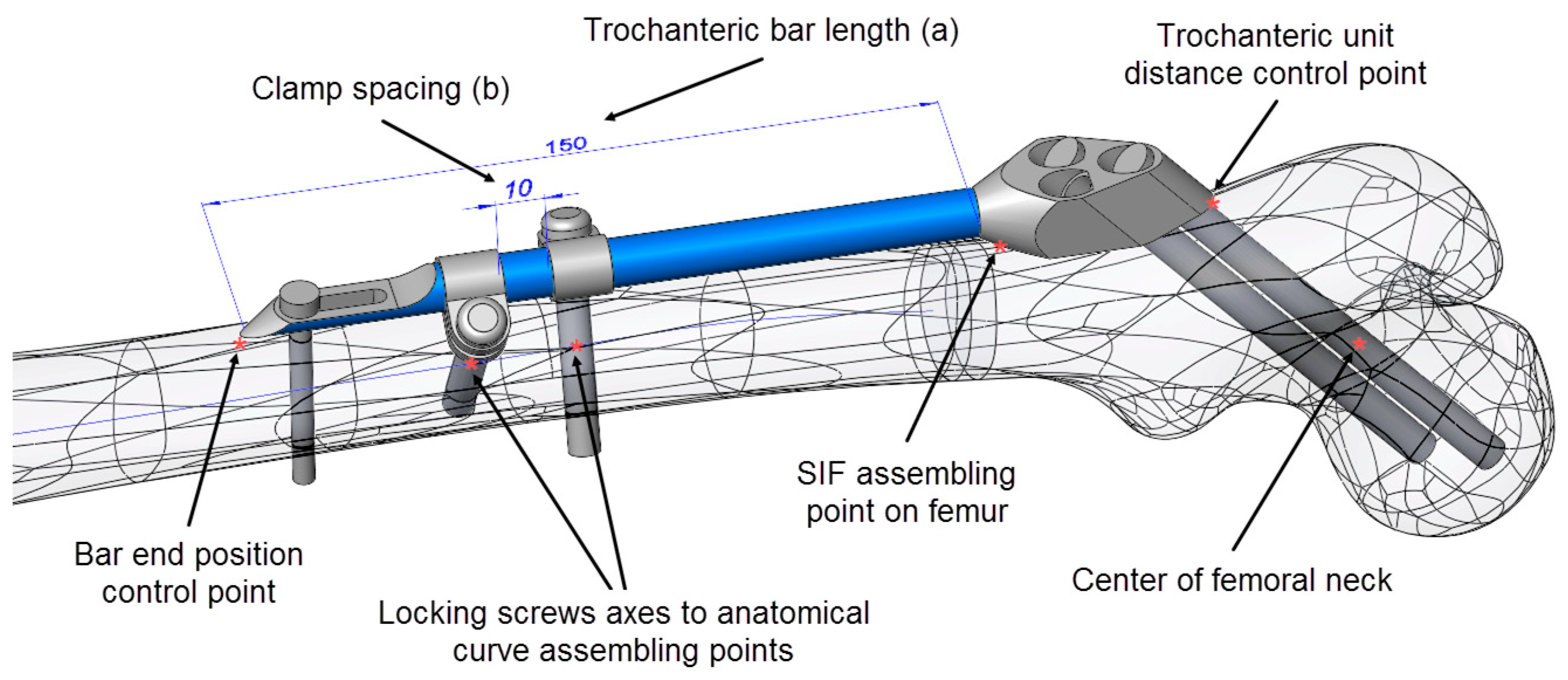
2.3. Anatomical Landmarks on the CAD Model of the Femur
2.4. SIF Configuration and Assembly Constraints
- Bar length (discrete)
- Clamp spacing (continuous)
- The coincidence of the symmetry plane of the trochanteric unit and a newly introduced point on the intersection of the femur surface and the A–P plane (the “SIF assembling point on femur” in Figure 3), placed distally from the initial breakthrough point on the femur surface and proximally from the fracture, at equal distances.
- The distance between the trochanteric unit and the femur surface (Figure 4).
- The positioning of the bar end, such that it closely followed the anatomical axis. This was achieved by projecting the anatomic curve on the femur surface in the direction parallel to the symmetry plane of the fixator and by creating an assembly component containing a single point, which was assembled both to the projected curve and the fixator end.
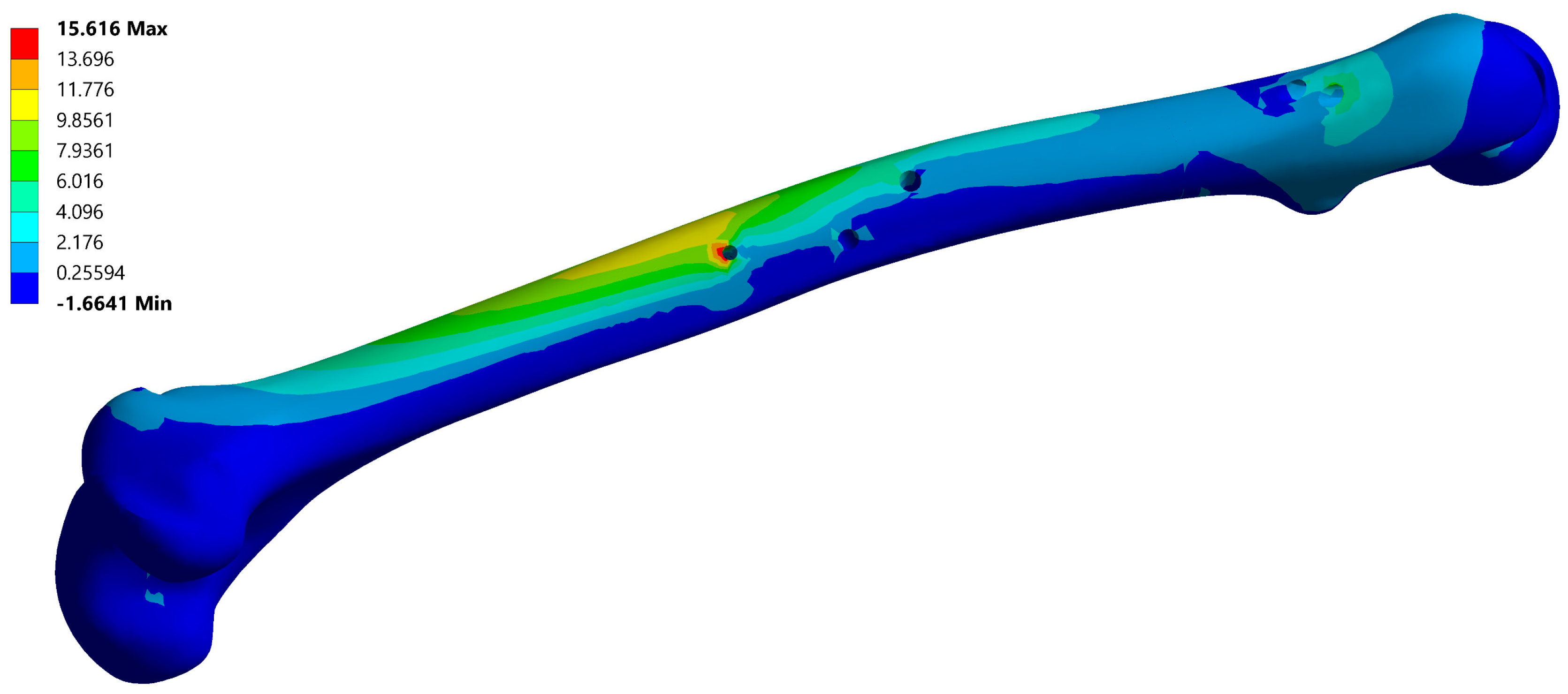
2.5. FE Model and Simulation
3. Results
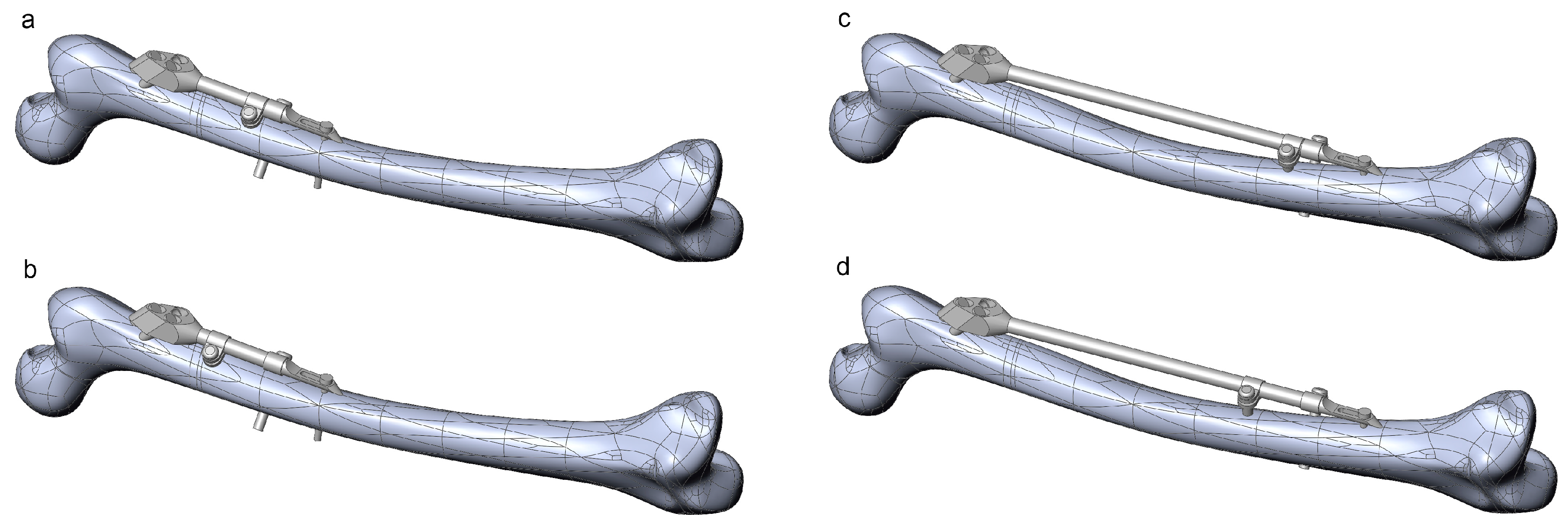
3.1. Instances of Femur–SIF CAD and FE Models
3.2. Sensitivity Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mittal, R.; Banerjee, S. Proximal femoral fractures: principles of management and review of literature. J. Clin. Orthop. Trauma 2012, 3, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Perren, S. Evolution of the internal fixation of long bone fractures: the scientific basis of biological internal fixation:Choosing a new balance between stability and biology. J. Bone Jt. Surg. Br. Vol. 2002, 84, 1093–1110. [Google Scholar] [CrossRef]
- Floyd, J.; O’toole, R.; Stall, A.; Forward, D.; Nabili, M.; Shillingburg, D.; Hsieh, A.; Nascone, J. Biomechanical comparison of proximal locking plates and blade plates for the treatment of comminuted subtrochanteric femoral fractures. J. Orthop. Trauma 2009, 23, 628–633. [Google Scholar] [CrossRef] [PubMed]
- Lunsjö, K.; Ceder, L.; Tidermark, J.; Hamberg, P.; Larsson, B.E.; Ragnarsson, B.; Knebel, R.W.; Allvin, I.; Hjalmars, K.; Norberg, S. Extramedullar fixation of 107 subtrochanteric fractures: A randomized multicenter trial of the Medoff sliding plate versus 3 other screw–plate systems. Acta Orthop. Scand. 1999, 70, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Pavić, A.; Kodvanj, J.; Surjak, M. Determining the stability of novel external fixator by using measuring system Aramis. The. Vjesn. 2013, 20, 995–999. [Google Scholar]
- Christensen, P.; Klarbring, A. An Introduction to Structural Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Vol. 153, pp. 1–214. [Google Scholar]
- Eberle, S.; Gerber, C.; Von Oldenburg, G.; Högel, F.; Augat, P. A biomechanical evaluation of orthopaedic implants for hip fractures by finite element analysis and in–vitro tests. Proc. Inst. Mech. Eng., Part H J. Eng. Med. 2010, 224, 1141–1152. [Google Scholar] [CrossRef] [PubMed]
- Samsami, S.; Saberi, S.; Sadighi, S.; Rouhi, G. Comparison of three fixation methods for femoral neck fracture in young adults: Experimental and numerical investigations. J. Med. Biol. Eng. 2015, 35, 566–579. [Google Scholar] [CrossRef] [PubMed]
- Sowmianarayanan, S.; Chandrasekaran, A.; Kumar, K. Finite element analysis of a subtrochanteric fractured femur with dynamic hip screw, dynamic condylar screw, and proximal femur nail implants-a comparative study. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2008, 222, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yang, M.; Wu, L.; Niu, W. A biomechanical comparison of two intramedullary implants for subtrochanteric fracture in two healing stages: A finite element analysis. Appl. Bionics Biomech. 2015, 2015, 7. [Google Scholar] [CrossRef]
- Yuan, G.X.; Shen, Y.H.; Chen, B.; Zhang, W.B. Biomechanical comparison of internal fixations in osteoporotic intertrochanteric fracture. A finite element analysis. Saudi Med. J. 2012, 33, 732–739. [Google Scholar]
- Castro, A.; Completo, A.; Simões, J.; Flores, P. Modelling and simulation of alternative designs for the femur–implant interface of Journey patellofemoral prosthesis. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 1464420718774074. [Google Scholar] [CrossRef]
- Konya, M.; Verim, Ö. Numerical optimization of the position in femoral head of proximal locking screws of proximal femoral nail system; biomechanical study. Balk. Med. J. 2017, 34, 425. [Google Scholar] [CrossRef] [PubMed]
- Korunović, N.; Trajanović, M.; Mitković, M.; Vitković, N.; Stevanović, D. A parametric study of selfdynamisable internal fixator used in femoral fracture treatment. In Proceedings of the NAFEMS World Congress 2015 inc. the 2nd International SPDM Conference, San Diego, CA, USA, 21–24 June 2015; p. 17. [Google Scholar]
- Simeonov, M.; Korunović, N.; Trajanović, M.; Zehn, M.; Mitković, M. Sensitivity of selfdynamisable internal fixator to change of bar length and clamp distance. In Proceedings of the 7th International Conference on Information Society and Techology ICIST, Kopaonik, Serbia, 12–15 March 2017. [Google Scholar]
- Lee, C.H.; Hsu, C.C.; Chaing, L. An Optimization Study for the Bone-Implant Interface Performance of Lumbar Vertebral Body Cages Using a Neurogenetic Algorithm and Verification Experiment. J. Med. Biol. Eng. 2018, 38, 22–32. [Google Scholar] [CrossRef]
- Guo, L.X.; Yin, J.Y. Finite element analysis and design of an interspinous device using topology optimization. Med. Biol. Eng. Comput. 2019, 57, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Smith, R. Structural analysis and optimization of the support device used for a proximal fracture of the femur. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2008. [Google Scholar]
- Zou, Z.; Liao, S.H.; Luo, S.D.; Liu, Q.; Liu, S.J. Semi–automatic segmentation of femur based on harmonic barrier. Comput. Methods Programs Biomed. 2017, 143, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Chu, C.; Bai, J.; Wu, X.; Zheng, G. MASCG: Multi–atlas segmentation constrained graph method for accurate segmentation of hip CT images. Med. Image Anal. 2015, 26, 173–184. [Google Scholar] [CrossRef] [PubMed]
- Almeida, D.; Ruben, R.; Folgado, J.; Fernandes, P.; Audenaert, E.; Verhegghe, B.; De Beule, M. Fully automatic segmentation of femurs with medullary canal definition in high and in low resolution CT scans. Med. Eng. Phys. 2016, 38, 1474–1480. [Google Scholar] [CrossRef] [PubMed]
- Rudek, M.; Gumiel, Y.; Canciglierir Jr, O.; Asofu, N.; Bichinho, G. A CAD–based conceptual method for skull prosthesis modelling. Facta Univ. Ser. Mech. Eng. 2017, 16, 285–296. [Google Scholar] [CrossRef]
- Huang, H.; Xiang, C.; Zeng, C.; Ouyang, H.; Wong, K.K.L.; Huang, W. Patient–specific geometrical modeling of orthopedic structures with high efficiency and accuracy for finite element modeling and 3D printing. Australas. Phys. Eng. Sci. Med. 2015, 38, 743–753. [Google Scholar] [CrossRef]
- Ehlke, M.; Ramm, H.; Lamecker, H.; Hege, H.C.; Zachow, S. Fast generation of virtual X–ray images for reconstruction of 3D anatomy. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2673–2682. [Google Scholar] [CrossRef]
- Kainmueller, D.; Lamecker, H.; Zachow, S.; Hege, H.C. An Articulated Statistical Shape Model for Accurate Hip Joint Segmentation. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 6345–6351. [Google Scholar]
- Stojkovic, M.; Veselinovic, M.; Vitkovic, N.; Marinkovic, D.; Trajanovic, M.; Arsic, S.; Mitkovic, M. Reverse Modelling of Human Long Bones Using T–Splines–Case of Tibia. The. Vjesn. 2018, 25, 1753–1760. [Google Scholar]
- Almeida, D.; Ruben, R.; Folgado, J.; Fernandes, P.; Gamelas, J.; Verhegghe, B.; De Beule, M. Automated femoral landmark extraction for optimal prosthesis placement in total hip arthroplasty. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2844. [Google Scholar] [CrossRef] [PubMed]
- Edwards, B.; Miller, R.; Derrick, T. Femoral strain during walking predicted with muscle forces from static and dynamic optimization. J. Biomech. 2016, 49, 1206–1213. [Google Scholar] [CrossRef] [PubMed]
- Phillips, A. The femur as a musculo–skeletal construct: A free boundary condition modelling approach. Med. Eng. Phys. 2009, 31, 673–680. [Google Scholar] [CrossRef] [PubMed]
- Pakhaliuk, V.; Poliakov, A. Simulation of wear in a spherical joint with a polymeric component of the total hip replacement considering activities of daily living. Facta Univ. Ser. Mech. Eng. 2018, 16, 51–63. [Google Scholar] [CrossRef]
- Mitkovic, M.; Milenkovic, S.; Micic, I.; Mladenovic, D.; Mitkovic, M. Results of the femur fractures treated with the new selfdynamisable internal fixator (SIF). Eur. J. Trauma Emerg. Surg. 2012, 38, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Micic, I.; Mitkovic, M.; Park, I.H.; Mladenovic, D.; Stojiljkovic, P.; Golubovic, Z.; Jeon, I.H. Treatment of subtrochanteric femoral fractures using Selfdynamisable internal fixator. Clin. Orthop. Surg. 2010, 2, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Trajanović, M.; Korunović, N.; Milovanović, J.; Vitković, N.; Mitković, M. Application of computer models of Mitković selfdynabizable internal fixator in rehabilitation of femur traumas. Facta Univ. Ser. Mech. Eng. 2010, 8, 27–38. [Google Scholar]
- Vitković, N.; Milovanović, J.; Korunović, N.; Trajanović, M.; Stojković, M.; Mišić, D.; Arsić, S. Software system for creation of human femur customized polygonal models. Comput. Sci. Inf. Syst. 2013, 10, 1473–1497. [Google Scholar] [CrossRef]
- ANSYS®. Academic Research Mechanical, Release 17.1, Help System, Workbench User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Korunovic, N.; Trajanovic, M.; Stevanovic, D.; Vitkovic, N.; Stojkovic, M.; Milovanovic, J.; Ilic, D. Material characterization ISSUES in FEA of long bones. In Proceedings of the SEECCM III 3rd South–East European Conference on Computational Mechanics—An ECCOMAS and IACM Special Interest Conference, Kos Island, Greece, 12–14 June 2013; pp. 12–14. [Google Scholar]
- Taddei, F.; Schileo, E.; Helgason, B.; Cristofolini, L.; Viceconti, M. The material mapping strategy influences the accuracy of CT–based finite element models of bones: an evaluation against experimental measurements. Med. Eng. Phys. 2007, 29, 973–979. [Google Scholar] [CrossRef]
- Ishida, T.; Nishimura, I.; Tanino, H.; Higa, M.; Ito, H.; Mitamura, Y. Use of a genetic algorithm for multiobjective design optimization of the femoral stem of a cemented total hip arthroplasty. Artif. Organs 2011, 35, 404–410. [Google Scholar] [CrossRef]
- Chanda, S.; Gupta, S.; Pratihar, D.K. A combined neural network and genetic algorithm based approach for optimally designed femoral implant having improved primary stability. Appl. Soft Comput. 2016, 38, 296–307. [Google Scholar] [CrossRef]
- Chen, X.; He, K.; Chen, Z.A. Novel Computer–Aided Approach for Parametric Investigation of Custom Design of Fracture Fixation Plates. Comput. Math. Methods Med. 2017, 2017, 7. [Google Scholar] [CrossRef]
- Bah, M.; Nair, P.; Browne, M. Mesh morphing for finite element analysis of implant positioning in cementless total hip replacements. Med. Eng. Phys. 2009, 31, 1235–1243. [Google Scholar] [CrossRef]
- Viceconti, M.; Casali, M.; Massari, B.; Cristofolini, L.; Bassini, S.; Toni, A. The ‘standardized femur program’proposal for a reference geometry to be used for the creation of finite element models of the femur. J. Biomech. 1996, 29, 1241. [Google Scholar] [CrossRef]





| Component | Material | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|---|
| SIF | Stainless steel (ASTM F138-03) | 210 | 0.3 | min. 680 |
| Femur | Bone | 5 | 0.25 | 105 |
| Fracture zone | Callus | 1.16 | 0.25 | 105 |
| Instance Number | Bar Length (a) (mm) | Clamp Spacing (b) (mm) | Maximal Fixator Stress (MPa) |
|---|---|---|---|
| 1 | 100 | 1 | 353.26 |
| 2 | 100 | 10 | 341.41 |
| 3 | 100 | 19 | 330.54 |
| 4 | 100 | 28 | 333.15 |
| 5 | 150 | 1 | 307.04 |
| 6 | 150 | 10 | 317.18 |
| 7 | 150 | 19 | 297.94 |
| 8 | 150 | 28 | 312.13 |
| 9 | 200 | 1 | 270.38 |
| 10 | 200 | 10 | 261.84 |
| 11 | 200 | 19 | 255.28 |
| 12 | 200 | 28 | 251.45 |
| 13 | 250 | 1 | 222.59 |
| 14 | 250 | 10 | 217.08 |
| 15 | 250 | 19 | 216.63 |
| 16 | 250 | 28 | 208.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korunovic, N.; Marinkovic, D.; Trajanovic, M.; Zehn, M.; Mitkovic, M.; Affatato, S. In Silico Optimization of Femoral Fixator Position and Configuration by Parametric CAD Model. Materials 2019, 12, 2326. https://doi.org/10.3390/ma12142326
Korunovic N, Marinkovic D, Trajanovic M, Zehn M, Mitkovic M, Affatato S. In Silico Optimization of Femoral Fixator Position and Configuration by Parametric CAD Model. Materials. 2019; 12(14):2326. https://doi.org/10.3390/ma12142326
Chicago/Turabian StyleKorunovic, Nikola, Dragan Marinkovic, Miroslav Trajanovic, Manfred Zehn, Milorad Mitkovic, and Saverio Affatato. 2019. "In Silico Optimization of Femoral Fixator Position and Configuration by Parametric CAD Model" Materials 12, no. 14: 2326. https://doi.org/10.3390/ma12142326
APA StyleKorunovic, N., Marinkovic, D., Trajanovic, M., Zehn, M., Mitkovic, M., & Affatato, S. (2019). In Silico Optimization of Femoral Fixator Position and Configuration by Parametric CAD Model. Materials, 12(14), 2326. https://doi.org/10.3390/ma12142326






