Microstructure and Texture Evolution of Mg–Gd–Y–Zn–Zr Alloy by Compression–Torsion Deformation
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
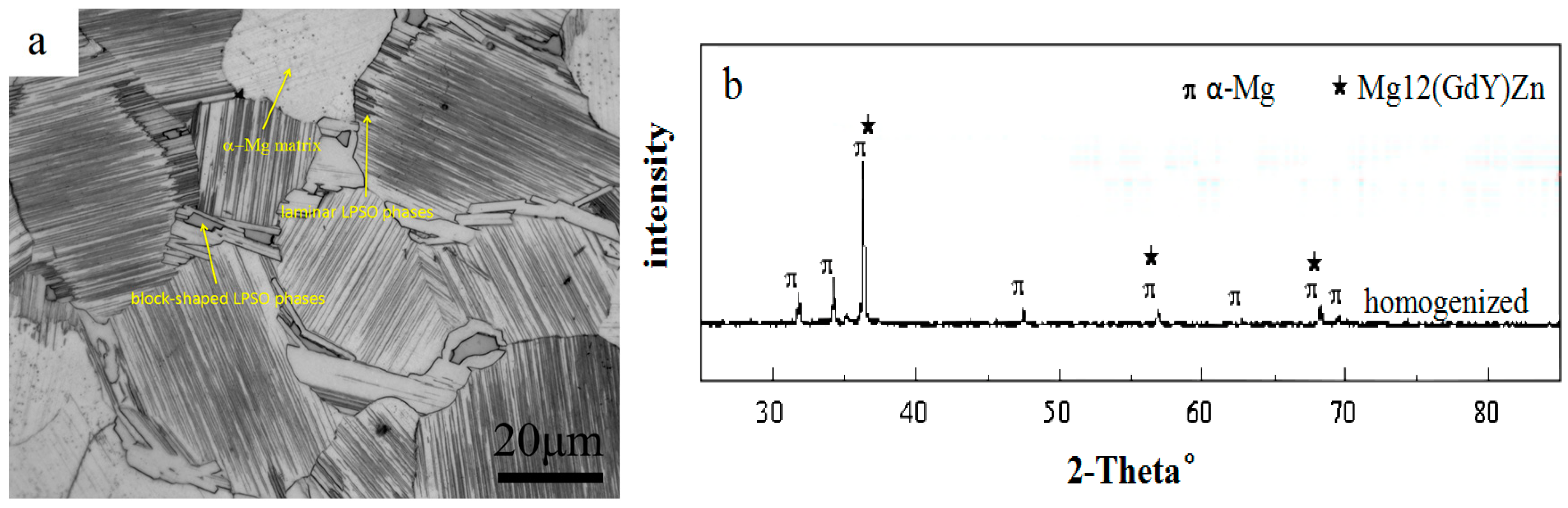
3.1. Microstructure of the Alloy before Compression–Torsion Deformation
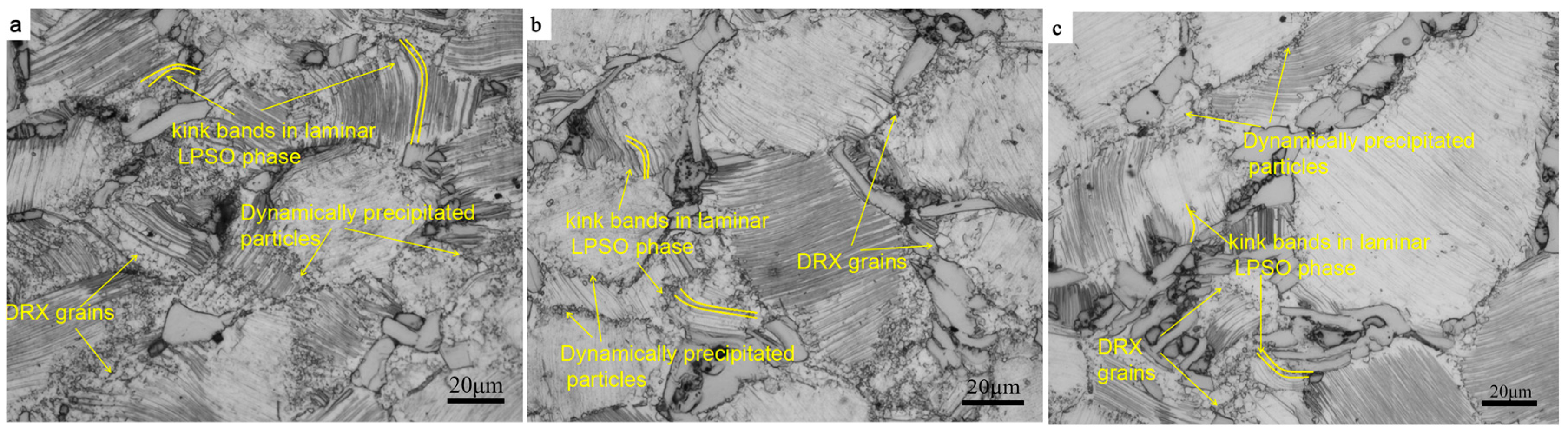
3.2. Evolution of Edge Microstructure at Different Strain Rates
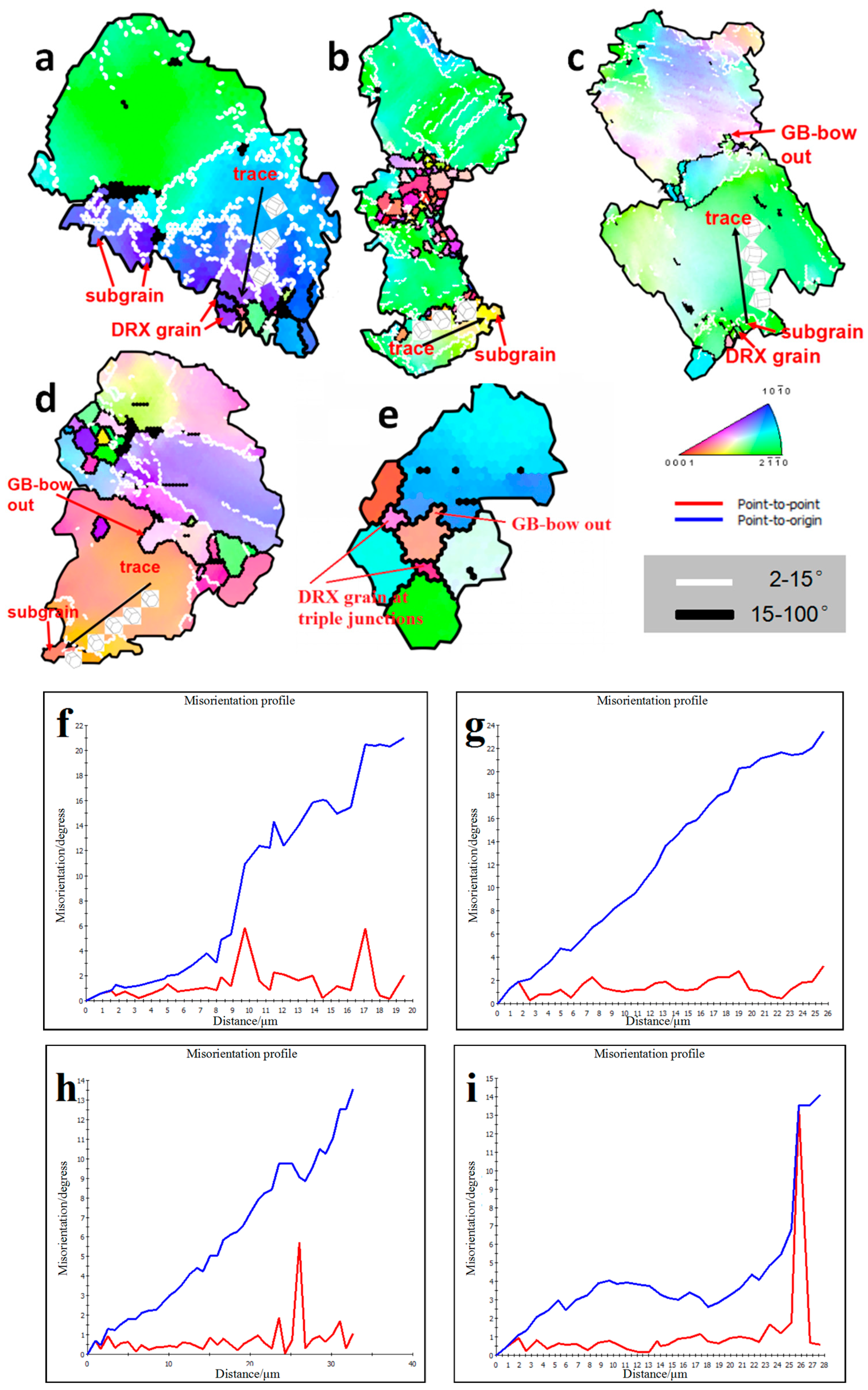
3.2.1. Observation of Microstructure
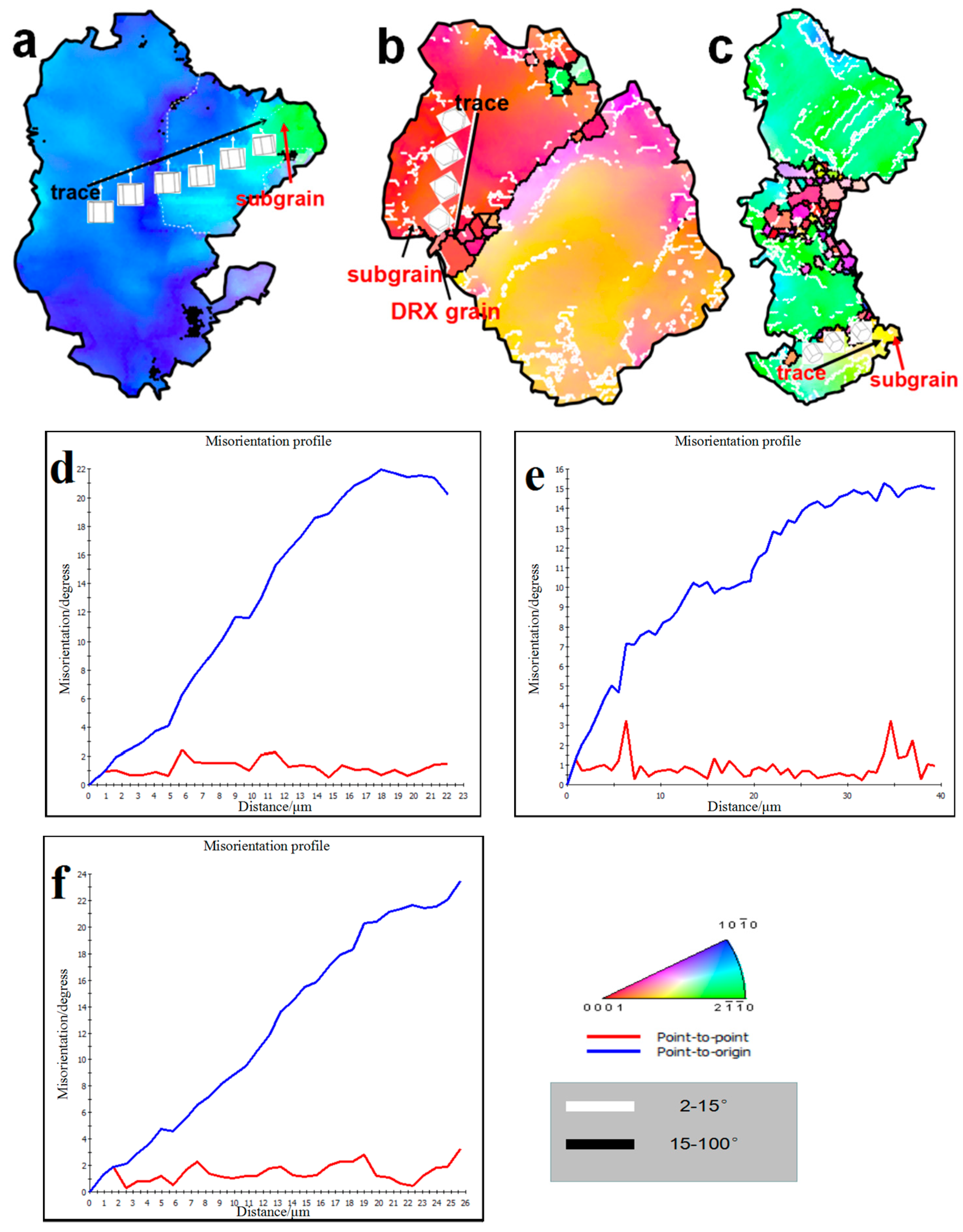
3.2.2. Dynamic Crystallization Mechanism
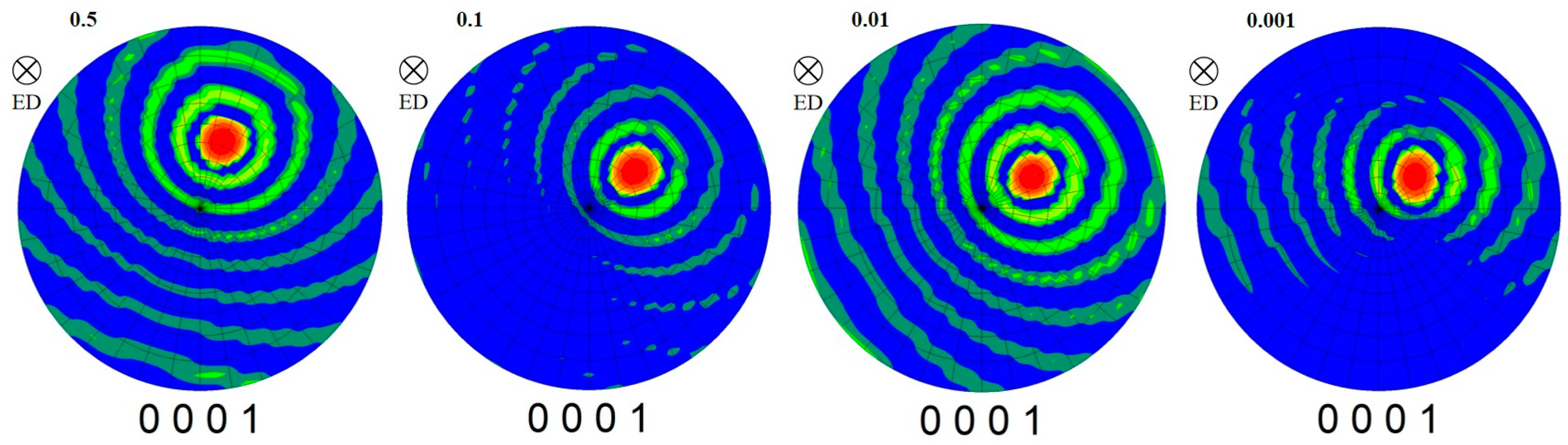
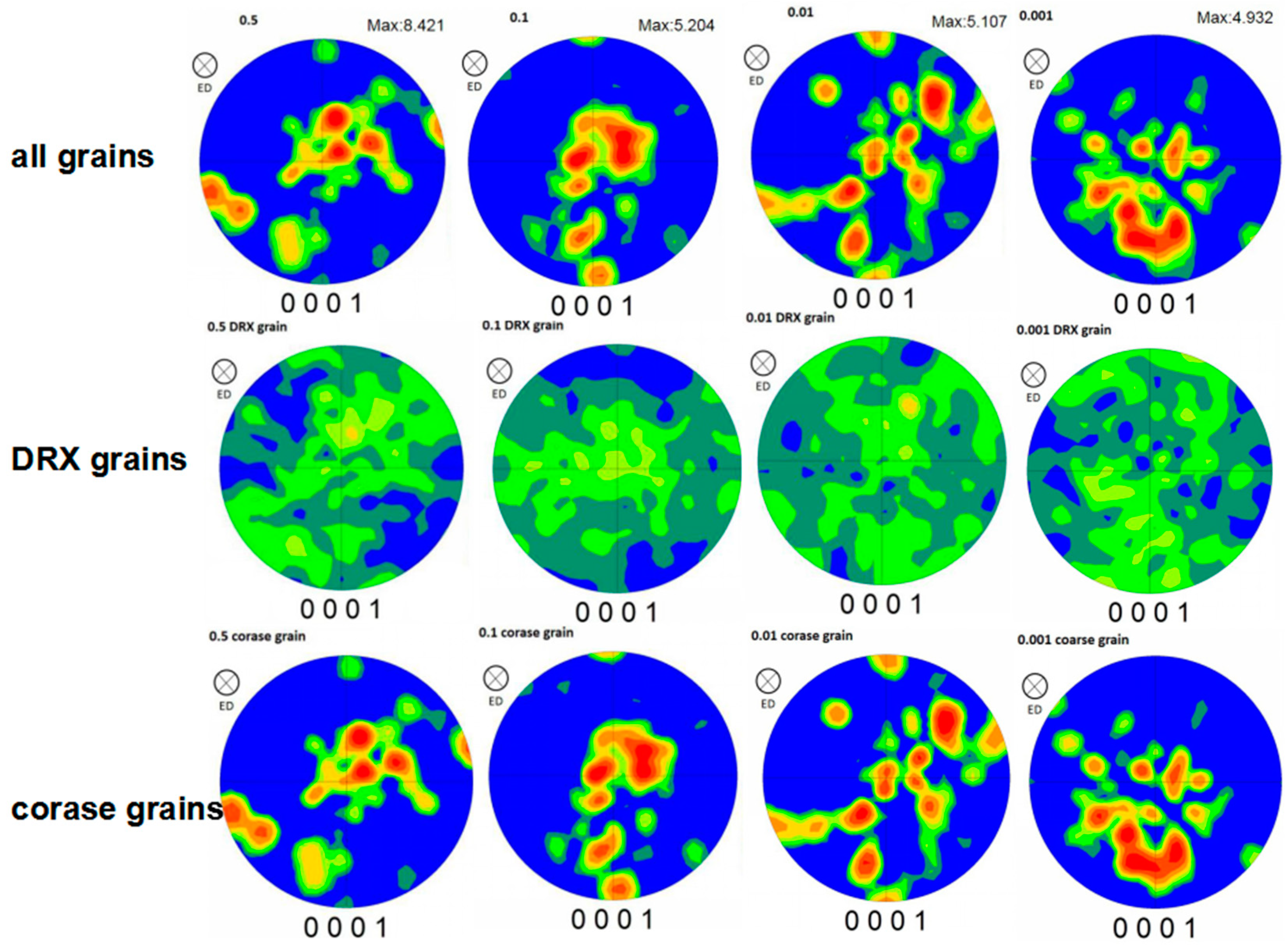
3.3. Texture Evolution of Edge Part under Different Strain Rates
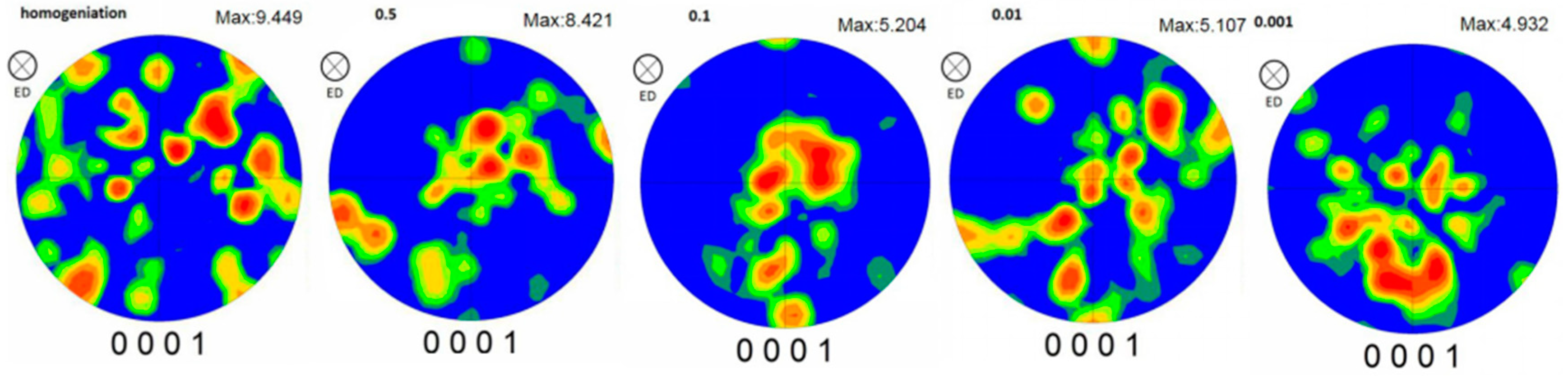
3.3.1. Evolution of Texture
3.3.2. Effect of Recrystallizing on Texture
3.4. Evolution of Gradient Microstructure in Compression–Torsion Deformation
3.4.1. Microstructure
3.4.2. Dynamic Crystallization Mechanism
3.4.3. Texture Evolution of Gradient Microstructure
4. Conclusions
- The number of kink bands in the microstructure is gradually reduced with the decrease of the strain rate, and basically disappears when the strain rate is 0.01 s−1. The number of dynamic precipitated particles increased with the decrease of strain rate; its distribution is more uniform, and its morphology develops from a single sphere to a state of spheroidal and acicular coexistence. The number of dynamic precipitated particles and the number of kink bands increase in the direction of the increasing radius.
- The number of DRXs increased gradually with the decrease of the strain rate; the number of DRXs increased greatly from 0.5 s−1 to 0.1 s−1, which increased little between the strain rates 0.1–0.001 s−1. The type of DRX mechanism changed from CDRX to DDRX, and the DRXs grew under the effect of thermal activation energy at the strain rate of 0.001 s−1. As the strain increases along the direction of radius increase, the number of DRXs in the microstructure increased along the direction of increasing radius. The DRX types along the radius increase are all CDRX types when the strain rate was 0.1 s−1.
- The compression–torsion deformation will weaken the texture, and the degree of texture weakening was increased with the decrease of strain rate. The position of the maximum pole intensity and the compression direction deflected by about 45° at each strain rate. The strength texture was mainly contributed by the undeformed coarse grains. The texture increased weakly along the direction of the radius increase, and the angle deviating from the compression direction increased.
Author Contributions
Funding
Conflicts of Interest
References
- Honma, T.; Ohkubo, T.; Hono, K.; Kamado, S. Chemistry of nanoscale precipitates in Mg–2.1Gd–0.6Y–0.2Zr (at.%) alloy investigated by the atom probe technique. Mater. Sci. Eng. A 2005, 395, 301–306. [Google Scholar] [CrossRef]
- Oñorbe, E.; Garcés, G.; Pérez, P.; Adeva, P. Effect of the LPSO volume fraction on the microstructure and mechanical properties of Mg–Y2X–ZnXalloys. J. Mater. Sci. 2012, 47, 10851093. [Google Scholar] [CrossRef]
- Wang, J.M.; Song, P.F.; Gao, S.; Wei, Y.Y.; Pan, F.S. Influence of Y on the phase composition and mechanical properties of as-extruded Mg–Zn–Y–Zr magnesium alloys. J. Mater. Sci. 2012, 47, 20052010. [Google Scholar] [CrossRef]
- Wang, J.F.; Gao, S.; Song, P.F.; Huang, X.F.; Shi, Z.Z.; Pan, F.S. Effects of phase composition on the mechanical properties and damping capacities of as-extruded Mg–Zn–Y–Zr alloys. J. Alloys Compd. 2011, 509, 8567–8572. [Google Scholar] [CrossRef]
- Homma, T.; Kunito, N.; Kamado, S. Fabrication of extraordinary high-strength magnesium alloy by hot extrusion. Scr. Mater. 2009, 61, 644–647. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, M.Y.; Xu, S.W.; Wu, K.; Wang, E.D.; Fan, G.H.; Kamado, S.; Wang, G.J.; Lv, X.Y. Ultra high-strength Mg–Gd–Y–Zn–Zr alloy sheets processed by large-strain hot rolling and ageing. Mater. Sci. Eng. A 2012, 547, 93–98. [Google Scholar] [CrossRef]
- Nie, K.B.; Wu, K.; Wang, X.J.; Deng, K.K.; Wu, Y.W.; Zheng, M.Y. Multidirectional forging of magnesium matrix composites: Effect on microstructures and tensile properties. Mater. Sci. Eng. A 2010, 527, 7364–7368. [Google Scholar] [CrossRef]
- Sakamoto, M.; Akiyama, S.; Ogi, K. Suppression of ignition and burning of molten Mg alloys by Ca bearing stable oxide film. J. Mater. Sci. 1997, 16, 1048–1050. [Google Scholar]
- Li, L.; Zhang, X.X. Hot compression deformation behavior and processing parameters of a cast Mg–Gd–Y–Zr alloy. Mater. Sci. Eng. A 2011, 528, 1396–1401. [Google Scholar] [CrossRef]
- Xu, C.; Pan, J.P.; Nakata, T.; Qiao, X.G.; Chi, Y.Q.; Zheng, M.Y.; Kamado, S. Hot compression deformation behavior of Mg–9Gd–2.9Y–1.9Zn–0.4Zr–0.2Ca (wt%) alloy. Mater. Char. 2017, 124, 40–49. [Google Scholar] [CrossRef]
- Zhang, D.X.; Tan, Z.; Huo, Q.H.; Xiao, Z.Y.; Fang, Z.W.; Yang, X.Y. Dynamic recrystallization behaviors of Mg–Gd–Y–Zn–Zr alloy with different morphologies and distributions of LPSO phases. Mater. Sci. Eng. A 2018, 715, 389–403. [Google Scholar] [CrossRef]
- Hagihara, K.; Yokotani, N.; Umakoshi, Y. Plastic deformation behavior of Mg12YZn with 18R long-period stacking ordered structure. Intermetallics 2009, 18, 267–276. [Google Scholar] [CrossRef]
- Lv, B.J.; Peng, J.; Wang, Y.J.; An, X.Q.; Zhong, L.P.; Tang, A.T.; Pan, F.S. Dynamic recrystallization behavior and hot workability of Mg–2.0Zn–0.3Zr–0.9Y alloy by using hot compression test. Mater. Des. 2014, 53, 357–365. [Google Scholar] [CrossRef]
- Jahedi, M.; Paydar, M.H. Study on the feasibility of the torsion extrusion (TE) process as a severe plastic deformation method for consolidation of Al powder. Mater. Sci. Eng. A 2010, 527, 5273–5279. [Google Scholar] [CrossRef]
- Kim, Y.H.; Park, J.H. Upper bound analysis of torsional backward extrusion process. J. Mater. Process. Technol. 2003, 143, 735–740. [Google Scholar] [CrossRef]
- Chino, Y.; Sassa, K.; Mabuch, M. Enhancement of tensile ductility of magnesium alloy produced by torsion extrusion. Scr. Mater. 2008, 59, 399–402. [Google Scholar] [CrossRef]
- Chen, H.B.; Liu, T.M.; Zhang, Y.; Zhai, Y.B.; He, J.J. Reducing tension–compression yield asymmetry by free end torsion in extruded Mg alloy. Mater. Sci. Technol. 2016, 32, 111–118. [Google Scholar] [CrossRef]
- Song, B.; Shu, X.G.; Pan, H.C.; Li, G.Q.; Guo, N.; Liu, T.T.; Chai, L.J.; Xin, R.L. Influence of Torsion Route on the Microstructure and Mechanical Properties of Extruded AZ31 Rods. Adv. Eng. Mater. 2017, 19, 1700267. [Google Scholar] [CrossRef]
- Yu, J.M.; Zhang, Z.M.; Xu, P.; Dong, B.B.; Wang, Q.; Meng, M.; Hao, H.Y.; Li, X.B.; Yin, X.Y. Dynamic recrystallization behavior of Gd-containing Mg alloy under torsion deformation. J. Alloys Compd. 2019, 787, 239–253. [Google Scholar] [CrossRef]
- Chen, Y.L.; Jin, L.; Dong, J.; Wang, F.H.; Li, Y.X.; Li, Y.J.; Pan, H.C.; Nie, X. Effects of LPSO/α-Mg interfaces on dynamic recrystallization behavior of Mg 96.5 Gd 2.5 Zn 1 alloy. Mater. Char. 2017, 134, 253–259. [Google Scholar] [CrossRef]
- Jiang, M.G.; Yan, H.; Chen, R.S. Enhanced mechanical properties due to grain refinement and texture modification in an AZ61 Mg alloy processed by small strain impact forging. Mater. Sci. Eng. A 2015, 621, 204–211. [Google Scholar] [CrossRef]
- Li, X.; Jiao, F.; Al-Samman, T.; Ghosh Chowdhury, S. Influence of second-phase precipitates on the texture evolution of Mg–Al–Zn alloys during hot deformation. Scr. Mater. 2012, 66, 159–162. [Google Scholar] [CrossRef]
- Park, S.H.; You, B.S. Effect of homogenization temperature on the microstructure and mechanical properties of extruded Mg–7Sn–1Al–1Zn alloy. J. Alloys Compd. 2015, 637, 332–338. [Google Scholar] [CrossRef]
- Wang, S.R.; Ma, R.; Yang, L.Y.; Wang, Y.; Wang, Y.J. Precipitates effect on microstructure of as-deformed and as-annealed AZ41 magnesium alloys by adding Mn and Ca. J. Mater. Sci. 2011, 46, 3060–3065. [Google Scholar] [CrossRef]
- Ding, H.L.; Liu, L.F.; Kamado, S.; Ding, W.J.; Kojima, Y. Study of the microstructure, texture and tensile properties of as-extruded AZ91 magnesium alloy. J. Alloys Compd. 2008, 456, 400–406. [Google Scholar] [CrossRef]
- Wang, R.M.; Eliezer, A.; Gutman, E. Microstructures and dislocations in the stressed AZ91D magnesium alloys. Mater. Sci. Eng. A 2003, 344, 279–287. [Google Scholar] [CrossRef]
- Saboori, A.; Dadkhah, M.; Pavese, M.; Manfredi, D.; Biamino, S.; Fino, P. Hot deformation behavior of Zr–1%Nb alloy: Flow curve analysis and microstructure observations. Mater. Sci. Eng. A 2017, 696, 366–373. [Google Scholar] [CrossRef]
- Sitdikov, O.; Kaibyshev, R.; Sakai, T. Dynamic recrystallization based on twinning in coarse-grained Mg. Mater. Sci. Forum. 2003, 419, 422. [Google Scholar] [CrossRef]
- Jiang, M.G.; Yan, H.; Chen, R.S. Twinning, recrystallization and texture development during multi-directional impact forging in an AZ61 Mg alloy. J. Alloys Compd. 2015, 650, 399–409. [Google Scholar] [CrossRef]
- Garces, G.; Morris, D.G.; Muñoz-Morris, M.A.; Perez, P.; Tolnai, D.; Mendis, C.; Stark, A.; Lim, H.K.; Kim, S.; Shell, N.; et al. Plasticity analysis by synchrotron radiation in a Mg97Y2Zn1 alloy with bimodal grain structure and containing LPSO phase. Acta Mater. 2015, 94, 78–86. [Google Scholar] [CrossRef]








| Mg | Gd | Y | Zn | Zr | Si | Cu | Fe |
|---|---|---|---|---|---|---|---|
| Balance | 12.88 | 4.00 | 2.00 | 0.50 | <0.01 | <0.01 | <0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Yu, J.; Zhang, Z. Microstructure and Texture Evolution of Mg–Gd–Y–Zn–Zr Alloy by Compression–Torsion Deformation. Materials 2019, 12, 2773. https://doi.org/10.3390/ma12172773
Xu P, Yu J, Zhang Z. Microstructure and Texture Evolution of Mg–Gd–Y–Zn–Zr Alloy by Compression–Torsion Deformation. Materials. 2019; 12(17):2773. https://doi.org/10.3390/ma12172773
Chicago/Turabian StyleXu, Ping, Jianmin Yu, and Zhimin Zhang. 2019. "Microstructure and Texture Evolution of Mg–Gd–Y–Zn–Zr Alloy by Compression–Torsion Deformation" Materials 12, no. 17: 2773. https://doi.org/10.3390/ma12172773
APA StyleXu, P., Yu, J., & Zhang, Z. (2019). Microstructure and Texture Evolution of Mg–Gd–Y–Zn–Zr Alloy by Compression–Torsion Deformation. Materials, 12(17), 2773. https://doi.org/10.3390/ma12172773




