Complete Stress–Strain Curves of Self-Compacting Steel Fiber Reinforced Expanded-Shale Lightweight Concrete under Uniaxial Compression
Abstract
1. Introduction
2. Preparation of Experimental Study
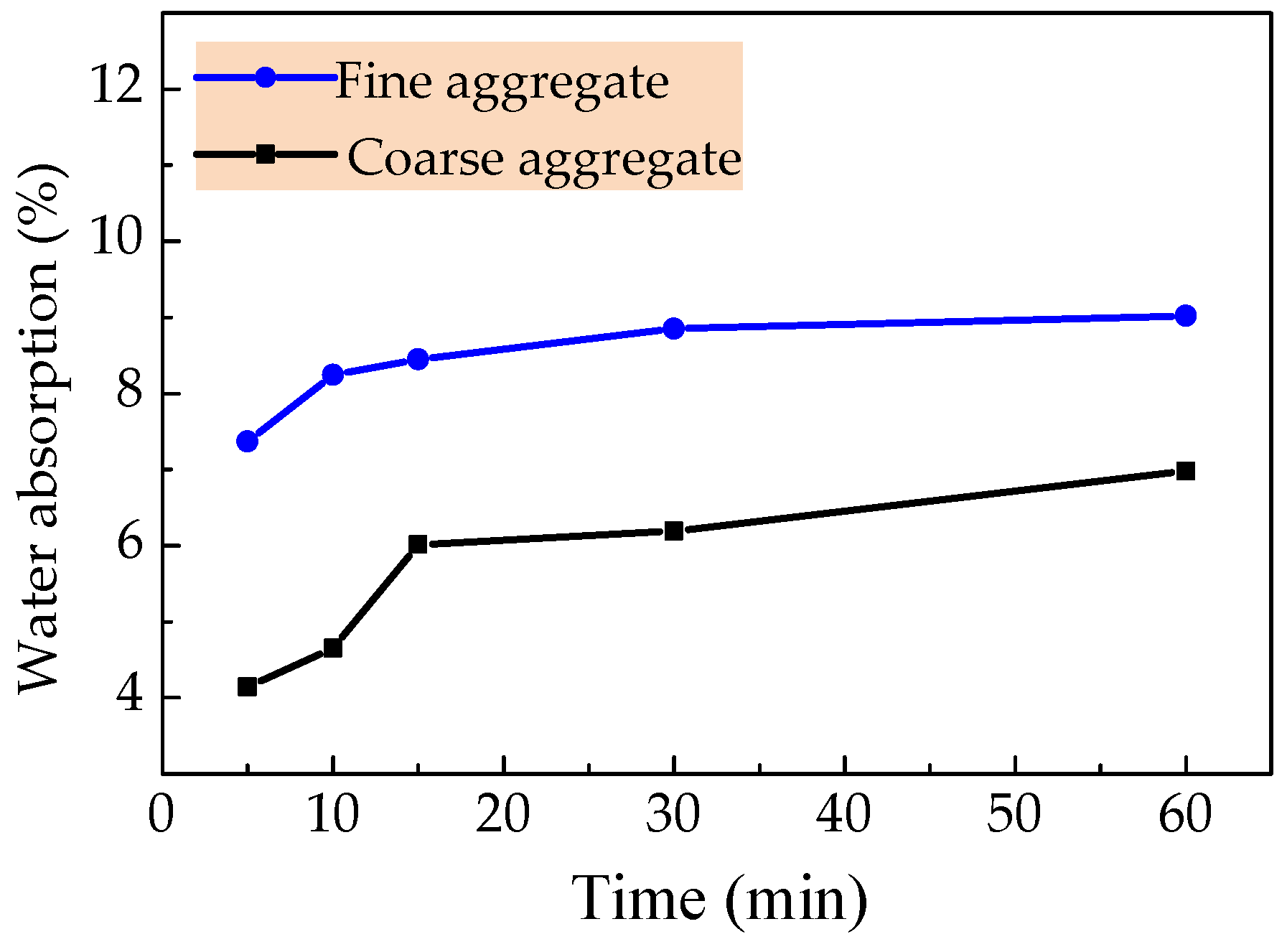
2.1. Raw Materials
2.2. Mix Proportions
2.3. Test Methods
3. Results and Analysis
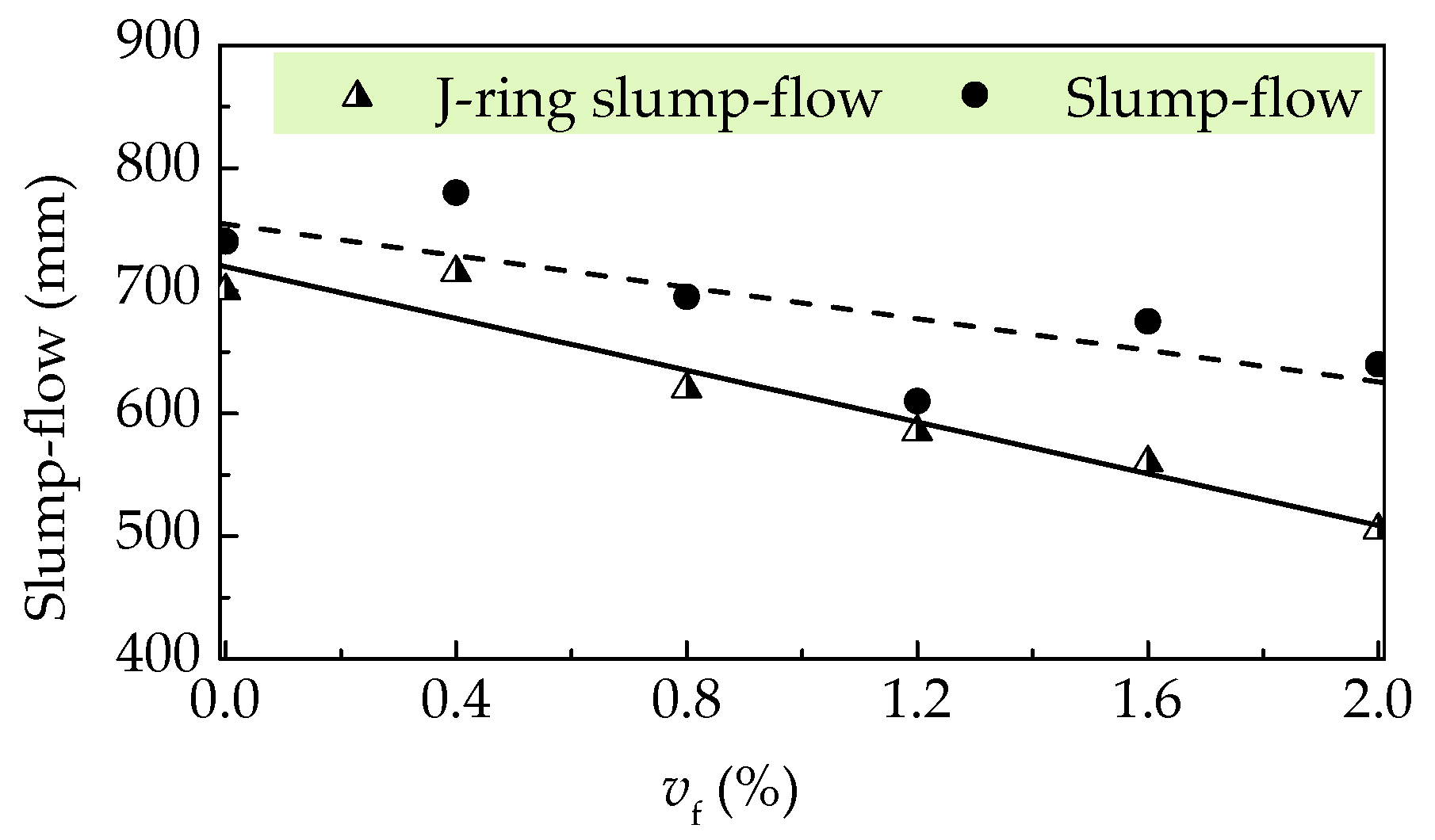
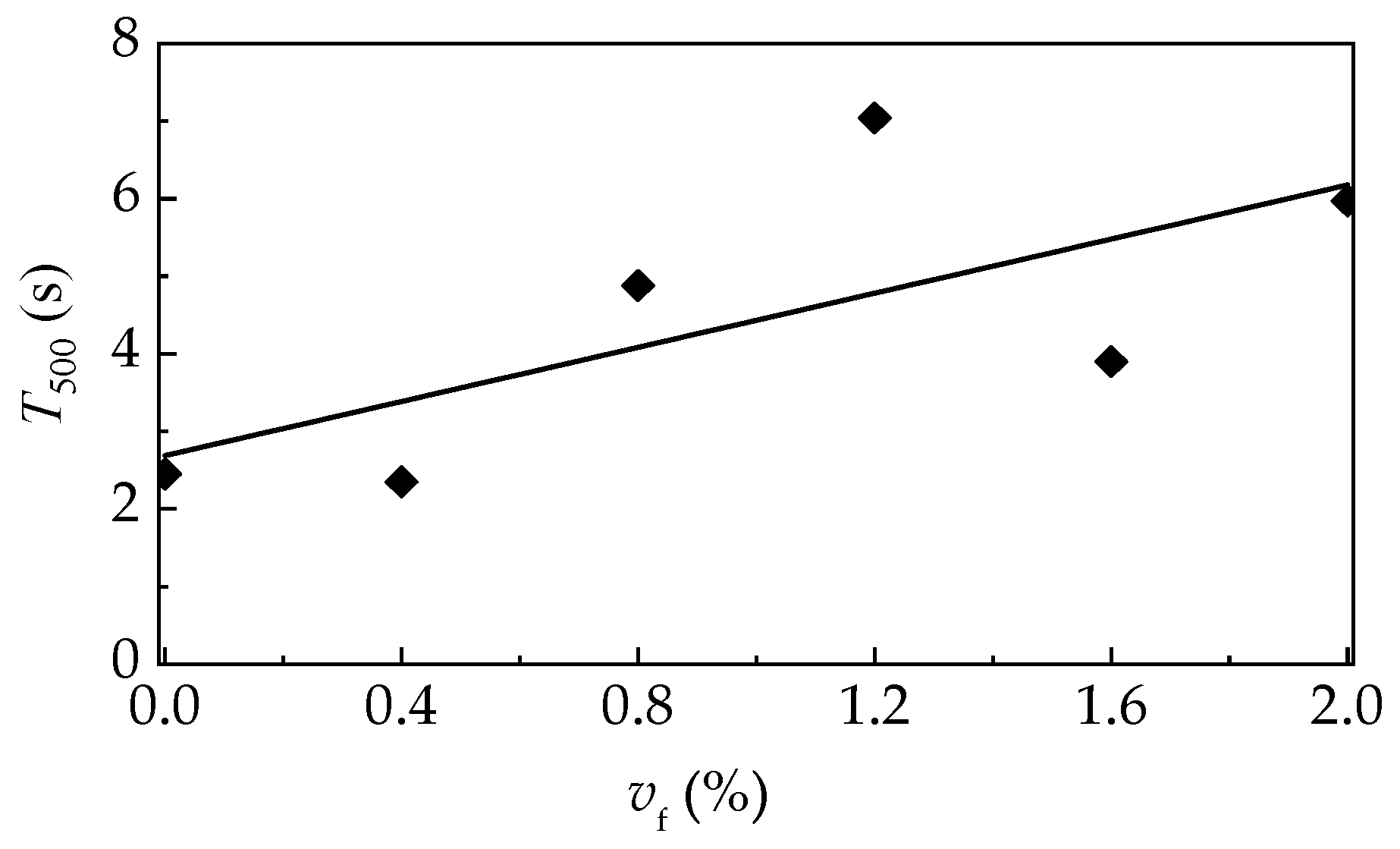
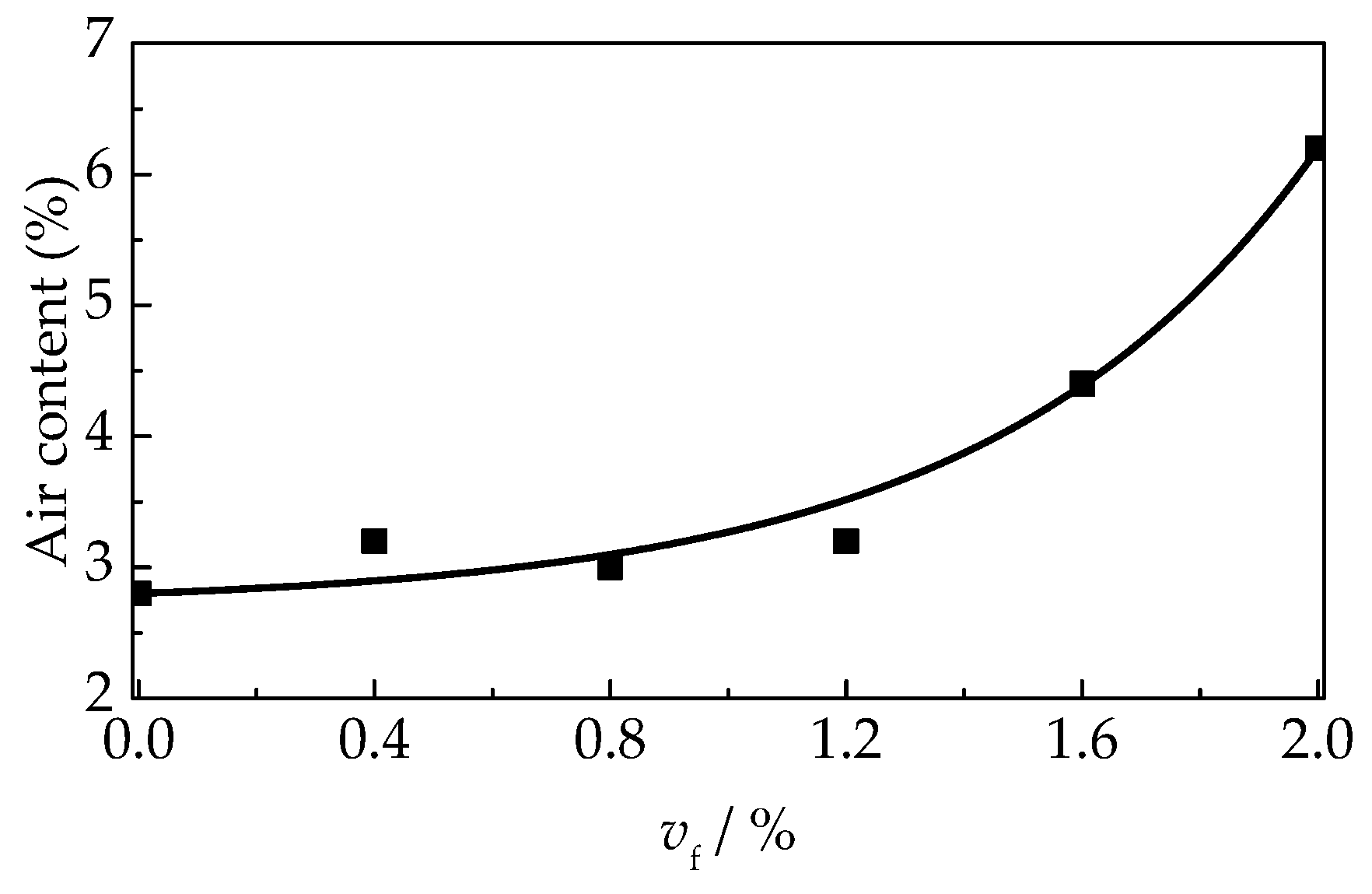
3.1. Workability and Density
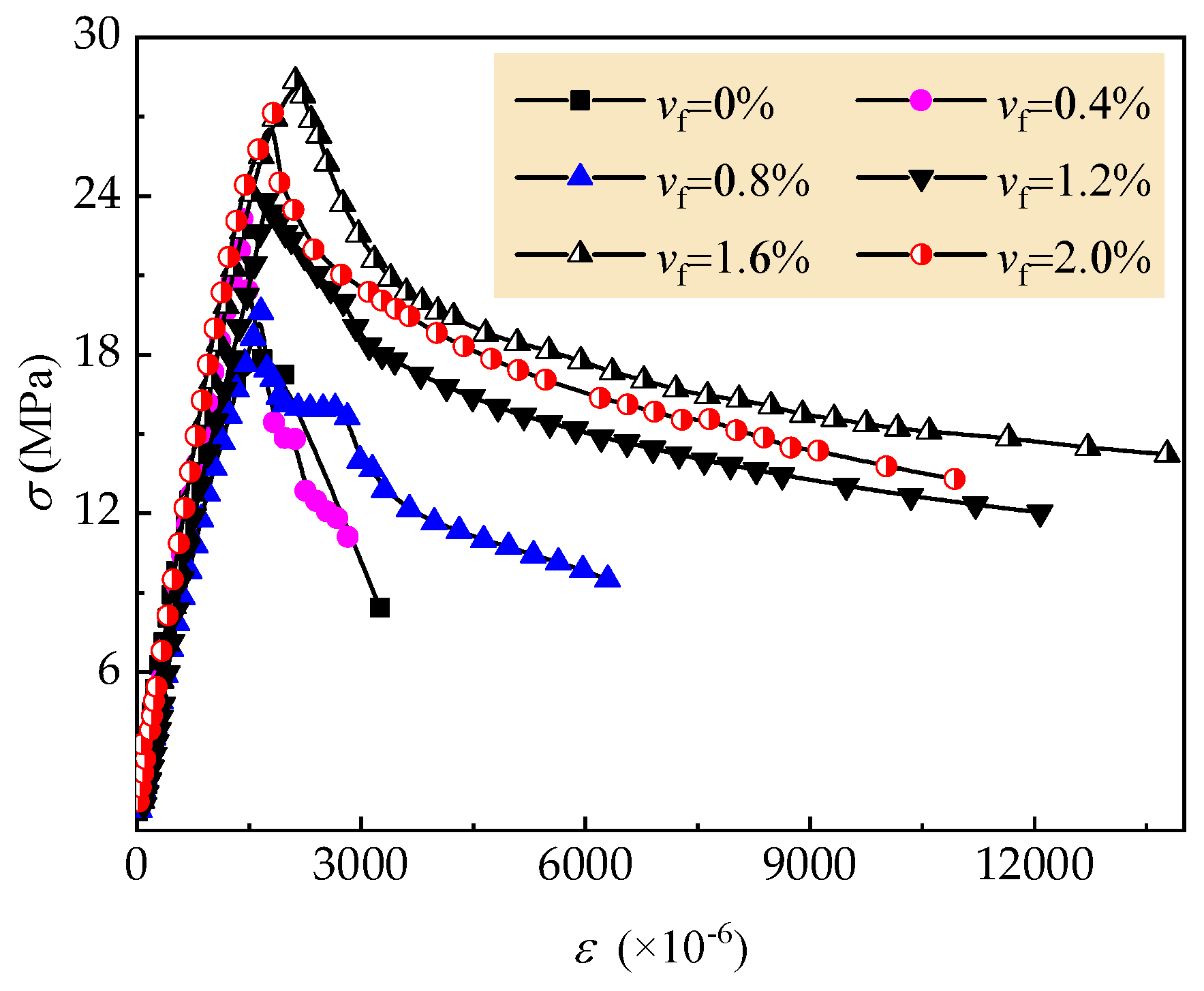
3.2. Uniaxial Compressive Stress-Strain Curves of Self-Compacting SFRELC
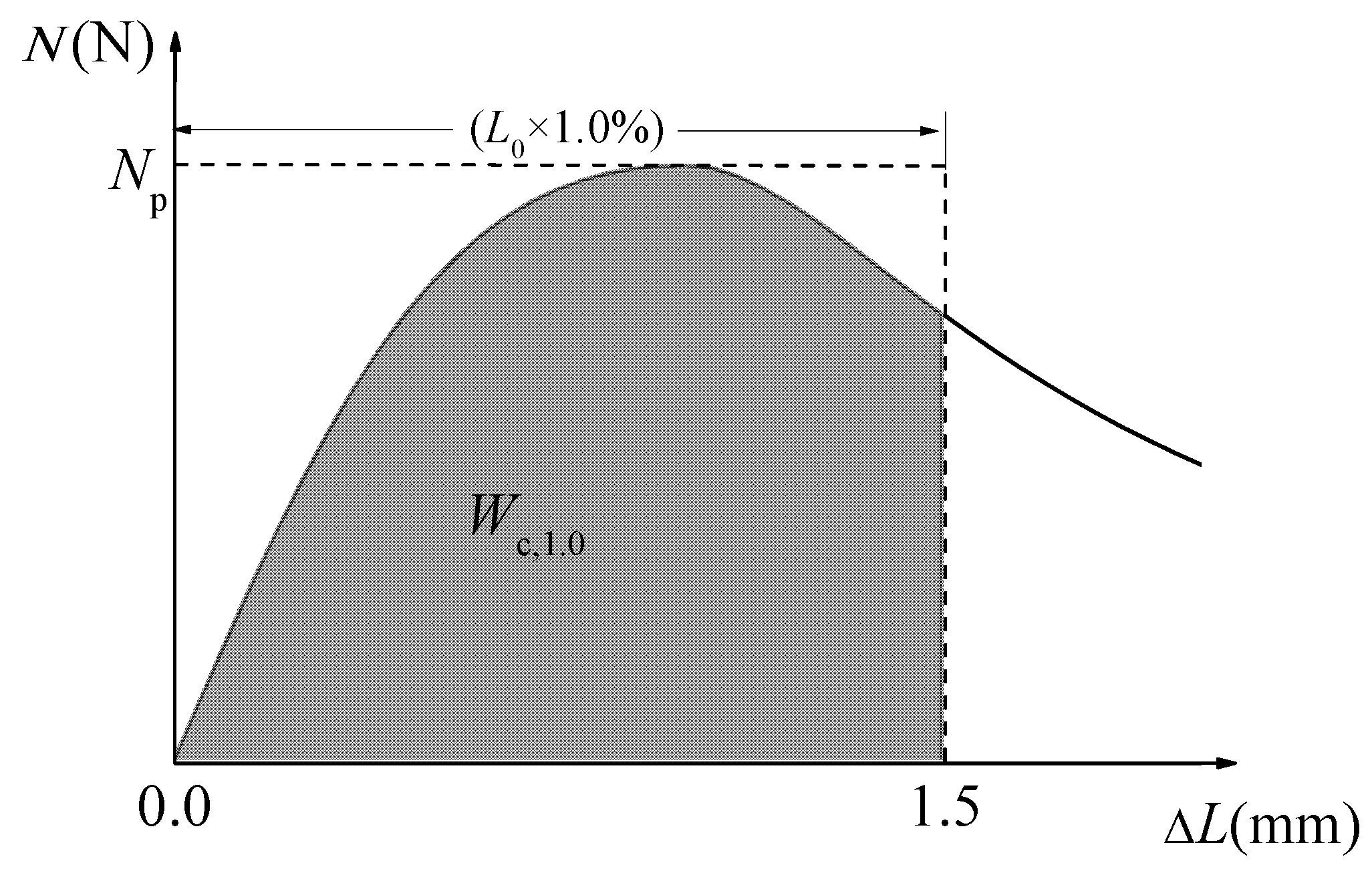
3.3. Compression Toughness
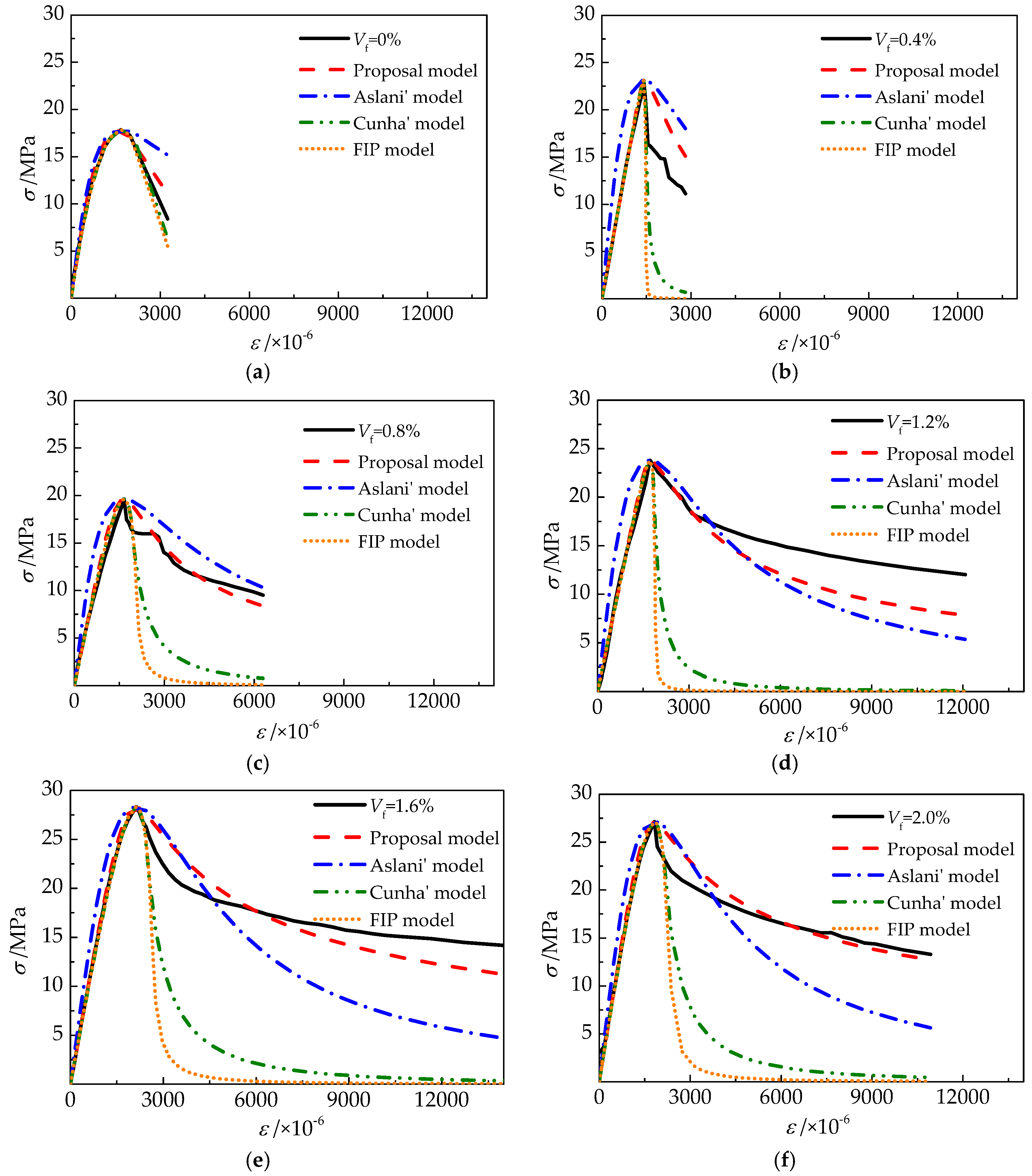
4. Evaluation for Compressive Stress-Strain Curve of Self-Compacting SFRELC
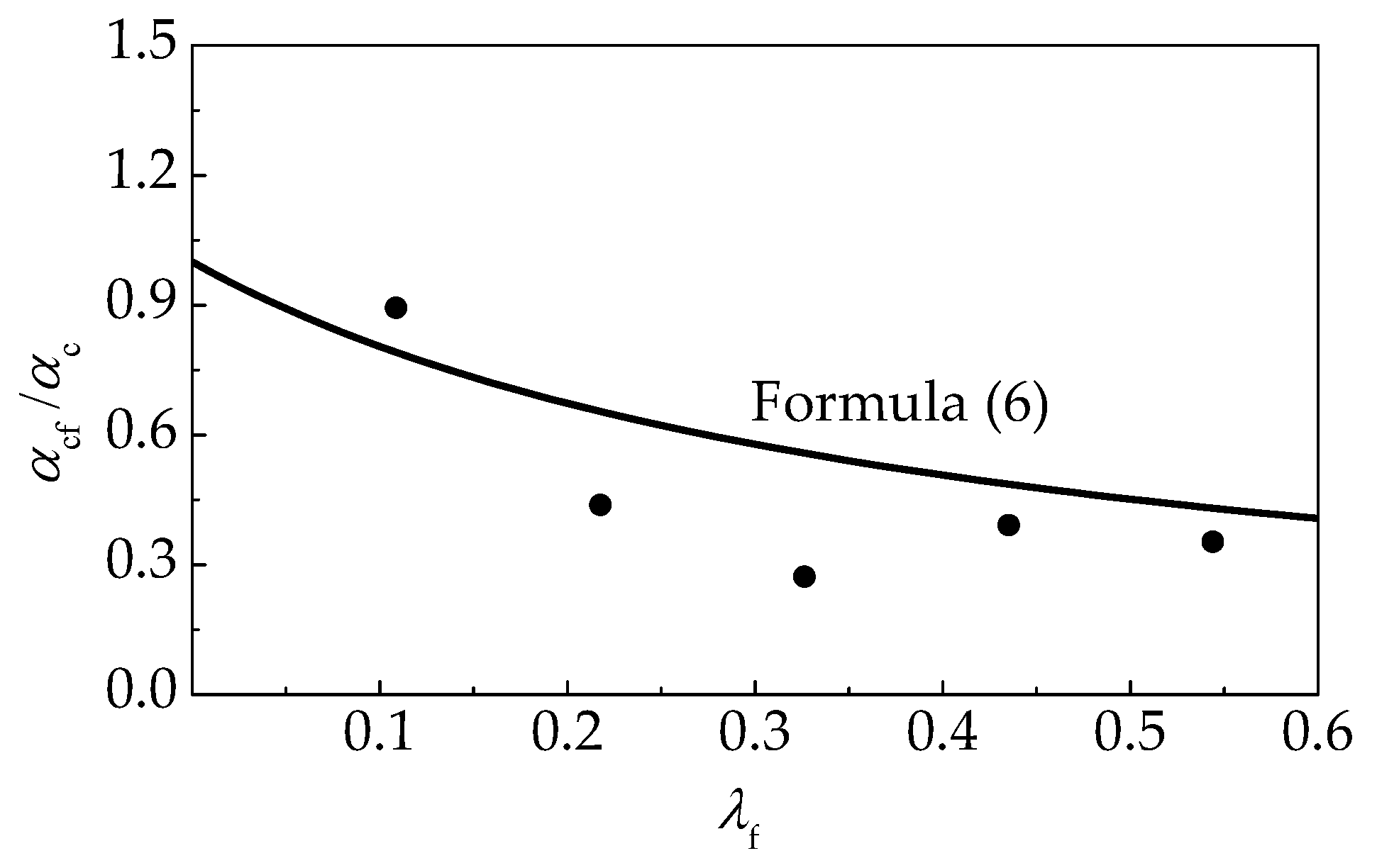
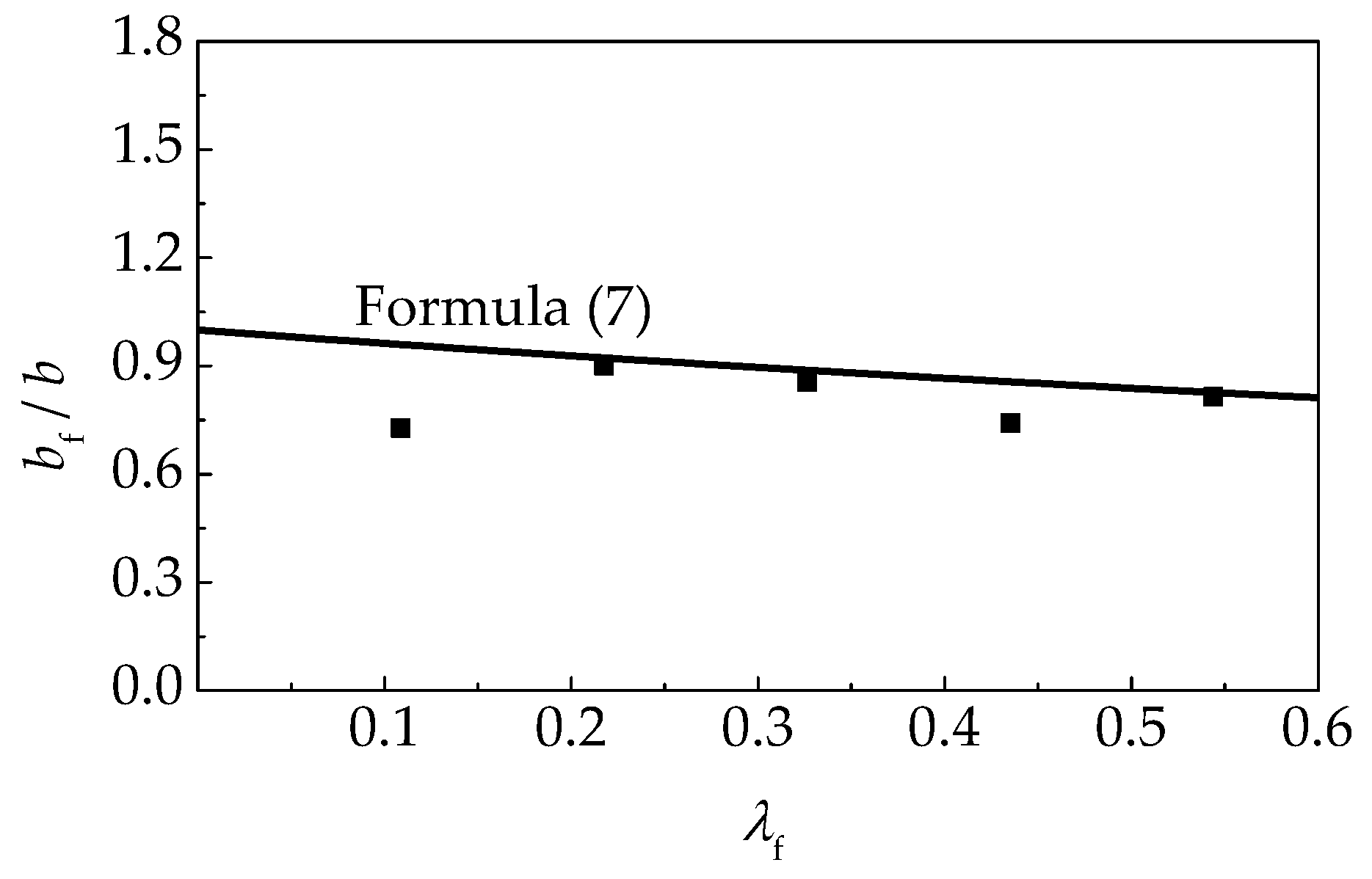
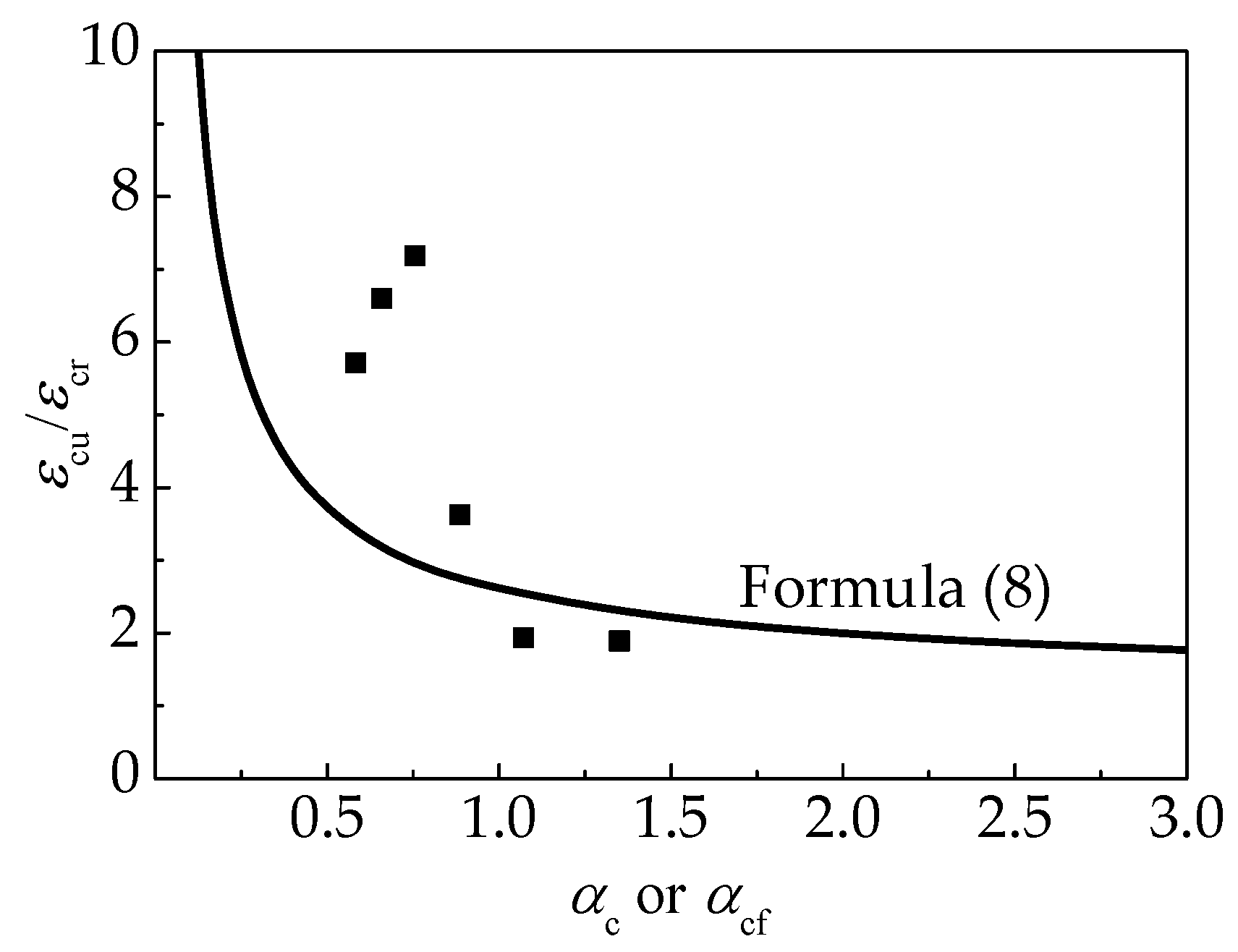
4.1. The Proposal Model
4.2. Aslani’ Model
4.3. Cunha’ and FIP Model
4.4. Fitness with Tested Curves
5. Conclusions
- (1)
- Self-compacting SFRELC with a slump flow of larger than 600 mm was prepared in this experiment. Slump-flow and J-ring slump-flow decreased while slump-flow time (T500) increased with the increase of vf. Drying densities increased about 12.2% with the vf increased from 0% to 2.0%.
- (2)
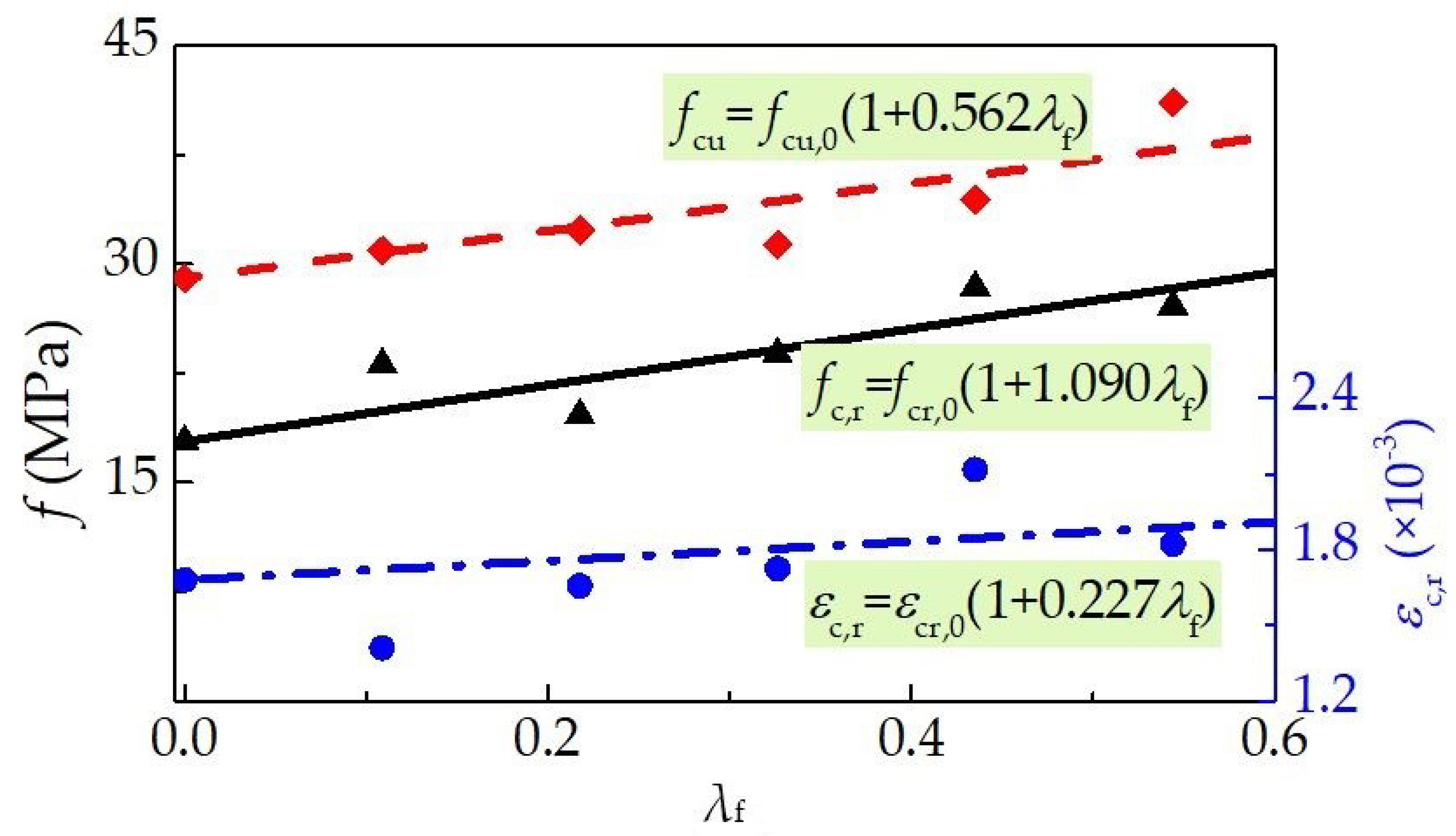
- With the increasing vf, the uniaxial compressive stress-strain curves of self-compacting SFRELC trends to be steep at ascending portion and a slower slope at descending portion. With the vf varying from 0% to 2.0%, the increments of fcu, fc,r and εc,r are 35.5%, 51.3% and 27.1% respectively. Values of fc,r are about 0.6–0.8 times fcu, which may be attributed to the loading rate being slower than that used in the test of axial compressive strength. The residual strengths increased with the increase of volume fraction of steel fiber.
- (3)
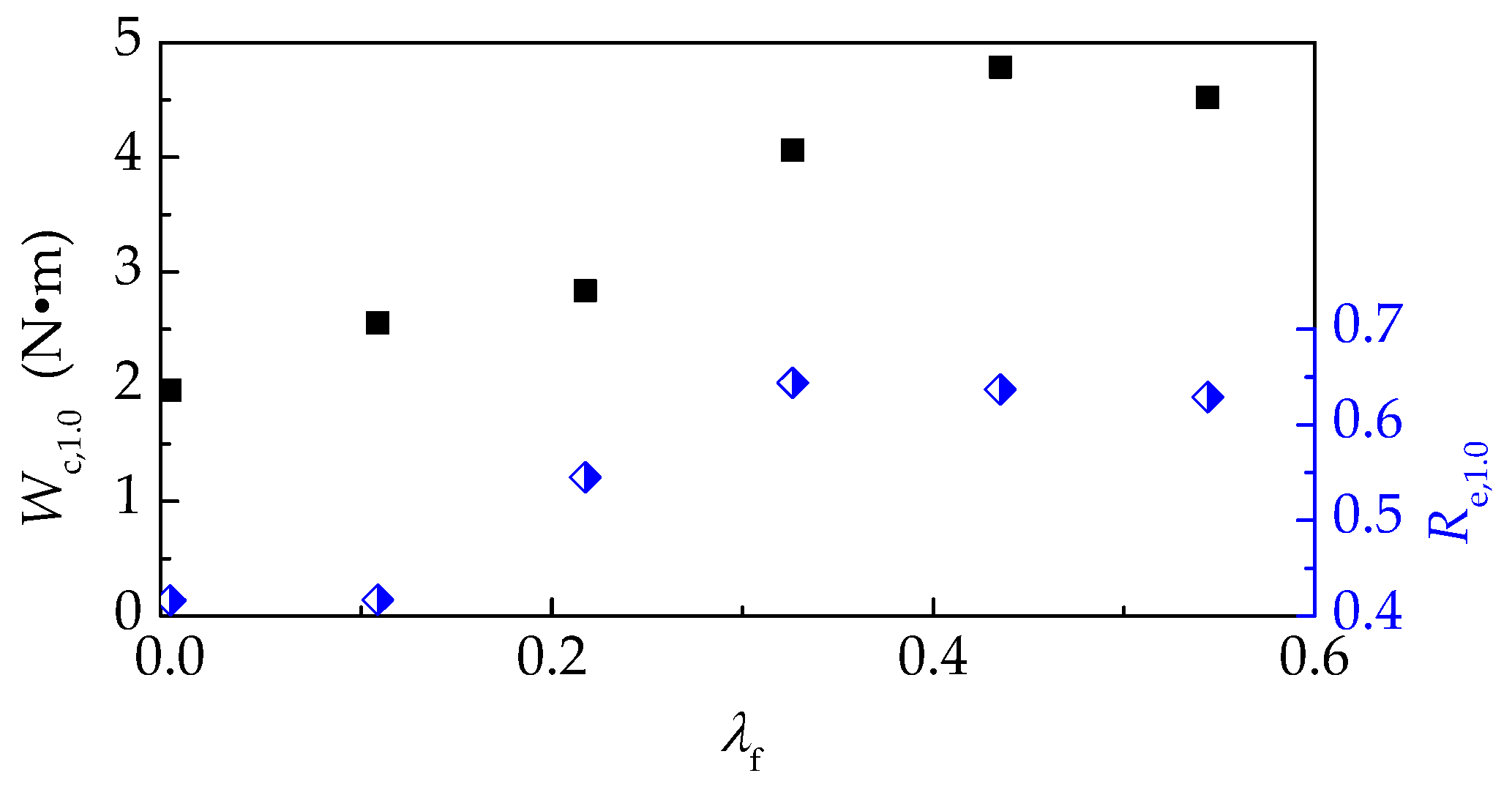
- With the vf varied from 0.4% to 1.2%, the toughening effect of steel fiber was outstanding, and the increments of Wc,1.0 and Re,1.0 are 59% and 54.5%, respectively. When the vf reached to 1.6% and 2.0%, the Wc,1.0 and Re,1.0 had no significant promotion. Therefore, the optimal vf for self-compacting SFRELC can be taken as 1.2%.
- (4)
- Based on the values of AVG and COV for the predictive ratios, and a comparison of calculations and test curves, the proposed model has a good fitness with the tested curves of self-compacting SFRELC, and Aslani’s model is slightly worse. Cunha’s model and the FIP model are suitable for the ascending portion, but inappropriate for the descending portion. As such, the proposed model is suggested in this paper.
Author Contributions
Funding
Conflicts of Interest
References
- JGJ 51-2002. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Specification of Lightweight Aggregate Concrete; China Building Industry Press: China, Beijing, 2002. (In Chinese) [Google Scholar]
- JGJ12-2006. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Specification for Lightweight Aggregate Concrete Structures; China Building Industry Press: China, Beijing, 2006. (In Chinese) [Google Scholar]
- Hassanpour, M.; Shafigh, P.; Mahmud, H.B. Lightweight aggregate concrete fiber reinforcement—A review. Constr. Build. Mater. 2012, 37, 452–461. [Google Scholar] [CrossRef]
- Zhao, S.B.; Li, C.Y.; Qian, X.J. Experimental study on mechanical properties of steel fiber reinforced full lightweight concrete. Geotech. Special Pub. 2011, 212, 233–239. [Google Scholar]
- Pan, L.Y.; Yuan, H.; Zhao, S.B. Experimental study on mechanical properties of hybrid fiber reinforced full lightweight aggregate concrete. Adv. Mater. Res. 2011, 197–198, 911–914. [Google Scholar] [CrossRef]
- Li, C.Y.; Chen, H.; Zhao, S.B. Mechanical properties of steel fiber reinforced light-aggregate concrete. Adv. Mater. Res. 2012, 366, 12–15. [Google Scholar] [CrossRef]
- Li, X.K.; Shen, Z.; Chen, M.H.; Zhao, M.S. Experimental study on compressive properties of steel-fiber-reinforced lightweight-aggregate fly-ash concrete. J. Guangxi Univ. Nat. Sci. Ed. 2015, 1, 106–111. (In Chinese) [Google Scholar]
- Shen, Z.; Chen, M.H.; Zhao, M.S.; Li, X.K. Experimental study on tensile properties of steel fiber reinforced lightweight-aggregate fly-ash flowable concrete. In Architectural Engineering and New Materials; DEStech Publications, Inc.: Lancaster, PA, USA, 2015; pp. 1–8. [Google Scholar]
- Zhao, M.L.; Zhao, M.S.; Chen, M.H.; Li, J.; Law, D. An experimental study on strength and toughness of steel fiber reinforced expanded-shale lightweight concrete. Constr. Build. Mater. 2018, 183, 493–501. [Google Scholar] [CrossRef]
- Li, X.K.; Zhang, X.Y.; Li, M.Q.; Zhao, M.S.; Li, C.Y. Experiments on development of strength and carbonization of steel fiber reinforced full-lightweight concrete. J. Civ. Eng. Manage. 2017, 2, 46–50. (In Chinese) [Google Scholar]
- Zhao, S.B.; Zhao, M.S.; Zhang, X.Y.; Peng, Z.J.; Huang, T.H. Study on complete stress-strain curves of steel fiber reinforced lightweight-aggregate concrete under uniaxial compression. J. Build. Struct. 2019, 5, 181–190. (In Chinese) [Google Scholar]
- Li, X.K.; Li, C.Y.; Zhao, M.L.; Yang, H.; Zhou, S.Y. Testing and prediction of shear performance for steel fiber reinforced expanded-shale lightweight concrete beams without web reinforcements. Materials 2019, 12, 1594. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.S.; Zhang, X.Y.; Song, W.H.; Li, C.Y.; Zhao, S.B. Development of steel fiber reinforced expanded-shale lightweight concrete with high freeze-thaw resistance. Adv. Mater. Sci. Eng. 2018, 2018, 9573849. [Google Scholar]
- Zhao, S.B.; Li, C.Y.; Zhao, M.S.; Zhang, X.Y. Experimental study on autogenous and drying shrinkage of steel fiber reinforced lightweight-aggregate concrete. Adv. Mater. Sci. Eng. 2016, 2016, 2589383. [Google Scholar] [CrossRef]
- Li, J.J.; Chen, Y.H.; Wan, C.J. A mix-design method for lightweight aggregate self-compacting concrete based on packing and mortar film thickness theories. Constr. Build. Mater. 2017, 157, 621–634. [Google Scholar] [CrossRef]
- Wu, Z.M.; Zhang, Y.G.; Zheng, J.J.; Ding, Y.N. An experimental study on the workability of self-compacting lightweight concrete. Constr. Build. Mater. 2009, 23, 2087–2092. [Google Scholar] [CrossRef]
- Wang, Y.M.; Liu, X.J. Mix proportion design and basic mechanical property experiment of self- compacting lightweight concrete. Concrete 2012, 6, 111–113. (In Chinese) [Google Scholar]
- Wu, X.; Wang, J.F.; Fan, X.L.; Zhang, X.; Wu, Z.M. Thermal behavior of self-compacting lightweight concrete subjected to the elevated temperature. J. Mater. Sci. Eng. 2014, 32, 313–317. (In Chinese) [Google Scholar]
- Iqbal, S.; Ali, A.; Holschemacher, K.; Bier, T.A. Mechanical properties of steel fiber reinforced high strength lightweight self-compacting concrete (SHLSCC). Constr. Build. Mater. 2015, 98, 325–333. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Wu, X.; Bi, Q.W. Shrinkage and creep performance of self-consolidating lightweight concrete. J. Mater. Sci. Eng. 2014, 32, 35–39. (In Chinese) [Google Scholar]
- Wu, X.; Fu, T.F.; Wu, Z.M. Experimental study on double-K fracture parameters and fracture energy of self-consolidating lightweight concrete. Eng. Mech. 2010, 27, 249–254. (In Chinese) [Google Scholar]
- Wang, Z.Y.; Ding, J.T.; Guo, Y.S. Stress-strain curves of structural lightweight aggregate concretes. Concrete. 2005, 3, 39–41. (In Chinese) [Google Scholar]
- Liu, X.; Yin, J.; He, Y.Q.; Hou, Y. Experimental study of stress-strain curves of lightweight aggregate concrete. J. Inner Mongolia Univ. Sci. Technol. 2010, 29, 277–280. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wang, C.R.; Chen, Y.X.; Ni, Y. Stress-strain relationships for concrete in axial compression. J. Tianjin Univ. 1983, 2, 29–40. (In Chinese) [Google Scholar]
- Campione, G.; Mendola, L.L. Behavior in compression of lightweight fiber reinforced concrete confined with transverse steel reinforcement. Cem. Concr. Compos. 2004, 26, 645–656. [Google Scholar] [CrossRef]
- Floyd, O.S.; Arthur, H.N.; Salvador, M. Mechanical properties of high-strength lightweight concrete. ACI J. 1986, 83, 606–613. [Google Scholar]
- Zhang, M.H.; Gjvorv, O.E. Mechanical Properties of High-Strength Lightweight Concrete. Aci Mater. J. 1991, 88, 240–247. [Google Scholar]
- Shannag, M.J. Characteristics of lightweight concrete containing mineral admixtures. Constr. Build. Mater. 2011, 25, 658–662. [Google Scholar] [CrossRef]
- Oğuz, A.D.; Rüstem, G.; Abdulkadir, C.A. Effect of steel fibers on the mechanical properties of natural lightweight aggregate concrete. Mater. Lett. 2005, 59, 3357–3363. [Google Scholar]
- Shafigh, P.; Mahmud, H.; Jumaat, M.Z. Effect of steel fiber on the mechanical properties of oil palm shell lightweight concrete. Mater. Des. 2011, 32, 3926–3932. [Google Scholar] [CrossRef]
- Lucyna, D. Modification of properties of structural lightweight concrete with steel fibres. J. Civ. Eng. Manag. 2011, 17, 36–44. [Google Scholar]
- Ding, X.X.; Li, C.Y.; Li, Y.Z.; Lu, Y.Z.; Song, C.; Zhao, S.B. Experimental and numerical study on stress-strain behavior of self-compacting SFRC under uniaxial compression. Constr. Build. Mater. 2018, 185, 30–38. [Google Scholar] [CrossRef]
- Aslani, F.; Nejadi, S. Mechanical characteristics of self-compacting concrete with and without fibres. Mag. Concr. Res. 2013, 65, 608–622. [Google Scholar] [CrossRef]
- Aslani, F.; Nejadi, S. Self-compacting concrete incorporating steel and polypropylene fibers: Compressive and tensile strengths, moduli of elasticity and rupture, compressive stress–strain curve, and energy dissipated under compression. Compos. Part B Eng. 2013, 53, 121–133. [Google Scholar] [CrossRef]
- Cunha, V.M.C.F.; Barros, J.A.O.; Sena-Cruz, J. Modelling the influence of age of steel fibre reinforced self-compacting concrete on its compressive behavior. Mater. Struct. 2008, 41, 465–478. [Google Scholar] [CrossRef]
- Aslani, F.; Natoori, M. Stress-strain relationships for steel fiber reinforced self-compacting concrete. Struct. Eng. Mech. 2013, 46, 295–322. [Google Scholar] [CrossRef]
- Comité Euro–International du Béton. CEB-FIP Model Code 1990–Design Code; Redwood Books: Trowbridge, UK, 1993. [Google Scholar]
- GB 175-2007. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Common Portland Cement; China Standard Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- GB/T 1596-2005. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Fly Ash Used for Cement and Concrete; China Standard Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- GB/T 17431.2-2010. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Lightweight aggregates and Its Test Methods—Part 2: Test Methods for Lightweight Aggregates; China Building Industry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- JGJ/T 283-2012. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Specification for Application of Self-compacting Concrete; China Building Industry Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- GB/T 50081-2002. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Standard for Test Method of Mechanical Properties on Ordinary Concrete; China Building Industry Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- CECS 13:2009. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Standard Test Methods for Fiber Reinforced Concrete; China Standard Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- American Concrete Institute. Design Considerations for Steel Fiber Reinforced Concrete; ACI 544.4R; ACI Committee 544: Farmington Hills, MI, USA, 1988. [Google Scholar]
- GB 50010-2010. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Code for Design of Concrete Structures; China Building Industry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]

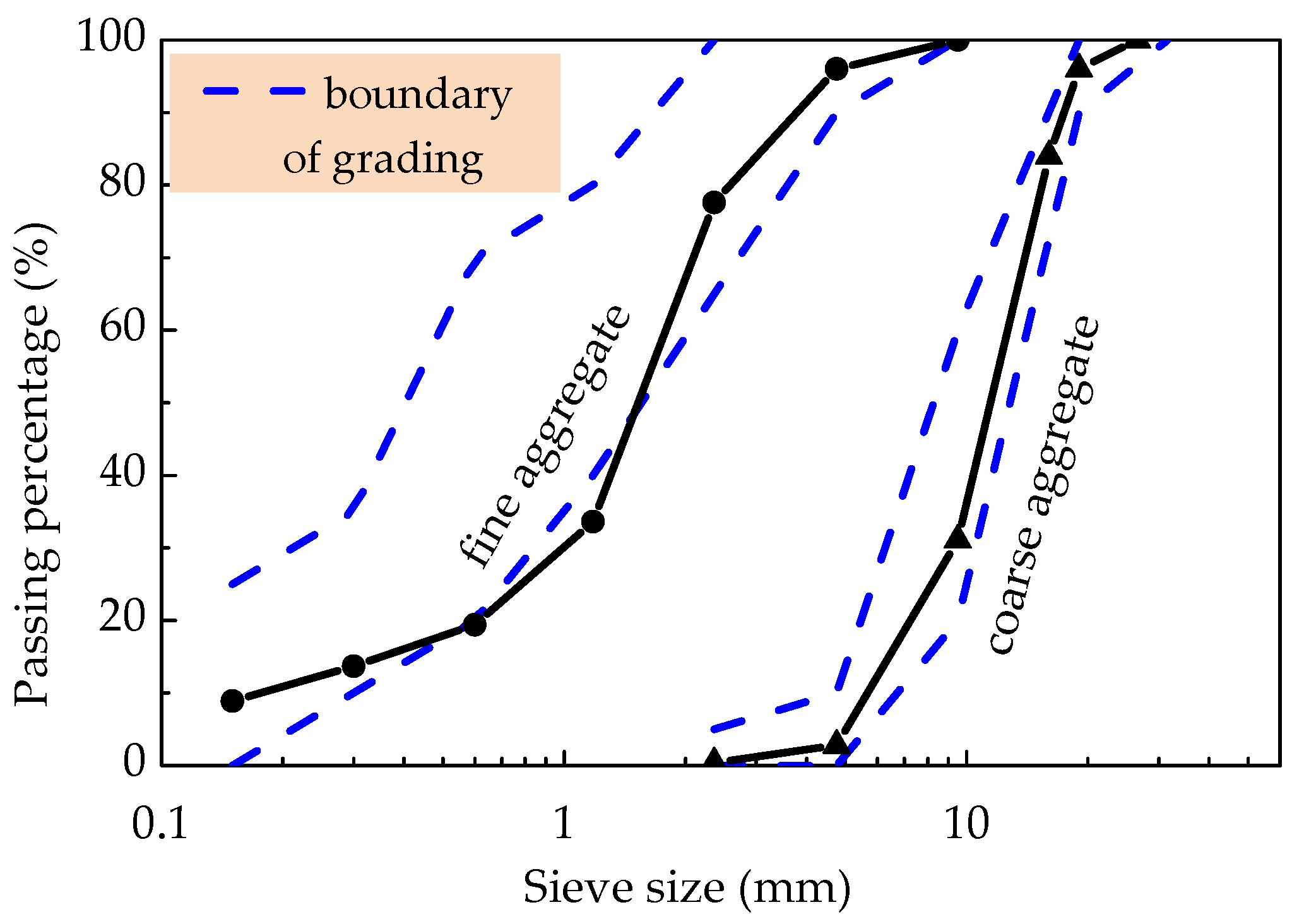




| Density (kg/m3) | Water Requirement of Normal Consistency (%) | Setting Time (min) | Compressive Strength (MPa) | Flexural Strength (MPa) | |||
|---|---|---|---|---|---|---|---|
| Initial | Final | 3d | 28d | 3d | 28d | ||
| 3085 | 26.4 | 160 | 245 | 29.4 | 54.7 | 6.2 | 9.4 |
| Particle Size (mm) | Apparent Density (kg/m3) | Bulk Density (kg⋅m3) | 1 h Water Absorption (%) | Mud Content (%) | Cylinder Compressive Strength (MPa) |
|---|---|---|---|---|---|
| 5–20 | 1262 | 827 | 6.98 | 0.7 | 7.4 |
| 0.16–5 | 1350 | 850 | 9.02 | 0.11 | - |
| w/b | vf (%) | Volume Ratio of Sand (%) | Cement (kg/m3) | Fly Ash (kg/m3) | Coarse Aggregate (kg/m3) | Fine Aggregate (kg/m3) | Super-Plasticizer (kg/m3) |
|---|---|---|---|---|---|---|---|
| 0.30 | 0 | 50 | 408 | 175 | 424 | 417 | 0.210 |
| 0.4 | 50 | 419 | 422 | 0.210 | |||
| 0.8 | 50 | 413 | 428 | 0.210 | |||
| 1.2 | 52 | 391 | 450 | 0.214 | |||
| 1.6 | 54 | 368 | 472 | 0.222 | |||
| 2.0 | 56 | 346 | 494 | 0.231 |
| w/c | vf (%) | λf | fcu (MPa) | fc,r (MPa) | εc,r (×10−3) | εc,u (×10−3) | Ec (GPa) | Wc,1.0 (N·mm) | Re,1.0 |
|---|---|---|---|---|---|---|---|---|---|
| 0.30 | 0 | 0 | 29.01 | 17.84 | 1.6801 | 3.1765 | 21.57 | 196766.1 | 0.42 |
| 0.4 | 0.1088 | 30.92 | 23.13 | 1.4116 | 2.7317 | 17.14 | 255427.2 | 0.42 | |
| 0.8 | 0.2176 | 32.28 | 19.62 | 1.6569 | 6.0114 | 15.35 | 283445.1 | 0.55 | |
| 1.2 | 0.3264 | 31.30 | 23.8 | 1.7252 | 12.3964 | 15.13 | 406151.2 | 0.64 | |
| 1.6 | 0.4352 | 34.41 | 28.35 | 2.1190 | 13.9847 | 17.42 | 478505.5 | 0.64 | |
| 2.0 | 0.544 | 41.12 | 27.13 | 1.8224 | 10.4132 | 19.72 | 452164.4 | 0.63 |
| vf/% | Proposal Model | Aslani’s Model | Cunha’s Model | FIP Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ascending Portion | Ascending Portion | Ascending Portion | Descending Portion | Ascending Portion | Descending Portion | Ascending Portion | Descending Portion | |||||||||
| AVG | COV | AVG | COV | AVG | COV | AVG | COV | AVG | COV | AVG | COV | AVG | COV | AVG | COV | |
| 0 | 1.017 | 0.177 | 1.08 | 0.144 | 0.875 | 0.198 | 1.234 | 0.309 | 0.875 | 0.181 | 0.947 | 0.138 | 0.458 | 0.345 | 0.807 | 0.281 |
| 0.4 | 1.018 | 0.023 | 1.303 | 0.101 | 1.603 | 0.2 | 1.413 | 0.143 | 1.019 | 0.023 | 0.359 | 0.981 | 1.019 | 0.023 | 0.153 | 2.152 |
| 0.8 | 0.988 | 0.134 | 1.025 | 0.088 | 1.38 | 0.125 | 1.158 | 0.051 | 0.969 | 0.122 | 0.456 | 0.837 | 0.969 | 0.122 | 0.3 | 1.396 |
| 1.2 | 1.101 | 0.127 | 0.867 | 0.156 | 1.665 | 0.273 | 0.832 | 0.265 | 1.098 | 0.13 | 0.189 | 1.557 | 1.098 | 0.13 | 0.092 | 2.765 |
| 1.6 | 1.018 | 0.019 | 0.991 | 0.111 | 1.266 | 0.09 | 0.811 | 0.356 | 0.995 | 0.023 | 0.318 | 1.091 | 0.995 | 0.023 | 0.198 | 1.739 |
| 2.0 | 0.935 | 0.185 | 1.036 | 0.065 | 1.153 | 0.168 | 0.825 | 0.315 | 0.911 | 0.177 | 0.304 | 1.099 | 0.911 | 0.177 | 0.182 | 1.685 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Zhang, B.; Shang, P.; Fu, Y.; Zhang, X.; Zhao, S. Complete Stress–Strain Curves of Self-Compacting Steel Fiber Reinforced Expanded-Shale Lightweight Concrete under Uniaxial Compression. Materials 2019, 12, 2979. https://doi.org/10.3390/ma12182979
Zhao M, Zhang B, Shang P, Fu Y, Zhang X, Zhao S. Complete Stress–Strain Curves of Self-Compacting Steel Fiber Reinforced Expanded-Shale Lightweight Concrete under Uniaxial Compression. Materials. 2019; 12(18):2979. https://doi.org/10.3390/ma12182979
Chicago/Turabian StyleZhao, Mingshuang, Bingxin Zhang, Pengran Shang, Yan Fu, Xiaoyan Zhang, and Shunbo Zhao. 2019. "Complete Stress–Strain Curves of Self-Compacting Steel Fiber Reinforced Expanded-Shale Lightweight Concrete under Uniaxial Compression" Materials 12, no. 18: 2979. https://doi.org/10.3390/ma12182979
APA StyleZhao, M., Zhang, B., Shang, P., Fu, Y., Zhang, X., & Zhao, S. (2019). Complete Stress–Strain Curves of Self-Compacting Steel Fiber Reinforced Expanded-Shale Lightweight Concrete under Uniaxial Compression. Materials, 12(18), 2979. https://doi.org/10.3390/ma12182979





