Thermodynamic Properties of Stoichiometric Non-Superconducting Phase Y2BaCuO5
Abstract
:1. Introduction
2. Materials and Methods
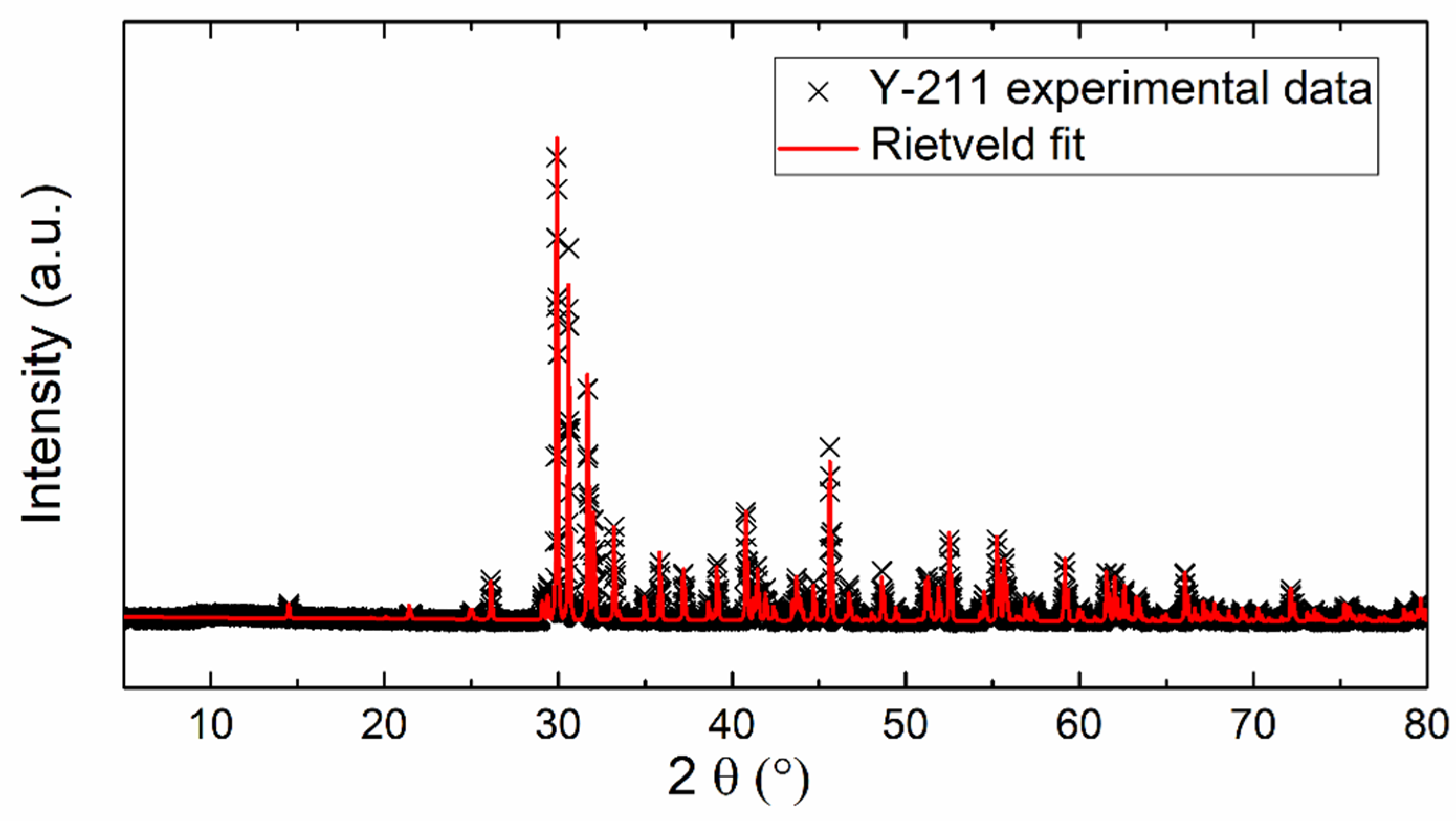
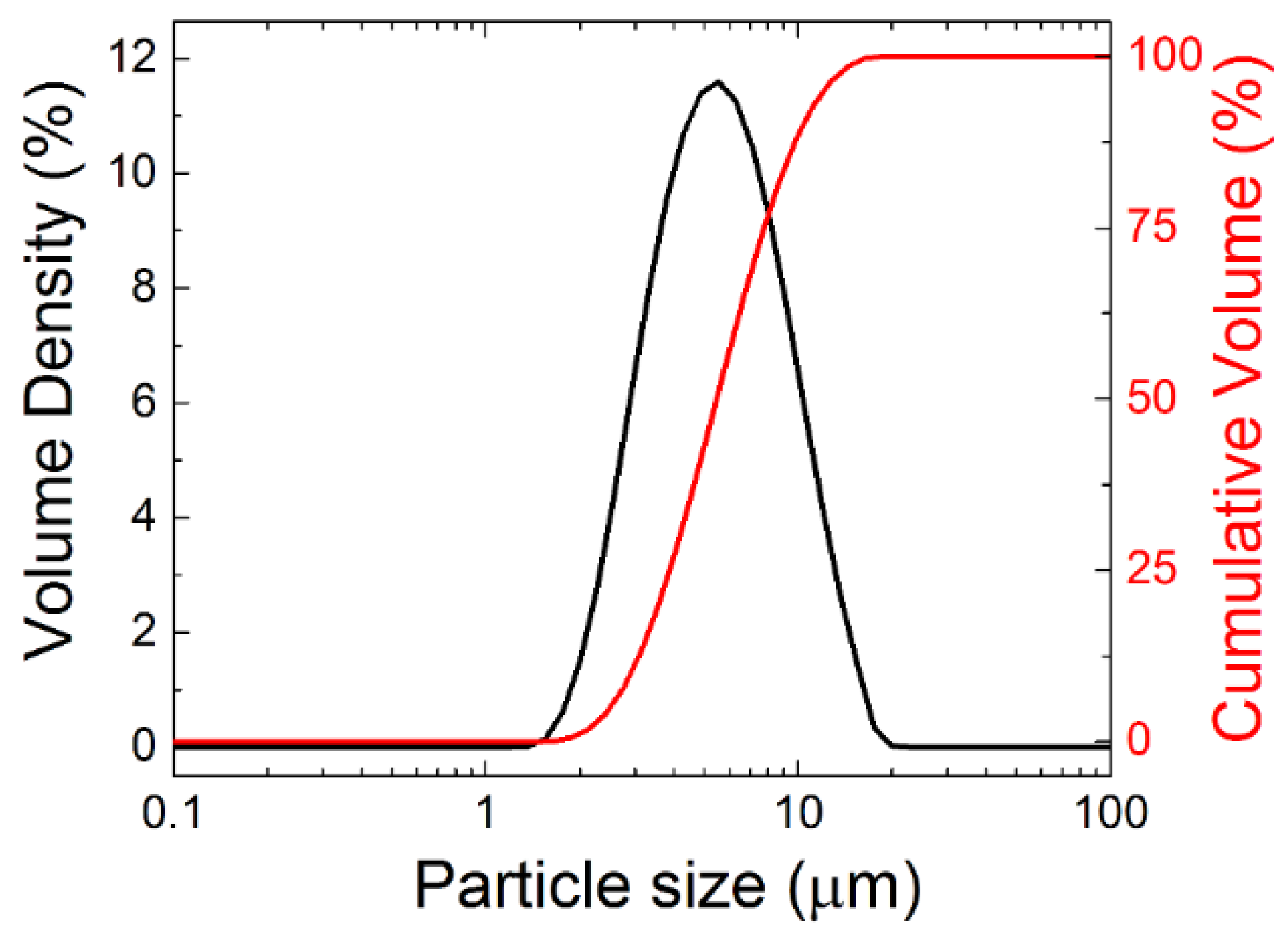
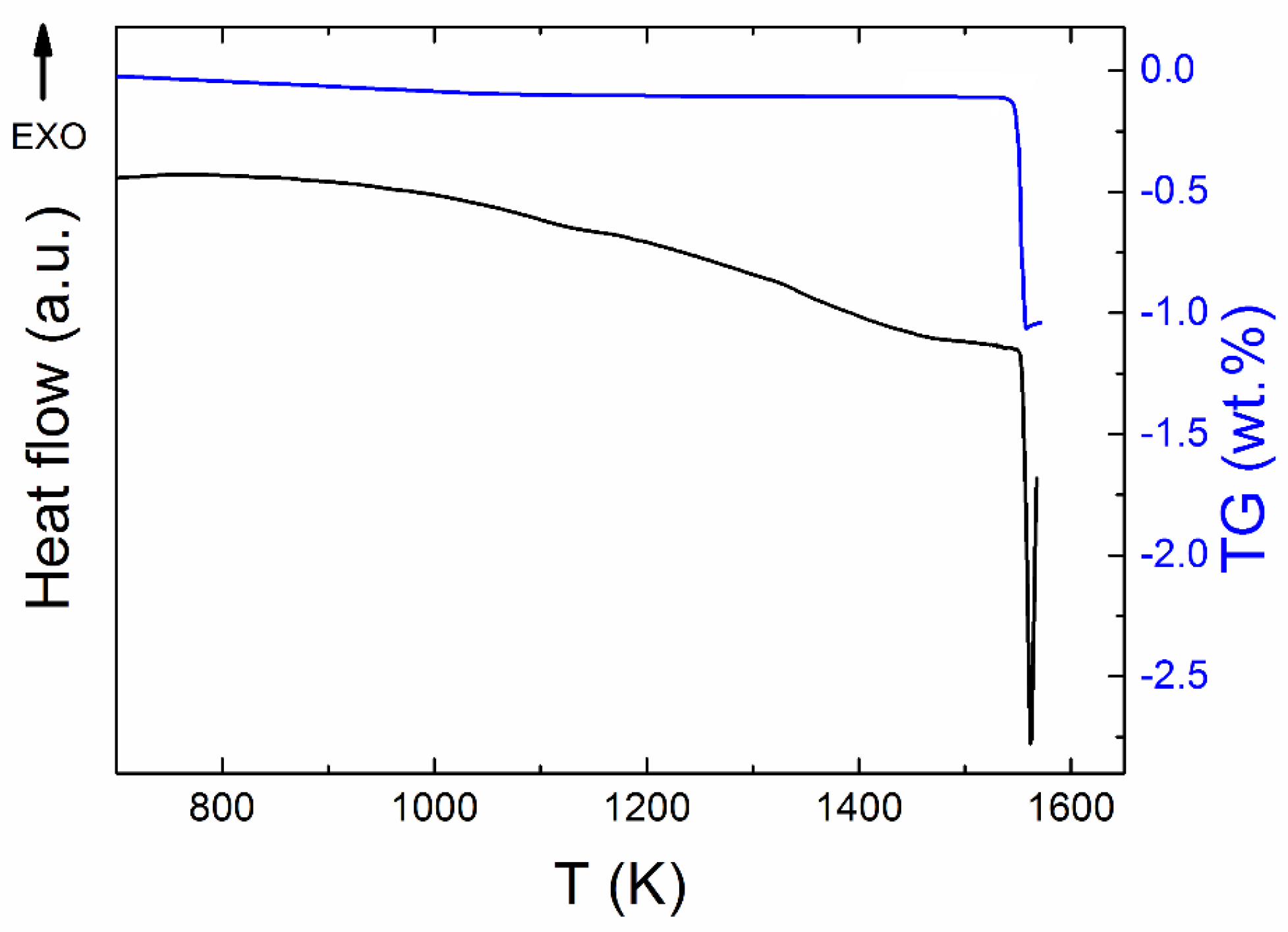
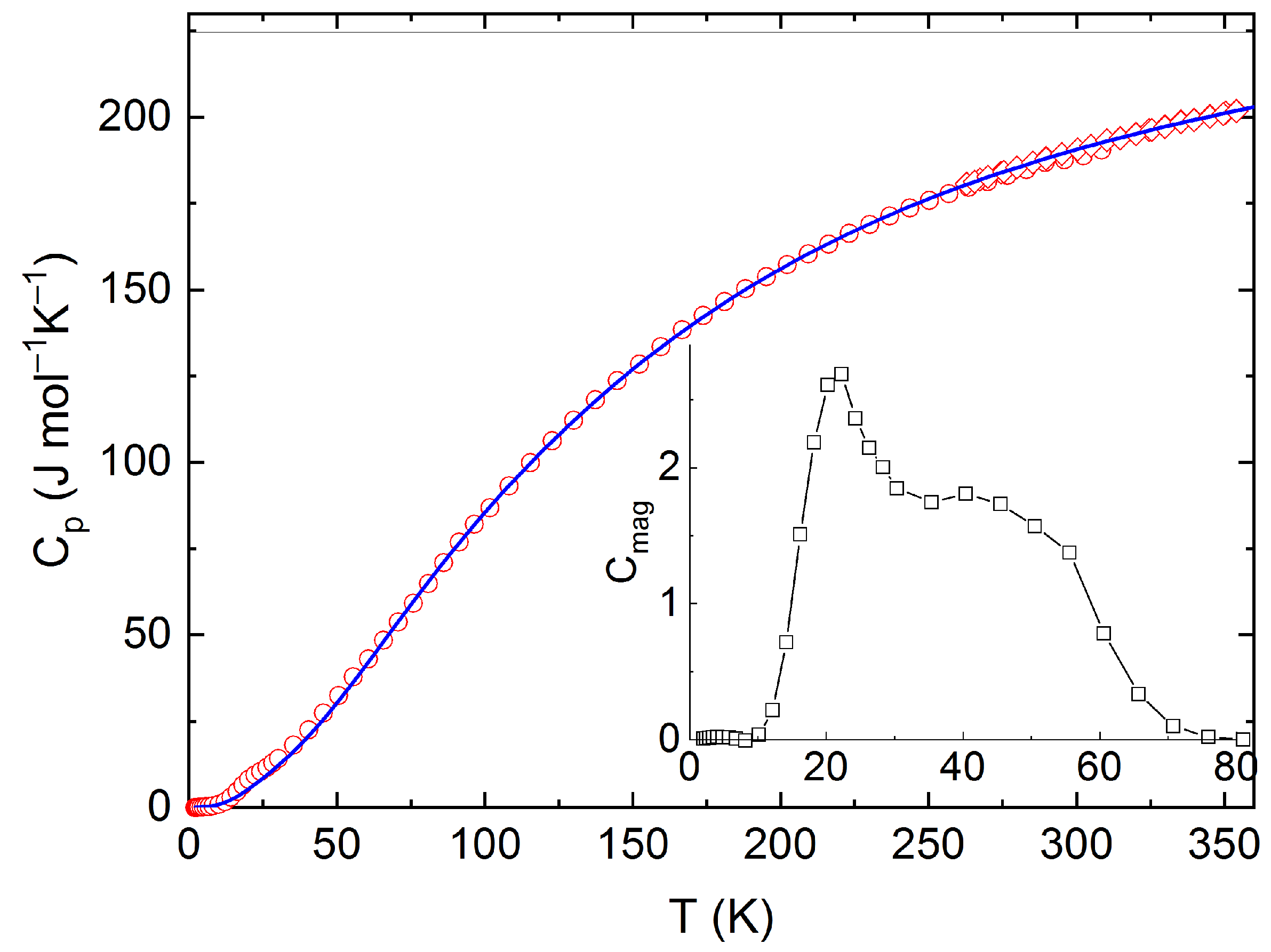
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, C.; Wu, H.B.; Xie, Y.; Lou, X.W. Mixed transition-metal oxides: Design, synthesis, and energy-related applications. Angew. Chem. Int. Ed. 2014, 53, 1488–1504. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Yan, B.; Xiong, D.; Li, D.; Lawes, S.; Sun, X. Recent developments and understanding of novel mixed transition-metal oxides as anodes in lithium ion batteries. Adv. Energy Mater. 2016, 6, 1502175. [Google Scholar] [CrossRef]
- Jankovský, O.; Sedmidubský, D.; Šimek, P.; Sofer, Z.; Ulbrich, P.; Bartůněk, V. Synthesis of MnO, Mn2O3 and Mn3O4 nanocrystal clusters by thermal decomposition of manganese glycerolate. Ceram. Int. 2015, 41, 595–601. [Google Scholar] [CrossRef]
- Bartůněk, V.; Huber, Š.; Sedmidubský, D.; Sofer, Z.; Šimek, P.; Jankovský, O. CoO and Co3O4 nanoparticles with a tunable particle size. Ceram. Int. 2014, 40, 12591–12595. [Google Scholar] [CrossRef]
- Kang, M.-G.; Cho, K.-H.; Kim, J.-S.; Nahm, S.; Yoon, S.-J.; Kang, C.-Y. Post-calcination, a novel method to synthesize cobalt oxide-based thermoelectric materials. Acta Mater. 2014, 73, 251–258. [Google Scholar] [CrossRef]
- Prasad, K.R.; Miura, N. Electrochemically synthesized MnO2-based mixed oxides for high performance redox supercapacitors. Electrochem. Commun. 2004, 6, 1004–1008. [Google Scholar] [CrossRef]
- Rao, K.; Smakula, A. Dielectric properties of cobalt oxide, nickel oxide, and their mixed crystals. J. Appl. Phys. 1965, 36, 2031–2038. [Google Scholar] [CrossRef]
- Van Schalkwijk, W.; Scrosati, B. Advances in lithium ion batteries introduction. In Advances in Lithium-Ion Batteries; Kluwer Academic/Plenum Publisher: London, UK, 2002; pp. 1–5. [Google Scholar]
- Andersen, N.I.; Serov, A.; Atanassov, P. Metal oxides/CNT nano-composite catalysts for oxygen reduction/oxygen evolution in alkaline media. Appl. Catal. B Environ. 2015, 163, 623–627. [Google Scholar] [CrossRef]
- Jayalakshmi, M.; Rao, M.M.; Venugopal, N.; Kim, K.-B. Hydrothermal synthesis of SnO2–V2O5 mixed oxide and electrochemical screening of carbon nano-tubes (CNT), V2O5, V2O5–CNT, and SnO2–V2O5–CNT electrodes for supercapacitor applications. J. Power Sour. 2007, 166, 578–583. [Google Scholar] [CrossRef]
- Ito, S.; Makari, Y.; Kitamura, T.; Wada, Y.; Yanagida, S. Fabrication and characterization of mesoporous SnO2/ZnO-composite electrodes for efficient dye solar cells. J. Mater. Chem. 2004, 14, 385–390. [Google Scholar] [CrossRef]
- Rusevova, K.; Kopinke, F.-D.; Georgi, A. Nano-sized magnetic iron oxides as catalysts for heterogeneous Fenton-like reactions—Influence of Fe (II)/Fe (III) ratio on catalytic performance. J. Hazard. Mater. 2012, 241, 433–440. [Google Scholar] [CrossRef]
- Leitner, J.; Bartůněk, V.; Sedmidubský, D.; Jankovský, O. Thermodynamic properties of nanostructured ZnO. Appl. Mater. Today 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible highT c superconductivity in the Ba−La−Cu−O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Rotter, M.; Tegel, M.; Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2. Phys. Rev. Lett. 2008, 101, 107006. [Google Scholar] [CrossRef]
- Tallapally, V.; Damma, D.; Darmakkolla, S.R. Facile synthesis of size-tunable tin arsenide nanocrystals. Chem. Commun. 2019, 55, 1560–1563. [Google Scholar] [CrossRef]
- Sleight, A.W.; Gillson, J.; Bierstedt, P. High-temperature superconductivity in the BaPb1−xBixO3 system. Solid State Commun. 1993, 88, 841–842. [Google Scholar] [CrossRef]
- Paglione, J.; Greene, R.L. High-temperature superconductivity in iron-based materials. Nat. Phys. 2010, 6, 645. [Google Scholar] [CrossRef]
- Jankovský, O.; Antončík, F.; Hlásek, T.; Plecháček, V.; Sedmidubský, D.; Huber, Š.; Lojka, M.; Bartůněk, V. Synthesis and properties of YBa2Cu3O7-δ–Y2Ba4CuWO10. 8 superconducting composites. J. Eur. Ceram. Soc. 2018, 38, 2541–2546. [Google Scholar] [CrossRef]
- Drozdov, A.; Eremets, M.; Troyan, I.; Ksenofontov, V.; Shylin, S. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Lv, Y.; Gao, W.; Yang, L.; Yu, R.; Li, F.; Jin, C. The superconductivity at 18 K in LiFeAs system. Solid State Commun. 2008, 148, 538–540. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.S.; Wang, L.; Chua, C.K.; Sofer, Z.; Jankovský, O.; Pumera, M. High temperature superconducting materials as bi-functional catalysts for hydrogen evolution and oxygen reduction. J. Mater. Chem. A 2015, 3, 8346–8352. [Google Scholar] [CrossRef]
- Goldschmidt, D.; Reisner, G.; Direktovitch, Y.; Knizhnik, A.; Gartstein, E.; Kimmel, G.; Eckstein, Y. Tetragonal superconducting family (CaxLa1−x)(Ba1.75−xLa0.25+x)Cu3Oy: The effect of cosubstitution on the transition temperature. Phys. Rev. B 1993, 48, 532. [Google Scholar] [CrossRef]
- Mirmelshtein, A.; Podlesnyak, A.; Bobrovskii, V.; Davydov, S.; Karkin, A.; Kozhevnikov, V.; Goshchitskii, B.; Cheshnitskii, S. Electrical crystal field effects in high-temperature superconductor HoBa2Cu3O7. Phys. C Supercond. 1988, 153, 176–177. [Google Scholar] [CrossRef]
- Maple, M.; Dalichaouch, Y.; Ferreira, J.; Hake, R.; Lee, B.; Neumeier, J.; Torikachvili, M.; Yang, K.; Zhou, H.; Guertin, R. RBa2Cu3O7–δ (R = Rare earth) High-Tc magnetic superconductors. In Proceedings of the Yamada Conference XVIII on Superconductivity in Highly Correlated Fermion Systems, Sendai, Japan, 31 August–3 September 1987; Elsevier: Amsterdam, The Netherlands, 1987; pp. 155–162. [Google Scholar]
- Jankovský, O.; Sedmidubský, D.; Rubešová, K.; Sofer, Z.; Leitner, J.; Ružička, K.; Svoboda, P. Structure, non-stoichiometry and thermodynamic properties of Bi1. 85Sr2Co1.85O7. 7−δ ceramics. Thermochim. Acta 2014, 582, 40–45. [Google Scholar] [CrossRef]
- Jankovský, O.; Sedmidubský, D.; Sofer, Z.; Šimek, P.; Hejtmánek, J. Thermodynamic behavior of Ca3Co3. 93O9+δ ceramics. Ceram. Silik. 2012, 56, 139–144. [Google Scholar]
- Jankovský, O.; Sedmidubský, D.; Sofer, Z. Phase diagram of the pseudobinary system Bi–Co–O. J. Eur. Ceram. Soc. 2013, 33, 2699–2704. [Google Scholar] [CrossRef]
- Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Kawamura, R.; Yanagi, H.; Kamiya, T.; Hosono, H. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 2006, 128, 10012–10013. [Google Scholar] [CrossRef]
- Wu, M.-K.; Ashburn, J.R.; Torng, C.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.; Chu, A. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908. [Google Scholar] [CrossRef]
- Schneemeyer, L.; Waszczak, J.; Siegrist, T.; Van Dover, R.; Rupp, L.; Batlogg, B.; Cava, R.J.; Murphy, D. Superconductivity in YBa2Cu3O7 single crystals. Nature 1987, 328, 601. [Google Scholar] [CrossRef]
- Watkins, S.; Fronczek, F.; Wheelock, K.; Goodrich, R.; Hamilton, W.; Johnson, W. Structure of Y2BaCuO5. Acta Crystallogr. Sect. C 1988, 44, 3–6. [Google Scholar]
- Lee, D.; Selvamanickam, V.; Salama, K. Influences of Y2BaCuO5 particle size and content on the transport critical current density of YBa2Cu3Ox superconductor. Phys. C Supercond. 1992, 202, 83–96. [Google Scholar] [CrossRef]
- McGinn, P.; Chen, W.; Zhu, N.; Tan, L.; Varanasi, C.; Sengupta, S. Microstructure and critical current density of zone melt textured YBa2Cu3O6+x/Y2BaCuO5 with BaSnO3 additions. Appl. Phys. Lett. 1991, 59, 120–122. [Google Scholar] [CrossRef]
- Jin, S.; Tiefel, T.; Kammlott, G. Effect of Y2BaCuO5 inclusions on flux pinning in YBa2Cu3O7−δ. Appl. Phys. Lett. 1991, 59, 540–542. [Google Scholar] [CrossRef]
- Hlásek, T.; Shi, Y.; Durrell, J.H.; Dennis, A.R.; Namburi, D.K.; Plecháček, V.; Rubešová, K.; Cardwell, D.A.; Jankovský, O. Cost-effective isothermal top-seeded melt-growth of single-domain YBCO superconducting ceramics. Solid State Sci. 2019, 88, 74–80. [Google Scholar] [CrossRef]
- Golosovsky, I.; Böni, P.; Fischer, P. Magnetic structure of Y2BaCuO5. Solid State Commun. 1993, 87, 1035–1037. [Google Scholar] [CrossRef]
- Štejfa, V.; Fulem, M.; Růžička, K.; Červinka, C. Thermodynamic study of selected monoterpenes III. J. Chem. Thermodyn. 2014, 79, 280–289. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Dudarev, S.; Botton, G.; Savrasov, S.; Humphreys, C.; Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Forsyth, J.; Brown, P.; Wanklyn, B. Magnetism in cupric oxide. J. Phys. C 1988, 21, 2917. [Google Scholar] [CrossRef]
- Martin, C. Simple treatment of anharmonic effects on the specific heat. J. Phys. Condens. Matter 1991, 3, 5967. [Google Scholar] [CrossRef]
- Hengzhong, Z.; Zheng, F.; Pingmin, Z.; Xinmin, C. Enthalpies of formation of some phases present in the Y−Ba−Cu−O system by solution calorimetry. J. Solut. Chem. 1995, 24, 565–578. [Google Scholar] [CrossRef]
- Zhou, Z.; Navrotsky, A. Thermochemistry of the Y2O3–BaO–Cu–O system. J. Mater. Res. 1992, 7, 2920–2935. [Google Scholar] [CrossRef]

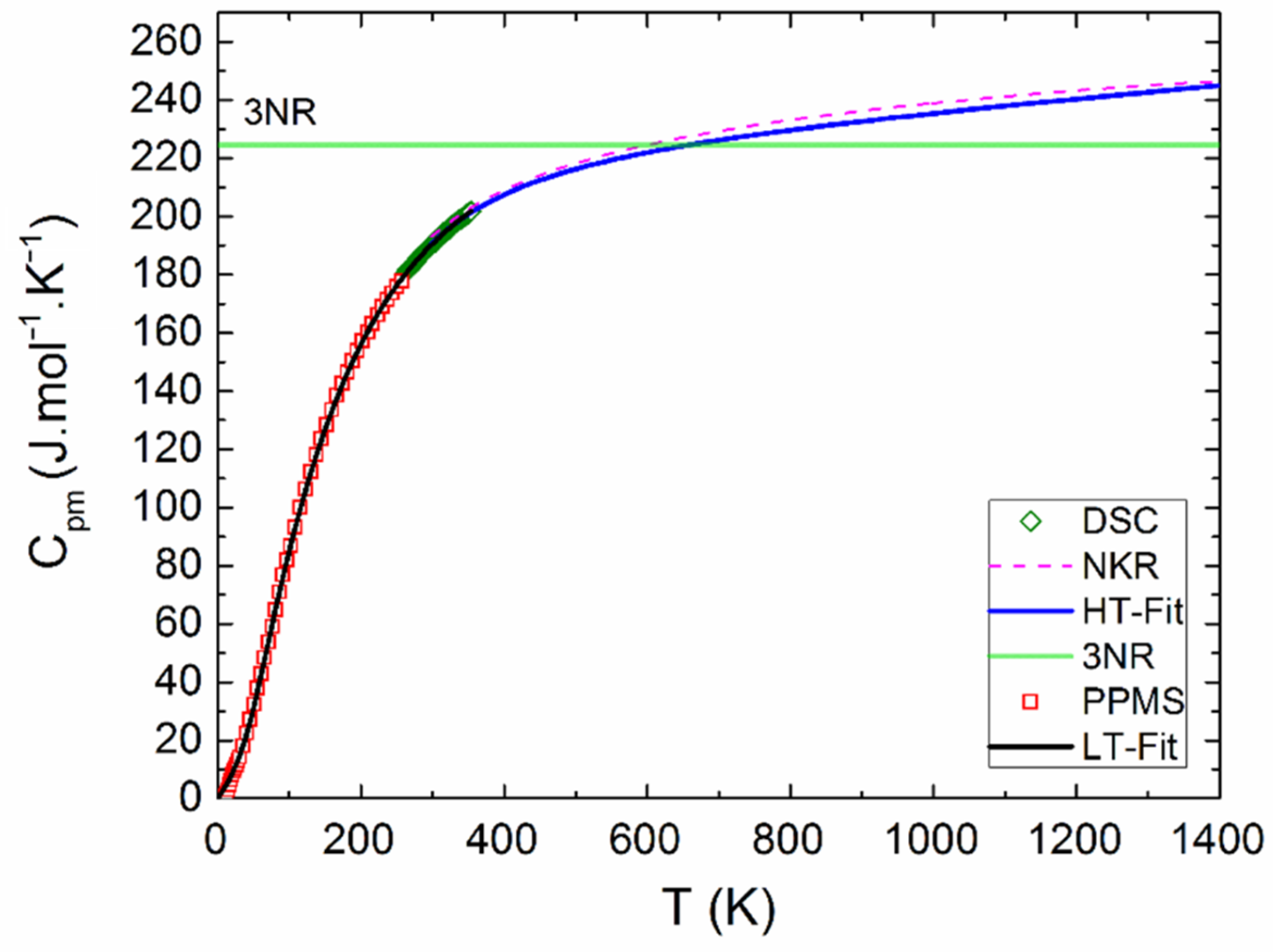
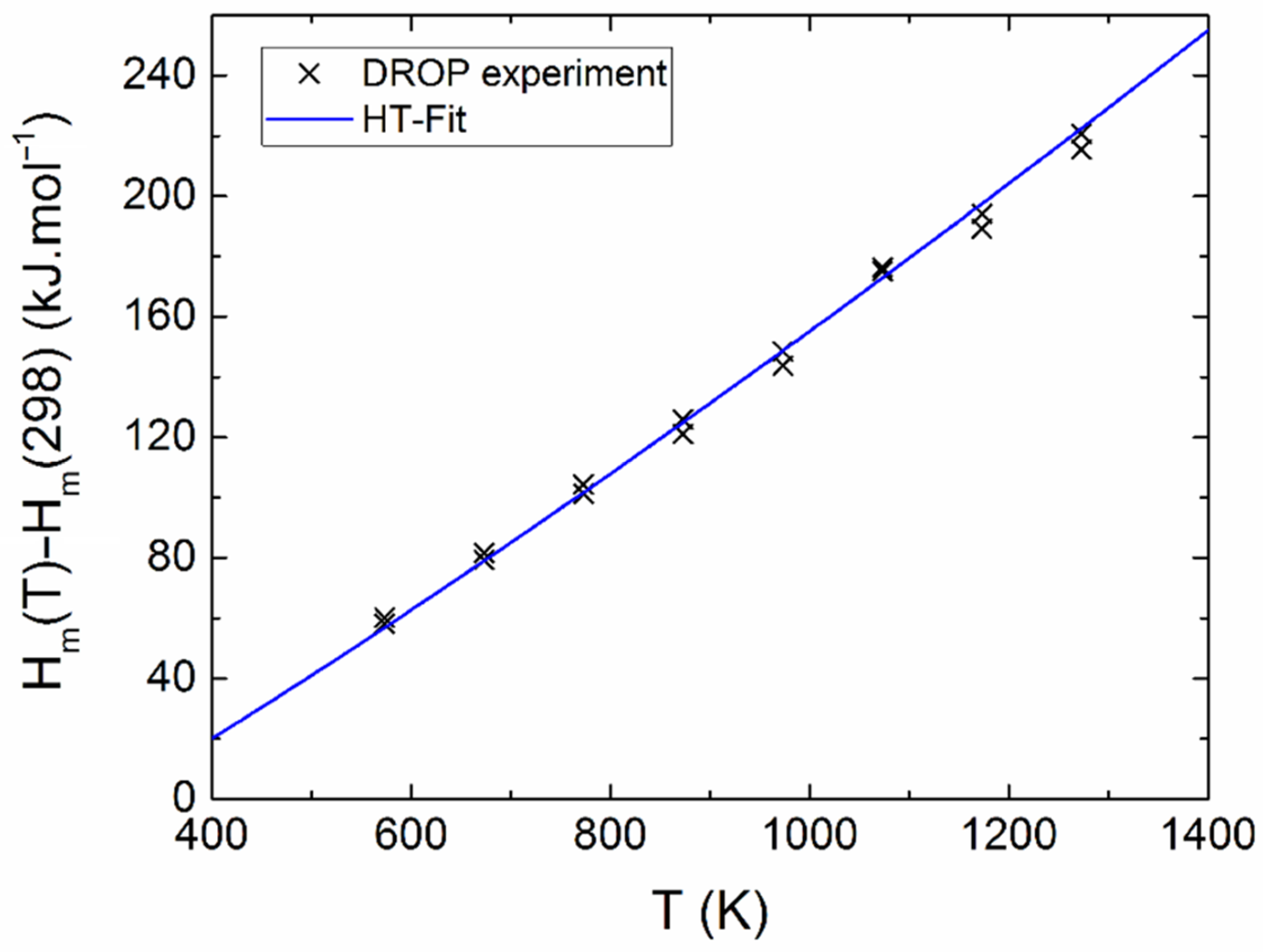

| Mode (i) | D | E1 | E2 | E3 | D |
|---|---|---|---|---|---|
| wi | 3 | 8 | 8 | 8 | - |
| θi/K | 116.3 ± 1.7 | 263.6 ± 2.0 | 406.7 ± 3.0 | 774.0 ± 3.9 | (6.584 ± 0.120) × 10−4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antončík, F.; Sedmidubský, D.; Jiříčková, A.; Lojka, M.; Hlásek, T.; Růžička, K.; Jankovský, O. Thermodynamic Properties of Stoichiometric Non-Superconducting Phase Y2BaCuO5. Materials 2019, 12, 3163. https://doi.org/10.3390/ma12193163
Antončík F, Sedmidubský D, Jiříčková A, Lojka M, Hlásek T, Růžička K, Jankovský O. Thermodynamic Properties of Stoichiometric Non-Superconducting Phase Y2BaCuO5. Materials. 2019; 12(19):3163. https://doi.org/10.3390/ma12193163
Chicago/Turabian StyleAntončík, Filip, David Sedmidubský, Adéla Jiříčková, Michal Lojka, Tomáš Hlásek, Květoslav Růžička, and Ondřej Jankovský. 2019. "Thermodynamic Properties of Stoichiometric Non-Superconducting Phase Y2BaCuO5" Materials 12, no. 19: 3163. https://doi.org/10.3390/ma12193163
APA StyleAntončík, F., Sedmidubský, D., Jiříčková, A., Lojka, M., Hlásek, T., Růžička, K., & Jankovský, O. (2019). Thermodynamic Properties of Stoichiometric Non-Superconducting Phase Y2BaCuO5. Materials, 12(19), 3163. https://doi.org/10.3390/ma12193163







