Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder
Abstract
:1. Introduction
2. Experimental Method and DEM Modeling
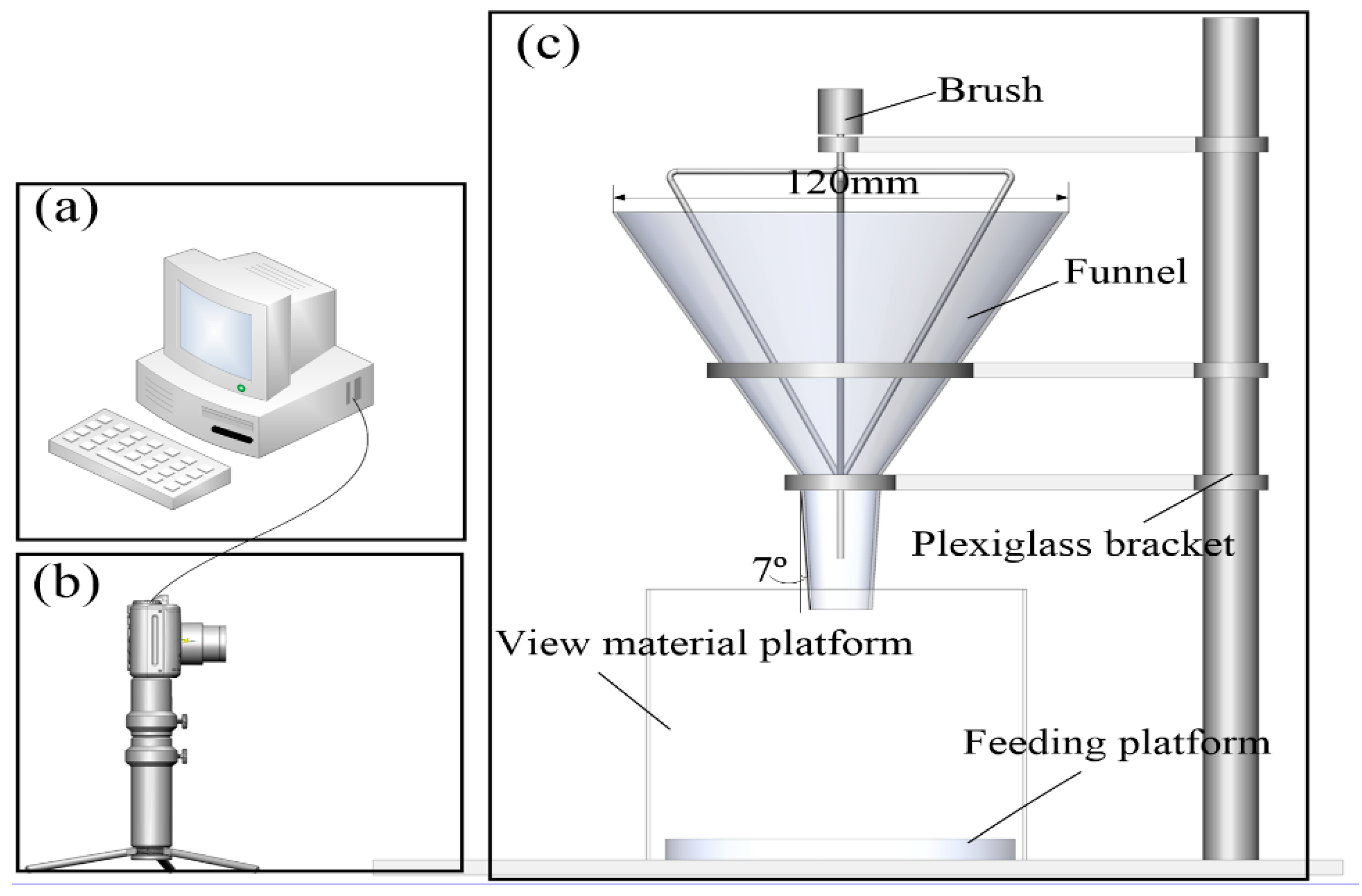
2.1. Funnel Flow Meter Test Device
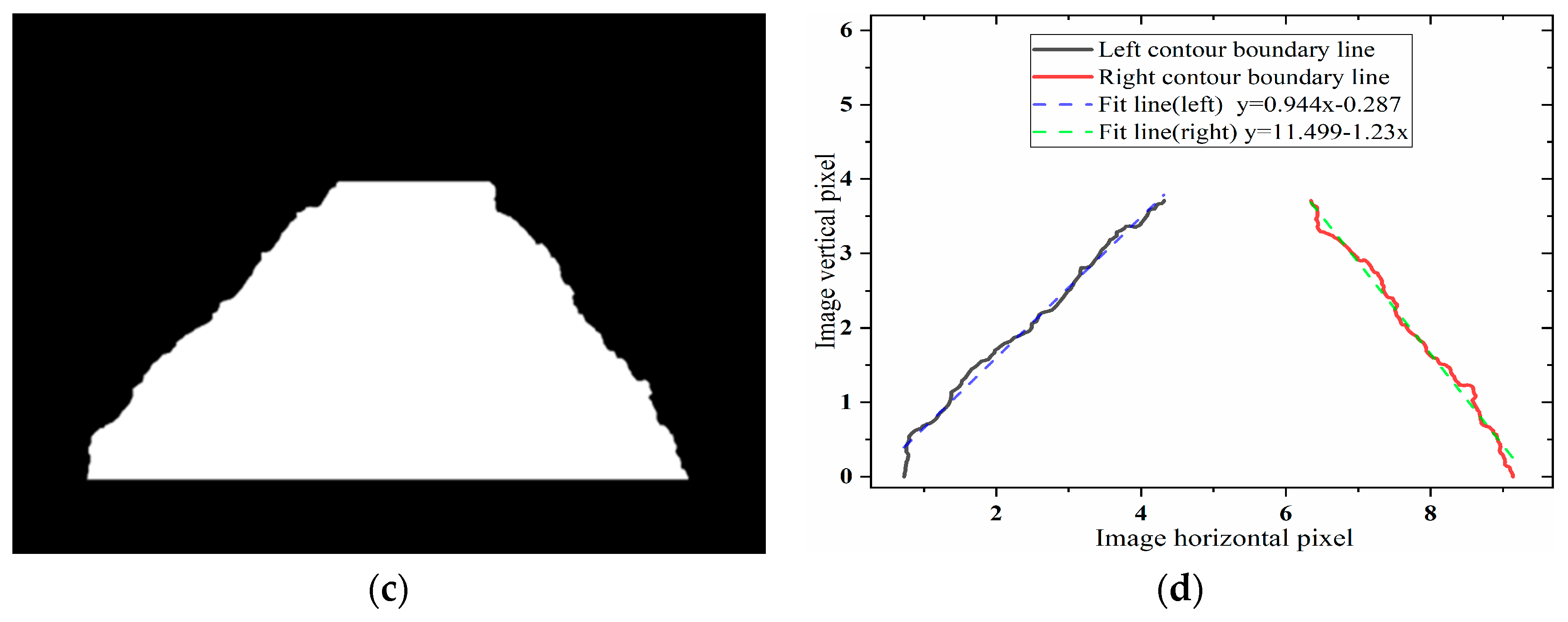
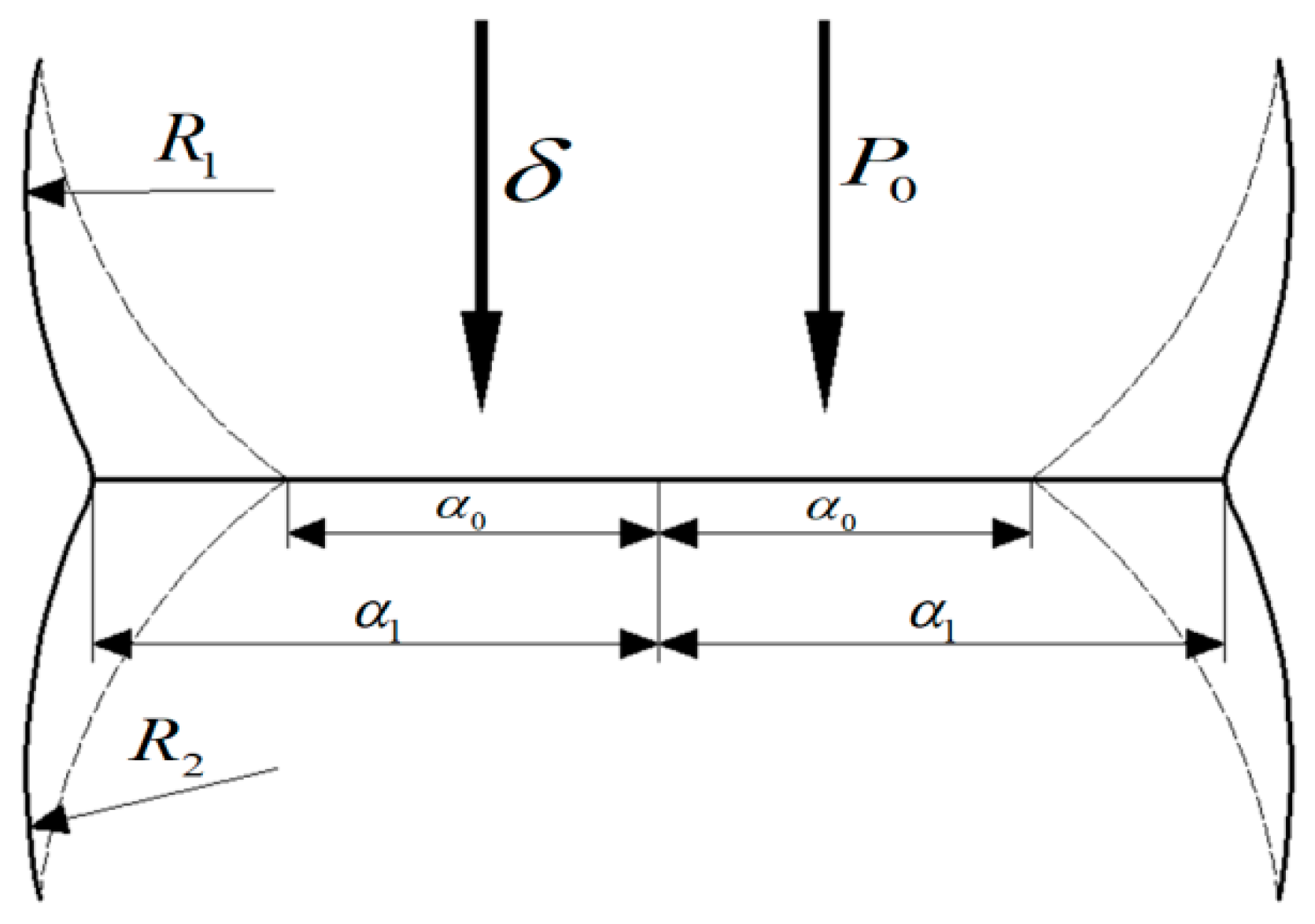
2.2. Angle-of-Repose Measurement
2.3. DEM Virtual Test Model
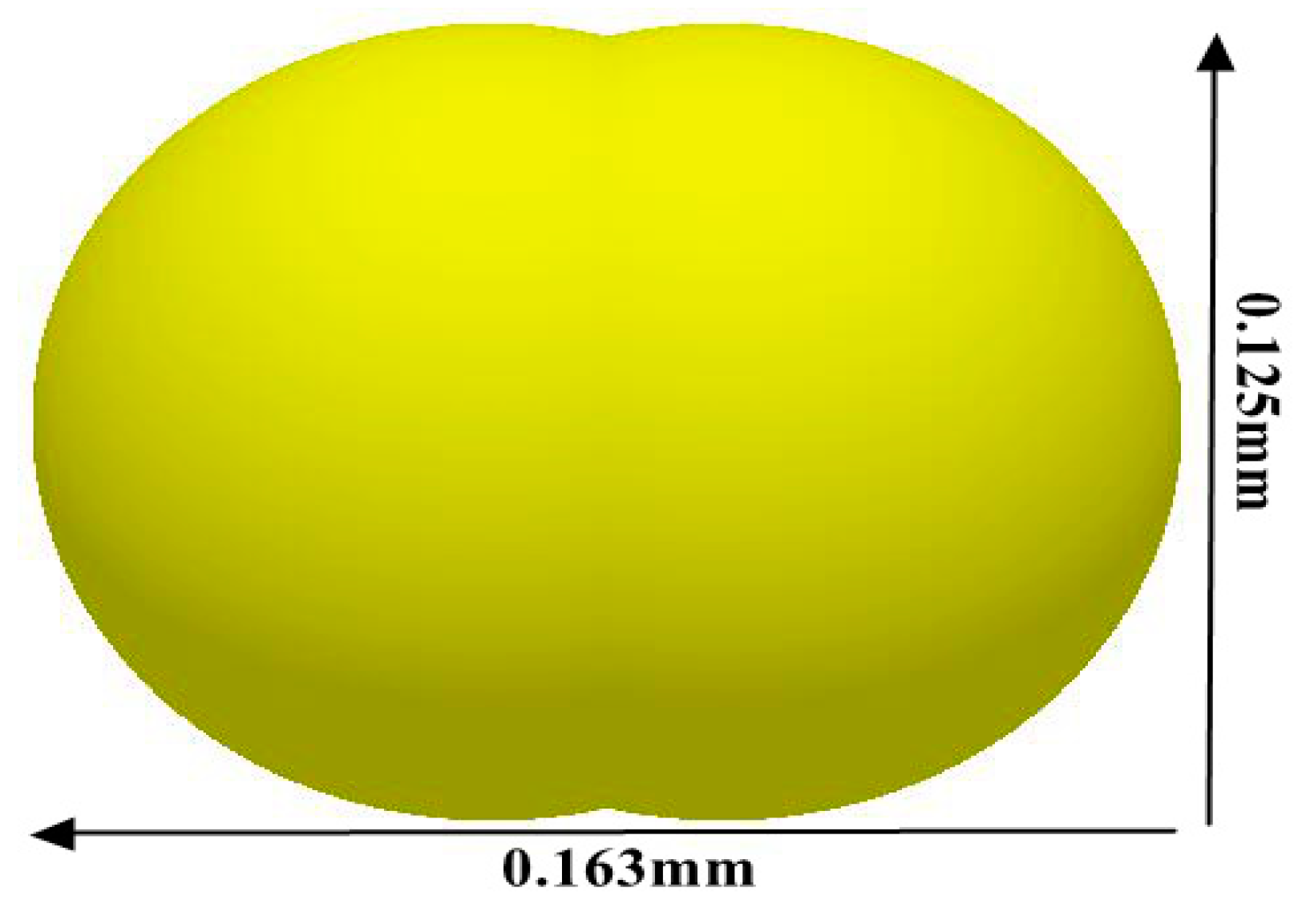
2.3.1. Coarse-Grain Modeling of the Particle Discrete Element Based on the JKR Contact Model
2.3.2. DEM Simulation Tests
2.3.3. Sensitivity Analysis of the Particle Intrinsic Parameters
3. Development and Application of the BP Prediction Model
3.1. BP Neural Network Database
- (1)
- Divide each random variable into N equal-probability subintervals , and obtain the midpoint of each subinterval as a sample representative of the corresponding random variable.
- (2)
- For each random variable Xi, extract a sample representative and arrange it according to a random number, and arrange the samples of all the random variables according to random numbers, resulting in N random arrangements. Each sample contains a sample of all the random variables representing .
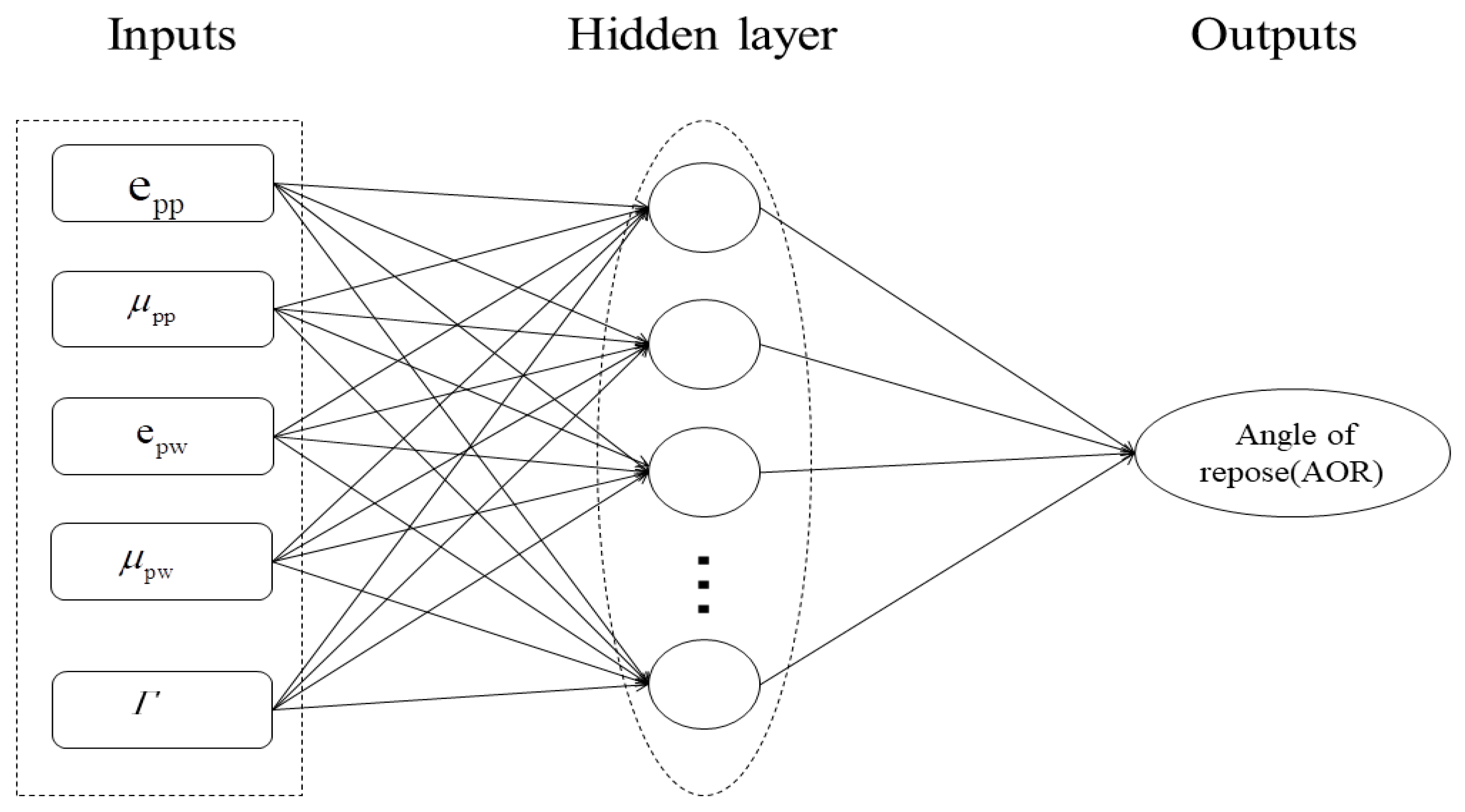
3.2. BP Neural Network Structure Design
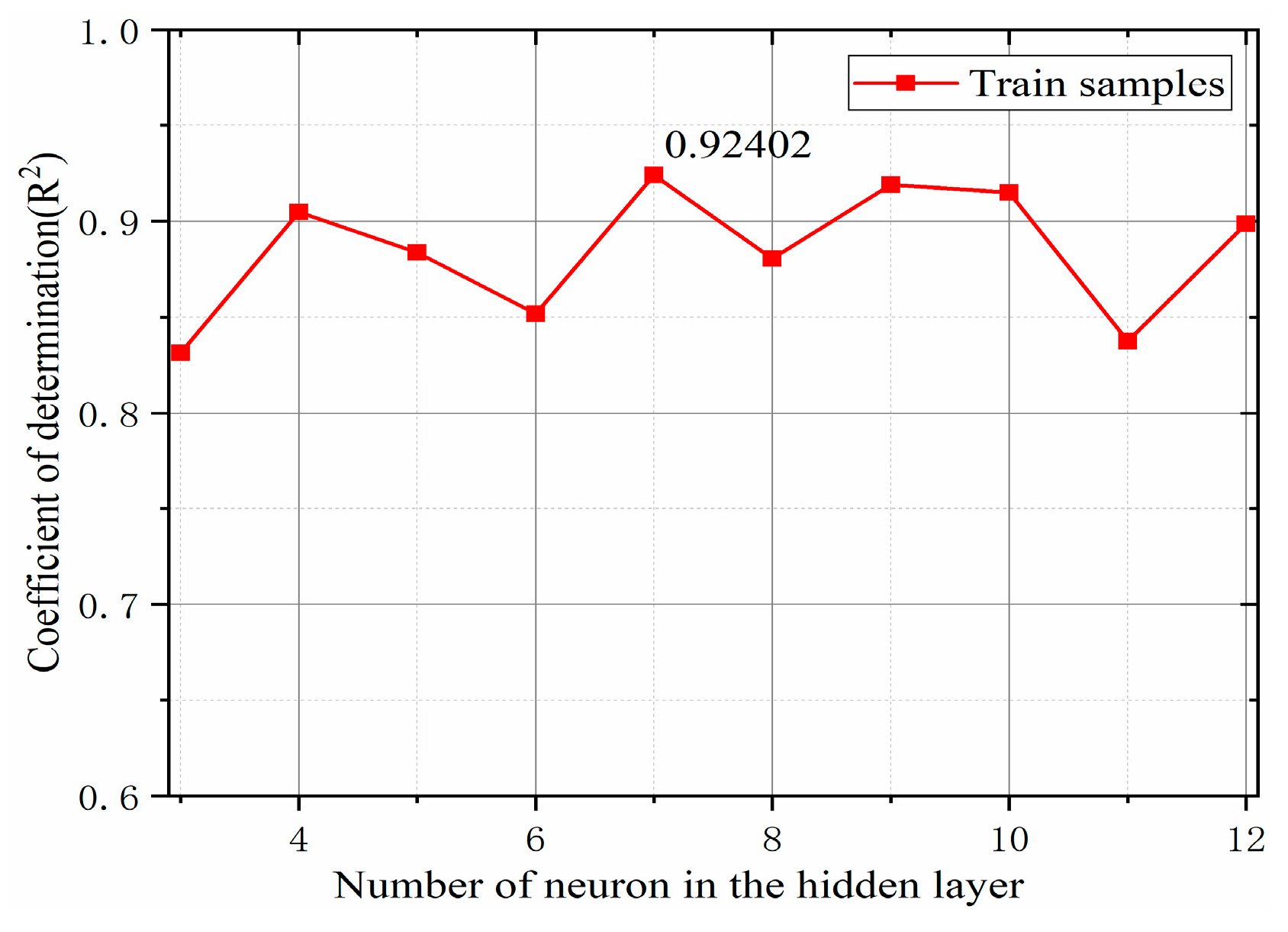
3.3. Optimization of the BP Neural Network Performance on the Basis of the GA
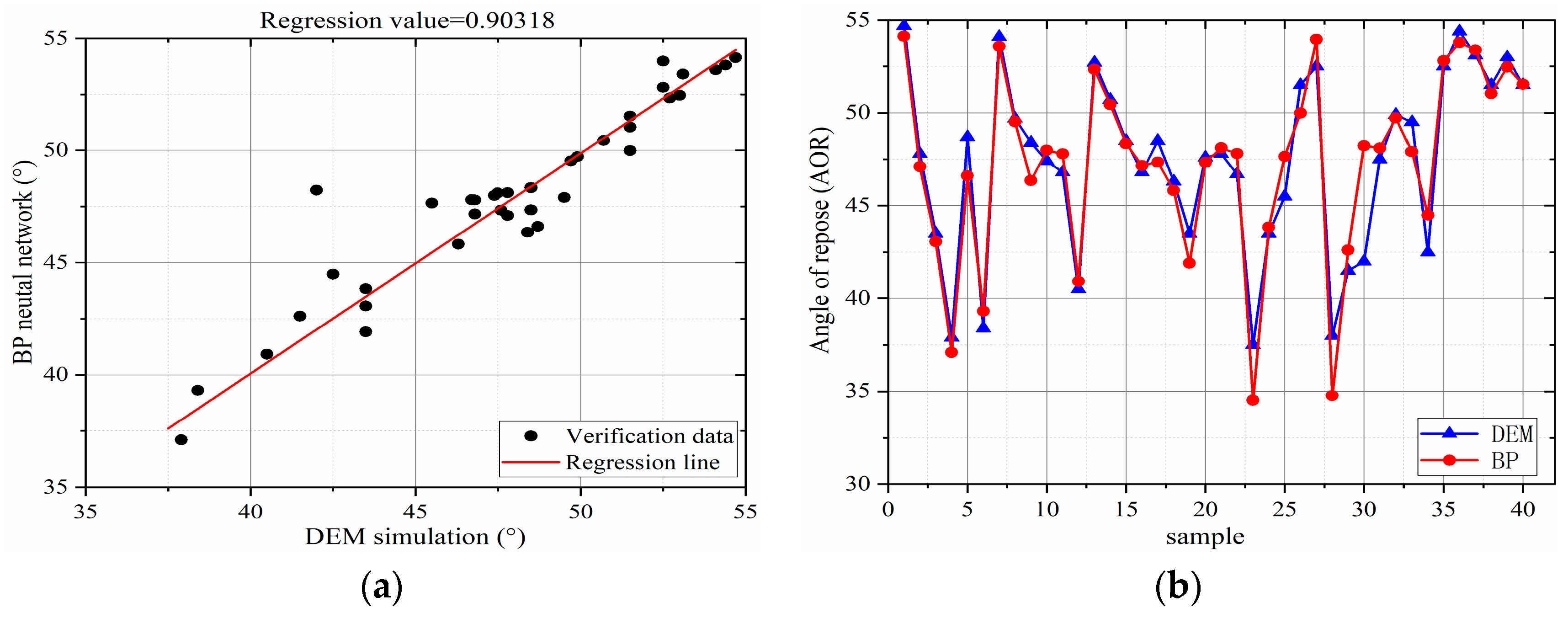
3.4. Prediction Results and Discussion
3.5. Application of the BP Prediction Model
3.5.1. BP Model Predictive Value of the Angle-of-Repose Search
- (1)
- initialize the sample point i, and predict the output value ;
- (2)
- identify whether the sample point i exceeds 300 sample points;
- (3)
- filter the predicted values of the BP prediction model according to the AORTol tolerance range and store them in a new sample space;
- (4)
- repeat steps (2) and (3) until 300 sample points have been searched, resulting in a new sample space as depicted in Figure 14b.
3.5.2. Mean-Shift Cluster Analysis
3.6. Verification Instance
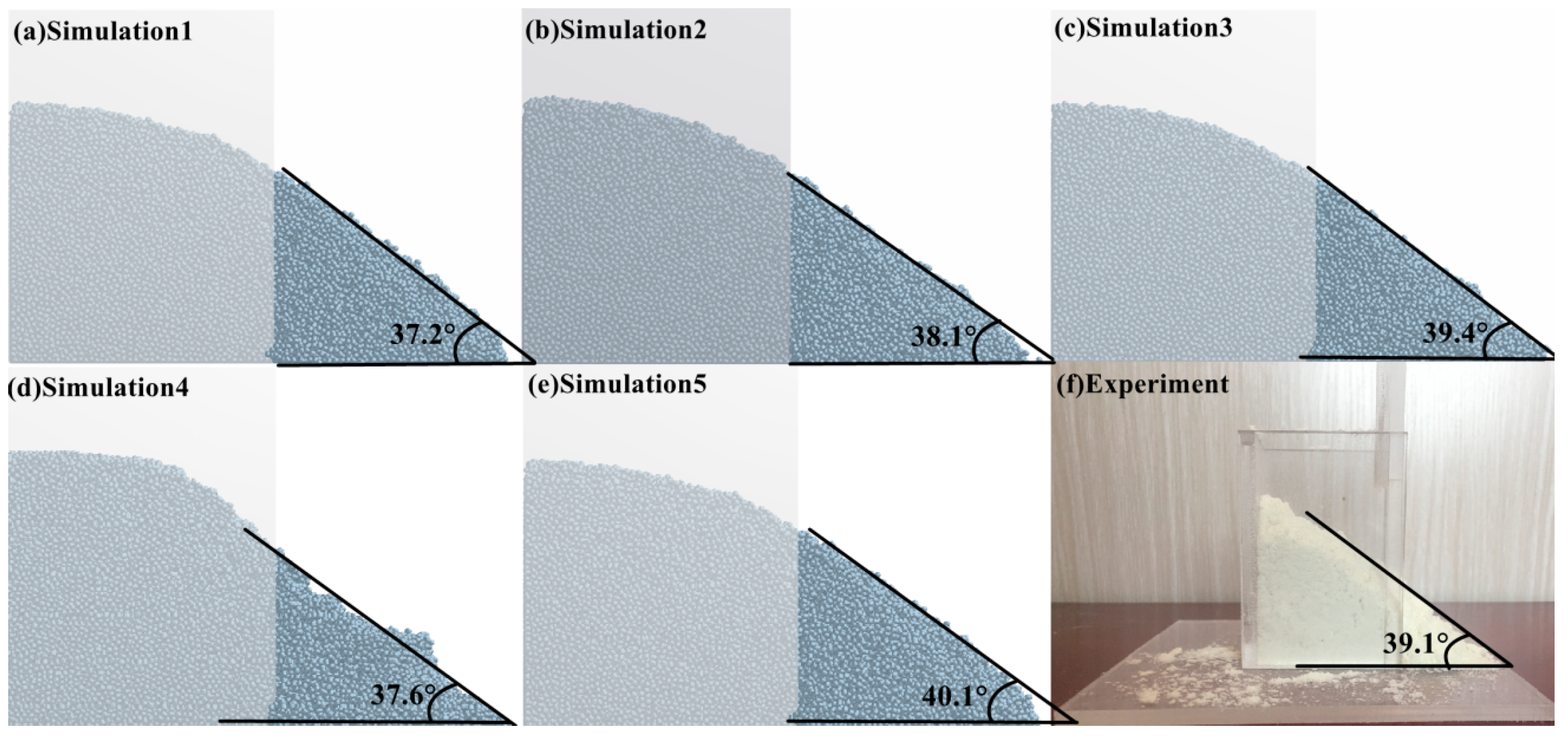
3.6.1. DEM Parameter Verification Under Quasi-Static Conditions
3.6.2. Dynamic Condition DEM Parameter Verification
3.6.3. Results and Discussion
4. Conclusions
- To achieve the DEM parameter calibration of the micron-scale material samples, the concept of cohesion number proposed by Bharadwaj et al. [23] for coarse-grained discrete element modeling can improve the calibration efficiency without affecting the calibration accuracy.
- In the DEM parameter calibration process, the BP approximation model modified using the GA can easily converge into the global sample space to avoid local optimal solutions, which would result in large errors in the calibration results.
- The study found that the rotating drum as a verification example of dynamic conditions can be used to verify the DEM parameter set of the funnel flow meter more accurately than the baffle lift test under static conditions and that the relative error is 0.63%–2.72%.
- The intrinsic parameters of the particles were explored during the simulation. The small range of the intrinsic parameters of the particles did not strongly influence the angle of repose; however, reducing the shear modulus was observed to considerably reduce the calculation cost.
- To avoid large dispersion and overlap between the predicted value and the simulated target value, a combination of the cyclic search algorithm and mean-shift cluster analysis can be used to find the optimal solution for each subclass in the sample space.
- Although the ultrafine agglomerated PU powder exhibited poor reproducibility with respect to the angle of repose during the stacking test, the baffle lifting method verified that the predicted output value of the BP model after training agreed with the angle obtained in the actual stacking test.
- During this calibration process, we observed that the DEM parameter calibration results are not a set of solution sets; each output value (angle) has multiple sets of mapping relations with the input DEM parameters. This also revealed the calibration work of the DEM parameter, which is a search process of the parameter set “best combination.” Based on a test design method, AOR was used as the target response value to find a suitable mapping relation for application in this study.
- In the future, a large number of variables (bulk density, time step) can be added as the response value of the output layer of the prediction model, and the influence of the DEM parameters on the angle of repose can be further investigated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| AOR (°) | Predicted value AOR (°) | |||||
|---|---|---|---|---|---|---|
| 0.148014 | 0.355076 | 0.135264 | 0.736817 | 0.736817 | 37.5 | - |
| 0.312023 | 0.537557 | 0.258614 | 1.551627 | 1.551627 | 43.2 | - |
| 0.327493 | 0.555877 | 0.270874 | 1.641178 | 1.641178 | 46.5 | - |
| 0.446438 | 0.689714 | 0.358998 | 2.222321 | 2.222321 | 52.2 | - |
| 0.141479 | 0.34653 | 0.130286 | 0.711667 | 0.711667 | 38.5 | - |
| 0.304733 | 0.531433 | 0.25321 | 1.52806 | 1.52806 | 46.5 | - |
| 0.16831 | 0.378255 | 0.152086 | 0.849553 | 0.849553 | 38.5 | - |
| 0.126852 | 0.331476 | 0.12139 | 0.649442 | 0.649442 | 38.5 | - |
| 0.423007 | 0.663505 | 0.341825 | 2.115487 | 2.115487 | 52.5 | - |
| 0.121281 | 0.323449 | 0.115855 | 0.604728 | 0.604728 | 36.5 | - |
| 0.333261 | 0.56006 | 0.272745 | 1.657726 | 1.657726 | 46.6 | - |
| 0.21847 | 0.432949 | 0.187752 | 1.096404 | 1.096404 | 44.5 | - |
| 0.241529 | 0.458257 | 0.205444 | 1.213885 | 1.213885 | 45.5 | - |
| 0.107443 | 0.308152 | 0.105226 | 0.545632 | 0.545632 | 33.7 | - |
| 0.212468 | 0.425678 | 0.183951 | 1.053621 | 1.053621 | 42.5 | - |
| 0.418222 | 0.65724 | 0.338593 | 2.095684 | 2.095684 | 50.9 | - |
| 0.276442 | 0.497534 | 0.231542 | 1.372128 | 1.372128 | 48.5 | - |
| 0.423445 | 0.667499 | 0.344465 | 2.128864 | 2.128864 | 51.5 | - |
| 0.319158 | 0.546443 | 0.262997 | 1.586359 | 1.586359 | 47.5 | - |
| 0.288473 | 0.512738 | 0.2408 | 1.444792 | 1.444792 | 47.5 | - |
| 0.296496 | 0.519416 | 0.246191 | 1.468489 | 1.468489 | 48.6 | - |
| 0.207081 | 0.420897 | 0.18249 | 1.038653 | 1.038653 | 44.5 | - |
| 0.299113 | 0.524424 | 0.247849 | 1.495777 | 1.495777 | 47.5 | - |
| 0.374274 | 0.610314 | 0.305546 | 1.878514 | 1.878514 | 48.8 | - |
| 0.153651 | 0.360635 | 0.14243 | 0.782299 | 0.782299 | 37.5 | - |
| 0.117663 | 0.32115 | 0.113377 | 0.589483 | 0.589483 | 35.5 | - |
| 0.151342 | 0.358549 | 0.138751 | 0.763457 | 0.763457 | 38.5 | - |
| 0.200513 | 0.412871 | 0.175436 | 1.01327 | 1.01327 | 43.2 | - |
| 0.272885 | 0.492047 | 0.228874 | 1.3599 | 1.3599 | 48.5 | - |
| 0.447476 | 0.690637 | 0.3602 | 2.243708 | 2.243708 | 53 | - |
| 0.462514 | 0.708098 | 0.371081 | 2.30172 | 2.30172 | 53.2 | - |
| 0.49869 | 0.747369 | 0.397784 | 2.498688 | 2.498688 | 54.9 | - |
| 0.408619 | 0.648391 | 0.330753 | 2.043503 | 2.043503 | 50.4 | - |
| 0.229198 | 0.443187 | 0.195137 | 1.144559 | 1.144559 | 46.3 | - |
| 0.124055 | 0.327711 | 0.117612 | 0.624993 | 0.624993 | 37.5 | - |
| 0.391213 | 0.627576 | 0.319341 | 1.959905 | 1.959905 | 50.6 | - |
| 0.468248 | 0.714486 | 0.376739 | 2.335572 | 2.335572 | 54.5 | - |
| 0.367979 | 0.60188 | 0.30052 | 1.838435 | 1.838435 | 48.4 | - |
| 0.146516 | 0.350077 | 0.134187 | 0.722417 | 0.722417 | 38.5 | - |
| 0.471483 | 0.717974 | 0.379428 | 2.364548 | 2.364548 | 53.6 | - |
| 0.221485 | 0.43738 | 0.191663 | 1.114118 | 1.114118 | 43.6 | - |
| 0.135678 | 0.340273 | 0.125432 | 0.679225 | 0.679225 | 36.8 | - |
| 0.48366 | 0.732491 | 0.387561 | 2.425036 | 2.425036 | 54.2 | - |
| 0.377803 | 0.61492 | 0.309358 | 1.88945 | 1.88945 | 48.8 | - |
| 0.188603 | 0.400831 | 0.165758 | 0.947453 | 0.947453 | 41.4 | - |
| 0.452653 | 0.694399 | 0.363694 | 2.255973 | 2.255973 | 52.6 | - |
| 0.25078 | 0.470105 | 0.21425 | 1.25443 | 1.25443 | 48.6 | - |
| 0.380085 | 0.617621 | 0.312161 | 1.908359 | 1.908359 | 49.1 | - |
| 0.433769 | 0.678038 | 0.351069 | 2.17868 | 2.17868 | 51.7 | - |
| 0.306967 | 0.533354 | 0.256798 | 1.544442 | 1.544442 | 45.4 | - |
| 0.23591 | 0.450782 | 0.201923 | 1.181499 | 1.181499 | 47.5 | - |
| 0.224564 | 0.442093 | 0.192686 | 1.117348 | 1.117348 | 45.8 | - |
| 0.16351 | 0.374564 | 0.148299 | 0.817834 | 0.817834 | 39.5 | - |
| 0.302886 | 0.52835 | 0.251428 | 1.513066 | 1.513066 | 48.3 | - |
| 0.131847 | 0.336389 | 0.124413 | 0.655122 | 0.655122 | 35.5 | - |
| 0.23827 | 0.456382 | 0.202916 | 1.189952 | 1.189952 | 47.5 | - |
| 0.260284 | 0.481961 | 0.221172 | 1.305584 | 1.305584 | 46.7 | - |
| 0.254459 | 0.475788 | 0.215289 | 1.27702 | 1.27702 | 47.5 | - |
| 0.441856 | 0.685963 | 0.355206 | 2.206748 | 2.206748 | 51.5 | - |
| 0.32147 | 0.550521 | 0.266212 | 1.60286 | 1.60286 | 46.5 | - |
| 0.324843 | 0.552813 | 0.269607 | 1.623838 | 1.623838 | 46.3 | - |
| 0.18121 | 0.390041 | 0.160593 | 0.909805 | 0.909805 | 41.5 | - |
| 0.162969 | 0.369847 | 0.145247 | 0.803433 | 0.803433 | 38.4 | - |
| 0.19726 | 0.411867 | 0.173669 | 0.994007 | 0.994007 | 44.5 | - |
| 0.340307 | 0.573351 | 0.281061 | 1.707059 | 1.707059 | 47.1 | - |
| 0.170813 | 0.381489 | 0.153139 | 0.851311 | 0.851311 | 39.5 | - |
| 0.104023 | 0.307472 | 0.103119 | 0.526815 | 0.526815 | 31.8 | - |
| 0.387796 | 0.625467 | 0.317023 | 1.94451 | 1.94451 | 49.4 | - |
| 0.385571 | 0.619061 | 0.314785 | 1.926352 | 1.926352 | 49.3 | - |
| 0.410039 | 0.65005 | 0.333638 | 2.052398 | 2.052398 | 50.5 | - |
| 0.370615 | 0.604706 | 0.304686 | 1.852664 | 1.852664 | 48.6 | - |
| 0.282934 | 0.506236 | 0.236888 | 1.41209 | 1.41209 | 48.7 | - |
| 0.475776 | 0.723432 | 0.381433 | 2.371023 | 2.371023 | 53.7 | - |
| 0.102568 | 0.300973 | 0.101261 | 0.516099 | 0.516099 | 31.3 | - |
| 0.401425 | 0.640962 | 0.326776 | 2.003317 | 2.003317 | 50.4 | - |
| 0.432507 | 0.672806 | 0.347558 | 2.150266 | 2.150266 | 51.6 | - |
| 0.29331 | 0.516569 | 0.244004 | 1.465484 | 1.465484 | 47.9 | - |
| 0.361881 | 0.592732 | 0.297125 | 1.807417 | 1.807417 | 48.4 | - |
| 0.177314 | 0.389413 | 0.159907 | 0.886797 | 0.886797 | 39.4 | - |
| 0.259868 | 0.477258 | 0.218398 | 1.291127 | 1.291127 | 48.7 | - |
| 0.496221 | 0.742673 | 0.395921 | 2.48252 | 2.48252 | 54.7 | 54.1343 |
| 0.263487 | 0.487348 | 0.223437 | 1.31955 | 1.31955 | 47.8 | 47.09626 |
| 0.195801 | 0.408062 | 0.170152 | 0.983121 | 0.983121 | 43.5 | 43.07308 |
| 0.13885 | 0.342139 | 0.129412 | 0.694485 | 0.694485 | 37.9 | 37.10446 |
| 0.248251 | 0.468067 | 0.210299 | 1.239911 | 1.239911 | 48.7 | 46.61237 |
| 0.157703 | 0.365908 | 0.143041 | 0.798988 | 0.798988 | 38.4 | 39.31297 |
| 0.483311 | 0.729671 | 0.387418 | 2.409156 | 2.409156 | 54.1 | 53.59277 |
| 0.394428 | 0.632054 | 0.321426 | 1.975155 | 1.975155 | 49.7 | 49.52709 |
| 0.246637 | 0.461935 | 0.209964 | 1.220124 | 1.220124 | 48.4 | 46.35139 |
| 0.347334 | 0.580223 | 0.28592 | 1.737206 | 1.737206 | 47.4 | 47.99007 |
| 0.336898 | 0.566945 | 0.277764 | 1.684021 | 1.684021 | 46.8 | 47.7934 |
| 0.1753 | 0.383506 | 0.156862 | 0.876854 | 0.876854 | 40.5 | 40.91912 |
| 0.454227 | 0.697562 | 0.367317 | 2.278103 | 2.278103 | 52.7 | 52.33081 |
| 0.41565 | 0.65385 | 0.336594 | 2.068696 | 2.068696 | 50.7 | 50.44045 |
| 0.363435 | 0.596835 | 0.29987 | 1.833117 | 1.833117 | 48.5 | 48.34836 |
| 0.267718 | 0.488204 | 0.225227 | 1.33657 | 1.33657 | 46.8 | 47.16393 |
| 0.278919 | 0.500717 | 0.233969 | 1.388731 | 1.388731 | 48.5 | 47.34501 |
| 0.232639 | 0.448623 | 0.198307 | 1.166255 | 1.166255 | 46.3 | 45.81617 |
| 0.185732 | 0.396439 | 0.164037 | 0.919877 | 0.919877 | 43.5 | 41.91603 |
| 0.283575 | 0.507758 | 0.239619 | 1.417782 | 1.417782 | 47.6 | 47.3336 |
| 0.35404 | 0.58545 | 0.290478 | 1.772903 | 1.772903 | 47.8 | 48.11718 |
| 0.335475 | 0.565447 | 0.275944 | 1.672342 | 1.672342 | 46.7 | 47.80509 |
| 0.11331 | 0.314101 | 0.108047 | 0.558355 | 0.558355 | 37.5 | 34.5128 |
| 0.205706 | 0.417912 | 0.17927 | 1.032569 | 1.032569 | 43.5 | 43.83734 |
| 0.31594 | 0.542452 | 0.260678 | 1.566943 | 1.566943 | 45.5 | 47.65645 |
| 0.405597 | 0.642057 | 0.328437 | 2.026057 | 2.026057 | 51.5 | 49.98852 |
| 0.490435 | 0.74106 | 0.394663 | 2.464506 | 2.464506 | 52.5 | 53.97321 |
| 0.115208 | 0.317845 | 0.110801 | 0.572423 | 0.572423 | 38 | 34.75902 |
| 0.192786 | 0.404665 | 0.167635 | 0.95128 | 0.95128 | 41.5 | 42.62196 |
| 0.358329 | 0.590099 | 0.293082 | 1.790835 | 1.790835 | 42 | 48.23795 |
| 0.352469 | 0.58337 | 0.287791 | 1.764129 | 1.764129 | 47.5 | 48.10753 |
| 0.398763 | 0.637235 | 0.322779 | 1.988032 | 1.988032 | 49.9 | 49.7124 |
| 0.344042 | 0.57628 | 0.284129 | 1.718395 | 1.718395 | 49.5 | 47.90788 |
| 0.216065 | 0.427818 | 0.187274 | 1.070227 | 1.070227 | 42.5 | 44.48258 |
| 0.464179 | 0.709876 | 0.3729 | 2.331597 | 2.331597 | 52.5 | 52.80379 |
| 0.48677 | 0.735263 | 0.391804 | 2.44262 | 2.44262 | 54.4 | 53.80025 |
| 0.478557 | 0.724111 | 0.384023 | 2.388136 | 2.388136 | 53.1 | 53.39367 |
| 0.427445 | 0.668181 | 0.345401 | 2.139559 | 2.139559 | 51.5 | 51.03914 |
| 0.457369 | 0.701879 | 0.369677 | 2.284386 | 2.284386 | 53 | 52.46019 |
| 0.438178 | 0.678875 | 0.354788 | 2.185601 | 2.185601 | 51.5 | 51.52571 |
| Test Sequence | Simulation AOR (°) | Test Sequence | Simulation AOR (°) | Test Sequence | Simulation AOR (°) |
|---|---|---|---|---|---|
| 1 | 45.5 | 35 | 50.5 | 69 | 48.4 |
| 2 | 46.4 | 36 | 47 | 70 | 48.3 |
| 3 | 47.4 | 37 | 48.1 | 71 | 48.9 |
| 4 | 48.3 | 38 | 49.4 | 72 | 46.7 |
| 5 | 47.2 | 39 | 46.8 | 73 | 48.6 |
| 6 | 46.3 | 40 | 48.6 | 74 | 47.2 |
| 7 | 47.5 | 41 | 49.5 | 75 | 47.2 |
| 8 | 43.6 | 42 | 47.5 | 76 | 48.3 |
| 9 | 45.8 | 43 | 47.9 | 77 | 45.6 |
| 10 | 48.3 | 44 | 50.1 | 78 | 46.9 |
| 11 | 49.2 | 45 | 48.2 | 79 | 48.6 |
| 12 | 48.4 | 46 | 47.2 | 80 | 48.5 |
| 13 | 49.2 | 47 | 48.3 | 81 | 48.5 |
| 14 | 47.5 | 48 | 45.4 | 82 | 47.8 |
| 15 | 46.8 | 49 | 48.1 | 83 | 48.4 |
| 16 | 49.5 | 50 | 50.1 | 84 | 48.3 |
| 17 | 49.5 | 51 | 49.4 | 85 | 48.5 |
| 18 | 46.3 | 52 | 50.2 | 86 | 48.5 |
| 19 | 48.9 | 53 | 46.3 | 87 | 46.9 |
| 20 | 47.3 | 54 | 48.3 | 88 | 49.2 |
| 21 | 48.9 | 55 | 46.8 | 89 | 47.7 |
| 22 | 48.8 | 56 | 47.6 | 90 | 48.2 |
| 23 | 47.9 | 57 | 48.4 | 91 | 49.3 |
| 24 | 47.1 | 58 | 47.4 | 92 | 47.9 |
| 25 | 46.5 | 59 | 45.2 | 93 | 49.6 |
| 26 | 45.9 | 60 | 44.5 | 94 | 48.5 |
| 27 | 48.2 | 61 | 47.9 | 95 | 49.4 |
| 28 | 45.6 | 62 | 48.9 | 96 | 41.2 |
| 29 | 49.2 | 63 | 47.1 | 97 | 40.5 |
| 30 | 48.5 | 64 | 47.5 | 98 | 49.8 |
| 31 | 46.8 | 65 | 48.9 | 99 | 49.9 |
| 32 | 45.8 | 66 | 48.9 | 100 | 48.8 |
| 33 | 49.5 | 67 | 48.4 | ||
| 34 | 50.2 | 68 | 47.8 | ||
| The average value of the static angle of the bulk accumulation experiment is 47.801°. | |||||
References
- Wu, Z.; Liu, Z.; Liu, G. Research on Crushing and Regeneration Mechanism of Thermosetting Plastic Based on Mechanical and Physical Method. China Mech. Eng. 2012, 23, 1639–1644. [Google Scholar]
- Yang, W.; Dong, Q.; Liu, S.; Xie, H.; Liu, L.; Li, J. Recycling and Disposal Methods for Polyurethane Foam Wastes. Procedia Environ. Sci. 2012, 16, 167–175. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Z. Preparation and Performance Analysis of Regenerated Materials for Thermosetting Polyurethane Based on Coupled Thermo-mechanical Model. China Mech. Eng. 2016, 27, 2540–2546. [Google Scholar]
- Barrios, G.K.P.; De Carvalho, R.M.; Kwade, A.; Tavares, L.M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technol. 2013, 248, 84–93. [Google Scholar] [CrossRef]
- Freireich, B.; Ketterhagen, W.R.; Wassgren, C. Intra-tablet coating variability for several pharmaceutical tablet shapes. Chem. Eng. Sci. 2011, 66, 2535–2544. [Google Scholar] [CrossRef]
- Luo, S.; Yuan, Q. Parameters Calibration of Vermicomposting Nursery Substrate with Discrete Element Method Based on JKR Contact Model. Trans. Chin. Soc. Agric. Eng. 2018, 49, 343–350. [Google Scholar]
- Wangchai, S.; Hastie, D.B.; Wypych, P.W. The simulation of particle flow mecha nisms in dustiness testers. In Proceedings of the 11th International Conference on Bulk Materials Storage, Handling and Transportation, Newcaslte, Australia, 2 July–4 July 2013; pp. 1–10. [Google Scholar]
- Marigo, M.; Stitt, E.H. Discrete Element Method (DEM) for Industrial Applications: Comments on Calibration and Validation for the Modelling of Cylindrical Pellets. KONA Powder Part. J. 2015, 32, 236–252. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Jia, F.; Tang, Y. Influence of granular coefficient of rolling friction on accumulation characteristics. Acta Phys. Sin. 2014, 63, 1–7. [Google Scholar]
- Wu, L.; Qu, F.; Li, S. Inversion on discrete element model parameters of conditioned soil of earth pressure balance shield machine. J. Dalian Univ. Technol. 2010, 50, 860–866. [Google Scholar]
- Cheng, H.; Shuku, T.; Thoeni, K. Probabilistic calibration of discrete element simulations using the sequential quasi-Monte Carlo fifilter. Granul. Matter. 2018, 20, 11–12. [Google Scholar] [CrossRef]
- Rackla, M.; Hanleyb, K. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Hu, Z.; Chen, J.; Lv, X.; Xie, N. Calibration of DEM models for irregular particles based on experimental design method and bulk experiments. Powder Technol. 2018, 332, 210–223. [Google Scholar] [CrossRef]
- Do, H.Q.; Aragón, A.M.; Schott, D.L. A calibration framework for discrete element model parameters using genetic algorithms. Adv. Powder Technol. 2018, 29, 1393–1403. [Google Scholar] [CrossRef]
- Alizadeh, M.; Asachi, M.; Ghadiri, M.; Bayly, A.; Hassanpour, A. A methodology for calibration of DEM input parameters in simulation of segregation of powder mixtures, a special focus on adhesion. Powder Technol. 2018, 339, 789–800. [Google Scholar] [CrossRef] [Green Version]
- Nasato, D.S.; Goniva, C.; Pirker, S.; Kloss, C. Coarse Graining for Large-scale DEM Simulations of Particle Flow—An Investigation on Contact and Cohesion Models. Procedia Eng. 2015, 102, 1484–1490. [Google Scholar] [CrossRef]
- Hærvig, J.; Kleinhans, U. On the adhesive JKR contact and rolling models for reduced particle stiffness discrete element simulations. Powder Technol. 2017, 319, 472–482. [Google Scholar] [CrossRef] [Green Version]
- Yile, G.; Ali, O. A modified cohesion model for CFD–DEM simulations of fluidization. Powder Technol. 2016, 296, 17–28. [Google Scholar]
- Ye, F.; Wheeler, C.; Chen, B.; Hu, J.; Chen, K.; Chen, W. Calibration and verification of DEM parameters for dynamic particle flow conditions using a backpropagation neural network. Adv. Powder Technol. 2019, 30, 292–301. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, X.; Wu, W. Study of the critical angles of granular material in rotary drums aimed for fast DEM model calibration. Powder Technol. 2018, 340, 563–569. [Google Scholar] [CrossRef]
- Mehta, A.; Barker, G.C. The dynamics of sand, reports. Prog. Phys. 1994, 57, 383–416. [Google Scholar] [CrossRef]
- Härtl, J.; Ooi, J.Y. Numerical investigation of particle shape and particle friction on limiting bulk friction in direct shear tests and comparison with experiments. Powder Technol. 2011, 212, 231–239. [Google Scholar] [CrossRef]
- Bharadwaj, R.; Ketterhagen, W.R.; Hancock, B.C. Discrete element simulation study of a Freeman powder rheometer. Chem. Eng. Sci. 2010, 65, 5747–5756. [Google Scholar] [CrossRef]
- Kendall, K.L.J.; Roberts, A.D. Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. Lond. 1971, 324, 301–313. [Google Scholar]
- Johnson, K.L.; Greenwood, J.A. An Adhesion Map for the Contact of Elastic Spheres. J. Coll. Interface Sci. 1997, 192, 326–333. [Google Scholar] [CrossRef]
- Thornton, C.; Ning, Z. A theoretical model for the stick/bounce behaviour of adhesive, elastic-plastic spheres. Powder Technol. 1998, 99, 154–162. [Google Scholar] [CrossRef]
- Behjani, M.A.; Rahmanian, N.; Ghani, N.F.B.A.; Hassanpour, A. An investigation on process of seeded granulation in a continuous drum granulator using DEM. Adv. Powder Technol. 2017, 28, 2456–2464. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, M.; Dai, Z. Simulation on Adhesion of Microscale Contact of Rough Polyurethane Surface. J. Nanjing Univ. Aeronaut. Astronaut. 2007, 39, 471–474. [Google Scholar]
- Al-Hashemi, H.M.B.; Al-Amoudi, O.S.B. A review on the angle of repose of granular materials. Powder Technol. 2018, 330, 397–417. [Google Scholar] [CrossRef]
- Zhao, M.; Cui, W.-C. Application of the optimal Latin hypercube design and radial basis function network to collaborative optimization. J. Mar. Sci. Appl. 2008, 6, 24. [Google Scholar] [CrossRef]
- He, Q. BP Neural Network and Its Application Research; Chongqing Jiaotong University: Chongqing, China, 2004. [Google Scholar]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Antony, S.J.; Zhou, C.H.; Wang, X. An integrated mechanistic-neural network modelling for granular systems. Appl. Math. Model. 2006, 30, 116–128. [Google Scholar] [CrossRef] [Green Version]
- Ji, G. Review of Genetic Algorithms. J. Comput. Appl. Softw. 2004, 21. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Li, B. Research on the Method of Determining the Number of Nodes in BP Neural Network Implicit Layer. Comput. Technol. Dev. 2018, 28, 37–41. [Google Scholar]
- Duong, T.; Beck, G.; Azzag, H.; Lebbah, M. Nearest neighbour estimators of density derivatives, with application to mean shift clustering. Pattern Recognit. Lett. 2016, 80, 224–230. [Google Scholar] [CrossRef]
- Guo, Y.; Şengür, A.; Akbulut, Y.; Shipley, A. An effective color image segmentation approach using neutrosophic adaptive mean shift clustering. Measurement 2018, 119, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.X.; Sun, B.; Lu, R.; Zhang, C.; Wu, H. A method for detecting high-frequency oscillations using semi-supervised k-means and mean shift clustering. Neurocomputing 2019, 350, 102–107. [Google Scholar] [CrossRef]










| DEM Parameter | Symbol | Value/Interval |
|---|---|---|
| Polyurethane Poisson’s ratio | 0.35–0.39 | |
| Polyurethane Young’s modulus (Pa) | ||
| Polyurethane density (kg·m−3) | 30–100 | |
| Poisson’s ratio of steel | 0.3 | |
| Young’s modulus of steel (Pa) | ||
| Steel density (kg·m−3) | 7850 | |
| Poisson’s ratio of Plexiglas | 0.4 | |
| Shear modulus of Plexiglas (Pa) | ||
| Density of Plexiglas (kg·m−3) | 1385 | |
| Collision recovery coefficient (particle–particle) | ★0.1–0.5 | |
| Static friction coefficient (particle–particle) | ★0.3–0.75 | |
| Rolling friction coefficient (particle–particle) | 0.001 | |
| Collision recovery coefficient (particle–wall) | ★0.1–0.6 | |
| Static friction coefficient (particle–wall) | ★0.5–2.5 | |
| Rolling friction coefficient (particle–wall) | 0.001 | |
| JKR surface energy (J/m2) | Γ | ★3–8 |
| Group | Calibrated DEM Parameters | ||||
|---|---|---|---|---|---|
| 1 | 0.320426 | 0.353256 | 0.490065 | 0.930533 | 5.974576 |
| 2 | 0.267255 | 0.371349 | 0.565715 | 0.670134 | 4.38862 |
| 3 | 0.295006 | 0.327425 | 0.506216 | 1.734846 | 4.818618 |
| 4 | 0.301659 | 0.350872 | 0.537846 | 1.660376 | 3.609546 |
| 5 | 0.262054 | 0.336516 | 0.519476 | 0.792432 | 7.318412 |
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | |
|---|---|---|---|---|---|
| Simulation of rotating drum/(°) | 47.5 | 48.5 | 49.1 | 49.1 | 48.1 |
| Rotating drum test/(°) | 47.1 | ||||
| Rotating drum contrast test (relative error) | 0.85% | 2.97% | 4.25% | 4.25% | 2.12% |
| Simulation of baffle lift/(°) | 37.2 | 38.1 | 39.4 | 37.6 | 40.1 |
| Baffle lift test/(°) | 39.1 | ||||
| Baffle lift contrast test (relative error) | 4.86% | 2.56% | 0.77% | 3.84% | 2.56% |
| Funnel flow meter test/(°) | 47.801 | ||||
| Funnel flow meter test and baffle lift simulation (relative error) | 22.18% | 20.29% | 17.57% | 21.34% | 16.11% |
| Funnel flow meter test and rotary drum simulation (relative error) | 0.63% | 1.46% | 2.72% | 2.72% | 0.63% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, P.; Fan, Y.; Pan, B.; Zhu, Y.; Liu, J.; Zhu, D. Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder. Materials 2019, 12, 3350. https://doi.org/10.3390/ma12203350
He P, Fan Y, Pan B, Zhu Y, Liu J, Zhu D. Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder. Materials. 2019; 12(20):3350. https://doi.org/10.3390/ma12203350
Chicago/Turabian StyleHe, Ping, Yiwei Fan, Banglong Pan, Yinfeng Zhu, Jing Liu, and Darong Zhu. 2019. "Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder" Materials 12, no. 20: 3350. https://doi.org/10.3390/ma12203350
APA StyleHe, P., Fan, Y., Pan, B., Zhu, Y., Liu, J., & Zhu, D. (2019). Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder. Materials, 12(20), 3350. https://doi.org/10.3390/ma12203350





