Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature
Abstract
:1. Introduction
2. Investigated SMC Material and Processing
3. Experimental Procedure
3.1. Transverse Modulus in Thickness Direction
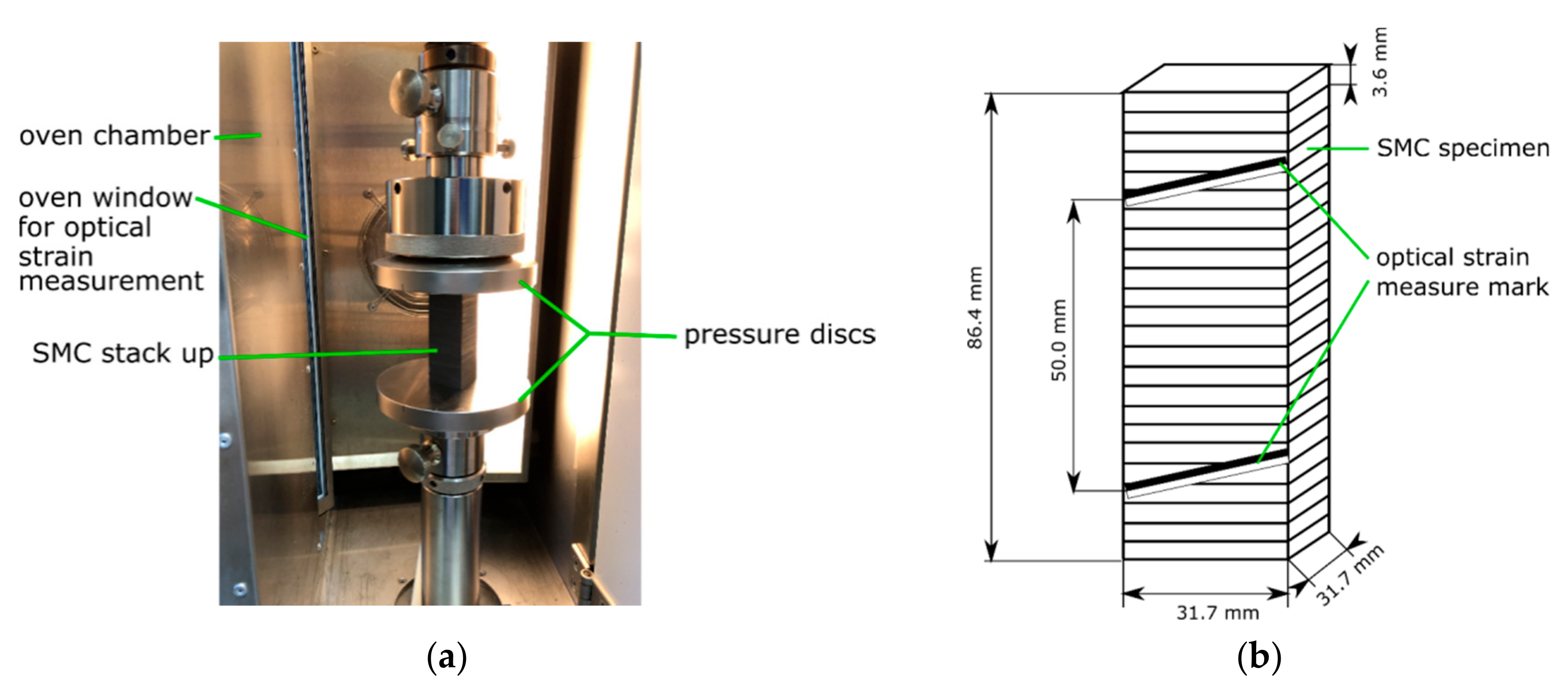
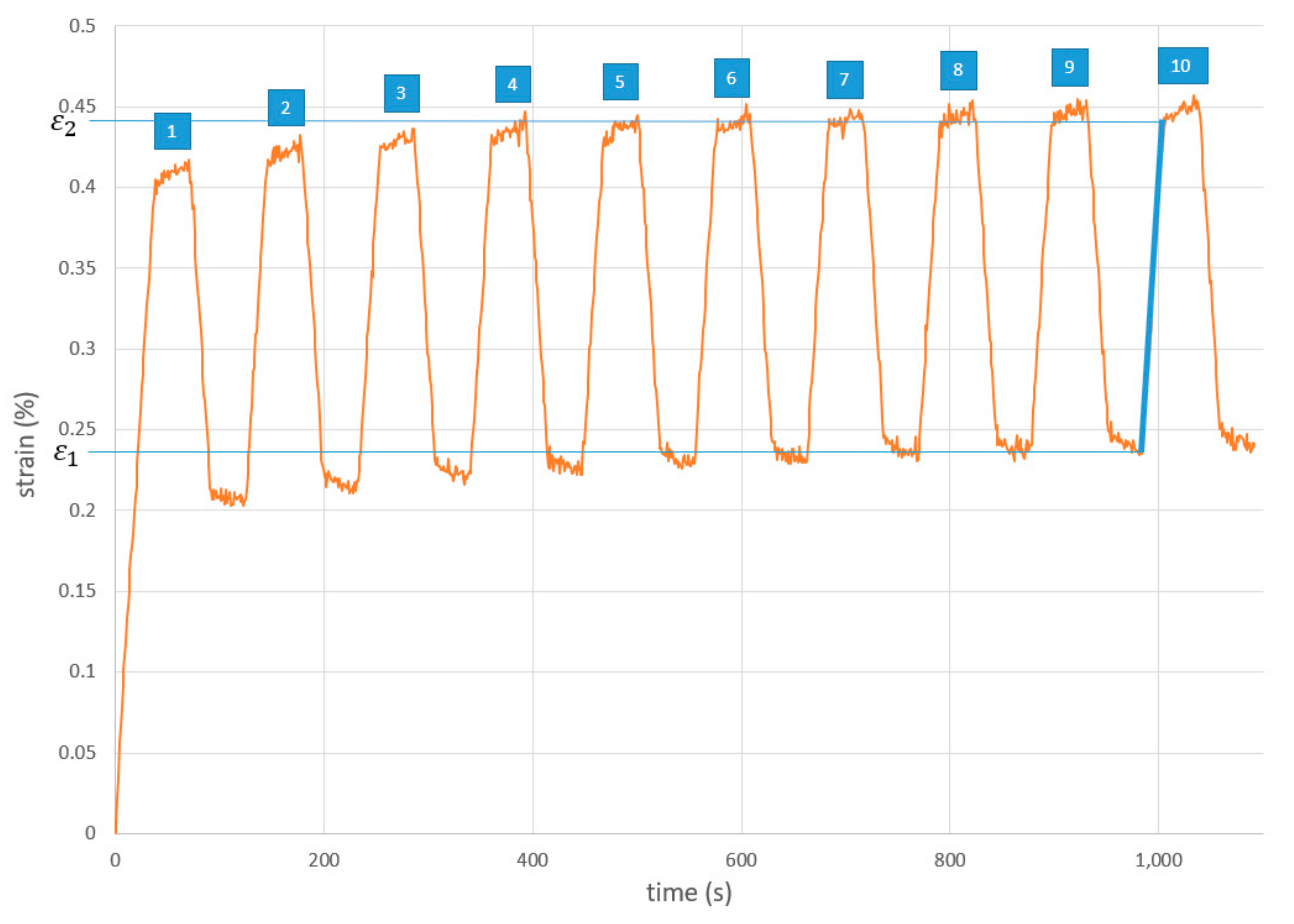
3.2. Compressive Creep Test
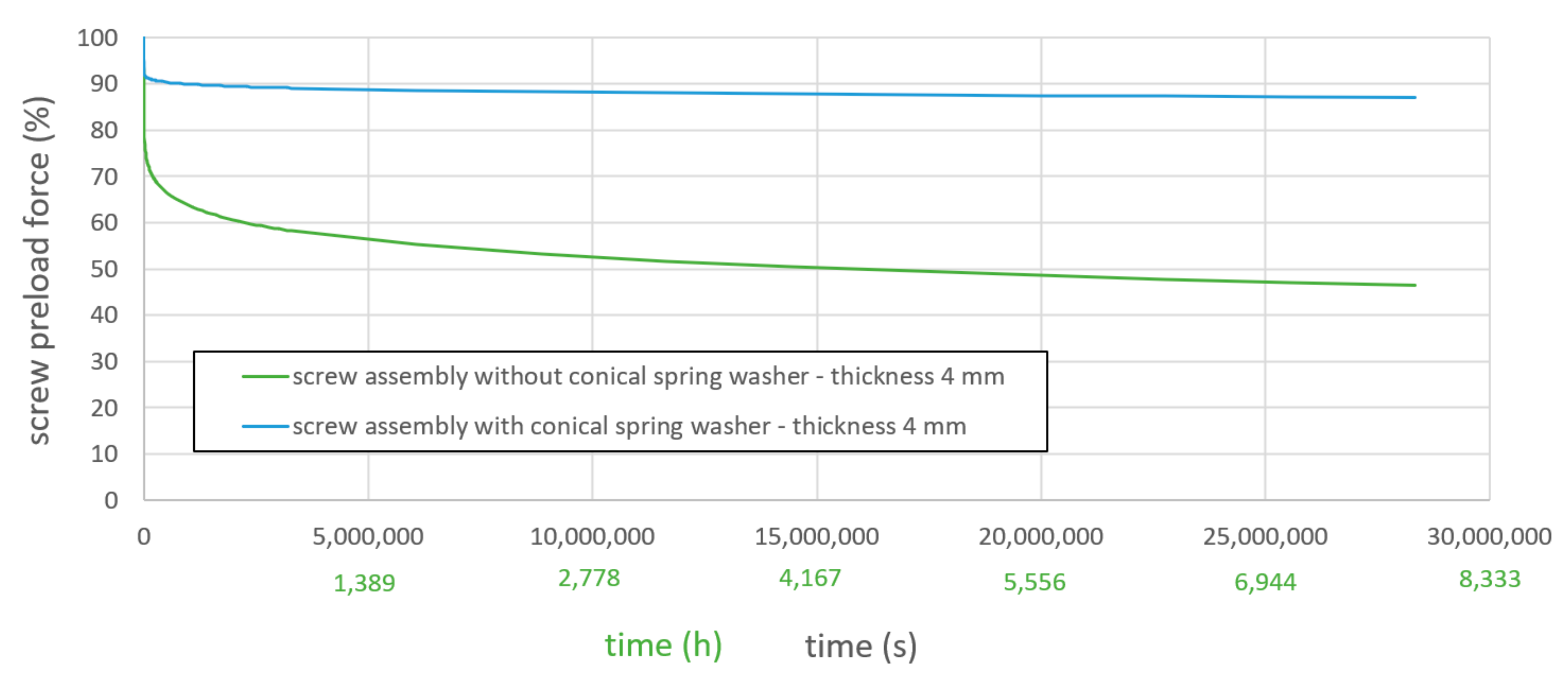
3.3. Preload Loss of Pretensioned Bolts
4. Simulation Procedure
4.1. Simulation of ‘Compressive Creep Test’
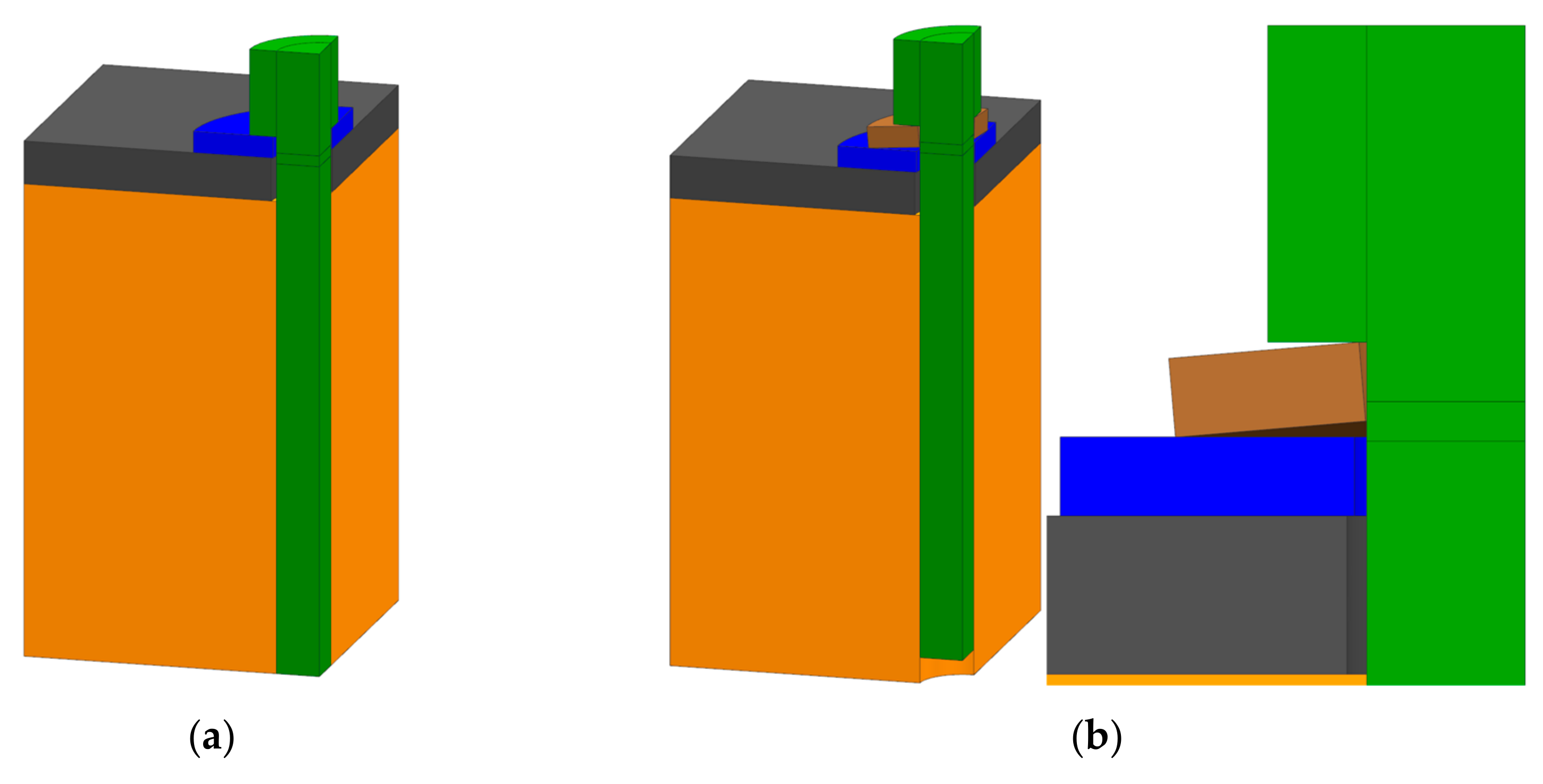
4.2. Simulation of ‘Preload Loss of Pretensioned Bolts’
4.3. Example of Application
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Nord-Lock Ltd. Why Do Bolts Loosen? 2018. Available online: https://www.nord-lock.com/en-gb/insights/knowledge/2018/why-do-bolts-loosen/ (accessed on 23 May 2019).
- Helfrich, B. Schriftenreihe Band 123—Untersuchung des Reibwerteinflusses auf die Krafteinleitung in endloskohlenstofffaserverstärkte Polymerwerkstoffe [Publication Series 123—Investigation of Influence of Friction at Force Transmission into Continuous CFRP]; Institute for Composite Materials (IVW): Kaiserslautern, Germany, 2016. [Google Scholar]
- Wang, J.; Li, Y.; Dai, F. A micromechanical relaxation model of composite bolted connections based on viscoelastic theory. Compos. Struct. 2016. [Google Scholar] [CrossRef]
- Gibson, R.F.; Thoppul, S.D. Composite Materials and Joining Technologies for Composites; Springer: New York, NY, USA, 2013; Volume 7. [Google Scholar] [CrossRef]
- Shivakumar, K.N.; Crews, J.H. NASA Technical Memorandum 83268—Bolt Clampup Relaxation in a Graphite/Epoxy Laminate; NASA: Washington, DC, USA, 1982.
- Lu, Z.; Dai, W. Bolt Assembly Optimization and Life Prediction Based on Creep Curve. Procedia CIRP 2016. [Google Scholar] [CrossRef]
- Timke, J. Thermomechanische Bewertung einer Composite-Metall Schraubenverbindung am Beispiel einer Elektromotorkompenente [Thermomechanical Evaluation of a Composite-Metal Screw Connection at a Electric Engine Component]; RWTH Aachen—Institute of polymer processing (IKV): Aachen, Germany, 2018. [Google Scholar]
- Miravalles, M. The Creep Behaviour of Adhesives—A Numerical and Experimental Investigation; Chalmers University Of Technology: Gothenburg, Sweden, 2007. [Google Scholar]
- Scattina, A.; Roncato, D.; Belingardi, G.; Martino, G. Investigation of creep phenomenon on composite material for bolt connections. Compos. Struct. 2015. [Google Scholar] [CrossRef]
- Schuermann, H. Konstruieren mit Faser-Kunststoff-Verbunden, 2. Auflage [Designing with Fiber-Polymer-Composites, ], 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- The MacNeal-Schwendler Corporation (MSC). MSC Nastran 2019.0; The MacNeal-Schwendler Corporation (MSC): Newport Beach, CA, USA, 2019. [Google Scholar]
- Simulia (Dassault Systèmes). ABAQUS UNIFIED FEA 2019; Simulia (Dassault Systèmes): Johnston, RI, USA, 2019. [Google Scholar]
- ANSYS Inc. ANSYS Workbench 2019 R3; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Siemens PLM Software. Siemens NX Simcenter 12; SIEMENS AG: Munich, Germany, 2019. [Google Scholar]
- Bielecki, M.; Badur, J. Comparison of Various Models of Creep Coupled With Damage Evolution; POLITECHNIKI BIAŁOSTOCKIEJ: Białystok, Poland, 2001. [Google Scholar]
- Kastner, J. Prozesscharakterisierung und thermomechanische Eigenschaften von GF/CF-SMC Hybridmaterialien [Process characterization and thermomechanical properties of GF/CF-SMC hybrid-materials]; Technische Hochschule Nürnberg Georg Simon Ohm: Nuremburg, Germany, 2019. [Google Scholar]
- International Standards Organization. ISO 527-4: Determination of Tensile Properties—Part 4: Test Conditions for Isotropic and Orthotropic Fibre-Reinforced Plastic Composites; International Standards Organization: Geneva, Switzerland, 1997. [Google Scholar]
- Polynt Composites Germany GmbH. Datasheet—SMCarbon 80 CF60-3K/2; Polynt Composites Germany GmbH: Miehlen, Germany, 2017. [Google Scholar]
- Hornbogen, E.; Eggeler, G.; Ewald, W. Werkstoffe: Aufbau und Eigenschaften von Keramik-, Metall-, Polymer- und Verbundwerkstoffen 8. Auflage [Materials: Structure and Properties of Ceramic-, Metal-, Polymer- und Composite-Materials 8. edition]; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mesarovic, S.D. Dislocation creep: Climb and glide in the lattice continuum. Crystals 2017, 7, 243. [Google Scholar] [CrossRef]
- Friedrich, C.; Hubbertz, H. Friction behavior and preload relaxation of fastening systems with composite structures, Compos. Structures 2014. [Google Scholar] [CrossRef]
- Szymanski, N.K. Self Healing of Deformation-Induced Damage in Fe-W Alloys; Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Batchelor, A.W.; Loh, N.L.; Chandrasekaran, M. Materials Degradation and Its Control by Surface Engineering; Imperial College Press: London, UK, 2011. [Google Scholar]
- Trivikrama, B.P.; Joga, R.I. Creep Failure Analysis and Shelf Life Determination (Prevention) of Injection Molded Parts with and with out Gamma Irradiation; New Jersey Institute of Technology: Newark, NJ, USA, 2017. [Google Scholar]
- May, D.L.; Gordon, A.P.; Segletes, D.S. The Application of the Norton–Bailey Law for Creep Prediction Through Power Law Regression. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- International Standards Organization. DIN EN ISO 7093-1: Flache Scheiben—Große Reihe [DIN EN ISO 7093-1: Flat Washers—Large Line]; International Standards Organization: Geneva, Switzerland, 2000. [Google Scholar]
- International Standards Organization. DIN EN ISO 3506-1: Mechanische Eigenschaften von Verbindungselementen aus nichtrostenden Stählen—Teil 1 [DIN EN ISO 3506-1: Mechanical Properties of Corrosion-Resistant Stainless Steel Fasteners—Part 1]; International Standards Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Schmidt, W.; Dietrich, H. Praxis der mechanischen Werkstoffprüfung: Was nicht in Normen und Lehrbüchern steht [Experience in Mechanical Material Testing: What is not Written in Standards and Textbooks]; Expert: Tübingen, Germany, 1999. [Google Scholar]
- Siemens Product Lifecycle Management Inc. Basic Nonlinear Analysis User’s Guide; SIEMENS AG: Munich, Germany, 2014. [Google Scholar]
- Murthy, P. NASA Glenn Research Center—Integrated Composite Analyzer (ICAN/JAVA). 2011. Available online: https://www.grc.nasa.gov/WWW/StructMech/ICAN/html/ican.choose.html (accessed on 30 July 2019).
- Siemens Product Lifecycle Management Inc. NX Nastran 10—Advanced Nonlinear Theory and Modeling Guide; SIEMENS AG: Munich, Germany, 2014. [Google Scholar]
- Jamil, A.; Vashney, V. A user-defined subroutine for numerical modelling of failure due to creep under compression in carbon fibre reinforced composite materials. Mater. Res. Express. 2019, 6, 085609. [Google Scholar] [CrossRef]
- Schuermann, H.; Elter, A. Beitrag zur Gestaltung von Schraubverbindungen bei Laminaten aus Faser-Kunststoff-Verbunden [Design of Bolted Joints for Laminates made of Fiber Reinforced Plastics]. Konstruktion - Fachaufsatz Verbindungstechnik 2013. [Google Scholar]
- Kalweit, A.; Paul, C.; Peters, S.; Wallbaum, R. Handbuch für Technisches Produktdesign—Material und Fertigung, Entscheidungsgrundlagen für Designer und Ingenieure [Textbook for Technical Product Design—Material and Manufacturing, Decision Basis for Designers and Engineers]; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Deutsches Institut für Normung (DIN). DIN 6796: Spannscheiben für Schraubenverbindungen [DIN 6796: Conical spring washers for bolted connections]; Deutsches Institut für Normung (DIN): Berlin, Germany, 2009. [Google Scholar]
- SCHNORR GmbH. SCHNORR Produktprogramm Tellerfedern Schraubensicherungs-Systeme [SCHNORR Product line—Conical Spring Washers and Screw Protection Systems]; SCHNORR GmbH: Sindelfingen, Germany, 2012. [Google Scholar]






| Material Property | Mean Value ± One SD |
|---|---|
| Modulus in-plane (measured) | 46,765 MPa ± 2994 MPa |
| Modulus in-plane (datasheet) | 46,000 MPa |
| Strength in-plane (measured) | 312 MPa ± 16 MPa |
| Strength in-plane (datasheet) | 240 MPa |
| Glass transition temperature (datasheet) | 150 °C |
| Fiber weight fraction (datasheet) | 60% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finck, D.; Seidel, C.; Hausmann, J.; Rief, T. Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature. Materials 2019, 12, 3598. https://doi.org/10.3390/ma12213598
Finck D, Seidel C, Hausmann J, Rief T. Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature. Materials. 2019; 12(21):3598. https://doi.org/10.3390/ma12213598
Chicago/Turabian StyleFinck, David, Christian Seidel, Joachim Hausmann, and Thomas Rief. 2019. "Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature" Materials 12, no. 21: 3598. https://doi.org/10.3390/ma12213598
APA StyleFinck, D., Seidel, C., Hausmann, J., & Rief, T. (2019). Creep-Induced Screw Preload Loss of Carbon-Fiber Sheet Molding Compound at Elevated Temperature. Materials, 12(21), 3598. https://doi.org/10.3390/ma12213598






