Critical Damage Values of R200 and 100Cr6 Steels Obtained by Hot Tensile Testing
Abstract
:1. Introduction
- Brittle fracture, where material cohesion is disrupted due to atomic bond breaking;
- Ductile fracture, where extensive plastic deformation takes place without disrupting material cohesion.
2. Experimental Tests
2.1. Compression Test
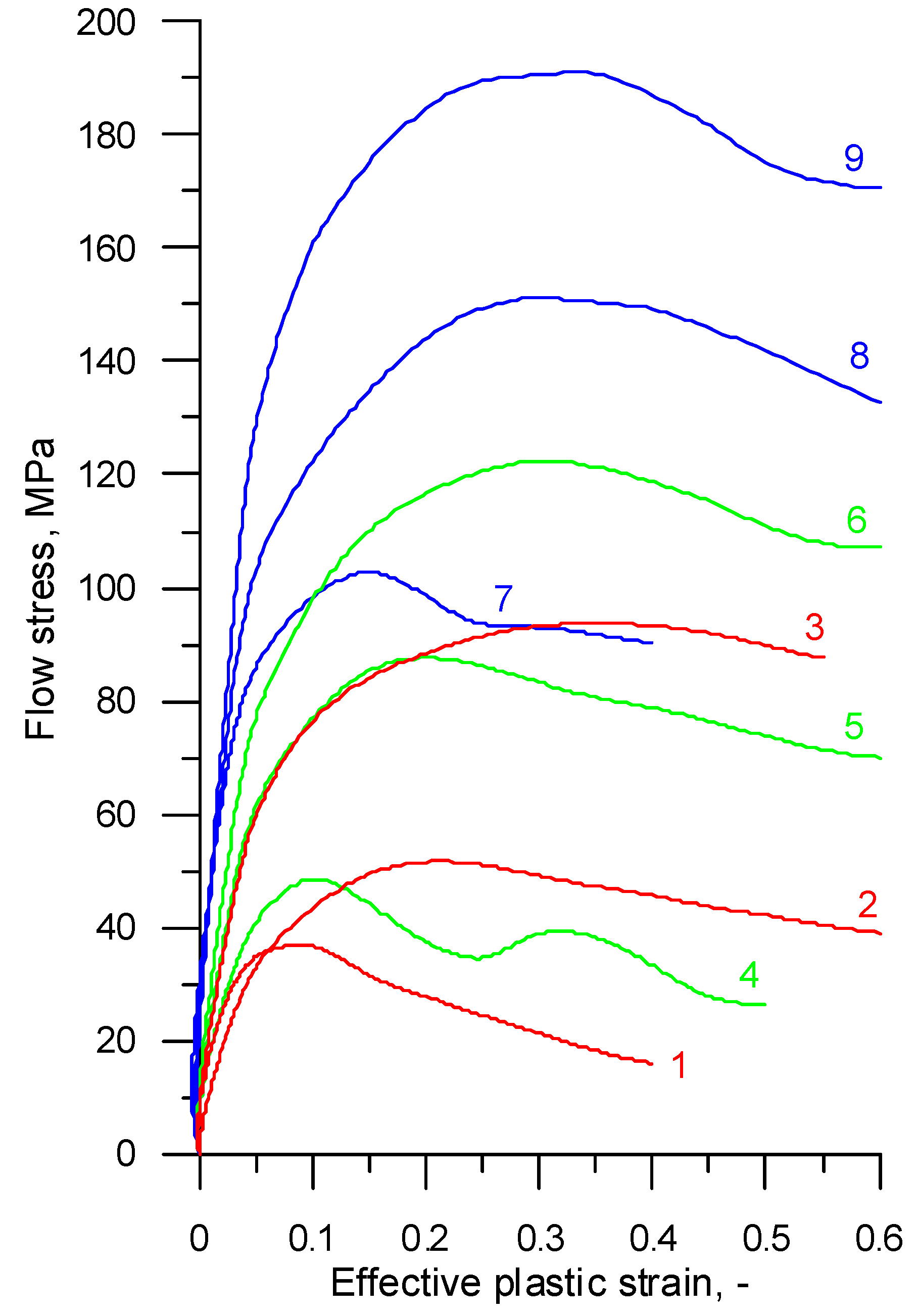
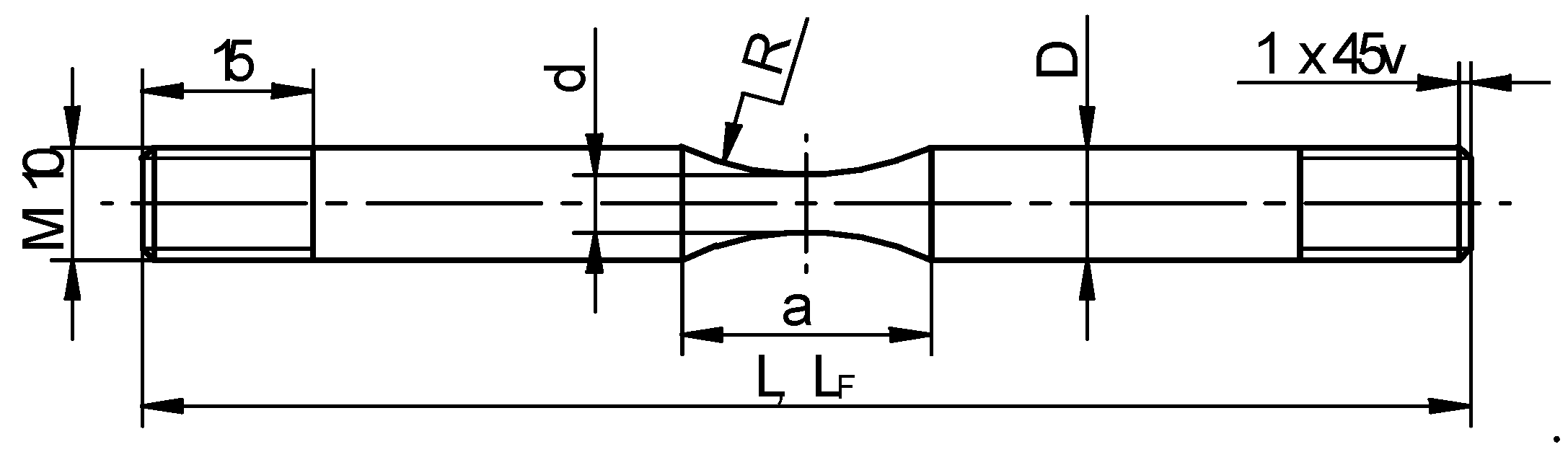
2.2. Tensile Test
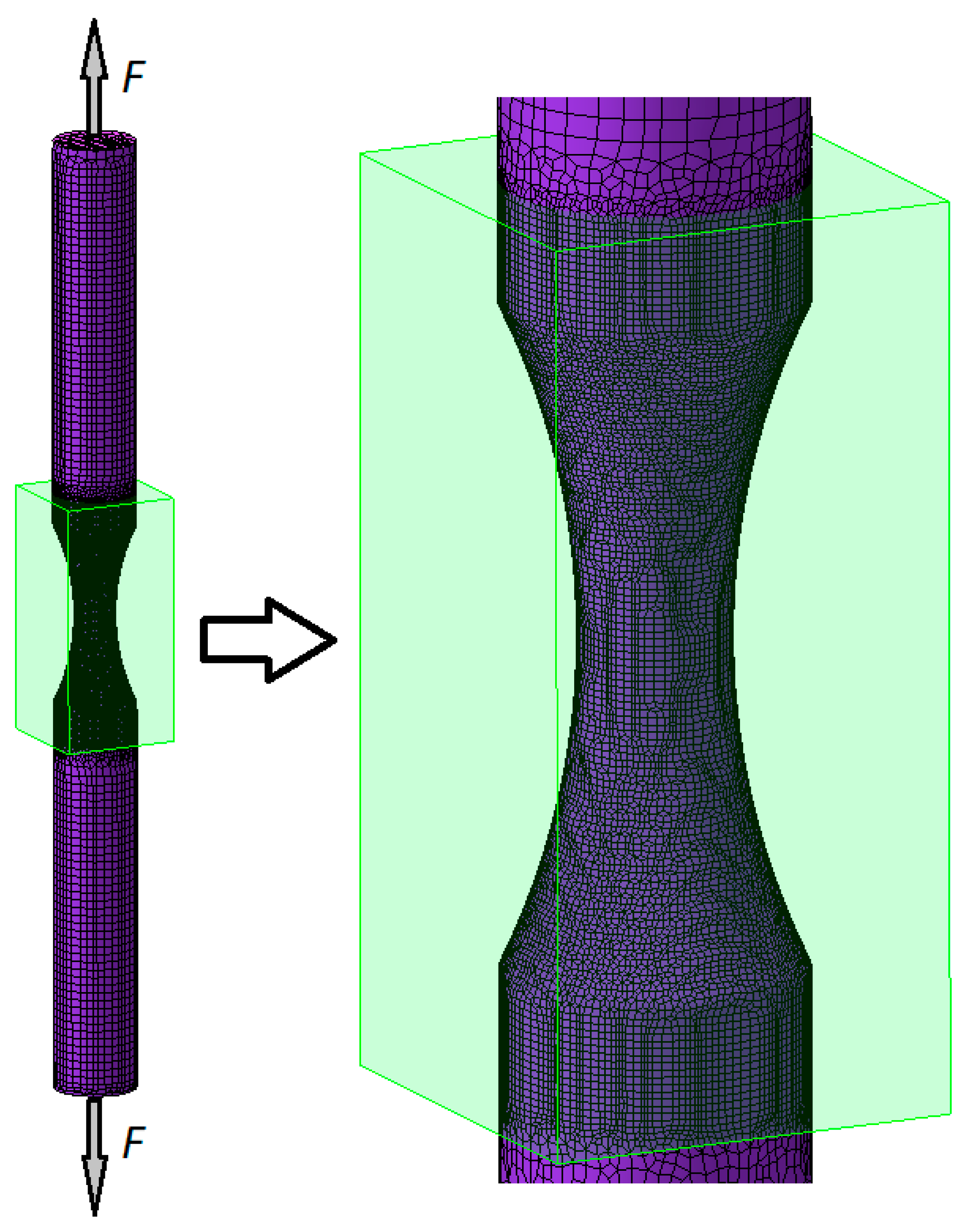
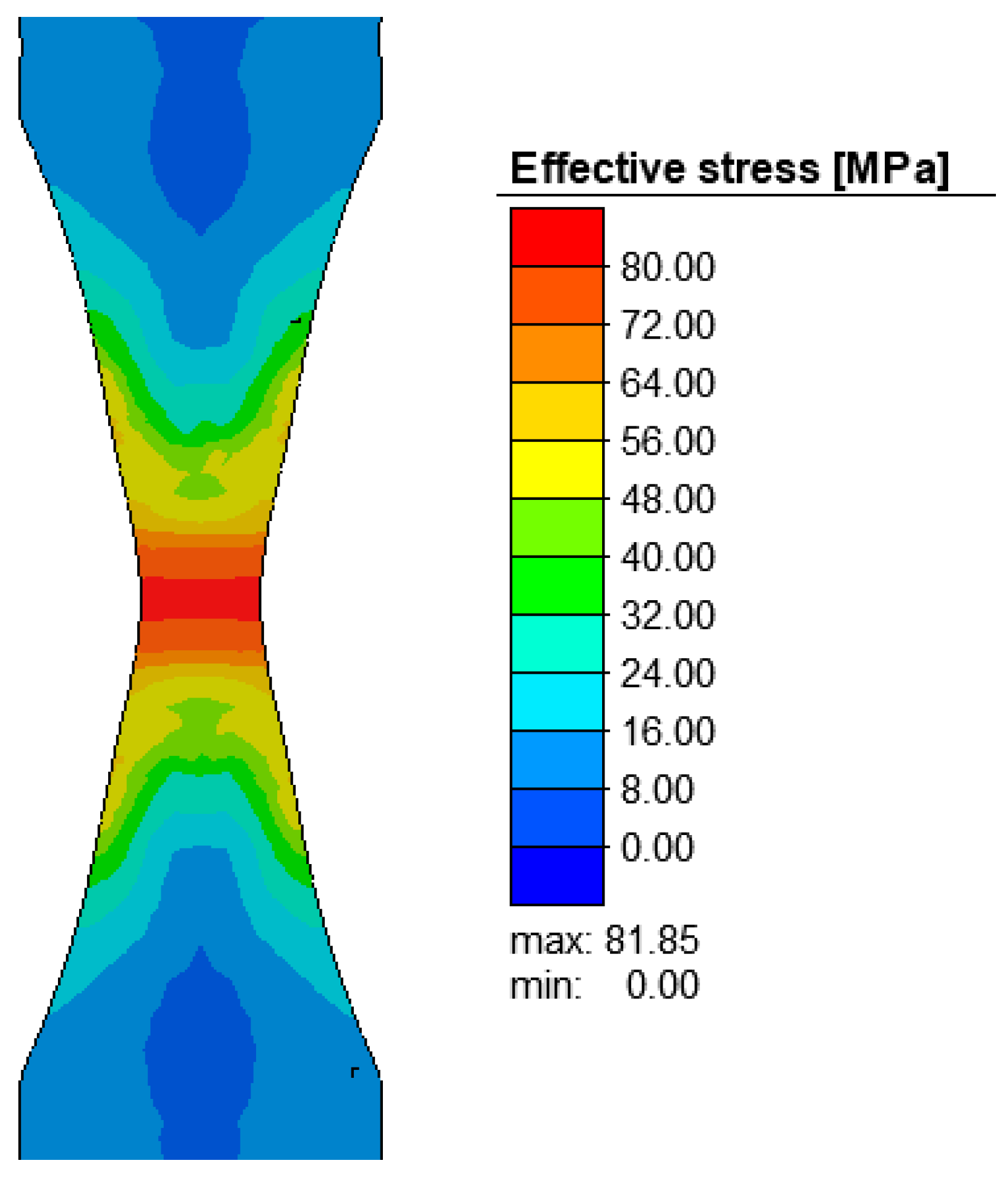
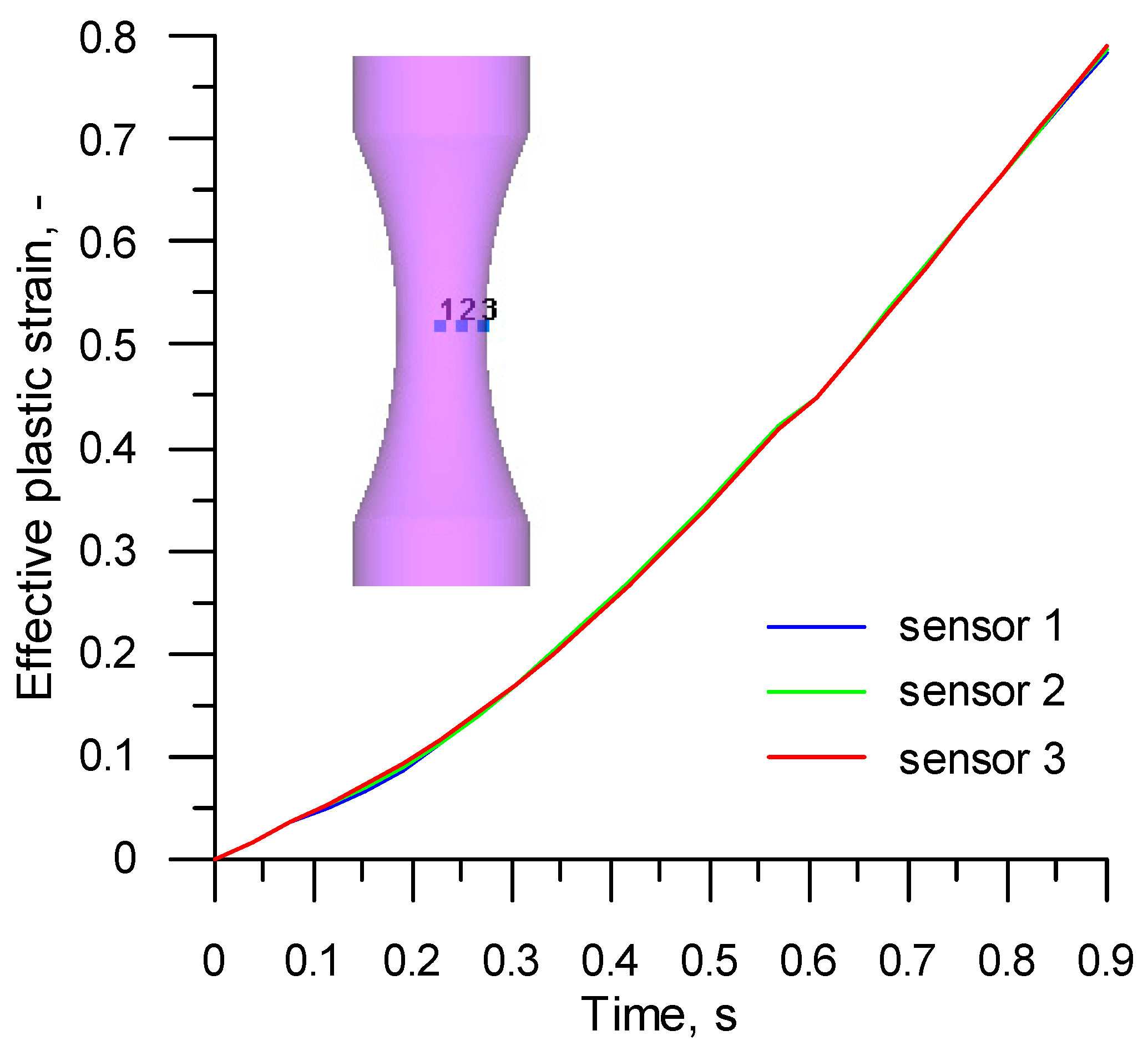
3. Numerical Analysis
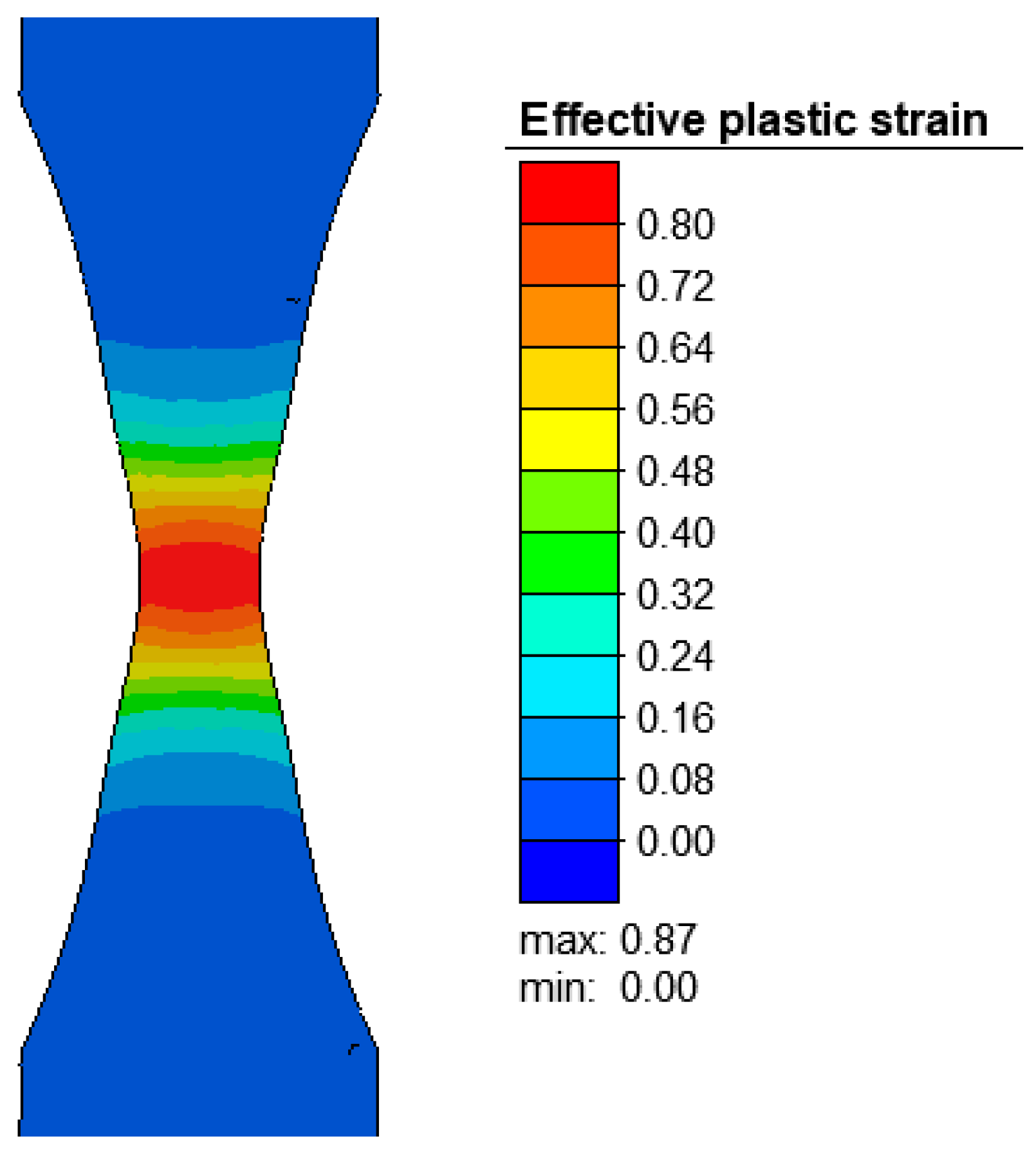
4. Results and Discussions
5. Conclusions
- Critical damage values in hot working conditions can be determined by a tensile test of notched round bars;
- The employed method for determining critical damage values is highly universal, and hence can be employed in hot forming processes for all metals and alloys;
- Critical damage values depend on the steel grade, particularly its strength properties and hot-workability;
- Critical damage values depend on the forming temperature;
- The critical damage values obtained for R200 and 100Cr6 steel grades for the temperature range of 1000–1200 °C are listed in Table 6.
Author Contributions
Funding
Conflicts of Interest
References
- Kim, S.W.; Lee, Y.S. Comparative Study on Failure Prediction in Warm Forming Processes of Mg Alloy Sheet by the FEM and Ductile Fracture Criteria. Metall. Mater. Trans. B 2014, 45, 445–453. [Google Scholar] [CrossRef]
- Li, H.; Fu, M.W.; Lu, J.; Yang, H. Ductile fracture: Experiments and computations. Int. J. Plast. 2014, 27, 147–180. [Google Scholar]
- Yan, Y.; Wang, H.; Wan, M. Prediction of fracture in press bend forming of aluminum alloy high-stiffener integral panels. Comput. Mater. Sci. 2011, 50, 2232–2244. [Google Scholar]
- Wu, Z.; Li, S.; Zhang, W.; Wang, W. Ductile fracture simulation of hydropiercing process based on various criteria in 3D modelling. Mater. Des. 2010, 31, 3661–3671. [Google Scholar] [CrossRef]
- Otzurk, F.; Lee, D. A New Methodology for Ductile Fracture Criteria to Predict the Forming Limits. J. Mater. Eng. Perform. 2007, 62, 224–228. [Google Scholar]
- Otzurk, F.; Lee, D. Analysis of forming limits using ductile fracture criteria. J. Mater. Process. Technol. 2004, 147, 397–404. [Google Scholar]
- Hambli, R.; Reszka, M. Fracture criteria identification using an inverse technique method and blanking experiment. Int. J. Mech. Sci. 2002, 44, 1349–1361. [Google Scholar] [CrossRef]
- Kraisnik, M.; Vilotic, D.; Sidanin, L.; Stefanovic, M. Various Approaches to Defining the Criteria of Ductile Crack in Cold Bulk Forming Processes. Ann. Fac. Eng. Hunedoara 2015, 13, 213–218. [Google Scholar]
- Bjorklund, O.; Govik, A.; Nilsson, L. Prediction of fracture in a dual-phase steel subjected to non-linear straining. J. Mater. Process. Technol. 2014, 214, 2748–2758. [Google Scholar]
- Yu, S.; Feng, W. Experimental research on ductile fracture criterion in metal forming. Appl. Mech. Mater. 2011, 6, 308–311. [Google Scholar]
- Coppola, T.; Cortese, L.; Folgarait, P. The effect of stress invariants on ductile fracture limit in steels. Eng. Fract. Mech. 2009, 76, 1288–1302. [Google Scholar] [CrossRef]
- Goijarets, A.M.; Govaert, L.E.; Baaijens, F.P.T. Evaluation of ductile fracture models for different metals in blanking. J. Mater. Process. Technol. 2001, 110, 312–323. [Google Scholar] [CrossRef] [Green Version]
- Bjorklund, O.; Larsson, R.; Nilsson, L. Failure of high strength steel sheets: Experiments and modelling. J. Mater. Process. Technol. 2013, 213, 1103–1117. [Google Scholar] [CrossRef] [Green Version]
- Dunand, M.; Mohr, D. Hybrid experimental-numerical analysis of basic ductile fracture experiments for sheet metals. Int. J. Solids Struct. 2010, 47, 1130–1143. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, W.J. Failure prediction of magnesium alloy sheets deforming at warm temperatures using the Zener-Holloman parameter. Mech. Mater. 2010, 42, 293–303. [Google Scholar]
- Yu, S.; Zhao, J. Investigation on Blanking of Thick Sheet Metal Using the Ductile Fracture Initiation and Propagation Criterion. J. Shanghai Jiaotong Univ. (Sci.) 2012, 17, 531–536. [Google Scholar] [CrossRef]
- Cesar de Sa, J.M.A.; Areias, P.M.A.; Zheng, C. Damage modeling in metal forming problems using an implicit non-local gradient model. Comput. Method Appl. Mech. 2006, 195, 6646–6660. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.W.; Song, W.J.; Kang, B.S. Analytical and numerical approach to prediction of forming limit in tube hydroforming. Int. J. Mech. Sci. 2005, 47, 1023–1037. [Google Scholar]
- Lee, Y.W.; Wierzbicki, T. Fracture prediction of thin plates under localized impulsive loading. Part II: Discing and pedaling. Int. J. Impact Eng. 2005, 31, 1277–1308. [Google Scholar] [CrossRef]
- Takuda, H.; Mori, K.; Hatta, N. The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals. J. Mater. Process. Technol. 1999, 95, 116–121. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, W.; Zhang, F.; Zhao, Y.; Zhang, X.; Wang, K. A new methodology for prediction of fracture initiation in hot compression of Ti40 titanium alloy. Mater. Sci. Eng. A 2012, 553, 112–118. [Google Scholar] [CrossRef]
- Watanabe, A.; Fujikawa, S.; Ikeda, A.; Shiga, N. Prediction of ductile fracture in cold forging. Procedia Eng. 2014, 81, 425–430. [Google Scholar]
- Landre, J.; Pertence, A.; Cetlin, P.R.; Rodrigues, J.M.C.; Martins, P.A.F. On the utilization of ductile fracture criteria in cold forging. Finite Elem. Anal. Des. 2003, 39, 175–186. [Google Scholar]
- MacCormack, C.; Monaghan, J. Failure analysis of cold forging dies using FEA. J. Mater. Process. Technol. 2001, 117, 209–215. [Google Scholar] [CrossRef]
- Venkata Reddy, N.; Dixit, P.M.; Lal, G.K. Ductile fracture criteria and its prediction in axisymmetric drawing. Int. J. Mach. Tool Manuf. 2000, 40, 95–111. [Google Scholar]
- Novella, M.F.; Ghiotti, A.; Bruschi, S.; Bariani, P.F. Ductile damage modeling at elevated temperature applied to the cross wedge rolling of AA6082-T6 bars. J. Mater. Process. Technol. 2015, 222, 259–267. [Google Scholar] [CrossRef]
- Shi, D.; Hu, P.; Ying, L. Comparative study of ductile fracture prediction of 22MnB5 steel in hot stamping process. Int. J. Adv. Manuf. Technol. 2016, 84, 895–906. [Google Scholar]
- Pater, Z.; Tomczak, J.; Bulzak, T. An innovative method for forming balls from scrap rail heads. Adv. Sci. Technol. Res. J. 2016, 10, 151–157. [Google Scholar] [CrossRef]
- Tomczak, J.; Pater, Z.; Bulzak, T. The Flat Wedge Rolling Mill for Forming Balls from Heads of Scrap Railway Rails. Arch. Metall. Mater. 2018, 63, 5–12. [Google Scholar]
- Pater, Z.; Tomczak, J.; Bulzak, T. An innovative method for producing balls from scrap rail heads. Int. J. Adv. Manuf. Technol. 2018, 97, 893–901. [Google Scholar] [Green Version]





| Criterion (year) | Formula |
|---|---|
| Freudenthal (1950) | |
| Cockcroft and Latham (1968) | |
| Rice and Tracey (1969) | |
| Brozzo et al. (1972) | |
| Oyane (1972) | |
| Ayada (1984) | |
| Zhan et al. (2009) |
| C | Mn | Si | P | Cr | S | Al | N | V | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 0.38–0.62 | 0.65–1.25 | 0.13–0.60 | ≤0.04 | ≤0.15 | ≤0.035 | ≤0.004 | ≤0.01 | ≤0.03 | balance |
| C | Mn | Si | P | S | Cr | Ni | Cu | Ni+Cu | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 0.95–1.1 | 0.25–0.45 | 0.15–0.35 | ≤0.027 | ≤0.020 | 1.3–1.65 | ≤0.30 | ≤0.30 | ≤0.50 | balance |
| Steel Grade | T, °C | D, mm | d, mm | a, mm | L, mm | LF, mm |
|---|---|---|---|---|---|---|
| R200 | 1000 | 9.97 | 5.10 | 21.93 | 116.70 | 120.77 |
| 1100 | 9.95 | 5.09 | 21.85 | 116.55 | 121.05 | |
| 1200 | 10.00 | 4.99 | 21.88 | 116.72 | 119.75 | |
| 100Cr6 | 1000 | 10.00 | 5.00 | 21.92 | 116.40 | 120.25 |
| 1100 | 10.04 | 5.18 | 21.98 | 116.31 | 120.32 | |
| 1200 | 9.90 | 5.05 | 22.12 | 116.58 | 119.34 |
| Parameter | R200 | 100Cr6 | ||||
|---|---|---|---|---|---|---|
| T = 1000 °C | T = 1100 °C | T = 1200 °C | T = 1000 °C | T = 1100 °C | T = 1200 °C | |
| εf, - | 0.929 | 0.854 | 0.540 | 0.633 | 0.518 | 0.410 |
| σ1, MPa | 118.87 | 86.70 | 54.72 | 149.48 | 75.81 | 51.84 |
| σi, MPa | 106.11 | 81.30 | 53.21 | 143.04 | 75.70 | 52.16 |
| σm, MPa | 48.16 | 32.50 | 19.27 | 54.15 | 25.35 | 17.07 |
| Criterion | R200 | 100Cr6 | ||||
|---|---|---|---|---|---|---|
| T = 1000 °C | T = 1100 °C | T = 1200 °C | T = 1000 °C | T = 1100 °C | T = 1200 °C | |
| Freudenthal C1 | 91.697 | 61.100 | 25.094 | 82.734 | 35.797 | 19.689 |
| Cockcroft and Latham C2 | 1.010 | 0.895 | 0.563 | 0.652 | 0.529 | 0.418 |
| Rice and Tracey C3 | 1.148 | 1.033 | 0.652 | 0.759 | 0.618 | 0.487 |
| Brozzo et al. C4 | 1.013 | 0.894 | 0.564 | 0.651 | 0.528 | 0.414 |
| Oyane C5 | 1.095 | 0.992 | 0.626 | 0.730 | 0.596 | 0.470 |
| Ayada C6 | 0.392 | 0.325 | 0.203 | 0.229 | 0.183 | 0.142 |
| Zhan et al. C7 | 61.140 | 40.880 | 16.793 | 55.401 | 23.996 | 13.263 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pater, Z.; Gontarz, A. Critical Damage Values of R200 and 100Cr6 Steels Obtained by Hot Tensile Testing. Materials 2019, 12, 1011. https://doi.org/10.3390/ma12071011
Pater Z, Gontarz A. Critical Damage Values of R200 and 100Cr6 Steels Obtained by Hot Tensile Testing. Materials. 2019; 12(7):1011. https://doi.org/10.3390/ma12071011
Chicago/Turabian StylePater, Zbigniew, and Andrzej Gontarz. 2019. "Critical Damage Values of R200 and 100Cr6 Steels Obtained by Hot Tensile Testing" Materials 12, no. 7: 1011. https://doi.org/10.3390/ma12071011
APA StylePater, Z., & Gontarz, A. (2019). Critical Damage Values of R200 and 100Cr6 Steels Obtained by Hot Tensile Testing. Materials, 12(7), 1011. https://doi.org/10.3390/ma12071011






