4D Printing Self-Morphing Structures
Abstract
1. Introduction
2. Conceptual Design
2.1. FG 4D Printing
2.2. Materials and Printing
3. Theoretical Modeling
3.1. SMP Model
3.2. FE Methodology
3.2.1. In-house FE method
3.2.2. FE Abaqus
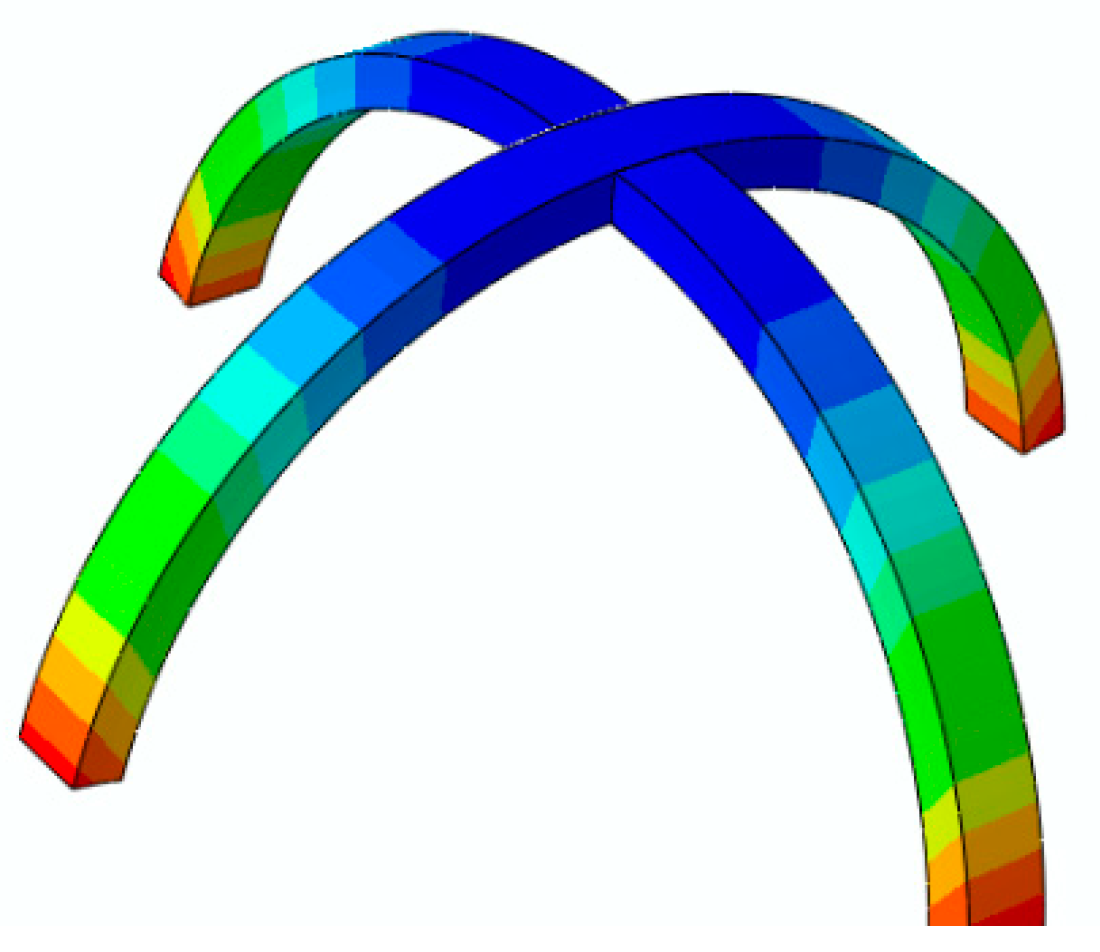
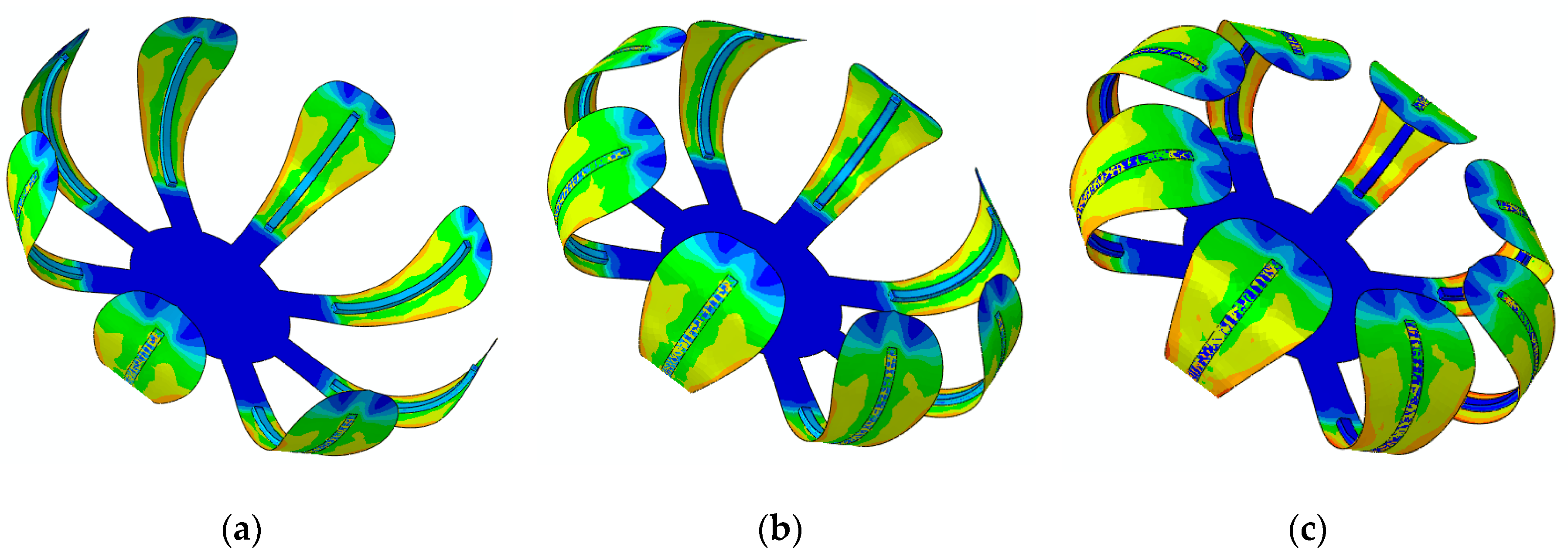
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rengier, F.; Mehndiratta, A.; Von Tengg-Kobligk, H.; Zechmann, C.M.; Unterhinninghofen, R.; Kauczor, H.U.; Giesel, F.L. 3D printing based on imaging data: review of medical applications. Int. J. Comput. Assist. Radiol. Surg. 2010, 5, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Hull, C.W. Apparatus for Production of Three-Dimensional Objects by Stereolithography. U.S. Patent 4,575,330, 8 August 1984. [Google Scholar]
- Tymrak, B.; Kreiger, M.; Pearce, J.M. Mechanical properties of components fabricated with open-source 3-D printers under realistic environmental conditions. Mater. Des. 2014, 58, 242–246. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.; Bellehumeur, C.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Tran, P.; Ngo, T.D.; Ghazlan, A.; Hui, D. Bimaterial 3D printing and numerical analysis of bio-inspired composite structures under in-plane and transverse loadings. Compos. Part B-Eng. 2017, 108, 210–223. [Google Scholar] [CrossRef]
- Melnikova, R.; Ehrmann, A.; Finsterbusch, K. 3D printing of textile-based structures by Fused Deposition Modelling (FDM) with different polymer materials. IOP Conf. Ser. Mater. Sci. Eng. 2014, 62, 1–6. [Google Scholar] [CrossRef]
- Caulfield, B.; McHugh, P.; Lohfeld, S. Dependence of mechanical properties of polyamide components on build parameters in the SLS process. J. Mater. Process. Technol. 2007, 182, 477–488. [Google Scholar] [CrossRef]
- Garcia, C.R.; Correa, J.; Espalin, D.; Barton, J.H.; Rumpf, R.C.; Wicker, R.; Gonzalez, V. 3D printing of anisotropic metamaterials. Prog. Electromagn. Res. 2012, 34, 75–82. [Google Scholar] [CrossRef]
- Endo, F.; Saiga, N. Thermoplastic Polymer Composition and Medical Devices Made of the Same. E.U. Patent 0568451, 28 April 1995. [Google Scholar]
- Wang, Q.; Tian, X.; Huang, L.; Li, D.; Malakhov, A.V.; Polilov, A.N. Programmable morphing composites with embedded continuous fibers by 4D printing. Mater. Des. 2018, 155, 404–413. [Google Scholar] [CrossRef]
- Hu, J.; Meng, H.; Li, G.; Ibekwe, S.I. A review of stimuli-responsive polymers for smart textile applications. Smart Mater. Struct. 2012, 21, 053001. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical performance of additively manufactured meta-biomaterials. Acta Biomater. 2018, 85, 41–59. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1041. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 20, 1800864. [Google Scholar] [CrossRef]
- Wang, K.; Chang, Y.-H.; Chen, Y.; Zhang, C.; Wang, B. Designable dual-material auxetic metamaterials using three-dimensional printing. Mater. Des. 2015, 67, 159–164. [Google Scholar] [CrossRef]
- Mirzaali, M.; Caracciolo, A.; Pahlavani, H.; Janbaz, S.; Vergani, L.; Zadpoor, A. Multi-material 3D printed mechanical metamaterials: Rational design of elastic properties through spatial distribution of hard and soft phases. Appl. Phys. Lett. 2018, 113, 241903. [Google Scholar] [CrossRef]
- Yang, H.; Wang, B.; Ma, L. Designing hierarchical metamaterials by topology analysis with tailored Poisson’s ratio and Young’s modulus. Compos. Struct. 2019, 214, 359–378. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Hu, G.; Liao, W.H. Large deformations of soft metamaterials fabricated by 3D printing. Mater. Des. 2017, 131, 81–91. [Google Scholar] [CrossRef]
- Lee, A.Y.; An, J.; Chua, C.K. Two-way 4D printing: a review on the reversibility of 3D-printed shape memory materials. Engineering 2017, 3, 663–674. [Google Scholar] [CrossRef]
- Tibbits, S.; McKnelly, C.; Olguin, C.; Dikovsky, D.; Hirsch, S. 4D Printing and universal transformation. In Proceedings of the 34th Annual Conference of the Association for Computer Aided Design in Architecture, Los Angeles, CA, USA, 23–25 October 2014; pp. 539–548. [Google Scholar]
- Zhang, Q.; Zhang, K.; Hu, G. Smart three-dimensional lightweight structure triggered from a thin composite sheet via 3D printing technique. Sci. Rep. 2016, 6, 22431. [Google Scholar] [CrossRef]
- Jamal, M.; Kadam, S.S.; Xiao, R.; Jivan, F.; Onn, T.M.; Fernandes, R.; Nguyen, T.D.; Gracias, D.H. Bio-origami hydrogel scaffolds composed of photocrosslinked PEG bilayers. Adv. Healthc. Mater. 2013, 2, 1142–1150. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Liao, W.H. Adaptive metamaterials by functionally graded 4D printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Teoh, J.; An, J.; Feng, X.; Zhao, Y.; Chua, C.; Liu, Y. Design and 4D printing of cross-folded origami structures: A preliminary investigation. Materials 2018, 11, 376. [Google Scholar] [CrossRef]
- Yang, C.; Boorugu, M.; Dopp, A.; Ren, J.; Martin, R.; Han, D.; Choi, W.; Lee, H. 4D printing reconfigurable, deployable and mechanically tunable metamaterials. Mater. Horiz. 2019. [Google Scholar] [CrossRef]
- Bodaghi, M.; Liao, W.H. 4D printed tunable mechanical metamaterials with shape memory operations. Smart Mater. Struct. 2019, 28, 045019. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kaynak, A.; Yang Khoo, S.; Zhang, J.; Nahavandi, S.; Kouzani, A. control-oriented modelling of a 3D-printed soft actuator. Materials 2019, 12, 71. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 1–11. [Google Scholar] [CrossRef]
- Yu, K.; Yin, W.; Sun, S.; Liu, Y.; Leng, J. Design and analysis of morphing wing based on SMP composite. Proc. SPIE 2009, 7290, 72900S. [Google Scholar]
- Tao, R.; Yang, Q.S.; He, X.Q.; Liew, K.M. Parametric analysis and temperature effect of deployable hinged shells using shape memory polymers. Smart Mater. Struct. 2016, 25, 115034. [Google Scholar] [CrossRef]




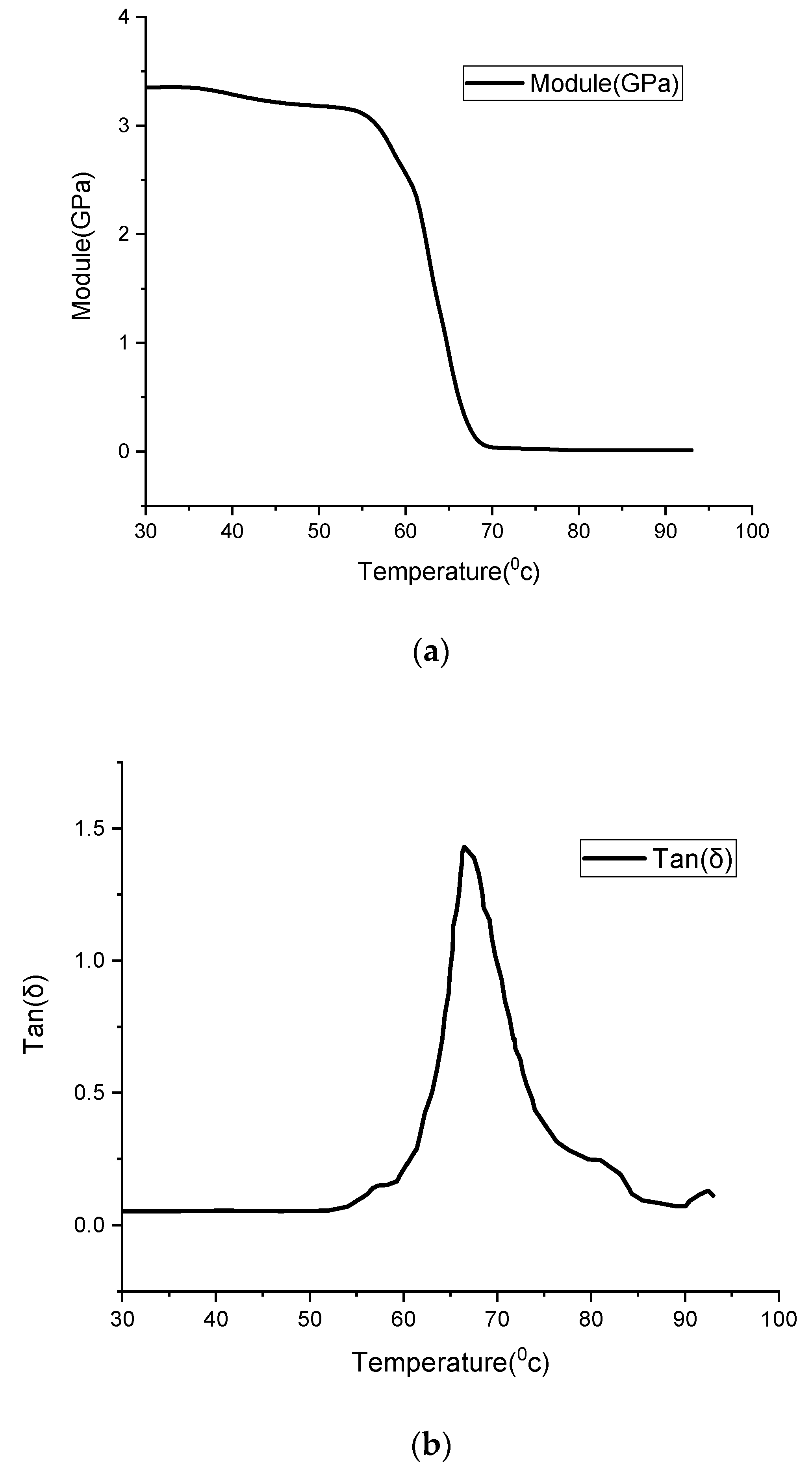







| T (°C) | 30 | 40 | 50 | 52 | 54 | 56 | 60 | 62 | 64 | 66 | 68 |
| Storage module | 0.0524 | 0.055 | 0.0540 | 0.0561 | 0.0701 | 0.1134 | 0.2116 | 0.383 | 0.6753 | 1.2890 | 1.2295 |
| tan(δ) | 3.3510 | 3.288 | 3.1880 | 3.1682 | 3.1402 | 3.0777 | 2.6378 | 2.0433 | 1.2807 | 0.5393 | 0.1459 |
| T(°C) | 70 | 72 | 74 | 76 | 78 | 80 | 82 | 84 | 88 | 90 | 93 |
| Storage module | 0.9875 | 0.658 | 0.434 | 0.3292 | 0.2758 | 0.2483 | 0.221 | 0.1398 | 0.0774 | 0.0723 | 0.1248 |
| tan(δ) | 0.030 | 0.026 | 0.0218 | 0.0138 | 0.0117 | 0.0117 | 0.0117 | 0.0117 | 0.0117 | 0.0117 | 0.030 |
| T (°C) | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|
| E (MPa) | 3350 | 3280 | 3166 | 2554 | 48 | 18 | 14 |
| αi(1/°C) | Sp(mm/s) | ||
|---|---|---|---|
| 20 | 40 | 70 | |
| α1 | −0.00400 | −0.00480 | −0.00680 |
| α2 | −0.00320 | −0.00384 | −0.00544 |
| α3 | −0.00240 | −0.00288 | −0.00408 |
| α4 | −0.00160 | −0.00192 | −0.00272 |
| α5 | −0.00080 | −0.00096 | −0.00136 |
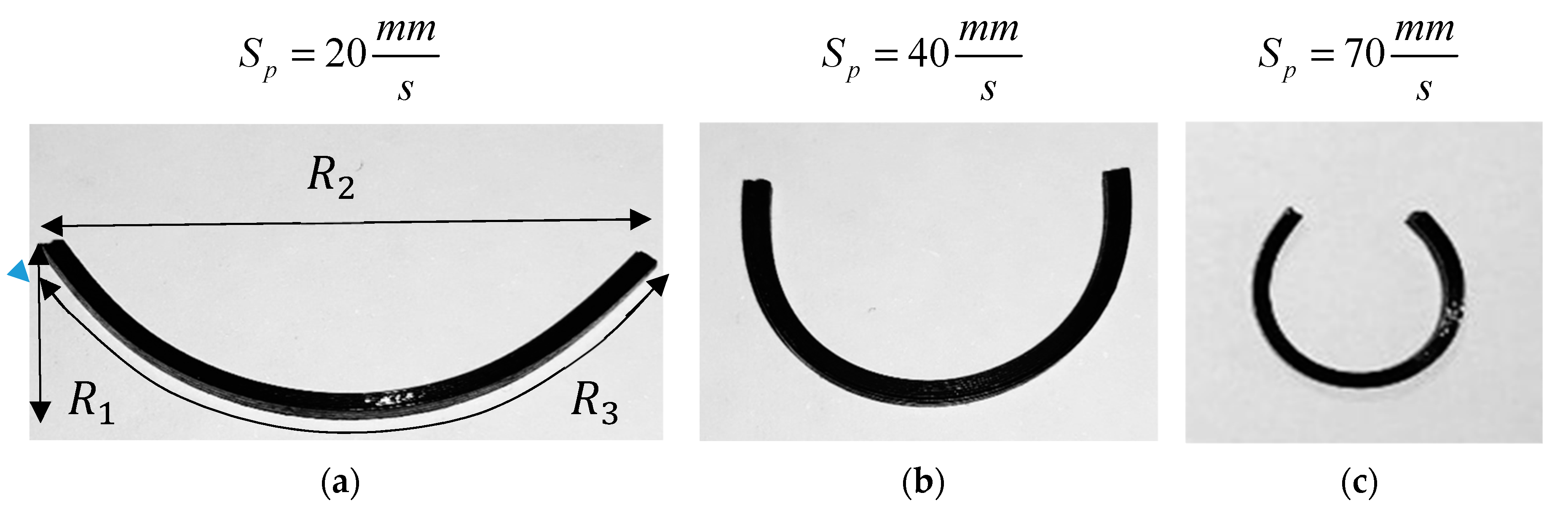
| Method | Vp (mm/s) | R1 (mm) | R2 (mm) | R3 (mm) |
|---|---|---|---|---|
| Experiments | 20 | 8.20 | 21.00 | 29.50 |
| 40 | 9.60 | 12.40 | 29.10 | |
| 70 | 10.70 | 5.90 | 28.50 | |
| FE Abaqus | 20 | 8.31 | 21.20 | 29.55 |
| 40 | 9.75 | 12.34 | 29.00 | |
| 70 | 10.57 | 6.08 | 28.60 | |
| In-house FE method | 20 | 8.32 | 21.30 | 29.47 |
| 40 | 9.79 | 12.41 | 29.01 | |
| 70 | 10.66 | 6.02 | 28.49 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodaghi, M.; Noroozi, R.; Zolfagharian, A.; Fotouhi, M.; Norouzi, S. 4D Printing Self-Morphing Structures. Materials 2019, 12, 1353. https://doi.org/10.3390/ma12081353
Bodaghi M, Noroozi R, Zolfagharian A, Fotouhi M, Norouzi S. 4D Printing Self-Morphing Structures. Materials. 2019; 12(8):1353. https://doi.org/10.3390/ma12081353
Chicago/Turabian StyleBodaghi, Mahdi, Reza Noroozi, Ali Zolfagharian, Mohamad Fotouhi, and Saeed Norouzi. 2019. "4D Printing Self-Morphing Structures" Materials 12, no. 8: 1353. https://doi.org/10.3390/ma12081353
APA StyleBodaghi, M., Noroozi, R., Zolfagharian, A., Fotouhi, M., & Norouzi, S. (2019). 4D Printing Self-Morphing Structures. Materials, 12(8), 1353. https://doi.org/10.3390/ma12081353







